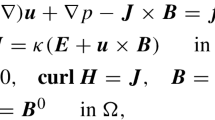Skip to main content
SpringerLink
Log in

An unconditionally stable implicit method for hyperbolic conservation laws

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Summary

We construct a space-centered self-adjusting hybrid difference method for one-dimensional hyperbolic conservation laws. The method is linearly implicit and combines a newly developed minimum dispersion scheme of the first order with the recently developed second-order scheme of Lerat. The resulting method is unconditionally stable and unconditionally diagonally dominant in the linearized sense. The method has been developed for quasi-stationary problems, in which shocks play a dominant role. Numerical results for the unsteady Euler equations are presented. It is shown that the method is non-oscillatory, robust and accurate in several cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. H. Araki et al., editors, Proc, 8th Int. Conf. on Num. Meth. in Fl. Dyn., Springer Leet. Notes in Phys. 170 (1982).

  2. R. Beam and R.F. Warming, An implicit finite difference algorithm for hyperbolic systems in conservation law form, J. of Comp. Phys. 11 (1976) 87–110.

    Google Scholar 

  3. R. Courant and K.O. Friedrichs, Supersonic flow and Shock Waves, Springer, reprint (1976).

  4. A. Harten and G. Zwas, Self-adjusting hybrid schemes for shock computations, J. of comp. Phys. 6 (1972) 568–583.

    Google Scholar 

  5. A. Harten, The artificial compression method for computation of shocks and contact discontinuities: III: Self-adjusting hybrid schemes, Math. of Comp. 32 (1978) 363–389.

    Google Scholar 

  6. D.N. Holla and P.C. Jain, Implicit dissipative schemes for solving systems of conservation laws, J. of Eng. Math. 13 (1979) 257–270.

    Google Scholar 

  7. E. Issacson and H. Keller, Analysis of Numerical Methods, Wiley (1966).

  8. J. of Comp. Phys. 48 (1982) no. 2.

  9. A. Lerat, Sur le calcul des solutions faibles des systèmes hyperboliques de lois de conservation à l'aide de schèmas aux diffèrences, thesis, Univ. Pierre et Marie Curie (1981). Also Publication ONERA 1981-1.

  10. A. Lerat, J. Sidès and V. Daru, An implicit finite volume method for solving the Euler equations, Proc. 8th Int. Conf. on Num. Meth. in Fl. Dyn., ed. H. Araki et al., Springer (1982).

  11. A. Lerat, private communication (1983).

  12. A. Lerat, Implicit methods of second-order accuracy for the Euler equations, Proc. 6th AIAA Comp. Fl. Dyn. Conf. (1983).

  13. J.H. Varah, On the solution of block-tridiagonal systems arising from certain finite difference equations, Math. of Comp. 26 (1972) 859–868.

    Google Scholar 

  14. P. Wilders, Minimization of Dispersion in Difference Methods for Hyperbolic Conservation Laws, Thesis, Univ. of Amsterdam (1984).

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Delft University of Technology, P.O. Box 356, 2600 AJ, Delft, The Netherlands

    P. Wilders

Authors
  1. P. Wilders
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wilders, P. An unconditionally stable implicit method for hyperbolic conservation laws. J Eng Math 19, 33–44 (1985). https://doi.org/10.1007/BF00055039

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF00055039

Keywords

Search

Navigation