The response of a confined gas to a thermal disturbance: rapid boundary heating

Summary

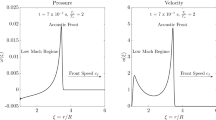
An inert compressible gas confined between infinite parallel planar walls is subjected to significant heat addition at the boundaries. The wall temperature is increased during an interval which is scaled by the acoustic time of the container, defined as the passage time of an acoustic wave across the slab. On this time scale heat transfer to the gas occurs in thin conductive boundary layers adjacent to the walls. Temperature increases in these layers cause the gas to expand such that a finite velocity exists at the boundary-layer edge. This mechanical effect, which is like a time-varying piston motion, induces a planar linear acoustic field in the basically adiabatic core of the slab. A spatially homogeneous pressure rise and a bulk velocity field evolve in the core as the result of repeated passage of weak compression waves through the gas. Eventually the thickness of the conduction boundary layers is a significant fraction of the slab width. This occurs on the condition time scale of the slab which is typically a factor of 10⁶ larger than the acoustic time. The further evolution of the thermomechanical response of the gas is dominated by a conductive-convective balance throughout the slab. The evolving spatially-dependent temperature distribution is affected by the homogeneous pressure rise (compressive heating) and by the deformation process occurring in the confined gas. Superimposed on this relatively slowly-varying conduction-dominated field is an acoustic field which is the descendent of that generated on the shorter time scale. The short-time-scale acoustic waves are distorted as they propagate through a slowly-varying inhomogeneous gas in a finite space. Solutions are developed in terms of asymptotic expansions valid when the ratio of the acoustic to conduction time scales is small. The results provide an explicit expression for the piston analogy of boundary heat addition.