Cohesive cracks versus nonlocal models: Closing the gap

Abstract

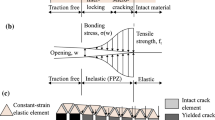
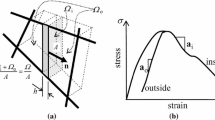
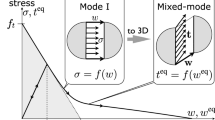
Fracture of quasi-brittle materials, particularly concrete and cement-based material, has been treated in the past using a number of mildly related models. Hillerborg's fictitious crack model (also called cohesive crack model and Dugdale-Barenblatt model), Bažant's crack band model, and nonlocal models, are three of the most used for theoretical as well as for applied analysis. Using a uniaxial formulation and a Rankine-type model, the present work shows that the cohesive crack may be obtained as a particular case of a fully nonlocal formulation. The discussion of the generalization of the uniaxial formulation to triaxial behavior suggests that a directional averaging, rather than an isotropic one, may be necessary.