Abstract
Two non-empty sets A, B of a metric space (X, d) are called parallel if \(d(a,B)=d(A,B)=d(A,b)\) for any points \(a\in A\) and \(b\in B\). Answering a question posed on mathoverflow.net, we prove that for a cover \({\mathscr {C}}\) of a metrizable space X by compact subsets, the following conditions are equivalent: (i) the topology of X is generated by a metric d such that any two sets \(A,B\in {\mathscr {C}}\) are parallel; (ii) the cover \({\mathscr {C}}\) is disjoint, lower semicontinuous and upper semicontinuous.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
In this paper we shall prove a “parallel” metrization theorem answering a question [1] of the Mathoverflow user116515. The question concerns parallel sets in metric spaces.
Two non-empty sets A, B in a metric space (X, d) are called parallel if
Here \(d(A,B)=\inf \{ d(a,b):a\in A,\, b\in B\}\) and  for \(x\in X\). Observe that two closed parallel sets A, B in a metric space are either disjoint or coincide.
for \(x\in X\). Observe that two closed parallel sets A, B in a metric space are either disjoint or coincide.
Let \({\mathscr {C}}\) be a family of non-empty closed subsets of a topological space X. A metric d on X is defined to be \({\mathscr {C}}\)-parallel if any two sets \(A,B\in {\mathscr {C}}\) are parallel with respect to the metric d.
A family \({\mathscr {C}}\) of subsets of X is called a compact cover of X if \(X=\bigcup {\mathscr {C}}\) and each set \(C\in {\mathscr {C}}\) is compact.
([1]) For which compact covers \({\mathscr {C}}\) of a topological space X the topology of X is generated by a \({\mathscr {C}}\)-parallel metric?
A metric generating the topology of a given topological space will be called admissible. A necessary condition for the existence of an admissible \({\mathscr {C}}\)-parallel metric is the upper and lower semicontinuity of the cover \({\mathscr {C}}\).
A family \({\mathscr {C}}\) of subsets of a topological space X is called
lower semicontinuous if for any open set \(U\subset X\) its \({\mathscr {C}}\)-star
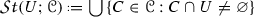 is open in X;
is open in X;upper semicontinuous if for any closed set \(F\subset X\) its \({\mathscr {C}}\)-star
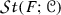 is closed in X;
is closed in X;continuous if \({\mathscr {C}}\) is both lower and upper semicontinuous;
disjoint if any distinct sets \(A,B\in {\mathscr {C}}\) are disjoint.
The following theorem is the main result of the paper, answering Problem.
For a compact cover \({\mathscr {C}}\) of a metrizable topological space X the following conditions are equivalent:
- (i)
the topology of X is generated by a \({\mathscr {C}}\)-parallel metric;
- (ii)
the family \({\mathscr {C}}\) is disjoint and continuous.
(i) \(\Rightarrow \) (ii). Assume that d is an admissible \({\mathscr {C}}\)-parallel metric on X. The disjointness of the cover \({\mathscr {C}}\) follows from the obvious observation that two closed parallel sets in a metric space are either disjoint or coincide.
To see that \({\mathscr {C}}\) is lower semicontinuous, fix any open set \(U\subset X\) and consider its \({\mathscr {C}}\)-star  . To see that
. To see that  is open, take any point
is open, take any point  and find a set \(C\in {\mathscr {C}}\) such that \(s\in C\) and \(C\cap U\ne \varnothing \). Fix a point \(u\in U\cap C\) and find \(\varepsilon >0\) such that the \(\varepsilon \)-ball \(B(u;\varepsilon )=\{ x\in X:d(x,u)<\varepsilon \}\) is contained in U. We claim that
and find a set \(C\in {\mathscr {C}}\) such that \(s\in C\) and \(C\cap U\ne \varnothing \). Fix a point \(u\in U\cap C\) and find \(\varepsilon >0\) such that the \(\varepsilon \)-ball \(B(u;\varepsilon )=\{ x\in X:d(x,u)<\varepsilon \}\) is contained in U. We claim that  . Indeed, for any \(x\in B(s;\varepsilon )\) we can find a set \(C_x\in {\mathscr {C}}\) containing x and conclude that \(d(C_x,u)=d(C_x,C)\leqslant d(x,s)<\varepsilon \) and hence \(C_x\cap U\ne \varnothing \) and
. Indeed, for any \(x\in B(s;\varepsilon )\) we can find a set \(C_x\in {\mathscr {C}}\) containing x and conclude that \(d(C_x,u)=d(C_x,C)\leqslant d(x,s)<\varepsilon \) and hence \(C_x\cap U\ne \varnothing \) and  .
.
To see that \({\mathscr {C}}\) is upper semicontinuous, fix any closed set \(F\subset X\) and consider its \({\mathscr {C}}\)-star  . To see that
. To see that  is closed, take any point
is closed, take any point  and find a set \(C\in {\mathscr {C}}\) such that \(s\in C\). It follows from
and find a set \(C\in {\mathscr {C}}\) such that \(s\in C\). It follows from  that \(C\cap F=\varnothing \) and hence
that \(C\cap F=\varnothing \) and hence  by the compactness of C. We claim that
by the compactness of C. We claim that  . Assuming the opposite, we can find a point
. Assuming the opposite, we can find a point  and a set \(C_x\in {\mathscr {C}}\) such that \(x\in C_x\) and \(C_x\cap F\ne \varnothing \). Fix a point \(z\in C_x\cap F\) and observe that \(d(C,F)\leqslant d(C,z)=d(C,C_x)\leqslant d(s,x)<\varepsilon =d(C,F)\), which is a desired contradiction.
and a set \(C_x\in {\mathscr {C}}\) such that \(x\in C_x\) and \(C_x\cap F\ne \varnothing \). Fix a point \(z\in C_x\cap F\) and observe that \(d(C,F)\leqslant d(C,z)=d(C,C_x)\leqslant d(s,x)<\varepsilon =d(C,F)\), which is a desired contradiction.
(ii) \(\Rightarrow \) (i). The proof of this implication is more difficult. Assume that \({\mathscr {C}}\) is disjoint and continuous. Fix any admissible metric \(\rho \leqslant 1\) on X.
Let \({\mathscr {U}}_0(C)=\{X\}\) for every \(C\in {\mathscr {C}}\).
FormalPara ClaimFor every \(n\in {\mathbb {N}}\) and every \(C\in {\mathscr {C}}\) there exists a finite cover \({\mathscr {U}}_n(C)\) of C by open subsets of X such that
- (a)
each set \(U\in {\mathscr {U}}_n(C)\) has \(\rho \)-diameter \(\leqslant 1/{2^n}\);
- (b)
if a set \(A\in {\mathscr {C}}\) meets some set \(U\in {\mathscr {U}}_n(C)\), then \(A\subset \bigcup {\mathscr {U}}_n(C)\) and A meets each set \(U'\in {\mathscr {U}}_n(C)\).
Using the paracompactness [2, 5.1.3] of the metrizable space X, choose a locally finite open cover \({\mathscr {V}}\) of X consisting of sets of \(\rho \)-diameter \(<1/{2^n}\).
For every compact set \(C\in {\mathscr {C}}\) consider the finite subfamily  of the locally finite cover \({\mathscr {V}}\). Since the cover \({\mathscr {C}}\) is upper semicontinuous, the set
of the locally finite cover \({\mathscr {V}}\). Since the cover \({\mathscr {C}}\) is upper semicontinuous, the set  is closed and disjoint with the set C. Since \({\mathscr {C}}\) is lower semicontinuous, for any open set \(V\in {\mathscr {V}}(C)\) the set
is closed and disjoint with the set C. Since \({\mathscr {C}}\) is lower semicontinuous, for any open set \(V\in {\mathscr {V}}(C)\) the set  is open and hence
is open and hence  is an open neighborhood of C.
is an open neighborhood of C.
Put  and observe that \({\mathscr {U}}_n\) satisfies condition (a).
and observe that \({\mathscr {U}}_n\) satisfies condition (a).
Let us show that the cover \({\mathscr {U}}_n(C)\) satisfies condition (b). Assume that a set \(A\in {\mathscr {C}}\) meets some set \(U\in {\mathscr {U}}_n(C)\). First we show that \(A\subset \bigcup {\mathscr {U}}_n(C)\). Find a set \(V\in {\mathscr {V}}(C)\) such that \(U=W(C)\cap V\). It follows from \(\varnothing \ne A\cap U\subset A\cap W(C)\) that the set A meets W(C) and hence is contained in W(C) and is disjoint with \(F_C\). Hence

Next, take any set \(U'\in {\mathscr {U}}_n(C)\) and find a set \(V'\in {\mathscr {V}}(C)\) with \(U'=W(C)\cap V'\). The relation \(A\cap W(C)\cap V=A\cap U\ne \varnothing \) and the definition of the set \(W(C)\supset A\) imply that A intersects the set \(V'\in {\mathscr {V}}(C)\) and hence intersects the set \(U'=W(C)\cap V'\). \(\blacksquare \)
Given two points \(x,y\in X\) let

Adjust the function \(\delta \) to a pseudometric d letting

where the infimum is taken over all sequences \(x=x_0\), \(\dots \), \(x_m=y\). Condition (a) of Claim implies that \(\rho (x,y)\leqslant \delta (x,y)\) and hence \(\rho (x,y)\leqslant d(x,y)\) for any \(x,y\in X\). So, the pseudometric d is a metric on X such that the identity map \((X,d)\rightarrow (X,\rho )\) is continuous. To see that this map is a homeomorphism, take any point \(x\in X\) and \(\varepsilon >0\). Find \(n\in {\mathbb {N}}\) such that \(1/{2^n}<\varepsilon \) and choose a set \(C\in {\mathscr {C}}\) with \(x\in C\) and a set \(U\in {\mathscr {U}}_n(C)\) with \(x\in U\). Then for any \(y\in U\) we get \(d(y,x)\leqslant \delta (x,y)\leqslant 1/{2^n}<\varepsilon \), which means that the map \(X\rightarrow (X,d)\) is continuous.
Finally, let us prove that the metric d is \({\mathscr {C}}\)-parallel. Pick any two distinct compact sets \(A,B\in {\mathscr {C}}\). We need to show that \(d(a,B)=d(A,B)=d(A,b)\) for any \(a\in A\), \(b\in B\). Assuming that this inequality is not true, we conclude that either \(d(a,B)>d(A,B)>0\) or \(d(A,b)>d(A,B)>0\) for some \(a\in A\) and \(b\in B\).
First assume that \(d(a,B)>d(A,B)\) for some \(a\in A\). Choose points \(a'\in A\), \(b'\in B\) such that \(d(a',b')=d(A,B)<d(a,B)\). By the definition of the distance \(d(a',b')<d(a,B)\), there exists a chain \(a'=x'_0, x'_1,\dots ,x'_m=b'\) such that \(\sum _{ i=1}^{ m}\delta (x'_{i-1},x'_i)<d(a,B)\). We can assume that the points \(x'_0,\dots ,x'_m\) are pairwise distinct, so for every \(i\leqslant m\) there exist \(n_i\geqslant 0\) such that \(\delta (x'_{i-1},x'_i)= 1/{2^{n_i}}\) and hence \(x'_{i-1},x'_i\in U_i'\) for some \(C_i\in {\mathscr {C}}\) and \(U_i'\in {\mathscr {U}}_{n_i}(C_i)\). For every \(i\leqslant m\) let \(A_i\in {\mathscr {C}}\) be the unique set with \(x_i'\in A_i\). Then \(A_0=A\) and \(A_m=B\).
Using condition (b), we can inductively construct a sequence of points \(a=x_0,x_1,\dots ,x_m\in B\) such that for every positive \(i\leqslant m\) the point \(x_i\) belongs to \(A_i\) and the points \(x_{i-1},x_i\) belong to some set \(U_i\in {\mathscr {U}}_{n_i}(C_i)\). The chain \(a=x_0,x_1,\dots ,x_m\in A_m=B\) witnesses that

which is a desired contradiction. By analogy we can prove that the case \(d(A,B)<d(A,b)\) leads to a contradiction. \(\square \)
References
user116515: Making compact subsets “parallel”. https://mathoverflow.net/questions/284544/making-compact-subsets-parallel. Accessed 27 Oct 2017
Engelking, R.: General Topology. Sigma Series in Pure Mathematics, vol. 6, 2nd edn. Heldermann, Berlin (1989)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Banakh, T., Hryniv, O. A parallel metrization theorem. European Journal of Mathematics 6, 110–113 (2020). https://doi.org/10.1007/s40879-018-00311-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40879-018-00311-6




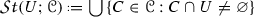 is open in X;
is open in X;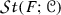 is closed in X;
is closed in X;