Skip to main content
SpringerLink
Log in

Influence of different subgrid-scale models in low-order LES of supersonic jet flows

  • Technical Paper
  • Published:
Journal of the Brazilian Society of Mechanical Sciences and Engineering Aims and scope Submit manuscript

Abstract

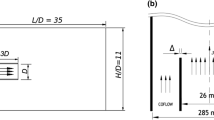
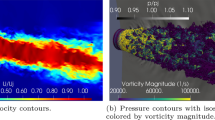
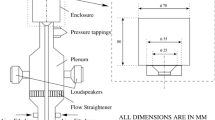
The present work is concerned with a study of large eddy simulations (LES) of unsteady turbulent jet flows. In particular, the present analysis is focused on the effects of the subgrid-scale modeling used when a second-order spatial discretization methodology is employed for the numerical simulations. The present effort addresses perfectly expanded supersonic jets, because the authors want to emphasize the effects of the jet mixing phenomena. The LES formulation is discretized using the finite difference approach, after the equations are rewritten in a generalized coordinate system. Both space and time discretizations are second-order accurate and an explicit time march is adopted. Special care is dedicated to the discretization of the energy equation to appropriately model the set of filtered equations appearing in the LES formulation. The classical Smagorinsky, the dynamic Smagorinsky and the Vreman models are the subgrid-scale closures selected for the present work. The computational results are compared to data in the literature to validate the present simulation tool. Results indicate that the characteristics of numerical discretization can be as important as the effects of the subgrid-scale models for such low-order spatial discretization schemes. A detailed analysis is presented for the performance of each subgrid closure in the numerical context here considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23
Fig. 24

Similar content being viewed by others

References

  1. ANSYS. http://www.ansys.com/. Accessed 13 May 2016

  2. Bigarella EDV (2002) Three-dimensional turbulent flow over aerospace configurations. MSc thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brasil,

  3. Bigarella EDV (2007) Advanced turbulence modeling for complex aerospace applications. PhD thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brasil

  4. Bodony DJ, Lele SK (2008) Current status of jet noise predictions using large-eddy simulations. AIAA J 46(2):364–380

    Article  Google Scholar 

  5. Bogey C, Marsden O, Bailly C (2011) Large-eddy simulation of the flow and acoustic fields of a Reynolds number \(10^{5}\) subsonic jet with tripped exit boundary layers. Phys Fluids 23(3):035104

    Article  Google Scholar 

  6. Brès GA, Jaunet V, Le Rallic M, Jordan P, Colonius T, Lele SK (2015) Large eddy simulation for jet noise: the importance of getting the boundary layer right. In: AIAA Paper No. 2015-2535, Proceedings of the 21st AIAA/CEAS aeroacoustics conference, Dallas, TX

  7. Bridges J, Wernet MP (2008) Turbulence associated with broadband shock noise in hot jets. In: AIAA Paper No. 2008-2834, Proceedings of the 14th AIAA/CEAS aeroacoustics conference, Vancouver, Canada

  8. Choi H, Moin P (2012) Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys Fluids 24(1):011702

    Article  Google Scholar 

  9. Clark RA, Ferziger JZ, Reynolds WC (1979) Evaluation of subgrid-scale models using an accurately simulated turbulent flow. J Fluid Mech 91:1–16

    Article  MATH  Google Scholar 

  10. Deardorff JW (1970) A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J Fluid Mech 4(part 2):453–480

    Article  MATH  Google Scholar 

  11. Garnier E, Adams N, Sagaut P (2009) Large eddy simulation for compressible flows.Springer, New York

    Book  MATH  Google Scholar 

  12. Germano M (1990) Averaging invariance of the turbulent equations and similar subgrid scale modeling. In: Center for Turbulence Research Manuscript 116. Stanford University and NASA Ames Research Center

  13. Germano M, Piomelli U, Moin P, Cabot WH (1991) A dynamic subgrid-scale eddy viscosity model. Phys Fluids A Fluid Dyn 3(7):1760–1765

    Article  MATH  Google Scholar 

  14. Jameson A, Mavriplis D (1986) Finite volume solution of the two-dimensional Euler equations on a regular triangular mesh. AIAA J 24(4):611–618

    Article  MATH  Google Scholar 

  15. Jameson A, Schmidt W, Turkel E (1981) Numerical solutions of the Euler equations by finite volume methods using Runge–Kutta time-stepping schemes. In: AIAA Paper No. 81–1259, Proceedings of the AIAA 14th fluid and plasma dynamics conference, Palo Alto, California, USA

  16. Junqueira-Junior C (2016) Development of a parallel solver for large eddy simulation of supersonic jet flow. PhD thesis, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brazil

  17. Junqueira-Junior C, Yamouni S, Azevedo JLF, Wolf WR (2015) Large eddy simulations of supersonic jet flows for aeroacoustic applications. In: AIAA Paper No. 2015-3306, Proceedings of the 33rd AIAA applied aerodynamics conference, Dallas, TX

  18. Junqueira-Junior C, Yamouni S, Azevedo JLF, Wolf WR (2016) Influence of different subgrid scale models in LES of supersonic jet flows. In: AIAA Paper No. 2016-4093, Proceedings of the 46th AIAA fluid dynamics conference, AIAA Aviation Forum, Washington, DC

  19. Leonard A (1974) Energy cascade in large eddy simulations of turbulent fluid flows. Adv Geophys A18:237–248

    Google Scholar 

  20. Li Y, Wang ZJ (2015) A priori and a posteriori evaluation of subgrid stress models with the Burger’s equation. IN: AIAA Paper No. 2015-1283, Proceedings of 53rd AIAA aerospace sciences meeting, Kissimmee, FL

  21. Lilly DK (1965) On the computational stability of numerical solutions of time-dependent non-linear geophysical fluid dynamics problems. Mon Weather Rev 93(1):11–25

    Article  Google Scholar 

  22. Lilly DK (1967) The representation of small-scale turbulence in numerical simulation experiments. In: IBM Form No. 320–1951, Proceedings of the IBM scientific computing symposium on environmental sciences. Yorktown Heights, NY, pp 195–210

  23. Long LN, Khan M, Sharp HT (1991) A massively parallel three-dimensional Euler/Navier–Stokes method. AIAA J 29(5):657–666

    Article  Google Scholar 

  24. Mendez S, Shoeybi M, Sharma A, Ham FE, Lele SK, Moin P (2010) Large-eddy simulations of perfectly-expanded supersonic jets: quality assessment and validation. In: AIAA Paper No. 2010–0271, Proceedings of the 48th AIAA aerospace sciences meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL

  25. Mendez S, Shoeybi M, Sharma A, Ham FE, Lele SK, Moin P (2012) Large-eddy simulations of perfectly-expanded supersonic jets using an unstructured solver. AIAA J 50(5):1103–1118

    Article  Google Scholar 

  26. Moin P, Squires K, Cabot W, Lee S (1991) A dynamic subgrid-scale model for compressible turbulence and scalar transport. Phys Fluids A Fluid Dyn (1989–1993) 3(11):2746–2757

    Article  MATH  Google Scholar 

  27. Sagaut P (2002) Large eddy simulation for incompressible flows. Springer, Berlin

    Book  MATH  Google Scholar 

  28. Smagorinsky J (1963) General circulation experiments with the primitive equations: I. The basic experiment. Mon Weather Rev 91(3):99–164

    Article  Google Scholar 

  29. Turkel E, Vatsa VN (1994) Effect of artificial viscosity on three-dimensional flow solutions. AIAA J 32(1):39–45

    Article  MATH  Google Scholar 

  30. Vreman AW (1995) Direct and large-eddy simulation of the compressible turbulent mixing layer. PhD thesis, Universiteit Twente, The Netherlands

  31. Vreman AW (2004) An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys Fluids 16(10):3670–3681

    Article  MATH  Google Scholar 

  32. Vreman B, Geurts B, Kuerten H (1996) Large-eddy simulation of the turbulent mixing layer using the Clark model. Theor Comput Fluid Dyn 8(4):309–324

    Article  MATH  Google Scholar 

  33. Wang ZJ (2015) Large eddy simulations of turbulent flows using discontinuous high order methods. In: 22nd AIAA computational fluid dynamics conference, invited talk, Dallas, TX

  34. Wolf WR, Azevedo JLF, Lele SK (2012) Convective effects and the role of quadrupole sources for aerofoil aeroacoustics. J Fluid Mech 708:502–538

    Article  MathSciNet  MATH  Google Scholar 

  35. Yoshizawa A (1986) Statistical theory for compressible turbulent shear flows, with the application to subgrid modeling. Phys Fluids 29(7):2152–2164

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors gratefully acknowledge the partial support for this research provided by Conselho Nacional de Desenvolvimento Científico e Tecnológico, CNPq, under the Research Grant nos. 309985/2013-7, 400844/2014-1 and 443839/2014-0. The authors are also indebted to the partial financial support received from Fundação de Amparo à Pesquisa do Estado de São Paulo, FAPESP, under the Research Grant nos. 2013/07375-0 and 2013/21535-0. The authors further acknowledge the National Laboratory for Scientific Computing, LNCC/MCTIC, for providing high-performance computing resources through the Santos Dumont supercomputer, which have contributed to the research results reported within this paper.

Author information

Authors and Affiliations

  1. Instituto de Aeronáutica e Espaço, DCTA/IAE/ALA, São José dos Campos, SP, 12228-904, Brazil

    Carlos Junqueira-Junior & João Luiz F. Azevedo

  2. Instituto Tecnológico de Aeronáutica, DCTA/ITA, São José dos Campos, SP, 12228-900, Brazil

    Sami Yamouni

  3. Faculdade de Engenharia Mecânica, Universidade Estadual de Campinas, Rua Mendeleyev, 200, Campinas, SP, 13083-860, Brazil

    William R. Wolf

Authors
  1. Carlos Junqueira-Junior
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sami Yamouni
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. João Luiz F. Azevedo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. William R. Wolf
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sami Yamouni.

Additional information

Technical Editor: André Cavalieri.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Junqueira-Junior, C., Yamouni, S., Azevedo, J.L.F. et al. Influence of different subgrid-scale models in low-order LES of supersonic jet flows. J Braz. Soc. Mech. Sci. Eng. 40, 258 (2018). https://doi.org/10.1007/s40430-018-1182-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40430-018-1182-9

Keywords

Search

Navigation