Abstract
The paper discusses the possibility of detecting local damages in complex structures typical of civil engineering, as multispan beams and trusses. Namely, it describes a procedure to identify localised cracks in structures in the elastic range of behaviour using only the values of natural frequencies in the intact configuration and in the damaged one evaluated by means of dynamic tests. The error minimisation procedure described in the paper selects the solution within a set of finite element models that simulate a range of positions and levels of damage, by identifying the damaged configuration as the one whose modal frequencies minimise the least-square difference with the measured data. The accuracy of the method is first investigated by applying it to the damage detection of a two-span steel beam, whose modal frequencies were obtained by means of experimental tests. To explore the accuracy of the proposed procedure, numerically simulated data with random noise were also generated for several positions and levels of damage and for different values of the random noise. The procedure was then extended, by means of numerical simulations, to the case of a beam with two localised damages. Finally, the procedure proposed for multispan beams is adapted to the damage identification of plane truss structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The last decades have witnessed an increasing attention to health monitoring of civil structures, above all in case of existing buildings, for which retrofitting interventions are often required to guarantee prescribed performances during the time. A first step in this direction is the definition of an accurate numerical model of the structure in its actual conditions, including the identification of possible damages. To this respect, the identification of modal properties, as natural frequencies, modal damping coefficients and mode shapes in a linear elastic structure can be used to verify the correspondence of a Finite Element (FE) model of the structure to its real behaviour, updating the numerical model on the base of experimental tests (D’Ambrisi et al. 2012; Diaferio et al. 2015, 2018; Gentile and Saisi 2010; Potenza et al. 2015; Ivorra et al. 2016; Antonacci et al. 2012; Sepe et al. 2005a, b, 2017; Valente et al. 2016; Bedon et al. 2016). Moreover, the experimental modal analysis techniques are able to highlight some peculiarities of the structural response that are usually neglected or that are difficult to be evaluated in the design process (as the influence of the non-structural elements on the dynamical response of the building, the presence of inhomogeneities, etc.).
On the other side, the remarkable progress in the resolution and sensitivity of the measurement devices for structural response acquirement, the possibility of implementing wireless acquisition chains (laptop, electronic acquisition board, accelerometers, etc.) and the continuously improved efficiency of the software for the treatment of experimental data, make realistic the possibility to monitor existing structures, even for ordinary buildings, through the evaluation of their dynamical parameters at different times (Cerri and Vestroni 2003; Greco et al. 2007; Sepe and Bellizzotti 2009; Rahai et al. 2007; Moaveni et al. 2008, 2009; Ramos et al. 2010; Amani et al. 2007). The importance of this tool is also confirmed by the recent development of new modal identification procedures (Pioldi et al. 2017) which make use of short duration and non-stationary data related to heavy structural damping. These techniques pave the way for damage detection in any forcing conditions.
In case of a damage localised in small parts of a linear elastic structure, e.g., in few sections of a beam or in a rod of a truss, as considered in this paper, the comparison between dynamical parameters of the damaged and undamaged structures should, therefore, allow to identify at least the main characteristics of the damage, as location and severity.
However, the occurrence of damage is usually associated with small variations of the modal parameters which can be also due to other sources, as environmental temperature modifications; as a consequence, many authors are cautious about the possibility of detecting the damage through the analysis of the variations of these parameters. Nevertheless, many methods that use such parameters have been proposed.
In Xia and Hao (2000), a method to select the measurement points and the modes to be used in model updating for damage identification is discussed; in Lee and Shin (2002) a frequency-domain method of structural damage identification for beam structures is presented. In Amani et al. (2007), the damage is estimated by means of SSI-Cov method and a modal analysis of the structural ambient vibrations.
In Rahai et al. (2007), an algorithm for damage detection is proposed that utilises incomplete measured mode shapes and natural frequencies. The algorithm proceeds solving the damage equations, which are written using the incomplete measured mode shapes, through an optimization method.
Amongst the others, Moaveni et al. (2008, 2009), Ramos et al. (2010) provide experimental validation of damage identification procedures in the frequency and time domains.
The aforementioned procedures have been applied mainly to detect the damage in beam-like structures, i.e. structures whose main behaviour is flexural. Differently from damage identification in beams or frames, the damage identification in truss structures has instead received a limited attention in the scientific literature. However, the typical characteristics of these structures, dominated by extensional behaviour, do not allow to simply extend to them the procedures developed for beams and frames, i.e. structures dominated by flexural behaviour.
In Liu (1995), the damage is detected by minimising the error norm of the eigen-equation of the truss which is written in accordance with the finite element approach and introducing the experimental modal parameters.
In Liu and Chen (1996), the transient response of the truss is used for identifying its element properties; in detail, the spectral finite element method is adopted to formulate the equilibrium equation and the unknown truss properties are estimated by minimising the error function that is defined in terms of unbalanced forces of the equilibrium equations. Finally, the damage is detected by comparing the identified element properties with the ones of the undamaged configuration.
In the damage detection method proposed in Castello et al. (2002), the eigen-problem for the FE model of the examined structure is written and then the model is updated by introducing the modal properties experimentally evaluated. In fact, the FE model is defined as a function of a damage parameter that represents the updating parameter and that is evaluated by minimising a global error derived from the dynamic residue vectors. The method is applied for the damage detection of beam-like and truss-like structures.
Liu and Yang (2006) proposed a method based on a FE model of the original structure and on the experimental frequency values and mode shapes. As a first step, the method proceeds establishing the number of the damaged elements which is assumed equal to the number of nonzero eigenvalues of the damage matrix, defined as the product of the mode shape matrix and the residual force matrix; subsequently, the position and the level of damage are evaluated by means of a damage localization matrix.
In Kopsaftopoulos and Fassois (2010), the effectiveness of statistical time series methods is discussed with regard to the estimation of damage in a lightweight aluminium truss structure.
The present paper investigates such issue both from an experimental and a numerical point of view. Namely, it describes situations of increasing complexity for multispan beams and truss structures.
In Sect. 2, the main features of the procedure are discussed.
Section 3 describes the tests conducted on a steel beam which is supported at both ends and in correspondence of the central cross section; in this way, two spans with the same length are obtained (Bellizzotti 2009). Moreover, a cross section of the beam was partially cut to simulate a localised damage. The dynamic tests have been carried out by applying an impulsive force by means of a hammer, and the subsequent results of the dynamic identification have been utilised for applying a procedure which identifies the place and the level of damage by minimising an error function which depends on the numerical and experimental natural frequencies. As it will be described in the following, to evaluate this function, several finite element (FE) models have been defined by varying the location and the depth of the notch in a given range; to automatise minimization procedure, the modal frequencies in the damaged cases are collected into a data-base characterised by three different indexes: the mode number, the damage position, and the level of damage. The construction of such data base allows to establish how the natural frequencies and the modes order number vary depending on the position and severity of damage.
Section 4 shows how the procedure developed for a multispan beam characterised by flexural behaviour (Sect. 3) can be extended to truss structures, whose dynamic behaviour is mainly due to axial deformations. For this kind of structure, a wide numerical investigation on a sample case shows the applicability and efficacy of the proposed procedure.
Damage detection based on experimental and numerical frequency values
Damage
In the present study, the damage in the beam is considered due to a notch which reduces the transversal section for the whole width and for a depth p, and it is assumed that the structural mass does not change. In these hypotheses, the damaged section can be modelled through a rotational spring whose flexural stiffness can be expressed in accordance with the formulation proposed by Chondros and Dimarogonas (1998) as follow:
where E is the elastic modulus of the beam, I is the area moment of inertia, ν is the Poisson coefficient, h is the thickness of the beam and \(\varPhi_{1}\) is a non-dimensional coefficient which can be expressed, according to Chondros and Dimarogonas (1998), as
where \(\alpha\) is the ratio between the depth of the cut p and the beam thickness h.
For a truss, whose dynamical behaviour is dominated by axial effects (Sect. 4), the damage is instead modelled in the following by means of a reduction (denoted by r) of the axial stiffness.
The damage identification procedure
The identification procedure discussed in this paper turns out the position and level of damage by minimising an error function that includes the measured values of the natural frequencies of the structure, both in the undamaged and damaged configurations (see also Cerri and Vestroni 2003; Greco et al. 2007 for other kinds and complexity of structures). The damage modifies in fact the natural frequencies, depending on its position and level. As a consequence, if a database is built of all the values of the natural frequencies of the structure obtained varying the position and the level of damage in a realistic interval, the actual state of damage can be detected as the one for which the difference between numerical and experimental frequency values is minimum.
The damage detection, i.e. position s and damage level p for a beam, element number # and stiffness reduction r for a truss, is performed by an error function which is defined as the square difference between the non-dimensional variation of the natural frequencies experimentally evaluated and the one obtained through the finite element model of the examined structure. Two different functions are introduced, \(G(s,\;p)\) and \(G(\# ,\;r)\) for the damage detection of a beam and of a truss, respectively:
where N is the number of the experimentally identified natural modes, \(\omega_{i}^{\text{U}}\) is the measured undamaged ith natural frequency, \(\omega_{i}^{\text{D}}\) denotes the damaged ith natural frequency, while \(\omega_{{i,{\text{FE}}}}^{\text{U}}\) is the ith frequency of the undamaged FE model; for a beam, \(\omega_{{i,{\text{FE}}}}^{\text{D}} (s,\;p)\) denotes the ith frequency of the FE model with a damage at position s and with level p, while for a truss \(\omega_{{i,{\text{FE}}}}^{\text{D}} (\# ,\;r)\) denotes the ith frequency of the FE model with a damage in the element number # and with a stiffness reduction r.
It must be underlined that the error functions have been defined as the least squared error between the percentage variation of the frequencies of the real structure and the one of the numerical models. In this way, the influence of possible differences between the FE model and the structure may be significantly reduced.
As discussed in Sect. 3.2, the accuracy of the identification procedure is related to the number of natural frequencies taken into account in the Eq. (3).
Cerri and Vestroni (2003) and Greco et al. (2007) have taken the first three natural frequencies into account; while for the cases here considered, it is shown that, due to the presence of noise in the data, the accuracy of the procedure requires a higher number of modes.
A good criterion is, therefore, to choose the widest set of reliable experimental modal frequencies; some of the available frequencies may in fact be not relevant on the identification problem (e.g., a crack in the inflection point of a given mode does not produce any variation of its frequency value). Moreover, increasing the number of the considered natural frequencies, the effects of noise can also be reduced.
Two-span beam
Damage detection for a multispan beam
To verify the accuracy of the described technique, the case of a two-span beam is considered. Namely, the beam has a rectangular transversal section 40 mm × 8 mm and a length of 100 cm for each span.
As a first step, it has been studied the accuracy of the procedure with regard to the number and combination of the natural modes included in the error function G; this analysis has been performed on pseudo-experimental (i.e. numerically simulated) data, that are discussed in Sect. 3.2.
The validation of the procedure by means of experimental tests is illustrated in Sect. 3.3.
Finally, the procedure has been extended, by means of a numerical investigation, to a damage configuration characterised by two notches localised in two different sections of the beam (see Sect. 3.4).
The experimental investigation (see for further details in Bellizzotti 2009) has been performed in the Material Testing Laboratory of the Department of Engineering and Geology of the University “G. D’Annunzio” of Chieti-Pescara; a steel model of a two-span simply supported beam has been tested, with a total length of 2200 mm and a rectangular cross section of 8-mm thick and 40-mm wide (see Figs. 1, 2).
The vibrations of the beam have been recorded by means of 12 accelerometers, with ± 2g full scale range, installed in the points denoted as 1, 3, 4, 5, 6, 8, 11, 14, 15, 17, 18, 19 in Fig. 2; masses equivalent to those of the accelerometers (16 g each) have been added in the other 7 measurement points, so to have an almost uniform mass distribution. The time-histories of accelerations have been sampled at 1000 Hz.
The beam has been forced by applying impulsive loads with a hammer.
After dynamical tests on the undamaged beam, a damaged configuration has been obtained by cutting with a disk saw a notch deep p = 4.2 mm at 501 mm from one of the beam ends.
The elastic linear finite element model (FEM) of the steel beam consists of 109 beam elements with a length of 20 mm each. The elastic modulus E = 2.032 × 105 N/m2 has been selected to minimise the difference between numerical and measured frequencies of the first six FEM modes in the undamaged configuration, with assumed values of 7813 kg/m3 for the mass density and 0.3 for the Poisson coefficient.
Starting from the aforementioned FE model and assuming that the notch is cut in a single section of the beam, it was chosen to discretize the beam with a step equal to 20 mm, thus obtaining 109 cross sections. Regarding the damage level, it was assumed that its depth may vary between 2 and 7 mm (70 steps). On such basis, 7630 different damaged configurations have been considered in the data base of FE models.
In accordance with Sect. 3.1, in each FE model, the damaged section was substituted by a rotational spring whose stiffness is given by Eqs. (1) and (2); the frequency values of the first six natural modes in the damaged configurations were then estimated. Consequently, each element of the frequency database is characterised by three indices: number of the natural mode, damage position and notch depth.
The FE model has also been used to generate the pseudo-experimental data (i.e. numerically simulated).
The natural frequencies to be included in the error function have been evaluated, both in the experimental test and in the pseudo-experimental simulation, by means of an impulsive force applied in a single section.
The accuracy of the damage detection procedure
The influence of noise and of the errors connected with the operational modal analysis makes reasonable to perform the damage identification procedure considering 5–6 modes, even if, from a theoretical point of view, fewer modes may be sufficient for a good estimation of the damage, as it is also confirmed in this paragraph.
To verify the influence of the number and combination of the modes included in the error function, a numerical simulation of the damaged case with s = 420 mm and p = 4.2 mm has been performed; to simulate the effects of a random measurement noise, the frequency values for the examined damaged case have been modified introducing an error ranging between − 20% and 20% of the difference between damaged and undamaged frequencies.
The damage detection has been performed varying the number of natural modes in Eq. (3) between 3 and 6, chosen among the lowest natural modes, as they are the ones that can be better identified by means of dynamical tests. The results of this analysis are shown in Table 1.
It can be observed that in the range of modes between 3 and 5, the detection of the damage position is quite accurate and lightly influenced by the combination of the considered modes, with the highest error around 1.85% of the span length. On the contrary, the natural modes selected to be included in the error function G can highly influence the estimation of the damage level that, in fact, can even reach an error of about the 17% of the notch depth.
Quite obviously, the accuracy level is strictly connected to the value of the random noise. In fact, considering the same damaged configuration (s = 420 mm and p = 4.2 mm) and the same number and combination of natural modes, the damage estimation varies with the maximum value of the random noise.
In detail, three different cases have been considered: the case A in which the random noise ranges between − 20% and 20% of the difference between damaged and undamaged frequencies, the case B in which the random noise ranges between − 25% and 25%, and the case C in which the random noise ranges between − 30% and 30% (see Table 2). As shown in Table 2, when the random noise value increases, the accuracy of the procedure decreases even when six natural modes have been considered. In this sense, the procedure could give good results only considering a higher number of natural modes, or repeating several times the dynamical tests and assuming as frequency values the mean ones, so to filter out the effects of random noise.
Experimental validation of the procedure
As it has been previously explained, the procedure has been validated detecting the damage in the aforementioned two-span beam; in particular, the damage was obtained by cutting the transversal section at s = 501 mm from the left end and considering two different cut depths, p = 3.2 mm and p = 3.8 mm, respectively.
To increase the visibility of the error function minima, in Fig. 3, the level curves of the dimensionless error function are plotted, obtained by dividing the error function G (see Eq. (3)) by its minimum value Gmin. As expected, in Fig. 3 they are visible two minima which are symmetric respect to the internal support. The damage identification procedure of Sect. 2 is able to identify with good accuracy the damage position (s = 500 mm, exact), while it overestimates the notch depth (p = 3.4 mm and 3.9 mm in Fig. 3b, d, respectively, corresponding to an error of about 3–6%).
Level curves of the error function G. Experimental data, damage at the location s = 501 mm with two different notch depths p. For each case, G(s, p) is normalised to its minimum value. ap = 3.2 mm; b zoom at the local minimum s = 500 mm and p = 3.4 mm; cp = 3.8 mm; d zoom at the local minimum s = 500 mm and p = 3.9 mm
Multiple damage
From a theoretical point of view, the abovementioned approach can be extended for detecting damage at multiple sites, even if the computational effort, due to the large number of the FE models related to the different combinations of position and level of damage, will be unacceptable for practical applications. As intermediate step, the two-span beam of Fig. 2 has been examined considering the damage localised into two different transversal sections.
In this case, the error function G is the natural extension of the one defined in Eq. (3), and it is obtained considering its dependence on four parameters: the two damage positions \(\bar{s}_{1} ,\;\bar{s}_{2}\) and the two damage levels \(\bar{p}_{1} ,\;\bar{p}_{2}\). The minimization procedure is performed through two steps: in the first step, for each s1, s2 pair, the domain \(G^{*} (s_{1} ,\;s_{2} )\) of the minima of G for all the possible combinations of p1, p2 is built; in the second step, the two positions of damage \(\bar{s}_{1} ,\;\bar{s}_{2}\) are detected evaluating the absolute minimum of \(G^{*} (s_{1} ,\;s_{2} )\). Once evaluated the positions \(\bar{s}_{1} ,\;\bar{s}_{2}\) of damage, the depths of the notches \(\bar{p}_{1} ,\;\bar{p}_{2}\) are estimated by minimising the function \(G(\bar{s}_{1} ,\;\bar{s}_{2} ,.,.)\). To verify the performance of the proposed procedure, a numerical simulation of the two-span beam affected by a double damage (s1= 960 mm, p1= 3.2 mm, s2= 620 mm, p2= 4.2 mm) has been performed, and the results have been plotted in Fig. 4.
Nevertheless, the described step-by-step approach to the minimization procedure cannot guarantee, from a theoretical point of view, that the estimated damage parameters \(\bar{s}_{1} ,\;\bar{s}_{2}\), \(\bar{p}_{1} ,\;\bar{p}_{2}\) correspond to the absolute minimum of the error function G. The global minimum has, therefore, to be checked in the neighbourhood of the point \(G(\bar{s}_{1} ,\;\bar{s}_{2} ,\;\bar{p}_{1} ,\;\bar{p}_{2} )\), taking into account all the possible combinations of the damage parameters; in all the examined cases, the results of the abovementioned procedure have been confirmed.
To evaluate the influence of the random noise, the frequency values of the 6 natural modes have then been contaminated with ± 0.3% error, which is about a quarter of the mean differences between the undamaged and damaged frequency values. As Fig. 4 shows, in the examined damaged configuration, this approach is able to give an accurate estimation of the damage, and this seems a quite promising result for the application of the proposed procedure to multiple damage configurations.
In Table 3, the results of the damage detection for the double damaged configuration s1= 1240 mm, p1= 3.2 mm, s2= 620 mm, p2= 4.2 mm are shown for three different levels of the random noise: (1) exact pseudo-experimental frequencies; (2) pseudo-experimental frequencies with a ± 0.10% error; (3) pseudo-experimental frequencies with a ± 0.25% error, which is about a quarter of the mean differences between the undamaged and damaged frequency values.
Numerical investigation on trusses
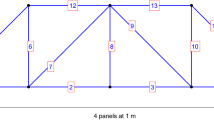
For plane trusses consisting of rods connected to each other by hinges, as the one in Fig. 5, global and local modes can be distinguished, with extensional or flexural deformations, respectively.
For the simply supported steel plane truss in Fig. 5, Table 4 reports cross-sectional characteristics of the rods; elastic modulus E = 200000 MPa and density ρ = 7850 kg/m3 have been also assumed.
In the following it will be assumed a damage in one truss element, that both modifies the extensional and flexural stiffness, and therefore affects both global and local modes.
Different sensors distributions are required to evaluate the experimental modal frequencies of global and local modes. While the structural response in the nodal points allows to obtain the frequencies of global modes (i.e. the modal properties used in the procedure described here) and their modal shapes (not used in the procedure described here, but included in other techniques based on modal properties (Liu 1995; Liu and Yang 2006)), the experimental evaluation of local modes requires a more close distribution of measurement sensors, including sensors in intermediate points of the truss elements. In fact, although all natural modes (both global and local ones) contribute from a theoretical point of view to the structural response and can, therefore, be both revealed by sensors in nodal points of the truss, in the writers’ experience, the small contribution of local modes to the frequency spectrum identified from measured response in nodal points can be (and is) in practice masked by measuring errors or noise.
Therefore, it has been assumed here that only global frequencies (Fig. 6) are available both in the damaged and in the undamaged cases, derived by nodal time-histories of the response.
First 12 natural modes of the plane truss in Fig. 5 (undamaged case)
Following a procedure analogous to the one described in Sect. 2 for beams, an undamaged FE model (denoted as reference model) and a database of damaged FE models have been considered. In particular, 248 FE models have been built, obtained considering the damage localised in each one of the 31 truss elements (the symmetry of the structure has been taken into account, see Fig. 5) and varying the extensional stiffness reduction in the range 5–40% with a step equal to 5% (8 different damage levels). The database is composed by 2976 elements (the first 12 frequencies for each damaged configuration).
For the reasons already discussed, the numerical investigation described in the following simulates an experimental campaign based on measuring sensors located in the nodes of the truss, that allow to identify—with classical procedures in the frequency domain—the global modes of the truss, i.e. those modes related to extensional behaviour of the truss elements.
According to the measuring setup assumed, on the other hand, the frequency variation of local modes is considered here as unidentifiable, and therefore, no reduction is considered for the flexural stiffness of the damaged truss element. The frequency variations in the examined damaged configurations relative to the undamaged state are plotted in Fig. 7.
As a sample case, a stiffness reduction of 35% is considered in the truss element #15, i.e. the fourth diagonal member from the left end of the truss (Fig. 5).
To simulate a realistic experimental result, the undamaged and damaged “measured” natural frequencies have been obtained by adding to the exact undamaged and damaged frequencies a random error up to ± 0.2 Hz, and ten different realisations of such an error have been considered in the following.
According to the procedure already discussed in Sect. 2, the following error function is assumed
that includes the undamaged (\(\omega_{i}^{\text{U}}\)) and damaged (\(\omega_{i}^{\text{D}}\)) natural frequencies of the first 12 global modes for any simulated set of “measures” (here numerically simulated, as said before, by adding a sample realisation of the random error to the exact damaged and undamaged frequencies); the difference between such frequencies is compared, in the error function, with the difference between the corresponding exact values of undamaged (\(\omega_{{i,{\text{FE}}}}^{\text{U}}\)) and damaged frequencies (\(\omega_{{i,{\text{FE}}}}^{\text{D}} (\# ,\;r)\)) in a database of FE models, representing all possible damaged configurations in a realistic range (one truss element at a time, extensional stiffness reduction between 5 and 40% with an increment step of 5% in the numerical investigation here reported).
As shown by the error function plotted in Figs. 8, 9, 10, 11, 12, 13 and 14, for this kind of structures, the proposed procedure is quite sensitive to measuring errors.
35% of stiffness reduction r in the truss element #15. Error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering “pseudo-experimental” data, both for undamaged and damaged configurations, contaminated with an error of maximum value ± 0.2 Hz (random noise). Several minima can be observed (#13 with r = 30–35%, #15 with r = 25–35%, #16 with r = 40%, #19 with r = 20–30%), including the exact one (#15 with r = 35%)
35% of stiffness reduction r in the truss element #15. Error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering “pseudo-experimental” data, both for undamaged and damaged configurations, contaminated with an error of maximum value ± 0.1 Hz (random noise). Several minima can be observed (#15 with r = 30–35%) around the exact value
35% of stiffness reduction r in the truss element #15. Error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering pseudo-experimental data, both for undamaged and damaged configurations, contaminated with an error of maximum value ± 0.3 Hz (random noise). Several minima can be observed (e.g. #13 with r = 25–40%, #16 with r = 40%, #19 with r = 15–30%, and so on), not including the exact one (#15 with r = 35%)
35% of stiffness reduction r in the truss element #15. Mean error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering ten sample cases of pseudo-experimental data, both for undamaged and damaged configurations, contaminated with an error of maximum value ± 0.2 Hz (random noise). The exact minimum (#15 with r = 35%) is identified
35% of stiffness reduction r in the truss element #15. Mean error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering ten sample cases of “pseudo-experimental” data, both for undamaged and damaged configurations, contaminated with an error of maximum value ± 0.3 Hz (random noise). Several minima can be observed (#15 with r = 30–40%) around the exact value (r = 35%)
35% of stiffness reduction r in the truss element #15. Error function \(G(\# ,\;r)\) normalised to its minimum value and evaluated considering pseudo-experimental data, both for undamaged and damaged configurations, contaminated with a systematic error of + 0.1 Hz. The damaged element (#15) is correctly identified, while the damage level is underestimated (r = 25–30%, instead of 35%)
While an exact knowledge of both undamaged (\(\omega_{i}^{\text{U}}\)) and damaged (\(\omega_{i}^{\text{D}}\)) natural frequencies—here discussed only as an ideal target and reported in Fig. 8—allows an exact identification of the damaged truss element (#15) and of the damage level (reduction of extensional stiffness r = 35%), the presence of “measuring” errors influences the identified solution, as shown for the sample case in Fig. 9, corresponding to measuring errors on the first 12 frequencies ranging between ± 0.2 Hz, i.e. for accurate but realistic experimental data. In this sample case, the error function shows in fact several local minima, that cannot allow to confine the region of the truss that includes the damaged element; more generally, it has been found that the damage detection based on a single set of simulated frequencies (i.e. a sample case of random error added to the exact frequencies) can be less or more accurate depending on the specific “noise” of that realisation, and therefore it is not reliable.
Quite obviously, the damage is better identified for smaller “measuring” errors (see Fig. 10, where the errors added to natural frequencies have been halved), while larger “measuring” errors imply an even worse identification of damage (see Fig. 11, where the errors added to natural frequencies have been increased).
To overcome this inconvenience, the statistical approach discussed in the following has been proven to be effective; it uses, both in the undamaged and in the damaged case, multiple experimental measures (namely “pseudoexperimental”, i.e. numerically generated, in the cases discussed here).
For the same case of Fig. 9 (“measuring” errors ranging between ± 0.2 Hz), ten different random sequences of “noise” have been considered both for the undamaged and damaged frequencies, evaluating for each of them the error function for all the damaged frequencies in the FEM database.
Although, as already discussed, the error function for a single pseudo-experimental “measure” does not allow an accurate damage identification, the random nature of measuring errors allows to filter out such uncertainties when a mean error function is considered, obtained as an average of the error functions evaluated for each random noise sequence.
As shown in Fig. 12, in fact, the damage identification is in this case quite accurate (compare with Fig. 9) for measuring errors ranging between ± 0.2 Hz, and keeps maintaining an acceptable accuracy also for larger random errors, when the identification based on a sample case may be completely unreliable (e.g. Fig. 13, with measuring errors ranging between ± 0.3 Hz; compare with Fig. 11).
On the other hand, systematic errors on the measured frequencies (i.e. all in excess or in fault of a given quantity) do not imply relevant effects on the damage location, while of course they affect the identified damage level. An example is shown in Fig. 14, where the frequencies evaluated by means of the FE model with a damage in the diagonal element #15 and with a reduction stiffness of 35% have been contaminated with a systematic error of + 0.1 Hz: as expected by observing the structure of the error function (Eq. 4), the damage location is correctly found (diagonal element #15), while the procedure obviously underestimates the damage level as a consequence of systematic frequencies overestimation.
Although the numerical results discussed so far cannot yet be considered as general, as they need to be validated by means of a wider numerical and experimental analysis, in the writer’s opinion, they confirm the possibility of extending to truss structures the proposed procedure, already experimentally validated for multispan beams (Sect. 3).
Conclusions
The paper deals with the identification of localised damage in linear elastic structures through measured dynamical parameters.
It analyses from a numerical and an experimental point of view multispan beams and trusses. The damage detection considers the possibility to monitor such structures by performing dynamic tests at the initial service conditions, i.e. intact structure, and during the time when the damage may occur. In this way, the natural frequencies at different times may be evaluated and utilised to identify the occurrence of damage.
To verify the accuracy and the limits of the procedure, dynamic tests have been carried out on a steel beam with three simple supports, two at the ends and one at the middle section. In detail, the model was loaded by the impact of a hammer (Bellizzotti 2009). The beam was considered damaged in a single transversal section, such condition was described in the FE model of the structure by a spring whose rotational stiffness was evaluated in accordance with Eqs. (1) and (2); in the experimental tests described in Sect. 3, the notch is obtained with a disk saw.
Location and severity of damage are found (see Sect. 2.2) by minimising (in the least squares sense) an error function that considers the difference of some modal frequencies between the undamaged and damaged configurations (six in the sample case of Sect. 3) and compares them with the frequency variations for a wide set of damaged configurations, which are obtained varying the location and severity of the damage. Based on experimental results, Sect. 3 also discusses the possible extension of the proposed procedure to multiple damages, in the perspective of a future research activity.
Section 4 deals with the application of such procedure to truss-like structures, dominated by axial deformations. The accuracy of the damage detection procedure is analysed by applying it to a single bay simply supported plane truss and by considering pseudo-experimental data contaminated with errors of different levels, introduced to simulate random noise.
As shown in other papers of the writers’, such procedure can also be extended to multispan and multi-floor framed structures, where only higher-order modes are significantly affected by local damage, by means of a substructure approach (Bellizzotti 2009; Sepe and Bellizzotti 2009; Sepe et al. 2009; Diaferio and Sepe 2016). In Sepe and Bellizzotti (2009), the possibility of applying such a procedure when the damaged span of a multispan beam is not directly accessible is also discussed.
References
Amani MG, Riera JD, Curadelli RO (2007) Identification of changes in the stiffness and damping matrices of linear structures through ambient vibrations. Struct Control Health Monit 14:1155–1169
Antonacci E, De Stefano A, Gattulli V, Lepidi M, Matta E (2012) Comparative study of vibration-based parametric identification techniques for a three-dimensional frame structure. Struct Control Health Monit 19(5):579–608
Bedon C, Dilena M, Morassi A (2016) Ambient vibration testing and structural identification of a cable-stayed bridge. Meccanica 51(11):2777–2796
Bellizzotti G (2009) Dynamic identification of structures and damage identification by non-destructive dynamic tests, Ph.D. dissertation. University “G. D’Annunzio” of Chieti-Pescara, Italy (in Italian)
Castello DA, Stutz LT, Rochinha FA (2002) A structural defect identification approach based on a continuum damage model. Comp Struct 80:417–436
Cerri MN, Vestroni F (2003) Identification of damage due to open cracks by changes of measured frequencies. In: Proceedings of the 16th conference of theoretical and applies mechanics AIMETA, Ferrara
Chondros TG, Dimarogonas AD (1998) A continuos cracked beam theory. J Sound Vib 215(1):17–34
D’Ambrisi A, Mariani V, Mezzi M (2012) Seismic assessment of a historical masonry tower with nonlinear static and dynamic analyses tuned on ambient vibration tests. Eng Struct 36:210–219
Diaferio M, Sepe V (2016) Modal identification of damaged frames. Struct Control Health Monit 23(1):82–102
Diaferio M, Foti D, Giannoccaro NI (2015) Identification of the modal properties of a squat historic tower for the tuning of a FE model. In: Proceedings of 6th international operational modal analysis conference, IOMAC 2015, Abba Hotel, Gijon, 12–14 May 2015; Code 112375
Diaferio M, Foti D, Potenza F (2018) Prediction of the fundamental frequencies and modal shapes of historic masonry towers by empirical equations based on experimental data. Eng Struct 156:433–442
Gentile C, Saisi A (2010) FE modeling of a historic masonry tower and vibration-based systematic model tuning. Adv Mater Res 133–134:435–440
Greco A, Pau A and Vestroni F. (2007) Damage identification in a parabolic arch. In: Proceedings of the 18th conference of Italian Association for theoretical and applied mechanics, AIMETA, Brescia
Ivorra S, Brotóns V, Foti D, Diaferio M (2016) A preliminary approach of dynamic identification of slender buildings by neuronal networks. Int J Non-Linear Mech 80:183–189
Kopsaftopoulos FP, Fassois SD (2010) Vibration based health monitoring for a lightweight truss structure: experimental assessment of several statistical time series methods. Mech Syst Signal Process 24:1977–1997
Lee U, Shin J (2002) A frequency domain method of structural damage identification formulated from the dynamic stiffness equation of motion. J Sound Vib 257(4):615–634
Liu PL (1995) Identification and damage detection of trusses using modal data. J Struct Eng 121:599–608
Liu PL, Chen CC (1996) Parametric identification of truss structures by using transient response. J Sound Vib 191(2):273–287
Liu JK, Yang QW (2006) A new structural damage identification method. J Sound Vib 297:694–703
Moaveni B, He X, Conte JP (2008) Damage identification of a composite beam based on changes of modal parameters. Comp Aided Civ Infrastruct Eng 23(5):339–359
Moaveni B, Conte JP, Hemez FM (2009) Uncertainty and sensitivity analysis of damage identification results obtained using finite element model updating. Comput Aided Civ Infrastruct Eng 24(5):320–334
Pioldi F, Ferrari R, Rizzi E (2017) Seismic FDD modal identification and monitoring of building properties from real strong-motion structural response signals. Struct Control Health Monit 24:e1982. https://doi.org/10.1002/stc.1982
Potenza F, Federici F, Lepidi M, Gattulli V, Graziosi F, Colarieti A (2015) Long-term structural monitoring of the damaged Basilica S. Maria di Collemaggio through a low-cost wireless sensor network. J Civ Struct Health Monit 5:655–676
Rahai A, Bakhtiari-Nejad F, Esfandiari A (2007) Damage assessment of structure using incomplete measured mode shapes. Struct Control Health Monit 14:808–829
Ramos L, De Roeck G, Lourenço P, Campos-Costa A (2010) Damage identification on arched masonry structures using ambient and random impact vibrations. Eng Struct 32(1):146–162
Sepe V, Bellizzotti G (2009) Identification of damage in structural elements not directly accessible. In: Procedeings of the 3rd IOMAC, Portonovo-Ancona
Sepe V, Capecchi D, De Angelis M (2005a) Modal model identification of structures under unmeasured seismic excitations. Earthq Eng Struct D 34:807–824
Sepe V, Vestroni F, Vidoli S, Mele R, Tisalvi M (2005b) Train induced vibrations of masonry railway bridges. In: Sixth European conference on structural dynamics EURODYN 2005, Vol 1. Paris, pp 161–166
Sepe V, Bellizzotti G, Diaferio M (2009) Identification of local damage in beams and frames. In: Proceedings of the 19th conference on Italian Association for theoretical and applied mechanics, AIMETA XIX, Ancona
Sepe V, Valente C, Zuccarino L, Siano R, Iezzi F (2017) Identification of frame models under unmeasured base motion: experimental validation. In: 10th International conference on structural dynamics, EURODYN 2017, Rome, 10–13 September 2017, PROC ENG, vol 199, pp 1008–1013, Elsevier Ltd, ISSN: 1877-7058. https://doi.org/10.1016/j.proeng.2017.09.265
Valente C, Sepe V, Di Pilla M, Iezzi F, Siano R, Zuccarino L (2016) Modal analysis of a frame model under unmeasured seismic input. ECCOMAS Congress 2016—VII European Congress on Computational Methods in Applied Sciences and Engineering, vol III, pp 5742–5752, Institute of Structural Analysis and Antiseismic Research, School of Civil Engineering, NTUA, ISBN: 978-618-82844-0-1, Crete Island, 5–10/06/2016
Xia Y, Hao H (2000) Measurement selection for vibration-based structural damage identification. J Sound Vib 236(1):89–104
Acknowledgements
The authors gratefully acknowledge the funding by the University “G. D’Annunzio” of Chieti-Pescara. Prof. Fabrizio Vestroni, University of Rome “La Sapienza”, is gratefully acknowledged for his help to one of the authors (G.B.) during his visiting period as PhD Student in Rome, in the framework of a 1-year fellowship of Regione Abruzzo (POR C3/IC4E, 2007–2008).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Diaferio, M., Sepe, V. & Bellizzotti, G. Modal identification of localised damage in beams and trusses: experimental and numerical results. Int J Adv Struct Eng 11, 421–437 (2019). https://doi.org/10.1007/s40091-019-00243-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40091-019-00243-9