Abstract
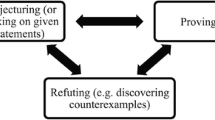
Dynamic geometry environment (DGE) has been a catalytic agent driving a paradigm shift in the teaching and learning of school geometry in the past two decades. It opens up a pedagogical space for teachers and students to engage in mathematical explorations that niche across the experimental and the theoretical. In particular, the drag-mode in DGE has been a unique pedagogical tool that can facilitate and empower students to experiment with dynamic geometrical objects which can lead to generation of mathematical conjectures. Furthermore, the drag-mode seems to open up a new methodology and even a new discourse to acquire geometrical knowledge alternative to the traditional Euclidean deductive reasoning paradigm. This discussion paper proposes an epistemic model of techno-pedagogic mathematic task design which serves as a theoretical combined-lens to view mathematics knowledge acquisition. Three epistemic modes for techno-pedagogic mathematical task design are proposed. They are used to conceptualize design of dynamic geometry tasks capitalizing the unique drag-mode nature in DGE that opens up an explorative space for learners to acquire mathematical knowledge.








Similar content being viewed by others
References
Ainley, J., Pratt, D., & Hansen, A. (2006). Connecting engagement and focus in pedagogic task design. British Educational Research Journal, 32(1), 21–36.
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practices in Cabri environments. Zentralblatt für Didaktik der Mathematik, 34(3), 66–72.
Baccaglini-Frank, A., & Mariotti, M. A. (2010). Generating conjectures in dynamic geometry: The maintaining dragging model. International Journal of Computers for Mathematical Learning, 15, 225–253.
Baccaglini-Frank, A., Mariotti, M. A., & Antinini, S. (2009). Different perceptions of invariants and generality of proof in dynamic geometry. In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 89–96). Thessaloniki, Greece: PME.
Brown, J. (2005). Affordances of a technology-rich teaching and learning environment. In P. Clarkson, A. Downton, D. Gronn, M. Horne, A. McDonough, R. Pierce, M. Horne, & A. Roche (Eds.), Building connections: Theory, research, and practice, Proceedings of the 28th annual conference of the Mathematics Education Research Group of Australasia, Melbourne (Vol. 1, pp. 177–184). Sydney: MERGA.
Duval, R. (1995). Geometrical pictures: Kinds of representation and specific processing. In R. Sutherland & J. Mason (Eds.), Exploiting mental imagery with computers in mathematics education (pp. 142–157). New York: Springer.
Freudenthal, H. (1968). Why to teach mathematics so as to be useful. Educational Studies in Mathematics, 1, 3–8.
Freudenthal, H. (1991). Revisiting mathematics education. Dordrecht: Kluwer Academic Publishers.
Gibson, J. J. (1979). The ecological approach to visual perception. Boston: Houghton Mifflin.
Laborde, C. (2005). Robust and soft constructions: Two sides of the use of dynamics geometry environments. In Proceedings of the Tenth Asian Technology Conference in Mathematics (pp. 22–35). Korea National University of Education, Cheong-Ju, South Korea.
Leung, A. (2003) Dynamic geometry and the theory of variation. In N. A. Pateman, B. J. Dougherty, & J. Zilliox (Eds.), Proceedings of PME 27: Psychology of Mathematics Education 27th International Conference (Vol. 3, pp. 197–204). Honolulu, USA.
Leung, A. (2008). Dragging in a dynamic geometry environment through the lens of variation. International Journal of Computers for Mathematical Learning, 13, 135–157.
Leung, A. (2009). Written proof in dynamic geometry environment: Inspiration from a student’s work. In Proceedings of the ICMI 19 Study Conference: Proof and Proving in Mathematics Education (Vol. 2, pp. 15–20). Taipei, Taiwan.
Leung, A., Chan, Y. C., & Lopez-Real, F. (2006). Instrumental genesis in dynamic geometry environments. In Proceedings of the ICMI 17 Study Conference: Technology Revisited, Part 2 (pp. 346–353). Hanoi, Vietnam.
Leung, A., & Lopez-Real, F. (2002). Theorem justification and acquisition in dynamic geometry: A case of proof by contradiction. International Journal of Computers for Mathematical Learning, 7, 145–165.
Leung, A., & Or, A. (2009). Cognitive apprehension in Cabri 3D environment. In M. Tzekaki, M. Kaldrimidou, & H. Sakonidis (Eds.), Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 1, p. 417). Thessaloniki, Greece: PME.
Lopez-Real, F., & Leung, A. (2006). Dragging as a conceptual tool in dynamic geometry environments. International Journal of Mathematical Education in Science and Technology, 37(6), 665–679.
Mariotti, M. A. (2002). Influence of technologies advances on students’ maths learning. In L. English, M. Bartolini Bussi, G. Jones, R. Lesh, & D. Tirosh (Eds.), Handbook of international research in mathematics education (pp. 695–721). New Jersey: Lawrence Erlbaum Associates.
Mason, J., & Johnston-Wilder, S. (2006). Designing and using mathematical tasks. St. Albans: Tarquin Publications.
Noss, R., & Hoyles, C. (1996). Windows on mathematical meanings. Dordrecht: Kluwer Academic Publishers.
Pratt, D., & Noss, R. (2010). Designing for mathematical abstraction. International Journal of Computers for Mathematical Learning, 15, 81–97.
Restrepo, A. M. (2008). Genese instrumentale du deplacement en geometrie dynamique chez des eleves de 6eme. Unpublished Ph.D. Thesis. Universite Joseph Fourier.
Talmon, V., & Yerushalmy, M. (2004). Understanding dynamic behaviour: Parent–child relations in dynamic geometry environments. Educational Studies in Mathematics, 57, 91–119.
Vérillon, P., & Rabardel, P. (1995). Cognition and artifacts: A contribution to the study of thought in relation to instrumented activity. European Journal of Psychology of Education, 10(1), 77–101.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Leung, A. An epistemic model of task design in dynamic geometry environment. ZDM Mathematics Education 43, 325–336 (2011). https://doi.org/10.1007/s11858-011-0329-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11858-011-0329-2