Introduction

High-velocity oxygen fuel (HVOF) is a thermal spray technique that was introduced in 1980s (Ref 1). It is a particulate deposition process in which microsized particles of metals, alloys, or cermets are propelled and heated in a sonic/supersonic combusting gas stream and are deposited on a substrate at high speeds to form a layer of coating. Compared with plasma spray, coatings sprayed by the HVOF process have outstanding characteristics including higher density, bond strength, and toughness, as a result of the significantly higher particle velocity at impact and relatively lower particle temperature. High-velocity oxygen fuel sprayed functional coatings are now widely used in various industries to enhance performance, extend product life, and reduce maintenance cost. Representative examples include WC/Co-based wear-resistant coatings for drilling tools, YSZ-based thermal barrier coatings for turbine blades, and nickel-base corrosion-resistant coatings for chemical reactors. More recently, the HVOF process has been used for processing nanostructured coatings using microsized nanocrystalline powder particles (Ref 2-4), which exhibit superior properties over conventional counterparts in terms of microhardness, elastic modulus, wear resistance, and thermal conductivity.

Modeling and control play an important role in the design and operation of the HVOF thermal spray process, partly because of its inherent complexity. Generally, the relationship among processing conditions, particle characteristics, and the resulting coating properties is highly nonlinear and might not be thoroughly revealed by experimental studies. As a result, the optimization of HVOF thermal spray based on the conventional design of experiments (DOE) methodology could be limited, especially when the HVOF system is significantly modified (Ref 5). Mathematical modeling is an excellent complement to the experimental approach. It provides a fundamental understanding of the underlying momentum and heat-transfer mechanisms, which in turn, might be used to guide system design and operation (Ref 6, 7). Moreover, the compensation of feed disturbances and process variability during real-time process operation becomes essential in order to fabricate coatings of a consistent quality. This motivates the development and implementation of real-time control systems in HVOF thermal spray to suppress variations in the particle temperature and velocity at the point of impact on the substrate. Such efforts have been facilitated by recent advances in the gas and particle velocity and temperature measurements via real-time diagnostic techniques (Ref 8).

Modeling of HVOF Thermal Spray

Multiscale Character of HVOF Thermal Spray

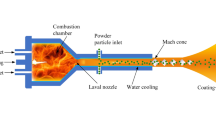
Figure 1 shows a schematic of a representative HVOF thermal spray system (Sulzer Metco Diamond Jet Hybrid 2700, Sulzer Metco, Westbury, NY). In this process, the premixed fuel gas (typically propylene or hydrogen) and oxygen are fed to the air cap, where they react to produce high-temperature combustion gases. The exhaust gases, together with the air injected from the annular inlet orifice, expand through the nozzle to reach supersonic velocity. The air cap is cooled by both water and air to prevent it from melting. The powder particles are injected at the central inlet nozzle using nitrogen as the carrier gas. Consequently, rapid momentum and heat transfer between the gas and the powder particles lead to acceleration and heating of the particles. The molten or semimolten particles are carried toward the substrate by the expanding gas jet. The particles hit the substrate, cool, and solidify, forming a thin layer of coating material with low porosity.

Fig. 1
figure 1

Diamond Jet Hybrid thermal spray gun

Full size image

The multiscale character of a typical HVOF thermal spray process is shown in Fig. 2 (Ref 9). The microstructure of HVOF sprayed coatings results from the deformation, solidification, and sintering of the deposited particles, which are dependent on the substrate properties (e.g., substrate temperature) as well as the physical and chemical state (e.g., temperature, velocity, melting ratio, and oxidant content) of the particles at the point of impact on the substrate. The particle in-flight behavior, however, is coupled with the gas dynamics, which are directly related to various processing conditions such as gas flow rate, fuel/oxygen ratio, spray distance, and so forth. While the macroscopic thermal/flow field can be readily described by continuum-type differential equations governing the compressible two-phase flow, the process of particle deposition is stochastic and discrete in nature and is best described by stochastic simulation methods (Ref 9).

Fig. 2
figure 2

Multiscale character of the HVOF thermal spray process (Ref 9, 27)

Full size image

Gas Dynamics

The gas and particle dynamics in the HVOF thermal spray are coupled with each other. To simplify the analysis, the assumption of one-way coupling is usually made when the particle loading, which is defined as the ratio of mass flow rate of particles to that of gases, is low (about 4-5%). Under such an assumption, the existence of particles has a minimal influence on the gas thermal and flow dynamics, while the particle in-flight behavior is derived from the particle momentum and heat-transfer equations (Ref 10, 11). The modeling of the two-way coupling of the gas and particulate phases is also possible at the expense of a higher computational cost (Ref 12).

The gas flow in HVOF thermal spray is essentially a compressible reacting flow process featured with turbulence and subsonic/sonic/supersonic transitions (Ref 13). A comprehensive description of this process requires time-consuming direct numerical simulations. To simplify the simulation, the Reynolds-Averaged Navier-Stokes (RANS) equations are usually used so that the small-scale turbulent fluctuations might not be directly solved. To convert the Navier-Stokes equations into the ensemble-averaged form, the Boussinesq hypothesis (Ref 14) is employed to represent the Reynolds stresses (with fluctuation terms) with the mean velocity gradients (without fluctuation terms). Specifically, the governing equations include the conservations of mass, momentum, energy, species transport, turbulent kinetic energy, dissipation rate, and so forth (Ref 11). The equations written in Cartesian tensor notation are:

Continuity:

$$ \frac{\partial \uprho }{\partial t} + \frac{\partial }{{\partial x_{j} }}(\uprho v_{j} ) = 0 $$
(1)

where ρ is the density, t is the time, and v j are the velocity components in each of the x j directions.

Momentum balance:

$$ \begin{aligned} \frac{\partial }{\partial t}(\uprho v_{i} ) + \frac{\partial }{{\partial x_{j} }}(\uprho v_{i} v_{j} ) \hfill \\ = - \frac{\partial p}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left[ {\upmu \left( {\frac{{\partial v_{i} }}{{\partial x_{j} }} + \frac{{\partial v_{j} }}{{\partial x_{i} }} - \frac{2}{3}\updelta_{ij} \frac{{\partial v_{l} }}{{\partial x_{l} }}} \right)} \right] + \frac{\partial }{{\partial x_{j} }}( - \uprho \overline{{v^{\prime}_{i} v^{\prime}_{j} }} ),\quad i = 1,2,3 \hfill \\ \end{aligned} $$
(2)

where p is the pressure, μ is the molecular viscosity, δ ij is the Kronecker delta, and \( - \uprho \overline{{v^{\prime}_{i} v^{\prime}_{j} }} \) is the Reynolds stress term representing the effect of turbulence. Based on the Boussinesq approximation,

$$ - \uprho \overline{{v^{\prime}_{i} v^{\prime}_{j} }} = \upmu_{\text{t}} \left( {\frac{{\partial v_{i} }}{{\partial x_{j} }} + \frac{{\partial v_{j} }}{{\partial x_{i} }}} \right) - \frac{2}{3}\left( {\uprho k + \upmu_{\text{t}} \frac{{\partial v_{l} }}{{\partial x_{l} }}} \right)\updelta_{ij} $$

where μt is the turbulent viscosity [\( \upmu_{\text{t}} = \uprho c_{\upmu } \left( {k^{ 2} /\upepsilon } \right) \)] and k is the turbulence kinetic energy (k = ½\( {\overline{{v}_{i}^{\prime 2}}} \)).

Turbulence model (using the k-\( \upepsilon \) model as an example):

$$ \frac{\partial }{\partial t}(\uprho k) + \frac{\partial }{{\partial x_{i} }}(\uprho v_{i} k) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\upmu + \frac{{\upmu_{\text{t}} }}{{\upsigma_{\text{k}} }}} \right)\frac{\partial k}{{\partial x_{j} }}} \right] + G_{\text{k}} + G_{\text{b}} - \uprho \upepsilon - Y_{\text{M}} $$
(3)

and

$$ \frac{\partial }{\partial t}(\uprho \upepsilon ) + \frac{\partial }{{\partial x_{i} }}(\uprho v_{i} \upepsilon ) = \frac{\partial }{{\partial x_{j} }}\left[ {\left( {\upmu + \frac{{\upmu_{\text{t}} }}{{\upsigma_{\upepsilon } }}} \right)\frac{\partial \upepsilon }{{\partial x_{j} }}} \right] + C_{1\upepsilon } \frac{\upepsilon }{k}(G_{\text{k}} + C_{3\upepsilon } G_{\text{b}} ) - C_{2\upepsilon } \uprho \frac{{\upepsilon^{2} }}{k} $$
(4)

where \( \upepsilon \) is the turbulence dissipation rate, G k and G b are the generations of turbulence kinetic energy caused by the mean velocity gradients and buoyancy, respectively, and Y M is the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate. \( C_{1\upepsilon } \) = 1.44, \( C_{2\upepsilon } \) = 1.92, C μ = 0.09, σk = 1.0, and \( \upsigma_{\upepsilon } \) = 1.3.

Species transport:

$$ \frac{\partial }{\partial t}(\uprho y_{i} ) + \frac{\partial }{{\partial x_{j} }}(\uprho v_{j} y_{i} ) = - \frac{\partial }{{\partial x_{j} }}(J_{i} ) + R_{i} ,\quad i = 1, \ldots ,N - 1 $$
(5)

where y i is the mass fraction of each species, J i is the diffusion flux of species i calculated by Maxwell-Stefan equations, R i is net rate of production of species i by chemical reaction, and N is total number of species involved in the reaction.

Energy balance:

$$ \frac{\partial }{\partial t}(\uprho H) + \frac{\partial }{{\partial x_{i} }}(\uprho v_{i} H) = \frac{\partial }{{\partial x_{j} }}\left( {\Upgamma \frac{\partial H}{{\partial x_{j} }}} \right) + S_{\text{H}} $$
(6)

where Γ is the ratio of the effective viscosity and the Prandtl number, H is the total enthalpy defined by \( H = \sum_{i = 1}^{N} {H_{i} } y_{i} \) and S H is the source term (e.g., heat generated by the exothermic reaction).

Ideal gas law:

$$ p = \uprho RT $$
(7)

where R is the specific gas constant, or the molecular gas constant divided by the molecular weight of the gas.

In the modeling of HVOF thermal spray, it is very important to note that because of the high operating temperature, combustion products will dissociate into a number of species with low molecular weight, for example, OH and H and so forth (Ref 5, 13). The predicted temperature could be significantly higher if such a dissociation is not taken into account. Depending on the computational time, single or multistep reduced reaction chemistry models may be used. In the literature, different approaches have been used to model the reaction rate, including: (a) infinitely fast reaction rate (e.g., Ref 10, 13, 15, 16) or instantaneous chemical equilibrium at the entrance of the combustion chamber, (b) finite reaction rate in Arrhenius form (e.g., Ref 17-20), (c) finite reaction rate limited by turbulent mixing (e.g., Ref 11, 12, 21-25) or the reaction is faster than the mixing rate so that the overall combustion process is limited by the latter.

In many practical situations such as the HVOF thermal spray, the eddy-dissipation model describes the limiting rate, and thus knowledge of accurate Arrhenius rate data is not needed (Ref 12). Based on the fact that the gas residence time in the combustion chamber (convergent section of the nozzle) is much longer than the one in the subsequent sections, it is reasonable to assume that the reaction occurs primarily in the combustion chamber following a global one-step equilibrium chemistry model, which can be determined by minimizing the Gibbs free energy under constant enthalpy and constant pressure using existing equilibrium codes (Ref 26). The pressure can be measured at the operating conditions. Alternatively, if the mass flow rates of oxygen and fuel are available, a previously developed approach (Ref 11) can be used to determine the chamber pressure. Specifically, with the given oxygen and fuel flow rates, a combustion pressure is assumed, based on which a quasi-one-dimensional model is used to calculate the equilibrium composition and temperature at the combustion chamber. The total mass flow rate at the throat of the nozzle is then calculated, based on which the pressure is adjusted until the discrepancy between the calculated and the specified total mass flow rates falls below a user-specified tolerance (Ref 27).

The computational fluid dynamic (CFD) simulation is able to provide the detailed temperature and velocity information of the gas field. For example, Fig. 3 shows the temperature contour in the combustion chamber of the Diamond Jet 2700 gun (Ref 11). The function of air is clearly demonstrated; the hot flame is surrounded by the cooling air around the torch wall, thus protecting the hardware from being overheated. Figure 4 shows the contour and centerline profile of static pressure in the internal and external gas fields. The pressure gradually decreases from 6.2 bar in the combustion chamber to 0.6 bar (or a gage pressure of −0.4 bar) at the exit of the nozzle, which is close to a −0.3 bar gage pressure measured by the manufacturer (Ref 11). Because this pressure is less than the ambient pressure, the flow is underexpanded and a mach disk is formed downstream of the nozzle exit. The flow adjusts to the ambient pressure by a series of shock waves, which are usually observed experimentally.

Fig. 3
figure 3

Contour of static temperature in the combustion chamber (Ref 11)

Full size image
Fig. 4
figure 4

Contours of the static pressure in the Diamond Jet HVOF thermal spray gun (Ref 11)

Full size image

For a quasi-one-dimensional analysis, the assumptions of instantaneous equilibrium at the entrance of the combustion chamber and frozen flow along the nozzle can be used (Ref 28). The mathematical model accounting for wall friction and water cooling is described by (Ref 29):

$$ \frac{{{\text{d}}M^{2} }}{{M^{2} }} = \frac{{1 + [(\upgamma - 1)/2]M^{2} }}{{1 - M^{2} }}\left( { - 2\frac{{{\text{d}}A}}{A} + \uplambda \upgamma M^{2} \frac{{{\text{d}}x}}{D} + \frac{{1 + \upgamma M^{2} }}{{1 + [(\upgamma - 1)/2]M^{2} }}\frac{{{\text{d}}q}}{{c_{\text{p}} T}}} \right) $$
(8)
$$ \frac{{{\text{d}}T}}{T} = \frac{{(\upgamma - 1)M^{2} }}{{1 - M^{2} }}\left( {\frac{{{\text{d}}A}}{A} - \uplambda \frac{{\upgamma M^{2} }}{2}\frac{{{\text{d}}x}}{D} + \frac{{1 - \upgamma M^{2} }}{{(\upgamma - 1)M^{2} }}\frac{{{\text{d}}q}}{{c_{\text{p}} T}}} \right) $$
(9)

where A is the cross-sectional area perpendicular to the flow direction, D is the diameter of the nozzle, γ is the heat capacity ratio, and M is the mach number (note that v/M = a = \( \sqrt {\upgamma RT} \) is the sonic velocity. At the throat of the nozzle, where the flow area reaches the minimum, the mach number is 1). λ is the Darcy friction coefficient correlated as a function of the Reynolds number of the equivalent roughness of the wall by the Colebrook equation (Ref 30):

$$ \frac{1}{\sqrt \uplambda } = - 2\log_{10} \left( {\frac{\varepsilon /D}{3.72} + \frac{2.51}{Re\sqrt \uplambda }} \right) $$
(10)

The term −(dq/dx) is the heat-removal rate per unit length of the nozzle, which might be estimated by fitting experimental data and model prediction (Ref 31). Equations 8 and 9 are integrated simultaneously using the Runge-Kutta method.

For an even simpler analysis neglecting friction or cooling (this is reasonable from the combustion chamber to the nozzle throat in HVOF guns such as the Sulzer Metco Diamond Jet Hybrid 2700 (Sulzer Metco, Westbury, NY) and the Praxair-Tafa JP-5000 (Praxair Surface Technologies, Indianapolis, IN)), the following isentropic equations may also be used to relate the temperature, pressure, and density at two points along the nozzle (Ref 32):

$$ \frac{{T_{2} }}{{T_{1} }} = \frac{{1 + [(\upgamma - 1)/2]M_{1}^{2} }}{{1 + [(\upgamma - 1)/2]M_{2}^{2} }} $$
(11)
$$ \frac{{p_{2} }}{{p_{1} }} = \left\{ {\frac{{1 + [(\upgamma - 1)/2]M_{1}^{2} }}{{1 + [(\upgamma - 1)/2]M_{2}^{2} }}} \right\}^{[\upgamma /(\upgamma - 1)]} $$
(12)
$$ \frac{{\uprho_{2} }}{{\uprho_{1} }} = \left\{ {\frac{{1 + [(\upgamma - 1)/2]M_{1}^{2} }}{{1 + [(\upgamma - 1)/2]M_{2}^{2} }}} \right\}^{[1/(\upgamma - 1)]} $$
(13)
$$ \frac{{A_{2} }}{{A_{1} }} = \frac{{M_{1} }}{{M_{2} }}\left\{ {\frac{{1 + [(\upgamma - 1)/2]M_{2}^{2} }}{{1 + [(\upgamma - 1)/2]M_{1}^{2} }}} \right\}^{[(\upgamma + 1)/2(\upgamma - 1)]} $$
(14)

Based on the aforementioned relationships, it can be derived that the total mass flow rate is:

$$ \dot{m} = \frac{{p_{0} }}{{\sqrt {T_{0} } }}A_{\text{th}} \sqrt {\frac{{\upgamma \bar{M}_{\text{pr}} }}{{R_{\text{g}} }}\left( {\frac{2}{\upgamma + 1}} \right)^{[(\upgamma + 1)/(\upgamma - 1)]} } $$
(15)

where A th is the cross-sectional area at the throat (where the area is the minimum), R g is the molecular gas constant, \( \bar{M}_{\text{pr}} \) is the average molecular weight of the combustion products, and T 0 and p 0 are, respectively, the stagnation temperature and stagnation pressure in the combustion chamber. This equation clearly reveals that the mass flow rate and the combustion pressure are not independent, which explains why the combustion pressure should be solved using an iterative procedure when the flow rates of oxygen and fuel are provided. Table 1 shows a comparison between predicted and experimentally measured chamber pressures under various operating conditions of a Diamond Jet thermal spray gun using the approach developed in Ref 27. The discrepancy is generally less than 6%, which validates the assumption of chemical equilibrium in the chamber.

Table 1 Comparison of computational and experimental results (Ref 21) for a Diamond Jet thermal spray gun using a quasi-one-dimensional model (Ref 27)
Full size table

Equations 8 and 9 or 11 to 14 are only applicable in the internal flow field. For a one-dimensional analysis of the external field, empirical formulas might be correlated from experimental measurement (Ref 28, 33-36). Tawfik and Zimmerman provided the following correlation formulas for typical HVOF processing conditions (Ref 29):

$$ \frac{v}{{v_{\text{e}} }} = \left\{ {\begin{array}{*{20}c} {1,} \hfill & {x \le x_{\text{c}} } \hfill \\ {1 - \exp \left( {\frac{0.85}{{1 - x/x_{\text{c}} }}} \right),} \hfill & {x > x_{\text{c}} } \hfill \\ \end{array} } \right. $$
(16)
$$ \frac{{T - T_{\text{a}} }}{{T_{\text{e}} - T_{\text{a}} }} = \left\{ {\begin{array}{*{20}c} {1,} \hfill & {x \le x_{\text{c}} } \hfill \\ {1 - \exp \left( {\frac{1.25}{{1 - x/x_{\text{c}} }}} \right),} \hfill & {x > x_{\text{c}} } \hfill \\ \end{array} } \right. $$
(17)

where the subscripts “a” and “e” stand for ambient condition and nozzle exit condition, respectively, and x c is the potential core length (x c/D e = 4.2 + 1.1 \( M_{\text{e}}^{2} \), Ref 29). Figure 5 shows the axial profiles of gas velocity and static temperature along the centerline in a Metco Diamond Jet thermal spray process based on a simplified quasi-one-dimensional model (Ref 27, 37) and a CFD model (Ref 11). It can be seen that the general trends are similar, while the centerline temperature derived from the one-dimensional model is higher than the one from the CFD model. This is because the former is not able to handle the mixing of cold carrier gas and the hot combustion flame in the combustion chamber, which is multidimensional in nature.

Fig. 5
figure 5

Comparison of (a) axial gas velocity and (b) static temperature along the centerline solved using a simplified quasi-one-dimensional model (Ref 27, 37) and a CFD model (Ref 11)

Full size image

Particle Dynamics

The modeling of particulate phase in the HVOF thermal spray is typically based on the Lagrangian approach. First, the average distance between individual particles in the HVOF thermal spray process can be estimated based on the analysis of Crowe et al. (Ref 38). Specifically,

$$ \frac{{L_{\text{d}} }}{{d_{\text{p}} }} = \left[ {\frac{\uppi }{6}\frac{1 + \upkappa }{\upkappa }} \right]^{1/3} $$
(18)

where L d is the distance between two particles and κ is the ratio of particle loading to particle/gas density ratio. Based on a particle loading of 4% and a density ratio of 103 to 104, L d/d p is about 20-50, which implies that the individual powder particles are isolated from each other (Ref 37). Therefore, it is reasonable to assume that particle coagulation is negligible (Ref 11, 27), and thus the powder size distribution does not change during flight (Ref 22). In the modeling of particle dynamics, it is usually assumed that the major force acting on a particle in the HVOF thermal spray process is the drag force, and other forces, such as the Basset history term, gravitational force, forces caused by pressure gradients, and so forth, can be neglected (Ref 21, 39). With these assumptions, the particle motion along the axial direction in the Cartesian coordinates is described by:

$$ m_{\text{p}} \frac{{{{d}}v_{\text{p}} }}{{{{d}}t}} = \frac{1}{2}C_{\text{D}} \uprho_{\text{g}} A_{\text{p}} \left( {v_{\text{g}} - v_{\text{p}} } \right)\left| {v_{\text{g}} - v_{\text{p}} } \right|,\quad \frac{{{{d}}x_{\text{p}} }}{{{{d}}t}} = v_{\text{p}} $$
(19)

where m p, v p, d p, and x p are the mass, velocity, diameter, and position of the particle, respectively. A p is the projected area of the particle on the plane perpendicular to the flow direction. v g and ρg are the velocity and density of the gas. C D is the drag coefficient, which is a function of the local Reynolds number (Re) defined by Re = (d p|v g − v p|ρg)/μg, where μg is the gas viscosity (Ref 30). In the processing of nanostructured coatings, the particles are typically not spherical (Ref 16) and the corresponding shape factor can be taken into account in the C D calculation in this case (Ref 40, 41). Note that the particles experience forces from all three spatial directions and equations similar to Eq 19 should also be solved in the other two Cartesian coordinates.

Assuming spherical particles, the particle heating can be described by a partial different equation (Ref 42):

$$ \begin{aligned} \uprho_{\text{p}} c_{{p_{\text{p}} }} \frac{{\partial T_{\text{p}} (r,t)}}{\partial t} & = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \uplambda_{\text{p}} \frac{{\partial T_{\text{p}} (r,t)}}{\partial r}} \right),\quad 0 \le r \le r_{\text{p}} \\ B.C. \\ \frac{{\partial T_{\text{p}} (0,t)}}{\partial r} & = 0 \\ \uplambda_{\text{p}} \frac{{\partial T_{\text{p}} (r_{\text{p}} ,t)}}{\partial r} & = h(T_{\text{g}} - T_{\text{p}} (r_{\text{p}} ,t)) \\ \end{aligned} $$
(20)

where r p is the radius of the particle, λ is the thermal conductivity of the gas, and h is the heat-transfer coefficient correlated by the Ranz-Marshall empirical equation (Ref 30):

$$ h = \frac{{\uplambda_{\text{g}} }}{{d_{\text{p}} }}\left[ {2 + 0.6Re^{1/2} Pr^{1/3} } \right] $$
(21)

where the Prandtl number (Pr) is calculated by \( Pr = c_{{p_{\text{g}} }} \upmu_{\text{g}} /\uplambda_{\text{g}} \) where \( c_{{p_{\text{g}} }} \), μg, and λg are the heat capacity, viscosity, and thermal conductivity of the gas, respectively.

In general, particles in the HVOF thermal spray process experience melting and solidification (Ref 42). In such a case, Eq 20 should be modified to account for the propagation of the melting/solidification front toward/from the particle center. This is a Stefan problem with moving boundaries (Ref 25, 43). Further work on the breakup, cooling, and solidification of metal particles is also available in the literature (Ref 44, 45). For good heat-conducting particles, if the Biot number (Bi = hd p/6λp) is less than 0.1, the internal particle temperature gradients can be ignored. In such a case, Eq 20 can be simplified to the following form (Ref 27):

$$ hA^{\prime}_{{\text{p}}} (T_{{\text{g}}} - T_{{\text{p}}} ) = \left\{ {\begin{array}{ll} {m_{{\text{p}}} c_{{{\text{p}}_{{\text{p}}} }} \frac{{{\text{d}}T_{{\text{p}}} }}{{{\text{d}}t}},} \hfill & {(T_{{\text{p}}} < T_{{\text{m}}} ,f = 0)} \hfill \\ {\Updelta H_{{\text{m}}} m_{{\text{p}}} \frac{{{\text{d}}f_{{\text{p}}} }}{{{\text{d}}t}},} \hfill & {(T_{{\text{p}}} = T_{{\text{m}}} )} \hfill \\ {m_{{\text{p}}} c_{{{\text{p}}_{{\text{l}}} }} \frac{{{\text{d}}T_{{\text{p}}} }}{{{\text{d}}t}},} \hfill & {(T_{{\text{p}}} > T_{{\text{m}}} ,f = 1)} \hfill \\ \end{array} } \right.$$
(22)

where \( A^{\prime}_{\text{p}} \) is the surface area of the particle, T m is the melting point of the particle, ΔH m is the enthalpy of melting, and f p is the melting ratio, or the ratio of the melted mass to the total mass of the particle (0 ≤ f p ≤ 1). A numerical integration method is provided in Ref 27 for the particle heating/cooling with phase transitions. As mentioned previously, because of the high turbulence in the fluid flow, the particles are likely to be affected by the instantaneous fluctuation in the fluid phase. However, either the RANS equations or the quasi-one-dimensional model solves only for the mean fluid velocity. In order to account for the turbulent dispersion of particles, the stochastic tracking approach can be used in which a random velocity fluctuation term is added to the mean gas phase velocity (Ref 22). The fluctuation velocity component in each spatial direction is kept constant over the characteristic lifetime of the eddies and is updated in each time interval. Each run of the above discrete random walk model provides a snapshot profile of particle motion in the gas field. A statistical effect of the turbulence on particle dispersion may be obtained by computing the particle trajectories in this manner for a sufficiently large number of independent simulations.

Key conclusions from the modeling of particle dynamics (Ref 11, 22, 27, 46, 47) are summarized in the following paragraphs.

Particles are affected by the gas field to different extents depending on their size. Small particles may be accelerated and heated up to very high velocities and temperatures. However, because of the entrainment of the ambient air in the external field, the gas velocity and temperature decay downstream of the potential core (Fig. 5). As a result, the velocities and temperatures of small particles drop more sharply than those of larger particles because of their smaller momentum and thermal inertias. In some cases, small particles may reach the melting point in a short period of time and become fully melted during flight. However, they may eventually be in a liquid/solid or even solid state as they reach the substrate. For particles of large sizes, the periods for acceleration and heating are both longer, and the velocity (or temperature) profiles become nearly flat after their velocity and temperature are higher than those of the gas. A typical profile of particle velocity, temperature, and melting degree is shown in Fig. 6 (Ref 37).

Fig. 6
figure 6

Profiles of (a) particle velocity and (b) temperature along the centerline (Ref 22)

Full size image

The effect of particle turbulence dispersion is shown in Fig. 7 (Ref 22). This snapshot profile of the particle trajectories in the flow field is obtained by feeding 100 particles to the HVOF thermal spray system from 5 uniformly distributed radial locations in the carrier nitrogen stream and 20 uniformly distributed sizes between 1 and 20 μm. It is seen that although most particles are highly concentrated in the centerline inside of the HVOF torch, the particles tend to expand toward the radial direction when they approach the substrate, due to substantial radial gas velocities (Ref 22). Small particles are significantly influenced by the gas flow pattern close to the substrate. They are also sensitive to the fluctuations in the gas phase and have more random trajectories. Some of them might even follow the gas stream and will not be deposited on the substrate. Note that submicron particles might be deposited on the substrate by thermophoretic force; however, this force is not as strong as the turbulent dispersion. For this reason, particles used in the HVOF thermal spray coating process cannot be too small. This is true even for the processing of nanostructured coatings, in which the powders comprise micron-sized agglomerates with grain size below 100 nm.

Fig. 7
figure 7

Trajectories of different size particles injected at different radial locations in the flow field (Ref 22)

Full size image

The particle velocity and temperature at impact are strongly dependent on particle size and also on the trajectory that the particle takes. The maximum of particle velocity and temperature generally occur at median particle sizes. When the same size particles take different trajectories (due to differences in the initial injection location and random fluctuations in the gas phase), they might achieve different velocities and temperatures upon impact, see Fig. 8. This behavior is consistent with experimental observations of Zhao et al. (Ref 48).

Fig. 8
figure 8

(a) Axial particle velocity and (b) temperature upon impact as a function of particle size (Ref 22)

Full size image

It is also demonstrated in the modeling study that the particle temperature can be strongly affected by the axial injection location and initial injection velocity while the particle velocity is more robust with respect to these two parameters. This is also validated by the studies of Hanson et al. (Ref 49, 50). However, the axial injection location is not a variable to be adjusted in real time, and therefore its application in automatic control might be limited.

While mathematical modeling can provide general trends and important insight into the behavior of the HVOF thermal spray process, a perfect match between model prediction and measurement is very difficult to obtain. For example, the CFD simulations typically underpredict the particle temperature (Ref 6), partly due to the negligence of exothermic particle oxidation (Ref 12) and the contribution of viscous dissipation to the two-phase heat-transfer coefficient (Ref 51). A particle oxidation model has been recently accounted for in the CFD model by Zeoli et al. (Ref 52).

Powder Size Distribution

It is very important to note that the powder particles used in the HVOF thermal spray process are typically polydisperse, and therefore the powder size distribution is an important parameter that should be accounted for in the evaluation of the average in-flight particle characteristics. Two commonly used two-parameter powder size distribution functions in HVOF thermal spray are log normal and Rosin-Rammler. A log normal powder size function has following form (Ref 53):

$$ f(d_{\text{p}} ) = \frac{1}{{\sqrt {2\uppi } \upsigma d_{\text{p}} }}\exp \left[ { - \frac{{(\ln \,d_{\text{p}} - \upmu )^{2} }}{{2\upsigma^{2} }}} \right] $$
(23)

where μ and σ2 are two dimensionless parameters corresponding to the mean and the variance of ln d p, which obeys the normal distribution. For particles that are log normally distributed, μ and σ can be determined using (Ref 46, 47):

$$ \begin{aligned} \upmu = & \ln \root{3}\of{{d_{10} d_{50} d_{90} }} - 1.831\left( {\ln \sqrt {\frac{{d_{90} }}{{d_{10} }}} } \right)^{2} \\ \upsigma = & 0.781\,\ln \sqrt {\frac{{d_{90} }}{{d_{10} }}} \\ \end{aligned} $$
(24)

where d 10, d 50, and d 90 are three characteristic diameters that can be obtained experimentally (Ref 2).

The Rosin-Rammler powder size distribution function is:

$$ f(d_{\text{p}} ) = \frac{n}{{\bar{d}_{\text{p}} }}\left( {\frac{{d_{\text{p}} }}{{\bar{d}_{\text{p}} }}} \right)^{n - 1} \exp \left[ { - \left( {\frac{{d_{\text{p}} }}{{\bar{d}_{\text{p}} }}} \right)^{n} } \right] $$
(25)

or

$$ M_{{d_{\text{p}} }} = \exp \left[ { - \left( {\frac{{d_{\text{p}} }}{{\bar{d}_{\text{p}} }}} \right)^{n} } \right] $$
(26)

where \( M_{{d_{\text{p}} }} \) is the retained weight fraction (weight fraction of particles with diameter greater than d p), \( \bar{d}_{\text{p}} \) is the mean particle size, and n is the spread factor. n and \( \bar{d}_{\text{p}} \) in the Rosin-Rammler distribution function are the slope and the inverse of the exponential of the intercept slope ratio of the straight line represented by ln d p versus ln(−ln \( M_{{d_{\text{p}} }} \)) (Ref 22).

Because of the polydispersity in the size distribution and the strong effect of particle size on particle velocity and temperature, it is more appropriate to relate the coating properties with volume-averaged powder properties \( \left( {\overline{PP} } \right) \) instead of a single particle size because larger particles have a stronger influence on coating properties than smaller ones. The volume-averaged powder properties are defined as:

$$ \overline{PP} = \frac{{\int_{{d_{\text{lb}} }}^{{d_{\text{ub}} }} {\frac{1}{6}\uppi d_{\text{p}}^{3} PP(d_{\text{p}} )f(d_{\text{p}} ){\text{d}}(d_{\text{p}} )} }}{{\int_{{d_{\text{lb}} }}^{{d_{\text{ub}} }} {\frac{1}{6}\uppi d_{\text{p}}^{3} f(d_{\text{p}} ){\text{d}}(d_{\text{p}} )} }} $$
(27)

where d lb and d ub are the lower and upper bounds in the particle size such that the denominator is larger than 0.99.

Particle Impact and Coating Growth

Splat formation and coating growth have been studied extensively (Ref 6, 54, 55), and a comprehensive review has been provided by Fauchais et al. (Ref 56) to summarize the effect of particle properties (temperature, velocity, molten state, oxidization state, etc.) and substrate conditions (roughness, composition, crystallinity, etc.) on particle flattening, splashing, and solidification. Most of the available research work is based on fully melted particles (which is typical of plasma spray processes), which might not reflect the fact that particles at impact on the substrate in HVOF thermal spray may be in mixed melting states (fully melted, partially melted, or solid) due to different sizes and different trajectories in the gas flow field. This has been substantiated by both experimental studies (Ref 57) and numerical simulations (Ref 11, 27). Moreover, in the HVOF thermal spray processing of carbides with binding metals, such as the WC-Co powders, only the metals may be in a molten state because the gas temperature in a conventional HVOF thermal spray process is not high enough for melting carbides, which have high melting points (e.g., 3143 K for tungsten carbide) (Ref 58). Ivosevic et al. (Ref 42) studied the deformation of HVOF sprayed polymer particles using the volume of fluid (VoF) method and found that when particles are partially melted, the internal temperature distribution has a significant effect on the final shape of the splat. Their mathematical model successfully explained the experimentally observed “fried-egg” shape of the splat, which features a low-temperature, nearly hemispherical core located in the center of a thin disk (Ref 42). Therefore, to simulate the coating growth in HVOF sprayed coatings, it is necessary to account for partially or unmelted particles.

A rule-based stochastic simulation approach was developed for the formation of HVOF sprayed coatings in which the particles of mixed melting states are accounted for (Ref 59). The general procedure is shown in Fig. 9. Specifically, it is assumed that the coating formation process is a sequence of independent discrete events of each individual particle landing on the previously formed coating layer. The powder size and landing location are derived from random number generators, which follow the powder size distribution function and a uniform distribution function (due to the movement of the HVOF thermal spray gun), respectively. The particle properties upon impact are then determined based on the gas and particle models presented previously. The splat is formed and added to the previously deposited coating layer following appropriate rules discussed in the next paragraph. The particle deposition is repeated until a desired coating thickness is reached. The program then calculates the coating porosity, surface roughness, and deposition efficiency.

Fig. 9
figure 9

Multiscale modeling of the HVOF thermal spray process (Ref 9)

Full size image

The rules governing the particle deformation and coating growth are summarized (Ref 59):

  • The deformation of fully melted particles follows the law of Madejski (Ref 60):

    $$ \xi = \frac{{D_{\text{s}} }}{{d_{\text{p}} }} = \xi (Re,We,Pe) $$
    (28)

    where D s is the diameter of the thin disk formed by the particle and ξ is the flattening ratio that depends on several dimensionless parameters characterizing the impact and spreading processes: (a) the Reynolds number, which represents the viscous dissipation of the inertia forces, (b) the Weber number, which quantifies the conversion of the kinetic energy into surface energy, and (c) the Peclet number, which expresses the freezing rate. For partially melted particles, this assumption is modified such that the unmelted part will form a hemisphere with the equivalent volume and the melted part will form a ring around this hemisphere, whose flattening ratio can be calculated using the same formula, see Fig. 10. This rule is based on experimental observations (Ref 42).

    Fig. 10
    figure 10

    Deformation of partially melted particle upon impact on the substrate (Ref 59)

    Full size image

  • When a particle hits the substrate, the melted part of the particle will fit to the surface as much as possible. The splat will move forward until it is in close contact with the previously deposited coating surface.

  • If the unmelted part of a partially melted particle hits at the point of the previously deposited layer that is formed by an unmelted particle, particle rebound might occur and consequently a hole is formed in the center of the disk. Otherwise, it will attach on the coating surface as a hemisphere.

  • If the splat comes to a vertical drop during spreading, the ratio of the splat that has not been settled down will be calculated. If the step does not continue with a gap that can be covered by the splat, the splat will break or cover the corner of the step according to the ratio and the height of the step. Otherwise, the gap will be covered by the splat and a pore will be formed.

  • If the splat encounters a dead end, it will first fill the available space, and then flow over the outer surface depending on the remaining volume.

The effect of melting state on the coating microstructure is shown in Fig. 11 (Ref 11). When all the particles are fully melted, an ideal lamellar microstructure is formed. However, under normal HVOF processing conditions, many particles might be partially melted or even unmelted. When these particles are embedded in the coating, the microstructure and resulting physical and mechanical properties could be different. The fact that the particles are not necessarily to be fully melted to achieve excellent coating microstructure is consistent with practice. This is very important for the fabrication of nanostructured coatings, since the nanostructure in the unmelted particles is preserved during flight. However, under certain conditions where the particle melting ratio is very low, unmelted particles may bounce off the substrate, resulting in a high-porosity coating with a low deposition efficiency.

Fig. 11
figure 11

Simulated microstructure of coatings formed by fully melted particles and particles with mixed melting states (Ref 11)

Full size image

Several results from the stochastic simulations of coating growth have been verified by experimental studies (Ref 59). For example, the simulation pointed out that a high melting degree (which occurs at an equivalence ratio of about 1.2, or a fuel-rich condition, where the gas and particle temperatures are the highest) and a high total mass flow rate would enhance a low coating porosity. This is validated by the studies of NiWCrBSi coatings processing using a Praxair-TAFA JP-5000 HVOF thermal spray system (TAFA Inc., Concord, NH, acquired by Praxair Surface Technologies, Indianapolis, IN) (Ref 61). Similar conclusions have been drawn in NiAl coatings processing using a UTP TopGun HVOF gun (UTP, Bad Krozingen, Germany) (Ref 62) and in steel coatings processing using a Praxair-TAFA JP-5000 HVOF gun (Ref 50). The simulation also shows that a better particle melting condition would enhance the deposition efficiency, which is consistent with experimental studies (Ref 50, 62, 63).

A comparison of simulation results (Ref 11) with experimental studies (Ref 50) shows that the porosity predicted by the model is higher than the experimentally measured value under similar operating conditions. One possible reason is that the CFD model usually underpredicts particle temperature (Ref 12). Further development is still necessary to more accurately predict coating microstructure and resulting properties from macroscopic operating conditions using multiscale models. For example, residual stress is a key criterion of coating property that may be affected by particle characteristics (Ref 63-66). Finite element analysis of residual stress of HVOF sprayed coating has been developed (Ref 67, 68). However, the effect of partially molten particles on residual stress is yet to be explicitly accounted for.

Control of HVOF Thermal Spray

As pointed out by Moreau (Ref 69), some automatic control systems have been developed and implemented in the thermal spray processing to regulate variables such as gas flow and material feed rates, substrate temperature, and robot trajectory. However, the more challenging task is what and how control actions should be taken to compensate for a drift in the particle characteristics observed in the processing. This requires a fundamental understanding of the relationship between manipulated inputs (i.e., key operating conditions) and controlled outputs (i.e., particle properties at the point of impact on the substrate) derived from off-line parametric analysis (e.g., plasma spray, Ref 70 and HVOF spray, Ref 49, 71) as well as the integration of real-time diagnostics and control algorithms in a feedback loop. Current research and development of online diagnostic and control systems are mainly focused on plasma spray processes, for example, real-time diagnostics and control of particle velocity and temperature in plasma spray using PID (Ref 72) and using artificial neural networks and fuzzy logic (Ref 73, 74). For the HVOF thermal spray process, a feedback control system is shown in Fig. 12. In such a closed-loop system, the particle information from the online measurement system is compared with the desired set point. The difference is sent to the feedback controller, which adjusts the processing parameters until the difference becomes zero. The development of such a feedback control system would require online measurement and diagnostic techniques, control-relevant parametric analysis as well as controller design and implementation.

Fig. 12
figure 12

A schematic of feedback control of HVOF thermal spray

Full size image

A variety of online sensing and diagnostic tools have been developed for the thermal spray processes to directly measure gas enthalpy and particle characteristics. For example, DPV-2000 (Tecnar Automation, Saint-Bruno, QC, Canada) is a commercial optical sensing device that provides online measurement of individual particle characteristics including temperature (1000-4000 °C, precision: 3%), velocity (5-1200 m/s, precision: 3%) and size (10-300 μm). The working principle of DPV-2000 is based on two-wavelength pyrometry and a dual-slit optical device (Ref 75). Due to the presence of a photomask between the two slits, a particle passing the measurement volume will generate a signal with two-peaks. This signal is then transmitted through an optical fiber bundle to the detection module, where the light passes through a dichroic mirror and two interference band-pass filters (around 790 and 990 nm, respectively) and is then imaged on two photodetectors. The signals from the photodetectors are amplified, filtered, and transmitted to the control module where the particle characteristics are calculated. Specifically, the particle velocity is calculated from the distance between the image of the two slits in the measurement volume and the time-of-flight between the two peaks of the particle signal. The temperature is deduced from the ratio of signals from the two photodetectors (or energies radiated at the two wavelengths) with the assumption that the particles behave as gray bodies. The diameter is calculated from the signal at one wavelength after a calibration procedure. The analysis rate of DPV-2000 can be up to 4000 particles/s, depending on the spraying conditions. If supplemented with CPS-2000, the sensing system is able to characterize cold particles that are otherwise not detected. The CPS-2000 is a cold particle sensor that employs a diode laser tuned on one of the pyrometer’s wavelength to characterize the cold particles. Similar techniques have been developed by Idaho National Laboratory (Ref 76-79). The particle size and velocity are measured from a laser-particle sizing system and a dual crossed-beam laser Doppler velocimeter. The temperature measurement is also based on the two-color pyrometry. Both ensemble and single-particle techniques are available to provide either time-resolved/spatially averaged or spatially resolved/time-averaged information. Oseir Ltd. (Tampere, Finland) also developed a commercial product (SprayWatch) that uses a high-speed charge-coupled device (CCD) camera to measure the particle velocity and a two-color pyrometer to measure the particle temperature (Ref 80). This system is able to analyze particle characteristics of the entire jet when only the averaged particle information is provided.

The online diagnostic techniques supplemented with other measurement tools have significantly facilitated the development of process maps for HVOF process optimization. These experimental investigations studied the effect of operating parameters including gun type, fuel type, feedstock type and size, combustion pressure, fuel/oxygen ratio, spray distance on the particle temperature, velocity, melting ratio, oxidant content and the resulting coating microstructure, porosity, hardness, wear abrasion, and corrosion resistance (e.g., Ref 3, 28, 34, 48-50, 61, 62, 65, 71, 81-92). The experimental studies have been supplemented by CFD modeling efforts (Ref 10-13, 15-21, 23), which provide fundamental understanding of the gas dynamics, particle in-flight, and impact. The studies reveal that particle characteristics upon impact on the substrate (i.e., velocity, temperature, and melting degree) are key parameters that affect coating porosity, bond strength, and residual stress. To develop a feedback control system for the HVOF thermal spray process, it is necessary to choose the processing parameters that can be manipulated in real time to suppress the variation in these particle characteristics. It is widely acknowledged that the particle velocity and temperature (or melting degree) can be almost independently regulated by manipulating pressure in the combustion chamber and the fuel/oxygen ratio (Ref 27, 34), respectively. Both of them are functions of the flow rates of fuel and oxygen (the dependence of chamber pressure on gas flow rates is shown in Eq 15). Therefore, the manipulated input can be chosen to be the gas flow rates. The effect of gas flow rates on particle velocity and temperature is shown in Fig. 13. The baseline conditions used in the analysis are the recommended processing conditions for WC-Co coatings (Ref 11). When the total mass flow increases from 50 to 150% of its baseline value, the velocity does not change much but the density increases linearly. As a result, the gas momentum flux \( \left( {\uprho v_{\text{g}}^{2} } \right) \) is tripled, which implies a significant increase in the drag force for particle motion. This is because the drag force is roughly proportional to \( \uprho v_{\text{g}}^{2} \) if v p ≪ v g. [Strictly speaking, the drag force would not increase by as high as three times because of the change in C D. In fact, based on a drag formula C D = (24/Re) (1 + 0.15Re 0.687) valid for Re < 1000 (Ref 30), one can derive that F D = (1/2)C Dρg A p(v g − v p)| v g − v p| = 3πμd p (v g − v p)(1 + 0.15Re 0.687). Therefore, the drag force might be only doubled at most]. However, the gas temperature, difference of which from the particle temperature provides the driving force for particle heating, increases about only 4%. When the total mass flow rate is fixed, the gas temperature varies with the fuel/oxygen ratio with an optimal value slightly larger than the stoichiometric value, and a change in the fuel/oxygen ratio with a fixed total mass flow rate has little effect on the gas pressure as well as on the gas momentum flux. Similar experimental studies are shown in Fig. 14 (Ref 71). In the control of HVOF spray, it should be noted that the gas temperature varies only about 12-13% in the equivalence ratio range of interest (0.55-1.8; the peak temperature occurs at an equivalence ratio of around 1.2, corresponding to a fuel rich condition), which suggests that the window for particle temperature control in the HVOF thermal spray is rather narrow. This is different from the plasma spray process where the particle temperature can be adjusted in a wider range by manipulating the torch current (Ref 72).

Fig. 13
figure 13

Influence of (a) total mass flow rate and (b) equivalence ratio on the gas properties at the throat of the nozzle. Normalized based on a baseline condition (Ref 37)

Full size image
Fig. 14
figure 14

(a) Velocity and (b) temperature of aluminum particles as a function of total mass flow rate and fuel/oxygen ratio using Praxair HV-2000 spray gun with propylene as the fuel (Ref 71)

Full size image

Based on model predictions and available experimental observations, the control problem for the HVOF process is formulated as the one of regulating the volume-based averages of velocity and temperature (or melting degree) of particles at impact on the substrate by manipulating the flow rates of fuel and oxygen at the entrance of the HVOF thermal spray gun. The volume-averaged instead of number-averaged particle properties are chosen in the control formulation because large particles contribute more to the coating volume. The information of individual particle size should be available in order to calculate the volume-based particle characteristics upon impact. In the absence of particle size measurements, the control objective could be the number-averaged particle properties, similar to the work of Fincke et al. (Ref 72) in feedback control of plasma spray. The manipulation of combustion pressure and equivalence ratio is realized by adjusting the flow rate of fuel, u 1 (t), and oxygen, u 2 (t). Owing to the almost decoupled nature of the manipulated input/controlled output pairs, two proportional integral (PI) controllers were proposed in Ref 27 and 47 to regulate the process. Specifically, the controllers have the following form:

$$ \begin{aligned} \dot{\zeta }_{i}& = y_{{{\text{sp}}_{i} }} - y_{i} ,\quad \zeta_{i} (0) = 0,\ i = 1,2 \\ u^{\prime}_{i}& = K_{{{\text{c}}_{i} }} \left[ {\left( {y_{{{\text{sp}}_{i} }} - y_{i} } \right) + \frac{1}{{\tau_{{{\text{c}}_{i} }} }}\zeta_{i} } \right] + u^{\prime}_{{0_{i} }} ,\quad i = 1,2 \\ \left\{ {u_{1} ,u_{2} } \right\}& = f(u^{\prime}_{1} ,u^{\prime}_{2} ) \\ \end{aligned} $$
(29)

where \( y_{{{\text{sp}}_{i} }} \) is the desired set-point value and y i is the value of the output obtained from the measurement system (y 1 is the volume-based average of particle velocity, and y 2 is the volume-based average of particle temperature or melting degree), \( u_{1}^{\prime } \) is the combustion pressure and \( u_{2}^{\prime } \) is the equivalence ratio. f is the mapping between the flow rates and the chamber pressure as well as the equivalence ratio. \( K_{{{\text{c}}_{i} }} \) is the proportional gain and \( \tau_{{{\text{c}}_{i} }} \) is the integral time constant. If the gas phase measurement is available, a model-based scheme can be used to estimate the particle properties through the dynamic particle in-flight model (Ref 93). Interested readers may also refer to literature for the design of model-based feedback control systems employing nonlinear control techniques for various particulate processes (Ref 94-100).

Closed-loop simulations under the control scheme of Eq 29 have been carried out to demonstrate the effectiveness of the proposed control formulation (Ref 37). It is assumed in the computer simulation that the responses of gas and particle dynamics to the change of gas flow rates are very fast, which is reasonable for such a supersonic flow. With this simplification, it has been demonstrated that the feedback controllers are very effective with respect to set-point changes in both particle velocity and temperature (i.e., 5% increase in both particle velocity and melting degree). As seen in Fig. 15, both the flow rates of oxygen and fuel increase in order to have a higher particle velocity. However, the temperature increases and exceeds its desired value because of the increased chamber pressure. As a result, the changing rate of oxygen flow becomes slower than that of fuel after a short time, which lowers the equivalence ratio and drives the temperature down to its set point. Figure 16 demonstrates the response of the feedback controller in order to maintain the same particle velocity and temperature levels in the presence of a 10% decrease in the spray distance (process disturbance). The particle velocity does not change much while the particle temperature increases significantly. Under feedback control, the manipulated inputs drive the process outputs to their original steady-state values in 10 s, which demonstrates the robustness of the controller.

Fig. 15
figure 15

Profiles of (a) controlled outputs (average particle velocity and melting ratio) and (b) manipulated inputs (flow rates of propylene and oxygen) under the request of 5% increase in particle velocity and 5% increase in melting ratio (Ref 37)

Full size image
Fig. 16
figure 16

Profiles of (a) controlled outputs (average particle velocity and melting ratio) and (b) manipulated inputs (flow rates of propylene and oxygen) in the presence of 10% decrease in spray distance (Ref 37)

Full size image

Concluding Remarks

The HVOF thermal spray is an enabling technique for the processing of functional coatings. Mathematical modeling has been an excellent complement to experimental studies to provide systematic understanding of the underlying physics of the process and to enhance coating performance through optimized system design and operation. However, detailed model development is still needed in some areas, for example, the oxidation, melting, and solidification of particles during flight, deformation of partially melted and unmelted particles, and its effect on coating microstructure evolution and residual stress, especially when the particles are of irregular shape (which is common in the processing of nanostructured particles). Further modeling efforts should also include the validation and refining of mathematical models to better match experimental measurements (e.g., gas-particle heat transfer accounting for viscous dissipation).

In addition to modeling, feedback control systems have been designed in which the particle velocity and temperature are controlled by adjusting the flow rates of oxygen and fuel, and their effectiveness and robustness have been tested through computer simulations. Further research efforts should focus on the development of a demonstration prototype by integrating real-time diagnostics and feedback control systems in an experimental HVOF thermal spray process.