1 Introduction

For scientists and engineers, the analysis of nonlinear dynamical systems is an important field of research since the solutions of these systems can exhibit counterintuitive and sometimes unexpected behavior. To obtain useful information from these systems, the multiple scales perturbation method can play an important role.

Nowadays, the multiple time-scales perturbation method for differential equations is well developed, well accepted, and a very popular method to approximate solutions of weakly nonlinear differential equations. For difference equations, this perturbation method is recently improved by Van Horssen [1] such that it can be applied to a large class of problems. In [1], a version of the multiple scales perturbation method is presented in a complete “difference operator” setting. This method can for instance be applied to problems for systems with time-varying masses. Examples of such systems can be found in robotics, rotating crankshafts, conveyor systems, excavators, cranes, biomechanics, and in fluid-structure interaction problems [2, 3]. The oscillations of electric transmission lines and cables of cable-stayed bridges with water rivulets on the surface are also examples of time-varying dynamic systems [4]. For these mechanical constructions, the 1-mode Galerkin approximation of the continuous model will lead to a single degree-of-freedom oscillator (sdofo)-equation. These sdofos are considered to be representative models for testing numerical methods and for studying forces which are acting on the system [5]. In [6] and [7], the forced vibrations of a linear sdofo with a time-varying mass were studied. The forced vibrations are due to small masses which are periodically hitting and leaving the oscillator with different velocities. In [8], the vibrations of a damped, linear sdofo with a time-varying mass were studied, and the stability properties for the free, and for the forced vibrations (due to small masses and an external force (for instance, a windforce)) were presented for various parameter values. A system of two nonlinear ordinary difference equations (OΔEs) is obtained when also windforces are included in the model. To analyze the system of OΔEs, numerical methods were used. In the analysis, a small parameter ε was defined for the relative mass which is added periodically. Then, also a perturbation method can be applied. In this paper, we are going to study similar systems of OΔEs. It will be shown how the improved multiple scales perturbation method can be applied to such systems of OΔEs. Moreover, several bifurcation problems will be studied in detail.

2 Problem definition

In this paper, we consider a weakly nonlinear perturbed system of two first-order OΔEs. A nice representation for such a system can be written as

$$\lefteqn{\begin{cases}x_{n+1}=f_{1,0}(x_n,y_n)+\varepsilon f_{1,1}(x_n,y_n)+O(\varepsilon ^2),\\y_{n+1}=f_{2,0}(x_n,y_n)+\varepsilon f_{2,1}(x_n,y_n)+O(\varepsilon^2),\end{cases}} $$
(1)

where

$$\begin{cases}f_{1,0}(x_n,y_n)=a_{11}x_n+a_{12}y_n,\\f_{2,0}(x_n,y_n)=a_{21}x_n+a_{22}y_n,\\f_{1,1}(x_n,y_n)=b_{10}+b_{11}x_n+b_{12}y_n+b_{13}x_n^2\\\hspace{2cm}+\,b_{14}x_ny_n+b_{15}y_n^2+b_{16}x_n^3\\\hspace{2cm}+\,b_{17}x_n^2y_n+b_{18}x_ny_n^2+b_{19}y_n^3,\\f_{2,1}(x_n,y_n)=b_{20}+b_{21}x_n+b_{22}y_n+b_{23}x_n^2\\\hspace{2cm}+\,b_{24}x_ny_n+b_{25}y_n^2+b_{26}x_n^3\\\hspace{2cm}+\,b_{27}x_n^2y_n+b_{28}x_ny_n^2+b_{29}y_n^3,\\\end{cases} $$
(2)

and where a ij and b ij are real constants, and 0<ε≪1.

In our work, by using the multiple scales perturbation method in terms of difference operators, we will obtain secular-free solutions of system (1) which can be used to analyze, for example, systems with time-varying masses. Furthermore, our analysis will give a complete bifurcation analysis of system (1) when the eigenvalues of matrix

(3)

are complex valued. This analysis strongly depends on the eigenvalues of the problem when ε=0. The most interesting case from the applicational point of view is the case when the eigenvalues of matrix A are complex valued with nonzero real and imaginary parts, and are in modulus smaller than or equal to 1. The analysis in this paper will be restricted to this case.

3 The multiple scales perturbation method for OΔEs

In this section, the multiple scales perturbation method for OΔEs will be presented in a complete “difference operator” setting. Before introducing this method, several operators have to be defined (and motivated). The well-known shift operator E, the difference operator Δ, and the identity operator I are defined as follows:

$$\lefteqn{\begin{aligned}&Ex_n=x_{n+1},\quad\Delta x_n=x_{n+1}-x_n,\quad\mbox{and}\\&Ix_n=x_n.\end{aligned}} $$
(4)

The relationship between these operators easily follows from (4):

$$E=\Delta+I \quad\Leftrightarrow\quad\Delta=E-I. $$
(5)

The solution of a weakly perturbed OΔE usually contains a rapidly changing part in n, and a slowly changing part in n. This is usually referred to as multiple scales behavior. It should be observed that these notations are similar to the ones used in the multiple timescales perturbation method for ODEs. Now it is assumed that x n =x(n,εn). This assumption implies that the solution of the OΔE depends on two variables. So, the OΔE actually becomes a partial difference equation. For that reason also, partial shift operators and partial difference operators have to be defined. The following definitions are proposed [1]:

$$\lefteqn{\begin{aligned}[c] E_1x(n,\varepsilon n)&=x(n+1,\varepsilon n),\\E_\varepsilon x(n,\varepsilon n)&=x \bigl(n,\varepsilon(n+1) \bigr),\\\Delta_1x(n,\varepsilon n)&=x(n+1,\varepsilon n)-x(n,\varepsilon n)\\&=(E_1-I)x(n,\varepsilon n),\\\Delta_\varepsilon x(n,\varepsilon n)&=x \bigl(n,\varepsilon(n+1)\bigr)-x(n, \varepsilon n)\\&=(E_\varepsilon-I)x(n,\varepsilon n).\end{aligned}} $$
(6)

From (4), (5), and (6), it follows that (assuming x n =x(n,εn)):

(7)

And so, it follows that

$$\Delta=\Delta_1+\Delta_\varepsilon+\Delta_1\Delta_\varepsilon,\quad\mbox{and}\quad E=E_1E_\varepsilon. $$
(8)

Furthermore, for the partial difference operators Δ1 and Δ ε it is assumed that [1]:

$$\lefteqn{\begin{aligned}[c]&\Delta_1x(n,\varepsilon n)=O \bigl(x(n,\varepsilon n) \bigr),\quad \mbox{and}\\&\Delta_\varepsilon x(n,\varepsilon n)=O \bigl (\varepsilon x(n,\varepsilon n) \bigr).\end{aligned}} $$
(9)

In fact, this assumption (9) implies that the variation in the dependent variable x(n,εn) with respect to one of the independent variables is proportional to the product of the absolute value of the dependent variable and the variation in that particular independent variable.

When x n depends on m+1 scales, the given definitions can readily be generalized, yielding (for j=0,1,…,m):

$$\lefteqn{\begin{aligned}[c]&x_n=x \bigl(n,\varepsilon n,\varepsilon^2n,\ldots,\varepsilon^mn \bigr),\\&E_{\varepsilon^j}x \bigl(n,\ldots,\varepsilon^mn \bigr)\\&\quad=x \bigl(n,\varepsilon n,\ldots,\varepsilon^j(n+1),\ldots,\varepsilon^mn\bigr),\\&\Delta_{\varepsilon^j}x \bigl(n,\ldots,\varepsilon^mn\bigr)=(E_{\varepsilon^j}-I)x \bigl(n,\ldots,\varepsilon^mn \bigr),\\&E=E_1E_\varepsilon E_{\varepsilon^2}\cdots E_{\varepsilon^m},\\&\Delta=(\Delta_1+I) (\Delta_\varepsilon+I)\cdots(\Delta_{\varepsilon^m}+I)-I,\\&\Delta_{\varepsilon^j}x \bigl(n,\ldots,\varepsilon^mn \bigr)=O\bigl(\varepsilon^jx \bigl(n,\ldots,\varepsilon^mn \bigr)\bigr).\end{aligned}} $$
(10)

Now it will be shown how these operators can be used for system (1). Using (4) and (5), it follows that (1) can be rewritten in:

$$\lefteqn{\begin{cases}Ex_n=f_{1,0}(x_n,y_n)+\varepsilon f_{1,1}(x_n,y_n)+O(\varepsilon^2),\\Ey_n=f_{2,0}(x_n,y_n)+\varepsilon f_{2,1}(x_n,y_n)+O(\varepsilon^2).\end{cases}} $$
(11)

Assuming that x n and y n depend on two scales (a fast scale n, and a slow scale εn), it follows that x n =x(n,εn) and y n =y(n,εn). By using (8), (11) becomes

$$\lefteqn{\begin{cases}(\Delta_1+\Delta_\varepsilon+\Delta_1\Delta_\varepsilon +I)x_n\\\quad=f_{1,0}(x_n,y_n)+\varepsilon f_{1,1}(x_n,y_n)+O(\varepsilon ^2),\\(\Delta_1+\Delta_\varepsilon+\Delta_1\Delta_\varepsilon +I)y_n\\\quad=f_{2,0}(x_n,y_n)+\varepsilon f_{2,1}(x_n,y_n)+O(\varepsilon^2).\end{cases}} $$
(12)

To construct an approximation for x n and y n , one now has to substitute into (12) a formal power series (in ε) for x n and y n , that is,

$$\lefteqn{\begin{cases}x_n=x(n,\varepsilon n)=x_0(n,\varepsilon n)+\varepsilon x_1(n,\varepsilon n)\\\hspace{67pt}+\,\varepsilon^2 x_2(n,\varepsilon n)+\cdots,\\y_n=y(n,\varepsilon n)=y_0(n,\varepsilon n)+\varepsilon y_1(n,\varepsilon n)\\\hspace{67pt}+\,\varepsilon^2 y_2(n,\varepsilon n)+\cdots.\end{cases}} $$
(13)

Then, by taking together those terms of equal powers in ε, one obtains as O(1)-problem

$$\begin{cases}(\Delta_1+I)x_0=f_{1,0}(x_0,y_0),\\(\Delta_1+I)y_0=f_{2,0}(x_0,y_0),\end{cases} $$
(14)

where x 0=x 0(n,εn) and y 0=y 0(n,εn), and as O(ε)-problem

$$\begin{cases}\varepsilon((\Delta_1+I)x_1-f_{1,0}(x_1,y_1))\\\quad=\varepsilon f_{1,1}(x_0,y_0)-(\Delta_\varepsilon+\Delta_1\Delta_\varepsilon )x_0,\\\varepsilon((\Delta_1+I)y_1-f_{2,0}(x_1,y_1))\\\quad=\varepsilon f_{2,1}(x_0,y_0)-(\Delta_\varepsilon+\Delta_1\Delta_\varepsilon)y_0,\end{cases} $$
(15)

where x 1=x 1(n,εn), y 1=y 1(n,εn).

4 Two complex eigenvalues

When the O(1)-problem has two complex valued eigenvalues (namely, λ 1 and λ 2), we restrict ourselves to two cases for r: 0<r<1, or r=1, where r is the absolute value of the complex eigenvalues. It follows from (14) that

(16)

where \(c_{1}=\frac{\lambda_{1}-a_{22}}{a_{21}}\) and \(c_{2}=\frac{\lambda _{2}-a_{22}}{a_{21}}\) are complex conjugates, and where g 0(εn) and h 0(εn) are still arbitrary functions which can be used to avoid unbounded behavior in x 1(n,εn) and y 1(n,εn) on the \(O(\frac {1}{\varepsilon})\) iteration scale. Then, by substituting (16) into the O(ε)-problem (15), and after rearranging terms, one finally obtains as O(ε)-problem

(17)

where M ij (for i=1,2, and j=0,…,9) are given by

$$\lefteqn{\begin{aligned}[c]&\begin{pmatrix}M_{10}\\M_{20}\end{pmatrix}= \varepsilon \begin{pmatrix}b_{10}\\b_{20}\end{pmatrix},\\&\begin{pmatrix}M_{11}\\M_{21}\end{pmatrix}=\begin{pmatrix}\varepsilon(b_{11}c_1+b_{12})g_0-c_1\lambda_1\Delta_\varepsilon g_0(\varepsilon n)\\\varepsilon(b_{21}c_1+b_{22})g_0-\lambda_1\Delta_\varepsilon g_0(\varepsilon n)\end{pmatrix},\\&\begin{pmatrix}M_{12}\\M_{22}\end{pmatrix}=\begin{pmatrix}\varepsilon(b_{11}c_2+b_{12})h_0-c_2\lambda_2\Delta_\varepsilon h_0(\varepsilon n)\\\varepsilon(b_{21}c_2+b_{22})h_0-\lambda_2\Delta_\varepsilon h_0(\varepsilon n)\end{pmatrix},\\&\begin{pmatrix}M_{13}\\M_{23}\end{pmatrix}= \varepsilon \begin{pmatrix}b_{13}c_1^2+b_{14}c_1+b_{15}\\b_{23}c_1^2+b_{24}c_1+b_{25}\end{pmatrix}g_0^2,\\&\begin{pmatrix}M_{14}\\M_{24}\end{pmatrix}= \varepsilon \begin{pmatrix}2b_{13}c_1c_2+b_{14}(c_1+c_2)+2b_{15}\\2b_{23}c_1c_2+b_{24}(c_1+c_2)+2b_{25}\end{pmatrix}g_0h_0,\\&\begin{pmatrix}M_{15}\\M_{25}\end{pmatrix}= \varepsilon \begin{pmatrix}b_{13}c_2^2+b_{14}c_2+b_{15}\\b_{23}c_2^2+b_{24}c_2+b_{25}\end{pmatrix}h_0^2,\\&\begin{pmatrix}M_{16}\\M_{26}\end{pmatrix}= \varepsilon \begin{pmatrix}b_{16}c_1^3+b_{17}c_1^2+b_{18}c_1+b_{19}\\b_{26}c_1^3+b_{27}c_1^2+b_{28}c_1+b_{29}\end{pmatrix}g_0^3,\\&\begin{pmatrix}M_{17}\\M_{27}\end{pmatrix}= \varepsilon \begin{pmatrix}3b_{16}c_1^2c_2+b_{17}c_1(c_1+2c_2)+b_{18}(2c_1+c_2)+3b_{19}\\3b_{26}c_1^2c_2+b_{27}c_1(c_1+2c_2)+b_{28}(2c_1+c_2)+3b_{29}\end{pmatrix}g_0^2h_0,\\&\begin{pmatrix}M_{18}\\M_{28}\end{pmatrix}= \varepsilon \begin{pmatrix}3b_{16}c_1c_2^2+b_{17}c_2(2c_1+c_2)+b_{18}(c_1+2c_2)+3b_{19}\\3b_{26}c_1c_2^2+b_{27}c_2(2c_1+c_2)+b_{28}(c_1+2c_2)+3b_{29}\end{pmatrix}g_0h_0^2,\\&\begin{pmatrix}M_{19}\\M_{29}\end{pmatrix}= \varepsilon \begin{pmatrix}b_{16}c_2^3+b_{17}c_2^2+b_{18}c_2+b_{19}\\b_{26}c_2^3+b_{27}c_2^2+b_{28}c_2+b_{29}\end{pmatrix}h_0^3,\end{aligned}} $$
(18)

where g 0=g 0(εn) and h 0=h 0(εn). In system (17) for x 1(n,εn) and y 1(n,εn), it is obvious that the right-hand side contains terms (i.e., multiples of \((c_{1},1)^{T}\lambda_{1}^{n}\) and of \((c_{2},1)^{T}\lambda_{2}^{n}\), where T refers to the transpose of the matrix), which are solutions of the homogeneous system. For the case 0<r<1, it follows from (17) that only two vectors \((M_{11},M_{21})^{T}\lambda_{1}^{n}\) and \((M_{12},M_{22})^{T}\lambda_{2}^{n}\) contain secular, and also nonsecular terms. Therefore, we decompose the sum of these vectors into two linearly independent directions to separate secular and nonsecular terms,

(19)

where M k (for k=1,…,4) are obtained based on the relationship between the eigenvalues λ 1 and λ 2, see Table 1. From (19), we obtain

$$\begin{cases}m_1=\frac{c_2M_2-M_1}{c_2-c_1},\\m_2=\frac{M_1-c_1M_2}{c_2-c_1},\\m_3=\frac{c_2M_4-M_3}{c_2-c_1},\\m_4=\frac{M_3-c_1M_4}{c_2-c_1}.\end{cases} $$
(20)

To avoid secular behavior in x 1(n,εn) and y 1(n,εn), it follows that m 1=0 and m 4=0, that is,

$$M_1=c_2M_2,\quad\mbox{and}\quad M_3=c_1M_4. $$
(21)

If we solve system (21) for Δ ε g 0(εn) and Δ ε h 0(εn), for the case 0<r<1 and based on Table 1, it follows that

$$\begin{cases}\Delta_\varepsilon g_0(\varepsilon n)=\varepsilon k_1g_0(\varepsilon n),\\\Delta_\varepsilon h_0(\varepsilon n)=\varepsilon k_2h_0(\varepsilon n),\end{cases} $$
(22)

where

$$\lefteqn{\begin{aligned}[c]&k_1=\frac{c_1b_{11}+b_{12}-c_1c_2b_{21}-c_2b_{22}}{\lambda _1(c_1-c_2)},\quad\mbox{and}\\& k_2=-\frac{c_2b_{11}+b_{12}-c_1c_2b_{21}-c_1b_{22}}{\lambda_2(c_1-c_2)}.\end{aligned}} $$
(23)

Since, for the complex eigenvalues, c 1 and c 2 are complex conjugates, and so k 1 and k 2 are, and since the solutions x 0(n,εn) and y 0(εn) need to be real, it then follows that \(h_{0}(\varepsilon n)=\overline {g_{0}(\varepsilon n)}\), where the overline refers to complex conjugates. Therefore, system (22) can be reduced to a single equation

$$\Delta_\varepsilon g_0(\varepsilon n)=\varepsilon k_1g_0(\varepsilon n), $$
(24)

which has as a solution

$$g_0(\varepsilon n)=g_0(0) (1+\varepsilon k_1)^{n}. $$
(25)

From (24), it then follows that if |1+εk 1| is less than 1, then the equilibrium point (x(n,εn),y(n,εn))=(0 +O(ε),0+O(ε)) of system (1) is an asymptotically stable focus, if |1+εk 1| is bigger than 1, then the equilibrium point (x(n,εn),y(n,εn))=(0+O(ε),0+O(ε)) of system (1) is an unstable focus, and if k 1 is zero, then the equilibrium point (x(n,εn),y(n,εn))=(0+O(ε),0+O(ε)) is a higher singularity and the O(ε 2)-problem for x 2(n,εn) and x 2(n,εn) has to be studied (which is outside the scope of this paper).

Table 1 Values of M k (for k=1,…,4) in (19) for some representations of the absolute value of the eigenvalues λ 1 and λ 2
Full size table

For the case r=1 and when the eigenvalues of matrix A in (3) are complex with nonzero real and imaginary parts, it follows from (17) that only four vectors \((M_{11},M_{21})^{T}\lambda_{1}^{n}\), \((M_{12},M_{22})^{T}\lambda_{2}^{n}\), \((M_{17},M_{27})^{T}\lambda_{1}^{2n}\lambda_{2}^{n}\), and \((M_{18},M_{28})^{T}\lambda_{1}^{n}\lambda_{2}^{2n}\) contain secular, and also nonsecular terms. Therefore, we decompose the sum of these vectors into two linearly independent directions to separate secular and nonsecular terms which follow from the same equation as (19), for the case r=1, where M k (for k=1,…,4) are obtained based on the relationship λ 1 λ 2=1, see Table 1. If we solve system (21) for Δ ε g 0(εn) and Δ ε h 0(εn), where \(h_{0}(\varepsilon n)=\overline{g_{0}(\varepsilon n)}\), for the case r=1, and based on Table 1, we have again a single equation

$$\Delta_\varepsilon g_0(\varepsilon n)=\varepsilon g_0(\varepsilon n) \bigl(k_1+k_3g_0(\varepsilon n)\overline{g_0(\varepsilon n)}\, \bigr), $$
(26)

where

(27)

Consider

$$\lefteqn{\begin{aligned}[c]&g_0(\varepsilon n)=g_{0,1}(\varepsilon n)+ig_{0,2}(\varepsilon n),\\&k_1=k_{11}+ik_{12},\quad\mbox{and}\\& k_3=k_{31}+ik_{32},\end{aligned}} $$
(28)

where g 0,1(εn) and g 0,2(εn) are real functions, and where k 11,k 12,k 31, and k 32 are real constants. Then (26) becomes

$$\begin{cases}\Delta_\varepsilon g_{0,1}=\varepsilon\{[k_{11}+k_{31}(g_{0,1}^2+g_{0,2}^2)]g_{0,1}\\\hspace*{40pt}-[k_{12}+\,k_{32}(g_{0,1}^2+g_{0,2}^2)]g_{0,2}\},\\\Delta_\varepsilon g_{0,2}=\varepsilon\{[k_{11}+k_{31}(g_{0,1}^2+g_{0,2}^2)]g_{0,2}\\\hspace*{40pt}+\,[k_{12}+k_{32}(g_{0,1}^2+g_{0,2}^2)]g_{0,1}\},\end{cases} $$
(29)

where g 0,1=g 0,1(εn) and g 0,2=g 0,2(εn). As far as we know, there are no exact solutions available for system (29). However system (29) has always an equilibrium point in (g 0,1,g 0,2)=(0,0), and an equilibrium “circle”

$$g_{0,1}^2+g_{0,2}^2=-\frac{k_{11}k_{31}+k_{12}k_{32}}{k_{31}^2+k_{32}^2}, $$
(30)

when k 31 k 12=k 32 k 11.

For an additional analysis, we define a new variable R, where \(R^{2}=g_{0,1}^{2}+g_{0,2}^{2}\). After doing some computations, it follows from (29) that

(31)

Since the dynamics of the system is mostly influenced by the O(ε)-problem rather than O(ε 2)-problem we consider O(ε) terms in (31) for the analysis. Then it follows that if k 11 and k 31 have different signs, and if k 11 is positive, there is a stable limit cycle, and if k 11 is negative then the limit cycle is unstable. To compute the radius of this limit cycle, the right-hand side of (31) is set equal to zero, that is, Δ ε (R ∗ 2)=0. To construct an approximation for R ∗ 2, one now has to substitute into the right-hand side of (31) a formal power series (in ε) for R ∗ 2, that is,

$${R^*}^2=R_0^*+\varepsilon R_1^*+\varepsilon^2 R_2^*+O \bigl(\varepsilon^3\bigr), $$
(32)

One solution of Δ ε (R ∗ 2)=0 is the origin, that is R ∗=0. To find a nontrivial approximation, by taking together those terms of equal powers in ε, one obtains as O(1)-problem

$$k_{11}+k_{31}R_0^*=0, $$
(33)

which has as a nontrivial solution

$$R_0^*=-\frac{k_{11}}{k_{31}}, $$
(34)

when \(-\frac{k_{11}}{k_{31}}>0\), and, as O(ε)-problem

(35)

which has as a solution

$$R_1^*=-\frac{(k_{31}k_{12}-k_{11}k_{32})^2}{2k_{31}^3}, $$
(36)

and, as O(ε 2)-problem

(37)

which has as a solution

$$R_2^*=\frac{k_{32}(k_{31}k_{12}-k_{11}k_{32})^3}{2k_{31}^5}, $$
(38)

and so on. So, nontrivial equilibrium points follow from

$$\lefteqn{\begin{cases}g_{0,1}^{*2}+g_{0,2}^{*2}=R^{*2},\\(k_{11}+k_{31}{R^*}^2)g_{0,1}^*-(k_{12}+k_{32}{R^*}^2)g_{0,2}^*=0,\\(k_{11}+k_{31}{R^*}^2)g_{0,2}^*+(k_{12}+k_{32}{R^*}^2)g_{0,1}^*=0,\end{cases}} $$
(39)

where R ∗ 2 is defined in (32). Now, we expand a formal power series (in ε) for \(g_{0,1}^{*}\) and \(g_{0,2}^{*}\), that is,

$$\begin{cases}g_{0,1}^*=a_0+\varepsilon a_1+\varepsilon^2a_2+O(\varepsilon^3),\\g_{0,2}^*=b_0+\varepsilon b_1+\varepsilon^2b_2+O(\varepsilon^3).\end{cases} $$
(40)

Then, we substitute (40) into (39) and take together those terms of equal powers in ε to find a 0,b 0,a 1,b 1,…. One obtains as O(1)-problem

$$\begin{cases}a_0^2+b_0^2=R_0^*,\\a_0(k_{11}+k_{31}R_0^*)-b_0(k_{12}+k_{32}R_0^*)=0,\\b_0(k_{11}+k_{31}R_0^*)+a_0(k_{12}+k_{32}R_0^*)=0,\end{cases} $$
(41)

where \(R_{0}^{*}\) is defined in (34). It follows from (34) that (41) has nontrivial solutions for a 0 and b 0 if and only if k 11 k 32=k 12 k 31 and \(a_{0}^{2}+b_{0}^{2}=-\frac{k_{11}}{k_{31}}\). And, as O(ε)-problem

$$\begin{cases}2a_0a_1+2b_0b_1=R_1^*,\\(a_0k_{31}-b_0k_{32})R_1^*+a_1(k_{11}+k_{31}R_0^*)\\\quad-\,b_1(k_{12}+k_{32}R_0^*)=0,\\(b_0k_{31}+a_0k_{32})R_1^*+b_1(k_{11}+k_{31}R_0^*)\\\quad+\,a_1(k_{12}+k_{32}R_0^*)=0,\end{cases} $$
(42)

where \(R_{1}^{*}\) is defined in (36). Then it follows that, if k 11 k 32=k 12 k 31, (42) has nontrivial solution for a 1 and b 1 if and only if a 0 a 1+b 0 b 1=0.

If we define g 0,1=Rcos(ϕ) and g 0,2=Rsin(ϕ), after doing some computations, it follows from (29) that

$$\Delta_\varepsilon\biggl(\frac{g_{0,2}}{g_{0,1}} \biggr)=\frac {\varepsilon(k_{12}+k_{32}R^2)R^2}{g_{0,1}(\varepsilon n)g_{0,1}(\varepsilon(n+1))}. $$
(43)

or, after expanding the right-hand side with respect to ε, it follows that

$$\Delta_\varepsilon\biggl(\frac{g_{0,2}}{g_{0,1}} \biggr)=\frac {\varepsilon(k_{12}+k_{32}R^2)R^2}{g_{0,1}^2}\Biggl[1-\frac{\varepsilon(k_{11}g_{0,1}-k_{12}g_{0,2}+(g_{0,1}k_{31}-g_{0,2}k_{32})R^2)}{g_{0,1}}\sum_{m=0}^{\infty}\biggl(\frac{-\varepsilon}{g_{0,1}} \biggr)^m \Biggr], $$
(44)

where g 0,1=g 0,1(εn) and g 0,2=g 0,2(εn). It follows from (31) and (44) that if k 11 k 32=k 12 k 31 there are infinitely many equilibrium points and as a result singularity exists, therefore, for this case we need higher order terms when we compute secular terms. But if k 11 k 32≠k 12 k 31, then the system has only one equilibrium point (which is located in the origin). And, by linearization of (29) around origin, it follows that if |1+εk 1| is less than 1, then the equilibrium point (x(n,εn),y(n,εn))=(0+O(ε),0+O(ε)) of system (1) is an asymptotically stable focus, if |1+εk 1| is bigger than 1, then the equilibrium point (x(n,εn),y(n,εn))=(0+O(ε),0+O(ε)) of system (1) is an unstable focus, and if k 1 is zero, then the equilibrium point (x(n,εn),y(n,εn))=(0+O(ε),0+O(ε)) is a higher singularity and the O(ε 2)-problem for x 2(n,εn) and x 2(n,εn) has to be studied (which is outside the scope of this paper). Then it also follows from (16) that the real solutions for x 0(n,εn) and y 0(n,εn), for the case when r=1, are as follows:

$$\begin{pmatrix}x_0(n,\varepsilon n)\\y_0(n,\varepsilon n)\end{pmatrix}=2R(\varepsilon n)\begin{pmatrix}\frac{1}{a_{21}}[\cos(\phi(\varepsilon n)+(n+1)\theta)-a_{22}\cos (\phi (\varepsilon n)+n\theta)]\\\cos(\phi(\varepsilon n)+n\theta)\end{pmatrix}, $$
(45)

where λ 1=cos(θ)+isin(θ) and \(\lambda _{2}=\overline {\lambda_{1}}\).

5 Conclusions and remarks

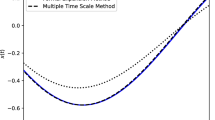
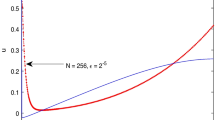
In this paper, by applying the multiple scales perturbation method to a general system of two first-order ordinary difference equations, including linear, quadratic, and qubic terms, we obtain approximations of the solutions which are valid on long iteration scales. We considered two cases for which the eigenvalues are complex with nonzero real and imaginary parts, and the modulus is less than or equal to 1. For the case when the modulus is smaller than 1, we found conditions for which the solutions are stable, and for the case when the modulus is equal to 1, and for some special values of the constants, we encounter limit cycles, and a circle of equilibrium points. Our results are in nice agreement with numerical results in [9] when ε is considered to be small. The stable and unstable limit cycles in the phase plane shown by [9] show this agreement.

The methodology that we used in this paper can also be expanded in the same way to the other cases such as two distinct real eigenvalues, and two coinciding real eigenvalues, and based on the values for the constants a ij and b ij we can have the bifurcation diagrams as well. The obtained results help us in a better understanding of the behavior of nonlinear oscillations. In particular, all kinds of bifurcations can be studied in detail.