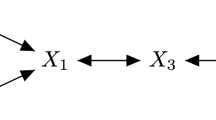Abstract
A fully probabilistic approach to reconstructing Gaussian graphical models from distance data is presented. The main idea is to extend the usual central Wishart model in traditional methods to using a likelihood depending only on pairwise distances, thus being independent of geometric assumptions about the underlying Euclidean space. This extension has two advantages: the model becomes invariant against potential bias terms in the measurements, and can be used in situations which on input use a kernel- or distance matrix, without requiring direct access to the underlying vectors. The latter aspect opens up a huge new application field for Gaussian graphical models, as network reconstruction is now possible from any Mercer kernel, be it on graphs, strings, probabilities or more complex objects. We combine this likelihood with a suitable prior to enable Bayesian network inference. We present an efficient MCMC sampler for this model and discuss the estimation of module networks. Experiments depict the high quality and usefulness of the inferred networks.
Similar content being viewed by others
1 Introduction
Gaussian graphical models (GGMs) have amassed prolific interest in recent years due to its intuitive mechanism of representing and visualizing complex connectedness between objects. They provide a rigid formalism to represent high-dimensional distributions of random variables (objects). Given a n×d-dimensional random matrix X with n objects and d i.i.d. measurements (observations), GGMs infer the network of dependencies amongst these n objects through their pairwise partial correlations. The partial correlations are seen as a measure of conditional dependence between objects and are obtained from the inverse of the covariance matrix. Conditional independence is asserted between any two objects if the pairwise partial correlation is zero and this indicates the absence of an edge between these objects in the network. Identifying networks—estimating dependencies between objects and thereby determining their underlying graph structure—is a challenging problem. The problem is more pronounced in high-dimensional settings i.e. when the number of objects is far larger than the measurements themselves and when the unknown network structure has to be learned from noisy observed measurements. The noisiness and high-dimensionality add degrees of complexity in interpreting and analyzing networks. Further, traditional network inference models depend on geometric translations of the data which require knowledge of the underlying geometric coordinates. In many real-world scenarios, especially those dealing with non-vectorial objects like strings, graphs etc, one rarely has access to the objects’ underlying vectorial representations but only to their pairwise distances implying that the geometric translations are entirely lost. Therefore, it becomes pertinent to devise a network inference procedure that looks from the angle of pairwise distances, hence being devoid of any vectorial representations of the objects. To our knowledge, the problem of recovering networks solely from pairwise relational information has not been addressed in the literature so far, except for the case of classical GGMs where the standard Wishart likelihood effectively depends only on pairwise inner products. This dependency on inner products, however, implies a strong assumption about the origin of the underlying space, and we show in our experiments that the success of network inference based on the standard Wishart likelihood crucially depends on the fulfillment of this geometric assumption. Focusing on situations in which the relational information between objects is all that we can observe (because, for instance, we are dealing with structured objects like strings, graphs etc for which no generic vectorial representation exists), it is basically impossible to correct for (or even to check) this implicit geometric assumption that is encoded into the standard Wishart likelihood. This problem was the main motivation for us to search for variants of GGMs which are invariant against assumptions about the origin of the underlying coordinate system. Note that this invariance essentially describes the transition from inner products (which necessarily depend on the origin) to distances (which do not).
In the current paper, we introduce a novel sparse network inference mechanism called the Translation-invariant Wishart Network (TiWnet) model that is designed solely to work on pairwise distances. This applicability to situations in which we can only observe distance information constitutes the strength of this new model over similar approaches involving the matrix-valued Gaussian likelihood (Allen and Tibshirani 2010). We denote by D n×n , the matrix that contains the pairwise distances between n objects. To the best of our knowledge this is the first paper that deals with network structure discovery in situations where no vectorial representation of objects is available and only pairwise distances are observed. Additionally, the presence of certain objects having a relatively higher confluence of edges gives rise to central hub regions. Extracting the network structure from amongst hubs given noisy measurements makes it, in general, difficult to summarize the entire network succinctly. To handle this, we present the construction of module networks where networks are learned on groups of variables called modules, thereby effectively reducing n to the number of modules.
Graphical abstract
For clarity, we provide a graphical abstract (Fig. 1) that captures the focus of this paper. The top panel shows the classical operational regime for GGMs that uses the vectorial representation of an object for network recovery. These vectors are present in the observed X n×d matrix where n is the number of objects and d the measurements. The bottom panel sketches the regime our paper focuses on which deals with the non-vectorial representations of objects. These objects can be those having a structure like graphs, strings, probability distributions etc. For such objects, it is natural to look into their pairwise representations and therefore for network recovery, we make use of their pairwise representations assembled in a pairwise distance D n×n matrix.
Graphical abstract. Consider the space of objects having a vectorial or non-vectorial representation. (Top) Classical GGMs operate in a vectorial regime where networks are extracted from objects represented as vectors in an observed X n×d matrix with n objects of interest and d observations. (Bottom) Current focus of this paper deals with objects possessing a non-vectorial representation i.e. these objects have a structure like a string or graph. For such objects, it is natural to consider their pairwise representations rather than vectorial representations. To enable network extraction for such structured objects, we use their pairwise representations collected in a pairwise distance D n×n matrix
Outline of the paper
In Sect. 2, we explain the classical setting for GGMs. The underlying problems with existing methods are elaborated in Sect. 3. In Sect. 4, we discuss the solution to these problems and further explain how our model, TiWnet, caters to this solution. Section 5 details the TiWnet network inference model. We describe module networks in Sect. 6. Comparison experiments on simulated data along with three real-world application areas are demonstrated in Sect. 7. In Sect. 8, we discuss TiWD (Vogt et al. 2010) that uses the same likelihood as TiWnet and TiWD’s incapability to extract networks. The contributions of TiWnet are highlighted in Sect. 9 and we conclude the paper in Sect. 10.
2 Classical GGMs
To set the stage, we begin with a description of the classical framework for estimating sparse GGMs. One usually starts with a n×d observed data matrix X o (the superscript o means “original” and is used here only for notational consistency), its d columns interpreted as the outcome of a measuring procedure in which some property of the n objects of interest is measured. In a biological setting, for instance, the objects could be n genes and one set of measurements (one column) could be gene expression values from one microarray. All d columns in X o are assumed to be i.i.d. according to \(\mathcal{N}(\textbf{0}, \varSigma)\). Then, the inner product matrix \(S^{o} = \frac{1}{d}X^{o} (X^{o})^{t}\) follows a central Wishart distribution \(\mathcal{W}_{d}(\varSigma)\) in d degrees of freedomFootnote 1 (Muirhead 1982) (if d≥n otherwise S o is pseudo-WishartFootnote 2), and its likelihood as a function of the inverse covariance Ψ:=Σ −1 is
The corresponding generative model is sketched in Fig. 2. Every algorithm for network reconstruction relies on some potentially interesting sparsity structure garnered within the inverse covariance matrix Ψ:=Σ −1. Ψ contains the (scaled) partial correlations between the n random variables forming the nodes in the network: a zero entry in Ψ ij concurs to no edge prevailing between the pair of random variables (i,j) in the network.
Assumed underlying generative process in classical GGMs. Black arrows indicate the workflow when drawing samples from this model; n, d: matrix dimensions. Every dth draw from the n-dimensional Gaussian is an i.i.d. replication and stacked as a column of X o. A draw represents a set of observations and a row denotes an object of interest
Related work
There exists a plethora of literature on network structure estimation using i.i.d. samples. To infer the underlying network, it is straightforward (at least from a methodological viewpoint) to maximize the Wishart likelihood while ensuring that Ψ is sparse. This is exactly the approach followed in graph lasso (Friedman et al. 2007) where a ℓ 1 sparsity constraint on Ψ is used:
where λ controls the amount of penalization and ∥Ψ∥1=∑ i |Ψ i |, the ℓ 1 norm which is the sum of absolute values of the elements in Ψ. A methodologically similar, but simplified approach that decouples this joint estimation problem into n independent neighborhood-selection problems is dealt in Meinhausen and Bühlmann (2006). The neighborhood selection problem is cast into a standard regression problem and is solved efficiently using a ℓ 1 penalty. The model presented in Kolar et al. (2010b) deals with conditional covariance selection where the neighborhoods of nodes are conditioned on a random variable that holds information about the associations between nodes. They employ a logistic regression model with a ℓ 1/ℓ 2 penalty for the neighborhood-selection problem while additionally assuming this conditioning variable which steers sparsity of edges. Another method to extract networks called walk-summable graphs is introduced in Johnson et al. (2005b) where a neighborhood is constructed based on walks accumulated by every node in the graph and weighted as a function of the edgewise partial correlations present in Ψ.
3 Underlying problems with existing methods
The above papers and related approaches, however, have been built on an assumption that the d columns in X o are i.i.d. This particular assumption of considering columns to be identically distributed might be too restrictive: even if the underlying Gaussian generative process is a valid model, different column-wise bias terms are common in practice. In the above biological example, there might be global expression differences between the d microarrays. It is therefore indispensable to model these unknown shifts (biases) for valid network inference. An ensuing consequence of modeling these biases is that the column i.i.d. assumption gets relaxed i.e., one ends up working with just independent data since the columns now come from different distributions.
Employing non-i.i.d. data for network recovery has been dealt with in the past, primarily in the area of time-varying data. Here, the data are no longer identically distributed since observations are taken at d discrete time points. In this case, the time-varying GGMs aim in capturing the longitudinal relational structure between objects. Examples of such work that deal with transient non-i.i.d. data due to discrete time points can be found in Kolar et al. (2010a), Zhou et al. (2010) and Carvalho and West (2007). In these references, it must be noted that every observation assumes to have been generated from either a common-mean discrete-distribution Ising model (Kolar et al. 2010a) or zero-mean multivariate normal distribution (Zhou et al. 2010 and Carvalho and West 2007). At this juncture, our work differs from this fraternity in that although we also deal with non-i.i.d. data, the non-i.i.d. nature arises not due to the time component but due to admitting different column-wise biases.
To model these column-wise biases in TiWnet, they are included in the generative model by introducing a shifting operation in which scalar bias terms b (i=1,…,d) are added to the “original” column vectors \(\boldsymbol{x}^{o}_{i}\), which results in a mean-shifted vector x i , forming the ith column in X, cf. Fig. 3 (purple-outlined boxes). Hence the columns come from different distributions i.e. they cease to be identically distributed. In the classical case of not considering column biases, X o is distributed as \(\mathcal{N}(\boldsymbol{0}, \varSigma)\), but in TiWnet which now accommodates these column biases, the joint distribution of all matrix elements is expressed, that here is matrix normal \(X\sim\mathcal{N}(M, \varOmega)\) with mean matrix \(M:=\boldsymbol{1}_{n} \boldsymbol{b}_{d}^{t}\) and covariance tensor Ω:=Σ n×n ⊗I d . This model implies that \(S=\frac{1}{d}XX^{t}\) follows a non-central Wishart distribution \(S \sim\mathcal {W}_{d}(\varSigma, \varTheta)\) with non-centrality matrix Θ:=Σ −1 MM t (Gupta and Nagar 1999). Practical use of the non-central Wishart for network inference, however, is severely hampered by its complicated form and more so, the problem of estimating the unknown non-centrality matrix Θ based on only one observation of S which is problematically analogous to identifying the mean of any distribution given only a single data point.
Assumed underlying generative process. Black arrows indicate the workflow when drawing samples from this model; n, d: matrix dimensions. The red arrows highlight the same distance matrix D produced from either the “original data” X o (consisting of i.i.d. samples) or the “mean-shifted” data X (purple-outlined boxes) (Color figure online)
It is, thus, desirable to use a simpler distribution. One possible way of handling such column biases is to “center” the columns by subtracting the empirical column means \(\hat{b}_{i}\), and using the matrix \(S_{C} = \frac{1}{d}(X-\boldsymbol{1} \hat{\boldsymbol{b}}{}^{t})(X-\boldsymbol{1} \hat{\boldsymbol{b}}{}^{t})^{t}\) in the standard central Wishart model. Since the entries in the ith column, {x 1i ,…,x ni }, are not independent but coupled via the Σ-part in Ω, this centering, however, brings about undesired side effects; apart from removing the additive shift, the original columns are modified with the resulting column-centered matrix S C being rank deficient. As a consequence, \(S_{C} \nsim\mathcal{W}(\varSigma)\) i.e. S C is not central Wishart distributed. Instead, S C follows the more complicated translation invariant Wishart distribution, see (12) below.
Figure 4 exemplifies these problems where we depict the performance of graph lasso (Friedman et al. 2007) based on (i) the original unshifted data generated using Fig. 2 (GL.o), (ii) mean-shifted data generated using Fig. 3 (GL.s) and (iii) column-centered data (GL.C). Graph lasso maximizes the Wishart likelihood using a ℓ 1 sparsity constraint (see (2)) and works best in case (i) where the model assumptions are met. The boxplots in Fig. 4 confirm that the presence of column-wise biases (case ii) significantly deteriorates the performance of graph lasso and even column-centering (case iii) does not augment the performance. Thus column-biases are not only a theoretical problem of model mismatch but also a severe practical problem for inferring the underlying network.
Left: Example network, artificially created from a data generator. Right: performance of edge recovery for the graph lasso (GL) method which maximizes the standard Wishart likelihood with a ℓ 1 sparsity penalty. The leftmost boxplot refers to the original (unshifted) data (GL.o), meaning that the model assumptions are correct, the rightmost boxplot refers to data with column shifts (GL.s), and the middle boxplot refers to empirically centering the columns (GL.C). Refer Sect. 7 for details on sample generation, methods, model selection and evaluation criteria
Another problem-arising situation is where even observing X n×d is not valid, instead one assumes access to a measuring procedure which directly returns pairwise relationships between n objects. Two variants are considered: either a positive definite similarity matrix identified with the matrix S is measured, or pairwise squared distances arranged in a matrix D is measured, defined component-wise as D ij =S ii +S jj −2S ij . In the first case with S or in the second case with D, column-centering is still possible by the usual “centering” operation in kernel PCA (Schölkopf et al. 1998): S C =QSQ t=−(1/2)QDQ t, with \(Q_{ij} = \delta_{ij}-\frac{1}{n}\). However, using this column-centered matrix S C in the standard Wishart model induces obviously the same problems related to model mismatch as in the vectorial case above (Fig. 4).
4 Novel solution to network inference
To overcome the above intertwined problems of having to work with column-wise biases and the complicated non-central Wishart we need to rely on a model that makes use of only pairwise distances. Figure 5 shows how one can move from X↦S↦D and the information loss involved therein. When one moves from X to S, the rotational information is lost and when one moves from S to D, the translational information is lost. Once in D, we are devoid of any relevant geometric information i.e. D is both translation and rotation invariant. Since we consider D to contain the squared-Euclidean pairwise distances, the distances are preserved throughout. On the other hand, the mappings from D↦S and S↦X are not unique and this non-uniqueness is the problem that requires careful handling. We explain more on this non-uniqueness and how we handle it in the following.
Relationship between data matrix X, similarity matrix S and pairwise distance matrix D and the information loss procured by moving between them. The straight lines from X↦S, X↦D and S↦D show a unique mapping whereas the dotted lines from D↦S and S↦X show a non-unique mapping. Since we deal with squared-Euclidean pairwise distances throughout, the distances are preserved. It is the non-uniqueness that poses the real problem which requires attention
Since by assumption D contains squared Euclidean distances, there is a set of inner product matrices S that fulfill D ij =S ii +S jj −2S ij (McCullagh 2009). If S ∗ is one (any) such matrix, the equivalence class of these matrices mapping to a single D is formally described as set \(\mathbb{S}(D) = \{S| S = S_{*} + \boldsymbol{1} \boldsymbol{v}^{t} + \boldsymbol{v} \boldsymbol{1}^{t} , S \succeq0,\boldsymbol{v} \in\mathbb{R}^{n} \}\). The elements in \(\mathbb{S}(D)\) can be seen as Mercer kernels that represent many objects ranging from graphs to probability distributions to strings etc. Mercer kernels are kernels that satisfy Mercer’s theorem conditions (Vapnik 1998 and Cristianini and Shawe-Taylor 2000). These kernels are viewed as similarity measures between structured objects that have no direct vectorial representation.Footnote 3 For example, Fig. 6 represents a structured object like a graph for which different Mercer kernels S 1 and S 2 can be constructed wherein \(S_{1},S_{2} \in\mathbb{S}(D)\) and therefore map to the same D. This \(\mathbb{S}\) is exactly the set of inner product matrices that can be constructed by arbitrarily biasing the column vectors in X n×d . Shifting the viewpoint from column to row vectors, this invariance means that the density does not depend on the origin of the coordinate system in which the n objects are represented as vectors containing d different measurements. Column-wise biases referred to before reduce in this view to simple shifts of the origin of an underlying coordinate system.
A structured object like a graph for which two different similarity matrices (Mercer kernels) S 1 and S 2 exist that give rise to the same D. In this case, the choice of S for usage in a probabilistic setup is irrelevant whereas if they did not map to the same D, then the choice of S is critical for the probabilistic model. In a discriminative framework, the choice of S is irrelevant
Most of the methods used for constructing kernels have no information about the origin of the kernel’s underlying space meaning that we have no knowledge whether the probability distribution of either S 1 or S 2 is that of S C i.e. the S having zero-column shifts. This indicates that as long as the kernels belong to set \(\mathbb{S}(D)\), the exact form of the kernel matrix is irrelevant. On the other hand, were S 1 or S 2 ∉ \(\mathbb{S}(D)\), then the choice of S is critical in the framework of probabilistic models whereas for discriminative classifiers, the choice of S does not pose a problem. Most supervised kernel methods like SVMs are invariant against choosing different representatives in \(\mathbb{S}\), and in common unsupervised kernel methods like kernel PCA (Schölkopf et al. 1998) the rows of X are considered i.i.d. implying that subtracting the empirical column means (leading to S C ) is the desired centering procedure for selecting a candidate in \(\mathbb{S}(D)\). However, the sampling model for GGMs is not invariant against choosing \(S \in\mathbb{S}\). If one adopts column centering, then this reduces to selecting one specific representative S C from the set of all possible \(S \in \mathbb{S}(D)\), namely the one whose origin is at the sample mean. This leads to implicitly assuming the underlying vectorial space. Such column centering, however, destroys the central Wishart property of S (assuming it was a Wishart matrix before) as discussed in Sect. 3. The strategy is therefore to avoid the selection of a representative \(S \in\mathbb{S}\) altogether.
Instead, the proposed solution is to use a probabilistic model for squared Euclidean distances D. We use a likelihood model in TiWnet that depends only on D where these distances are not affected by any column-wise shifts (translations), cf. the red arrows in Fig. 3. The likelihood model invariant to shifts has been studied before in the Translational-invariant Wishart Dirichlet (TiWD) cluster process (Vogt et al. 2010). In Sect. 8, we discuss further the TiWD model and its unsuitability for network extraction.
5 The TiWnet model
In this section, we discuss the likelihood model common to both TiWD and TiWnet, the prior construction we use suitable for network inference and the network inference mechanism.
5.1 Likelihood model
One starts with an observed matrix D containing pairwise squared distances between row vectors of an unobserved matrix \(X\sim\mathcal{N}(M, \varOmega)\). This means that in addition to the classical framework for GGMs, arbitrary column biases b (i=1,…,d) are now allowed which “shift” the columns in X but leave the pairwise distances unaffected.
As elaborated in Sect. 4 and depicted in Fig. 6, there exists \(\mathbb{S}(D)\), the set of kernel matrices mapping to the same D. We can now work with either D or with any \(S \in\mathbb{S}(D)\) i.e. a specific S is not required. Since there exists no convenient expression for the distribution of D, the likelihood in terms of D can be computed based on the distribution of S (McCullagh 2009). Here, it is shown that the distribution of an arbitrary \(S \in\mathbb{S}\) can be derived analytically as a singular Wishart distribution with a rank-deficient covariance matrix. The likelihood is developed through the concept of marginal likelihood (Patterson and Thompson 1971; Harville 1974). Below, we explain the constructs for marginal likelihood and then define it in terms of D.
Marginal likelihood
The term marginal likelihood is not consistently used in the literature. What is sometimes called the “classical” marginal likelihood, (Patterson and Thompson 1971; Harville 1974), is a decomposition of the likelihood into one part which depends on the parameters of interest and a second one depending only on “nuisance” parameters. The “Bayesian” marginal likelihood, on the other hand, is computed by integrating out the nuisance parameters after placing prior distributions on them. In the following we will use the first definition, which involves a partition of the likelihood into an “interesting” part and a “nuisance” part. In some cases, this classical marginal likelihood coincides with the profile likelihood, which is obtained by replacing the nuisance parameters with their maximum likelihood (ML)-estimates. This interpretation indeed holds true in our case, implying that here the intuitive idea of plugging-in the ML estimates leads to a valid likelihood function (which is not always true for profile likelihoods). Further technical details on this equivalence between profile- and marginal likelihood are given in the Appendix, and a discussion of these likelihood concepts from a Bayesian viewpoint can be found in Berger et al. (1999).
Let the data matrix X be distributed according to p(X|α,θ), where the distribution is parametrized by the interest parameter α and the nuisance parameter θ. Assume there exists a statistic t(X) whose distribution depends only on α. Then p(X|α,θ) can be decomposed as follows:

We base our inference on p(t(X)|α) which is the “classical” marginal likelihood based on the interest parameter alone. We notate p(t(X)|α) as \(\mathcal{L}(\alpha;t(X))\) where \(t(X)= \frac{(X - \mathbf{1}_{n}\hat{\boldsymbol{b}^{t}})}{\|X - \mathbf {1}_{n}\hat {\boldsymbol{b}^{t}}\|}\) is the standardized statistic and the interest parameter α=Ψ. The nuisance parameters θ consist of bias estimates \(\hat{\boldsymbol{b}}\) and scale factor τ. Note that this specific statistic t(X) is constant on the set of all X and S matrices that map to the same D. Therefore t(X) can be seen as a function that depends only on the scaled version of D i.e. \(f(\frac{D}{\|D\|})\).
Proposition 1
(McCullagh 2009)
Consider the standardized statistic \(t(X)= \frac{(X - \mathbf {1}_{n}\hat {\boldsymbol{b}^{t}})}{\|X - \mathbf{1}_{n}\hat{\boldsymbol{b}^{t}}\|}\) where t(X) is a function \(f(\frac{D}{\|D\|})\) depending only on (scaled) D. The interest parameter is Ψ. The shift- and scale- invariant likelihood in terms of D is:
where \(\widetilde{\varPsi} = f(\varPsi) = \varPsi- (\boldsymbol{1}^{t}_{n} \varPsi \boldsymbol{1}_{n} )^{-1} \varPsi\boldsymbol{1}_{n} \boldsymbol{1}^{t}_{n} \varPsi\).
The proof of Proposition 1 is given in the Appendix.
Thus, there is a valid probabilistic model underlying (4), and with a suitable prior Bayesian inference for Ψ is well-defined.
The reader should notice that (4) can be computed either from the distances D, or from any inner product matrix \(S \in\mathbb{S}(D)\). Rather than choosing any S and implicitly fixing the underlying coordinate system, our solution is to make the distribution invariant to the choice of any S (refer Sect. 4). This is achieved by working directly with D whereby any \(S \in\mathbb{S}(D)\) can be used. The practical advantage of this property is that one can now make use of the large “zoo” of Mercer kernels that represent structured objects whose vectorial representations are generally unknown. With TiWnet based on D, we make no assumption of the underlying coordinate system and can now use these Mercer kernels for reconstructing GGMs without being dependent on the choice of \(S \in\mathbb{S}\).
5.2 Prior construction
For network inference in a Bayesian framework, we complement the likelihood (4) with a prior over Ψ. We develop a new prior construction that enables network inference. This prior is similar to the spike and slab model introduced in Mitchell and Beauchamp (1988). In principle, any distribution over symmetric positive definite matrices can be used. The likelihood has a simple functional form in \(\widetilde{\varPsi}\), but our main interest is in Ψ, since zeros in Ψ determine the topology. Unfortunately, the likelihood in Ψ is not in standard form making it plausible to use a MCMC sampler. For any two Σ matrices, Σ 1 and Σ 2 that are related by Σ 2=Σ 1+1 v t+v 1 t, the likelihood is the same for Σ 1 and Σ 2 (McCullagh 2009). This means that Ψ is non-identifiable and a sampler will have problems with such constant likelihood regions by continuing to visit them unless a prior is used that breaks this symmetry.
To deal with this problem, we quantize the space of possible Ψ-matrices such that any two candidates have different likelihood. This is achieved with a two-component prior: P 1(Ψ) is uniform over the discrete set \(\mathcal{A}\) of symmetric diagonally-dominant matrices with off-diagonal entries in {−1,+1,0}, and diagonal entries are deterministic, conditioned on the off-diagonal elements i.e. Ψ ii =∑ j≠i |Ψ ij |+ϵ where ϵ is a positive constant added to ensure full rank of Ψ. Thus \(\mathcal{A} = \{\varPsi|\varPsi_{ij} \in\{-1, +1, 0\},\varPsi_{ji} = \varPsi_{ij}, \varPsi_{ii} = \sum_{j\neq i} |\varPsi_{ij}| + \epsilon\}\). Note that we treat only the off-diagonal entries as random variables. Enforcing such a diagonally-dominant matrix construction ensures that the matrix will be positive definite. The usage of diagonally-dominant matrices for network reconstruction is further justified since these matrices form a strict subclass of GGMs that are walk summable (Johnson et al. 2005a) and in Anandkumar et al. (2011) theoretical guarantees are provided establishing that walk-summable graphs make consistent sparse structure estimation possible. It is clear that such a three-level quantization of the prior which differentiates only between positive, negative and zero partial correlations encodes a strong prior belief about the expected range of the partial correlations. However, it is straightforward to use more quantization levels, or even switch to continuous priors like the ones introduced in Harry (1996), Daniels and Pourahmadi (2009) which parametrize the “semi-partial” correlations. On the other hand, our simulation experiments below suggest that the simple three-level prior performs very well in terms of structure recovery.
The second component of the prior is a sparsity-inducing prior P 2(Ψ). This corresponds to a Laplacian prior over the number of edges for each node and is given by \(P_{2}(\varPsi|\lambda) \propto\exp(-\lambda\sum_{i=1}^{n} (\varPsi_{ii}-\epsilon))\) where (Ψ ii −ϵ) denotes the number of edges for the ith node and λ is equivalent to the regularization parameter controlling the sparsity of the connecting edges.
5.3 Inference in TiWnet
To enable Bayesian inference in our model, we make use of the likelihood given in (4) and the two-component prior described in Sect. 5.2. For inference we devise a Metropolis-within-Gibbs sampler where the Metropolis-Hastings step proposes an appropriate Ψ matrix by iteratively sample one row/column in the upper triangle part of Ψ, conditioning on the rest, and the Gibbs iteration involves repeating the Metropolis-Hastings step for every node.
The proposal distribution defines a symmetric random walk on the row/column vector taking values in {−1,+1,0} by randomly selecting one value and resampling it with identical probability to the two other possible values. After updating the ith row/column in the upper triangle matrix and copying the values to the lower triangle, the corresponding diagonal element is imputed deterministically as Ψ ii =∑ j≠i |Ψ ij |+ϵ. This creates \(\widetilde{\varPsi}_{\text{proposed}}\) which is then accepted according to the usual Metropolis-Hastings equations based on the posterior ratio \(P(\widetilde{\varPsi}_{\text{proposed}}| \bullet) / P(\widetilde {\varPsi }_{\text{old}}| \bullet)\). The acceptance threshold is given by just the posterior ratio since we implement a symmetric random walk Metropolis sampling. The entire Metropolis-within-Gibbs sampler is described in Algorithm 1.
Algorithm 1
(Metropolis-within-Gibbs sampler)
in ith row/column vector in upper triangle of Ψ
-
1:
Uniformly select index k, k ∈{1,…,i−1,i+1,…,n}
-
2:
Resample value at Ψ ik by drawing with equal probability from {−1,+1,0}
-
3:
Set Ψ ki = Ψ ik and update Ψ ii and Ψ kk (to ensure diagonal dominance). This is \(\widetilde{\varPsi}_{\text{proposed}}\)
-
4:
Compute \(P(\tilde{\varPsi}| \bullet) \propto\mathcal{L}(\widetilde{\varPsi}) P_{1}(\varPsi) P_{2}(\varPsi) \)
-
5:
Calculate the acceptance threshold a = min (1, \(\frac {P(\widetilde{\varPsi}_{\text{proposed}}| \bullet)}{ P(\widetilde {\varPsi }_{\text{old}}| \bullet)}\))
-
6:
Sample u ∼ Unif(0,1)
-
7:
if (u<a) accept \(\widetilde {\varPsi }_{\text{proposed}}\), else reject.
end
Since the proposal distribution, \(\widetilde{\varPsi}_{\text{proposed}}\), defines a symmetric random walk on set \(\mathcal{A}\) consisting of diagonally-dominant matrices, one can reach any other element in \(\mathcal{A}\) with non-zero probability after a sufficient number of \(\frac{n(n-1)}{2}\) steps that account for number of elements in the upper triangle of Ψ. This construction ensures ergodicity in the Markov chain.
Note that the (usually unknown) degrees of freedom d in the shift- and scale-invariant likelihood (4) appears only in the exponents and, thus, has the formal role of an annealing parameter. In the annealing framework, the likelihood equation is seen as the energy function with d as the annealing temperature. We use this property of d during the burn-in period, where d is slowly increased to “anneal” the system until the acceptance probability reaches below a certain threshold, and then the sampled Ψ-matrices are averaged to approximate the posterior expectation. If a truly sparse solution is desired, the annealing is continued until a network is “frozen”.
Implementation & complexity analysis
Presumably the most efficient way to recompute \(P(\widetilde{\varPsi}| \bullet)\) after a row/column update of Ψ is through the identity: \(\det(\widetilde {\varPsi}) = (\det({\varPsi}) / \boldsymbol{1}^{t} \varPsi\boldsymbol{1})\cdot n\) (McCullagh 2009). Assume now we have a QR factorization of Ψ old before the update. Then the new \(\varPsi= \varPsi_{\text{old}} + \boldsymbol{v}_{i} \boldsymbol {v}_{i}^{t} + \boldsymbol{v}_{j} \boldsymbol{v}_{j}^{t}\) where i,j are the row/column indices of Ψ old to be updated along with the corresponding diagonal elements and this accounts for two rank-one updates. Thus the QR factorization of the new \(\widetilde{\varPsi}\) can also be computed in O(n 2) time and \(\det(\widetilde{\varPsi})\) is then derived as ∏ i R ii . The trace \(\operatorname{tr}( \widetilde{\varPsi}D)\) is also computed in O(n 2) time, as it is the sum of the element-wise products of the entries in \(\widetilde{\varPsi}\) and D. It is clear that this scaling behavior is prohibitive for very large matrices, but matrices of size in the hundreds can be easily handled, and for larger matrices with a “complex” inverse covariance structure the statistical significance of the reconstructed networks is questionable anyway, unless a really huge number of measurements is available. Moreover there is an elegant way of avoiding such large matrices by reconstructing module networks as outlined in the next section.
6 Inferring module networks
A particularly interesting property of TiWnet is its applicability to learning module networks. We define a module as a completely-connected subgraph, forming nodes in a module network. As a motivating example we refer to our gene-expression example of X n×d where the measurements consist of d microarrays for n genes. In usual situations having far more objects than measurements, one should not be too optimistic to reconstruct a meaningful network, in particular if the measurements are noisy and if the underlying network has “hubs”—nodes with high degrees. Generally when the node neighborhoods are small, networks can be learned well whereas when the neighborhoods tend to grow larger as in the case with hubs, learning networks gets difficult due to the higher-order dependencies existing between nodes. Unfortunately, both high noise and existence of hubs are common in such data. To address these issues, we present the computationally-attractive method of initially creating clusters of objects, that we connote as modules, over which networks are learned. Considering the gene-expression example, there are usually groups of genes which have highly correlated expressions and can often be jointly represented by one cluster without losing too much relevant information, due to high noise. To create clusters, we begin with the d-dimensional expression profile vectors, \(\textbf{\emph{x}} \in\mathbb{R}^{d}\), of the n genes and use a mixture model to cluster these expression vectors into “modules”, reducing n to the effective number of modules. The mixture model density is given by \(p(\textbf{\emph{x}}) = \sum_{k=1}^{K} \pi_{k} p_{k}(\textbf{\emph{x}})\) where π k is the mixing coefficient and \(p_{k}(\textbf{\emph{x}})\) is the component distribution of the kth module. Partition matrices can be viewed as block-diagonal covariances (see McCullagh and Yang 2008; Vogt et al. 2010), and in the terminology of Gaussian graphical models the blocks define independent subgraphs with completely connected nodes, which is what we have defined as modules.
The link to learn networks on top of these modules goes via kernels defined on probability distributions. We can use kernels like Bhattacharyya kernel (Jebara et al. 2004):
or the Jensen-Shannon kernel (Martins et al. 2008):
(where \(\mathcal{H}\) is the Shannon entropy) over the component distributions of the modules to compute an inner-product matrix of the modules. Network inference is then performed using this resulting inner-product matrix.
Usually, there is no information available about the origin of the underlying space, and by reconstructing networks from such kernels we heavily rely on the geometric invariance encoded in the TiWnet model. This elegant solution for inferring module networks overcomes statistical problems, and is also a principled way of applying the TiWnet to large problem instances. An example of this strategy is presented in Sect. 7.
7 Experiments
7.1 Toy examples
The TiWnet is compared with the graph lasso method (Friedman et al. 2007) and with its non-invariant counterpart Wnet on artificial data. The graph lasso maximizes the standard Wishart likelihood under a sparsity penalty on the inverse covariance matrix, see (2). Wnet replaces the invariant Wishart used in TiWnet with the standard Wishart (1), but uses otherwise exactly the same MCMC code.
Sample generation
For these experiments we implemented a data generator that mimics the assumed generative model as shown in Fig. 3. First, a sparse inverse covariance matrix \(\varPsi\in\mathbb{R}^{n\times n}\) with n=25 is sampled. Networks with uniformly sampled node degrees are relatively easy to reconstruct for most methods, while networks with “hubs” are better suited for showing differences. Hubs are nodes with high degrees that appear naturally in many real networks since they often are scale-free i.e. their node degrees follow a power law. We simulate such networks by drawing node degrees from a Pareto(7×10−5,0.5)-distribution and use these values as parameters in a binomial model for sampling 0/1 entries in the rows/columns of Ψ. The sign of these entries is randomly flipped, and scaled with samples from a Gamma- or uniform distribution (see below for a precise description of the distribution of the edge weights). The diagonal elements are imputed as the row-sums of absolute values plus some small constant ϵ(=0.1) to ensure full rank. We draw d vectors \(\boldsymbol{x}^{o}_{i} \in\mathbb{R}^{n}\) from \(\mathcal {N}(\boldsymbol{0}_{n}, \varPsi )\), and arrange them as columns in X o. \(S^{o} = \frac{1}{d}X^{o}(X^{o})^{t}\) is then a central Wishart matrix. To study the effect of biased measurements, we randomly generate biases b (i=1,…,d), resulting in the mean-shifted vectors x i in Fig. 3. The resulting matrix S is non-central Wishart with non-centrality matrix Θ=Σ −1 MM t, and M=1 b t. In fact, we always sample two i.i.d. replicates of the matrices S o and S, and we use the second ones as a test set to tune all model parameters of the respective methods (the ℓ 1 regularization parameter in graph lasso and the corresponding λ-parameter in the prior P 2(Ψ) of TiWnet and Wnet) by maximizing the predictive likelihood on this test set. In order to separate the effects of parameter tuning from the “true” differences in the models themselves, we additionally compared all models by tuning them to the same sparsity level. Figure 7 shows an example network drawn from our data generator together with a Gamma(2,4)-distribution of the absolute values of the edge weights.
Simulations
In a first experiment, we compare the performance of TiWnet with graph lasso and Wnet. The quality of the reconstructed networks is measured as follows: A binary vector l of size n(n−1)/2 encoding the presence of an edge in the upper triangle matrix of Ψ is treated as “true” edge labels, and this vector is compared with a vector \(\hat {\boldsymbol{l}}\) containing the absolute values of elements in the reconstructed \(\hat {\varPsi}\) after zeroing those elements in \(\hat{\boldsymbol{l}}\) which are not sign-consistent with the nonzero entries in Ψ (meaning that sign-inconsistent estimates will always be counted as errors). The agreement of l and \(\hat{\boldsymbol{l}}\) is measured with the F-measure, i.e. the highest harmonic mean of precision and recall under thresholding the elements in \(\hat{\boldsymbol{l}}\). The left panel in Fig. 8 shows boxplots of F-scores obtained in 20 experiments with randomly generated Ψ-matrices for graph lasso, TiWnet, and Wnet. For graph lasso, a series of \(\hat{\varPsi}\) estimates with increasing ℓ 1 penalty parameter is computed using the glassopath function from the glasso R-package.Footnote 4 For the MCMC-based methods TiWnet and Wnet, \(\hat{\varPsi}\) is computed as the sample average of networks drawn from the Gibbs samples after a certain burn-in period. The right panel shows the outcome of a Friedman test (i.e. non-parametric ANOVA) with post-hoc analysis for assessing the significance of the differences, see figure caption for further details. From the results we conclude that for the methods relying on the standard Wishart distribution (i.e. graph lasso and Wnet), column centering does not overcome the problem of model mismatch due to column biases. Further, TiWnet using only the pairwise distances D performs as well as graph lasso on the original (not shifted) data. Note that for the original S o, graph lasso might indeed serve as a “gold standard”, since the model assumptions are exactly met. And last but not least, the invariance properties of the likelihood used in TiWnet are indeed essential for its good performance, since its non-invariant counterpart Wnet uses exactly the same MCMC code (apart from using the standard Wishart likelihood, of course).
Left: Boxplots of F-scores obtained in 20 experiments with randomly generated Ψ-matrices for graph lasso (GL): GL.o uses original S o and GL.C uses column-centered S, TiWnet, and Wnet. Right: Boxplot of the pairwise differences together with color-coded significance (green, if multiple-testing-corrected p<0.05) computed by a non-parametric Friedman test with post-hoc analysis (Wilcoxon-Nemenyi-McDonald-Thompson test, see Hollander and Wolfe 1999) (Color figure online)
The left column of Fig. 9 shows the networks reconstructed by the different methods (networks with highest predictive likelihood for graph lasso and sample average in the case of TiWnet and Wnet). The right column depicts the thresholded networks according to the best F-score with respect to the known ground truth. Analyzing the reconstructed networks in the left column of Fig. 9, it is obvious that the graph lasso networks are very dense, and that thresholding the edge weights is essential for a high F-score. Note, however, that such thresholding is only possible if the ground truth is known. The average TiWnet/Wnet result is also dense, since it represents the empirical distribution of networks sampled during the MCMC iterations. Thresholding the edges is also essential here, but for the MCMC models we can easily compute a truly sparse network by annealing the Markov chain without having access to the ground truth. Further studying this effect leads us to a second experiment, where we directly compare the lasso-type networks reconstructed using a sequence of ℓ 1 regularization parameters with the “frozen” TiWnet after annealing. In this comparison, however we do not allow for further thresholding the edge weights when computing the F-score (i.e. we replace the entries in \(\hat {\boldsymbol{l}}\) by their sign). The left panel in Fig. 10 shows that TiWnet clearly outperforms all other methods. We conclude that model selection in the lasso methods does not work satisfactorily, probably because the ℓ 1 penalty not only sparsifies the solution, but also globally shrinks the parameters. As a result, truly sparse solutions have a relatively small predictive likelihood. Further, it is obvious that in the case of TiWnet, the annealing mechanism in our MCMC sampler produces very sparse networks of very high quality. The direct comparison with the non-invariant Wnet model shows that the invariance in the Wishart likelihood is indeed the essential ingredient of TiWnet.
Left column: networks with highest predictive likelihood for graph lasso (GL): GL.o uses original S o and GL.C uses column-centered S and sample averages for TiWnet, and Wnet. Right column: Optimally thresholded networks according to the best F-score with respect to the known ground truth. The underlying ground truth network is the one depicted in Fig. 7
Left: F-scores without additional thresholding for graph lasso (GL): GL.o uses original S o and GL.C uses column-centered S, (model selected according to best predictive likelihood) and TiWnet/Wnet (also selected according to predictive likelihood, then annealed). Right: Corresponding boxplots of the pairwise differences
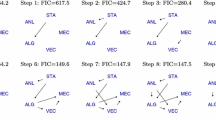
It is clear that the results of the previous experiment crucially depend on the model selection step. To exclude differences caused by model selection, in a third experiment we additionally investigated the performance of the models after tuning all of them to the same sparsity level as the annealed network obtained by TiWnet. The results are presented in Fig. 11. It is obvious that TiWnet clearly outperforms its competitors. Inspecting the recovered networks for the graph lasso, we see that under these restrictive sparsity constraints, the lasso selection has particular problems to recover the edges connecting hubs in the network.
F-scores obtained by tuning the models to (roughly) the same sparsity level as the annealed TiWnet, averaged over 20 randomly drawn networks (top left). Other panels: networks recovered by graph lasso (GL): GL.o uses original S o and GL.C uses column-centered S and TiWnet in one of the 20 experiments. The underlying ground truth network is again the one depicted in Fig. 7
We test the dependency of these results on the validity of the model assumptions, in a fourth experiment. The TiWnet in its simplest form uses only three levels for edge weights: 0,+1,−1. It is clear that this simple model will have problems recovering networks with a very high dynamic range of edge weights (the generalization to more than 3 levels, however, is straight forward). Since the edge weight distribution in the previous experiments was relatively concentrated around the mode of the gamma distribution (see Fig. 7), we changed the distribution to a uniform distribution over the interval [0.2,20]. This choice implies a uniform dynamic range over two decades. The performance of TiWnet measured in terms of the F-score, however, did not change significantly, see the top row in Fig. 12 in comparison to Fig. 8.
Top row: Testing the quality of the three-level prior on the elements in the inverse covariance matrix by simulating edge-weights with a uniform distribution on the interval [0.2,20] for graph lasso (GL) (GL.o uses original S o and GL.C uses column-centered S) and TiWnet/Wnet. Bottom row: Results using a multivariate Student-t distribution in three degrees of freedom instead of a normal distribution to generate the columns in X o
In order to further test the robustness under model mismatches, in a fifth experiment, we substituted the Gaussian to produce X o with a Student-t distribution in our data generator. The resulting plot of F-scores (Fig. 12, bottom row) has the same overall-structure as in Fig. 8, which shows that TiWnet is relatively robust under such model mismatches. In summary, we conclude from these experiments that TiWnet significantly outperforms its competitors, and that the main reason for this good performance is indeed attributed to the invariant Wishart likelihood.
7.2 Real-world examples
A module network of Escherichia coli genes
For inferring module networks in a biological context, we applied the TiWnet to a published dataset of promoter activity data from ≈1100 Escherichia coli operons (Zaslaver et al. 2006). The promoter activities were recorded with high temporal resolution as the bacteria progressed through a classical growth curve experiment experiencing a “diauxic shift”. Certain groups of genes are induced or repressed during specific stages of this growth curve. Cluster analysis of the promoter activity data was performed using a spherical Gaussian mixture model with shared variance σ: \(p(x)=\sum_{k}\pi_{k} \mathcal{N}(x|\mu_{k},\sigma)\) along with a Dirichlet-process prior to automatically select the number of clusters. This revealed the presence of 14 distinct gene clusters (see expression profiles of nodes in Fig. 13). Network inference with TiWnet was carried out on a Bhattacharyya kernel K B computed over the Gaussian clusters where \(K_{B}(k,j)=\exp^{ -\|\mu_{k} - \mu_{j}\|^{2}/ 8\sigma^{2}}\) (see Jebara et al. 2004). When the clusters were analyzed, genes known to be co-regulated were predominantly found in the same or nearby clusters with positive partial correlations. For example, during the diauxic shift experiment, the transcriptional activator CRP induces a certain set of genes in a specific growth phase (Keseler et al. 2011). Strikingly, of the 72 known CRP regulated operons in the dataset, 43 genes are found in cluster 6 or the four neighboring clusters (3,9,11,13). Likewise, genes involved in specific molecular functions (those coding for proteins involved in amino acid biosynthesis pathways) were found in close proximity in the network, for example in nodes 1 and 2 (Fig. 13). Physiologically, this co-regulation makes sense since protein biosynthesis (carried out by the ribosome) depends on a constant supply of synthesized amino acids. Thus TiWnet can successfully identify connections between genes co-regulated by the same molecular factor, or are involved in interlinked molecular processes.
“Landscape” of chemical compounds with in vitro activity against HIV-1
As a second real-world example TiWnet is used to reconstruct a network of chemical compounds. We enriched a small list of compounds identified in an AIDS antiviral screen by NCI/NIH available at http://dtp.nci.nih.gov/docs/aids/searches/list.html#NPorA with all currently available anti-HIV drugs, yielding a set of 86 compounds. Chemical hashed fingerprints were computed from the chemical structure of the compounds that was encoded in SMILES strings (Weininger 1988). The Tanimoto kernel, a similarity matrix S of inner-product type, is constructed by the pairwise Tanimoto association scores (Rogers and Tanimoto 1960) between the compounds. Since the geometric position of the underlying Euclidean space is unclear, we again relied heavily on the geometric invariance inherent in TiWnet. The resulting network (Fig. 14) shows several disconnected components which nicely correspond to chemical classes (the node colors). Currently available anti-HIV drugs are indicated by their chemical and commercial names alongside their 2D-structures depicting the chemical similarity underlying this network. These drugs belong to the functional groups “Nucleoside reverse transcriptase inhibitors (NRTI)”, “Non-nucleoside reverse transcriptase inhibitors (NNRTI)”, “Protease inhibitors”, “Integrase inhibitors”, or “Entry inhibitors”, and most compounds of a certain functional type cluster together in the graph. Medically, this network can be very useful to predict “cross resistance” between resistant HIV-1 variants and drugs and is especially distinctive for NRTIs. The pairs lamivudine-emtricitabine, tenofovir-abacavir, and d4T-zidovudine(ZDV) show almost the same resistance profiles (Johnson et al. 2010). This similarity is very well reflected by our network where these pairs are in close proximity.
It is worth noting that graph lasso has similar difficulties on this dataset as in the toy examples. When following the solution path by varying the penalty parameter, it is difficult to find a good compromise between sparsity and connectivity: either the obtained graphs are very dense being difficult to plot and harder to interpret, or are increasingly sparse in which, however, several interesting structural connections are lost since many singleton nodes are created. For a graphical depiction, refer Figs. 1–3 in Supplementary material A. The R and C++ source code for this experiment using TiWnet is available at http://bmda.cs.unibas.ch/TiWnet.
The “Landscape” of glycosidase enzymes of Escherichia coli.
In yet another real-world experiment, we use TiWnet to extract the network of Glycosidase enzymes of Escherichia coli. Every enzyme is represented by its vectorized contact map computed from their PDB (Protein Data Bank) files. A contact map is a compact representation of the topological information of the 3D protein structure, present in the PDB file, into a symmetric, binary 2D matrix consisting of pairwise, inter-residue contacts: for a protein with R amino acid residues, the contact map (see Fig. 15) would be a R×R binary matrix CM where CM ij =1 if residues i and j are similar or 0 otherwise. The starting point for TiWnet is the contact map representation of an enzyme whose row-wise vectors serve as strings. To obtain the pairwise distances between strings in these contact maps, we compute the Normalized Compression Distance (NCD) (Li et al. 2004) which is an approximation to the Normalized Information Distance (NID). The NID (Li et al. 2004) is a distance metric minimizing any admissible metric between objects. Given strings x and y, NID is proportional to the length of the shortest program that computes x|y as well as y|x and is defined as
where K(x) is the Kolmogorov complexity of the string x. The real-world approximated version of NID is given by NCD and is calculated as follows:
where C(xy) represents the size of the file obtained by compressing the concatenation of x and y. We use the ProCKSI-Server (Barthel et al. 2007; Krasnogor and Pelta 2004) to compute NCD(x,y).
The network extracted by TiWnet from the NCD values is shown in Fig. 16. The network shows a clear formation of subnets of enzymes given by node colors. To further analyze the obtained subnets, we look at their corresponding Gene Ontology (GO) annotations. The GO annotations are part of a Directed Acyclic Graph (DAG), covering three orthogonal taxonomies: molecular function, biological process and cellular component. For two subnets (shown in dotted circles in Fig. 16), we inspect the GO subgraphs that are subsets of the entire GO graph. The three taxonomic components of the GO subgraphs explain the proteins in these subnets and show the relevance of these proteins through the color-scaling scheme where red accounts for highly-frequent enzymes. As depicted, the GO subgraphs plotted for the two subnets consist of many highly-significant enzymes thus emphasizing that the subnets so obtained using TiWnet are not random, but instead consist of groups of enzymes having shared annotations. Subnets of this kind are beneficial to identify the most important GO domains for a given set of enzymes and also suggest biological areas that warrant further study.
Top: “Landscape” of Glycosidase enzymes of Escherichia coli. Black/green edges = positive/negative partial correlation. For two subnets, Subnet 1 and 2 (encircled by dots), the corresponding Gene Ontology (GO) subgraphs (centre and bottom) are given that explain the enzymes present in the subnet. The multiple red/orange-hued boxes in the GO subgraph signal highly-frequent enzymes thus showing that the subnets extracted by TiWnet are not random but instead contain groups of enzymes having shared annotations (Color figure online)
8 TiWD versus TiWnet
In this section, we describe the Translational-invariant Wishart Dirichlet (TiWD) cluster process (Vogt et al. 2010) (previously mentioned in Sect. 4) and explain why it is unsuited for extracting networks. TiWD is a fully-probabilistic model for clustering and is specifically devised to work with pairwise Euclidean distances by suitably encoding the translational and rotational invariances. Although the TiWD clustering model and TiWnet use identical likelihoods, the priors in both models are different.
The TiWD clustering model uses a Dirichlet-Multinomial type prior over clusters with the priors being restricted to block-diagonal form. This kind of prior construction is incompetent for network inference since if such a prior is used, all networks would always decompose into separated clusters which are maximal cliques i.e. fully connected within themselves. Therefore, to enable network recovery an enhanced prior construction is necessary and to this end, TiWnet uses a prior that relaxes the block-diagonal form. The two-component TiWnet prior (Sect. 5.2) is designed that, along with the invariance encoded in the likelihood, leads to sparse network recovery. The resulting Ψ is constructed to be a sparse diagonally-dominant matrix.
We illustrate the difference between the TiWnet and TiWD prior constructions in Fig. 17. The top panel of Fig. 17 depicts the original network generated using Ψ (no longer block-diagonal) meant for network inference and the inferred network using TiWnet. The black/green edges depict the positive/negative partial correlations between the nodes. The bottom panel of Fig. 17 shows the inferred block-diagonal Ψ (left) obtained from TiWD clustering that uses a block-diagonal prior and different views of the network obtained using this Ψ: the center plot shows that the network is densely connected bearing no resemblance to the original network and the right plot highlights that the network gets decomposed into separate fully-connected clusters (maximal cliques). Moreover, the network fails to capture the positive/negative partial correlations between the nodes since the inferred Σ in the case of TiWD clustering only contains information regarding the cluster structure but without signs.
Illustration of the difference between TiWnet and TiWD clustering (Vogt et al. 2010) using data generated from Ψ (no longer block-diagonal) designed for network inference. Top: Left: Original network. Right: Inferred sparse network using TiWnet. The black/green edges denote positive/negative partial correlations between nodes. Bottom: Left: Inferred Ψ using TiWD clustering that has a block-diagonal structure which leads to fully-connected clusters (maximal cliques). Center: Densely-connected network obtained using this block-diagonal Ψ. The edges do not differentiate between positive/negative partial correlations. Right: The same network as in the center now showing that the network decomposes into separate maximal cliques. Here the network decomposes into 5 clusters viz. 3 fully-connected and 2 singletons (Color figure online)
From the above discussion, it is obvious that clustering is a specialized case of network inference and that general networks cannot be recovered using the TiWD clustering model of Vogt et al. (2010). Thus the prior designed for use in TiWnet is not of the block-diagonal form thereby allowing any possible internodal interaction. Combining this enhanced prior suitable for network reconstruction with the likelihood, we are able to perform Bayesian network inference in TiWnet. We refer the reader to the Sect. 5 for complete details of our inference mechanism.
9 Contributions of TiWnet
TiWnet deals with distance data and is therefore, shift invariant
Classical GGMs extract networks from vectorial representations of objects and are based on the standard (central) Wishart likelihood model. The central Wishart model is only justified for zero column-shifts (i.i.d. data). These methods have solely relied on the i.i.d. assumption and not catered to the inherent column-shifts, thereby possibly generating biased networks. Graph lasso’s performance on column-shifts (Fig. 4) and our extensive comparison experiments in Sect. 7 validate that not handling the column-wise biases is detrimental to network extraction. Instead, TiWnet based on D is shift-invariant and can therefore handle non-i.i.d. data (non-vectorial data). We show that in practical applications this shift invariance is an essential ingredient for recovering correct networks. Due to this, network reconstruction is possible using any D induced by a Mercer kernel that represents objects with structures for which the underlying vectorial space is unknown.
Generate module networks
Being able to derive networks from such complex objects, for example graphs and probability distributions, further leads to the development of module networks which addresses the high-dimensionality problem setting. A module connotes a cluster of homogeneous objects, thereby reducing the number of objects to that of the overall clusters, where each module is now represented by a probabilistic distribution or a graph over which a Mercer kernel can be constructed and used for network discovery.
TiWnet provides a distribution over networks
Graph lasso was devised for estimating a truly sparse network from the data. Since TiWnet is fully probabilistic, on output we not only obtain a single network but a distribution of networks explaining the data. For many cases in reality, this is more meaningful since one has access to possible structural variations of the extracted networks.
TiWnet provides an annealed network
Further, if required, our method has the flexibility to yield a single MAP-estimate network by simulated annealing and this is possible even without knowing the underlying ground truth. On the contrary, obtaining such an equivalent sparse network with graph lasso would require thresholding the edge weights and this too is only possible if the ground truth is known. The graph lasso’s sparse networks obtained by the highest predictive likelihood are comparatively less better than TiWnet’s (Fig. 10). This could probably be to the improper model selection in the lasso-based models in the presence of column-shifts in the data.
TiWnet can extract hub nodes
Comparing TiWnet with graph lasso and Wnet based on the same sparsity level, we see that graph lasso clearly fails in recovering hub nodes (Fig. 11). TiWnet still returns a sparse annealed network with these desirable properties that seem difficult to be achieved by graph lasso. Thus, the experiments justify TiWnet’s superior performance against lasso-based non-invariant models and the reason can be clearly attributed to the translation-invariance encoded in the Wishart likelihood.
10 Conclusion
The TiWnet model is a fully probabilistic approach to inferring GGMs from pairwise Euclidean distances obtained from inner-product similarity matrices (i.e. kernels) of n objects. Traditional models for reconstructing GGMs, for example lasso-type methods, are based on the central Wishart likelihood parametrized by the inverse covariance, and sparsity of the latter is usually enforced by some penalty term. Assuming a central Wishart, however, is equivalent to assuming that the origin of the coordinate system is known. If these methods use on input only kernel matrices, then usually only the kernels’ pairwise distance information is truly relevant. Since traditional methods solely rely on the origin implicitly encoded in any such kernel, they might generate biased networks. Our TiWnet method is specifically designed to work with pairwise distances since the likelihood used in inference depends only on these distances. Combining this likelihood with a prior suited for sparse network recovery, we are able to extract sparse networks using only pairwise distances. This property opens up a huge new application field for GGMs, because network inference can now be carried out on any such distance matrix induced by a Mercer kernel on graphs, probability distributions or more complex structures. We also present an efficient MCMC sampler for TiWnet making it applicable to medium-size instances, and the possibly remaining scaling issues may be overcome by inferring module networks using kernels defined on probability distributions over groups of nodes. Comparisons with competing methods demonstrate the high quality of networks obtained from TiWnet, evoking the effectiveness of working with pairwise distances. TiWnet is also robust to model mismatches unlike existing methods. The three real-world examples provide an insight into the huge variety of possible applications.
Notes
The central standard Wishart distribution is defined for S o=X o(X o)t. Throughout the paper, we use \(S^{o} = \frac {1}{d}X^{o} (X^{o})^{t}\) so that d appears in the central Wishart distribution and can be later used as an annealing parameter in the inference procedure.
The names of the Wishart distribution are inconsistent in the literature. We use the notation in Díaz-García et al. (1997).
This does not necessarily imply that it is meaningful to use any Mercer kernel for reconstructing a Gaussian graphical model. The main focus here is not on kernels as a means for mapping input vectors to high-dimensional feature spaces in order to exploit nonlinearity in the input space but as similarity measures.
The central standard Wishart distribution is defined for S o=X o(X o)t. Throughout the paper, we use \(S^{o} = \frac {1}{d}X^{o} (X^{o})^{t}\) so that d appears in the central Wishart distribution and can be later used as an annealing parameter in the inference procedure.
References
Allen, G. I., & Tibshirani, R. (2010). Transposable regularized covariance models with an application to missing data imputation. Annals of Applied Statistics, 4(2), 764–790.
Anandkumar, A., Tan, V., & Willsky, A. S. (2011). High-dimensional graphical model selection: tractable graph families and necessary conditions. Advances in Neural Information Processing Systems, 24, 1863–1871.
Barthel, D., Hirst, J. D., Blazewicz, J., Burke, E. K., & Krasnogor, N. (2007). ProCKSI: a decision support system for protein (structure) comparison, knowledge, similarity and information. BMC Bioinformatics, 8(416), 3250–3264.
Berger, J. O., Liseo, B., & Wolpert, R. L. (1999). Integrated likelihood methods for eliminating nuisance parameters. Statistical Science, 14(1), 1–28.
Carvalho, C. M., & West, M. (2007). Dynamic matrix-variate graphical models. Bayesian Analysis, 2(1), 69–97.
Cristianini, N., & Shawe-Taylor, J. (2000). An introduction to support vector machines. Cambridge: Cambridge University Press.
Daniels, M. J., & Pourahmadi, M. (2009). Modeling covariance matrices via partial autocorrelations. Journal of Multivariate Analysis, 100(10), 2352–2363.
Díaz-García, J. A., Gutierrez Jáimez, R., & Mardia, K. V. (1997). Wishart and pseudo-Wishart distributions and some applications to shape theory. Journal of Multivariate Analysis, 63, 73–87.
Friedman, J., Hastie, T., & Tibshirani, R. (2007). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9, 432–441.
Gupta, A. K., & Nagar, D. K. (1999). Matrix variate distributions. London/Boca Raton: Chapman & Hall/CRC Press. ISBN 978-1584880462.
Harry, J. (1996). Families of m-variate distributions with given margins and m(m−1)/2 bivariate dependence parameters. In L. Rüschendorf, B. Schweizer, & M. D. Taylor (Eds.), IMS lecture notes: Vol. 28. Distributions with fixed marginals and related topics (pp. 120–141). Providence: AMS.
Harville, D. A. (1974). Bayesian inference for variance components using only error contrasts. Biometrika, 61(2), 383–385.
Hollander, M., & Wolfe, D. A. (1999). Nonparametric statistical methods (2nd ed.). New York: Wiley-Interscience.
Jebara, T., Kondor, R., & Howard, A. (2004). Probability product kernels. Journal of Machine Learning Research, 5, 819–844.
Johnson, J. K., Malioutov, D. M., & Willsky, A. S. (2005a). Walk-summable Gaussian networks and walk-sum interpretation of Gaussian belief propagation (Technical Report—2650). LIDS, MIT.
Johnson, J. K., Malioutov, D. M., & Willsky, A. S. (2005b). Walk-sum interpretation and analysis of Gaussian belief propagation. In Advances in neural information processing systems 18 (pp. 579–586).
Johnson, V. A., Brun-Vezinet, F., Clotet, B., et al. (2010). Update of the drug resistance mutations in HIV-1: Dec 2010. Topics in HIV Medicine, 18(5), 156–163.
Keseler, I. M., Collado-Vides, J., Santos-Zavaleta, A., et al. (2011). Ecocyc: a comprehensive database of Escherichia coli biology. Nucleic Acids Research, 39, D583–D590.
Kolar, M., Song, L., Ahmed, A., & Xing, E. P. (2010a). Estimating time-varying networks. Annals of Applied Statistics, 4(1), 94–123.
Kolar, M., Parikh, A. P., & Xing, E. P. (2010b). On sparse nonparametric conditional covariance selection. In Proceedings of the 27th international conference on machine learning (pp. 559–566).
Krasnogor, N., & Pelta, D. A. (2004). Measuring the similarity of protein structures by means of the universal similarity metric. Bioinformatics, 20(7), 1015–1021.
Li, M., Chen, X., Li, X., Ma, B., & Vitanyi, P. M. B. (2004). The similarity metric. IEEE Transactions on Information Theory, 50(12), 3250–3264.
Martins, A. F. T., Figueiredo, M. A. T., Aguiar, P. M. Q., Smith, N. A., & Xing, E. P. (2008). Nonextensive entropic kernels. In Proceedings of the 25th international conference on machine learning (pp. 640–647).
McCullagh, P. (2009). Marginal likelihood for distance matrices. Statistica Sinica, 19, 631–649.
McCullagh, P., & Yang, J. (2008). How many clusters? Bayesian Analysis, 3, 101–120.
Meinhausen, N., & Bühlmann, P. (2006). High dimensional graphs and variable selection with the Lasso. The Annals of Statistics, 38, 1436–1462.
Mitchell, T. J., & Beauchamp, J. J. (1988). Bayesian variable selection in linear regression. Journal of the American Statistical Association, 83(404), 1023–1032.
Muirhead, R. J. (1982). Aspects of multivariate statistical theory. New York: Wiley.
Patterson, D., & Thompson, R. (1971). Recovery of inter-block information when block sizes are unequal. Biometrika, 58(3), 545–554.
Prabhakaran, S., Metzner, K. J., Boehm, A., & Roth, V. (2012). Recovering networks from distance data. Journal of Machine Learning Research Workshop and Conference Proceedings, 25, 349–364.
Rogers, D. J., & Tanimoto, T. T. (1960). A computer program for classifying plants. Science, 132, 1115–1118.
Schölkopf, B., Smola, A., & Müller, K.-R. (1998). Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation, 10, 1299–1319.
Tunnicliffe-Wilson, G. (1989). On the use of marginal likelihood in time series model estimation. Journal of the Royal Statistical Society, Series B, 51, 15–27.
Uhlig, H. (1994). On singular Wishart and singular multivariate beta distributions. The Annals of Statistics, 22, 395–405.
Vapnik, V. (1998). Statistical learning theory. New York: Wiley.
Vogt, J. E., Prabhakaran, S., Fuchs, T. J., & Roth, V. (2010). The translation-invariant Wishart-Dirichlet process for clustering distance data. In Proceedings of the 27th international conference on machine learning (pp. 1111–1118).
Weininger, D. (1988). SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. Journal of Chemical Information and Computer Sciences, 28(1), 31–36.
Zaslaver, A., Bren, A., Ronen, M., et al. (2006). A comprehensive library of fluorescent transcriptional reporters for Escherichia coli. Nature Methods, 3(8), 623–628.
Zhou, S., Lafferty, J., & Wasserman, L. (2010). Time varying undirected graphs. Machine Learning, 83, 295–319.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editors: Zhi-Hua Zhou, Wee Sun Lee, Steven Hoi, Wray Buntine, and Hiroshi Motoda.
A. Böhm is deceased.
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Appendix: Proof of Proposition 1
Appendix: Proof of Proposition 1
The marginal likelihood in terms of D, \(\mathcal{L}(\varPsi;t(X))\), is developed indirectly through the distribution of S. Here, \(t(X)= \frac{(X - \mathbf{1}_{n}\hat{\boldsymbol {b}^{t}})}{\|X - \mathbf{1}_{n}\hat{\boldsymbol{b}^{t}}\|}\) is the standardized statistic and is constant on the set of all X and S mapping to the same D. Therefore t(X) can be seen as a function of the scaled version of D alone i.e \(f(\frac{D}{\|D\|})\). Our interest parameter is Ψ. McCullagh (2009) shows that the distribution of an arbitrary \(S \in \mathbb{S}(D)\) can be analytically derived as a singular Wishart distribution with a rank-deficient covariance matrix.
We first explain the linear transformation and its kernel applied to S necessary to formulate the marginal likelihood and then proceed with the derivation of the marginal likelihood in D.
Linear transformation and kernel
Given a transformation matrix \(\mathbb{L}\) with kernel \(\mathcal{K}\), i.e. \(\mathbb{L}\mathcal{K}=\mathbf{0}\) and a generalized Gaussian random variable in \(\mathcal{R}^{n}\), \(X \sim\mathcal{N}(\mathcal {K},\pmb {\mu},\varSigma)\), then the linearly transformed vector \(\mathbb{L}X\) is distributed as \(\mathcal{N}(\mathbb{L}\pmb {\mu },\mathbb{L}\varSigma\mathbb{L}^{t})\). Under \(\mathcal{K}=\mathbf{1}_{n}\), two parameter values (\(\pmb{\mu}_{1}\), Σ 1) and (\(\pmb{\mu}_{2}\), Σ 2) are equivalent when \(\mathbb{L}(\pmb {\mu }_{1} - \pmb{\mu}_{2})=\mathbf{0}\) and \(\mathbb{L}(\varSigma_{1}-\varSigma_{2})\mathbb{L}^{t}=\mathbf{0}\) i.e. when \((\pmb{\mu}_{1}-\pmb{\mu}_{2}) \in\mathbf{1}_{n}\) and \((\varSigma_{1}-\varSigma_{2}) \in\{\mathbf{1}_{n}\boldsymbol {v}^{t}+\boldsymbol{v}\mathbf{1}_{n}^{t}; \boldsymbol{v} \in\mathcal{R}^{n}\}\), the space denoted by \(sym^{2}(\mathbf{1}_{n} \otimes\mathcal{R}^{n})\). Equivalent parameter values denote the same distribution. Corresponding to the generalized distribution of X with kernel \(\mathcal{K} = \mathbf{1}_{n}\), the similarity matrix \(S=\frac{1}{d}XX^{t}\) is now distributed as \(S \sim \mathcal{W}_{d}(\mathbf{1}_{n},\varSigma)\). D exhibits the negative definiteness property i.e. x t D x=−2x t S x≤0 for any x:x t 1 n =0. The same property holds when x is replaced by a symmetric positive semi-definite matrix Q i.e. QDQ=−2QSQ≤0 for any Q:Q 1 n =0.
Now we consider the case of having a generalized Gaussian random matrix for kernel \(\mathcal{K}\): \(X_{n \times d} \sim\mathcal{MN} (\mathcal{K},M,\varOmega)\) with mean matrix M:=1 n b t where b i is the ith-column bias of X and covariance tensor Ω:=Σ n×n ⊗I d . For the mean-shifted X, the exponent term in the matrix normal distribution of X will be:
The corresponding exponent term in the distribution of the transformed X, \(\mathbb{L}X\), is now:
We define \(Q= \varSigma\mathbb{L}^{t} (\mathbb{L} \varSigma\mathbb {L}^{t})^{-1} \mathbb{L}\) or \(\varPsi Q =\mathbb{L}^{t} (\mathbb{L} \varSigma\mathbb{L}^{t})^{-1} \mathbb {L}\) (where Ψ=Σ −1) as a unique orthogonal projection with \(\mathcal{K} = \mathbf{1}_{n}\). Q can be written as \((\mathbf{I} - \mathbf{1}_{n}(\mathbf{1}^{t}_{n}\varPsi \mathbf{1}_{n})^{-1}\mathbf{1}^{t}_{n}\varPsi)\) which is the orthogonal projection onto the orthogonal complement of the space spanned by symmetric positive semi-definite Σ matrices constructed by \(\varSigma+ \mathbf{1}_{n}\hat{\boldsymbol{v}}{}^{t} + \hat {\boldsymbol{v}} \mathbf {1}_{n}^{t}; \boldsymbol{v} \in\mathcal{R}^{n}\). Note that Q is rank deficient with rank=n−1.
Based on \(\mathbb{L}X\), the corresponding S follows a generalized Wishart distribution in d degrees of freedom \(S \sim\mathcal {W}_{d}(\mathbf{1},\varSigma_{n \times n})\). McCullagh (2009) shows that D ij =S ii +S jj −2S ij is a linear transformation on symmetric matrices with transformation kernel \(\mathcal{K}=sym^{2}(\mathbf{1}_{n} \otimes\mathcal{R}^{n})\), implying that D follows a generalized Wishart distribution \(-D \sim\mathcal{W}_{d}(\mathbf{1},2\varSigma) \) defined with respect to a transformation kernel \(\mathcal{K} = \mathbf{1} \subset\mathcal{R}^{n}\). The generalized distribution is different from the standard Wishart distribution in that Ψ is replaced by \(\widetilde{\varPsi} = \varPsi Q = \varPsi(\mathbf{I} - \mathbf {1}_{n}(\mathbf {1}^{t}_{n}\varPsi\mathbf{1}_{n})^{-1}\mathbf{1}^{t}_{n}\varPsi)\) and the |⋅| symbol for determinant is replaced by the generalized det(⋅) which is the product of non-zero eigenvalues of its argument. \(\widetilde{\varPsi}\) is rank deficient with rank=n−1.
Shift- and scale-invariant marginal likelihood in D
Using the above formulation of linear transformation and kernel on symmetric positive semi-definite S matrices, McCullagh (2009) derives the marginal likelihood in D based on the standardized statistic \(t(X)= \frac{(X - \mathbf{1}_{n}\hat{\boldsymbol{b}^{t}})}{\|X - \mathbf {1}_{n}\hat {\boldsymbol{b}^{t}}\|}\) and the interest parameter α=Ψ (3). The nuisance parameters θ are bias estimates \(\hat{\boldsymbol {b}}\) and scale parameter τ.
Given \(X_{n \times d}^{o}\), the corresponding \(S^{o} = \frac{1}{d}X^{o} (X^{o})^{t}\) follows a central Wishart distributionFootnote 5 and its likelihood as a function of the inverse covariance Ψ is:
We consider the statistic for mean-shifted X as \((X-\boldsymbol{1}_{n} \hat{\boldsymbol{b}})\). In terms of this statistic, \(S=\frac {1}{d}(X-\boldsymbol{1}_{n} \hat{\boldsymbol{b}}{}^{t}) (X-\boldsymbol{1}_{n} \hat{\boldsymbol{b}}{}^{t})^{t}\) and (9) becomes:
In (10), we apply an arbitrary but fixed transformation \(\mathbb{L}\) with kernel \(\mathcal{K} = \mathbf{1}_{n}\) leading to \(\varPsi Q =\mathbb{L}^{t} (\mathbb{L} \varSigma\mathbb {L}^{t})^{-1} \mathbb{L}\) and replace the determinant |⋅| symbol by the generalized det(⋅) which is the product of non-zero eigenvalues of its argument (since Q is rank deficient) and obtain:
We substitute \(\widetilde{\varPsi} = \varPsi Q = \varPsi(\mathbf{I} - \mathbf{1}_{n}(\mathbf{1}^{t}_{n}\varPsi\mathbf{1}_{n})^{-1}\mathbf {1}^{t}_{n}\varPsi)\) to arrive at the shift-invariant form for marginal likelihood in S:
The likelihood in (12) is constant for all choices of \(S \in\mathbb{S}(D)\) and hence it depends only on D. Using the negative definiteness property of D i.e. \(\widetilde {\varPsi }S = (-\frac{1}{2})\widetilde{\varPsi}D\), (12) can be written in terms of D as:
Equation (13) is the shift-invariant marginal likelihood in D based on the statistic \((X-\boldsymbol{1}_{n} \hat{\boldsymbol{b}})\) and the rank-deficient inverse covariance \(\widetilde{\varPsi}\).
To remove the scalar terms, we base the marginal likelihood on the standardized statistic \(t(X)= \frac{(X - \mathbf{1}_{n}\hat{\boldsymbol{b}^{t}})}{\|X - \mathbf {1}_{n}\hat {\boldsymbol{b}^{t}}\|}\). Consider the scale parameter \(\tau= \frac{1}{\|X - \mathbf{1}_{n}\hat {\boldsymbol{b}}^{t}\|}\). Equation (10) now becomes:
Applying the same procedure as before i.e. using \(\mathcal{K} = \mathbf {1}_{n}\) leading to ΨQ, replacing |⋅| with det(⋅) symbol and substituting for \(\widetilde{\varPsi}\), we get:

since \(\mathrm{rank}(\widetilde{\varPsi}) =(n-1)\) and det(cA)h=c h⋅rank(A)det(A)h for any constants c and h and a nonsingular matrix A. Notice here that the dependency on biases \(\hat{\boldsymbol{b}}\) is removed.
Next, we differentiate (15) and set the derivative to zero.


By canceling terms and rearranging (17), we obtain:
and then substitute the expression for τ 2 back in (15):
where the dependency on τ vanishes.
Ignoring constant terms, we obtain the shift- and scale-invariant likelihood in S (Tunnicliffe-Wilson 1989; McCullagh 2009):
which is constant for all \(S \in\mathbb{S}(D)\). Thus the likelihood depends only on (the scaled version of) D and by the negative definiteness property of D, we finally arrive at the shift- and scale-invariant marginal likelihood in D:
Rights and permissions
About this article
Cite this article
Prabhakaran, S., Adametz, D., Metzner, K.J. et al. Recovering networks from distance data. Mach Learn 92, 251–283 (2013). https://doi.org/10.1007/s10994-013-5370-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-013-5370-7