Pinned Solutions in a Heterogeneous Three-Component FitzHugh–Nagumo Model

Abstract

We analyse pinned front and pulse solutions in a singularly perturbed three-component FitzHugh–Nagumo model with a small jump-type heterogeneity. We derive explicit conditions for the existence and stability of these type of pinned solutions by combining geometric singular perturbation techniques and an action functional approach. Most notably, in certain parameter regimes we can explicitly compute the pinning distance of a localised solution to the defect.

1 Introduction

Systems of partial differential equations (PDEs) with spatial heterogeneities, i.e. defect systems, have received a lot of attention in the literature over the past few decades [1, 3, 17, 18, 30, 34, 35, 36, 37, 50, 54, 59, 60, 61, 62, e.g.] and defect systems have been mentioned as potentially being used in device applications [27, 43, e.g.]. In this manuscript, we study a singularly perturbed three-component FitzHugh–Nagumo defect model

$$\begin{aligned} \left\{ \begin{aligned} U_t&= \varepsilon ^2 U_{xx} + U - U^3 - \varepsilon (\alpha V + \beta W + \gamma (x)) \,,\\ \tau V_t&= V_{xx} + U - V \,,\\ \theta W_t&= D^2 W_{xx} + U - W \, , \end{aligned} \right. \end{aligned}$$

(1)

with a small jump-type heterogeneity, or defect, at $x=0$:

$$\begin{aligned} \gamma (x) = \left\{ \begin{aligned} \gamma _1\,,&\quad \text {for }x\le 0\,, \\ \gamma _2\,,&\quad \text {for }x >0\,. \end{aligned} \right. \end{aligned}$$

(2)

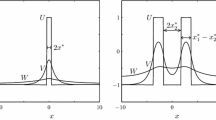
Here, $0 < \varepsilon \ll 1; D>1; \tau ,\theta >0; (x,t) \in \mathbb {R} \times \mathbb {R}^+; \alpha , \beta , \gamma _{1,2} \in \mathbb {R}$ and all parameters are a priori assumed to be $\mathcal {O}(1)$ with respect to $\varepsilon$. We are particularly interested in stationary localised solutions supported by (1) whose interfaces are pinned away from the defect, see, for instance, panels “c–e” of Fig. 1. Following [24], we call this type of pinned solutions local defect solutions and we call the distance of the interface to the defect the pinning distance.

For completeness, we first recall the definitions of the big-$\mathcal {O}$-notation and the big-$\varTheta$-notation.

Definition 1

(Adapted from [29])

• $h_1 = \mathcal {O}(\phi _1)$ as $\varepsilon \downarrow \varepsilon _0$ if there are constants $k_0>0$ and $\varepsilon _1$ such that $|h_1(\varepsilon )| \le k_0|\phi _1(\varepsilon )|$ for $\varepsilon _0< \varepsilon < \varepsilon _1$.

• $h_2 = \varTheta (\phi _2)$ as $\varepsilon \downarrow \varepsilon _0$ if there are constants $k_0, k_1>0$ and $\varepsilon _1$ such that $k_1|\phi _2(\varepsilon )| \le |h_2(\varepsilon )| \le k_0|\phi _2(\varepsilon )|$ for $\varepsilon _0< \varepsilon < \varepsilon _1$.

Fig. 1

Pinned defect pulse and front solutions supported by (1) obtained by simulating the time-independent version of (1), i.e. by simulating (10), on a domain of length 24. The system parameters used for the simulations in panels a–c are $(\alpha , \beta , D, \gamma _1, \gamma _2, \varepsilon ) = (3,2,5,2,2.5,0.02)$, while the system parameters used in the panels d–f are $(\alpha , \beta , D, \gamma _1, \gamma _2, \varepsilon ) = (3,-2,5,0.02,-5,0.02)$

By combining Geometrical Singular Perturbation Theory (GSPT) [25, 31, 32] with an action functional approach [52], we derive the following result related to the the existence and stability of local defect front and pulse solutions.

Main Result 1

Let $\varepsilon$ be small enough and let $\tau$ and $\theta$ be bounded by some $\mathcal {O}(1)$-constant.¹

If $\gamma _1 = \varepsilon \tilde{\gamma }_1$, with $\tilde{\gamma }_1=\varTheta (1)$, $(\alpha , \beta , D,$$\gamma _2)$ are $\varTheta (1)$ such that $\tilde{\gamma }_1-{\gamma }_2 = \varTheta (1)$ and if there exist an $x_d>0$ solving

$$\begin{aligned} 2 \tilde{\gamma }_1 - \frac{1}{2} \gamma _2f(x_d) =0\,, \quad \text {with} \quad f(x_d):= \alpha e^{-x_d}+ \beta e^{-x_d/D}\,, \end{aligned}$$

(3)

then (1) supports a local defect front solution $Z_{f,ld}^{\ell }=(U_{f,ld}^{\ell }, V_{f,ld}^{\ell }, W_{f,ld}^{\ell })$ that asymptotes to $\pm 1 + \mathcal {O}(\varepsilon )$ as $x \rightarrow \pm \infty$ and which is pinned to the left of the defect with leading order pinning distance $x_d$. The local defect front solution $Z_{f,ld}^{\ell }$ is stable if and only if

$$\begin{aligned} \gamma _2 g(x_d) >0 \,, \quad \text {with} \quad g(x_d):= \alpha e^{-x_d}+ \frac{\beta }{D} e^{-x_d/D} \,. \end{aligned}$$

(4)

If $(\alpha , \beta , D, \gamma _1, \gamma _2)$ are $\varTheta (1)$ such that $\gamma _1-\gamma _2 = \varTheta (1)$ and if there exist an $x^*>0$ and $x_d>0$ solving

$$\begin{aligned} f(2x^*) = \gamma _2\,, \qquad f(x_d) = f(x_d+2x^*), \end{aligned}$$

(5)

then (1) supports a local defect pulse solution $Z_{p,ld}^{r}=(U_{p,ld}^{r}, V_{p,ld}^{r}, W_{p,ld}^{r})$ that asymptotes to $-1+ \mathcal {O}(\varepsilon )$ as $x \rightarrow \pm \infty$ and which is pinned to the right of the defect with leading order width²$2x^*$ and leading order pinning distance $x_d$. The local defect pulse solution $Z_{p,ld}^{r}$ is stable if and only if

$$\begin{aligned} \begin{aligned} g(2x^*)>0 \,, \quad {\text {and}}\quad (\gamma _2-\gamma _1) (g(x_d)-g(x_d+2x^*)) >0 \,. \end{aligned} \end{aligned}$$

(6)

To understand the implications of Main Result 1, we take a closer look at the existence conditions (3) and (5), and stability conditions (4) and (6). If $\alpha$ and $\beta$ have the same sign, then f is monotonic. Consequently, the existence condition (3) for local defect front solutions pinned to the left of the defect has at most one solution, while the existence conditions (5) for local defect pulse solutions pinned to the right of the defect has no solutions. In other words, if $\alpha$ and $\beta$ have the same sign—and if the other system parameters are chosen appropriately—then Main Result 1 gives the existence of a local defect front solutions pinned to the left of the defect. After noting that $g(x_d) = -f'(x_d)$, we get from (4) that this solution is stable only if $\alpha$ and $\gamma _2$ have the same sign.

If $\alpha$ and $\beta$ have opposite signs (however, see Remark 2), then, by the particulars of f, (3) has at most two distinct solutions. Consequently, and if the other system parameters are chosen appropriately, Main Result 1 gives the existence of (at most) two local defect front solutions pinned to the left of the defect and with different pinning distances. If $\alpha \gamma _2>0$, then the local defect front solution with the smaller pinning distance is stable, while the other local defect front solution is unstable. The opposite holds for $\alpha \gamma _2<0$. Main Result 1 also gives, if the other system parameters are chosen appropriately, the existence of (at most) two local defect pulse solutions pinned to the right of the defect and with different pinning distances. If $\beta< 0 <\alpha$ and $\gamma _2>\gamma _1$, then the local defect pulse solution with the smaller width is stable, while the other local defect front solution is unstable. Both local defect pulse solutions are unstable if $\beta< 0 <\alpha$ and $\gamma _2<\gamma _1$. The opposite holds for $\alpha< 0 <\beta$. See also Fig. 2. More details are given in the remainder of this manuscript, see, in particular, Sect. 3.2, Sect. 4.2, and Tables 1 and 2.

Fig. 2

Graphical representation of the existence condition (5) and the stability condition (6) of Main Result 1 related to local defect pulse solutions $Z_{p,ld}^{r}$. Here, the first existence condition $f(2x^*) = \gamma _2$ (5) has a unique solution $2x^*$ and since $g(x)=-f'(x)$, we have that $g(2x^*)>0$ (6). The second existence condition $f(x_d) = f(x_d+2x^*)$ (5) yields a unique pinning distance $x_d$ and $g(x_d)-g(x_d+2x^*)>0$. Thus, by (6), the related local defect pulse solution $Z_{p,ld}^{r}$ is stable if $\gamma _2>\gamma _1$ and unstable if $\gamma _2<\gamma _1$

For $x \ne 0$, (1) has the symmetries

$$\begin{aligned} (U,V,W,x,\gamma _1,\gamma _2) \mapsto -(U,V,W,x,\gamma _2,\gamma _1)\,, \end{aligned}$$

(7)

and

$$\begin{aligned} (x,\gamma _1,\gamma _2) \mapsto (-x,\gamma _2,\gamma _1) \,. \end{aligned}$$

(8)

From Main Result 1 and the symmetries one can directly derive existence and stability conditions for local defect front and pulse solutions that asymptote to $1+\mathcal {O}(\varepsilon )$ as $x \rightarrow -\infty$ and/or local defect front and pulse solutions that are pinned in the opposite $\gamma _i$-region (so on the other side of the defect). For brevity of presentation, we do not explicitly state these additional results. Furthermore, we assume, without loss of generality, that defect solutions asymptote to $-1 + \mathcal {O}(\varepsilon )$ as $x \rightarrow -\infty$ in the remainder of the manuscript (unless stated otherwise).

Remark 1

The results presented in Main Result 1 are not rigorous since not all the functional analytic details of the methodology of combining geometric singular perturbation techniques and an action functional approach have been fully worked out. Many of the functional analytic details of the approach are given in all detail in series of papers by Chen and collaborators [5,6,7,8,9,10,11,12] for slightly different problems and these methods can be generalised to the setting of the current manuscript, see also [52]. However, these generalisations are a nontrivial exercise and we decided to not proceed this direction (for the readability of the manuscript). Instead, we explain the essentials of the approach in some detail in Sect. 2, see, in particular, Sect. 2.2, and we test the results of Main Result 1 against numerical simulations and we get excellent agreement, see, in particular, Figs. 5, 6, 10, and 11. Further, in [52] we introduced this methodology for the homogeneous version of (1) and used it to explicitly replicate known rigorous results regarding the existence and stability of localised solutions from [23, 53, 55].

1.1 Background of the Model

A dimensional homogeneous version of (1)—so with $\gamma _1=\gamma _2=\gamma (x)$—was introduced in the nineties to study gas-discharge systems [42, 48]. Versions of the dimensional—and nondimisionalised—homogeneous model have been studied intensively afterwards, see [2, 15, 23, 28, 39, 46, 51, 52, 53, 55, 56, 57, 58, e.g.] and references therein. From a mathematical point of view, the homogeneous version of (1) is arguably the most mathematically rigorously studied singularly perturbed three-component reaction–diffusion equation. It is not a surprise that the homogeneous version of (1) supports stable slowly travelling front solutions with speed $c = \frac{3}{2} \sqrt{2} \varepsilon ^2 \gamma$ [55], since the homogeneous model can be seen as a weakly perturbed Allen-Cahn type equation [4, 15, 26]. Consequently, stationary front solutions exist only for $\gamma \equiv 0$. In [23], it was shown there exist a (family of) stationary pulse solution(s) with leading order width $2x^*$ if there is an $x^*>0$ solving $f(2x^*) =\gamma$, where f is defined in (3). By using the NonLocal Eigenvalue Problem approach for Evans functions [20,21,22], it was shown in [53] that the critical part of the spectrum associated with a stationary pulse solution consists of a translation invariance eigenvalue at the origin and a critical eigenvalue $\lambda = -3\sqrt{2}\varepsilon ^2 g(2x^*)$, where g is defined in (4). The remaining subset of the spectrum is contained in the left half-plane bounded away from the imaginary axis with an $\mathcal {O}(1)$-bound and there are no complex-valued eigenvalues for $\tau$ and $\theta$ of $\mathcal {O}(1)$. Thus, the stationary pulse solution is stable if $g(2x^*)>0$. In other words, the existence and stability conditions for homogeneous stationary pulse solutions coincide with the first conditions for the existence and stability of local defect pulse solutions of Main Result 1.

In [52], we reproduced the above mentioned existence and stability results for homogeneous stationary front and pulse solutions by combining GSPT techniques with an action functional approach. The action functional approach for a mono-stable or a bi-stable two-component FitzHugh–Nagumo model without small diffusion was pioneered by Chen and collaborators in a series of papers [5,6,7, 9, 10, 12]. In [52] it was shown that the action functional J for a stationary homogeneous pulse solution (u, v, w)—whose profile with unknown width is computed by GSPT—is given by

$$\begin{aligned} \begin{aligned} J(u) =&\int _{-\infty }^{\infty } \left( \frac{1}{2} \varepsilon ^2 u_x^2 + F(u) - F(\bar{u}_{\gamma })+ \frac{1}{2} \varepsilon \alpha (u\mathcal {L}_1u-\bar{u}_{\gamma }^2) \right. \\&\left. + \frac{1}{2} \varepsilon \beta (u\mathcal {L}_2u-\bar{u}_{\gamma }^2)+ \varepsilon \gamma (u-\bar{u}_{\gamma }) \right) dx, \end{aligned} \end{aligned}$$

(9)

with antiderivative $F(u) = \frac{1}{4} u^4 - \frac{1}{2} u^2 \,,$$\bar{u}_\gamma$ the steady state of the system near $-1$ (see (11)), $\mathcal {L}_1 := (-\frac{d^2}{dx^2}+1)^{-1}$, $\mathcal {L}_2 := (-D^2 \frac{d^2}{dx^2}+1)^{-1}$. Consequently, the existence condition determining the width of the pulse solution follows from the critical points of J (with respect to the unknown width) and the stability condition follows from the minimisers of J. We derive Main Result 1 for the heterogeneous model (1) by utilising, and extending, this action functional approach of [52] (however, see Remark 1).

(Versions of) the heterogeneous model (1), and the effect of the defect, have also been studied [24, 41, 54, 61, 62, e.g.]. We shortly discuss the results of [24, 54] as they are most relevant for this manuscript. Since the heterogeneous model (1) is, in contrast to the homogeneous model, not translation invariant, a stationary solution is typically isolated and does not come as a family of solutions. Moreover, since the defect is small it does not alter the spectrum in a leading order fashion and the perturbed translation invariant eigenvalue (at the origin for the homogeneous case) will determine the fate of the stability of a defect solution (there are no leading complex-valued eigenvalues since $\tau$ and $\theta$ are $\mathcal {O}(1)$ [53]). In [54] it was shown that, under certain parameter conditions, (1) supports so-called stable pinned global defect solutions [24]. That is, stationary front and pulse solutions with one of the interfaces pinned at the defect (this in contrast to local defect solutions were the interfaces are pinned away from the defect). In particular, it was shown that global defect front solutions exist if $\gamma _1 \gamma _2 < 0$ and that they are stable if, in addition, $\gamma _1>0$, see also panel “e” of Fig. 1. For the global defect pulse solutions it was shown that the widths of the pinned pulse solutions are, to leading order, given by $2x^*$, where $2x^*$ solves $f(2x^*)=\min \{\gamma _1,\gamma _2\}$, see also panel “a” of Fig. 1. That is, they correspond to the widths of the pulse solutions in the homogeneous case with $\gamma =\min \{\gamma _1,\gamma _2\}$.

Local defect solutions were investigated numerically in [54] since the analytic methods employed in [54] cannot be used directly to study local defect solutions. This is due to the fact that the interaction of the defect with the localised interfaces is weak—due to the $\varTheta (1)$-distance between them—and higher order computations are needed. For instance, a leading order GSPT analysis appended with a Melnikov integral [47] gives that the leading order width $2x^*$ of a local defect pulse solution is—again—given by the roots of $f(2x^*) = \gamma _i$, see also panels “b” and “c” of Fig. 1. In other words, the widths of the pinned pulse solutions are in essence not affected by the introduction of the small defect. However, the pinning distance $x_d$ cannot be determined from this leading order analysis.

Since the system parameters used for the simulations of the pinned pulse (front) solutions in Fig. 1 are all the same, we have the co-existence of local and global defect pulse (front) solutions. Moreover, the numerically stable local defect pulse solution shown in panel “c” of Fig. 1 is pinned in the region to the right of the defect (where $\gamma (x)= \gamma _2$), while the numerically stable global defect pulse solution shown in panel “a” of Fig. 1 is pinned in the opposite region to the left of the defect (where $\gamma (x)= \gamma _1$). The two stable pinned pulse solutions are separated by a numerically unstable pinned pulse solution shown in panel “b” of Fig. 1. This unstable pulse is pinned at the defect in the $\gamma _2$-region and has a width similar as the stable local defect pulse solution. This unstable pinned pulse solution acts as the separatrix between the two stable pinned pulse solutions and is called the scatter solution [39,40,41, 50, 62].

In [24], the authors used geometric methods to study the persistence of heteroclinic and homoclinic orbits for a general system of ordinary differential equations (ODEs) with a weak defect and under generic conditions on the nonlinearities. The ODE associated to pinned defect solutions of (1) (see (10)) fits into an extended version of this general system, see also Remark 1.13 of [24]. Consequently, some of the results of [24] are directly applicable here.

Theorem 2

(adopted from Thms. 4.7 and 4.8 of [24]) Let $\gamma (x)$ be as in (2) and let $\varepsilon$ be small enough. Moreover, let $\alpha>0, \beta >0, \gamma _2 \in \mathbb {R}$ be $\mathcal {O}(1)$ with respect to $\varepsilon$.

• If $\gamma _1=0$, then (1) supports a local defect front solution $Z_{f,ld}^{\ell }=(U_{f,ld}^{\ell }, V_{f,ld}^{\ell },$$W_{f,ld}^{\ell })$ that asymptotes to $\pm 1 +\mathcal {O}(\varepsilon )$ as $x \rightarrow \pm \infty$ and with its front pinned to the left of the defect.

• If $0<\gamma _1< \alpha +\beta$, then (1) supports a local defect pulse solution $Z_{p,ld}^{\ell }=(U_{p,ld}^{\ell }, V_{p,ld}^{\ell }, W_{p,ld}^{\ell })$ that asymptotes to $-1 +\mathcal {O}(\varepsilon )$ as $x \rightarrow -\infty$ and with its pulse pinned to the left of the defect.

Whilst Theorem 2 partly settles the question related to the existence of local defect front and pulse solutions supported by (1), it has several limitations. Firstly, it requires that both $\alpha$ and $\beta$ are positive and does not provide any insights for $\alpha$ and/or $\beta$ negative. See, however, Remark 2. Secondly, Theorem 2 does not provide any information regarding the profiles—and thus also not regarding the pinning distances—of the local defect solutions. Thirdly, for the existence of local defect front solutions it is required that $\gamma _1 = 0$—this to ensure the existence of a stationary front solution in the homogeneous case [55]—while one would also expect local defect front solutions for $\gamma _1$ small, but not zero. Finally, Theorem 2 does not provide any information regarding the stability of the local defect solutions. The results of this manuscript as stated in Main Result 1 (partly) address the above issues and thus significantly extend the results of [24]. In particular, we put a priori no additional restrictions on the parameters and determine leading order expressions for the pinning distances $x_d$. In addition, we also determine the stability of the local defect solutions.

Remark 2

From Main Result 1 it follows that the most interesting results of this manuscript relate to the case where $\alpha \beta <0$. For instance, the second existence condition of (5) implies that, in this case only, the pinning distance $x_d = \varTheta (1)$ (since f is monotonic for $\alpha \beta >0$). The original activator–inhibitor framework of the homogeneous version of (1) [42, 48, e.g.] actually required that both $\alpha$ and $\beta$ were positive. However, this restriction is mathematically not necessary and the dynamics of the homogeneous and heterogeneous model is much richer without it. See, for instance, [23, 24, 58].

1.2 Outlook

We derive Main Result 1 by combining GSPT techniques with the action functional approach of [52]. In short, GSPT techniques will provide the profile of a local defect solution—with unknown width (for a pulse) and unknown pinning distance (for both a front and a pulse). The critical points of the action functional landscape of the derived profile determine the potential widths and pinning distances of the local defect solution under consideration and only the minimisers of the action functional yield stable local defect solutions. In Sect. 2, we discuss this action functional approach in more detail and show how to append the action functional (9) of the homogeneous case as to deal with the heterogeneity of (1).

Besides local and global defect solutions, another type of defect solutions—the trivial defect solution – was introduced in [24]. This type of defect solution is characterised by the fact that it stays $\mathcal {O}(\varepsilon )$-close to both asymptotic end states over the whole spatial domain. That is, a trivial defect solution is—in some sense—a small perturbation of a steady state solution and can thus be seen as the heterogeneous equivalent of a homogeneous steady state solution. It was shown in [24] that, under generic conditions, trivial defect solutions exist and are unique—in the sense that there is exactly one trivial defect solution near each of the steady states. The homogenous version of (1) has two steady state solutions (near $(U,V,W)=\pm (1,1,1)$) that fulfil these generic conditions, and, consequently, (1) has two trivial defect solutions $Z_{td}^{\pm }=(U_{td}^{\pm }, V_{td}^{\pm }, W_{td}^{\pm })$. Whilst pinned local defect solutions are the main subject of interest of this manuscript, we also explicitly determine the profiles of these trivial defect solutions $Z_{td}^{\pm }$ in “Appendix A”. We add the derivation of these profiles for completeness, but also to illustrate how the region around the defect should be handled from an asymptotic perspective.³ Specifically, we show that the defect introduces two new fast regions where the dynamics of the U-component dominates, one just to the left of the defect and one just to the right of the defect. To leading order, these additional fast regions do not contribute to the profile of the trivial defect solutions, i.e. the profiles are to leading order $\pm 1$ in both fast regions, but they do contribute at an $\mathcal {O}(\varepsilon )$-level. Heuristically, local defect solutions can be seen as a concatenation of the equivalent stationary solution to the homogenous model with one of the trivial defect solutions.⁴ Therefore, obtaining insights in these trivial defect solutions is also a first crucial step towards understanding local defect solutions.

In Sect. 3, we derive the part of Main Result 1 related to local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect and determine the profile—up to and including $\mathcal {O}(\varepsilon )$-terms—of these solutions. We also use the action functional approach to study global defect front solutions $Z_{f,gd}$ and reproduce the key results of [54] related to the existence ($\gamma _1\gamma _2<0$) and stability ($\gamma _1>0>\gamma _2$) of these global defect front solutions (note that only leading order computations are needed to obtain these results). Finally, we combine the results for local and global defect front solutions and we numerically investigate the stationary version of (1) to confirm the asymptotic findings.

In Sect. 4, we follow the same procedure as in Sect. 3 but now for defect pulse solutions. That is, we derive the part of Main Result 1 related to local defect pulse solutions $Z_{p,ld}^r$ pinned to the right of the defect and determine the profile—up to and including $\mathcal {O}(\varepsilon )$-terms—of these solutions. Most of this derivation has been placed in “Appendix B” since it is very similar to the derivation in Sect. 3 and it is only algebraically more involved (the GSPT procedure now determines the profiles up to two unknowns, the pinning distance $x_d$ and the pulse width $2x^*$). We also discuss the connection of the action functional approach and the results for global defect pulse solutions $Z_{p,gd}$ from [54] and combine these results to obtain a broader picture for pinned pulse solutions. Finally, we numerically investigate the stationary version of (1) to confirm the asymptotic findings.

We end this manuscript with a summary and a short outlook on future projects.

2 GSPT and the Action Functional Approach

Pinned solutions to (1) solve the following system of ODEs

$$\begin{aligned} \left\{ \begin{aligned} 0&= \varepsilon ^2 u_{xx} + u - u^3 - \varepsilon (\alpha v + \beta w + \gamma (x)) \,,\\ 0&= v_{xx} + u -v \,,\\ 0&= D^2 w_{xx} + u - w \, , \end{aligned} \right. \end{aligned}$$

(10)

and they asymptote to the asymptotic end states$(\bar{u}_{\gamma _i},\bar{u}_{\gamma _i},\bar{u}_{\gamma _i})$ and/or $(\hat{u}_{\gamma _i},\hat{u}_{\gamma _i},\hat{u}_{\gamma _i})$ of (1). These are solutions of (1) in the regions $|x| \gg 1$ that are to leading order constant in time and space and they are determined by two of the roots of the cubic polynomial $u^3-u+\varepsilon ((\alpha +\beta )u+\gamma _i)=0$.⁵ In particular, $\bar{u}_{\gamma _i}$ and $\hat{u}_{\gamma _i}$ are given by

$$\begin{aligned} \begin{aligned} \bar{u}_{\gamma _i} := -1 +\frac{1}{2} \varepsilon (\alpha + \beta -\gamma _i) +\mathcal {O}(\varepsilon ^2)\,, \hat{u}_{\gamma _i} := 1 -\frac{1}{2} \varepsilon (\alpha + \beta +\gamma _i) +\mathcal {O}(\varepsilon ^2)\,, \end{aligned} \end{aligned}$$

(11)

see, for instance, [23].

2.1 GSPT

The leading order profiles of trivial and local defect solutions to (1) (i.e. solutions of (10)) are relatively straightforward to determine. In short, we divide the spatial domain in $N+2$, asymptotically small, fast regions $I_f$ and $N+2$ slow regions $I_s$: a fast region around each of the N interfaces of the local defect solution, two fast regions around the defect at $x=0$ and $N+2$ slow regions away from the N interfaces and the defect. In particular, for a trivial defect solution $Z_{td}^{\pm }$ we have $N=0$, while $N=1$ for a local defect front solution $Z_{f,ld}$ and $N=2$ for a local defect pulse solution $Z_{p,ld}$. In the slow regions away from the interfaces and defect, the fastu-component of (10) is, due to the asymptotic smallness of its diffusion coefficient, close to one of its asymptotic end states (11). Consequently, the equations for the slow (v, w)-components can be solved to leading order. In the fast, asymptotically small, regions, the fast u-component of (10) is dominant, while the slow (v, w)-components are to leading order constant. To study the fast u-equation in these fast regions, we introduce the fast scaling $\xi :=x/\varepsilon$ and rewrite (10) in $\xi$:

$$\begin{aligned} \left\{ \begin{aligned} 0&= u_{\xi \xi } + u - u^3 - \varepsilon (\alpha v + \beta w + \gamma (\xi )) \,,\\ 0&= v_{\xi \xi } + \varepsilon ^2 (u -v) \,,\\ 0&= D^2 w_{\xi \xi } + \varepsilon ^2(u - w) \, , \end{aligned} \right. \end{aligned}$$

(12)

where we note that (10) and (12) are equivalent as long as $\varepsilon \ne 0$. The u-equation is to leading order solved by $\pm \tanh {((\xi -\hat{\xi })/\sqrt{2})}$, where $\hat{\xi }$ is an arbitrary translational constant that is determined by the location of the interface. Finally, we concatenate the solutions in the different slow and fast regions to construct the leading order profiles of the trivial and local defect solutions. For more details, see, in particular, “Appendix A”, the upcoming sections and [23, 54, 55].

Remark 3

The defining difference between a local defect solution $Z_{ld}$ and a global defect solution $Z_{gd}$ is the location of the interfaces of the solution with respect to the defect at $x=0$. If this pinning distance is $\varTheta (1)$ in the slow scaling x, then we have a local defect solution $Z_{ld}$, while we have a global defect solution $Z_{gd}$ if the pinning distance is $\mathcal {O}(1)$ in the fast scaling $\xi :=x/\varepsilon$. In other words, for global defect solutions $Z_{gd}$ the defect and one of the interfaces lie in the same fast field, while they lie in different fast fields—and are separated by a slow field—for local defect solutions $Z_{ld}$. So, the spatial domain has to be divided in $N+1$ fast and $N+1$ slow regions to study global defect solutions.

2.2 The Action Functional Approach

The Lagrangian associated with the homogenous version of (10) is a skew-gradient system [8] and is given by

$$\begin{aligned} \begin{aligned} L_0(u,v,w)&:=\frac{1}{2} \varepsilon ^2 u_x^2 + F(u) + \varepsilon \alpha \left( uv-\frac{1}{2} v_x^2-\frac{1}{2} v^2\right) \\&\quad + \varepsilon \beta \left( uw-\frac{1}{2} D^2 w_x^2-\frac{1}{2} w^2\right) + \varepsilon \gamma u +c_0\,. \end{aligned} \end{aligned}$$

(13)

Here, $F(u) = \frac{1}{4} u^4 - \frac{1}{2} u^2 \,$ and $c_0$ is a normalising constant so that we deal with finite critical values. With the second and third equations of (10) being linear, the associated Lagrangians are convex, which provide natural coercivity. Furthermore, straightforward calculations yield

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{\infty } (uv- v_x^2 - v^2) dx = 0\,,\quad \int _{-\infty }^{\infty } (uw- D^2 w_x^2- w^2) dx = 0\,, \end{aligned} \end{aligned}$$

(14)

if $u \in \mathcal {C}_0^\infty ({\mathbb {R}})$ or ${\mathbb {H}}^1(\mathbb R)$, and where v, respectively w, is the unique bounded solution of the second, respectively third, equation of (10). The solutions of the homogeneous version of (10) can be found from the critical points of a variational functional associated with the Lagrangian $L_0(u,v,w)$ [8]. This functional is strongly indefinite, which requires min-max arguments to show the existence of critical points. However, we may take advantage of the linearity of the second and third equations of (10). That is, we introduce $\mathcal {L}_1 := (-\frac{d^2}{dx^2}+1)^{-1}$ and $\mathcal {L}_2 := (-D^2 \frac{d^2}{dx^2}+1)^{-1}$, such that $\mathcal {L}_1u$ exactly solves the linear v-equation $0=v_{xx}+u-v$ for any given u, while $\mathcal {L}_2u$ exactly solves the linear w-equation $0=D^2 w_{xx}+u-w$, and use (14) to employ an action functional J defined by (9) to investigate the stationary solutions of the homogenous version of (10). From (14) it is clear that

$$\begin{aligned} \begin{aligned} \int _{-\infty }^{\infty } u\mathcal {L}_iu dx \ge 0\,, \qquad i=1,2, \end{aligned} \end{aligned}$$

a coercivity which enables us to seek minimisers of J. See also [5, 10, 11, 52], and references therein, for more details.

As in [52], the idea of Lyapunov-Schmidt reduction helps us to investigate the pinned front and pulse solutions; however, we need to further refine the argument to deal with the defect imposed on (10). Knowing that the defect is located at $x=0$, we adjust $L_0$ (13) for the different $\gamma$-values and split the integral associated to the action functional over the two domains $x<0$ and $x>0$. In particular, for a defect pulse solution we use the following action functional

$$\begin{aligned} \begin{aligned} J_p(u) =&\int _{-\infty }^{0} L(u; \bar{u}_{\gamma _1})dx + \int _{0}^{\infty } L(u; \bar{u}_{\gamma _2})dx\,, \end{aligned} \end{aligned}$$

(15)

with

$$\begin{aligned} \begin{aligned} L(u;\bar{u}_{\gamma _i})&:=\frac{1}{2} \varepsilon ^2 u_x^2 + F(u) - F(\bar{u}_{\gamma _i})+ \frac{1}{2} \varepsilon \alpha (u\mathcal {L}_1u-\bar{u}_{\gamma _i}^2) \\&\quad + \frac{1}{2} \varepsilon \beta (u\mathcal {L}_2u-\bar{u}_{\gamma _i}^2)+ \varepsilon \gamma _i (u-\bar{u}_{\gamma _i})\,, \end{aligned} \end{aligned}$$

(16)

and with $F(u), \bar{u}_{\gamma _i}$ and $\mathcal {L}_{1,2}$ as before. The admissible functions u are the profiles of the defect pulse solutions with unknown widths and pinning distances determined by the GSPT procedure outlined in Sect. 2.1. Thus, $u \in \mathbb {H}^1 + \hat{u}$, where $\hat{u}$ is a $C^{\infty }$ function and

$$\begin{aligned} \hat{u} = \left\{ \begin{aligned} \bar{u}_{\gamma _1}\,,&\quad \text {for }x< -1\,, \\ \bar{u}_{\gamma _2}\,,&\quad \text {for }x >1\,. \end{aligned} \right. \end{aligned}$$

Stationary front solutions are not studied in [52]⁶, but it is not hard to adapt the above action functional for defect pulse solutions to an action functional for defect front solutions. The main difference is that a defect front solution asymptotes to $(\hat{u}_{\gamma _2},\hat{u}_{\gamma _2},\hat{u}_{\gamma _2})$ as $x \rightarrow \infty$, hence, the action functional for a defect front solution becomes

$$\begin{aligned} \begin{aligned} J_f(u) =&\int _{-\infty }^{0} L(u; \bar{u}_{\gamma _1})dx + \int _{0}^{\infty } L(u; \hat{u}_{\gamma _2})dx\,, \end{aligned} \end{aligned}$$

(17)

with L given by (16) and $\hat{\bar{u}}_{\gamma _{1,2}}$ given by (11). The admissible functions u are now the profiles of the defect front solutions with unknown pinning distances, and, hence, $u \in \mathbb {H}^1 + \check{u}$, where $\check{u}$ is a $C^{\infty }$ function and

$$\begin{aligned} \check{u} = \left\{ \begin{aligned} \bar{u}_{\gamma _1}\,,&\quad \text {for }x< -1\,, \\ \hat{u}_{\gamma _2}\,,&\quad \text {for }x >1\,. \end{aligned} \right. \end{aligned}$$

The Maslov index derived in [7] can be used to study the stability of stationary pulse solutions of skew-gradient systems; in particular of FitzHugh–Nagumo equations [5, 9]. This index plays a similar role as the Morse index for the solutions of gradient systems and the Maslov index of a minimiser of $J_p$ is zero. In view of the skew-gradient structure for (10), the fact that the second and third equations are linear reduces the complexity of the calculations in the spectral analysis. For instance, both $-\frac{d^2}{dx^2}+1$ and $-D^2 \frac{d^2}{dx^2}+1$ are positive operators. In addition, suitably small $\tau$ and $\theta$ precludes the existence of non-real eigenvalues in the right half-plane [9, Lemma 4.1] and [53]. This assumption on $\tau$ and $\theta$ can thus be construed as keeping the system away from a strongly excitable situation, as might result, for instance, in Hopf bifurcations. So, similar to the results established in [7, 9], the minimisers of $J_p$ will correspond to stable pinned pulse solutions. Likewise, we can adapt the approach of [10] to assert that the minimisers of $J_f$ will correspond to stable pinned front solutions.

We now take a closer look to the individual terms of L (16) inside the action functionals (15) and (17). As discussed above, to construct the profiles of the defect front and pulse solutions we split the spatial domain into slow regions $I_s$—that are away from the defect and away from the interfaces—and fast regions $I_f$—near the defect and interfaces. In the slow regions $I_s$, the slow (v, w)-components are dominant and the fast u-component is slaved to the slow components. In particular, the fast u-component, as well as $\hat{\bar{u}}_{\gamma _{1,2}}$ (11), are to leading order $\pm 1$ (see also the upcoming sections and appendices). Consequently, the $\frac{1}{2} \varepsilon ^2 u_x^2$-terms in L of (15) and (17) are $\mathcal {O}(\varepsilon ^4)$ in the slow regions. For the antiderivative F(u), we have

$$\begin{aligned} F(\pm 1 + \varepsilon K_1 + \varepsilon ^2 K_2+\mathcal {O}(\varepsilon ^3)) = -\frac{1}{4} + \varepsilon ^2 K_1^2 + \mathcal {O}(\varepsilon ^3). \end{aligned}$$

(18)

Hence, the $F(u)-F(\hat{\bar{u}}_{\gamma _{1,2}})$-terms in L of (15) and (17) are $\mathcal {O}(\varepsilon ^2)$ in the slow regions. Consequently, the leading order terms of the action functionals in the slow region $I_s$ are actual $\mathcal {O}(\varepsilon )$. By using regular expansions for $u=u_0 + \varepsilon u_1 + \mathcal {O}(\varepsilon ^2)= \pm 1 + \varepsilon u_1 + \mathcal {O}(\varepsilon ^2)$ and $\hat{\bar{u}}_{\gamma _i} = \hat{\bar{u}}_{\gamma _i,0} + \varepsilon \hat{\bar{u}}_{\gamma _i,1}+ \mathcal {O}(\varepsilon ^2) = \pm 1 + \varepsilon \hat{\bar{u}}_{\gamma _i,1}+ \mathcal {O}(\varepsilon ^2)$ (11), we get that in the slow regions $I_s$

$$\begin{aligned}&L(u; \hat{\bar{u}}_{\gamma _i})|_{I_s} = \varepsilon L_1(u; \hat{\bar{u}}_{\gamma _i}) + \varepsilon ^2 L_2(u; \hat{\bar{u}}_{\gamma _i}) + \mathcal {O}(\varepsilon ^3)\,, \end{aligned}$$

with

$$\begin{aligned} L_1(u; \hat{\bar{u}}_{\gamma _i}) :=\frac{1}{2} \alpha (u_0\mathcal {L}_1u_0-1) + \frac{1}{2} \beta (u_0\mathcal {L}_2u_0-1)+ \gamma _i (u_0- \hat{\bar{u}}_{\gamma _i, 0} )\,, \end{aligned}$$

(19)

and

$$\begin{aligned} \begin{aligned} L_2(u; \hat{\bar{u}}_{\gamma _i}) :=&\,\,u_1^2 - (\hat{\bar{u}}_{\gamma _i,1})^2 + \frac{1}{2} \alpha (u_1\mathcal {L}_1u_0+u_0\mathcal {L}_1u_1-2\hat{\bar{u}}_{\gamma _i,0}\hat{\bar{u}}_{\gamma _i,1}) \\&+ \frac{1}{2} \beta (u_1\mathcal {L}_2u_0+u_0\mathcal {L}_1u_1-2\hat{\bar{u}}_{\gamma _i,0}\hat{\bar{u}}_{\gamma _i,1})+ \gamma _i (u_1-\hat{\bar{u}}_{\gamma _i,1}) \,.\end{aligned} \end{aligned}$$

(20)

In the fast, asymptotically small, regions $I_f$ the fast component is dominant and the slow components are effectively constant, see (12) and [23]. We use the fast scaling $\xi =x/\varepsilon$ to study the action functional in these fast regions. That is,

$$\begin{aligned} \begin{aligned} J_{f,p}(u) = \varepsilon \int _{-\infty }^{0} \bar{L}(u; \bar{u}_{\gamma _1})d\xi + \varepsilon \int _{0}^{\infty } \bar{L}(u; \hat{\bar{u}}_{\gamma _2})d\xi \,, \end{aligned} \end{aligned}$$

(21)

with

$$\begin{aligned} \begin{aligned} \bar{L}(u; \hat{\bar{u}}_{\gamma _i})&= \frac{1}{2} u_{\xi }^2 + F(u) - F(\hat{\bar{u}}_{\gamma _i})+ \frac{1}{2} \varepsilon \alpha (u\mathcal {L}_1u-\hat{\bar{u}}_{\gamma _i}^2) \\&\quad + \frac{1}{2} \varepsilon \beta (u\mathcal {L}_2u-\hat{\bar{u}}_{\gamma _i}^2)+ \varepsilon \gamma (u-\hat{\bar{u}}_{\gamma _i})\,, \end{aligned} \end{aligned}$$

where $F,\mathcal {L}_{1,2},$ and $\hat{\bar{u}}_{\gamma _i}$ (11) are as before and where we note the $\varepsilon$-term premultiplying the integrals of (21). By using a regular expansion in $\xi$ for the different components of $\bar{L}$, we get that in the fast regions $I_f$

$$\begin{aligned}&\bar{L}(u; \hat{\bar{u}}_{\gamma _i})|_{I_f} = \bar{L}_0(u; \hat{\bar{u}}_{\gamma _i}) + \varepsilon \bar{L}_1(u; \hat{\bar{u}}_{\gamma _i}) + \mathcal {O}(\varepsilon ^2)\,, \end{aligned}$$

with

$$\begin{aligned} \bar{L}_0(u; \hat{\bar{u}}_{\gamma _i}) := \frac{1}{2} (u_0)_{\xi }^2 + F(u_0) +\frac{1}{4} \,, \end{aligned}$$

(22)

and

$$\begin{aligned} \begin{aligned} \bar{L}_1(u; \hat{\bar{u}}_{\gamma _i})&:=(u_0)_{\xi }(u_1)_{\xi } + u_0 u_1 (u_0^2-1) + \frac{1}{2} \alpha (u_0\mathcal {L}_1u_0-1)\\&\quad + \frac{1}{2} \beta (u_0\mathcal {L}_2u_0-1) + \gamma _i (u_0 -\hat{\bar{u}}_{\gamma _{i,0}}) \,,\end{aligned} \end{aligned}$$

(23)

where we used (18) and the observation that $F(u_0+\varepsilon u_1 + \mathcal {O}(\varepsilon ^2)) = F(u_0)+\varepsilon u_0 u_1 (u_0^2-1) + \mathcal {O}(\varepsilon ^2)$.

3 Pinned Front Solutions

In this section, we focus on pinned front solutions supported by (1) and we first derive the part of Main Result 1 related to the existence and stability of local defect front solutions $Z_{f, ld}^\ell$ pinned to the left of the defect. In particular, we explicitly derive the relationship (3) determining the pinning distance of the interface of the local defect front solution to the defect. In Sect. 3.2, we combine these results with the results of [54] related to global defect front solutions to obtain a broader picture for pinned front solutions. Finally, we confirm our asymptotic findings by numerically investigating the stationary version of (1), that is, by investigating (10).

3.1 Local Defect Front Solutions $Z_{f, ld}^\ell$ Pinned to the Left of the Defect

In order to study local defect front solutions $Z_{f, ld}^\ell$ pinned to the left of the defect and as outlined in Sect. 2.1, we split the spatial domain into three slow regions $I_s^{1,3,6}$ and three fast regions $I_f^{2,4,5}$. In particular,

$$\begin{aligned} \begin{aligned}&I_s^1:=(-\infty ,-x_d-\sqrt{\varepsilon }]\,,&I_s^3:=[-x_d+\sqrt{\varepsilon }, -\sqrt{\varepsilon }]\,,&I_s^6:=[\sqrt{\varepsilon }, \infty )\,,&\\&I_f^2:=(-x_d-\sqrt{\varepsilon },-x_d+\sqrt{\varepsilon })\,,&I_f^4:=(-\sqrt{\varepsilon }, 0]\,,&I_f^5:=(0,\sqrt{\varepsilon })\,,&\end{aligned} \end{aligned}$$

(24)

Fig. 3

Schematic depiction of the three slow regions $I_s^{1,3,6}$ and three fast regions $I_f^{2,4,5}$ (24) used to study local defect front solutions $Z_{f, ld}^\ell$ pinned to the left of the defect

with $0<x_d=\varTheta (1)$ the, currently undetermined, pinning distance and with the defect located in between the fast fields $I_f^4$ and $I_f^5$. See also Fig. 3. We use a regular expansion in $\varepsilon$ and expand the profile of a local defect front solution $Z_{f, ld}^\ell (x)$

$$\begin{aligned} \begin{aligned} Z_{f, ld}^\ell (x)&= (U_{f, ld}^\ell ,V_{f, ld}^\ell ,W_{f, ld}^\ell )(x) = (U_{f, ld,0}^\ell ,V_{f, ld,0}^\ell ,W_{f, ld,0}^\ell )(x) \\&\qquad + \varepsilon (U_{f, ld,1}^\ell ,V_{f, ld,1}^\ell , W_{f, ld,1}^\ell )(x) + \mathcal {O}(\varepsilon ^2)\,. \end{aligned} \end{aligned}$$

(25)

Since the defect is small, it has no leading order influence on the profile and we can thus use the results from the homogeneous case. In particular, we have that

$$\begin{aligned} U_{f,ld,0}^\ell (x) = \left\{ \begin{aligned} -1\,, \qquad&{\text { in }} I_s^1\,,&\\ \tanh {\left( \frac{x+x_d}{\sqrt{2} \varepsilon }\right) }\,,\qquad&{\text { in }} I_f^2\,,&\\ 1\,, \qquad&{\text { in }} I_s^3 \cup I_f^4 \cup I_f^5 \cup I_s^6 \,,&\end{aligned} \right. \end{aligned}$$

(26)

see, for instance, [15, 54, 55] (and recall that $\tanh {((\xi -\hat{\xi })/\sqrt{2})}$ solves $u_{\xi \xi }+u-u^3=0$). The leading order components of the slow components are given by

$$\begin{aligned} V_{f,ld,0}^\ell (x) = \left\{ \begin{aligned} e^{x+x_d} -1\,, \qquad&{\text { in }} I_s^1\,,&\\ 0\,,\qquad&{\text { in }} I_f^2\,,&\\ -e^{-(x+x_d)}+1\,, \qquad&{\text { in }} I_s^3 \cup I_f^4 \cup I_f^5 \cup I_s^6 \,,&\end{aligned} \right. \end{aligned}$$

(27)

and

$$\begin{aligned} W_{f,ld,0}^\ell (x) = \left\{ \begin{aligned} e^{(x+x_d)/D} -1\,, \qquad&{\text { in }} I_s^1\,,&\\ 0\,,\qquad&{\text { in }} I_f^2\,,&\\ -e^{-(x+x_d)/D}+1\,, \qquad&{\text { in }} I_s^3 \cup I_f^4 \cup I_f^5 \cup I_s^6 \,.&\end{aligned} \right. \end{aligned}$$

(28)

Before we compute the higher order correction terms of $Z_{f,ld}^\ell$, we first look at the contribution of the leading order profile to the action functional $J_f$ (17). That is, we compute $J_{f,1}^{1,3}:=\int _{I_s^{1,3}} L_1(U_{f,ld}^\ell ;\bar{u}_{\gamma _1}) dx$, $J_{f,1}^{6}:=\int _{I_s^{6}} L_1(U_{f,ld}^\ell ;\hat{u}_{\gamma _2}) dx$, $J_{f,1}^{2,4}:=\int _{I_f^{2,4}} \bar{L}_0(U_{f,ld}^\ell ;\bar{u}_{\gamma _1}) d\xi$, and $J_{f,1}^{5}:=\int _{I_f^{5}} \bar{L}_0(U_{f,ld}^\ell ;\hat{u}_{\gamma _2}) d\xi$, see (19), respectively (22), for the definition of $L_1$, respectively $\bar{L}_0$. These computations will be similar in spirit to the computations in [52] for homogeneous pulse solutions (since the contributions of the weak defect enter only at the next level of the action functional). We first compute the leading order contributions of the three slow integrals $J_{f,1}^{1,3,6}$. We get

$$\begin{aligned} \begin{aligned} J_{f,1}^{1}&= \int _{I_s^{1}} L_1(U_{f,ld}^\ell ;\bar{u}_{\gamma _1}) dx \\ {}&= \int _{I_s^1} \left( \frac{1}{2} \alpha \left( U_{f,ld,0}^\ell V_{f,ld,0}^\ell -1\right) + \frac{1}{2} \beta \left( U_{f,ld,0}^\ell W_{f,ld,0}^\ell -1\right) \right. \\&\left. \qquad + \gamma _1 \left( U_{f,ld,0}^\ell +1\right) \right) dx \\&= -\int _{-\infty }^{-x_d} \left( \frac{1}{2} \alpha e^{x+x_d} + \frac{1}{2} \beta e^{(x+x_d)/D} \right) dx +\mathcal {O}(\sqrt{\varepsilon }) \\&= -\frac{1}{2} (\alpha + \beta D) +\mathcal {O}(\sqrt{\varepsilon }) \,, \end{aligned} \end{aligned}$$

(29)

where the $\mathcal {O}(\sqrt{\varepsilon })$-term stems from the fact that we shifted the limit of the integral from $-x_d-\sqrt{\varepsilon }$ to $-x_d$. Likewise, we get

$$\begin{aligned} \begin{aligned} J_{f,1}^{3}&= \frac{1}{2} \left( \alpha \left( e^{-x_d}-1\right) + \beta D \left( e^{-x_d/D}-1\right) \right) + 2 \gamma _1 x_d +\mathcal {O}(\sqrt{\varepsilon }) \,, \end{aligned} \end{aligned}$$

where we remark that the explicit $\gamma _1$-dependence follows from the fact that $U_{f,ld,0}^\ell = 1$ in $I_s^3$ while $\bar{u}_{\gamma _1} = -1$ in $I_s^3$, see Fig. 3. Similarly,

$$\begin{aligned} \begin{aligned} J_{f,1}^6&= -\frac{1}{2} \left( \alpha e^{-x_d} + \beta D e^{-x_d/D}\right) +\mathcal {O}(\sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

The integral over the first fast region $I_f^{2}$ gives

$$\begin{aligned} \begin{aligned} J_{f,1}^{2}&= \int _{I_f^{2}} \bar{L}_0(U_{f,ld}^\ell ;\bar{u}_{\gamma _1}) d\xi = \int _{I_f^2} \left( \frac{1}{2}(U_{f,ld,0}^\ell )_{\xi }^2 + F(U_{f,ld,0}^\ell )+\frac{1}{4} \right) d\xi \, \\&=\int _{0}^{1/\sqrt{\varepsilon }} \mathrm{{sech^4}}{\left( \frac{\xi }{\sqrt{2} }\right) }d\xi = \frac{2\sqrt{2}}{3} + \mathcal {O}(e^{-1/\sqrt{\varepsilon }})\,, \end{aligned} \end{aligned}$$

(30)

where we used that $\tanh ^4(\cdot ) - 2 \tanh ^2(\cdot )+1 = (\tanh ^2(\cdot )-1)^2= \mathrm{{sech^4}}(\cdot )$, see also [52], and the correction term again arises from changing the limit of the integral. The other two fast integrals do not yield a leading order contribution to the action functional since the U-profile is to leading order constant $+1$ over $I_{f}^{4,5}$, see (26). In particular, over these fields we have that $(U_{f,ld,0}^\ell )_\xi =0$ and $F(U_{f,ld,0}^\ell )=-1/4$ and, hence, $\bar{L}_0(U_{f,ld,0}^\ell , \hat{\bar{u}}_{\gamma _i})=0$ (22). So, by adding $J_{f,1}^{1,2,3}$ and $J_{f,1}^{6}$ we get that the action functional for a local defect front solution $Z_{f,ld}^\ell$ pinned to the left of the defect is given by

$$\begin{aligned} J_f(U_{f,ld}^\ell ) = \left( 2\gamma _1 x_d +\frac{2\sqrt{2}}{3}-(\alpha + \beta D) \right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,. \end{aligned}$$

(31)

As long as $\gamma _1 =\varTheta (1)$ (and thus unequal to 0), the critical points of $J_f(U_{f,ld}^\ell )$ with respect to the pinning distance $x_d$ are—to leading order—given by $x_d \rightarrow 0$ and $x_d \rightarrow \infty$. In other words, they approach the boundaries of the slow region $I_s^1$. Consequently, local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect do not exist if $\gamma _1 = \varTheta (1)$, and, as expected, the pinning distance $x_d$ of $Z_{f,ld}^\ell$ cannot be determined from the leading order computation.

Remark 4

By the symmetry (7) of (1), the action functional for a local defect front solution $Z_{f,ld}^r$ pinned to the right of the defect is given by

$$\begin{aligned} J_f(U_{f,ld}^r) = \left( -2\gamma _2 x_d+\frac{2\sqrt{2}}{3}-(\alpha + \beta D) \right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,, \end{aligned}$$

where $x_d>0$ is again the pinning distance. So, combining the results following from the action functionals for $U_{f,ld}^\ell$ and $U_{f,ld}^r$ also hints to the results for the existence and stability of global defect front solutions $Z_{f, gd}$ pinned at the defect as obtained in [54]: global defect front solutions exist if $\gamma _1\gamma _2<0$, and they are stable if and only if $\gamma _2<0<\gamma _1$. In more detail, for $\gamma _1>0$ the action functional $J_f(U_{f,ld}^\ell )$ indicates that a front solution to the left of the defect wants to move towards the defect (towards smaller $x_d>0$) to minimise its action functional, while it moves away from the defect for $\gamma _1<0$. Similarly, for $\gamma _2<0$ the action functional $J_f(U_{f,ld}^r)$ indicates that a front solution to the right of the defect wants to move towards the defect (towards smaller $x_d>0$) to minimise the action functional, while it moves away from the defect for $\gamma _2>0$.

3.1.1 The Next Order

As eluded to above, it is clear from (31) that, to leading order, we necessarily need that $\gamma _1=0$ for the existence of a local defect front solution $Z_{f,ld}^\ell$ pinned to the left of the defect. So, we set $\gamma _1 = \varepsilon \tilde{\gamma }_1$ with, a priori, $\tilde{\gamma }_1=\varTheta (1)$. To be able to determine the next order term of the action functional $J_f$ (17), we first compute the higher order correction terms $(U_{f,ld,1}^\ell , V_{f,ld,1}^\ell , W_{f,ld,1}^\ell )(x)$ (25) of $Z_{f,ld}^\ell$. In the slow fields $I_s^{1,3,6}$, we substitute the regular expansion (25)—with $U_{f,ld,0}^\ell , V_{f,ld,0}^\ell$ and $W_{f,ld,0}^\ell$ respectively given by (26)–(28)—into (10), to obtain

$$\begin{aligned} \left\{ \begin{aligned} \mathcal {O}(\varepsilon )&= U_{f,ld,1}^\ell -3 (U_{f,ld,0}^\ell )^2U_{f,ld,1}^\ell - (\alpha V_{f,ld,0}^\ell + \beta W_{f,ld,0}^\ell + \gamma (x)) \,,\\ \mathcal {O}(\varepsilon )&= (V_{f,ld,1}^\ell )_{xx} + U_{f,ld,1}^\ell -V_{f,ld,1}^\ell \,,\\ \mathcal {O}(\varepsilon )&= D^2 (W_{f,ld,1}^\ell )_{xx} + U_{f,ld,1}^\ell - W_{f,ld,1}^\ell \, . \end{aligned} \right. \end{aligned}$$

(32)

Since $(U_{f,ld,0}^\ell )^2=1$ in all three slow fields, the first equation yields that the higher order correction term $U_{f,ld,1}^\ell$ in the slow fields is given by

$$\begin{aligned} U_{f,ld,1}^\ell = -\frac{1}{2} \left( \alpha V_{f,ld,0} + \beta W_{f,ld,0} + \gamma (x)\right) , \end{aligned}$$

with $V_{f,ld,0}^\ell$, respectively $W_{f,ld,0}^\ell$, given by (27), respectively (28) and $\gamma (x)$ given by (2) with $\gamma _1 = 0$ (since $\gamma _1 = \varepsilon \tilde{\gamma }_1$ is a higher order term). This allows us to solve the second and third equations of (32) explicitly. In $I_s^1$ we obtain

$$\begin{aligned} I_s^1:\left\{ \begin{aligned} U_{f,ld,1}^\ell&= \frac{1}{2}(\alpha +\beta ) - \frac{1}{2} \left( \alpha e^{x+x_d} + \beta e^{(x+x_d)/D}\right) \,,\\ V_{f,ld,1}^\ell&= \frac{1}{2}(\alpha +\beta ) + C_{1,V} e^x +\frac{1}{8} \alpha (2x-1)e^{x+x_d} \\&\quad - \frac{1}{2} \beta \left( \frac{D^2}{D^2-1}\right) e^{(x+x_d)/D}\,,\\ W_{f,ld,1}^\ell&=\frac{1}{2}(\alpha +\beta ) + C_{1,W} e^{x/D} + \frac{1}{2} \alpha \left( \frac{1}{D^2-1}\right) e^{x+x_d} \\&\quad + \frac{1}{8} \beta \left( \frac{2x}{D}-1\right) e^{(x+x_d)/D} \, , \end{aligned} \right. \end{aligned}$$

where we used that both slow components need to be bounded as x approaches $-\infty$ and the fact that $\gamma _1 = 0$ to leading order. In $I_s^3$ we obtain

$$\begin{aligned} I_s^3:\left\{ \begin{aligned} U_{f,ld,1}^\ell&= -\frac{1}{2}(\alpha +\beta )+ \frac{1}{2} \left( \alpha e^{-(x+x_d)} + \beta e^{-(x+x_d)/D}\right) \,,\\ V_{f,ld,1}^\ell&=-\frac{1}{2}(\alpha +\beta ) + C_{3,V} e^x + D_{3,V} e^{-x} +\frac{1}{8} \alpha (2x+1)e^{-(x+x_d)} \\ {}&\qquad +\frac{1}{2} \beta \left( \frac{D^2}{D^2-1}\right) e^{-(x+x_d)/D} \,,\\ W_{f,ld,1}^\ell&=-\frac{1}{2}(\alpha +\beta ) + C_{3,W} e^{x/D} + D_{3,W} e^{-x/D} \\ {}&\qquad -\frac{1}{2} \alpha \left( \frac{1}{D^2-1}\right) e^{-(x+x_d)}+ \frac{1}{8} \beta \left( \frac{2x}{D}+1\right) e^{-(x+x_d)/D} \, , \end{aligned} \right. \end{aligned}$$

and in $I_s^6$ we have

$$\begin{aligned} I_s^6:\left\{ \begin{aligned} U_{f,ld,1}^\ell&= -\frac{1}{2}(\alpha +\beta +\gamma _2) + \frac{1}{2} \left( \alpha e^{-(x+x_d)} + \beta e^{-(x+x_d)/D}\right) \,,\\ V_{f,ld,1}^\ell&=-\frac{1}{2}(\alpha +\beta +\gamma _2) + D_{6,V} e^{-x} +\frac{1}{8} \alpha (2x+1) e^{-(x+x_d)} \\ {}&\qquad +\frac{1}{2} \beta \left( \frac{D^2}{D^2-1}\right) e^{-(x+x_d)/D} \,,\\ W_{f,ld,1}^\ell&=-\frac{1}{2}(\alpha +\beta +\gamma _2) + D_{6,W} e^{-x/D}-\frac{1}{2} \alpha \left( \frac{1}{D^2-1}\right) e^{-(x+x_d)} \\ {}&\qquad + \frac{1}{8} \beta \left( \frac{2x}{D}+1\right) e^{-(x+x_d)/D} \, , \end{aligned} \right. \end{aligned}$$

where we used that both slow components need to be bounded as x approaches $\infty$. In the three fast regions $I_f^{2,4,5}$, we use the fast scaling $\xi$ and substitute the regular expansion (25)—as function of $\xi$—into (12). By using the expressions of $U_{f,ld,0}^\ell , V_{f,ld,0}^\ell$ and $W_{f,ld,0}^\ell$, given by respectively (26)–(28), we obtain

$$\begin{aligned} \left\{ \begin{aligned} \mathcal {O}(\varepsilon )&= \left( U_{f,ld,1}^\ell \right) _{\xi \xi } +U_{f,ld,1}^\ell - 3\left( U_{f,ld,0}^\ell \right) ^2 U_{f,ld,1}^\ell \\ {}&\quad - \left( \alpha V_{f,ld,0}^\ell +\beta W_{f,ld,0}^\ell + \gamma (x)\right) \,,\\ \mathcal {O}(\varepsilon )&= \left( V_{f,ld,1}^\ell \right) _{\xi \xi } \,,\\ \mathcal {O}(\varepsilon )&= D^2 \left( W_{f,ld,1}^\ell \right) _{\xi \xi } \, , \end{aligned} \right. \end{aligned}$$

(33)

where we used that both $(V_{f,ld,0}^\ell )_{\xi \xi }$ and $(W_{f,ld,0}^\ell )_{\xi \xi }$ are $\mathcal {O}(\varepsilon ^2)$ in the fast fields. So, the slow components are solved by linear functions. However, the solutions have to stay bounded and therefore they are to leading order constant, see also “Appendix A”. Furthermore, since the fast fields are too small for the slow components to change significantly, see, for instance, [54], these slow components—as well as their derivatives—need to match over the fast fields. This gives

$$\begin{aligned} \begin{aligned} C_{1,V}&= -\frac{1}{4} \gamma _2 + \frac{1}{8} \alpha (-3+2x_d) e^{x_d} + \frac{1}{2} \beta \left( \frac{1}{D^2-1}\right) e^{x_d} \,,\quad C_{3,V} = -\frac{1}{4} \gamma _2 \,,\\ D_{3,V}&= \frac{1}{8} \alpha (3+2x_d) e^{-x_d}- \frac{1}{2} \beta \left( \frac{1}{D^2-1}\right) e^{-x_d}\,,\quad D_{6,V} =\frac{1}{4} \gamma _2 + D_{3,V}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} C_{1,W}&= -\frac{1}{4} \gamma _2 -\frac{1}{2} \alpha \left( \frac{D^2}{D^2-1}\right) e^{x_d/D} + \frac{1}{8} \beta \left( -3+\frac{2x_d}{D}\right) e^{x_d/D} \,,\\ C_{3,W}&= -\frac{1}{4} \gamma _2 \,,\\ D_{3,W}&= \frac{1}{2}\alpha \left( \frac{D^2}{D^2-1}\right) e^{-x_d/D} + \frac{1}{8} \beta \left( 3+\frac{2x_d}{D}\right) e^{-x_d/D}\,,\\ D_{6,W}&=\frac{1}{4} \gamma _2 + D_{3,W}\,. \end{aligned} \end{aligned}$$

So, we have completely determined the correction terms $V_{f,ld,1}^\ell$ and $W_{f,ld,1}^\ell$.

In the first fast field $I_f^2$, the U-equation of (33) reduces to

$$\begin{aligned} \mathcal {O}(\varepsilon ) = (U_{f,ld,1}^\ell )_{\xi \xi } +\left( 1- 3\tanh ^2{\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } \right) U_{f,ld,1}^\ell \,, \end{aligned}$$

where we used that the leading order computation implied that $\gamma _1 = \varTheta (\varepsilon )$. The above equation is explicitly solved by

$$\begin{aligned} \begin{aligned} U_{f,ld,1}^\ell (\xi )= & {} D_{2,U} \left( 2 \sinh {\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } \cosh {\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } +3\tanh {\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } \right. \\&+ \left. 3 \left( \frac{\xi +\xi _d}{\sqrt{2}}\right) \mathrm{sech}^2{\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } \right) +C_{2,U} \mathrm{sech}^2{\left( \frac{\xi +\xi _d}{\sqrt{2}}\right) } \,, \end{aligned} \end{aligned}$$

see Sect. 2 of [54]. However, to ensure that $U_{f,ld,1}^\ell$ stays bounded as $\xi$ approaches the boundaries of the fast field, which are to leading order in $\xi$ given by $\xi \rightarrow \pm \infty$, we have $D_{2,U} = 0$. Moreover, also $C_{2,U}$ can be taken identically zero since the original U-equation, upon substituting the leading order expressions of the slow components in the first fast field $I_f^2$ (see (27) and (28)), has no $\mathcal {O}(\varepsilon )$-terms. In particular, the u-equation of (12) in $I_f^2$ reduces to $\mathcal {O}(\varepsilon ^2)=u_{\xi \xi } + u - u^3$ and so no $\mathcal {O}(\varepsilon )$-correction term is expected, see also [53]. Thus,

$$\begin{aligned} U_{f,ld,1}^\ell (\xi )=0\,, \qquad \xi \in I_f^2. \end{aligned}$$

In the other two fast fields $I_{f}^{4,5}$, the U-equation of (33) reduces to

$$\begin{aligned} \mathcal {O}(\varepsilon ) = (U_{f,ld,1}^\ell )_{\xi \xi } -2U_{f,ld,1}^\ell - (\alpha (-e^{-x_d}+1)+\beta (-e^{-x_d/D}+1)+ \gamma (\xi )) \,. \end{aligned}$$

This equation is solved, see also “Appendix A”, by

$$\begin{aligned} U_{f,ld,1}^\ell (\xi )&= \left\{ \begin{aligned}&-\frac{1}{2}(\alpha +\beta )+ C_{4,U} e^{\sqrt{2} \xi }+D_{4,U} e^{-\sqrt{2} \xi } \\&\quad +\frac{1}{2}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,,&\quad \xi \in I_f^4 \,, \\&-\frac{1}{2}(\alpha +\beta +\gamma _2)+ C_{5,U} e^{\sqrt{2} \xi }+D_{5,U} e^{-\sqrt{2} \xi } \\&\quad +\frac{1}{2}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,,&\quad \xi \in I_f^5 \,. \end{aligned} \right. \end{aligned}$$

These two terms—as well as their derivatives—have to match at the defect point $x=0$. This gives $C_{4,U} +D_{4,U} = C_{5,U}+D_{5,U} -\frac{1}{2} \gamma _2$ and $C_{4,U} -D_{4,U} = C_{5,U}-D_{5,U}$. Moreover, matching with the slow fields gives $D_{4,U} = 0 = C_{5,U}$. Combining these gives $C_{4,U} = -\frac{1}{4} \gamma _2 = -D_{5,U}$. Hence, the correction term $U_{f,ld,1}^\ell$ is now also completely determined and given by

$$\begin{aligned} U_{f,ld,1}^\ell (x) = \left\{ \begin{aligned}&\frac{1}{2}(\alpha +\beta ) - \frac{1}{2} \left( \alpha e^{x+x_d} + \beta e^{(x+x_d)/D}\right) \,,&x \in I_s^1\,,&\\&0\,,&x \in I_f^2\,,&\\&-\frac{1}{2}(\alpha +\beta )+ \frac{1}{2} \left( \alpha e^{-(x+x_d)} + \beta e^{-(x+x_d)/D}\right) \,,&x \in I_s^3\,,&\\&-\frac{1}{2}(\alpha +\beta ) -\frac{1}{4} \gamma _2 e^{\sqrt{2} x/\varepsilon } +\frac{1}{2}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,,&x \in I_f^4\,,&\\&-\frac{1}{2}(\alpha +\beta +\gamma _2) + \frac{1}{4}\gamma _2 e^{-\sqrt{2} x/\varepsilon } \\&+\frac{1}{2}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,,&x \in I_f^5\,,&\\&-\frac{1}{2}(\alpha +\beta +\gamma _2)+ \frac{1}{2} \left( \alpha e^{-(x+x_d)} + \beta e^{-(x+x_d)/D}\right) \,,&x \in I_s^6\,.&\end{aligned} \right. \end{aligned}$$

(34)

We are now in the position to compute the higher order correction term of the action functional $J_f$ (17) for a front solution $Z_{f,ld}^\ell$ pinned to the left of the defect. We start by computing the higher order contributions to the action functional coming from the first slow region $I_s^1$. Recall that to obtain the leading order contribution from the first slow region $I_s^1$, i.e. (29), we shifted the upper limit of the integral of $J_{f,1}^1$ and this resulted in an  $\mathcal {O}(\sqrt{\varepsilon })$-error. Since we are now interested in the higher order contributions, we actually need to explicitly compute this error-term. From (29) we deduce

$$\begin{aligned} \begin{aligned} J_{f,1}^1&= -\frac{1}{2} (\alpha + \beta D) + \int _{-x_d-\sqrt{\varepsilon }}^{-x_d} \left( \frac{1}{2} \alpha e^{x+x_d} + \frac{1}{2} \beta e^{(x+x_d)/D} \right) dx \\&=-\frac{1}{2} (\alpha + \beta D) + \frac{1}{2} \left( \alpha \left( 1-e^{-\sqrt{\varepsilon }}\right) + \beta D\left( 1-e^{\sqrt{\varepsilon }/D}\right) \right) \\&= -\frac{1}{2} (\alpha + \beta D) + \frac{1}{2} (\alpha +\beta ) \sqrt{\varepsilon }- \frac{1}{4} \left( \alpha + \frac{\beta }{D} \right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon }) \,. \end{aligned} \end{aligned}$$

Next, we compute the contribution of the remaining correction terms of the profile in $I_s^1$. That is, we compute

$$\begin{aligned} \begin{aligned} J_{f,2}^1:&= \int _{I_s^{1}} L_2(U_{f,ld}^\ell ;\bar{u}_{\varepsilon \tilde{\gamma }_1}) dx \\&=\int _{I_s^1} \left( \left( U_{f,ld,1}^\ell \right) ^2 - \left( \bar{u}_{0,1}\right) ^2 + \frac{1}{2} \alpha \left( U_{f,ld,1}^\ell \mathcal {L}_1U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_1U_{f,ld,1}^\ell \right. \right. \\&\qquad \left. \left. +2\bar{u}_{0,1}\right) + \frac{1}{2} \beta \left( U_{f,ld,1}^\ell \mathcal {L}_2U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_1U_{f,ld,1}^\ell +2\bar{u}_{0,1}\right) \right. \\&\qquad \left. + \tilde{\gamma }_1 \left( U_{f,ld,0}^\ell +1\right) \right) dx \\&=\int _{I_s^1} \left( \left( U_{f,ld,1}^\ell \right) ^2 - \left( \bar{u}_{0,1}\right) ^2 + \frac{1}{2} \alpha \left( U_{f,ld,1}^\ell \mathcal {L}_1U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_1U_{f,ld,1}^\ell \right. \right. \\&\qquad \left. \left. +2\bar{u}_{0,1}\right) + \frac{1}{2} \beta \left( U_{f,ld,1}^\ell \mathcal {L}_2U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_1U_{f,ld,1}^\ell +2\bar{u}_{0,1}\right) \right) dx\,, \end{aligned} \end{aligned}$$

where we used the asymptotic scaling $\gamma _1 = \varepsilon \tilde{\gamma }_1$ and recall that $\bar{u}_{0,1}$ is the $\mathcal {O}(\varepsilon )$-term of the asymptotic end state near $-1$, see (11). For the clarity of the presentation, we compute the different components of the integral separately. We get

$$\begin{aligned} \begin{aligned}&\int _{I_s^1} \left( (U_{f,ld,1}^\ell )^2 - (\bar{u}_{0,1})^2\right) dx \\ {}&\quad = \int _{I_s^1} \frac{1}{4}\left( \alpha e^{x+x_d} + \beta e^{(x+x_d)/D}\right) \left( -2(\alpha +\beta ) + \left( \alpha e^{x+x_d} + \beta e^{(x+x_d)/D}\right) \right) dx \\ {}&\quad = -\frac{3}{8} (\alpha ^2+ \beta ^2 D) -\frac{1}{2} \alpha \beta \left( \frac{D^3-1}{D^2-1}\right) + \mathcal {O}(\sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

where the $\mathcal {O}(\sqrt{\varepsilon })$-term again appears due to the error made by shifting the limit of the integral. Similarly,

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \alpha \int _{I_s^1} \left( U_{f,ld,1}^\ell \mathcal {L}_1U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_1U_{f,ld,1}^\ell +2\bar{u}_{0,1} \right) dx\, \\ {}&\qquad = \frac{1}{2} \alpha \int _{I_s^1} \left( U_{f,ld,1}^\ell V_{f,ld,0}^\ell -V_{f,ld,1}^\ell +(\alpha +\beta )\right) dx \\ {}&\qquad =\frac{1}{2} \alpha \int _{I_s^1} \left( \left( \frac{1}{2}(\alpha +\beta ) - \frac{1}{2} \left( \alpha e^{x+x_d} + \beta e^{(x+x_d)/D}\right) \right) (e^{x+x_d}-1)- \right. \\&\qquad \qquad \left. \left( \frac{1}{2}(\alpha +\beta ) + \left( -\frac{1}{4} \gamma _2 + \frac{1}{8} \alpha e^{x_d} (-3+2x_d) + \frac{1}{2} \beta \frac{1}{D^2-1}e^{x_d}\right) e^x \right. \right. \\ {}&\qquad \qquad \left. \left. +\frac{1}{8} \alpha e^{x+x_d}(2x-1) - \frac{1}{2} \beta \frac{D^2}{D^2-1} e^{(x+x_d)/D}\right) +(\alpha +\beta )\right) dx \\&\qquad = \frac{1}{2} \alpha \int _{I_s^1} \left( \frac{1}{4} \gamma _2 e^x + \frac{1}{4}\alpha \left( 6-(x+x_d)\right) e^{x+x_d} -\frac{1}{2} \alpha e^{2(x+x_d)} \right. \\&\qquad \qquad \left. + \frac{1}{2} \beta \left( 1-\frac{1}{D^2-1}\right) e^{x+x_d} + \frac{1}{2} \beta \left( 1+\frac{D^2}{D^2-1}\right) e^{(x+x_d)/D} \right. \\&\qquad \qquad \left. -\frac{1}{2} \beta e^{x+x_d}e^{(x+x_d)/D}\right) dx \\ {}&\qquad = \frac{1}{2} \alpha \left( \frac{1}{4} \gamma _2 e^{-x_d} + \frac{3}{2} \alpha + \beta \left( \frac{D^3-1}{D^2-1}\right) \right) + \mathcal {O}(\sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\frac{1}{2} \beta \int _{I_s^1} \left( U_{f,ld,1}^\ell \mathcal {L}_2U_{f,ld,0}^\ell +U_{f,ld,0}^\ell \mathcal {L}_2U_{f,ld,1}^\ell +2\bar{u}_{0,1} \right) dx\, \\ {}&\qquad = \frac{1}{2} \beta \left( \frac{1}{4} \gamma _2 D e^{-x_d/D} + \alpha \left( \frac{D^3-1}{D^2-1}\right) + \frac{3}{2}\beta D \right) + \mathcal {O}(\sqrt{\varepsilon }) \,. \end{aligned} \end{aligned}$$

So, the total contribution to the action functional coming from the first slow field $I_s^1$ is given by

$$\begin{aligned} \begin{aligned} J_f|_{I_s^1}&= \varepsilon J_{f,1}^{1} + \varepsilon ^2 J_{f,2}^{1} + \mathcal {O}(\varepsilon ^3) \\&= -\frac{1}{2} (\alpha + \beta D) \varepsilon + \frac{1}{2} (\alpha +\beta ) \varepsilon \sqrt{\varepsilon }+ \left( - \frac{1}{4} \left( \alpha + \frac{\beta }{D} \right) + \frac{1}{8} \gamma _2\left( \alpha e^{-x_d} \right. \right. \\ {}&\qquad \left. \left. + \beta D e^{-x_d/D}\right) + \frac{3}{8}\left( \alpha ^2+ \beta ^2 D\right) + \frac{1}{2} \alpha \beta \left( \frac{D^3-1}{D^2-1}\right) \right) \varepsilon ^2 + \mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

Observe that the pinning distance $x_d$ and $\gamma _2$—but not $\tilde{\gamma }_1$—enter the $\mathcal {O}(\varepsilon ^2)$-term. We also expect that, after adding the contributions to the action functional from the other slow and fast regions, the $\mathcal {O}(\varepsilon \sqrt{\varepsilon })$-term above disappears (since the boundaries between the slow and fast fields are artificial in the sense we could have used any $\varepsilon ^{a}, a \in (0,1)$, as boundary instead of $\sqrt{\varepsilon }$, see also [23]).

We also compute the contributions to the action functional over the other two slow regions $I_s^{3,6}$. Using the same notation as above, i.e. $J_f|_{I_s^{3,6}} = \varepsilon J_{f,1}^{3,6} + \varepsilon ^2 J_{f,2}^{3,6} + \mathcal {O}(\varepsilon ^3),$ we get for $I_s^3$

$$\begin{aligned} \begin{aligned} J_{f,1}^3&= \frac{1}{2} \left( \alpha \left( e^{-x_d}-1\right) + \beta D \left( e^{-x_d/D}-1\right) \right) +\frac{1}{2}\left( \alpha \left( 1+e^{-x_d}\right) \right. \\ {}&\qquad \left. +\beta \left( 1+e^{-x_d/D}\right) \right) \sqrt{\varepsilon }+\frac{1}{4} \left( \alpha \left( e^{-x_d}-1\right) + \frac{\beta }{D} \left( e^{-x_d/D}-1\right) \right) \varepsilon \\ {}&\qquad + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{f,2}^3 :&= \int _{I_s^3} L_2(U_{f,ld}^\ell ; \bar{u}_{\varepsilon \tilde{\gamma }_1}) dx \\&= 2 \tilde{\gamma }_1 x_d + \frac{1}{8} \gamma _2 \left( \alpha (e^{-x_d}-1) + \beta D \left( e^{-x_d/D}-1\right) \right) +\frac{1}{8} \alpha ^2 \left( 3 - 3 e^{-x_d} \right. \\ {}&\qquad \left. - x_d e^{-x_d} \right) +\frac{1}{8} \beta ^2 \left( 3D - 3 De^{-x_d/D} - x_d e^{-x_d/D} \right) + \frac{1}{2} \alpha \beta \left( \frac{D^3-1}{D^2-1}\right) \\ {}&\qquad + \frac{1}{2} \alpha \beta \left( \frac{e^{-x_d}-D^3 e^{-x_d/D}}{D^2-1}\right) + \mathcal {O}(\sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

Observe that this term does explicitly depend on $\tilde{\gamma }_1$. Similarly, For $I_s^6$ we get

$$\begin{aligned} \begin{aligned} J_{f,1}^6&= -\frac{1}{2} (\alpha e^{-x_d} + \beta D e^{-x_d/D}) +\frac{1}{2}\left( \alpha e^{-x_d}+\beta e^{-x_d/D} \right) \sqrt{\varepsilon }\\ {}&\qquad - \frac{1}{4} \left( \alpha e^{-x_d}+\frac{\beta }{D} e^{-x_d/D} \right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{f,2}^6 :&= \int _{I_s^6} L_2(U_{f,ld}^\ell ; \hat{u}_{\gamma _2}) dx \\&= \frac{1}{8} \gamma _2 \left( \alpha \left( 1+2e^{-x_d}\right) + \beta D \left( 1+2e^{-x_d/D}\right) \right) + \frac{1}{8} \alpha ^2\left( 3+x_d\right) e^{-x_d} \\ {}&\quad + \frac{1}{8} \beta ^2\left( 3D+x_d\right) e^{-x_d/D} +\frac{1}{2} \alpha \beta \left( \frac{D^3 e^{-x_d/D}-e^{-x_d}}{D^2-1}\right) + \mathcal {O}(\sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

Next, we compute the higher order contribution of the action functional over the fast fields $I_f^{2,4,5}$. Unlike the case for the slow fields, the error terms of the leading order contributions arising from shifting the limits of the fast integrals are exponentially small and we thus do not have to revisit $I_{f,1}^{2,4,5}$. We start with computing the correction term $J_{f,2}^2$ coming from the first fast field $I_f^{2}$. There is no $\mathcal {O}(\varepsilon )$-correction term to the fast component in $I_f^{2}$, see (34), and, in addition, the slow components in $I_f^2$ are to leading order zero, see (27) and (28). So, since $\gamma _1=\varTheta (\varepsilon )$, (23) reduces, to leading order, to

$$\begin{aligned} J_{f,2}^{2}&:= \int _{I_f^2} \bar{L}_1(U_{f,ld}^\ell ;\bar{u}_{\varepsilon \gamma _1})d\xi = -\frac{1}{2} (\alpha + \beta )\int _{I_f^2} d\xi = -\frac{1}{\sqrt{\varepsilon }}(\alpha +\beta ) \,, \end{aligned}$$

and we have

$$\begin{aligned} J_f|_{I_f^2} = \frac{2\sqrt{2}}{3} \varepsilon - (\alpha +\beta )\varepsilon \sqrt{\varepsilon }+ \mathcal {O}(\varepsilon ^2\sqrt{\varepsilon })\,. \end{aligned}$$

The fast component is to leading order constant $+1$ over the two fast fields $I_f^{4,5}$ around the defect. So, $(U_{f,ld,0}^\ell )_{\xi } =0$ and $(U_{f,ld,0}^\ell )^2-1=0$ in both $I_f^{4}$ and $I_f^{5}$. In addition, since $\gamma (x)=\gamma _1=\varTheta (\varepsilon )$ in $I_f^4$, (23) becomes

$$\begin{aligned} \begin{aligned} J_{f,2}^4 :&= \int _{I_f^4} \bar{L}_1(U_{f,ld}^\ell ;\bar{u}_{\varepsilon \gamma _1})d\xi = -\frac{1}{2} \left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \int _{I_f^4} d\xi \\&= -\frac{1}{2} \frac{1}{\sqrt{\varepsilon }}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,. \end{aligned} \end{aligned}$$

In $I_f^5$, $\gamma (x)=\gamma _2$ but $U_{f,ld,0}^\ell - \hat{u}_{\gamma _2,0}=0$, and (23) again reduces to

$$\begin{aligned} \begin{aligned} J_{f,2}^5 :&=\int _{I_f^5} \bar{L}_1(U_{f,ld}^\ell ;\hat{u}_{\gamma _2})d\xi = -\frac{1}{2} \frac{1}{\sqrt{\varepsilon }}\left( \alpha e^{-x_d}+\beta e^{-x_d/D}\right) \,. \end{aligned} \end{aligned}$$

Combining the contributions from the slow and fast regions to the action functional gives—as expected—that the $\mathcal {O}(\varepsilon \sqrt{\varepsilon })$-terms from the fast regions cancel out with the $\mathcal {O}(\varepsilon \sqrt{\varepsilon })$-terms from the slow regions, and the total action functional of a local defect front solution $Z_{f,ld}^\ell$ pinned to the left of the defect becomes

$$\begin{aligned} \begin{aligned} J_f(U_{f,ld}^\ell ) =&\left( \frac{2\sqrt{2}}{3}- (\alpha +\beta D)\right) \varepsilon + \left( 2 \tilde{\gamma }_1 x_d + \frac{1}{2} \gamma _2\left( \alpha e^{-x_d}+ \beta D e^{-x_d/D}\right) \right. \\ {}&\quad \left. -\frac{1}{2}\left( \alpha + \frac{\beta }{D}\right) + \frac{3}{4}\left( \alpha ^2 + \beta ^2 D\right) + \alpha \beta \left( \frac{D^3-1}{D^2-1}\right) \right) \varepsilon ^2 \\&\quad + \mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

(35)

3.1.2 The Derivation of the First Part of Main Result 1

We study the critical points of the action functional $J_f(U_{f,ld}^\ell )$ (35) to derive the results for local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect as stated in Main Result 1. For more details regarding this approach, we refer to Sect. 2, [5,6,7, 9,10,11,12, 52] and references therein, however, see also Remark 1. In particular, expression (3) determining the pinning distance $x_d$ is obtained from the critical points of the action functional $J_f(U_{f,ld}^\ell )$ (35), and only the critical points that are minima yield stable solutions. That is, the minima of the action functional coincide with the stability condition (4). To this purpose, we differentiate the action functional $J_f(U_{f,ld}^\ell )$ (35) with respect to the unknown pinning distance $x_d$

$$\begin{aligned} \dfrac{d }{d x_d} (J_f(U_{f,ld}^\ell )) = 2 \tilde{\gamma }_1 - \frac{1}{2} \gamma _2\left( \alpha e^{-x_d}+ \beta e^{-x_d/D}\right) = 2 \tilde{\gamma }_1 - \frac{1}{2} \gamma _2 f(x_d)\,, \end{aligned}$$

and the second derivative is

$$\begin{aligned} \dfrac{d^2 }{d x_d^2} (J_f(U_{f,ld}^\ell )) = \frac{1}{2} \gamma _2\left( \alpha e^{-x_d}+ \frac{\beta }{D} e^{-x_d/D}\right) = \frac{1}{2} \gamma _2 g(x_d)\,. \end{aligned}$$

So, the critical points of the action functional $J_f(U_{f,ld}^\ell )$ (35) with respect to the pinning distance $x_d$ are exactly given by the existence condition (3) of Main Result 1, and a critical point is a minimum if the stability condition (4) of Main Result 1 holds.

3.2 Pinned Front Solutions

We further investigate the results of Main Result 1 related to local defect front solutions, and we combine these results with the results of [54] related to global defect front solutions, see also Remark 4. So, we aim to get a broad picture of pinned front solutions supported by (1). For this reason, we first shortly discuss the essential properties of f (as defined in (3)) and $g = -f'$ (as defined in (4)). For $\alpha \beta >0$ the function $\alpha f(x)$ is monotonically decreasing and strictly positive, while f(x) has an extremum $f_{ex}$ at $x_{ex}$ for $\alpha \beta <0$ and $|\alpha D| > |\beta |$ (recall that $D>1$ by assumption). In particular,

$$\begin{aligned} f_{ex} := -\alpha (D-1) \left( -\frac{\alpha D}{\beta }\right) ^{-D/(D-1)}, \quad x_{ex}:= \frac{D}{D-1}\log {\left( -\frac{\alpha D }{\beta }\right) }\,, \end{aligned}$$

(36)

and $f(x_{ex})=f_{ex}$ and $g(x_{ex})=0$. For convenience, we summarise these properties also in Table 1.

From Main Result 1 and these properties of f and g, we instantly get that there is a unique local defect front solution $Z_{f,ld}^\ell$ pinned to the left of the defect if $\alpha ,\beta >0$ and $0< 4 \tilde{\gamma }_1/\gamma _2 < \alpha + \beta$ and this solution is stable only if $\gamma _2>0$. A similar statement hold for $\alpha ,\beta <0$. For $\alpha \beta <0$ it directly follows that the situation is more complicated. In particular, the existence condition $\gamma _2 f(x_d) = 4\tilde{\gamma }_1$ (3) for local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect can have up to two solutions if $|\alpha D| > |\beta |$. Consequently, there can be two local defect front solutions pinned to the left of the defect with different pinning distances for the same parameter set. From (4) it follows that one of these front solutions will be a stable solution, while the other one is unstable. We summarise the results from Main Result 1 for local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect for the different parameter combinations in Table 2, and also refer to Figs. 4 and 5 for particular examples.

Table 1 Properties of $f(x) := \alpha e^{-x} + \beta e^{-x/D}$ and $g(x) := -f'(x) = \alpha e^{-x} + \frac{\beta }{D} e^{-x/D}$ for $x \in [0,\infty )$

Table 2 Number of local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect with pinning distances $x_d=\varTheta (1)$, and their stability properties, as derived from Main Result 1

Fig. 4

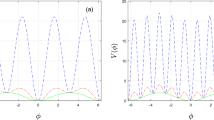
An example of $J_f(U_{f,ld}^\ell )$ (35), $f(x_d)$ and $g(x_d)$ for $sgn(\alpha ) \ne sgn(\beta ) = -1$, $|\alpha D|>|\beta |$ and $\alpha +\beta >0$. In particular, $(\alpha ,\beta ,D,\gamma _1,\gamma _2,\varepsilon ) = (3,-2,5,0.01,-5,0.01)$. Left panel: the action functional $J_f(U_{f,ld}^\ell )$ (35) and the numerically evaluated action functional $J_{f}^{NUM}(U_{f,ld}^\ell )$ (37) obtained from the asymptotically profile of a local defect front solution $Z_{f,ld}^\ell$ pinned to the left of the defect as function of the still undetermined pinning distance (and as derived in Sect. 3.1). The shape of the curve, as well as the location of the critical points are in good agreement, while the difference between the two curves appears to be, as expected, $\mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon })$. Right panel: the functions $f(x_d)$ and $g(x_d)$. For $f_{ex}<4\tilde{\gamma _1}/\gamma _2<0$ (see (36) for the definition of $f_{ex}$), there exist two different local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect. If $\gamma _2<0$, then the pinned front solution closest to the defect, i.e. with smallest pinning distance $x_d$, is unstable, while the larger one is stable

For $\gamma _1 \equiv 0$ it immediately follows from (3)—see also Table 2—that local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect with pinning distance $x_d = \varTheta (1)$ exist only for $\alpha \beta <0$. Since the local defect front solutions studied in [24], see also Theorem 2, required $\gamma _1 \equiv 0$ and $\alpha ,\beta >0$, we can conclude that these front solutions necessarily have pinning distances $x_d \gg 1$. However, see also Remark 5.

Fig. 5

Left panel: bifurcation diagram of the pinning distance $x_d$ of pinned defect front solutions for varying $\beta$ obtained by numerically simulating (10) on a domain of length $2L=54$. The other system parameters are kept fixed at $(\alpha , D, \varepsilon \tilde{\gamma }_1 , \gamma _2) = (3, 5, \varepsilon , -5)$ with $\varepsilon =0.02$. So, besides $\varepsilon$, the system parameters are similar to Fig. 4. The red curves represent numerically stable pinned defect front solutions, while the green curve represent numerically unstable pinned defect front solutions. The dashed blue curve shows the asymptotically predicted pinning distances $x_d$ for the local defect front solutions $Z_{f,ld}^\ell$ obtained from the existence condition (3) of Main Result 1. We observe excellent agreement between the asymptotic curve and the numerical curve, and also the stability results coincide. Right panels: the associated profiles of the pinned defect front solutions for $\beta =-2$. We have the co-existence of a stable global defect front solution (panel c) and two local defect front solutions (panels a, b). The local defect front solution with the larger pinning distance is stable (panel a), while the other one is unstable (panel b). Observe that the unstable local defect front solution in panel b indeed has the largest action functional value (Color figure online)

3.2.1 Numerical Results

Global defect front solutions $Z_{f,gd}$ exist only for $\gamma _1\gamma _2 <0$ [54]. So, from Table 2 it follows that $\alpha >0,\beta <0$ and $\alpha D>|\beta |$ is the most interesting parameter setting (since in this case we can have the co-existence of two local defect front solutions $Z_{f,ld}^\ell$ pinned to the left of the defect and a global defect front solution $Z_{f,gd}$). Therefore, we numerically investigate (10) for this parameter setting to further validate the asymptotic leading order results for pinned defect front solutions as stated in Main Result 1 and as derived in [54]. To determine the $\varepsilon$-dependent numerical profiles, we adapt the path following procedure for the homogeneous version of (10) outlined in [52]. This procedure is inspired by the predictor-corrector method of pseudo-arclength continuation [19, 33, 49]. From these profiles, we also compute the numerical action functional $J_{f,p}^{NUM}(u)$ by replacing the improper integrals of (15) and (17) by integrals from $-L$ to 0 and 0 to L. Here, 2L represents the length of the domain used in the numerical integration. So,

$$\begin{aligned} \begin{aligned} J_{f,p}^{NUM}(u) =&\int _{-L}^0 L(u;\bar{u}_{\gamma _1}) dx + \int _{0}^L L(u;\hat{\bar{u}}_{\gamma _2})dx\,. \end{aligned} \end{aligned}$$

(37)

See [52] for more details regarding the numerical techniques. We observe an excellent agreement between the numerically observed pinning distances and the leading order pinning distances computed from the existence condition (3) of Main Result 1, see the left panels of Figs. 4 and 5. Since $\gamma _2<0$ and $\tilde{\gamma }_1>0$, the stability condition (4) of Main Result 1 gives that—for fixed system parameters—the local defect front solution $Z_{f,ld}^\ell$ with the larger pinning distance is stable, while the other one is unstable, see also Table 2. This agrees with Fig. 4 as the extremum of $J_f(U_{f,ld}^\ell )$ with the larger pinning distance is a minimum. It also coincides with the numerically observed stability properties of the pinned front solutions—obtained from the spectrum of the discretised PDE—shown in Fig. 5. Furthermore, since $\gamma _2<0<\gamma _1$, the global defect front solution $Z_{f,gd}$ is expected to be stable [54] and this is again confirmed by the numerical results, see again Fig. 5.

4 Pinned Pulse Solutions

In this section, we focus on pinned pulse solutions supported by (1) and we derive the part of Main Result 1 related to the existence and stability of local defect pulse solutions $Z_{p, ld}^r$ pinned to the right of the defect. We follow the same procedure as for pinned front solutions and we combine GSPT techniques with the action functional approach. However, for the clarity of the presentation, and since the computations are similar in spirit (though algebraically more involved) as the computations for pinned front solutions, the derivation of the profile of a local defect pulse solution $Z_{p,ld}^r$—with unknown pulse half-width $x^*$ and unknown pinning distance $x_d$—and the computation of its action functional $J_p$ (15) is placed in “Appendix B”. In addition, we show that the action functional approach also reproduces some of the previously obtained results of [54] related to the existence of global defect pulse solutions $Z_{p,gd}$ and the non-existence of local defect pulse solutions $Z_{p,ld}^m$ with the defect pinned in between the two interfaces [54]. Finally, in Sect. 4.2, we confirm our asymptotic findings by numerically investigating (10).

4.1 The Derivation of the Second Part of Main Result 1

We need to compute the action functional $J_p(U_{p,ld}^r)$ (15) associated to a local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect to derive the parts of Main Result 1 related to local defect pulse solutions. We state the action functional below and refer to “Appendix B” for its proof.

Lemma 1

The action functional $J_p(U_{p,ld}^r)$ (15) associated to a local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect is given by

$$\begin{aligned} \begin{aligned} J_p(U_{p,ld}^r)&= \left( -2\alpha \left( 1-e^{-2x^*}\right) -2\beta D \left( 1-e^{-2x^*/D}\right) + 4 \gamma _2 x^* + \frac{4 \sqrt{2}}{3}\right) \varepsilon \\&\quad - \left( \alpha \left( 1-e^{-2x^*}\right) +\frac{\beta }{D} \left( 1-e^{-2x^*/D}\right) \right) \varepsilon ^2\\&\quad +2 \alpha \beta \frac{1}{D^2-1}\left( -\left( 1-e^{-2x^*}\right) +D^3\left( 1-e^{-2x^*/D}\right) \right) \varepsilon ^2 \\&\quad + \frac{1}{2} \alpha ^2 \left( 3-3e^{-2x^*}-2x^*e^{-2x^*}\right) \varepsilon ^2 \\ {}&\quad + \frac{1}{2} \beta ^2 \left( 3D-3De^{-2x^*/D}-2x^*e^{-2x^*/D}\right) \varepsilon ^2 \\ {}&\quad -\frac{1}{2} \gamma _1\left( \alpha e^{-x_d}\left( 1-e^{-2x^*}\right) + \beta D e^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \varepsilon ^2 \\ {}&\quad + \frac{1}{2} \alpha \gamma _2 \left( e^{-x_d}-e^{-(x_d+2x^*)}-4 x^*\right) \varepsilon ^2 \\ {}&\quad + \frac{1}{2} \beta \gamma _2 \left( De^{-x_d/D}-De^{-(x_d+2x^*)/D}-4 x^* \right) \varepsilon ^2 + \mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

(38)

with the pinning distance $x_d$ and the half-width of the pulse $x^*$ both positive and $\varTheta (1)$ with respect to $\varepsilon$.

Proof of Lemma 1

See “Appendix B”. $\square$

To derive the results of Main Result 1 related to local defect pulse solutions, we differentiate the action functional $J_p(U_{p,ld}^r)$ (38) with respect to the unknown pulse half-width $x^*$ and with respect to the unknown pinning distance $x_d$. Next, we equate the resulting expressions to zero. This gives

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial x^*} J_p(U_{p,ld}^r)= 0&\implies 4\left( -\alpha e^{-2x^*}-\beta e^{-2x^*/D}+ \gamma _2\right) \varepsilon = \mathcal {O}(\varepsilon ^2) \\&\implies 4\left( -f(2x^*)+\gamma _2\right) \varepsilon = \mathcal {O}(\varepsilon ^2)\,, \end{aligned} \end{aligned}$$

and

The first condition coincides, to leading order, with the first existence condition of (5), while the second condition coincides, to leading order, with the second existence condition of (5). The local defect pulse solutions that are minimisers of $J_p(U_{p,ld}^r)$ (38) correspond to stable pulse solutions. Since $J_p(U_{p,ld}^r)$ is a function of two unknowns, the second derivative test—see, for instance, Theorems 2.1 and 3.1 in Chapter 8 in [16]—determines these minimisers. However, since $J_p(U_{p,ld}^r)$ is to leading order independent of $x_d$, the second derivative test simplifies and the minimisers of $J_p(U_{p,ld}^r)$ are determined given by the critical points of $J_p(U_{p,ld}^r)$ such that both $\frac{\partial ^2 J }{\partial (x^*)^2}$ and $\frac{\partial ^2 J }{\partial (x_d)^2}$ are positive. So, a local defect pulse solution $Z_{p,ld}^r$ with half-width $x^*$ and pinning distance $x_d$ is stable if it is at a critical point of $J_p(U_{p,ld}^r)$ and if

$$\begin{aligned} \begin{aligned} \frac{\partial ^2 J }{\partial (x^*)^2}>0&\implies 8\left( \alpha e^{-2x^*} + \frac{\beta }{D} e^{-2x^*/D}\right) \varepsilon>0 \implies g(2x^*) >0\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\frac{\partial ^2 J }{\partial (x_d)^2}>0 \implies \\&\qquad \qquad \frac{1}{2} (\gamma _2-\gamma _1)\left( \alpha e^{-x_d} \left( 1-e^{-2x^*}\right) + \frac{\beta }{D} e^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right)>0\,, \\ {}&\qquad \qquad \,\,\,\,\, \implies (\gamma _2-\gamma _1)\left( g(x_d)-g(x_d+2x^*) \right) >0\,. \end{aligned} \end{aligned}$$

This completes the derivation of the second part of Main Result 1.

4.2 Pinned Pulse Solutions

We further investigate the results of Main Result 1 related to local defect pulse solutions, and we combine these results with the results of [54] related to global defect pulse solutions. So, we aim to get a broad picture of pinned pulse solutions supported by (1).

4.2.1 Numerical Results: Pulse Widths

Fig. 6

Bifurcation diagrams of the observed pulse widths $2x^*$ of pinned pulse solutions for varying $\gamma _2$ and for two different parameter sets. We observe an excellent agreement between the pulse widths obtained from numerically integrating (10) (green solid curves) and the asymptotically leading order widths determined by (5) of Main Result 1 (blue dashed curves) for pulse widths that are not too small. In the left panel the system parameters are kept fixed at $(\alpha , \beta , D, \gamma _1, \varepsilon ) = (3,2,5,2,0.02)$ such that $\alpha \beta >0$ and $2L=24$, while in the right panel the system parameters are set at $(\alpha , \beta , D, \gamma _1, \varepsilon ) = (4,-1,5,-0.2,0.05)$ such that $\alpha \beta <0$ and $2L=48$. The vertical dashed black lines indicate the homogeneous system were $\gamma _1=\gamma _2$. The pinned pulse profiles associated to $\gamma _2=2.5$ (dotted line) in the bifurcation diagram in the left panel are shown in Fig. 7, and the pinned pulse profiles associated to $\gamma _2=-0.3$ (dotted line) in the bifurcation diagram in the right panel are shown in Fig. 8 (Color figure online)

Fig. 7

The pinned pulse profiles associated to $\gamma _2=2.5$ in the bifurcation diagram in the left panel of Fig. 6 obtained by numerically integrating (10) over a domain of length $2L=24$. The other parameters are kept fixed at $(\alpha , \beta , D, \gamma _1, \varepsilon ) = (3,2,5,2,0.02)$. The profiles of panels b and c have the same leading order widths. The profiles of panels a and c are numerically stable, while the scatter solution [62] of panel b is numerically unstable. The small pulse profiles shown in panels d and e have not been analysed by the asymptotic methods of this manuscript

The action functional $J_p(U_{p,ld}^{r})$ (38) for a local defect pulse solution $Z_{p,ld}^{r}$ pinned to the right of the defect is—to leading order—independent of the pinning distance $x_d$, and, consequently, similar to the action functional for a homogeneous stationary pulse solution (with $\gamma = \gamma _2$), see Lemma 1 in [52]. As a result, the first existence condition (5) of Main Result 1 determining the width of the local defect pulse solution is the same as the existence condition for a stationary pulse solution in the homogeneous case (with $\gamma =\gamma _2$), see also [23]. In other words, the defect does not—to leading order—destroy the width of a stationary pulse solution. Combining the results of Main Result 1 and [54], and by using the symmetry (8), gives that the widths of both local and global pinned pulse solutions are to leading order determined by $f(2x^*) =\gamma _i$. So, to leading order, the widths of pinned pulse solutions to the right or left of the defect are independent from the pinning distance of the pulse to the defect. This is also observed numerically for pulses with widths that are not too small, i.e. in regions in parameter space where our asymptotic analysis is valid, see the bifurcation diagrams in Fig. 6. The profiles of the particular defect pulse solutions associated to Fig. 6, for a fixed value of $\gamma _2$, are shown in Fig. 7 (for $\alpha \beta >0$) and Fig. 8 (for $\alpha \beta <0$). Moreover, since $f(2x^*) = \gamma _i$ can have up to two solutions for a fixed parameter set, see Table 1 and [23], a pinned pulse solution can have up to four different leading order widths for a given parameter set $(\alpha ,\beta ,D,\gamma _1,\gamma _2)$. See, for instance, Fig. 8.

Fig. 8

The pinned pulse profiles associated to $\gamma _2=-0.3$ in the bifurcation diagram in the right panel of Fig. 6 obtained by numerically integrating (10) over a domain of length $2L=48$. The other parameters are kept fixed at $(\alpha , \beta , D, \gamma _1, \varepsilon ) = (4,-1,5,-0.2,0.05)$. The profiles of panels b and c have the same leading order width. Similarly, the profiles of panels d and e have the same leading order width, and also the profiles of panels f, g and h have the same leading order width

Fig. 9

Contour plot of the leading order part of the action functionals $J_p(U_{p,ld}^{r,\ell ,m})$ (38) and (39) (divided by $\varepsilon$) of local defect pulse solutions $Z_{p,ld}^{r,\ell ,m}$ as function of the interface locations $x_1^*$ and $x_2^*$—such that the leading order pulse width is $2x^*=x_2^*-x_1^*$—for $(\alpha ,\beta ,D,\gamma _1,\gamma _2)=(3,2,5,2,1)$. The level curves associated to the action functionals $J_p(U_{p,ld}^{r,\ell })$ in first and third quadrants are constant along the lines $x_2^*-x_1^*= K, K \in \mathbb {R}$, since these action functionals $J_p(U_{p,ld}^{r,\ell })$ depend only on $2x^*=x_2^*-x_1^*.$ The minimum in each of these two quadrants is indicated by the blue dashed curve and they are attained for $x_2^*-x_1^*= K^*_{1,2}$ with $f(K^*_{1,2})=\gamma _{1,2}$. In particular, $K_1^* \approx 1.6663$ and $K_2^* \approx 3.8096$. Since $\gamma _2 < \gamma _1$, we have—as expected—that $K_2^*> K_1^*$ and $\min \{J_p(U_{p,ld}^{r})\}< \min \{J_p(U_{p,ld}^{\ell })\}$. In addition, the leading order part of the action functional $J_p(U_{p,ld}^{m})$ (39) in the second quadrant becomes minimal for $(x_1^*,x_2^*) \rightarrow (0,K_2^*)$. The red dashed curve in the second quadrant indicates the minimum of the action functional $J_p(U_{p,ld}^{m})$ for a given $x_2^*$ fixed. Note that the action functional $J_p(U_{p,ld}^{m})$ decreases along the red curve for increasing $x_1^*$ (Color figure online)

Furthermore, it is clear that for fixed $x^*$ the action functional $J_p(U_{p,ld}^{r})$ (38) is smaller than the action functional $J_p(U_{p,ld}^{\ell })$⁷ associated to a local defect pulse solution pinned to the left of the defect if and only if $\gamma _1 > \gamma _2$. Consequently,

$$\begin{aligned} \min _{x^*} J_p(U_{p,ld}^{\ell })> \min _{x^*} J_p(U_{p,ld}^{r}) \quad \mathrm{if\, and\, only\, if} \quad \gamma _1 > \gamma _2\,. \end{aligned}$$

That is, a pinned pulse solution $Z_{p,ld}^{r}$ pinned to the right of the defect is favourable compared to a pinned pulse solution $Z_{p,ld}^{\ell }$ pinned to the left of the defect if and only if $\gamma _1 > \gamma _2$ (since only critical points that are local minima are stable). See also upcoming Fig. 9. This is consistent with the results for global defect pulse solutions $Z_{p,gd}$ presented in [54]: a global defect pulse solution $Z_{p,gd}^r$ pinned immediately to the right of the defect and with leading order width $2x^*$ exists if $\gamma _1>\gamma _2$ and if $x^*>0$ solves $f(2x^*) = \gamma _2$.

4.2.2 Local Defect Pulse Solutions $Z_{p,ld}^m$ Pinned Around the Defect

Local defect pulse solutions correspond to pulse solutions with their interfaces located away from the defect. So, there are potentially three different types of local defect pulse solutions: the defect is to the left of both interfaces, the defect is to the right of both interfaces, and the defect is in between both interfaces. In [54], it was shown that local defect pulse solutions with the defect pinned in between both interfaces do not exist. This result can also be explained by using the current approach. The leading order term of an action functional $J_p(U_{p,ld}^{m})$ for a local defect pulse solution $Z_{p,ld}^m$ with the defect located in between the two interfaces is slightly different from the leading order term of the action functional $J_p(U_{p,ld}^{r})$ (38) (and from the leading order term of the action functional $J_p(U_{p,ld}^{\ell })$). This difference comes from the final term $\gamma _i (u_0 -\hat{\bar{u}}_{\gamma _{i,0}})$ in the integral of the leading order part of the action functional over the slow field in between the interfaces, see (19). Integrating this term for a local defect pulse solution pinned completely to the left or right of the defect—as well as for a homogeneous pulse solution—gives $4 \gamma _i x^*$ (with $2x^*$ the leading order pulse width), while integrating this term for $Z_{p,ld}^{m}$ gives $2 \gamma _2x_2^*- 2 \gamma _1 x_1^*$, where $x_{1}^*<0<x_{2}^*$ denote the location of the two interfaces and with $x_2^* - x_1^*$ the leading order pulse width. In the end, this leads to the following action functional $J_p(U_{p,ld}^{m})$—which we present without proof, but we refer to [52] for more details—for a local defect pulse solution $Z_{p,ld}^m$ with the defect pinned in between the two interfaces

$$\begin{aligned} \begin{aligned} J_p(U_{p,ld}^m) =&\left( -2\alpha \left( 1-e^{-(x_2^*-x_1^*)}\right) -2\beta D \left( 1-e^{-(x_2^*-x_1^*)/D}\right) \right. \\&\qquad +\left. 2\left( \gamma _2 x_2^* - \gamma _1 x_1^*\right) + \frac{4 \sqrt{2}}{3}\right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

(39)

Unlike the leading order term of the action functional $J_p(U_{p,ld}^{r})$ (38) (and of $J_p(U_{p,ld}^{r,\ell })$), the action functional $J_p(U_{p,ld}^m)$ depends on two variables. Upon introducing $2x^*:=x_2^*-x_1^*>0$—such that $x^*$ again represents the pulse half-width—we rewrite (39) as

$$\begin{aligned} \begin{aligned} J_p(U_{p,ld}^m) =&\left( -2\alpha \left( 1-e^{-2x^*}\right) -2\beta D \left( 1-e^{-2x^*/D}\right) + 4 \min \{\gamma _1,\gamma _2\}x^* + \frac{4 \sqrt{2}}{3}\right) \varepsilon \\ {}&+ 2\varepsilon (\gamma _2-\gamma _1)y + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

with $y:=x_2^*$ for $\gamma _2>\gamma _1$ and $y:=x_1^*$ for $\gamma _1>\gamma _2$. By construction, only the linear term $2(\gamma _2-\gamma _1)y$ of the leading order part of $J_p(U_{p,ld}^m)$ depends on the variable y and this term is positive for both $\gamma _2>\gamma _1$ and $\gamma _1>\gamma _2$ (since $x_1^*<0<x_2^*$). Consequently, for $\gamma _2>\gamma _1$, $y \rightarrow 0$ (which implies that $x_2^* \rightarrow 0$) is a necessary condition for $J_p(U_{p,ld}^m)$ to be minimal, while $y \rightarrow 2x^*$ (which implies $x_1^* \rightarrow 0$) is a necessary condition for $J_p(U_{p,ld}^m)$ to be maximal. Similarly, for $\gamma _1>\gamma _2$, $y \rightarrow 0$ (which implies that $x_1^* \rightarrow 0$) is a necessary condition for $J_p(U_{p,ld}^m)$ to be minimal, while $y \rightarrow -2x^*$ (which implies $x_2^* \rightarrow 0$) is a necessary condition for $J_p(U_{p,ld}^m)$ to be maximal. In other words, for both $\gamma _2>\gamma _1$ and $\gamma _1>\gamma _2$ local defect pulse solutions $Z_{p,ld}^m$ with the defect in between the two interfaces move towards the boundary of the slow field, see also Fig. 9. So, as was already shown in [54], local defect pulse solutions $Z_{p,ld}^m$ with the defect in between the two interfaces do not exist as they move towards global defect pulse solutions $Z_{p,gd}$.

In addition, the part of the leading order term of the action functional $J_p(U_{p,ld}^m)$ that depends on the pulse half-width $x^*$ is identical to the leading order term of the action functionals $J_p(U_{p,ld}^{r,\ell })$ (38). Consequently, they have the same critical points $\{x^* | f(2x^*) = \gamma _i\}$ and thus also the same pulse half-widths and stability properties. For instance, for $\gamma _2>\gamma _1$, $J_p(U_{p,ld}^m)$ is minimal for $y=0, \{x^* | f(2x^*) = \gamma _1\}$ and $g(2x^*)>0$ and maximal for $y=2x^*$, $\{x^* | f(2x^*) = \gamma _2\}$ and $g(2x^*)<0$. So, again, smaller $\gamma _i$’s are favourable.

4.2.3 Numerical Results: Pinning Distances

For $\alpha \beta >0$ and $|\gamma _1-\gamma _2|=\varTheta (1)$, the first existence condition of (5) of Main Result 1 related to the width of a local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect is solvable if $\alpha \gamma _2>0$ and $0<|\gamma _2|< |\alpha +\beta |$. Furthermore, since f is monotonically decreasing or increasing, see Table 1, the second existence condition of (5) yields that—similar to the front case—the pinning distance $x_d \gg 1$. However, see Remark 5. From the stability conditions (6) of Main Result 1—with $x_d \gg 1$—it follows that these local defect pulse solutions $Z_{p,ld}^r$ pinned to the right of the defect are stable only if $\alpha ,\beta >0$ and $\gamma _2>\gamma _1$. For $\alpha , \beta <0$ all pinned pulse solutions will be unstable—independent of the defect—since the first stability condition of (6) is never satisfied. Combining this stability result for local defect pulse solutions $Z_{p,ld}^r$ with the results for global defect pulse solutions $Z_{p,gd}$ from [54], we obtain that for $\alpha , \beta >0$ and $0<\gamma _1<\gamma _2<\alpha +\beta$, (1) supports a stable global defect pulse solution $Z_{p,gd}^\ell$ pinned to the left of the defect and a stable local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect (with asymptotically large pinning distance $x_d$). These stable solutions are separated by an unstable scatter solution $Z_{p,gd}^r$ [62] pinned immediately to the right of the defect, see Figs. 6 and 7. The numerically computed action functional values $J_{p}^{NUM}$ (37) for the profiles in these figures confirm the asymptotic—and numerical—stability results. That is, the scatter solution $Z_{p,gd}^r$ has the largest action functional value. This unstable scatter solution can be further understood by observing that $J_p(U_{p,ld}^r)$ (38) also approaches a critical point—at least from one side—as $x_d \rightarrow 0$, and, similarly, $J_p(U_{p,ld}^m)$ (39) approaches a critical point—from the other side—as $x_1^* \rightarrow 0$.

Table 3 Pulse width $2x^*$, pinning distance $x_d$, pinning region, and stability properties (S $=$ stable, U $=$ unstable) of pinned pulse solutions obtained from Main Result 1, symmetry (8) and [54] for $(\alpha , \beta , D, \gamma _1, \gamma _2) = (4,-1,5,-0.2,-0.3)$, as well as their relation to the profiles of Fig. 8 obtained from simulating (10) on a domain of length $2L=48$

As for the front case, the results of Main Result 1 related to local defect pulse solutions are more interesting for $\alpha \beta <0$, see also Remark 2. In this case, stable and unstable local defect pulse solutions $Z_{p,ld}$ with different widths can be pinned in the same $\gamma$-region, see, for instance, Figs. 8, 10 and 11. Combining the result of this manuscript with the results for global defect pulse solutions $Z_{p,gd}$ of [54], and since the first existence condition $f(2x^*)= \gamma _i$ of Main Result 1 can have up to two solutions, shows that there can actually be a myriad of different pinned defect pulse solutions, especially for $0< |\gamma _{1,2}| < |\alpha + \beta |$ and $|\alpha D| > |\beta |$, see also Table 1. For instance, for $(\alpha , \beta , D, \gamma _1, \gamma _2) = (4,-1,5,-0.2,-0.3)$—the parameter values used in Figs. 6, 8, 10 and 11—the asymptotic results of this manuscript and [54] predict the existence of (at least) eight different pinned pulse solutions. Two of these eight pinned solutions are stable, while the other six are unstable. The asymptotic results for this particular parameter set are summarised in Table 3. Numerical simulations of (10) for the same parameter set on a domain of length $2L=48$ yield the same stable pinned pulse solutions, as well as six unstable pinned pulse solutions (and some small pulse profiles similar to the ones shown in panels “d” and “e” of Fig. 7). However, one of the unstable pinned pulse solutions from the asymptotic results of Main Result 1 is not found numerically on this domain of integration. This is due to the relative small size of the domain and we remark that we did find this solution by simulating on a larger domain, see Fig. 10 and also Remark 5. In addition, one of the numerically computed unstable pinned pulse solutions—shown in panel “h” of Fig. 8—is not found by the asymptotic results of Main Result 1. We postulate that this stems from the fact that the pinning distance for this pinned pulse solution is—asymptotically—much larger than one and a higher order analysis is needed to also find the pinning distance for this solution, see again Remark 5. Actually, we believe that there are potentially three more of these pinned pulse solutions that are pinned far away from the defect and that are not captured by the asymptotic results of this manuscript.

To further justify the above claims, we reinvestigate the pinned pulse solutions with leading order width $2x^* \approx 8.01$ for the same parameter set but on a larger domain—$2L=72$ instead of $2L=48$. Besides the unstable global defect pulse solution $Z_{p,gd}^{\ell ,2}$ we also found on the smaller domain, see Table 3, we discover two addition pinned pulse solutions with leading order width $2x^* \approx 8.01$: the missing unstable local defect pulse solution labelled $Z_{p,ld}^{\ell ,2}$ in Table 3 with pinning distance $x_d \approx 2.88$ and a defect pulse solution pinned far away from the defect, see the three panels on the left of Fig. 10.

Fig. 10

Left panels: the profiles of the three unstable pinned pulse solutions with leading order width $2x^* \approx 8.01$ obtained by numerically integrating (10) over a domain of length $2L=72$ and with $(\alpha , \beta , D, \gamma _1, \gamma _2, \varepsilon ) = (4,-1,5,-0.2,-0.3, 0.05)$. Right panel: bifurcation diagram of the numerically observed pinning distances $x_d$ (green solid curves) for these three pinned pulse solutions for varying $\gamma _2$. For $|\gamma _2-\gamma _1|$ not too small, we observe an excellent agreement between the numerically computed pinning distance of the local defect pulse solution $Z_{p,ld}^{\ell ,2}$ and the leading order pinning distance determined by Main Result 1 (blue dashed curves). The pinned pulse solutions on the lower branch of the bifurcation diagram correspond to the global defect pulse solution $Z_{p,gd}^{\ell ,2}$ in Table 3, see also panel a of Fig. 8. Furthermore, the pinned pulse solution in panel III, and the upper branch of the bifurcation diagram, are not captured by the analysis of this manuscript since the pinning distance for these pulses is asymptotically much larger than one, see also Remark 5 (Color figure online)

In Fig. 11, we show the bifurcation diagram of the pinning distances $x_d$ associated to the pinned defect pulse solutions shown in panels “f–h” of Fig. 8—so with leading order pulse width $2x^* \approx 2.20$, see also $Z_{p,gd}^{\ell ,1}$ and $Z_{p,ld}^{\ell ,1}$ in Table 3—for varying $\gamma _2$, while the other parameters are kept fixed, i.e. $(\alpha , \beta , D, \gamma _1) = (4,-1,5,-0.2)$. We observe that as long as $|\gamma _2-\gamma _1|$ is not too small, the asymptotically predicted pinning distances $x_d$ (indicated by the blue dashed line in Fig. 11) of Main Result 1 agree perfectly with the numerically observed pinning distances $x_d$ of the local defect pulse solutions. Moreover, both the asymptotical and numerical results predict that the middle branch of pinned pulse solutions is stable. The unstable upper branches in Fig. 11 relate to the pinned pulse solutions with asymptotically large pinning distances (e.g. panel “h” of Fig. 8 and panel III of Fig. 11) and that these branches connect with the middle branches for $|\gamma _2-\gamma _1|$ small—a region in parameter space where the results of Main Result 1 do not apply. See also the panel on the right of Fig. 10 where we observe similar behavior for the pinned pulse solutions with leading order pulse width $2x^* \approx 8.01$. The onset of these local defect solutions with asymptotically large pinning distances is unclear to us at this stage and whether these solutions fall in the category of bifurcations from infinity [45, e.g.] seems to deserve further investigation in the future.

Fig. 11

Left panel: bifurcation diagram of the observed pinning distance $x_d$ for varying $\gamma _2$ and $(\alpha , \beta , D, \gamma _1, \varepsilon ) = (4,-1,5,-0.2,0.05)$ for pinned pulse solutions with leading order width $2x^* \approx 2.20$ and associated to the profiles shown in panels f–h of Fig. 8 (as long as $\gamma _2<\gamma _1$). This bifurcation diagram is obtained by numerically integrating (10) over a domain of length $2L=48$. Right panel: the associated profiles of the pinned pulse solutions for $\gamma _2=-0.7$. The profiles associated to the branches to the right of $\gamma _2=\gamma _1$ are actually pinned to the right of the defect. For $|\gamma _2-\gamma _1|$ not too small, we observe an excellent agreement between the pinning distances obtained from numerically integrating (10) (red solid curves) and the asymptotically leading order pinning distances determined by (5) of Main Result 1 (blue dashed curves). Moreover, both the numerics and the results of Main Result 1 yield that these local defect pulse solutions $Z_{p,ld}$ with the smaller pinning distances $x_d$ are stable (red curves), while the other ones are unstable (green curves), see also Table 3. The unstable upper branches relate to the pinned pulse solutions with asymptotically large pinning distances (e.g. panel h of Fig. 8), and these branches connect with the middle branches for $|\gamma _2-\gamma _1|$ small (Color figure online)

Remark 5

Main Result 1 predicts that, under the conditions of Theorem 2, the pinning distance of a local defect front and pulse solution is much larger than one. However, the numerically observed pinning distances of local defect front and pulse solutions under these conditions do not appear to be much greater than one (see, for instance, the panel “c” of Fig. 1, Figures 4 and 5 in [54] and Figure 1 in [24]). We postulate that this stems from the fact that the numerical simulations are necessarily done on a bounded domain and this obviously influences the results on the pinning distances. Moreover, the asymptotic results from Main Result 1 hold only for small enough $\varepsilon$. See also Fig. 12, where we show numerically simulated profiles of local defect pulse solutions for $\alpha$ and $\beta$ positive—one of the conditions of Theorem 2—but for two different $\varepsilon$-values and on two different domains of integration.

Fig. 12

Top panels: local defect pulse solutions obtained by simulating the time-independent version of (1), i.e. by simulating (10), on a domain of length 24 for $(\alpha ,\beta ,D,\gamma _1,\gamma _2)= (3,2,5,2,1.5)$—so $\alpha \beta >0$—and for two different $\varepsilon$-values. Whilst the pulse widths appear to be the same in both simulations, the pinning distances $x_d$ differ significantly, see also Remark 5. Bottom panels: bifurcation diagrams of $\gamma _2$ versus the pinning distance $x_d$ for pinned pulse solutions for the same parameter set (but with $\gamma _2$ varying) and for two different $\varepsilon$-values and for two different domain lengths. The domain size, as well as the size of $\varepsilon$, have a leading order influence on the observed pinning distances

5 Discussion

5.1 Summary

In this manuscript, we studied a heterogeneous three-component FitzHugh–Nagumo model (1) and we derived existence and stability conditions for the simplest, but fundamental, localised pinned solutions—namely pinned front and pulse solutions—that are pinned away from the heterogeneity, see Main Result 1. In certain parameter regimes, we explicitly computed the relationship between the jump-type heterogeneity (2) and the pinning distance $x_d$ of a pinned localised solution, see, in particular, (3) and (5). In other parameter regimes, e.g. for $\alpha \beta >0$ for pinned pulse solutions, we showed that the pinning distances $x_d$ are much larger than one, see also Remarks 2 and 5, and higher order computations are needed to explicitly determine these pinning distances. These results were derived by combining GSPT techniques with an action functional approach. This combined approach was pioneered by us in [52] to study stationary localised solutions for the homogeneous three-component FitzHugh–Nagumo model. By appending the homogeneous action functional to deal with the defect, see (15) and (17), we showed that—due to the asymptotic scaling of the defect—the leading order width of the localised solution is not affected by the defect (see, however, Remark 1). In contrast, the pinning distance is determined at the next order (in $\varepsilon$) of the action functional. In essence, the defect destroys the translation invariance of the homogeneous problem and pinpoints—from the family of stationary localised solutions in the homogeneous case—a set of isolated locations for the localised pinned solutions. In addition, the defect also determines the fate of the translation invariance eigenvalue at zero—and thus the stability—of the localised pinned solutions, see (4) and (6).

5.2 Concluding Remarks and Future Work

5.2.1 Designing a Defect

Localised pinned solutions to (1) have been studied in detail before, see, in particular, [24, 54]. However, this is the first time that (1) has been studied in this generality and that the pinning distance $x_d$ has been computed explicitly. Actually, to the best of our knowledge this is the first time that this pinning distance has been computed analytically for local defect solutions for such systems of heterogeneous nonlinear reaction–diffusion equations. A direct consequence of explicitly characterising the pinning distance $x_d$ in terms of the system parameters and the strength of the defect is that it opens the path to solving the inverse problem of controlling the pinned solutions. That is, for a given width and location, can we find suitable system parameters and a heterogeneity such that (1) supports a stable localised pinned solution satisfying these prescribed conditions. For instance, say $(\alpha ,\beta ) = (3,-1)$ are given and we want to design a stable local defect pulse solution pinned to the right of the defect with width $2x^*=3$ and pinning distance $x_d=2.3$. Then, (5) of Main Result 1 holds for $D \approx 4.94$ and consequently $\gamma _2 = 3 e^{-3} - e^{-3/D} \approx -0.395$ (5). To ensure this pinned solution is also stable, i.e. such that (6) holds, it is required that $\gamma _1 < \gamma _2$ and $\gamma _1 \not \approx \gamma _2$.

5.2.2 Extensions Within the Action Functional Framework

The homogeneous version of (1) was originally developed for both $\alpha$ and $\beta$ positive, see also Remark 2. In contrast, the results of this manuscript give explicit information regarding the pinning distances $x_d$ of pinned localised solutions for $\alpha$ and $\beta$ of opposite sign only. For $\alpha$ and $\beta$ positive, the results only imply that the pinning distances $x_d$ are much larger than one. It is expected that an even higher order computation of the action functional will also provide the crucial information regarding the explicit pinning distances $x_d$ of pinned localised solutions for $\alpha$ and $\beta$ positive. The exploration of the next order term of the action functional is part of future work.

The homogeneous version of (1) also supports stable stationary symmetric 2-pulse solutions [23, 53]—and, under the right parameter conditions, also stationary asymmetric 2-pulse solutions or stationary symmetric 3-pulse solutions [52]—so it can be expected that (1) also supports these more exotic types of localised solutions. It is interesting to see if the explicit pinning distances of these more exotic solutions—as well as their stability—can also be explicitly determined by the action functional approach of this manuscript.

The heterogeneous model (1) has one small jump-type heterogeneity (2). However, there is a priori no reason to restrict to one jump and different types of heterogeneities have been investigated numerically before [41, 50, 54, e.g.]. For instance, in [54] (1) with a bump-type heterogeneity, i.e. $\gamma (x)=\gamma _1$ for $x \notin [-A,A]$ and $\gamma (x)=\gamma _2$ for $x \in [-A,A]$, was numerically simulated and it was observed that—under the right conditions on the parameters—local defect pulse solutions with the expected widths still form, see, in particular, the left panel of Figure 8 in [54]. The approach of the action functional used in this manuscript can be easily extended to handle several of these jump-type heterogeneities and is interesting to see if, for instance, the numerical observations of [54] can be shown analytically with the current approach. This bump-type heterogeneity is particularly interesting since a pinned solution in the region $[-A, A]$ (with $A=\varTheta (1)$) cannot have an asymptotically large pinning distance (as is the case for the jump-type heterogeneity for $\alpha$ and $\beta$ both positive).

5.2.3 Interaction Dynamics

Since we now understand—to a certain extend—pinned front and pulse solutions of (1), a next natural question to ask is the following. Suppose the homogeneous problem supports a stable stationary localised solution. What happens if you introduce a small jump heterogeneity far away from the position of the localised solution? Will the solution move towards the defect, or will it move away from it? That is, can we also understand the interaction dynamics of the heterogeneous model and can we, for example, derive the laws of motion that describe how front-like or pulse-like initial conditions of (1) evolve? For the homogeneous model these laws of motion are rigorously derived in [55] by using a Renormalization Group (RG) method [44]. By projecting the equations on the eigenspace associated to the small eigenvalues it is shown that an N-front-like initial condition evolves according to a N-dimensional system of ODEs. For instance, a pulse-like initial condition with initial width $x_w^0$ evolves according to

$$\begin{aligned} \dot{x}_w = 3\sqrt{2} \varepsilon ^2 (f(x_w) - \gamma ), \qquad x_w(0)=x_w^0\,, \end{aligned}$$

with f as given in (3). Actually, the derived systems of ODEs is a gradient flow with functional G, and the action functional approach can be seen as a direct way of computing (a scaled version of) this functional G, see Remark 4.3 in [55] and [52] for more details. It is interesting to see how the presence of the defect influences the dynamics of front-like and pulse-like initial conditions and whether the GSPT techniques and the action functional approach of this manuscript can be combined with the RG method of [55] to explicitly derive similar systems of ODEs describing the evolution in the defect case. Alternatively, one can try to adapt the formal approach of [38] in which the interface dynamics for similar defect models was derived. This approach is based on using the singular limit of the PDE to rewrite it into a free-boundary problem of mixed PDE-ODE-type and subsequently use a center manifold reduction to derive the interface dynamics, see [38] for more details.

5.2.4 Collision Dynamics

The importance of various types of defect solutions, such as scatter solutions, originated from numerical explorations of the collision dynamics between travelling pulse solutions and defects [41, 50, 62, e.g.], since understanding the structure of defect solutions would help understanding the dynamics of travelling pulse solutions when colliding with the heterogeneity. In the current setting with $\tau$ and $\theta$$\mathcal {O}(1)$, the homogeneous version of (1) does not support travelling pulse solutions [23]. However, for $\tau$ and/or $\theta$ large (in particular $\mathcal {O}(\varepsilon ^{-2})$) the homogeneous version does support stable and unstable travelling pulse solutions and these solutions travel with speed $c = \mathcal {O}(\varepsilon ^2)$ [23, 53, 55]. In addition, the homogeneous version also supports so-called breathing pulse solutions [23]. In [54], several numerical simulations were performed in this parameter regime and it appeared that, under the right parameter conditions, an initially breathing pulse solution could evolve to a travelling pulse solution after colliding with the defect, see, in particular, Figure 10 in [54]. It would be interesting to see whether this collision dynamics can be studied analytically and whether we can develop an understanding on how a defect influences travelling pulse solutions and breathing pulse solutions. One of the complications arising in this parameter regime stems from the fact that the essential spectrum of the linearised operator needed to determine stability lies asymptotically close to the imaginary axis and additional point eigenvalues (compared to the $\tau , \theta$$\mathcal {O}(1)$-case) potentially pop out of this essential spectrum, see [53] for more detail. Unfortunately, the action functional approach used in the current setting is not directly suitable to study these travelling pulse solutions, not even in the homogeneous case, see [52] for more details. However, an existence result for travelling pulse solutions supported by a mono-stable two-component FitzHugh–Nagumo model was established in [6] using a variational approach. Finally, observe that the general results of [24] are not applicable in this situation, since the underlying hypotheses in [24] are not met.

Appendices

Appendix A: Trivial Defect Solutions

From Lemma 1.7 in [24], we know that (1) supports two trivial defect solutions $Z_{td}^\pm = (U_{td}^{\pm },V_{td}^{\pm },W_{td}^{\pm })$ near $\pm (1,1,1)$. We use a regular expansion

$$\begin{aligned} Z_{td}^\pm = (U_{td}^{\pm },V_{td}^{\pm },W_{td}^{\pm })(x)&= \pm (1,1,1) + \varepsilon (U_{td,1}^{\pm },V_{td,1}^{\pm },W_{td,1}^{\pm })(x) + \mathcal {O}(\varepsilon ^2)\,, \end{aligned}$$

(40)

to determine the next order terms of these trivial defect solutions. Because of the different asymptotic scaling in the diffusion coefficients in (1)/(10)/(12), we expect that near the defect the profile of the U-component changes faster—in the sense that we expect its gradient (in space) to be steeper—than the profiles of the V and W components. Therefore, and as eluded to in Sect. 2, we split our spatial domain into four different regions $I_s^{\pm }$ and $I_f^{\pm }$. The two outer slow regions $I_s^{\pm }$ are away from the defect at $x=0$ and are given by $I_s^{-} = (-\infty ,-\sqrt{\varepsilon }]$, respectively, $I_s^{+} = [\sqrt{\varepsilon },\infty )$. In these slow regions, the spatial scaling as stated in (1) and (10)—the slow scaling—is used to accommodate the changes in the two slow V and W components, while the fast U-component does not change significantly (as it is already close to one of its asymptotic end states). The two inner fast regions $I_f^{\pm }$ near the defect deal with the changes in the fast U-component (due to the heterogeneity) and are given by $I_f^{-} = (-\sqrt{\varepsilon },0]$, respectively, $I_f^{+} = (0,\sqrt{\varepsilon })$. These fast regions are asymptotically small in x. Therefore, the two slow V and W components do not change significantly in these regions. To understand the changes in U over the fast regions, we use the fast scaling $\xi := x/\varepsilon$ and study (12). The crux behind the asymptotic $\sqrt{\varepsilon }$-scaling of the two slow regions and two fast regions is that the slow regions $I_s^{\pm }$ span—to leading order—the whole spatial domain in the slow scaling x, while the fast regions $I_f^{\pm }$ span—to leading order—the whole spatial domain in the fast scaling $\xi$ (since $I_f^{-} = (-1/\sqrt{\varepsilon },0]$ and $I_f^{+} = (0,1/\sqrt{\varepsilon })$ in the fast $\xi$-variable). Observe that similar spatial scalings are used to study the homogeneous version of (1), see [23, 53, e.g.].

We first compute the next order terms $(U_{td,1}^{-},V_{td,1}^{-},W_{td,1}^{-})$ of the trivial defect solution $Z_{td}^-$. Subsequently, the next order terms of the trivial defect solution $Z_{td}^+$ are obtained by applying both symmetries (7) and (8) to the $Z_{td}^-$-profile. In the first slow region $I_s^-$, implementing the regular expansion (40) into (10) gives

$$\begin{aligned} I_s^-: \left\{ \begin{aligned} \mathcal {O}(\varepsilon )&= -2U_{td,1}^{-}+ (\alpha +\beta -\gamma _1) \,,\\ \mathcal {O}(\varepsilon )&= \left( V_{td,1}^{-}\right) _{xx} + U_{td,1}^{-} -V_{td,1}^{-} \,,\\ \mathcal {O}(\varepsilon )&= D^2 \left( W_{td,1}^{-}\right) _{xx} + U_{td,1}^{-} - W_{td,1}^{-} \, . \end{aligned} \right. \end{aligned}$$

(41)

The U-equation shows that the first order correction term $U_{td,1}^{-}$ of the fast component in this region is constant. In particular, for $x \in I_s^-$ we get

$$\begin{aligned} U_{td,1}^{-}(x) =\frac{1}{2}(\alpha +\beta -\gamma _1)\,. \end{aligned}$$

This allows us to solve the leading order parts of the slow equations of (41) explicitly and we obtain

$$\begin{aligned} \begin{aligned} V_{td,1}^{-}(x) = C_{s,V}^- e^x + \frac{1}{2}(\alpha +\beta -\gamma _1)\,, \quad W_{td,1}^{-}(x) = C_{s,W}^- e^{\frac{x}{D}} + \frac{1}{2}(\alpha +\beta -\gamma _1) \,, \end{aligned} \end{aligned}$$

for $x \in I_s^-$ and with $C_{s,V}^-$ and $C_{s,W}^-$ integration constants that are determined later (the two other integration constant have been set to zero to ensure that the profiles stay bounded as $x \rightarrow -\infty$). Similarly, we obtain that the first order correction terms in the second slow region $I_s^+$ are given by

$$\begin{aligned} \begin{aligned} U_{td,1}^{-}(x)&= \frac{1}{2}(\alpha +\beta -\gamma _2)\,, \quad V_{td,1}^{-}(x) = C_{s,V}^+ e^{-x} + \frac{1}{2}(\alpha +\beta -\gamma _2)\,, \\ W_{td,1}^{-}(x)&= C_{s,W}^+ e^{-\frac{x}{D}} + \frac{1}{2}(\alpha +\beta -\gamma _2) \,, \end{aligned} \end{aligned}$$

with $C_{s,v}^+$ and $C_{s,W}^+$ two different integration constants.

We use the fast scaling $\xi$ in the fast regions $I_f^{\pm }$, and substituting the regular expansion (40) (in $\xi$) into (12) gives

$$\begin{aligned} I_f^\pm : \left\{ \begin{aligned} \mathcal {O}(\varepsilon )&= \left( U_{td,1}^{-}\right) _{\xi \xi } -2U_{td,1}^{-}+ (\alpha +\beta -\gamma _{1,2}) \,,\\ \mathcal {O}(\varepsilon )&= \left( V_{td,1}^{-}\right) _{\xi \xi } \,,\\ \mathcal {O}(\varepsilon )&= D^2\left( W_{td,1}^{-}\right) _{\xi \xi } \,. \end{aligned} \right. \end{aligned}$$

The leading order part of the U-equations is solved by

$$\begin{aligned} U_{td,1}^{-}(\xi ) =\frac{1}{2}(\alpha +\beta -\gamma _{1,2}) + C_{f,U}^{\pm } e^{\sqrt{2} \xi } + D_{f,U}^{\pm } e^{-\sqrt{2} \xi }\,, \end{aligned}$$

for $\xi \in I_f^\pm$ and with $C_{f,U}^{\pm }$ and $D_{f,U}^{\pm }$ four different integration constants. The equations for the slow components give

$$\begin{aligned} \begin{aligned} V_{td,1}^{-}(\xi )&= C_{f,V}^{\pm } + D_{f,V}^{\pm } \xi \,, \quad W_{td,1}^{-}(\xi ) = C_{f,W}^{\pm } + D_{f,W}^{\pm } \xi \,, \quad \xi \in I_f^\pm . \end{aligned} \end{aligned}$$

The solutions in the different regions—and their derivatives—should match at the boundaries of the particular slow and fast fields. Matching the fast U-component between the fast and slow fields gives—to leading order—$D_{f,U}^- = C_{f,U}^+=0$. To ensure that the profile U, and its derivative, match over the defect point $x=0$, we get $C_{f,U}^{-} = - D_{f,U}^{+}= -\frac{1}{4}(\gamma _{2}-\gamma _1)$. To ensure the boundedness of the profiles of the slow components, we get $D_{f,V}^{\pm } = D_{f,W}^{\pm }=0$ and matching at the defect point results in $C_{f,V}^{-}= C_{f,V}^{+}$ and $C_{f,W}^{-}= C_{f,W}^{+}$. Finally, matching the profiles of the V-component and their derivatives at the boundaries between the fast and slow regions gives $C_{f,V}^{+} = C_{s,V}^- = -C_{s,V}^+= -\frac{1}{4}(\gamma _2-\gamma _1)$. Similarly, $C_{f,W}^{+} = C_{s,W}^- = -C_{s,W}^+= - \frac{1}{4}(\gamma _2-\gamma _1)$.

In summary, the trivial defect solution $Z_{td}^-=(U_{td}^{-}, V_{td}^{-}, W_{td}^{-})(x)$ (40) is, to leading order, given by $(-1,-1,-1)$, and the first order correction terms are given by

$$\begin{aligned} U_{td,1}^{-}(x)&= \left\{ \begin{aligned}&\frac{1}{2}(\alpha +\beta -\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{\sqrt{2} x/\varepsilon } + \frac{1}{2}(\alpha +\beta -\gamma _{1}) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-\sqrt{2} x/\varepsilon } + \frac{1}{2}(\alpha +\beta -\gamma _{2}) \,,&\quad \mathrm{in} \quad I_f^+\,,\\&\frac{1}{2}(\alpha +\beta -\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,, \end{aligned} \right. \\ V_{td,1}^{-}(x)&= \left\{ \begin{aligned}&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{x} + \frac{1}{2}(\alpha +\beta -\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta ) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta )\,,&\quad \mathrm{in} \quad I_f^+\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-x} + \frac{1}{2}(\alpha +\beta -\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} W_{td,1}^{-}(x) = \left\{ \begin{aligned}&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{x/D} + \frac{1}{2}(\alpha +\beta -\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta ) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta )\,,&\quad \mathrm{in} \quad I_f^+\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-x/D} + \frac{1}{2}(\alpha +\beta -\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,. \end{aligned} \right. \end{aligned}$$

By applying both symmetries (7) and (8) to the above profile $Z_{td}^-$, we get that, to leading order, $Z_{td}^+$ (40) is given by (1, 1, 1), and the first order correction terms are given by

$$\begin{aligned} U_{td,1}^{+}(x)&= \left\{ \begin{aligned}&-\frac{1}{2}(\alpha +\beta +\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{\sqrt{2} x/\varepsilon } - \frac{1}{2}(\alpha +\beta +\gamma _{1}) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-\sqrt{2} x/\varepsilon } - \frac{1}{2}(\alpha +\beta +\gamma _{2}) \,,&\quad \mathrm{in} \quad I_f^+\,,\\&-\frac{1}{2}(\alpha +\beta +\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,, \end{aligned} \right. \\ V_{td,1}^{+}(x)&= \left\{ \begin{aligned}&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{x} - \frac{1}{2}(\alpha +\beta +\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) - \frac{1}{2}(\alpha +\beta ) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) - \frac{1}{2}(\alpha +\beta )\,,&\quad \mathrm{in} \quad I_f^+\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-x} - \frac{1}{2}(\alpha +\beta +\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} W_{td,1}^{+}(x) = \left\{ \begin{aligned}&\frac{1}{4}(\gamma _{1}-\gamma _2) e^{x/D} - \frac{1}{2}(\alpha +\beta +\gamma _1) \,,&\quad \mathrm{in} \quad I_s^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta ) \,,&\quad \mathrm{in} \quad I_f^-\,,\\&-\frac{1}{4}(\gamma _{1}+\gamma _2) + \frac{1}{2}(\alpha +\beta )\,,&\quad \mathrm{in} \quad I_f^+\,,\\&\frac{1}{4}(\gamma _{2}-\gamma _1) e^{-x/D} - \frac{1}{2}(\alpha +\beta +\gamma _2) \,,&\quad \mathrm{in} \quad I_s^+\,. \end{aligned} \right. \end{aligned}$$

Appendix B: Proof of Lemma 1

To prove Lemma 1 regarding the action functional of a local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect, we first need to determine the profile of $Z_{p,ld}^r$. With a slight abuse of notation, we split the spatial domain in four slow regions $I_s^{1,4,6,8}$ and four fast regions $I_s^{2,3,5,7}$:

$$\begin{aligned} \begin{aligned}&I_s^1 := x \in (-\infty , -\sqrt{\varepsilon }] \,,&I_f^2:= x \in (-\sqrt{\varepsilon },0] \,, \\&I_f^3:= x \in (0,\sqrt{\varepsilon })\,,&I_s^4:= x \in [\sqrt{\varepsilon }, x_d - \sqrt{\varepsilon }]\,, \\&I_f^5:= x \in ( x_d - \sqrt{\varepsilon }, x_d + \sqrt{\varepsilon })\,,&I_s^6:= x \in [x_d + \sqrt{\varepsilon }, x_d +2x^*- \sqrt{\varepsilon }] \,\\&I_f^7:= x \in (x_d +2x^*- \sqrt{\varepsilon },x_d +2x^*+ \sqrt{\varepsilon }) \,,&I_s^8:= x \in [x_d +2x^*+ \sqrt{\varepsilon },\infty )\,, \end{aligned} \end{aligned}$$

(42)

with the pinning distance $x_d$ and the pulse width $2x^*$ both positive and $\varTheta (1)$ with respect to $\varepsilon$. Since the defect (2) is small, it has no leading order influence on the profile of a local defect pulse solution $Z_{p,ld}^r$. So, $Z_{p,ld}^r$ is to leading order similar to the leading order profile of the homogeneous pulse solution. In particular, upon using the regular expansion $Z_{p,ld}^r=(U_{p,ld,0}^r,V_{p,ld,0}^r,W_{p,ld,0}^r)+ \varepsilon (U_{p,ld,1}^r,V_{p,ld,1}^r,W_{p,ld,1}^r) + \mathcal {O}(\varepsilon ^2)$, we get that

$$\begin{aligned}&U_{p,ld,0}^r (x)= \left\{ \begin{aligned} -1\,, \qquad&{\text { in }} I_s^1 \cup I_f^2 \cup I_f^3 \cup I_s^4\,,\\ \tanh {\left( \frac{x-x_d}{\sqrt{2} \varepsilon }\right) } \,, \qquad&{\text { in }} I_f^5\,,\\ 1\,, \qquad&{\text { in }} I_s^6\,,\\ -\tanh {\left( \frac{x-x_d-2x^*}{\sqrt{2} \varepsilon }\right) } \,, \qquad&{\text { in }} I_f^7\,,\\ -1\,, \qquad&{\text { in }} I_s^8 \,, \end{aligned} \right. \\&V_{p,ld,0}^r (x) = \left\{ \begin{aligned} -1 + \left( e^{x-x_d}-e^{x-x_d-2x^*}\right) \,, \qquad&{\text { in }}I_s^1 \cup I_f^2 \cup I_f^3 \cup I_s^4\,,\\ -e^{-2x^*} \,, \qquad&{\text { in }} I_f^5\,,\\ 1-\left( e^{x-x_d-2x^*}+e^{-(x-x_d)}\right) \,, \qquad&{\text { in }} I_s^6\,,\\ -e^{-2x^*} \,, \qquad&{\text { in }} I_f^7\,,\\ -1+ \left( e^{-(x-x_d-2x^*)} -e^{-(x-x_d)} \right) \,, \qquad&{\text { in }} I_s^8 \,, \end{aligned} \right. \, \end{aligned}$$

and

$$\begin{aligned}&W_{p,ld,0}^r (x) = \left\{ \begin{aligned} -1 + \left( e^{(x-x_d)/D}-e^{(x-x_d-2x^*)/D}\right) \,, \qquad&{\text { in }} I_s^1 \cup I_f^2 \cup I_f^3 \cup I_s^4\,,\\ -e^{-2x^*/D} \,, \qquad&{\text { in }} I_f^5\,,\\ 1-\left( e^{(x-x_d-2x^*)/D}+e^{-(x-x_d)/D}\right) \,, \qquad&{\text { in }} I_s^6\,,\\ -e^{-2x^*/D} \,, \qquad&{\text { in }} I_f^7\,,\\ -1+ \left( e^{-(x-x_d-2x^*)/D}- e^{-(x-x_d)/D}\right) \,, \qquad&{\text { in }} I_s^8 \,, \end{aligned} \right. \, \end{aligned}$$

see [23, 52, 54, e.g.]. To determine the next order correction terms, we use that—as for pinned front solutions—the fast component is still slaved to the slow components in the slow fields, see the first equation of (32). In particular, for x in the slow fields we have $U_{p,ld,1}^r = - \frac{1}{2} (\alpha V_{p,ld,0}^r + \beta W_{p,ld,0}^r + \gamma (x))$. So,

$$\begin{aligned}&U_{p,ld,1}^r (x) = \left\{ \begin{aligned} \frac{1}{2} (\alpha +\beta -\gamma _1) + \frac{1}{2} \alpha \left( e^{-2x^*}-1\right) e^{x-x_d} + \frac{1}{2} \beta \left( e^{-2x^*/D}-1\right) e^{(x-{x_d})/D}\,, \,\,&{\text { in }} I_s^1,\\ \frac{1}{2} (\alpha +\beta -\gamma _2) + \frac{1}{2} \alpha \left( e^{-2x^*}-1\right) e^{x-x_d} + \frac{1}{2} \beta \left( e^{-2x^*/D}-1\right) e^{(x-{x_d})/D}\,, \,\,&{\text { in }} I_s^4,\\ -\frac{1}{2}(\alpha +\beta +\gamma _2) +\frac{1}{2}\alpha \left( e^{x-x_d-2x^*}+e^{-(x-x_d)}\right) \,\,\,\,&\\ +\frac{1}{2}\beta \left( e^{(x-{x_d}-2x^*)/D}+e^{-(x-{x_d})/D}\right) \,, \,\,&{\text { in }} I_s^6,\\ \frac{1}{2}(\alpha +\beta -\gamma _2) - \frac{1}{2} \alpha \left( e^{2x^*}-1\right) e^{-(x-x_d)} \,\,\,\,&\\ -\frac{1}{2} \beta \left( e^{2x^*/D}-1\right) e^{-(x-{x_d})/D}\,,\,\,&{\text { in }} I_s^8 \,. \end{aligned} \right. \end{aligned}$$

(43)

By the second and third equations of (32), the above expressions allow us to compute—up to integration constants—the first order correction terms of the slow components in the slow fields. We get

$$\begin{aligned}&V_{p,ld,1}^r (x) = \left\{ \begin{aligned} \frac{1}{2}(\alpha +\beta -\gamma _1) +\frac{1}{8}\alpha (2x-1)\left( 1-e^{-2x^*}\right) e^{x-x_d} \,\,\,\,&\\ - \frac{1}{2} \beta \frac{D^2}{D^2-1}\left( 1-e^{-2x^*/D}\right) e^{(x-x_d)/D} + C_1^v e^x \,, \,\,&{\text { in }} I_s^1,\\ \frac{1}{2} (\alpha +\beta -\gamma _2) +\frac{1}{8}\alpha (2x-1)\left( 1-e^{-2x^*}\right) e^{x-x_d} \,\,\,\,\\ - \frac{1}{2} \beta \frac{D^2}{D^2-1}\left( 1-e^{-2x^*/D}\right) e^{(x-x_d)/D} + D_1^v e^x + D_2^ve^{-x} \,, \,\,&{\text { in }} I_s^4,\\ -\frac{1}{2}(\alpha +\beta +\gamma _2) +\frac{1}{8} \alpha \left( e^{x-x_d-2x^*} + e^{-(x-x_d)} \right. \,\,\,\,&\\ \left. -2x\left( e^{x-x_d-2x^*} - e^{-(x-x_d)}\right) \right) \,\,\,\,&\\ +\frac{1}{2}\beta \frac{D^2}{D^2-1}\left( e^{(x-x_d-2x^*)/D}+e^{-(x-x_d)/D}\right) + E_1^v e^x + E_2^ve^{-x} \,, \,\,&{\text { in }} I_s^6,\\ \frac{1}{2}(\alpha +\beta -\gamma _2) +\frac{1}{8} \alpha (1+2x) \left( 1-e^{2x^*}\right) e^{-(x-x_d)} \,\,\,\,&\\ +\frac{1}{2} \beta \frac{D^2}{D^2-1}\left( 1-e^{2x^*/D}\right) e^{-(x-x_d)/D} +F_2^ve^{-x} \,, \,\,&{\text { in }} I_s^8\,, \end{aligned} \right. \end{aligned}$$

(44)

and

$$\begin{aligned}&W_{p,ld,1}^r (x) =\left\{ \begin{aligned} \frac{1}{2}(\alpha +\beta -\gamma _1) +\frac{1}{8}\beta \left( \frac{2x}{D}-1\right) \left( 1-e^{-2x^*/D}\right) e^{(x-x_d)/D} \,\,\,\,\\ + \frac{1}{2} \alpha \frac{1}{D^2-1}\left( 1-e^{-2x^*}\right) e^{x-x_d} + C_1^w e^{x/D} \,, \,\,&{\text { in }} I_s^1,\\ \frac{1}{2}(\alpha +\beta -\gamma _2) +\frac{1}{8}\beta \left( \frac{2x}{D}-1\right) \left( 1-e^{-2x^*/D}\right) e^{(x-x_d)/D} \,\,\,\,\\ + \frac{1}{2} \alpha \frac{1}{D^2-1}\left( 1-e^{-2x^*}\right) e^{x-x_d}+D_1^w e^{x/D} + D_2^we^{-x/D}\,, \,\,&{\text { in }} I_s^4,\\ -\frac{1}{2}(\alpha +\beta +\gamma _2) +\frac{1}{8} \beta \left( e^{(x-x_d-2x^*)/D} + e^{-(x-x_d)/D} \right. \,\,\,\,\\ \left. -2\frac{x}{D}\left( e^{(x-x_d-2x^*)/D} - e^{-(x-x_d)/D}\right) \right) \,\,\,\,\\ -\frac{1}{2}\alpha \frac{1}{D^2-1}\left( e^{x-x_d-2x^*}+e^{-(x-x_d)}\right) + E_1^w e^{x/D} + E_2^we^{-x/D} \,, \,\,&{\text { in }} I_s^6,\\ \frac{1}{2}(\alpha +\beta -\gamma _2) +\frac{1}{8}\beta \left( 1+\frac{2x}{D}\right) \left( 1-e^{2x^*/D}\right) e^{-(x-x_d)/D} \,\,\,\,\\ -\frac{1}{2} \alpha \frac{1}{D^2-1}\left( 1-e^{2x^*}\right) e^{-(x-x_d)} + F_2^we^{-x/D} \,, \,\,&{\text { in }} I_s^8. \end{aligned} \right. \end{aligned}$$

(45)

Similar to the front case, the slow components—and their derivatives—do not change in the fast fields. Therefore, we require that they match up at the boundaries of the slow fields. This results in twelve conditions that determine the twelve unknown integration constants of (44) and (45). In the end, we find that

$$\begin{aligned} C_1^{v}= & {} \frac{1}{4}(\gamma _1-\gamma _2) + \frac{1}{8} \left( e^{-2x^*}-1\right) \left( 3\alpha +2\alpha x_d-4\beta \frac{1}{D^2-1}\right) e^{-x_d} + \frac{1}{2} \alpha x^* e^{-(x_d+2x^*)} \,, \\ D_1^v= & {} \frac{1}{8} \left( e^{-2x^*}-1\right) \left( 3\alpha +2\alpha x_d-4\beta \frac{1}{D^2-1}\right) e^{-x_d} + \frac{1}{2} \alpha x^* e^{-(x_d+2x^*)} \,, \\ D_2^{v}= & {} \frac{1}{4} (\gamma _2-\gamma _1)\,, \\ E_1^v= & {} \frac{1}{8} \left( 3\alpha +2\alpha x_d+4\alpha x^*-4\beta \frac{1}{D^2-1}\right) e^{-(x_d+2x^*)} \,,\\ E_2^v= & {} \frac{1}{4}(\gamma _2-\gamma _1) + \frac{1}{8} \left( 3\alpha -2\alpha x_d-4\beta \frac{1}{D^2-1}\right) e^{x_d} \,,\\ F_2^v= & {} \frac{1}{4}(\gamma _2-\gamma _1) +\frac{1}{8} \left( 1-e^{2x^*}\right) \left( 3\alpha -2\alpha x_d -4 \beta \frac{1}{D^2-1}\right) e^{x_d} + \frac{1}{2} \alpha x^* e^{x_d+2x^*} \,, \end{aligned}$$

and, similarly,

$$\begin{aligned} C_1^{w}= & {} \frac{1}{4}(\gamma _1-\gamma _2) +\frac{1}{8}\left( e^{-2x^*/D}-1\right) \left( 4\alpha \frac{D^2}{D^2-1}+3\beta +2 \beta \frac{x_d}{D} \right) e^{-x_d/D} \\&+ \frac{1}{2} \beta \frac{x^*}{D} e^{-(x_d+2x^*)/D} \,, \\ D_1^w= & {} \frac{1}{8}\left( e^{-2x^*/D}-1\right) \left( 4\alpha \frac{D^2}{D^2-1} + 3 \beta +2 \beta \frac{x_d}{D} \right) e^{-x_d/D} + \frac{1}{2} \beta \frac{x^*}{D} e^{-(x_d+2x^*)/D} \,, \\ D_2^{w}= & {} \frac{1}{4} (\gamma _2-\gamma _1)\,, \\ E_1^{w}= & {} \frac{1}{8} \left( 4\alpha \frac{D^2}{D^2-1}+ 3\beta +2\beta \frac{x_d}{D}+4\beta \frac{x^*}{D}\right) e^{-(x_d+2x^*)/D} \,, \\ E_2^w= & {} \frac{1}{4} (\gamma _2-\gamma _1)+ \frac{1}{8}\left( 4\alpha \frac{D^2}{D^2-1}+ 3\beta -2\beta \frac{x_d}{D}\right) e^{x_d/D}\,, \\ F_2^{w}= & {} \,\frac{1}{4}(\gamma _2-\gamma _1) + \frac{1}{8} \left( 1-e^{2x^*/D}\right) \left( 4\alpha \frac{D^2}{D^2-1}+ 3\beta -2\beta \frac{x_d}{D}\right) e^{x_d/D} \\&+ \frac{1}{2} \beta \frac{x^*}{D} e^{(x_d+2x^*)/D} \,. \end{aligned}$$

What remains to determine are the next order correction terms of the fast component in the fast fields. We first look into the fast fields $I_f^{2,3}$ around the defect. The fast equation in these fields, in the fast variable $\xi$, are given by the first equation of (12)—with $\gamma (x)=\gamma _1$ in $I_f^2$ and $\gamma (x)=\gamma _2$ in $I_f^3$. Plugging in the regular expansions for the local defect pulse solution $Z_{p,ld}^r$—and recalling that the slow components are constant in the fast fields—we get at the $\mathcal {O}(\varepsilon )$-level:

$$\begin{aligned} \begin{aligned} \left( U_{p,ld,1}^r\right) _{\xi \xi }&= 2U_{p,ld,1}^r - \alpha \left( 1+\left( e^{-2x^*}-1\right) e^{-x_d}\right) \\&\quad - \beta \left( 1+\left( e^{-2x^*/D}-1\right) e^{-x_d/D}\right) + \left\{ \begin{aligned} \gamma _{1} \,, \quad&{\text { in }} I_f^2\,,\\ \gamma _{2} \,, \quad&{\text { in }} I_f^3\,. \end{aligned} \right. \end{aligned} \end{aligned}$$

The solutions to these equations are given by

$$\begin{aligned} U_{p,ld,1}^r = \left\{ \begin{aligned} A_2e^{\sqrt{2} \xi } +B_2e^{-\sqrt{2} \xi } + \frac{1}{2}\alpha \left( 1+\left( e^{-2x^*}-1\right) e^{-x_d}\right) \qquad&\\ \qquad +\frac{1}{2} \beta \left( 1+\left( e^{-2x^*/D}-1\right) e^{-x_d/D}\right) - \frac{1}{2} \gamma _1\,, \quad&{\text { in }} I_f^2,\\ A_3e^{\sqrt{2} \xi } +B_3e^{-\sqrt{2} \xi } + \frac{1}{2}\alpha \left( 1+\left( e^{-2x^*}-1\right) e^{-x_d}\right) \qquad&\\ \qquad +\frac{1}{2} \beta \left( 1+\left( e^{-2x^*/D}-1\right) e^{-x_d/D}\right) -\frac{1}{2} \gamma _2\,, \quad&{\text { in }} I_f^3\,. \end{aligned} \right. \end{aligned}$$

Matching $U_{p,ld,1}^r$ at the left boundary of $I_f^2$ with $U_{p,ld,1}^r$ (43) at the right boundary of $I_s^1$ gives $B_2=0$. Similarly, matching at the right boundary of $I_f^3$ with the left boundary of $I_s^4$ gives $A_3=0$. Matching $U_{p,ld,1}^r$, as well as its derivative, at $\xi =0$ gives $-A_2 = B_3 = \frac{1}{4} (\gamma _2 - \gamma _1)$. Finally, the fast correction terms over the jump regions $I_f^{5,7}$ can, as for a local defect front solution, be set to zero since the fast equations over these fields have no $\mathcal {O}(\varepsilon )$-correction terms.

To compute the action functional $J_p(Z_{p,ld}^r)$ (38) and finalise the proof of Lemma 1, we split the action functional integral (15) according to the four slow and four fast regions (42)

$$\begin{aligned} \begin{aligned} J_p&= \underbrace{\int _{I_s^1} \cdot \,\, dx}_{:=J_p^1}+ \underbrace{\int _{I_f^2} \cdot \,\, dx}_{:=J_p^2}+ \underbrace{\int _{I_f^3} \cdot \,\, dx}_{:=J_p^3}+ \underbrace{\int _{I_s^4} \cdot \,\, dx}_{:=J_p^4}+ \underbrace{\int _{I_f^5} \cdot \,\, dx}_{:=J_p^5} + \underbrace{\int _{I_s^6} \cdot \,\, dx}_{:=J_p^6}+ \underbrace{\int _{I_f^7} \cdot \,\, dx}_{:=J_p^7} + \underbrace{\int _{I_s^8} \cdot \,\, dx}_{:=J_p^8}\,. \end{aligned} \end{aligned}$$

(46)

By using the observations of Sect. 2.2 and the profile of a local defect pulse solution $Z_{p,ld}^r$ constructed above, we compute the eight integrals $J^{i}_p = \varepsilon J^{i}_{p,1}+\varepsilon ^2 J^{i}_{p,2}+ \mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon }) , i=1,2,\ldots , 8$ of (46)⁸. We start with the integrals over the slow fields. The integral over the first slow field $I_s^1$ gives $J^{1}_p = \varepsilon J^{1}_{p,1}+\varepsilon ^2 J^{1}_{p,2}+ \mathcal {O}(\varepsilon ^2 \sqrt{\varepsilon })$ with, by (19) and (20),

$$\begin{aligned} \begin{aligned} J_{p,1}^1&= \int _{I_s^1} L_1(U_{p,ld}^r; \bar{u}_{\gamma _1}) dx \\&=\int _{I_s^1} -\frac{1}{2} \alpha \left( e^{x-x_d}-e^{x-x_d-2x^*}\right) + \frac{1}{2} \beta \left( e^{(x-x_d)/D}-e^{(x-x_d-2x^*)/D}\right) dx \\&= -\frac{1}{2} \left( \alpha e^{-x_d}\left( 1-e^{-2x^*}\right) + \beta De^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \\ {}&\quad \qquad + \frac{1}{2} \left( \alpha e^{-x_d}\left( 1-e^{-2x^*}\right) + \beta e^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \sqrt{\varepsilon }\\ {}&\quad \qquad - \frac{1}{4} \left( \alpha e^{-x_d}\left( 1-e^{-2x^*}\right) + \frac{\beta }{D} e^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \varepsilon + \mathcal {O}(\varepsilon \sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{p,2}^1&= \int _{I_s^1} L_2(U_{p,ld}^r; \bar{u}_{\gamma _1}) dx \\ {}&= -\frac{1}{2} \alpha \beta \frac{1}{D^2-1}\left( e^{-x_d}-e^{-\left( x_d+2x^*\right) }-D^3e^{-x_d/D}+D^3e^{-\left( x_d+2x^*\right) /D}\right) \\&\quad \quad + \frac{1}{8} \alpha ^2 \left( \left( 3+x_d\right) \left( 1-e^{-2x^*}\right) e^{-x_d} - 2x^* e^{-\left( x_d+2x^*\right) }\right) \\&\quad \quad + \frac{1}{8} \beta ^2\left( \left( 3D+x_d\right) \left( 1-e^{-2x^*/D}\right) e^{-x_d/D} - 2x^* e^{-\left( x_d+2x^*\right) /D}\right) \\&\quad \quad +\frac{1}{8}\gamma _1\left( \alpha \left( -1-2e^{-x_d}+2e^{-\left( x_d+2x^*\right) }\right) +\beta D\left( -1-2e^{-x_d/D}+2e^{-\left( x_d+2x^*\right) /D}\right) \right) \\&\quad \quad + \frac{1}{8} \gamma _2(\alpha + \beta D) +\mathcal {O}(\sqrt{\varepsilon }). \end{aligned} \end{aligned}$$

Similarly, the integral over the second slow field $I_s^4$ gives

$$\begin{aligned} \begin{aligned} J_{p,1}^4&= -\frac{1}{2} \left( \alpha \left( 1-e^{-x_d}\right) \left( 1-e^{-2x^*}\right) +\beta D \left( 1-e^{-x_d/D}\right) \left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{2} \left( \alpha \left( 1+e^{-x_d}\right) \left( 1-e^{-2x^*}\right) +\beta \left( 1+e^{-x_d/D}\right) \left( 1-e^{-2x^*/D}\right) \right) \sqrt{\varepsilon }\\&\quad \quad -\frac{1}{4} \left( \alpha \left( 1-e^{-x_d}\right) \left( 1-e^{-2x^*}\right) +\frac{\beta }{D} \left( 1-e^{-x_d/D}\right) \left( 1-e^{-2x^*/D}\right) \right) \varepsilon +\mathcal {O}(\varepsilon \sqrt{\varepsilon }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{p,2}^4&= \frac{1}{2} \alpha \beta \frac{1}{D^2-1}\left( -\left( 1-e^{-x_d}\right) \left( 1-e^{-2x^*}\right) +D^3\left( 1-e^{-x_d/D}\right) \left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{8} \alpha ^2 \left( 3\left( 1-e^{-x_d}\right) \left( 1-e^{-2x^*}\right) -x_de^{-x_d}\left( 1-e^{-2x^*}\right) -2x^*e^{-2x^*}\left( 1-e^{-x_d}\right) \right) \\&\quad \quad + \frac{1}{8} \beta ^2 \left( 3D\left( 1-e^{-x_d/D}\right) \left( 1-e^{-2x^*/D}\right) -x_de^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad -\frac{1}{4} \beta ^2 x^*e^{-2x^*/D}\left( 1-e^{-x_d/D}\right) + \frac{1}{8}\gamma _1\left( \alpha \left( 1-e^{-x_d}\right) + \beta D\left( 1-e^{-x_d/D}\right) \right) \\&\quad \quad -\frac{1}{8}\gamma _2\left( \alpha \left( 1-e^{-x_d}\right) \left( 3-2e^{-2x^*}\right) +\beta D \left( 1-e^{-x_d/D}\right) \left( 3-2e^{-2x^*/D}\right) \right) +\mathcal {O}(\sqrt{\varepsilon }). \end{aligned} \end{aligned}$$

The integral over the third slow region $I_s^6$ gives

$$\begin{aligned} \begin{aligned} J_{p,1}^6&= -\alpha \left( 1-e^{-2x^*}\right) - \beta D\left( 1-e^{-2x^*/D}\right) + 4 \gamma _2 x^* \\&\quad \quad + \left( \alpha \left( 1+e^{-2x^*}\right) + \beta \left( 1+e^{-2x^*/D}\right) - 4 \gamma _2 \right) \sqrt{\varepsilon }\\&\quad \quad + \left( -\frac{1}{2}\alpha \left( 1-e^{-2x^*}\right) - \frac{1}{2} \frac{\beta }{D}\left( 1-e^{-2x^*/D}\right) \right) \varepsilon +\mathcal {O}(\varepsilon \sqrt{\varepsilon }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{p,2}^6&= \alpha \beta \frac{1}{D^2-1}\left( -\left( 1-e^{-2x^*}\right) + D^3\left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{4} \alpha ^2 \left( 3-3e^{-2x^*}-2x^*e^{-2x^*}\right) \\&\quad \quad + \frac{1}{4} \beta ^2 \left( 3D-3De^{-2x^*/D}-2x^*e^{-2x^*/D}\right) \\&\quad \quad - \frac{1}{8}\gamma _1 \left( \alpha e^{-x_d}\left( 1-e^{-2x^*}\right) +\beta De^{-x_d/D}\left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{8}\gamma _2\left( \alpha \left( 4-16 x^*+e^{-x_d}-4e^{-2x^*}-e^{-(x_d+2x^*)}\right) \right) \\&\quad \quad +\frac{1}{8}\gamma _2\left( \beta \left( 4D-16 x^*+De^{-x_d/D}-4De^{-2x^*/D}-De^{-(x_d+2x^*)/D}\right) \right) +\mathcal {O}(\sqrt{\varepsilon }). \end{aligned} \end{aligned}$$

The integral over the last slow field $I_s^8$ gives

$$\begin{aligned} \begin{aligned} J_{p,1}^8&= -\frac{1}{2} \left( \alpha \left( 1-e^{-2x^*}\right) + \beta D\left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{2} \left( \alpha \left( 1-e^{-2x^*}\right) + \beta \left( 1-e^{-2x^*/D}\right) \right) \sqrt{\varepsilon }\\ {}&\quad \quad -\frac{1}{4} \left( \alpha \left( 1-e^{-2x^*}\right) + \frac{\beta }{D}\left( 1-e^{-2x^*/D}\right) \right) \varepsilon +\mathcal {O}(\varepsilon \sqrt{\varepsilon }), \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_{p,2}^8&= \frac{1}{2} \alpha \beta \frac{1}{D^2-1}\left( -\left( 1-e^{-2x^*}\right) + D^3\left( 1-e^{-2x^*/D}\right) \right) \\&\quad \quad +\frac{1}{8} \alpha ^2 \left( 3-3e^{-2x^*}-2x^*e^{-2x^*}\right) \\&\quad \quad + \frac{1}{8} \beta ^2 \left( 3D-3De^{-2x^*/D}-2x^*e^{-2x^*/D}\right) \\&\quad \quad + \frac{1}{8}\gamma _1 \left( \alpha e^{-(x_d+2x^*)} + \beta D e^{-(x_d+2x^*)/D}\right) \\&\quad \quad -\frac{1}{8}\gamma _2\left( \alpha \left( 2-2e^{-2x^*}+e^{-(x_d+2x^*)}\right) \right) \\&\quad \quad -\frac{1}{8}\gamma _2\left( \beta D\left( 2-2e^{-2x^*/D}+e^{-(x_d+2x^*)/D}\right) \right) +\mathcal {O}(\sqrt{\varepsilon }). \end{aligned} \end{aligned}$$

Next, we compute the integrals over the four fast fields. The leading order computation of the action functional over the fast fields yields $\frac{4 \sqrt{2}}{3}\varepsilon$—see [52] and (30)—and to determine the next order term we use (23). Around the defect point we get

$$\begin{aligned} \begin{aligned} J_p^2&= \varepsilon \int _{I_f^2} \bar{L}_0(U_{p,ld}^r;\bar{u}_{\gamma _1}) d \xi + \varepsilon ^2 \int _{I_f^2} \bar{L}_1(U_{p,ld}^r;\bar{u}_{\gamma _1}) d \xi \\&=-\frac{1}{2}\varepsilon ^2 \int _{-1/\sqrt{\varepsilon } }^{0} \left( \alpha \left( e^{-x_d}-e^{-x_d-2x^*}\right) + \beta \left( e^{-x_d/D}-e^{-(x_d+2x^*)/D}\right) \right) d\xi \\&\quad \qquad +\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon }) \\&=-\frac{1}{2}\left( \alpha \left( e^{-x_d}-e^{-x_d-2x^*}\right) + \beta \left( e^{-x_d/D}-e^{-(x_d+2x^*)/D}\right) \right) \varepsilon \sqrt{\varepsilon }+\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon })\,, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} J_p^3&= - \frac{1}{2}\left( \alpha \left( e^{-x_d}-e^{-x_d-2x^*}\right) + \beta \left( e^{-x_d/D}-e^{-(x_d+2x^*)/D}\right) \right) \varepsilon \sqrt{\varepsilon }\\ {}&\quad +\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon }) \,. \end{aligned}$$

The integral over the first fast jump, see also [52] and (30), gives

$$\begin{aligned} \begin{aligned} J_p^5&= \varepsilon \int _{I_f^5} \bar{L}_0(U_{p,ld}^r;\bar{u}_{\gamma _2}) d \xi + \varepsilon ^2 \int _{I_f^5} \bar{L}_1(U_{p,ld}^r;\bar{u}_{\gamma _2}) d \xi \\&= \frac{2 \sqrt{2}}{3} \varepsilon + \varepsilon ^2 \int _{-1/\sqrt{\varepsilon }}^{1/\sqrt{\varepsilon } } \left( \frac{1}{2} \alpha \left( -e^{-2x^*}\tanh {(\xi /\sqrt{2})}-1\right) \right. \\ {}&\quad \qquad \left. + \frac{1}{2} \beta \left( -e^{-2x^*/D}\tanh {(\xi /\sqrt{2})}-1\right) + \gamma _2 (\tanh {(\xi /\sqrt{2})}+1) \right) d\xi +\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon })\\&= \frac{2 \sqrt{2}}{3} \varepsilon + \left( -\alpha -\beta +2\gamma _2\right) \varepsilon \sqrt{\varepsilon }+\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon })\,. \end{aligned} \end{aligned}$$

Similarly,

$$\begin{aligned} J_p^7&= \frac{2 \sqrt{2}}{3} \varepsilon +(-\alpha -\beta +2\gamma _2)\varepsilon \sqrt{\varepsilon }+\mathcal {O}(\varepsilon ^2\sqrt{\varepsilon }) \,. \end{aligned}$$

So, adding the contributions of the slow and fast fields to the action functional together gives the action functional $J_p(U_{p,ld}^r)$ (38) of a local defect pulse solution $Z_{p,ld}^r$ pinned to the right of the defect. As expected, the $\mathcal {O}(\varepsilon \sqrt{\varepsilon })$-terms of the action functional from the slow and fast fields cancel out. This completes the proof of Lemma 1. $\square$