Abstract
Before a knock-out tournament starts, the participants are assigned to positions in the tournament bracket through a process known as seeding. There are many ways to seed a tournament. In this paper, we solve a discrete optimization problem of finding a seeding that maximizes spectator interest in a tournament when spectators are interested in matches with high competitive intensity (i.e., matches that involve teams comparable in strength) and high quality (i.e., matches that involve strong teams). We find a solution to the problem under two assumptions: the objective function is linear in quality and competitive intensity and a stronger team beats a weaker one with sufficiently high probability. Depending on parameters, only two special classes of seedings can be optimal. While one of the classes includes a seeding that is often used in practice, the seedings in the other class are very different. When we relax the assumption of linearity, we find that these classes of seedings are in fact optimal in a sizable number of cases. In contrast to existing literature on optimal seedings, our results are valid for an arbitrarily large number of participants in a tournament.


Similar content being viewed by others
Notes
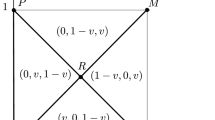
The share of close seedings in the set of all seedings is equal to \(\frac{2^{2^n-1}}{(2^n)!}\) while the share of distant seedings is the same number multiplied by \(\prod _{k=1}^{n-1}(2^k)!\).
References
Baumann R, Matheson VA, Howe C (2010) Anomalies in tournament design: the madness of March madness. J Quant Anal Sports. doi:10.2202/1559-0410.1233
Ely J, Frankel A, Kamenica E (2015) Suspense and Surprise. J Polit Econ 123(1):215–260
Forrest D, Simmons R (2002) Outcome uncertainty and attendance demand in sport: the case of English soccer. J R Stat Soc Ser D Stat 51 Part 2:229–241
Glickman ME (2008) Bayesian locally optimal design of knockout tournaments. J Stat Plann Inference 138:2117–2127
Groh C, Moldovanu B, Sela A, Sunde U (2012) Optimal seedings in elimination tournaments. Econ Theory 49:59–80
Horen J, Riezman R (1985) Comparing draws for single elimination tournaments. Oper Res 33:249–262
Hwang F (1982) New concepts in seeding knockout tournaments. Am Math Mon 89:235–239
Palomino F, Rigotti L (2000) The sport league’s dilemma: competitive intensity versus incentives to win. Working Paper, University of California, Department of Economics
Rosen S (1986) Prizes and incentives in elimination tournaments. Am Econ Rev 76(4):701–715
Ryvkin D (2005) The predictive power of noisy elimination tournaments. Working paper, Center for Economic Research and Graduate Education–Economic Institute, Prague
Schwenk A (2000) What is the correct way to seed a knockout tournament. Am Math Monthly 107:140–150
Vu TD (2010) Knockout tournament design: a computational approach. PhD dissertation, Stanford University, Department of Computer Science
Wright M (2014) OR analysis of sporting rules: a survey. Eur J Oper Res 232:1–8
Author information
Authors and Affiliations
Corresponding author
Additional information
Dmitry Dagaev is supported by The National Research University—Higher School of Economics Academic Fund Program in 2014/2015 (research grant No 14-01-0007).
Rights and permissions
About this article
Cite this article
Dagaev, D., Suzdaltsev, A. Competitive intensity and quality maximizing seedings in knock-out tournaments. J Comb Optim 35, 170–188 (2018). https://doi.org/10.1007/s10878-017-0164-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-017-0164-7