Abstract
We propose a theoretical model of a round-robin tournament with limited resources motivated by the fact that in real-world sport round-robin tournaments, participating teams are sometimes forced to distribute their effort over multiple matches. We assume that participating teams have a limited amount of effort that must be distributed between all matches of the tournament. We model the outcome of each match as a first-price all-pay auction. The prizes are awarded according to the ranking at the end of the tournament, based on the number of wins. The tournament with three teams is solved. In the case of identical budgets and low first prize, we find two types of equilibria—‘effort-saving’ and ‘burning-out’—both leading to unequal payoffs; when the first prize is large, we find multiple families of equilibria with both equal and non-equal payoffs. In the case of non-identical budgets, we show that there exist equilibria where a team with a lower budget gets a higher payoff than a team with a larger budget.







Similar content being viewed by others
Notes
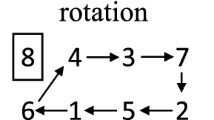
Though there are many ways to rank a round-robin tournament, usually, in practice, teams are ranked by the number of wins or by the number of points gained in all matches. As proved in Rubinstein (1980), ranking by the number of wins is the only aggregation method that satisfies anonymity, positive responsiveness, and the independence of irrelevant alternatives.
A formal definition is provided in Definition 3.
For the convenience of comparison, we adopt the notation of Laica et al. (2021) for our paper.
This corresponds to the case of \(k=n-1\), \(\alpha =1\) in Proposition 1 of the mentioned paper.
This assumption is not restrictive because one can define a one-to-one correspondence between games with teams A and B, teams being permuted. Note that A and B make their decisions simultaneously, and team C’s strategy in a match against A automatically determines team C’s effort in a match against B, so the update of information after the second match cannot be exploited.
Note that the latter condition implies that \(\beta >1\).
References
Amegashie JA, Cadsby CB, Song Y (2007) Competitive burnout: theory and experimental evidence. Games Econom Behav 59(2):213–239
Dechenaux E, Kovenock D, Sheremeta RM (2015) A survey of experimental research on contests, all-pay auctions and tournaments. Exp Econ 18(4):609–669
Deutscher C, Sahm M, Schneemann S, Sonnabend H (2021) Strategic investment decisions in multi-stage contests with heterogeneous players. Theory Decis 2021:1–37
Erez E, Sela A (2010) Round-Robin tournaments with effort constraints. In: Monaster Center for Economic Research Ben-Gurion University of the Negev. Discussion Paper, 10-09
Harbaugh R, Klumpp T (2005) Early round upsets and championship blowouts. Econ Inq 43(2):316–329
Ferrall C, Smith AA Jr (1999) A sequential game model of sports championship series: theory and estimation. Rev Econ Stat 81(4):704–719
Gross O, Wagner R (1950) A continuous colonel blotto game. In: RAND Corporation RM-408
Klumpp T, Konrad KA, Solomon A (2019) The dynamics of majoritarian Blotto games. Games Econ Behav 117:402–419
Konrad KA (2009) Strategy and dynamics in contests. Oxford University Press, Oxford
Kovenock D, Roberson B (2012) Coalitional Colonel Blotto games with application to the economics of alliances. J Public Econ Theory 14(4):653–676
Kovenock D, Roberson B (2020) Generalizations of the general lotto and colonel blotto games. Econ Theory 2020:1–36
Krumer A, Lechner M (2017) First in first win: evidence on schedule effects in round-robin tournaments in mega-events. Eur Econ Rev 100:412–427
Krumer A, Megidish R, Sela A (2017) First-mover advantage in round-robin tournaments. Soc Choice Welfare 48(3):633–658
Krumer A, Megidish R, Sela A (2020) The optimal design of round-robin tournaments with three players. J Sched 23:379–396
Laica C, Lauber A, Sahm M (2021) Sequential round-robin tournaments with multiple prizes. Games Econ Behav 129:421–448
Macdonell ST, Mastronardi N (2015) Waging simple wars: a complete characterization of two-battlefield Blotto equilibria. Econ Theor 58(1):183–216
Muehlheusser G (2006) Implications from the theory of contests for modelling and designing sports competitions. Handb Econ Sport 35:342
Nti KO (1999) Rent-seeking with asymmetric valuations. Public Choice 98(3–4):415–430
Roberson B (2006) The Colonel Blotto game. Econ Theor 29:1–24
Roberson B, Kvasov D (2012) The non-constant-sum Colonel Blotto game. Econ Theor 51(2):397–433
Rubinstein A (1980) Ranking the participants in a tournament. SIAM J Appl Math 38(1):108–111
Sahm M (2019) Are sequential round-robin tournaments discriminatory? J Public Econ Theory 21(1):44–61
Sela A, Erez E (2013) Dynamic contests with resource constraints. Soc Choice Welfare 41(4):863–882
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Dan Kovenock and Konstantin Sonin for their useful comments and suggestions. We have benefited from the comments of seminar participants at XVIII April International Academic Conference On Economic and Social Development (Moscow), the 1st International Conference on Economics of Football (Kazan), the 6th International Conference on Mathematics in Sport (Padova). Dmitry Dagaev gratefully acknowledges support from the Basic Research Program of the National Research University Higher School of Economics.
Andrey Zubanov: The work was done prior to joining Amazon, when the author was at the University of Wisconsin-Madison and HSE University.
Appendices
Appendix A
This Appendix contains formal proofs of statements from Sect. 3 (the case of identical budgets of effort).
1.1 Proof of Proposition 1
Define ex-ante payoff as the expected payoff that teams think of before a tie-break in Round 1 is realized. Interim payoff refers to the expected payoffs when the result of a tie-break in Round 1 is known, but the results of the other two games have not yet been determined. Ex-ante and interim payoffs differ only when teams’ efforts in Round 1 are equal.
When \(v>\frac{{1}}{2}\), the teams are strictly interested in winning a tournament. When \(v=\frac{1}{2}\), the teams are instead just interested in not being last. Consider the following cases:
1. If \(e_{a}+e_{b}>1\), then C can win the tournament with certainty by allocating efforts \(e_{c}>1-e_{a}\) in the second round against A and \(1-e_{c}>1-e_{b}\) in the third round against B. Then, for \(v>\frac{1}{2}\), all \(e_{c}\in (1-e_{a},e_{b})\) are the best responses for team C. Team C receives payoff v, the winner of the first round receives \(1-v\), and the loser of the first round receives 0.
Now, let \(v=\frac{1}{2}\). To finish among the top two teams with a probability of 1, it is necessary and sufficient for team C to defeat the loser of the match between teams A and B. Consequently, if A won over B in Round 1, any \(e_{c}\), such that \(1-e_{c}>1-e_{b}\), or \(e_{c}<e_{b}\), guarantees that team C will finish in at least second place; if B won over A in Round 1, any \(e_{c}>1-e_{a}\) works.
2. Let \(e_{a}+e_{b}=1\) and \(e_{a}>\frac{1}{2}\). The latter inequality means that A defeats B with certainty. If team C exerts less than \(1-e_{a}\) of effort in Round 2, then team A wins the tournament, and team C’s payoff is \(1-v\). Otherwise, team C can either tie the opponents’ efforts in the second and third rounds or win the second round and lose in the third. The latter strategy allows team C to obtain the expected payoff of \(\frac{{1}}{3}\), and the two other teams also get \(\frac{{1}}{3}\). Tying the opponents’ efforts in both rounds by playing \(e_{c}=1-e_{a}\) means:
-
with a probability of \(\frac{1}{4}\), C wins in both rounds and gets a payoff of v, teams A and B get \(1-v\) and 0, respectively;
-
with a probability of \(\frac{1}{4}\), C wins in Round 2 and loses in Round 3, which means that each team has 1 win and gets a payoff of \(\frac{1}{3}\);
-
with a probability of \(\frac{1}{4}\), C wins in Round 3 but loses in Round 2. Team C finishes second and gets \(1-v\), whereas team A receives v and team B — 0;
-
with a probability of \(\frac{1}{4}\), team C loses in both rounds and gets a payoff of 0. Teams A and B get v and \(1-v\), respectively.
Thus, the expected payoff of team C is \(\frac{{1}}{4}\cdot v+\frac{{1}}{4}\cdot \frac{{1}}{3}+\frac{{1}}{4}\cdot (1-v)=\frac{1}{3}\); the expected payoffs of teams A and B are \(\frac{1}{3}+\frac{{1}}{4}v\) and \(\frac{1}{3}-\frac{{1}}{4}v\), respectively. Compare the outcomes:
-
If \(v>\frac{2}{3}\), all strategies of \(e_{c}\ge 1-e_{a}\) are the best responses for team C. The corresponding payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\) if C chooses \(e_{c}>1-e_{a}\) and \((\frac{1}{3}+\frac{{1}}{4}v,\frac{1}{3}-\frac{{1}}{4}v,\frac{1}{3})\) if C chooses \(e_{c}=1-e_{a}\).
-
If \(\frac{1}{2}\le v<\frac{2}{3}\), team C will just win against the loser, team B, if possible. So, when \(e_{b}>0\), the best response of team C here is to play \(e_{c}<e_{b}\). When \(e_{b}=0\) and \(e_{a}=1\), team C gets \(\frac{1}{3}\) in any case. So, \(BR_{c}(1,0)=[0,1]\). When \(e_{c}>0\), every team gets a payoff of \(\frac{1}{3}\); when \(e_{c}=0\), the payoffs are \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\).
-
If \(v=\frac{2}{3}\), team C is indifferent. Then C can choose any \(e_{c}\in [0,e_{b}]\cup [1-e_{a},1]=[0,1]\). If \(e_{c}<e_{b}\), then payoffs are \((\frac{2}{3},0,\frac{1}{3})\); if \(e_{c}=e_{b}\), the payoff profile is \((\frac{1}{2},\frac{1}{6},\frac{1}{3})\); and if \(e_{c}>e_{b}\), then the payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\).
3. If \(e_{a}+e_{b}=1\) and \(e_{a}<\frac{1}{2}\) (B defeats A), the case is symmetric with the previous one.
-
If \(v>\frac{2}{3}\), all strategies \(e_{c}\le 1-e_{a}\) are the best responses for team C. The corresponding payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\) if C chooses \(e_{c}<1-e_{a}\) and \((\frac{1}{3}-\frac{{1}}{4}v,\frac{1}{3}+\frac{{1}}{4}v,\frac{1}{3})\) if C chooses \(e_{c}=1-e_{a}\).
-
If \(\frac{1}{2}\le v<\frac{2}{3}\), team C will win against the loser, team A, if possible. So, when \(e_{a}>0\), the best response of team C here is to play \(e_{c}>1-e_{a}\). When \(e_{a}=0\), and thus \(e_{b}=1\), then in any case team C gets \(\frac{1}{3}\). So, \(BR_{c}(0,1)=[0,1]\). When \(e_{c}>0\), every team gets payoff of \(\frac{1}{3}\), but when \(e_{c}=0\), the payoff profile is: \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{1}{4}v,\frac{1}{3})\).
-
If \(v=\frac{2}{3}\), team C is indifferent, and then C can choose any \(e_{c}\in [0,1]\). If \(e_{c}<1-e_{a}\), then payoffs are \((0,v,1-v\)); if \(e_{c}=1-e_{a}\), the payoff profile is \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{1}{4}v,\frac{1}{3})\); and if \(e_{c}>1-e_{a}\), then the payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\).
4. If \(e_{a}=e_{b}=\frac{{1}}{2}\), team C must choose one of two actions in each of the two states of the tie-break. Defeating the winner of Round 1 (say, team A) leads to payoffs of \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\). Defeating the loser of Round 1 (say, team B) gives payoffs of \((v,0,1-v)\). The best decision for team C here is similar to the previous case:
-
If \(\frac{1}{2}\le v<\frac{2}{3}\), it is better for C to win against the loser of Round 1.
-
If \(v=\frac{2}{3}\), any action is equally good for C: to defeat the winner, to defeat the loser, or to split its effort equally between both games. Three symmetric actions with respect to teams A and B bring the payoffs \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\). If C always prefers to defeat A, then the teams get \((\frac{1}{6},\frac{1}{2},\frac{1}{3})\); if C always prefers to defeat B, then the teams get \((\frac{1}{2},\frac{1}{6},\frac{1}{3})\). If C defeats winner A and splits its effort in case B wins, then the expected payoffs are \((\frac{1}{4},\frac{5}{12},\frac{1}{3})\). The same payoffs appear if C defeats loser A and splits its effort in case B wins. Similarly, the two opposite actions result in \((\frac{5}{12},\frac{1}{4},\frac{1}{3})\).
-
If \(v>\frac{2}{3}\) and A defeated B in a tie break, then all \(e_{c}\in [\frac{1}{2},1]\) are equally good for team C. If C chooses \(e_{c}\in (\frac{1}{2},1]\), then the payoff profile is \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), and if C exerts an effort level of \(\frac{1}{2}\), the interim payoff profile is \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\). The same works for the case in which B defeated A in a tie-break in Round 1. So, when C does play symmetric actions (with respect to a lottery outcome), the ex-ante payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\). If C plays \(e_{c}>\frac{1}{2}\) when A won in Round 1 but plays \(e_{c}=\frac{1}{2}\) when B won in Round 1, then the ex-ante payoffs are \(\left( \frac{1}{3}-\frac{{1}}{8}v,\frac{1}{3}+\frac{{1}}{8}v,\frac{1}{3}\right)\). Symmetrically, if C plays \(e_{c}<\frac{1}{2}\) when B won in Round 1 but plays \(e_{c}=\frac{1}{2}\) when A won in Round 1, then the ex-ante payoffs are \(\left( \frac{1}{3}+\frac{{1}}{8}v,\frac{1}{3}-\frac{{1}}{8}v,\frac{1}{3}\right)\).
5. If \(0<e_{a}+e_{b}<1\), team C cannot do better than to win one game and to lose another one.
-
When \(v>\frac{2}{3}\), the best decision is to defeat the winner of the first round and to get a payoff of \(\frac{{1}}{3}\).
-
When \(\frac{1}{2}\le v<\frac{2}{3}\), then for team C it is best to win over the loser of Round 1 (if possible; i.e., a loser spends strictly more than 0 in Round 1), getting payoffs \((v,0,1-v)\) if A won Round 1 and \((0,v,1-v)\) if B won Round 1. If \(e_{a}=0\) and \(e_{b}\in (0,1)\), then winning over B is better since it gives \(\frac{1}{3}\), but a tying effort against A will give only \(\frac{1}{2}(1-v)<\frac{1}{3}\). The same applies symmetrically to the case in which \(e_{b}=0\) and \(e_{a}\ne 0\).
-
When \(v=\frac{2}{3}\), team C is indifferent between defeating the winner and beating the loser of Round 1. To defeat the winner of Round 1, team C can choose any effort \(x>1-e_{a}\) if A won over B and any \(x<e_{b}\) if B won over A. All teams get \(\frac{1}{3}\). To beat the loser of Round 1, team C can choose any effort \(x<e_{b}\) if A won over B and any \(x>1-e_{a}\) if B won over A. So, the best action is to play \(x\in [0,e_{b})\cup (1-e_{a},1]\).
6. If \(e_{a}=e_{b}=0\), then
-
If \(v>\frac{2}{3}\), team C should spend all its effort in a game against the winner of Round 1. In this case, C gets a payoff of \(\frac{{1}}{2}\cdot \frac{{1}}{3}=\frac{1}{6}\), whereas both other teams get an ex-ante payoff of \(\frac{5}{12}\).
-
If \(\frac{1}{2}\le v<\frac{2}{3}\), it is better for team C to spend all its effort on the loser of Round 1, getting a payoff of \(\frac{1}{2}(1-v)\). The two other teams will get ex-ante payoffs of \(\frac{1}{2}(1-\frac{1}{2}(1-v))=\frac{1+v}{4}\).
-
If \(v=\frac{2}{3}\), C is indifferent between spending all its effort either in one or another game. \(\square\)
1.2 Proof of Theorem 1
Let \(v>\frac{{2}}{3}\). We check all pairs \((e_{a}^{*},e_{b}^{*})\) for the profitability of deviations assuming that C plays their best response.
-
If \(e_{a}^{*}+e_{b}^{*}>1\), the corresponding profile cannot be an equilibrium because playing 0 for one of the teams is certainly better.
-
If \(e_{a}^{*}=0,0<e_{b}^{*}<1\) or \(e_{b}^{*}=0,0<e_{a}^{*}<1\), all teams get \(\frac{1}{3}\). However, a team that exerts a positive level of effort can gain by decreasing it to 0. Thus, the corresponding strategies do not constitute an equilibrium.
-
If \(0<e_{a}^{*},e_{b}^{*}<\frac{{1}}{2}\), the payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). The deviation is unprofitable for both teams A and B if and only if team C chooses to defeat the winner of the first game in points \((e_{a}^{*},1-e_{a}^{*})\) and \((1-e_{b}^{*},e_{b}^{*})\). This leads to a set of equilibria \({{\mathcal {S}}}_{1}\).
-
Analogously, if \(0<e_{a}^{*}<\frac{{1}}{2}\) and \(\frac{{1}}{2}<e_{b}^{*}<1-e_{a}^{*}\), we obtain a set of equilibria \({{\mathcal {S}}}_{2}\), whilst case \(0<e_{b}^{*}<\frac{{1}}{2}\) and \(\frac{{1}}{2}<e_{a}^{*}<1-e_{b}^{*}\) brings a set of equilibria \({{\mathcal {S}}}_{3}\).
-
Suppose that \(0<e_{a}^{*}<\frac{{1}}{2}\) and \(e_{b}^{*}=\frac{{1}}{2}\). Team B would not deviate if \(e_{c}^{*}(e_{a}^{*},1-e_{a}^{*})<1-e_{a}^{*}\). It is necessary and sufficient for the existence of a profitable deviation for team A that team C responds to \((\frac{{1}}{2},\frac{{1}}{2})\) in such a way that C defeats B if B is the winner of the first game but equalizes the efforts of opponents if A won the first game. Thus, \({{\mathcal {S}}}_{4}\) is the set of equilibria in this case. Similarly, \({{\mathcal {S}}}_{5}\) is the set of equilibria if \(0<e_{b}^{*}<\frac{{1}}{2}\) and \(e_{a}^{*}=\frac{{1}}{2}\).
-
If \(e_{a}^{*}+e_{b}^{*}=1\), \(0<e_{a}^{*},e_{b}^{*}<1\), both teams A and B must receive \(\frac{{1}}{3}\) in equilibrium because both can guarantee a payoff of \(\frac{{1}}{3}\) by deviating. This is possible if and only if the strategy profile belongs to the set \({{\mathcal {S}}}_{6}\cup {{\mathcal {S}}}_{7}\cup {{\mathcal {S}}}_{8}\).
-
All strategy profiles from the set \({{\mathcal {S}}}_{9}\) are SPE: neither A nor B can get more than \(\frac{{5}}{12}\).
-
If \(e_{a}^{*}=0\), \(e_{b}^{*}=1\) and \(e_{c}^{*}\ne 1\), the payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), and team B would prefer to decrease their effort to 0. If \(e_{a}^{*}=0\), \(e_{b}^{*}=1\) and \(e_{c}^{*}=1\), the payoffs are \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{{1}}{4}v,\frac{1}{3})\), and no team is better off by deviating. This leads to a set of equilibria \({{\mathcal {S}}}_{11}\). Case \(e_{b}^{*}=0\), \(e_{a}^{*}=1\) is symmetric and leads to a set of equilibria \({{\mathcal {S}}}_{10}\). \(\square\)
1.3 Proof of Theorem 2
We check all pairs \((e_{a}^{*},e_{b}^{*})\) for the profitability of deviations, assuming that C plays their best response.
-
If \(2>e_{a}^{*}+e_{b}^{*}>1\), the corresponding profile cannot be an equilibrium because playing 0 for one of the teams is certainly better since it allows it to get at least \(\frac{{1}}{3}\).
-
If \(e_{a}^{*}=e_{b}^{*}=1\), neither team can profitably deviate if and only if team C ties the winner’s efforts at (1, 0) and (0, 1). This brings out equilibria from the set \({{\mathcal {S}}}_{12}\).
-
Any strategy profile such that \(0<e_{a}^{*},e_{b}^{*}<1\) or any strategy profile such that \(e_{a}^{*}=1,0<e_{b}^{*}<1\) or \(e_{b}^{*}=1,0<e_{a}^{*}<1\) cannot be an equilibrium because each of the teams A and B is able to guarantee a payoff of \(\frac{{1}}{3}\) by decreasing their efforts to 0.
-
If \(e_{a}^{*}=0,0<e_{b}^{*}<1\) or \(e_{b}^{*}=0,0<e_{a}^{*}<1\), all teams get \(\frac{1}{3}\). However, a team that exerts a positive level of effort can gain by decreasing its effort to 0. Thus, the corresponding strategies do not constitute an equilibrium.
-
If \(e_{a}^{*}=0\), \(e_{b}^{*}=1\) and \(e_{c}^{*}\ne 1\), the payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), and team B would prefer to decrease their effort to 0. If \(e_{a}^{*}=0\), \(e_{b}^{*}=1\) and \(e_{c}^{*}=1\), the payoffs are \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{{1}}{4}v,\frac{1}{3})\), and team A is better off by exerting all its effort in the first game against B, changing its own payoff to \(\frac{{1-v}}{2}\). Case \(e_{b}^{*}=0\), \(e_{a}^{*}=1\) is symmetric. There are no equilibria here.
-
It is easy to check that the strategy profiles from the set \({{\mathcal {S}}}_{9}\) are SPE: neither A nor B can increase their payoffs.
-
Other profiles that include \(e_{a}^{*}=e_{b}^{*}=0\) are not equilibria since either A would prefer \(e_{a}=1\) instead of \(e_{a}^{*}=0\) or B would prefer \(e_{b}=1\) instead of \(e_{b}^{*}=0\). \(\square\)
1.4 Proof of Theorem 3
An internal point of square PMNO (see 2) could be an equilibrium only if all teams get a payoff of \(\frac{{1}}{3}\): teams A and B can guarantee this payoff by decreasing their efforts in the first game to 0.
-
If \(e_{a}^{*}=e_{b}^{*}=1\), then no team has an incentive to deviate, if and only if team C ties the winner’s efforts in the subgames when \((e_{a},e_{b})=(1,0)\) and \((e_{a},e_{b})=(0,1)\). The payoff profile is then \(\frac{1}{2}(\frac{1}{3},0,\frac{2}{3})+\frac{1}{2}(0,\frac{1}{3},\frac{2}{3})=(\frac{1}{6},\frac{1}{6},\frac{2}{3})\).
-
If \(2>e_{a}^{*}+e_{b}^{*}>1\), these points do not satisfy the necessary condition. Thus, this is not an equilibrium.
-
If \(0<e_{a}^{*}+e_{b}^{*}\le 1\), \((e_{a}^{*},e_{b}^{*})\notin \{(0,1),(1,0)\}\), there exists an equilibrium in which team C always defeats the winner of the first round (if possible). The payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\).
-
If \(e_{a}^{*}=e_{b}^{*}=0\), all payoffs can occur in equilibrium if team C defeats the winner of the first round in points P and N, which lead to payoff of \((\frac{5}{12},\frac{5}{12},\frac{1}{6})\) when \(e_{c}^{*}(0,0,A)=0\) and \(e_{c}^{*}(0,0,B)=1\) or when \(e_{c}^{*}(0,0,A)=1\) and \(e_{c}^{*}(0,0,B)=0\). When \(e_{c}^{*}(0,0,A)=0\) and \(e_{c}^{*}(0,0,B)=0\), payoff profile \((\frac{1}{2},\frac{1}{3},\frac{1}{6})\) is realized. When \(e_{c}^{*}(0,0,A)=1\) and \(e_{c}^{*}(0,0,B)=1\), payoff profile \((\frac{1}{3},\frac{1}{2},\frac{1}{6})\) is realized.
-
Suppose that \(e_{a}^{*}=0\), \(e_{b}^{*}=1\). If \(e_{c}^{*}\ne 1\), the payoffs are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), and if \(e_{c}^{*}=1\), the payoffs are \((\frac{1}{6},\frac{1}{2},\frac{1}{3})\). In both cases, team A cannot deviate profitably. If \(e_{c}^{*}=1\), team B cannot deviate. If \(e_{c}^{*}\ne 1\), team B would not prefer to decrease their effort if the payoffs at point (0, 0) are \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\). This brings two types of equilibria. Case \(e_{b}^{*}=0\), \(e_{a}^{*}=1\) is symmetric. \(\square\)
1.5 Proof of Proposition 2
1.5.1 Case \(\frac{1}{2}\le v<\frac{2}{3}\)
This case contains only two types of Nash equilibria: \({{\mathcal {S}}}_{9}\) and \({{\mathcal {S}}}_{12}\) with payoff profiles \((\frac{1+v}{4},\frac{1+v}{4},\frac{1-v}{2})\) and \((\frac{1-v}{2},\frac{1-v}{2},v)\), respectively.
A profitable deviation from \({{\mathcal {S}}}_{9}\) would be from the coalition of teams A and C, which play \(e_{a}=1\) and \(e_{c}(1,0)=0\) (with the same off-path actions for team C as in equilibrium), while B still sticks to strategy \(e_{b}=0\). With this deviation, A wins against B with probability 1, while in two other matches, teams have equal chances to win against each other. The expected prizes would be \((\frac{1}{2}v+\frac{1}{4}\cdot \frac{1}{3}+\frac{1}{4}(1-v),\frac{1}{4}\cdot \frac{1}{3}+\frac{1}{4}(1-v),\frac{1}{4}v+\frac{1}{4}\cdot \frac{1}{3}+\frac{1}{4}(1-v))=(\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\). Note that here the prizes are larger both for A and for C than in equilibria from the set \({{\mathcal {S}}}_{9}\). Thus, \({{\mathcal {S}}}_{9}\) does not survive the strong Nash equilibrium refinement.
The other set of equilibria, \({{\mathcal {S}}}_{12}\), does not survive either. Consider a deviation from a coalition of teams A and B to \(e_{a}=0\), \(e_{b}=0\). Team C’s best response would be matching one of the opponents’ effort (i.e. play either \(e_{c}(0,0)=1\) or \(e_{c}(0,0)=0\)). The payoffs of the teams would be \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3},\frac{1}{3}-\frac{1}{4}v)\) if \(e_{c}(0,0)=0\), \((\frac{1}{3},\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v)\) if \(e_{c}(0,0)=1\), or \((\frac{1}{2},\frac{1}{2},0)\) in other cases. In any case, both A and B individually gain from cooperative deviation. Thus, \({{\mathcal {S}}}_{12}\) does not pass the strong Nash equilibrium refinement.
1.5.2 Case \(v>\frac{2}{3}\)
This case contains several types of equilibria: \({{\mathcal {S}}}_{1}\)-\({{\mathcal {S}}}_{8}\) with payoffs \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), \({{\mathcal {S}}}_{9}\) with payoffs \((\frac{5}{12},\frac{5}{12},\frac{1}{6})\), \({{\mathcal {S}}}_{10}\) and \({{\mathcal {S}}}_{11}\) with payoff profiles \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\) and \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{1}{4}v,\frac{1}{3})\), respectively.
In \({{\mathcal {S}}}_{9}\), teams A and C can deviate to \(e_{a}=1\) and \(e_{c}(1,0)=0\), which will yield them the payoffs of \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\). The latter payoffs are larger than in \({{\mathcal {S}}}_{9}\) since \(\frac{1}{3}+\frac{1}{4}v>\frac{5}{12}\) and \(\frac{1}{3}>\frac{1}{6}\).
In \({{\mathcal {S}}}_{10}\), teams B and C will prefer to deviate to \(e_{b}=1\) and \(e_{c}(1,1)=1\), and that would result in payoffs of \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3},\frac{1}{3}+\frac{1}{4}v)\). Both B and C will increase their payoffs compared to the profile from the set \({{\mathcal {S}}}_{10}\). The case \({{\mathcal {S}}}_{11}\) is symmetric to \({{\mathcal {S}}}_{10}\) up to the relabelling of teams A and B.
Consider now an equilibrium \((e_{a}^{*},e_{b}^{*},e_{c}^{*}(e_{a},e_{b},t(e_{a})))\) from sets \({{\mathcal {S}}}_{1}\)-\({{\mathcal {S}}}_{8}\). In this case, A and C can decide to play \(e_{a}=1\), \(e_{c}(1,e_{b}^{*})=0\), i.e. allocate all effort to the games against team B. Both A and C will defeat team B with certainty since B exerts positive effort in each round in each equilibrium from the sets \({{\mathcal {S}}}_{1}\)-\({{\mathcal {S}}}_{8}\). By spending all effort in their games against B, teams A and C would end up winning the game between them with the probability of \(\frac{1}{2}\), thus getting an expected prize of \(\frac{1}{2}\), which is larger than \(\frac{1}{3}\) they used to have. Thus, equilibria from the sets \({{\mathcal {S}}}_{1}\)-\({{\mathcal {S}}}_{8}\) do not survive the strong Nash refinement.
1.5.3 Case \(v=\frac{2}{3}\)
Very similar or exactly the same arguments work for the knife-edge case of \(v=\frac{2}{3}\). \(\square\)
1.6 Proof of Proposition 3
To prove the statement, for each value of v, we present an equilibrium from every class of equilibria \(\mathcal {S}_{i}\), which is eliminated after the refinement.
1.6.1 Case \(v>\frac{2}{3}\)
For auxiliary purposes, define
Note that \({\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\in BR_{c}(e_{a},e_{b},t(e_{a}))\). Using this function, for each \(\mathcal {S}_{i}\), we construct such pair \((e_{a}^{*},e_{b}^{*})\) and the best response \(e_{c}^{*}(e_{a},e_{b})\) of team C that the corresponding strategy profile does not survive after refinement. Here and below, we omit the tie-break argument of \(e_{c}^{*}\) when it does not lead to confusion.
\(\mathcal {S}_{1}\): Take \(e_{a}^{*}=\frac{1}{4}\), \(e_{b}^{*}=\frac{1}{8}\), and let \(e_{c}^{*}(\frac{1}{4},\frac{1}{8})=\frac{15}{16}\), whereas \(e_{c}^{*}(\frac{1}{8},\frac{1}{4})=\frac{1}{32}\). To ensure that the profile belongs to the set \(\mathcal {S}_{1}\), take other off-path actions as \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{16}\) and \(e_{c}^{*}(\frac{7}{8},\frac{1}{8})=\frac{9}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{4},\frac{1}{8}),(\frac{1}{8},\frac{1}{4}),(\frac{1}{4},\frac{3}{4}),(\frac{7}{8},\frac{1}{8})\}\). The strategy profile \((e_{a}^{*},e_{b}^{*},e_{c}^{*}(e_{a}^{*},e_{b}^{*}))\) belongs to \(\mathcal {S}_{1}\) but does not survive the equilibrium symmetry refinement.
\(\mathcal {S}_{2}\): Take \(e_{a}^{*}=\frac{1}{4}\), \(e_{b}^{*}=\frac{5}{8}\), and let \(e_{c}^{*}(\frac{1}{4},\frac{5}{8})=\frac{5}{16}\), whereas \(e_{c}^{*}(\frac{5}{8},\frac{1}{4})=\frac{31}{32}\). Take other off-path actions as \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{4},\frac{5}{8}),(\frac{5}{8},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{3}\): Take \(e_{a}^{*}=\frac{5}{8}\), \(e_{b}^{*}=\frac{1}{4}\), and let \(e_{c}^{*}(\frac{5}{8},\frac{1}{4})=\frac{31}{32}\), whereas \(e_{c}^{*}(\frac{1}{4},\frac{5}{8})=\frac{5}{16}\). Take other off-path actions as \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{15}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{4},\frac{5}{8}),(\frac{5}{8},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{4}\): Take \(e_{a}^{*}=\frac{1}{8}\), \(e_{b}^{*}=\frac{1}{2}\), and let \(e_{c}^{*}(\frac{1}{8},\frac{1}{2})=\frac{5}{16}\), whereas \(e_{c}^{*}(\frac{1}{2},\frac{1}{8})=\frac{31}{32}\). Take other off-path actions as \(e_{c}^{*}(\frac{1}{8},\frac{7}{8})=\frac{1}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{8},\frac{1}{2}),(\frac{1}{2},\frac{1}{8}),(\frac{1}{8},\frac{7}{8})\}\).
\(\mathcal {S}_{5}\): Take \(e_{a}^{*}=\frac{1}{2}\), \(e_{b}^{*}=\frac{1}{8}\), and let \(e_{c}^{*}(\frac{1}{2},\frac{1}{8})=\frac{11}{16}\), whereas \(e_{c}^{*}(\frac{1}{8},\frac{1}{2})=\frac{1}{32}\). Take other off-path actions as \(e_{c}^{*}(\frac{7}{8},\frac{1}{8})=\frac{15}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{8},\frac{1}{2}),(\frac{1}{2},\frac{1}{8}),(\frac{7}{8},\frac{1}{8})\}\).
\(\mathcal {S}_{6}\): Take \(e_{a}^{*}=\frac{3}{4}\), \(e_{b}^{*}=\frac{1}{4}\), and let \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{11}{16}\), whereas \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{32}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{7}\): Take \(e_{a}^{*}=\frac{1}{4}\), \(e_{b}^{*}=\frac{3}{4}\), and let \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{32}\), whereas \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{11}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{8}\): Take \(e_{a}^{*}=\frac{1}{2}\), \(e_{b}^{*}=\frac{1}{2}\), and let \(e_{c}^{*}(\frac{1}{2},\frac{1}{2},A)=\frac{13}{16}\), \(e_{c}^{*}(\frac{1}{2},\frac{1}{2},B)=\frac{3}{16}\). Additionally, \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{32}\), whereas \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{11}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(\frac{1}{2},\frac{1}{2}),(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{9}\): Take \(e_{a}^{*}=0\), \(e_{b}^{*}=0\), and \(e_{c}^{*}(0,0,A)=1\), \(e_{c}^{*}(0,0,B)=0\) together with \(e_{c}^{*}(1,0)=\frac{1}{2}\), \(e_{c}^{*}(0,1)=\) \(\frac{3}{4}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(0,0),(0,1),(1,0)\}\).
\(\mathcal {S}_{10}\): Take \(e_{a}^{*}=1\), \(e_{b}^{*}=0\), and \(e_{c}^{*}(1,0)=0\) while \(e_{c}^{*}(0,1)=1\). Let also \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{32}\), whereas \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{11}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(1,0),(0,1),(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
\(\mathcal {S}_{11}\): Take \(e_{a}^{*}=0\), \(e_{b}^{*}=1\), and \(e_{c}^{*}(0,1)=1\) while \(e_{c}^{*}(1,0)=0\). Let also \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{1}{32}\), whereas \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{11}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(1,0),(0,1),(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
For each \(i=1,\ldots ,11\), the strategy profile \((e_{a}^{*},e_{b}^{*},e_{c}^{*}(e_{a}^{*},e_{b}^{*}))\) belongs to \(\mathcal {S}_{i}\) but does not survive the equilibrium symmetry refinement.
1.6.2 Case \(\frac{1}{2}<v<\frac{2}{3}\)
Define
Again, \({\check{BR}}_{c}(e_{a},e_{b},t(e_{a}))\in BR_{c}(e_{a},e_{b},t(e_{a}))\).
\(\mathcal {S}_{9}\): Take \(e_{a}^{*}=0\), \(e_{b}^{*}=0\), and \(e_{c}^{*}(0,0,A)=1\), \(e_{c}^{*}(0,0,B)=0\) together with \(e_{c}^{*}(1,0)=\frac{1}{2}\), \(e_{c}^{*}(0,1)=\frac{3}{4}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\check{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(0,0),(0,1),(1,0)\}\).
\(\mathcal {S}_{12}\): Take \(e_{a}^{*}=1\), \(e_{b}^{*}=1\), and \(e_{c}^{*}(1,1,A)=\frac{1}{2}\), \(e_{c}^{*}(1,1,B)=\frac{3}{4}\) together with \(e_{c}^{*}(1,0)=0\) and \(e_{c}^{*}(0,1)=1\). Let also \(e_{c}^{*}(\frac{1}{4},\frac{3}{4})=\frac{7}{8}\), whereas \(e_{c}^{*}(\frac{3}{4},\frac{1}{4})=\frac{1}{16}\). Put \(e_{c}^{*}(e_{a},e_{b},t(e_{a}))={\check{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) for all other subgames, i.e. for \((e_{a},e_{b})\notin \{(0,1),(\frac{3}{4},\frac{1}{4}),(\frac{1}{4},\frac{3}{4})\}\).
1.6.3 Case \(v=\frac{1}{2}\)
The same examples from case \(\frac{1}{2}<v<\frac{2}{3}\) work for this case, too. \(\square\)
1.7 Proof of Proposition 4
It follows from definitions that \(\Pi '(v)\subseteq \Pi (v)\) for any v since \((\mathcal {S}_{i}\cap {\mathbb {S}}_{sym})\subseteq \mathcal {S}_{i}\) for any \(i=1,\ldots ,12\). In order to prove the proposition, for each payoff profile from \(\Pi (v)\), we find an equilibrium from\(\bigcup \limits _{i=1}^{12}\mathcal {S}_{i}\) with the same payoff profile that satisfies SYM. We will keep using notation \({\hat{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) and \({\check{BR}}_{c}(e_{a},e_{b},t(e_{a}))\) defined in the proof of Proposition 3. Consider three cases for different values of v:
1.7.1 Case \(v>\frac{2}{3}\)
According to Theorem 1, in this case, \(\Pi (v)=\{(\frac{1}{3},\frac{1}{3},\frac{1}{3}),(\frac{5}{12},\frac{5}{12},\frac{1}{6}),(\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}),(\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{1}{4}v,\frac{1}{3})\}\).
The following equilibrium from the set \(\mathcal {S}_{1}\) satisfies property SYM and ensures payoffs \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\):
The following equilibrium from the set \(\mathcal {S}_{9}\) satisfies property SYM and ensures payoffs \((\frac{5}{12},\frac{5}{12},\frac{1}{6})\):
The following equilibrium from the set \(\mathcal {S}_{10}\) satisfies property SYM and ensures payoffs \((\frac{1}{3}+\frac{1}{4}v,\frac{1}{3}-\frac{1}{4}v,\frac{1}{3})\):
The following equilibrium from the set \(\mathcal {S}_{11}\) satisfies property SYM and ensures payoffs \((\frac{1}{3}-\frac{1}{4}v,\frac{1}{3}+\frac{1}{4}v,\frac{1}{3})\):
1.7.2 Case \(\frac{1}{2}\le v<\frac{2}{3}\)
According to Theorem 2, in this case \(\Pi (v)=\{(\frac{1+v}{4},\frac{1+v}{4},\frac{1-v}{2}),(\frac{1-v}{2},\frac{1-v}{2},v)\}\).
The following equilibrium from the set \(\mathcal {S}_{9}\) satisfies property SYM and leads to payoffs \((\frac{1+v}{4},\frac{1+v}{4},\frac{1-v}{2})\):
The following equilibrium from the set \(\mathcal {S}_{12}\) satisfies property SYM and leads to payoffs \((\frac{1-v}{2},\frac{1-v}{2},v)\):
1.7.3 Case \(v=\frac{2}{3}\)
According to Theorem 3, in this case
For payoff profiles \((\frac{1}{3},\frac{1}{3},\frac{1}{3}),(\frac{5}{12},\frac{5}{12},\frac{1}{6})\), \((\frac{1}{2},\frac{1}{6},\frac{1}{3}),(\frac{1}{6},\frac{1}{2},\frac{1}{3})\), the same examples as in the case \(v>\frac{2}{3}\) would work. Analogously, for example, the payoff profile \((\frac{1}{6},\frac{1}{6},\frac{2}{3})\) can be borrowed from case \(\frac{1}{2}\le v<\frac{2}{3}\).
It remains to prove that payoffs \((\frac{1}{2},\frac{1}{3},\frac{1}{6})\) and \((\frac{1}{3},\frac{1}{2},\frac{1}{6})\) are ruled out by equilibrium symmetry refinement. Based on \(BR_{c}(e_{a},e_{b},t(e_{a}))\), \(e_{c}^{*}=0\) and \(e_{c}^{*}=1\) are the only possible actions of C on the equilibrium path. According to Theorem 3, payoff profiles \((\frac{1}{2},\frac{1}{3},\frac{1}{6}),(\frac{1}{3},\frac{1}{2},\frac{1}{6})\) happen only when \(e_{a}^{*}=e_{b}^{*}=0\). When \(e_{a}^{*}=e_{b}^{*}=0\), condition SYM is satisfied if I) \(e_{c}^{*}(0,0,A)=0\), \(e_{c}^{*}(0,0,B)=1\) or II) \(e_{c}^{*}(0,0,A)=1\), \(e_{c}^{*}(0,0,B)=0\), while cases III) \(e_{c}^{*}(0,0,A)=0\), \(e_{c}^{*}(0,0,B)=0\) and IV) \(e_{c}^{*}(0,0,A)=1\), \(e_{c}^{*}(0,0,B)=1\) are impossible. Both I) and II) lead to payoffs \((\frac{5}{12},\frac{5}{12},\frac{1}{6})\). \(\square\)
1.8 Proof of Proposition 5
1.8.1 Plan of the proof
We separately consider cases \(\frac{1}{2}\le v<\frac{2}{3}\) and \(v>\frac{2}{3}\). For both cases, the proof is carried out as follows:
-
1.
Equilibria from set \({{\mathcal {S}}}_{9}\) do not pass the refinement (see Definition 3):
-
(a)
We suggest a subgame \((e_{a},e_{b},t(e_{a}))\) and a set \({\tilde{S}}\) of actions in this subgame to be deleted. Note that we choose such \({\tilde{S}}\) that the strategy profile corresponding to \({{\mathcal {S}}}_{9}\) does not exist in \({\tilde{\beta }}\) anymore.
-
(b)
We show that at least one equilibrium of game \(\beta\) not belonging to set \({{\mathcal {S}}}_{9}\) is still an equilibrium in game \({\tilde{\beta }}\). It means that the set of SPE of game \({\tilde{\beta }}\) is non-empty.
-
(c)
We show that all equilibria of game \(\beta\), which are still equilibria in \({\tilde{\beta }}\), give a higher payoff to team C compared to what team C had in any equilibria from set \({{\mathcal {S}}}_{9}\) in game \(\beta\).
-
(d)
We show that there does not exist a new (that is, not corresponding to any equilibrium in \(\beta\)) equilibrium in \({\tilde{\beta }}\) which gives C a payoff, which is smaller or equal to that in \({{\mathcal {S}}}_{9}\).
-
(a)
-
2.
We show that the remaining equilibria pass the refinement by proving that for any subgame \((e_{a},e_{b},t(e_{a}))\) and set \({\tilde{S}}\), there does not exist an SPE in \({\tilde{\beta }}\) such that team C’s payoff is higher in this SPE than in equilibrium of \(\beta\) in consideration.
1.8.2 Case \(\frac{1}{2}\le v<\frac{2}{3}\)
First, consider case \(\frac{1}{2}\le v<\frac{2}{3}\). The only possible classes of equilibria in \(\beta\) are \({{\mathcal {S}}}_{9}\) and \({{\mathcal {S}}}_{12}\).
(1) We are going to prove now that \({{\mathcal {S}}}_{9}\) does not pass the refinement.
(1a) Consider \(e_{a}=0\), \(e_{b}=1\), and \({\tilde{S}}(0,1)=[0,1)\). In other words, we delete all actions other than \(e_{c}^{*}(0,1)=1\) in subgame \((e_{a},e_{b})=(0,1)\).
(1b) The strategy profiles from set \({{\mathcal {S}}}_{12}\) are still available in \({\tilde{\beta }}\) because team C can still play \(e_{c}^{*}(0,1)=1\) in subgame \((e_{a},e_{b})=(0,1)\). In subgame \((e_{a},e_{b})=(0,1)\) team C does not have a profitable deviation since \(e_{c}^{*}(0,1)=1\) is the only action. Team C does not have a profitable deviation in any other subgame because such \({\tilde{\beta }}\) shares actions and payoffs with \(\beta\), and the same arguments as in Theorem 2 work. Teams A and B do not have a profitable deviation from subgame \((e_{a},e_{b})=(1,1)\) to any other subgame than \((e_{a},e_{b})=(0,1)\) because otherwise it would be a profitable deviation from the equilibria in game \(\beta\). For team A, deviation from the subgame \((e_{a},e_{b})=(1,1)\) to the subgame \((e_{a},e_{b})=(0,1)\) is not profitable because in \((e_{a},e_{b},e_{c})=(0,1,1)\) team A gets \(\frac{1}{4}(\frac{1}{3}+1-v)=\frac{1}{3}-\frac{1}{4}v\) which is less than the payoff of \(\frac{1-v}{2}\) that team A gets in \({{\mathcal {S}}}_{12}\). Therefore, the set of SPE of game \({\tilde{\beta }}\) is non-empty.
(1c) All equilibria of game \(\beta\), which are not in \({{\mathcal {S}}}_{9}\), are from \({{\mathcal {S}}}_{12}\). Those equilibria give a maximum payoff of v to team C, which is larger than \(\frac{1-v}{2}\) that team C had in any equilibria from the set \({{\mathcal {S}}}_{9}\).
(1d) According to Fig. 1 and Table 3, \(\frac{1-v}{2}\) is the lowest possible payoff for team C. In \({\tilde{\beta }}\), it can happen only in the subgame \((e_{a},e_{b})=(0,0)\). Since \(e_{c}^{*}(0,1)=1\) in \({\tilde{\beta }}\), any profile with \((e_{a},e_{b})=(0,0)\) is not an equilibrium because team B would deviate to \(e_{b}=1\) in order to get payoff of \(\frac{1}{3}+\frac{1}{4}v\) instead of \(\frac{1+v}{4}\).
It follows from (1a), (1b), (1c), and (1d) that \({{\mathcal {S}}}_{9}\) does not pass the refinement by Definition 3.
(2) \({{\mathcal {S}}}_{12}\) leaves team C with the maximal possible payoff of v. Thus, it is impossible for C to get a higher payoff in some game \({\tilde{\beta }}\). By definition of the refinement concept, it means that \({{\mathcal {S}}}_{12}\) survives.
1.8.3 Case \(v>\frac{2}{3}\)
Now consider case \(v>\frac{2}{3}\). The set of all equilibria of \(\beta\) consists of sets \({{\mathcal {S}}}_{1}-{{\mathcal {S}}}_{11}\).
(1) We are going to prove now that \({{\mathcal {S}}}_{9}\) does not pass the refinement.
(1a) Let \(e_{a}=0\), \(e_{b}=1\), and \({\tilde{S}}(0,1)=[0,1)\). Again, team C must play \(e_{c}^{*}(0,1)=1\) now in the subgame since this is the only option.
(1b) Let \(e_{a}=\frac{3}{4}\), \(e_{b}=\frac{1}{4}\). Without any restrictions on actions that team C can choose, all strategy profiles from \({{\mathcal {S}}}_{6}\) satisfying the property \(e_{c}^{*}(0,1)=1\) will still be equilibria in \({\tilde{\beta }}\). Thus, the set of SPE of game \({\tilde{\beta }}\) is non-empty.
(1c) All equilibria of game \(\beta\) not belonging to \({{\mathcal {S}}}_{9}\) give team C the payoff of \(\frac{1}{3}\), which is larger than \(\frac{1}{6}\), the C’s payoff in \({{\mathcal {S}}}_{9}\).
(1d) Figure 3 shows all possible payoffs after certain actions of teams A and B and the best response of team C in \(\beta\). One can see that \(\frac{1}{6}\) is the lowest possible payoff after any actions of A and B and the best response of C. Thus, the only possible strategy profiles in \({\tilde{\beta }}\) which could give the payoff smaller or equal than \(\frac{{1}}{6}\) are those containing \((e_{a},e_{b})=(0,0)\). Since \(e_{c}^{*}(0,1)=1\) in any strategy profile in C, no profile with \((e_{a},e_{b})=(0,0)\) is an equilibrium. Team B would like to deviate by playing \(e_{b}=1\) in order to get a payoff of \(\frac{1}{3}+\frac{1}{4}v\) instead of \(\frac{5}{12}\).
(2) The only possible payoff larger than \(\frac{1}{3}\) that team C can get is v (see Figure 3 and Table 5). Team C can achieve the payoff of v only inside triangles PMR, RMN, inside interval RM, and in point M. We will demonstrate that these points cannot be part of some equilibrium of game \({\tilde{\beta }}\). Figure 3 and Table 5 are useful in understanding possible payoffs in \({\tilde{\beta }}\) because what team C can do is to choose a subset of payoffs in every point of Figure 3.
For any point inside PMR or RMN, the team which gets 0 (either A or B) has a deviation to a point inside triangle PNO by playing \(e_{a}^{*}=(1-e_{a})/2\) instead of \(e_{a}\) for team A or \(e_{b}^{*}=(1-e_{b})/2\) instead of \(e_{b}\) for team B. This deviation allows it to get the payoff of at least \(\frac{1}{3}\). The same deviations work from points on the interval RM.
For equilibria involving point M in any game \({\tilde{\beta }}\), the only possible deviations for teams A and B are to points P or N. According to the refinement concept, team C can restrict actions and possible payoffs in these subgames, but it cannot enlarge the set of possible payoffs since only the deletion of actions is possible. Thus a deviation of team A from \((e_{a},e_{b})=(1,1)\) to \((e_{a},e_{b})=(0,1)\) would yield the payoff of either \(\frac{1}{3}\) or \(\frac{1}{3}-\frac{1}{4}v\) which are both bigger than \(\frac{1-v}{2}\). Thus, team A always has a profitable deviation from M, and all equilibria involving \((e_{a},e_{b})=(1,1)\) are not possible in any \({\tilde{\beta }}\).
It follows that in any \({\tilde{\beta }}\) team C’s equilibrium payoff cannot exceed \(\frac{1}{3}\). Then, by definition, all equilibria from the sets \({{\mathcal {S}}}_{1}-{{\mathcal {S}}}_{8}\), \({{\mathcal {S}}}_{10}\), \({{\mathcal {S}}}_{11}\) pass the equilibrium choice refinement. \(\square\)
Appendix B
This Appendix contains formal consideration of non-generic triples of effort budgets \((1,\beta ,\gamma )\). We start by considering the case of a low first prize, \(v\in \left[ \frac{1}{2};\frac{2}{3}\right)\).
1.1 Low first prize: \(v\in \left[ \frac{1}{2};\frac{2}{3}\right)\)
For convenience, please refer to Fig. 6 to facilitate visual representation of cases.
Since \(\beta \geqslant 1\), the possible types of non-generic triples of effort budgets are:
-
1.
\(\beta =\gamma =1\) (Theorem 2);
- 2.
-
3.
\(\gamma =1\) and \(\beta \ne 1\) (Proposition 13, Proposition 15, part 1), and Proposition 16, part 1));
-
4.
\(\beta =\gamma \ne 1\) (Proposition 16, part 2));
-
5.
\(\beta =\gamma +1\) (Proposition 14 and Proposition 15, part 2));
-
6.
\(\gamma =\beta +1\) and \(\beta \ne 1\) (Proposition 7, part 3)).
The first case, \(\beta =\gamma =1\), was considered in Theorem 2. Next, we prove several auxiliary propositions for case 2 (\(\beta =1\) and \(\gamma \ne 1\)).
1.1.1 Symmetric teams A and B: \(\beta =1\) and \(\gamma \ne 1\)
First, assume that \(0<\gamma <1\).
Proposition 11
Suppose \(0<\gamma <1\). Then, the set of all equilibrium payoffs is:
-
1.
\(\varnothing\), if \(v\in \left[ \frac{1}{2},\frac{5}{9}\right)\);
-
2.
\(\left\{ \left( \frac{1+v}{4},\frac{1+v}{4},\frac{1-v}{2}\right) \right\}\), if \(v\in \left[ \frac{5}{9},\frac{2}{3}\right)\).
Proof
Fix a strategy profile that includes a pair of teams’ A and B strategies \((e_{a},e_{b})\). Since teams A and B are symmetric, it is enough to consider subgames with \(e_{a}\ge e_{b}\).
If \(e_{b}>1-\gamma\), team C can guarantee the payoff of \(1-v\) by defeating the winner of the first match. A and B can guarantee the equilibrium payoff of \(\frac{1}{3}\) by deviating to \(e_{a}^{*}=0\) or to \(e_{b}^{*}=0\), respectively (at those subgames, C is able to defeat the winner of the first match, but not the loser). Therefore, in SPE, the teams should get at least \(\frac{1}{3}+\frac{1}{3}+1-v>1\) altogether, which is impossible. Thus, there are no equilibria with \(e_{b}>1-\gamma\).
Suppose \(e_{a}>e_{b}=1-\gamma\). When \(e_{a}<1\), team C can either defeat A and lose to B or lose to A and exert the same effort as B in their game. The first option is better for C since it brings the payoff of \(\frac{1}{3}\) compared to the payoff of \(\frac{1}{2}(1-v)\) for the second option. Such a strategy of team C will lead to equal payoffs for all teams. In this scenario, B can deviate to \(e_{b}^{*}=1\), which would bring B the payoff of \(1-v\) (C would defeat both teams, and B wins over A). Therefore, there are no equilibria with \(1>e_{a}>e_{b}=1-\gamma\). When \(e_{a}=1\), team C has two options: to defeat A and lose to B or exert the same effort as the opponent in both games. The first option leads to the payoffs of \(\frac{1}{3}\) for all three teams. This is not an SPE: team A would be better off by playing \(e_{a}^{*}=0\), forcing team C to spend all effort in a match against B and leading to the payoff of \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot (1-v)=\frac{2}{3}-\frac{v}{2}>\frac{1}{3}\) for A. In the second option, the payoffs are \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\), and team B would be able to increase the payoff up to \(\frac{1}{3}\) by deviating to \(e_{b}^{*}=0\). To conclude, there are no SPE if \(e_{a}>e_{b}=1-\gamma\).
Now consider the case \(e_{a}=e_{b}=1-\gamma\). Team C should exert all effort in one of the matches. In the case of equalizing the effort of the winner of the first match, team C gets \(\frac{1}{6}\), while in the case of equalizing the effort of the loser of the first match, team C gets \(\frac{1}{2}(1-v)\). Since \(\frac{1}{2}(1-v)>\frac{1}{6}\), team C would prefer the latter, and the teams would get the ex-ante payoff of \(\left( \frac{1}{4}+\frac{v}{4},\frac{1}{4}+\frac{v}{4},\frac{1}{2}-\frac{v}{2}\right)\). Team A can consider deviation to \(e_{a}^{*}=0\). In this case, team C will spend all effort in a match against B, leading to the payoff of \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot (1-v)=\frac{2}{3}-\frac{v}{2}\) for A. It is easy to check that \(\frac{2}{3}-\frac{v}{2}>\frac{1}{4}+\frac{v}{4}\) iff \(v<\frac{5}{9}\), and there are no SPE if \(v<\frac{5}{9}\). If \(v\in \left[ \frac{5}{9},\frac{2}{3}\right)\), the strategy profile with \(e_{a}=e_{b}=1-\gamma\) leads to SPE: there are no incentives for A and B either to decrease the effort and lose the first game or to win the first game and get only \(\frac{1}{3}\) after losing the second.
The remaining case is \(e_{b}<1-\gamma\).
If \(e_{a}>1-\gamma >e_{b}\), C decides to defeat the winner of the first match, A, and the resulting payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). It cannot form an SPE because A can deviate to \(e_{a}^{*}=e_{b}\), getting the payoff of \(\frac{1}{2}\) (C would lose both matches, and A and B would exert the same effort in their match).
If \(e_{a}=1-\gamma >e_{b}\), team C’s best response is to exert all effort in the match against A, meaning that the expected payoff of team A is less than v. However, A can deviate to \(e_{a}^{*}=\frac{1-\gamma +e_{b}}{2}\), win both matches, and get the payoff of v.
If \(1-\gamma >e_{a}\ge e_{b}\), team C loses both games, and team B gets no more than \(\frac{1}{2}\). However, B can deviate to \(e_{b}^{*}=\frac{e_{a}+1-\gamma }{2}\) to win both games with certainty and get the payoff of v. Thus, there are no equilibria with \(e_{b}<1-\gamma\). \(\square\)
Now consider the case \(\gamma >1\).
Proposition 12
Suppose \(\gamma >1\). Then, the set of all equilibrium payoffs is \(\left\{ \left( \frac{1-v}{2},\frac{1-v}{2},v\right) \right\}\).
Proof
Fix a strategy profile that includes a pair of teams’ A and B strategies \((e_{a},e_{b})\). Note that team C can guarantee the payoff of \(1-v\) by winning over the loser of the first match. If \(e_{a}<1\) and \(e_{b}<1\), teams A and B can also guarantee the equilibrium payoff of \(1-v\) by spending all effort in the first match (C wins both matches in this case). Since \(3(1-v)>1\), there are no equilibria with \(e_{a}<1\) and \(e_{b}<1\).
If \(e_{a}=1\) and \(e_{b}<1\), C gets v by exerting \(\gamma -1\) in a match against A and 1 in a match against B. Thus, B loses to A and C and gets 0. However, B can deviate to \(e_{b}^{*}=1\) and get a positive payoff by collecting the second prize with the probability of 0.5. No equilibria in this case. The case of \(e_{a}<1\), \(e_{b}=1\) is symmetric.
If \(e_{a}=1\) and \(e_{b}=1\), C wins both matches, and the resulting payoff profile is \(\left( \frac{1-v}{2},\frac{1-v}{2},v\right)\). These strategies lead to SPE because, for both A and B, a decrease of effort in the first game would result in a loss as well as a zero payoff (C wins both matches in any of the subgames \((e_{a}^{*},1)\) and \((1,e_{b}^{*})\). \(\square\)
Propositions 11 and 12 provide a full characterization of the case \(\beta =1\), \(\gamma \ne 1\). Further, we will assume that \(\beta >1\).
1.1.2 Asymmetric teams A and B: \(\beta >1\)
We will organize consideration of non-generic cases by decreasing the value of \(\beta\): we will start with the case \(\beta >\gamma +1\), continue with the case \(\beta =\gamma +1\), and finish with the case \(\beta <\gamma +1\). If \(\beta >\gamma +1\), then the only non-generic case is \(\gamma =1\).
Proposition 13
Suppose \(\gamma =1\) and \(\beta >\gamma +1=2\). Then, the set of all equilibrium payoffs is \(\left\{ \left( \frac{1-v}{2},v,\frac{1-v}{2}\right) \right\}\).
Proof
Team B has a strategy that allows it to win in both matches, for example, \(e_{b}=1+\frac{\beta -(\gamma +1)}{2}\). It guarantees the payoff of v. Both A and C can each guarantee at least \(\frac{1-v}{2}\) by playing \(e_{a}=1\) and \(e_{c}=\gamma =1\), respectively. Since the sum of guaranteed payoffs for all players is 1 \(\left( \frac{1-v}{2}+v+\frac{1-v}{2}=1\right)\), the payoff profile \(\left( \frac{1-v}{2},v,\frac{1-v}{2}\right)\) is the only one that can happen in equilibrium. It does happen when \((e_{a},e_{b})=\left( 1,\frac{\beta }{2}\right)\). \(\square\)
Now assume that \(\beta =\gamma +1\).
Proposition 14
Suppose \(\beta =\gamma +1\) and \(\gamma >1\). Then, the set of all equilibrium payoffs is:
-
1.
\({\left\{ (0,v,1-v),\left( \frac{1}{6},\frac{v}{2}+\frac{1}{6},\frac{2}{3}-\frac{v}{2}\right) ,\left( \frac{1}{6}+\frac{v}{8},\frac{1}{6}+\frac{3v}{8},\frac{2}{3}-\frac{v}{2}\right) \right\} }\), if \(v\in \left[ \frac{20}{33};\frac{2}{3}\right)\);
-
2.
\({\left\{ (0,v,1-v),(0,1-v,v),\left( \frac{1}{6},\frac{v}{2}+\frac{1}{6},\frac{2}{3}-\frac{v}{2}\right) \right\} }\), if \(v\in \left[ \frac{5}{9},\frac{20}{33}\right)\);
-
3.
\({\{(0,v,1-v),(0,1-v,v)\}}\), if \(v\in \left[ \frac{1}{2},\frac{5}{9}\right)\).
Proof
First, if \(e_{a}=e_{b}=1\), there are two possible outcomes of a tie-break in a match between A and B. If B wins, team C will be strictly better off by defeating team A resulting in the payoffs of \((0,v,1-v)\). If A wins, then two alternatives are equally good for team C:
(1) to defeat A and lose to B. In this case, the payoff vector is \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\);
(2) to equalize the opponents’ effort in both matches, which leads to payoffs of \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\).
Depending on the choice of team C’s strategy, the ex-ante payoffs will be \(\left( \frac{1}{6},\frac{v}{2}+\frac{1}{6},\frac{2}{3}-\frac{v}{2}\right)\) or \(\left( \frac{1}{6}+\frac{v}{8},\frac{1}{6}+\frac{3v}{8},\frac{2}{3}-\frac{v}{2}\right)\). There are no profitable deviations for team A. As for team B, it can get the payoff of \(1-v\) by defeating team A. Note that \(\frac{v}{2}+\frac{1}{6}\ge 1-v\) iff \(v\ge \frac{5}{9}\), and \(\frac{1}{6}+\frac{3v}{8}\ge 1-v\) iff \(v\ge \frac{20}{33}\).
Second, if \(e_{a}=1\) and \(e_{b}>1\), team C wins both games, and the corresponding payoffs are \((0,1-v,v)\). These payoffs can be supported in SPE for \(v\in \left[ \frac{1}{2},\frac{20}{33}\right)\).
Third, if \(e_{a}=1\) and \(e_{b}<1\), it is not an SPE: team B gets only \(\frac{1}{3}\).
Last, if \(e_{a}<1\), team B wins both matches with certainty, whereas team C secures a win over A. The resulting payoffs are \((0,v,1-v)\). These payoffs can be supported in equilibrium, for example, when \((e_{a},e_{b})=\left( 0,\frac{3}{2}\right)\). Team C will defeat team A on the equilibrium path, for example, by spending \(\gamma\) in a match against A and 0 in a match against B. Team B does not have a profitable deviation since it already gets the maximal payoff, and team C does not have a profitable deviation by construction. Let’s now prove that A does not have a profitable deviation. For team A to have a profitable deviation, it should be able to at least exert the same amount of effort as C there (because B already spends more effort for a match with A than A’s total efforts). If A deviates to \(e_{a}^{*}\in \left( 0,\frac{1}{2}\right)\), and then if C exerts either more or the same against either of team A or B, C will lose its other match. In this case, the best option is to win against the loser of the first match, A, which results in payoffs of (\(0,v,1-v\)). Such payoffs ensure that this is not a profitable deviation for A. If A deviates to \(e_{a}^{*}\in \left( \frac{1}{2},1\right]\), then C can win both matches with certainty, resulting in payoff \((0,1-v,v)\), making it not a profitable deviation for A. If A deviates to \(e_{a}^{*}=\frac{1}{2}\), then C chooses between either winning against A or B for sure or spending equal efforts in matches with both. Winning against A yields \(1-v\), winning against B brings \(\frac{1}{3}\), equalizing the efforts gives C \(\frac{1}{4}\left( v+1-v+\frac{1}{3}+0\right) =\frac{1}{3}\), and thus C will choose to win against A resulting in payoffs of \((0,1-v,v)\), which is again not a profitable deviation for A. Thus, A does not have a profitable deviation, and \((0,v,1-v)\) is an equilibrium payoff. \(\square\)
Proposition 15
Suppose \(\beta =\gamma +1\) and \(\gamma \le 1\). Then, the set of all equilibrium payoffs is:
-
1.
\(\{(\frac{1-v}{2},v,\frac{1-v}{2})\}\), if \(\gamma =1\);
-
2.
\(\{(1-v,v,0)\}\) , if \(\gamma <1\).
Proof
(1) First, consider the case \(\gamma =1\), \(\beta =2\). Fix a pair of strategies \((e_{a},e_{b})\).
Let \(0<e_{a}<1\). If \((e_{a},e_{b})\) is a part of some SPE, then B can guarantee the payoff of v by playing \(e_{b}^{*}=\frac{1+e_{a}}{2}\). For all subgames with \(0<e_{a}<1\) and two wins for B, C can guarantee the payoff of \(1-v\) by playing \(e_{c}(e_{a},e_{b})=1\) and winning against A. It leads to the zero equilibrium payoff for A because the sum of prizes cannot exceed 1. However, A would deviate from all such subgames by playing \(e_{a}=0\), bringing a positive payoff since A exerts at least the same effort as C in their match. Thus, there are no equilibria with \(0<e_{a}<1\).
If \(e_{a}=0\), B also wins both matches with certainty. Thus, C’s best response in such games is to spend all effort in the match against A, because otherwise C is left with a zero payoff. It leads to the only possible equilibrium payoff profile \(\left( \frac{1-v}{2},v,\frac{1-v}{2}\right)\). A pair \((e_{a},e_{b})=(0,1)\) together with team C’s best response indeed lead to SPE. Team C spends all effort in a match against A on the equilibrium path. There are no reasons for A or C to equalize the effort of team B since the expected payoff will decrease from \(\frac{1-v}{2}\) to \(\frac{1}{6}\). Team B does not have profitable deviations because it already gets the maximal payoff.
Suppose \(e_{a}=1\).
When \(e_{a}=1\) and \(e_{b}<1\), the resulting payoff profile is \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) since C would choose to defeat A. Still, B plays suboptimally because deviating to \(e_{b}^{*}=1\) yields \(\frac{v}{2}+\frac{1}{6}\ge \frac{5}{12}>\frac{1}{3}\).
When \(e_{a}=1\) and \(e_{b}>1\), the payoff profile is \((0,1-v,v)\) since \(e_{c}(1,e_{b})=\frac{e_{b}-1}{2}\) allows team C to win both matches. Team A plays suboptimally because deviation to \(e_{a}^{*}=0\) allows it to get \(\frac{1-v}{2}\).
When \(e_{a}=1\) and \(e_{b}=1\), the payoff profile is \(\left( \frac{1}{6},\frac{v}{2}+\frac{1}{6},\frac{2}{3}-\frac{v}{2}\right)\) after team C’s win over A (this brings a higher payoff to C than \(e_{c}=0\), which brings \(\frac{1}{3}\)).
Thus, there are no equilibria with \(e_{a}=1\).
(2) Second, when \(\gamma <1\), team B can win both matches, while A can defeat C by playing \(e_{a}=0\). This leads to payoffs \((1-v,v,0)\). These payoffs can be supported in SPE, for example, if \((e_{a},e_{b})=\left( 0,1-\frac{\gamma }{2}\right)\). Obviously, team A cannot get more than the prize for second place, \(1-v\). \(\square\)
The next proposition deals with the case \(\beta <\gamma +1\).
Proposition 16
Suppose \(1<\beta <\gamma +1\). Then, the set of all equilibrium payoffs is:
-
1.
\(\varnothing\), if \(\gamma =1\).
-
2.
\(\{(0,1-v,v)\}\), if \(\gamma =\beta\).
The proof of Proposition 16 repeats all arguments from the proof of Proposition 7, so we omit it for the sake of brevity. To conclude the formal consideration of non-generic cases when the first prize is low, note that case 6) (\(\gamma =\beta +1\)) follows from Proposition 7, part 3).
1.2 High first prize: \(v\in \left( \frac{2}{3};1\right)\)
For convenience, please refer to Figure 7 to facilitate visual representation of cases.
The list of types of non-generic triples of effort includes the following cases:
-
1.
\(\beta =\gamma =1\) (Theorem 1);
- 2.
-
3.
\(\gamma =1\) and \(\beta \ne 1\) (Proposition 21);
-
4.
\(\beta =\gamma \ne 1\) (Proposition 23);
- 5.
-
6.
\(\gamma =\beta +1\) and \(\beta \ne 1\) (Proposition 10, part 1)).
The first case, \(\beta =\gamma =1\), was considered in Theorem 1. Next, we prove several auxiliary propositions for case 2 (\(\beta =1\) and \(\gamma \ne 1\)).
1.2.1 Symmetric teams A and B: \(\beta =1\) and \(\gamma \ne 1\)
Proposition 17
Suppose \(0<\gamma <1\). Then, the set of all equilibrium payoffs is \(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{5}{12},\frac{5}{12},\frac{1}{6}\right) \right\}\).
Proof
Fix a strategy profile that includes a pair of teams’ A and B strategies \((e_{a},e_{b})\). Since teams A and B are symmetric, it is enough to consider subgames with \(e_{a}\ge e_{b}\).
Let \(e_{b}>1-\gamma\). Team C can guarantee the payoff of \(\frac{1}{3}\) by defeating the winner of the first match. A and B can guarantee the payoff of \(\frac{1}{3}\) by deviating to \(e_{a}^{*}=0\) or \(e_{b}^{*}=0\), respectively (after such deviation, C would only be able to defeat the winner but not the loser of the first match). Thus, the teams should get \(\frac{1}{3}\) in such equilibrium. The payoff vector \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) can be supported in equilibrium if \(e_{a}=1-\frac{3}{4}\gamma\) and \(e_{b}=1-\frac{4}{5}\gamma\). In this case, A defeats B, C chooses to defeat A and lose to B, so all teams get \(\frac{1}{3}\). There are no profitable deviations: C can always defeat the winner of the first match, so neither A nor B can get more than \(\frac{1}{3}\) in equilibrium.
If \(e_{a}>e_{b}=1-\gamma\), team C would prefer to defeat A and get \(\frac{1}{3}\). The only possible payoff vector in SPE is \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). We already demonstrated that this payoff vector is realized in some (other) SPE.
If \(e_{a}=e_{b}=1-\gamma\), team C would be able to equalize the effort of the opponent in one of the matches. It is better to equalize the winner’s effort, which leads to the payoffs \(\left( \frac{5}{12},\frac{5}{12},\frac{1}{6}\right)\). Neither A nor B has incentives to deviate: decreasing the effort in the first game leads to the payoff of \(\frac{2}{3}-\frac{v}{2}<\frac{5}{12}\), whereas increasing the effort in the first game leads to the payoff of \(\frac{1}{3}<\frac{5}{12}\).
If \(e_{a}>1-\gamma >e_{b}\), team C would defeat A and lose to B, which yields the payoff of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). We already demonstrated that this payoff vector is realized in some (other) SPE.
Let \(e_{a}=1-\gamma >e_{b}\). Team C’s best response is to exert all effort in the match against A, which means that the expected payoff of A is less than v. Still, A can deviate to \(e_{a}^{*}=\frac{1-\gamma +e_{b}}{2}\), win both matches and get the payoff of v. No equilibria in this case.
Finally, if \(1-\gamma >e_{a}\ge e_{b}\), team C loses both games. Team B gets less than v but can deviate to \(e_{b}^{*}=\frac{e_{a}+1-\gamma }{2}\), win both games with certainty, and get the payoff of v. No equilibria in this case. \(\square\)
The case \(\gamma =1\) was considered in Section 3.
Proposition 18
Suppose \(1<\gamma <2\). Then, the set of all equilibrium payoffs is:
-
1.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1-v}{2},\frac{1-v}{2},v\right) \right\}\), if \(v\in \left( \frac{2}{3},\frac{8}{9}\right)\);
-
2.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1-v}{2},\frac{1-v}{2},v\right) ,\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) \right\}\), if \(v\in \left[ \frac{8}{9},1\right)\).
Proof
Fix a strategy profile that includes a pair of teams’ A and B strategies \((e_{a},e_{b})\). Team C guarantees the payoff of at least \(\frac{1}{3}\) in equilibrium by defeating the winner of the match between A and B.
Let \(e_{a}+e_{b}>2-\gamma\). In this case, C wins both matches. Thus, if \(e_{a}>e_{b}\), the payoffs are \((1-v,0,v)\); if \(e_{a}=e_{b}\), the payoffs are \(\left( \frac{1-v}{2},\frac{1-v}{2},v\right)\); if \(e_{a}<e_{b}\), the payoffs are \((0,1-v,v)\). A or B cannot get 0 in equilibrium, because the last-placed team can deviate by playing the same strategy as the opponent in the first match, which ensures at least \(\frac{1-v}{2}\). Payoffs \(\left( \frac{1-v}{2},\frac{1-v}{2},v\right)\) can be supported in SPE: consider \((e_{a},e_{b})=(1,1)\), \(e_{c}(1,1,A)=\frac{1+\gamma }{2}\), \(e_{c}(1,1,B)=\frac{1+\gamma }{2}\), \(e_{c}(1,e_{b}^{*})=\frac{\gamma -1}{2}\) for every \(e_{b}^{*}\in [0,1)\), and \(e_{c}(e_{a}^{*},1)=\frac{\gamma +1}{2}\) for every \(e_{a}^{*}\in [0,1)\). In this case, neither A nor B are interested in decreasing effort in the first game, because they would lose both games.
Suppose \(e_{a}+e_{b}<2-\gamma\). Team C’s budget of effort allows it to win one and only one match, so team C’s best response is to defeat the winner of the match between A and B. This leads to the payoffs of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). The latter payoff vector can be supported in SPE. For example, consider strategies \(e_{a}=e_{b}=0\). All teams get the payoff of \(\frac{1}{3}\) (C always defeats the winner of the first match). Neither A nor B are interested in increasing effort in the first game because a win in the first game will be followed by a loss in the second, with the payoff not exceeding \(\frac{1}{3}\).
The last case is \(e_{a}+e_{b}=2-\gamma\). If \(e_{a}>e_{b}\), then C has two options: either to spend all efforts against team A, the winner of the first match, or equalizing efforts with both teams. The former action leads to the payoffs of \(\frac{1}{3}\) for all teams, whereas the latter leads to the payoffs \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\). Payoffs \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) can be supported in the following SPE: \((e_{a},e_{b})=(2-\gamma ,0)\) with \(e_{c}(2-\gamma ,0)=\gamma\). Indeed, if A or B increases the effort in the first match, C wins both matches, so deviation leads to a lower payoff for A or B. If A decreases the effort in the first match, C defeats the winner of the first match, leading to the payoffs \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) — not a profitable deviation for A. Payoffs \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\) can be supported for any \(v\ge \frac{8}{9}\) in the following SPE: \((e_{a},e_{b})=(2-\gamma ,0)\) with \(e_{c}(2-\gamma ,0)=\gamma -1\). A has no incentives to deviate: choosing another strategy would result in a payoff of either \(\frac{1}{3}\) or \(1-v\). Team B can get \(1-v\) by deviating to \(e_{b}^{*}=1\). This deviation is profitable iff \(v<\frac{8}{9}\). Other deviations of team B would not result in a higher payoff. If \(v<\frac{8}{9}\), then payoffs \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\) cannot be supported in SPE: a deviation to \(e_{b}^{*}=1\) allows team B to get \(1-v>\frac{1}{3}-\frac{v}{4}\).
The logic is similar for the case \(e_{a}<e_{b}\) and the payoff vector \(\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right)\).
When \(e_{a}=e_{b}=1-\frac{\gamma }{2}\), there could not be any equilibrium payoffs aside from \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) because C guarantees the payoff of \(\frac{1}{3}\) by defeating the winner of the first game, whereas A and B can guarantee the payoff of \(\frac{1}{3}\) by deviating to \(e_{a}^{*}=0\) or \(e_{b}^{*}=0\), respectively. \(\square\)
Proposition 19
Suppose \(\gamma =2\). Then, the set of all equilibrium payoffs is:
-
1.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1-v}{2},\frac{1-v}{2},v\right) \right\}\), if \(v\in \left( \frac{2}{3},\frac{16}{21}\right)\);
-
2.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1-v}{2},\frac{1-v}{2},v\right) ,\left( \frac{1}{3}+\frac{1}{8}v,\frac{1}{3}-\frac{1}{8}v,\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{1}{8}v,\frac{1}{3}+\frac{1}{8}v,\frac{1}{3}\right) \right\}\), if \(v\in \left[ \frac{16}{21},1\right)\).
Proof
Fix a strategy profile that includes a pair of teams’ A and B strategies \((e_{a},e_{b})\). First, consider the case \(e_{a}>0\) and \(e_{b}>0\). In this case, C can defeat both teams with certainty and get the payoff of v. Teams A and B can guarantee the payoff of \(\frac{1-v}{2}\) by exerting all efforts in the first match because, in such a subgame, C would win both matches, and the team that exerts all effort in the first match ensures at least half of the second prize. Thus, the only possible equilibrium payoff vector is \(\left( \frac{1-v}{2},\frac{1-v}{2},v\right)\). It can be supported in equilibrium, for example, with \((e_{a},e_{b})=(1,1)\). Decreasing \(e_{a}\) or \(e_{b}\) is not profitable for A or B, respectively, because such a decrease leads to a zero payoff.
If \(e_{a}=0\) and \(e_{b}>0\), then it is not an equilibrium: A gets zero payoff and would deviate to \(e_{a}^{*}=1\) in order to get a positive payoff. Similarly, if \(e_{a}>0\) and \(e_{b}=0\), then \((e_{a},e_{b})\) is not a part of some SPE.
If \(e_{a}=e_{b}=0\), then C is indifferent between defeating the winner of the first match and equalizing the efforts of both teams. There are four types of the corresponding best responses of team C:
(a) \(e_{c}(0,0,A)=1\) and \(e_{c}(0,0,B)=1\), the payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\);
(b) \(e_{c}(0,0,A)=1\) and some \(e_{c}(0,0,B)<1\), the payoffs are \(\left( \frac{1}{3}+\frac{v}{8},\frac{1}{3}-\frac{v}{8},\frac{1}{3}\right)\);
(c) some \(e_{c}(0,0,A)>1\) and \(e_{c}(0,0,B)=1\), the payoffs are \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\);
(d) some \(e_{c}(0,0,A)>1\) and some \(e_{c}(0,0,B)<1\), the payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\).
Best responses of types a) and d) lead to SPE: deviations of A and B would always only lead to the payoff of \(1-v<\frac{1}{3}\) for the deviator. Best responses of types b) and c) lead to SPE iff deviations of A and B do not yield a higher payoff, i.e. when \(\frac{1}{3}-\frac{v}{8}\ge 1-v\), or \(v\ge \frac{16}{21}\). \(\square\)
Proposition 20
Suppose \(\gamma >2\). Then, the set of all equilibrium payoffs is \(\left\{ \left( \frac{1-v}{2},\frac{1-v}{2},v\right) \right\}\).
Proof
Team C wins both games with certainty. The distribution of the rest of the prize is between A and B and is based on the result of their match. Both teams will exert maximal effort in the first match resulting in the payoffs \(\left( \frac{1-v}{2},\frac{1-v}{2},v\right)\). \(\square\)
1.2.2 Asymmetric teams A and B: \(\beta >1\)
Now we move to cases when teams A and B are asymmetric.
Proposition 21
Suppose \(\gamma =1\) and \(\beta >\gamma +1=2\). Then, the set of all equilibrium payoffs is \(\{(\frac{1-v}{2},v,\frac{1-v}{2})\}\).
Proof
Note that the arguments from the proof of Proposition 13 can be repeated for this case. \(\square\)
The next possible case is \(1<\gamma =\beta\).
Proposition 22
Suppose \(1<\gamma =\beta\). If \(e_{a}\ge \beta -\gamma =0\) and \(e_{b}>\beta -\gamma =0\), then any SPE that contains \((e_{a},e_{b})\) leads to the payoff vector that belongs to the set:
-
1.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( 0,1-v,v\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) \right\}\), if \(v\in \left( \frac{2}{3},\frac{8}{9}\right)\);
-
2.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( 0,1-v,v\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) ,\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right) \right\}\), if \(v=\frac{8}{9}\);
-
3.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) ,\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right) \right\}\), if \(v\in \left( \frac{8}{9},1\right)\).
Proof
Suppose that \((e_{a},e_{b})\) satisfies conditions of the proposition.
If \(e_{b}>1\), team B saves for the second match less than \(\beta -1\), and team A saves for the second match no more than 1. Since \(\gamma =\beta\), team C will be able to defeat both opponents. Since A loses to B, the payoffs are \((0,1-v,v)\). If \(v>\frac{8}{9}\), these payoffs cannot be supported in equilibrium. Indeed, if \(e_{a}=0\), team B can get \(\frac{1}{3}\) by defeating A with a lower effort \(e_{b}^{*}=\frac{1}{2}\). In other cases, team B prefers to deviate to \(e_{b}^{*}=0\). Indeed, if \(0<e_{a}<1\), team C defeats A, and all teams get \(\frac{1}{3}\). If \(e_{a}=1\), team C can either defeat A and force the equal distribution of prizes or equalize the opponents’ effort in both matches leading to the payoffs of \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\). Since \(\frac{1}{3}-\frac{v}{4}>1-v\) iff \(v>\frac{8}{9}\), this is a profitable deviation. Thus, payoff vector \((0,1-v,v)\) is not supported in equilibrium for \(v>\frac{8}{9}\).
If \(e_{b}<1\), teams A and C can guarantee the equilibrium payoff of \(\frac{1}{3}\).
(1) Team C can win the game against the winner of the first match because the remaining efforts of team A for the last game will be not higher than \(1<\gamma\) and the remaining efforts of team B for the last game will be strictly less than \(\beta =\gamma\).
(2) Team A can guarantee the payoff of \(\frac{1}{3}\) by deviating to 0. Indeed, teams A and B will have the efforts of 1 and more than \(\gamma -1\), respectively, left for their matches against C. Therefore, team C can win only one game, and it will prefer to defeat B and lose to A.
(3) For team B, if \(e_{a}=0\), it guarantees the payoff of \(\frac{1}{3}\) by defeating A in the first match, e.g. with \(e_{b}^{*}=\frac{1}{2}\), and forcing team C to defeat B leading to payoffs \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). If \(e_{a}\in (0,1)\), team B can guarantee the equilibrium payoff of \(\frac{1}{3}\) by deviating to \(e_{b}^{*}=0\) and forcing team C to defeat A. If \(e_{a}=1\), team C is indifferent between two options: 1) defeating A and losing to B, the corresponding payoffs profile is \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\); and 2) equalizing the efforts of both teams, the corresponding payoffs profile is \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\). However, if \(v<\frac{8}{9}\), the first option cannot be reached in equilibrium: team B would be better off by defeating A in the first match and getting \(1-v\) for the second place in the tournament (team C will win both matches in this case) instead of \(\frac{1}{3}-\frac{v}{4}\).
Consider case \(e_{b}=1\). If \(e_{a}=1\), then team C wins both matches (the sum of the remaining efforts of teams A and B for the last game is \(0+\beta -1<\gamma\)). Team B would be better off by defeating team A in the first match with certainty, e.g. with \(e_{b}^{*}=\beta\), so this is not an equilibrium. If \(0<e_{a}<1\), then team C wins both matches (the sum of the remaining efforts of teams A and B for the last game is not higher than \(1-\beta +\gamma +\beta -1<\gamma\)), and team A loses both matches. Therefore, team A can profitably deviate to \(e_{a}^{*}=1\) to ensure a positive expected payoff. Finally, if \(e_{a}=0\), the sum of the remaining efforts of teams A and B for the last game is \(1-\beta +\gamma +\beta -1=\gamma\). Team C has two equally good options: to defeat team B, leading to the payoffs of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\), and to equalize the efforts of both A and B, leading to the payoffs of \(\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right)\). \(\square\)
Proposition 23
Suppose \(1<\gamma =\beta\). Then, the set of all equilibrium payoffs is
-
1.
\(\{\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( 0,1-v,v\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) \}\), if \(v\in (\frac{2}{3},\frac{8}{9})\);
-
2.
\(\{\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( 0,1-v,v\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) ,\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right) \}\), if \(v=\frac{8}{9}\);
-
3.
\(\{\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right) ,\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right) \}\), if \(v\in (\frac{8}{9},1)\).
Proof
Payoffs \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) can be obtained if \((e_{a},e_{b})=(1,0)\) and team C chooses to defeat A on the equilibrium path: \(e_{c}(1,0)=1\). There are no profitable deviations for any of the teams. Indeed, on the equilibrium path, team C can either defeat A or equalize the opponents’ efforts; both choices lead to the payoff of \(\frac{1}{3}\) for C. Team A will be defeated by C after any win over B, so A cannot increase the payoff. Team B can defeat team A in the first match, but in case of any win, B will be defeated by C in the second match. Thus, there are no profitable deviations for B.
If \(v\le \frac{8}{9}\), payoffs \(\left( 0,1-v,v\right)\) can be obtained if \((e_{a},e_{b})=(1,\beta )\) and team C chooses to equalize the efforts of A and B in the subgame (1, 0): \(e_{c}(1,0)=0\). Team C safely wins both matches, and team B wins a match against A. Team A cannot get a positive payoff since \(1<\gamma\), so team C always has enough effort to defeat A. Team B can pretend to a win over C only in case of deviating to \(e_{b}^{*}=0\).
Facing the strategies \((e_{a},e_{b})=(1,0)\), team C by construction chooses to equalize the efforts of A and B: \(e_{c}(1,0)=0\), so the payoffs after team B’s deviation are \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\). Since \(\frac{1}{3}-\frac{v}{4}\le 1-v\) iff \(v\le \frac{8}{9}\), we get SPE with the required payoffs.
For \(v\ge \frac{8}{9}\), consider the strategy profile such that \((e_{a},e_{b})=(1,0)\) and team C chooses to equalize the efforts of A and B in the subgame (1, 0): \(e_{c}(1,0)=0\) (at any other subgame, C plays any of their best responses). The teams get \(\left( \frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3}\right)\). Team B is not interested in getting \(1-v\) by defeating A in the first match because \(\frac{1}{3}-\frac{v}{4}\ge 1-v\). Team A obviously cannot get more given the opponents’ strategies.
Finally, payoffs \(\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right)\) happen in SPE if \((e_{a},e_{b})=(0,1)\) and team C chooses to equalize the efforts of both A and B: \(e_{c}(0,1)=1\). There are no profitable deviations for A: in case of deviating to \(0<e_{a}^{*}<1\), team A gets 0 after losing both matches; in case of deviating to \(e_{a}^{*}=1\), A gets \(\frac{1-v}{2}<\frac{1}{3}-\frac{v}{4}\). There are no profitable deviations for B: switching to \(e_{b}^{*}>1\) leads to a loss to C and the payoff of \(1-v<\frac{1}{3}+\frac{v}{4}\). In case of deviation to such \(e_{b}^{*}\) that \(0<e_{b}^{*}<1\), team C chooses to defeat B, so all teams will get \(\frac{1}{3}<\frac{1}{3}+\frac{v}{4}\). If B deviates to \(e_{b}^{*}=0\), then for any possible outcome of the tie-break in the first match, team B gets no more than \(\frac{1}{3}<\frac{1}{3}+\frac{v}{4}\).
From Proposition 22, it follows that other payoff vectors are impossible. \(\square\)
Next, consider non-generic cases with \(\beta =\gamma +1\).
Proposition 24
Suppose \(\beta =\gamma +1\) and \(\gamma >1\). Then, the set of all equilibrium payoffs is:
-
1.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right) \right\}\), if \(v\in \left( \frac{2}{3},\frac{5}{6}\right]\);
-
2.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) \right\}\), if \(v\in \left( \frac{5}{6},1\right)\).
Proof
Consider any SPE and denote the corresponding strategies of A and B by \(e_{a}\) and \(e_{b}\). First, if \(e_{a}=e_{b}=1\), there are two possible outcomes of the tie-break in a match between A and B. In each of these outcomes, team C has two options: to defeat A or to equalize the efforts of both A and B. The corresponding payoff vectors are provided in Table 7.
If B wins in a lottery against A, team C is strictly better off by equalizing efforts with both teams, resulting in the payoffs of \(\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right)\). If A wins, then two alternatives are equally good for team C. Depending on the choice of team C’s strategy, the ex-ante payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) or \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\). Payoff profile \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) can be supported in SPE if \(v\in (\frac{2}{3},\frac{5}{6}]\), e.g. when \(e_{a}=e_{b}=1\) and when \(e_{c}(1,1,A)=\frac{\gamma }{2}\) and \(e_{c}(1,1,B)=0\). Indeed, team B has no profitable deviations because any deviation would lead to one loss and the expected payoff not exceeding \(\frac{1}{3}\). Team A can consider deviations to \(e_{a}^{*}<1\). In that case, A loses to B; team C has two options:
(1) to get \(1-v\) by defeating A and losing to B by playing, for example, \(e_{c}={\frac{\gamma }{2}}\);
(2) to exert all effort in a match against B by playing \(e_{c}=0\). In this case, C gets \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot 0=\frac{1}{6}\).
Team C strictly prefers the first option if \(v<\frac{5}{6}\) and strictly prefers the second option if \(v>\frac{5}{6}\). Therefore, A will not choose \(e_{a}^{*}<1\) for \(v<\frac{5}{6}\). For \(v=\frac{5}{6}\), the strategy profile with an additional property \(e_{c}(e_{a}^{*},1)=\frac{\gamma }{2}\) for all \(e_{a}^{*}<1\) is an SPE.
Payoff profile \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) is reached if \((e_{a},e_{b})=(1,1)\), and team C equalizes efforts of both A and B in both outcomes of the tie-break (also, C plays their best response in other subgames). This is an SPE for any \(v>\frac{2}{3}.\) Indeed, for both A and B, a decrease of effort in the first match leads to a loss in that match, so the final payoff will not exceed \(\frac{1}{3}\). Also, B is not interested in playing \(e_{b}^{*}>1\) because B will defeat A, lose to C, and get the same payoff of \(\frac{1}{3}\). Therefore, there are no profitable deviations either for A or for B; team C plays their best response by construction.
Second, consider case \(e_{a}=1\), \(e_{b}\ne 1\). If \(e_{b}>1\), then C wins both matches with certainty, and B gets a payoff of \(1-v\). B would be willing to deviate to \(e_{b}=1\) to receive a payoff of at least \(\frac{1}{3}\). If \(e_{b}<1\), the payoffs of the teams are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) since team C would decide to defeat A and lose to B, but it has already been proven that such a payoff profile is realized in some equilibrium.
Finally, when \(e_{a}<1\), team B can get v by playing \(e_{b}^{*}=\frac{1+e_{a}}{2}\), whereas team C can secure the second place and the corresponding payoff \(1-v\) with \(e_{c}=1\). Thus, team A gets 0, so it plays suboptimally because deviation to \(e_{a}^{*}=1\) secures positive payoff. Consequently, there are no SPE with \(e_{a}<1\). \(\square\)
Proposition 25
Suppose \(\beta =\gamma +1\) and \(\gamma <1\). Then, the set of all equilibrium payoffs is:
-
1.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) \right\}\), if \(v\in \left( \frac{2}{3},\frac{8}{9}\right)\);
-
2.
\(\left\{ \left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right) \right\}\), if \(v\in \left[ \frac{8}{9},1\right)\).
Proof
Consider any SPE and denote the corresponding strategies of A and B by \(e_{a}\) and \(e_{b}\). As in the Proposition 24, strategies \(e_{a}=e_{b}=1\) lead to the ex-ante payoffs of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) or \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) depending on team C’s strategy.
Payoff profile \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) cannot be supported in equilibrium for \(v<\frac{8}{9}\) because team A would be better off by deviating to \(e_{a}^{*}=0\), which leads to the payoff of \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot (1-v)=\frac{2}{3}-\frac{v}{2}>\frac{1}{3}-\frac{v}{8}\) (team C equalizes team B’s effort in the last match). For \(v\ge \frac{8}{9}\), payoff profile \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) can be supported in equilibrium when \(e_{a}=e_{b}=1\) and \(e_{c}(1,1,A)=\frac{\gamma }{2}\). There are no profitable deviations either for A (any deviation to \(e_{a}^{*}<1\) would lead to the payoff not exceeding \(\frac{2}{3}-\frac{v}{2}\) after team C equalizes team B’s effort in the last match) or for B (any deviation would lead to one loss and the expected payoff not exceeding \(\frac{1}{3}\)). For the same reason, the payoff profile \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) is supported in equilibrium when \(e_{a}=e_{b}=1\) and C equalizes the efforts of both A and B if A wins the lottery in the first match.
Now consider the case \(e_{a}=1\), \(e_{b}\ne 1\). Playing \(e_{b}>1\) would result in C winning both matches with certainty and a payoff of at most \(1-v\) for B, so B plays suboptimally (playing \(e_{b}^{*}=1\) leads to the payoff of at least \(\frac{1}{3}\) for B). Playing \(e_{b}<1\) results in the payoff of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\) since team C would decide to defeat A and lose to B. Therefore, new equilibrium payoffs are impossible in this case.
If \(e_{a}<1\), team B secures the payoff of v by playing \(e_{b}^{*}=\frac{1+e_{a}}{2}\). Therefore, in equilibrium, team B must get v. In this case, team A can secure second place and the payoff of \(1-v\) by playing \(e_{a}^{*}=0\). Therefore, the only possible equilibrium payoff profile, in this case, is \((1-v,v,0)\). However, it cannot be supported in SPE since team A can get the expected payoff of \(\frac{1}{3}>1-v\) by spending all effort in the match against B. \(\square\)
Proposition 26
Suppose \(\beta =\gamma +1\) and \(\gamma =1\). Then, the set of all equilibrium payoffs is
-
1.
\(\{\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) \}\), if \(v\in \left( \frac{2}{3},\frac{8}{9}\right)\);
-
2.
\(\{\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right) ,\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right) \}\), if \(v\in [\frac{8}{9},1)\).
Proof
The proof mostly follows the proof of Propositions 24 and 25. We are going to prove that the payoff profile \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) can be supported in SPE iff \(v\ge \frac{8}{9}\). Such an equilibrium exists, for example, when \(e_{a}=e_{b}=1\) and \(e_{c}(1,1,A)=\frac{\gamma }{2}\). Consider a deviation of team A to \(e_{a}^{*}<1\).
Case 1. \(e_{a}^{*}=0\). In the subgame \((e_{a}^{*},e_{b})=(0,1)\), team C can either equalize the effort in the match against A (\(e_{c}(0,1)=1\)), yielding the payoff of \(\frac{1-v}{2}\), or equalize the effort in the match against B (\(e_{c}(0,1)=0\)), yielding payoff of \(\frac{1}{6}\). Since \(v>\frac{2}{3}\), the latter is the better option for C. Team A’s payoff in the same subgame is \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot (1-v)=\frac{2}{3}-\frac{v}{2}\). Note that \(\frac{2}{3}-\frac{v}{2}>\frac{1}{3}-\frac{v}{8}\) iff \(v<\frac{8}{9}\). Hence, \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) is not an equilibrium payoff if \(v<\frac{8}{9}\), and deviation to \(e_{a}^{*}=0\) is not profitable if \(v\in \left[ \frac{8}{9},1\right)\).
Case 2. \(0<e_{a}^{*}<1\). Now, team C has two options:
(1) to get \(1-v\) by defeating A and losing to B,
(2) to exert all effort in the match against B. In this case, C gets \(\frac{1}{2}\cdot \frac{1}{3}+\frac{1}{2}\cdot 0=\frac{1}{6}\).
We are still interested only in \(v\in \left[ \frac{8}{9},1\right)\). If \(v\ge \frac{8}{9}>\frac{5}{6}\), team C prefers to exert all effort in the match against B. Therefore, A gets \(\frac{2}{3}-\frac{v}{2}\). Since \(\frac{2}{3}-\frac{v}{2}>\frac{1}{3}-\frac{v}{8}\) iff \(v<\frac{8}{9}\), the deviation to \(e_{a}^{*}\) is not profitable for \(v\in \left[ \frac{8}{9},1\right)\). Therefore, \(\left( \frac{1}{3}-\frac{v}{8},\frac{1}{3}+\frac{v}{8},\frac{1}{3}\right)\) is supported in equilibrium iff \(v\ge \frac{8}{9}\).
The rest of the proof repeats the proof of Proposition 24. \(\square\)
Since the case \(\gamma =\beta + 1\) was investigated in Proposition 10, part 1), we completed the analysis of non-generic triples of budget when the first prize is high.
Appendix C
This Appendix contains formal proofs of Lemmas 1–7 from Section 5.
1.1 Proof of Lemma 1
Proof
Suppose that \((e_{a},e_{b})\) satisfies conditions of the Lemma.
If \(e_{a}<1-\gamma\), then team C loses both matches and gets 0. If additionally \(e_{a}=e_{b}\), then B can switch to \(e_{b}^{*}=\frac{e_{a}+(\beta -\gamma )}{2}\), which allows it to secure two wins instead of one win and one tie (with A), leading to a higher payoff. If \(e_{a}\ne e_{b}\), then the loser of a match between A and B can deviate and exert all effort in the first game. By doing so, this team guarantees the payoff of \(\frac{1}{3}\) because team C will win a match against the deviator leaving all teams with one win and one loss. Thus, there are no equilibria with \(e_{a}<1-\gamma\).
If \(e_{a}=1-\gamma\), then B can ensure the payoff of v by increasing efforts up to \(e_{b}^{*}=\frac{\beta -\gamma +e_{a}}{2}\). Team A can guarantee the payoff of \(\frac{1}{3}\) by deviating to \(e_{a}=1\) (team C definitely loses to B, so C will defeat A). Thus, there are no equilibria since the sum of the A and B’s guaranteed payoffs in equilibrium is not less than \(v+\frac{1}{3}>1\). \(\square\)
1.2 Proof of Lemma 2
Proof
Fix a pair \((e_{a},e_{b})\) that satisfies conditions of the Lemma.
First, consider case \(e_{b}>\beta -\gamma\). It follows from the assumptions that team B wins the first match versus A. Then, team C chooses to defeat the winner of the first game, team B, making the payoff equal to \(\frac{1}{3}\) for all teams. However, B can deviate to \(e_{b}^{*}=\frac{\beta -\gamma +e_{a}}{2}\) and get the payoff of v since it ensures a win against both opponents. Therefore, such \((e_{a},e_{b})\) cannot support an SPE.
Second, assume that \(e_{b}=\beta -\gamma\). Once again, team B wins the first match versus A. Team C can either defeat A and get the payoff of \(1-v\) or tie with B and get the payoff of \(\frac{1}{2}\cdot 0+\frac{1}{2}\cdot \frac{1}{3}=\frac{1}{6}\). Hence, if \(v>\frac{5}{6}\), team C prefers to tie team B, leading to the payoff vector \((\frac{2}{3}-\frac{v}{2},\frac{v}{2}+\frac{1}{6},\frac{1}{6})\); if \(v<\frac{5}{6}\), team C prefers to defeat A, leading to the payoff vector \((0,v,1-v)\); if \(v=\frac{5}{6}\), both options are equally good for C. However, team A can deviate to \(e_{a}^{*}=1\) and get the payoff of \(\frac{1}{3}\) by defeating B and losing to C. This would be a profitable deviation for A because \(\frac{2}{3}-\frac{v}{2}<\frac{1}{3}\). Thus, an equilibrium when \(e_{b}=\beta -\gamma\) is impossible in this case. \(\square\)
1.3 Proof of Lemma 3
Proof
Fix a pair \((e_{a},e_{b})\). Team A can ensure itself a payoff of \(\frac{1}{3}\) by deviating to \(e_{a}^{*}=1\), where A wins against B, and C’s optimal response would be to defeat A, yielding payoffs of \(\frac{1}{3}\) for all three teams. Due to the possibility of such a deviation, subgames where \(e_{b}\ge e_{a}\) would not lead to an equilibrium. Indeed, team C’s best strategy is to defeat A because there are not enough resources to even tie efforts against B. Therefore, A gets either 0, if \(e_{b}>e_{a}\), or \(\frac{1}{6}\), if \(e_{b}=e_{a}\), which makes a deviation to \(e_{a}^{*}=1\) profitable for A.
When \(e_{b}<e_{a}\), the only possible payoff profile is \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), because A defeats B, B defeats C, and C defeats A. \(\square\)
1.4 Proof of Lemma 4
Proof
If A wins the tie-break, then the payoffs are \(\frac{1}{3}\) for all three teams since C would like to win over the winner of the first match. If B wins the tie-break, C prefers to defeat A when \(v\in (\frac{2}{3},\frac{5}{6})\), which generates the payoff of \(1-v\) for C. When \(v\in (\frac{5}{6},1]\), team C would prefer to allocate all resources for the match against B which will generate the expected payoff of \(\frac{1}{2}\cdot 0+\frac{1}{2}\cdot \frac{1}{3}=\frac{1}{6}\). For \(v=\frac{5}{6}\), C is indifferent between two options. Now we can calculate the expected payoffs for all values of v. If \(v\in (\frac{2}{3},\frac{5}{6})\), then teams get \(\frac{1}{2}(\frac{1}{3},\frac{1}{3},\frac{1}{3})+\frac{1}{2}(0,v,1-v)=(\frac{1}{6},\frac{v}{2}+\frac{1}{6},\frac{2}{3}-\frac{v}{2})\). If \(v\in (\frac{5}{6},1]\), then the payoff vector is \(\frac{1}{2}(\frac{1}{3},\frac{1}{3},\frac{1}{3})+\frac{1}{4}(\frac{1}{3},\frac{1}{3},\frac{1}{3})+\frac{1}{4}(1-v,v,0)=(\frac{1}{2}-\frac{v}{4},\frac{1+v}{4},\frac{1}{4})\). If \(v=\frac{5}{6}\), both payoff vectors are possible. However, in all cases, team A would like to change its strategy to \(e_{a}=\frac{1+\beta -\gamma }{2}\), which allows it to defeat B with certainty. At the same time, the stock of effort of team C would be less than the sum of the remaining efforts of teams A and B for their matches with C. In this situation, C prefers to defeat A, which would result in the payoff of \(\frac{1}{3}\) for all three teams. This would be a profitable deviation for A (\(\frac{1}{2}-\frac{v}{4}<\frac{1}{3}\)), so no such equilibria exist. \(\square\)
1.5 Proof of Lemma 5
Proof
Fix a pair of strategies \((e_{a},e_{b})\). A strategy \(e_{a}\) that satisfies inequalities \(\beta -\gamma<e_{a}<1\) yields payoffs of \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\) because A wins the first match and C prefers to defeat A, the winner of the first match.
If \(e_{a}=1\), C can either defeat A, leading to the payoffs \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\), or equalize efforts in its both games, leading to the payoffs \((\frac{1}{3}+\frac{v}{4},\frac{1}{3}-\frac{v}{4},\frac{1}{3})\). The latter payoff vector cannot be supported in equilibrium for \(\beta >\gamma\): B can secure the payoff of \(\frac{1}{3}\) by decreasing the effort for the first game to, for example, \(e_{b}=\frac{\beta -\gamma }{2}\). In that case, A defeats B, B defeats C, and C chooses to defeat A, leading to the payoff of \(\frac{1}{3}\) for B.
These payoffs cannot also be supported in equilibrium if \(\beta =\gamma\) and \(v\in (\frac{2}{3},\frac{8}{9}]\): team B would be better off by defeating team A by playing, for example, \(e_{b}=\frac{1+\beta -\gamma }{2}\), and getting the payoff of \(1-v\) for the second place (\(1-v>\frac{1}{3}-\frac{v}{4}\) iff \(v<\frac{8}{9}\)). \(\square\)
1.6 Proof of Lemma 6
Proof
If \((e_{a},e_{b})\) satisfies conditions of the Lemma, team C can always defeat the winner of the first match and guarantee the payoff of \(\frac{1}{3}\) since the winner would have less than \(\gamma\) for its second match. Both teams A and B can guarantee the payoff of \(\frac{1}{3}\) by deviating to playing 0 in the first game. It would lead to a loss in the first match, but team C would be incentivized to defeat the winner of the first game. Since \(\gamma \le 1\), the loser of the first match would have enough effort to defeat team C (taking into account that C spends some effort against the winner of the first game). Hence, the payoff vector \((\frac{1}{3},\frac{1}{3},\frac{1}{3})\) is the only possibility. \(\square\)
1.7 Proof of Lemma 7
Proof
Suppose that \((e_{a},e_{b})\) satisfies conditions of the Lemma.
If \(e_{b}>1\), then team B saves less than \(\beta -1\) for the second match and team A saves for the second match no more than \(1-\beta +\gamma\). Therefore, team C will be able to defeat both opponents. Since A loses to B, the payoffs are \((0,1-v,v)\). These payoffs cannot be supported in equilibrium: team B prefers to deviate to \(e_{b}^{*}=0\) and get \(\frac{1}{3}\) instead.
If \(e_{b}<1\), then each team can guarantee the payoff of \(\frac{1}{3}\) in equilibrium. Team C can win one of its matches: the remaining effort of team A for the last game will be not higher than \(1-\beta +\gamma <\gamma\) and the remaining effort of team B for the last game will be strictly less than \(\beta -(\beta -\gamma )=\gamma\). Teams A and B can guarantee the payoff of \(\frac{1}{3}\) by deviating to 0 — in that case, team C will defeat the winner of the first game and lose to the loser of the first game (team C can win only one game because, after deviation to 0, the sum of remaining efforts of teams A and B will be not less than \(\beta >\gamma\)). Hence, the only possible equilibrium payoffs are \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\).
The last case is \(e_{b}=1\).
(1) If, additionally, \(e_{a}=1\), then team C wins both matches (the sum of the remaining efforts of teams A and B for the last game is \(0+\beta -1<\gamma\)). Team B would be better off by defeating team A in the first match with certainty, so this is not an equilibrium.
(2) If \(\beta -\gamma<e_{a}<1\), then team C wins both matches (the sum of the remaining efforts of teams A and B for the last game is not higher than \(1-\beta +\gamma +\beta -1<\gamma\)), and team A loses both matches. Therefore, team A can profitably deviate to \(e_{a}^{*}=1\), where it receives a positive payoff.
(3) Finally if \(e_{a}=\beta -\gamma\), the sum of the remaining efforts of teams A and B for the last game is \(1-\beta +\gamma +\beta -1=\gamma\). Team C has two equally good options: to defeat team B leading to the payoffs of \(\left( \frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\), and to equalize the efforts of both A and B, leading to the payoffs of \(\left( \frac{1}{3}-\frac{v}{4},\frac{1}{3}+\frac{v}{4},\frac{1}{3}\right)\). The latter case is not an equilibrium: team A can deviate to \(e_{a}^{*}=0\) and get the payoff of \(\frac{1}{3}\) (team C will strictly prefer to defeat B in that case). \(\square\)
Rights and permissions
About this article
Cite this article
Dagaev, D., Zubanov, A. Round-robin tournaments with limited resources. Soc Choice Welf 59, 525–583 (2022). https://doi.org/10.1007/s00355-022-01402-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00355-022-01402-w