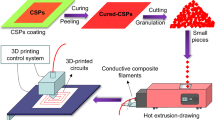
Abstract
In this work, new electrically conductive composite filaments are developed for the fabrication of conductive paths, 3D printed with FDM technology. These composite materials consist of electrically conductive copper powder and a polymer matrix. The influence of three different polymers (ABS, PLA, PS) on the electrical properties of the composites was examined. Electrical measurements of the composite filaments with the increasing copper powder concentrations, allow identifying the percolation threshold for elaborated composites. Results show that the lowest resistivity (0.156 × 10−5 Ωm) was achieved for the ABS/Cu composite at the 84.6 wt% Cu concentration. The obtained resistivity values are much lower than for other conductive composites and nanocomposites filaments reported in the literature. Voltage-current characteristics determined for each composite material showed that composites have Ohmic characteristics in low voltage regime. At high voltage regime, the electrical power dissipated in the composites caused a rapid increase in temperature. It was discovered that a polymer matrix influences the maximum value of the electrical power that can be dissipated in the filament before losing electrical conductivity. Examples of conductive 3D printed structures made from elaborated composites are also presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Additive manufacturing also called three-dimensional printing is a new manufacturing trend involving the fabrication of 3D objects directly from digital models. In recent years, 3D printing technology evolved rapidly, partially replacing and supplementing traditional manufacturing methods. Additive manufacturing is nowadays widely used in many manufacturing sectors from aerospace and the automotive industry to bioengineering and architecture [1,2,3,4,5,6]. Additive techniques offer a wide range of applications, suited in terms of production cost, minimum printing resolution, and the type of used materials [7, 8]. The most popular 3D printing techniques are stereolithography (SL), selective laser sintering (SLS), PolyJet and fused deposition modeling (FDM). PolyJet and SL techniques demonstrate very high printing resolution (below 20 µm) but these methods use relatively expensive machines and advanced photosensitive resins [9, 10]. On the other hand, the FDM technique is widely used due to process simplicity, low costs equipment, accessibility of materials and acceptable printing resolution (down to 50 µm) [11].
In FDM technique, the feedstock is in the form of a filament made of thermoplastic polymer. The filament is thermally melted (fused) inside a tube heater at a temperature above the melting point, extruded through the nozzle and deposited on to the build platform, in layer by layer manner. The FDM technology is used primarily to create low-cost prototypes in the production process. Thanks to the development of new materials, this technology is incorporated into the fabrication process of functional elements or to create customized products, that often cannot be made with traditional techniques, with the specific shape or color, depending on customer requirements [12, 13]. At this moment the availability of functional filaments is still limited so there is a need to develop new materials, including composite materials, with properties suited to the application.
On the other hand, we are dealing with the new trend in manufacturing, called structural electronics, involving electronic and electrical components, and circuits incorporated in the volume of protective or load-bearing structures, housing elements etc [14]. In order to enable the fabrication of advanced products, low-cost, and adaptable functional materials for FDM and other 3D printing techniques are necessary to develop. The main difficulty in the development of composites is the influence of a vast range of parameters on the final properties of the material and printed element. The material type and morphology of functional filler as well as the type and structure of the polymer matrix have an enormous impact on the properties of the composite [15]. In literature, we find experiments towards conductive composites with a graphene [16, 17], carbon black [18], carbon nanotubes [19] as a conductive filler. Such materials do not allow to achieve a low electrical resistivity of the filaments. Reposted results for composites filaments with graphene shown resistivity around 102 Ωm [17], with carbon black—10−1 Ωm [18] and with carbon nanotubes 10−2 Ωm [19]. The main advantage of using metallic powder as a filler is a higher electrical conductivity of the functional filler, what is directly influencing the conductivity of the final composite. Resistivity values in the range of 10−3–10−6 were reported in the literature for Ni/SiO2 and PEG/Ag composites [20, 21]. Electrically conductive composite filaments can be used in various fields of technology, for example in the production of supercapacitors, electromagnetic interferences shielding, printed antennas, sensors etc [18, 22]. Moreover, conventional polymer filaments and conductive filaments can be integrated together into the 3D printing process to make multi-material parts [23]. This offers the possibility to create electrical circuits, sensors, and elements inside 3D printed objects, fabricated in one process, on one machine.
The alternative approach used for fabrication of the structural electronics is to use single material FDM printers equipped with the additional printing head used to deposit conductive ink. The load structure of the element is printed from polymers and conductive paths are fabricated with Direct Write deposition using highly conductive, low-viscosity, silver-based inks. Printed conductive elements are cured at 90 °C to achieved final conductivity. Such hybrid FDM/DW printers are offered as commercial equipment by Voltera, Voxel 8 and V-One, introducing this hybrid technology with specialized, high-cost printers [24,25,26].
In this paper, we present the elaboration and evaluation of electrically conductive filaments based on copper powder as the functional phase and three different types of polymers used as matrix. Such composite filaments can be directly used in standard off-the-shelf FDM printers, to fabricate electrical circuits and other conductive electronic structures. It is important to evaluate the influence of the polymer matrix on the electrical properties of the filament and to measure current–voltage characteristics to discover the maximum power dissipated in the developed filaments, and its influence on the electrical properties. Furthermore, 3D printed demonstrators, a simple electrical circuit and human interface device (HID) printed with developed materials were presented.
2 Experimental procedure
2.1 Materials
In order to fabricate a conductive composite filament for use with an FDM 3D printer, two main materials need to be incorporated: a conductive phase and a thermoplastic matrix. For the conductive phase, copper micropowder filler was chosen, purchased from Makin Metal Powders. The purity of the copper powder was above 99% according to the datasheet. Metal was subjected to particle size analysis on a Malvern machine to evaluate the grain size distribution (Fig. 1). The average diameter of the filler particles was 57 µm. The shape of copper powder particles is shown on SEM picture (Fig. 2). Copper micropowder was chosen as filler due to its good electrical conductivity and widespread availability. The conductivity of the bulk copper is 5.96 × 107 S/m so using this material as a filler we should be able to develop highly conductive composite filaments.
To achieve good printability of composite filament, several thermoplastic polymers were chosen for the matrix material. Acrylonitrile butadiene styrene (ABS) polymer was chosen as the first matrix material, while it is a very popular and widely used polymer in FDM technology with good mechanical properties. The glass transition temperature of ABS is around 105 °C. Based on the supplier datasheet, the polymer density is 1.05 g/cm3.
Second polymer matrix used in the experiments was polylactic acid (PLA). It is a second, most popular polymer used in 3D printing. PLA is biodegradable and biocompatible thermoplastic aliphatic polyester with a melting temperature of around 150 °C and glass transition around 60 °C. PLA has also the highest density of 1.24 g/cm3 comparing to 1.05 g/cm3 for other used polymers.
Third used polymer for composite matrix was polystyrene (PS). It is a synthetic aromatic hydrocarbon polymer with a melting temperature of around 240 °C and a glass transition temperature of around 100 °C. The polymer density is 1.05 g/cm3 according to the datasheet.
All of the used polymer materials exhibit properties adequate for the extrusion process of obtained composite filaments on a standard FDM printer, without additional modification of extruder, hot-end or hot-bed.
2.2 Methods
To choose the appropriate filler ratio of the copper micropowder in the polymer matrix, two major effect needs to be evaluated: the percolation threshold influencing the electrical resistivity, and rheology influencing the viscosity. The percolation threshold is minimum filler content in the polymer matrix after which the properties of the composite rapidly change from dielectric to conductive. When percolation threshold is reached, the number of conductive paths and networks rise and resistivity of composite decreases. However, the amount of filler must be at low enough level so as to enable the filament to be extruded through printer nozzle. The optimal amount of copper powder must be obtained to comply with both conditions.
All composites were prepared by a two-stage solvent assisted processing method. The first stage consists of dissolving the polymer in a suitable organic solvent and mixing the metal filler with the obtained polymer solution. Afterward, the solvent is evaporated. The solvent used for polymers were: acetone for ABS, toluene for PS, and chloroform for PLA (Fig. 3). Solvent assisted processing method is preferable for this application over thermal plastification of polymer to reduce the thermal degradation of the polymer [27,28,29].
The samples were weighed using a Precisa 125A laboratory scale. 20 g of each polymer was used to prepare the solvent solution, with 40 ml of solvent added to each polymer sample and left overnight at room temperature to dissolve. The obtained polymer solution was mixed with a copper powder filler. Materials were mechanically mixed to achieve a homogeneous composition, poured into glass containers and placed in the heating oven at 90 °C for 2 h for the evaporation of the solvent.
Afterward, the resulting polymer composites were mechanically pelleted. To make the 3D printing filament, composite pellets were extruded on the specially adapted laboratory equipment in the hot mixing extrusion process. The single screw extruder machine (Fig. 4) with two heating zones was used to extrude filaments. Most popular filament’s diameters used in FDM technology are 1.75 mm and 3 mm. In our research, we decided to use 1.75 mm diameter filament to achieve stable thermal distribution in whole filament volume while printing. In the result the diameter of extruded filaments varied from 1.7 to 1.8 mm (Fig. 5). This range of diameters is good enough to print proper elements using standard FDM printer.
Depending on the polymer matrix, different extruding temperatures were used for each zone, summarized in Table 1. Higher temperature values caused the extruded filaments to be brittle, what is related to the thermal degradation of the polymer. Such materials could not be used in the 3D printing process and were eliminated from further experiments. On the other hand, below the selected temperature regime, there is a problem with the plastification of the polymer matrix and the extrusion process is impossible.
3 Results and discussion
3.1 Resistivity measurements
DC resistivity measurements were carried out using a four point method (Fig. 6). The resistance measurements were performed using an Escort 3145A multimeter on 10 cm filament sections with an average diameter of 1.75 mm. Due to the possible problems with high contact resistivity, a silver paste (DuPont 7145L) was used on the measurements contact points for lower contact resistance.
Each filament was measured in 30 randomly chosen fragments. Samples with resistance values above 200 MΩ were considered as non-conductive. To determinate the effect of the addition of copper powder to the polymer matrix, the volume resistivity \(\rho\) of each composite filament was calculated according to the equation below:
where \(\uprho\) is the volume resistivity, R is the resistance of filament, S is the cross-sectional area and l is a length of the measured section of the filament.
The influence of the amount of copper powder filler on the resistivity of the composite for all used polymers is presented in Fig. 7.
It is evident that the resistivity of filaments rapidly decreases with the increasing loading of filler. This indicates the formation of a large number of conductive paths, which is typical percolation phenomena. Change in the resistivity strongly depends on the type of polymer matrix. For each examined composite, different amount of copper powder is necessary to reach the percolation threshold. This is a typical dependence of the matrix material on the percolation threshold observed in other composites, regardless of the functional phase material [30]. After exceeding percolation threshold value, resistance stabilizes and we observe a plateau, regardless the further addition of conductive filler. The lowest measured resistivity was for ABS/Cu composite and highest for PS/Cu composite (Table 2).
It is also observed that resistivity of composites with an equal amount of copper powder strongly depends on the matrix polymer type. This is due to different polymer resistivity itself. The most noticeable is higher resistivity of PS/Cu composite even after reaching the percolation threshold. In literature can be found that resistivity values of PLA and ABS are similar and it is around 1012–1011 Ωm [13, 31]. Resistivity value of PS is definitely higher, around 1016 Ωm [32]. As that on the properties of composites affects both the filler and the matrix properties, it is obvious that PLA/Cu and ABS/Cu filaments will have similar electrical properties and PS/Cu will have noticeable worse electrical properties assuming a comparable ratio of filler and polymer.
Measured resistivity values for copper-based composite filaments are satisfyingly low compared to other composites we found in the literature. Resistance value above 0.1 × 10−2 Ωm for composite with carbon nanotubes as filler [19, 33], above 0.1 × 10−1 Ωm for composite with carbon black [23, 34], above 0.2 × 10−2 Ωm for composite with graphene oxide [35] are reported. The developed composites have also lower resistivity comparing with other metal-based composites: above 0.8 × 10 Ωm−1 for copper-based composite [36, 37] and around 0.17 Ωm for composite with nickel powder [36].
For each type of polymer matrix, one filament with optimal resistivity value was chosen to measure current–voltage characteristics—ABS/Cu with 81.8 vol%, PLA/Cu with 82.5 vol% and PS/Cu with 85.5 vol% of copper powder. All chosen filaments reach percolation threshold and using composites with a bigger amount of copper did not affect the electrical properties in a significant way. Measurements were carried out using two HM8112-3 Hameg multimeters, set as voltmeter and as ammeter, and Rigol DP832A power supply. I–V measurements show that all filaments have an Ohmic characteristic, which means that the relationship of the current and voltage is linear and corresponds to Ohm’s law (Fig. 8). Similar, Ohmics, I–V characteristics are typical also to other composites with the carbon nanotube [38]. During the measurements, there was also notice that the PLA/Cu composites are the least thermally stable, and the current values have a larger measuring spread compared to PLA and ABS-based composites. Characteristic of this material, however, is the typical conductor characteristic.
3.2 Maximum power dissipation measurements
The resistance of composite filaments was also measured at the higher voltage values (different for individual composites) until a significant increase in temperature, plasticization and permanent damage of measured filaments. Filaments with optimal resistivity were chosen for measurements—ABS/Cu with 81.8 vol%, PLA/Cu with 82.5 vol% and PS/Cu with 85.5 vol% of copper powder. We observed that each composite with different polymer matrix can dissipate different maximum value of electrical power. Above the sudden value of supply voltage, the temperature of the filament increases rapidly and polymer composite softens. At the same time, the resistivity of composite increases due to broken connections between filler particles [39]. The highest value of power is handled by the ABS/Cu composite due to the highest glass transition temperature of ABS polymer. Second is the PS/Cu composite and the least power can be dissipated by the PLA/Cu composite filament (Fig. 9). Results are also corresponding with the thermal conductivity of the polymer matrix. According to literature, thermal conductivity values are 0.13 Wm−1 K−1 for PLA, 0.14 Wm−1 K−1 for PS and 0.33 Wm−1 K−1 for ABS, respectively [40, 41]. The lower thermal conductivity of the polymer matrix cause that the composite exchange heat with the environment slower and material temperature increase faster [42]. Maximum values of power density for each composite are summarized in Table 3.
3.3 Percolation threshold
The percolation theory gives an idea about the resistivity near the percolation threshold value. The behavior of the resistivity near the percolation threshold showed a gentle change over the resistivity of the polymer matrix to the resistivity of the metallic filler. At lower concentration of filler, the metallic particles are isolated by the polymer, so resistivity of the composite is high. After reaching the percolation threshold, filler particles form conductive networks that decrease composite resistivity. At higher filler loading, more conductive paths are created and resistivity rapidly decreases. The percolation threshold values depend on properties of both polymer matrix and filler particles.
3.3.1 Percolation theory
To determinate the minimal theoretical amount of copper powder in polymer composite adequate to achieve electrical conductivity, the electrical percolation thresholds for each composite i.e., PLA/Cu, ABS/Cu and PS/Cu, were calculated using the following power law (according to Kirkpatric’s percolation model) [43, 44]:
where \(\sigma\) is composite conductivity, \(v\) is the volume of the copper powder phase, \({v_c}\) is its value at the copper powder volume for the percolation threshold and t is a critical exponent. The percolation threshold can be determinate by fitting experimentally obtained data to the classical percolation theory. Fit to the experimental values of \({\text{log}}\left( v \right)\) versus \({\text{log}}\left( {v - {v_c}} \right)\)for each composite with the different polymer matrix is shown in the inset to Fig. 10.
Percolation thresholds for all composites are shown in Fig. 10. For ABS/Cu composite an excellent fit to the measured values was obtained by a filler concentration of 29.20 vol% (77.8 wt%) and t = 1.42. For PLA/Cu composite calculate percolation threshold was higher than for ABS/Cu and the \({v_c}\) value was equal to 34.11 vol% (78.7 wt%) and t = 1.83. For PS/Cu composite, the \({v_c}\) value was calculated at 35.46 vol% (79.7 wt%) of copper powder in composite—the highest of all tested materials—and t = 1.55. Percolation threshold values are in agreement with data from the literature, related to the experiments on polymer composites with copper powder or other metal powders as the conductive filler. In such publications, \({v_c}\) values were obtained between 25 and 40 vol% [45, 46]. Other experiments described in the literature regarding low-density polyethylene (LDPE)/Cu and linear low-density polyethylene (LLDPE)/Cu composites, with copper powder particles size below 38 µm, suggest \({v_c}\) values of 18.7 vol% [37]. The obtained \({v_c}\) value is lower due to smaller filler particles size [45, 47]. A similar relationship was observed for composites with nanosilver powder (150 nm) as a filler. Depending on the polymer matrix, the \({v_c}\) value was calculated between 8.2 vol% to 18 vol% [48].
It was observed that critical copper powder content varies depended on matrix type. It is well known that the percolation threshold is sensitive to polymer type. This characteristic was also noticed in carbon particles-filled polymer composites [49]. Critical value of percolation threshold can be dependent on many polymer parameters. The most important is the viscosity of each matrix, which is strongly connected with processing temperature. Other parameters that have an impact on percolation threshold are the molecular weight of polymers, which can be varied even for the same polymer but obtained in a different process, the polarity of polymer and chain length of a polymer [50, 51].
3.4 Temperature coefficient and conductive mechanism
Table 4 shows the resistance of each composite, ABS/Cu with 81.8 vol%, PLA/Cu with 82.5 vol% and PS/Cu with 85.5 vol% of copper powder, in two different temperatures: room temperature (20 °C) and 120 °C. For all polymer/metal composites, the resistance increases in higher temperature. According to those measurements, TCR parameter can be calculated using the formula:
As is known, the TCR value allows us to obtain information about the conductivity mechanism [52]. In some cases, TCR values are negative which means that resistance of composite is decreasing in function of temperature. This phenome took place when composite show semiconductive characteristic. The conductive mechanism in semiconductors is strongly based on the tunnelling of electrons. In electron tunnelling theory, it is believed that conductive particles of filler don’t have mechanical contacts to each other and electrons can flow through composite thanks to the quantum mechanics process—tunnelling [53]. Increasing temperature in this composite can cause increasing electrons energy and make them easier to jump across gaps and tunnel through energy barrier between conductive phase and isolating matrix. Thanks to that, the resistance of material may decrease in higher temperature [54].
In other composites with positive TCR values, the conductive mechanism is based on mechanical connections between conductive filler particles. This kind of conductive mechanism took place in composite with high filler percentage due to forming a huge number of conductive paths. In most cases, the polymer matrix is expanding more than the conductive filler due to their different physical properties. Expanding the polymer matrix cause increasing distance between conductive filler grains and less conductive paths can be formed so resistance is increasing [53]. With a high number of conductive paths, composite behave like typical conductor and resistance of material decrease in increasing temperature [55].
We observed that TCR value for all composite ale similar and have positive values. The high amount of filler in each measured composites and positive values of TCR let assume that conductive mechanism in these composites is based on mechanical connections between filler particles and are similar to typical metal conductors.
3.5 3D-printed electrical circuits—demonstrators
In order to demonstrate the functionality of elaborated conductive filaments for printing 3D, different electrical structures were fabricated using low-cost, unmodified, dual extruder FDM printer. Simple, three-dimensional electrical circuit composed of two conductive paths in insulator housing was designed and printed. Conductive paths were made of ABS/Cu composite filament containing 80 wt% of Cu filler. The housing of structure was made with pure ABS filament. The developed composite filament was printed with standard parameters. Nozzle temperature was set to 250 °C and printing speed was set to 50 mm/s. Conductive elements were printed with 100% infill. To one side of the system the LED was connected and to the other side, the 9 V battery. Due to the low resistivity of printed elements, LED could be successfully powered by a 9 V battery (Fig. 11a). Further tests have shown that a 2.8 V power supply is also enough to power the LED but with lower efficiency (Fig. 11b).
Conductive filaments can also be used to print capacitive sensors. Many different types of sensors, like humidity [56], fluid level [57], pressure [58], position [59], acceleration [60] are based on capacitance measurement. Another wide application of capacitive sensors is a human interface device (HID) class. HID is a type of computer device that interacts directly with, and most often takes input from, humans and may deliver outputs to humans. As an example of a 3D printed HID device, a printed keyboard with three capacitive buttons was designed and fabricated. When the user touches the printed conductive buttons, the capacitance of buttons increases, a signal is sent to the Arduino board and output pin is triggered. Triggering output pin is visualized by turning the LED on and off. To implement capacitive sensors, CapSense Arduino library was used. This library turns two Arduino input pins into the capacitive sensor. The functional device is presented in Fig. 12 and a short presentation in supplementary materials.
4 Conclusion
This paper describes the preparation and characterization of conductive copper-based filaments for FDM technology. Three different polymer materials were used for the composite matrix. Lowest resistivity was exhibited by ABS/Cu composite and highest by PS/Cu composite. Resistivity value below 10−3 Ωm was achieved for ABS and PLA-based composites containing copper filler loading above 80 wt% and resistivity value below 0.01 Ωm for PS/Cu composite containing copper filler loading above 84 wt%. I–V measurements have shown that composites have Ohmics characteristic, which means that they have constant resistivity value, voltage independent. This is true for the low values of the supply voltage. The maximum amount of power dissipated by the composites depends on polymer matrix properties: its glass transition temperature and thermal conductivity. Above the maximum value of dissipated power (up to 500 mW for ABS/Cu) composite softens and resistance increase rapidly. Developed materials were used to print demonstrators of simple electrical circuit and human interface device (HID). They prove that copper-based composites filaments can be used at any commercially available FDM printer, without the complicated and costly modifications. In order to obtain more functional composite filaments, many types of research can be carried out in the future. Other metal powders, like nickel, iron or mixes if different metal powders, as well as nanoparticles, can be used as a conductive phase. The influence of the size and shape of the functional phase particles must also be investigated. It is also important to examine non-standard polymer matrixes—high temperature, high impact, low-density polymers—and its influence on composite properties. This kind of functional materials open possibilities for a vast range of applications in existing and new fields of industry, allowing to create high-tech products with low-cost materials and readily available equipment.
References
R. Petzold, H.-F. Zeilhofer, W.A. Kalender, Comput. Med. Imaging Graph. 23, 277 (1999)
J. Winder, R. Bibb, J. Oral. Maxillofac. Surg. 63, 1006 (2005)
B. Berman, Bus. Horiz. 55, 155 (2012)
Y.L. Yap, W.Y. Yeong, Virtual and Phys. Prototyping 9, 195 (2014)
S.K. Moon, Y.E. Tan, J. Hwang, Y.-J. Yoon, Int. J. of Precis. Eng. and Manuf.-Green Tech. 1, 223 (2014)
H. Yoshida, T. Igarashi, Y. Obuchi, Y. Takami, J. Sato, M. Araki, M. Miki, K. Nagata, K. Sakai, S. Igarashi, ACM Trans. on Graph. (TOG) 34, 88 (2015)
K.V. Wong, A. Hernandez, ISRN Mech. Eng. 2012, 208760 (2012)
X. Wang, M. Jiang, Z. Zhou, J. Gou, D. Hui, Compos. Part B Eng. 110, 442 (2017)
M.P. Lee, G.J.T. Cooper, T. Hinkley, G.M. Gibson, M.J. Padgett, L. Cronin, Sci. Rep. 5, 9875 (2015)
A. Cazón, P. Morer, L. Matey, In: Proceedings of the institution of mechanical engineers, part B. J. Eng. Manuf. 228, 1664 (2014)
R.D. Farahani, K. Chizari, D. Therriault, Nanoscale 6, 10470 (2014)
O.S. Carneiro, A.F. Silva, R. Gomes, Mater. Des. 83, 768 (2015)
D. Espalin, D.W. Muse, E. MacDonald, R.B. Wicker, Int. J. Adv. Manuf. Technol. 72, 963 (2014)
D.A. Roberson, R.B. Wicker, E. MacDonald, J. Electron. Packag. 137, 031004 (2015)
H.S. Göktürk, T.J. Fiske, D.M. Kalyon, J. Appl. Polym. Sci. 50, 1891 (1993)
S. Dul, L. Fambri, A. Pegoretti, Compos. Part A Appl. Sci. Manufac. 85, 181 (2016)
X. Wei, D. Li, W. Jiang, Z. Gu, X. Wang, Z. Zhang, Z. Sun, Sci. Rep. 5, 11181 (2015)
S.J. Leigh, R.J. Bradley, C.P. Purssell, D.R. Billson, D.A. Hutchins, PLoS ONE 7, e49365 (2012)
L. Sithiprumnea Dul, Fambri, A. Pegoretti, Nanomaterials 8, 49 (2018)
D. Toker, D. Azulay, N. Shimoni, I. Balberg, O. Millo, Phys. Rev. B 68, 041403 (2003)
D.C. Hyun, M. Park, C. Park, B. Kim, Y. Xia, J.H. Hur, J.M. Kim, J.J. Park, U. Jeong, Adv. Mater. 23, 2946 (2011)
M.L. Clingerman, J.A. King, K.H. Schulz, J.D. Meyers, J. Appl. Polym. Sci. 83, 1341 (2001)
S.W. Kwok, K.H.H. Goh, Z.D. Tan, S.T.M. Tan, W.W. Tjiu, J.Y. Soh, Z.J.G. Ng, Y.Z. Chan, H.K. Hui, K. E. J. Goh, Appl. Mater. Today 9, 167 (2017)
Y. Dong, X. Min, W.S. Kim, IEEE Sens. J. 18, 2959 (2018)
V. Muthu, P. Chatterjee, T.K. Jet, In: IEEE Region 10 Conference (TENCON) (IEEE, Singapore, 2016), pp. 2327–2333 (2016)
Y. Dong, C. Bao, W.S. Kim, Joule 2, 579 (2018)
N. Najafi, M.C. Heuzey, P.J. Carreau, P.M. Wood-Adams, Polym. Degrad. Stab. 97, 554 (2012)
Z. Peng, L.X. Kong, Polym. Degrad. Stab. 92, 1061 (2007)
T. Kuilla, S. Bhadra, D. Yao, N.H. Kim, S. Bose, J.H. Lee, Prog. Polym. Sci. 35, 1350 (2010)
W. Bauhofer, J.Z. Kovacs, Compos. Sci. and Technol. 69, 1486 (2009)
W. Urbaniak-Domagala, J. Electrostat. 71, 456 (2013)
X.-Y. Qi, D. Yan, Z. Jiang, Y.-K. Cao, Z.-Z. Yu, F. Yavari, N. Koratkar, ACS Appl. Mater. Interfaces. 3, 3130 (2011)
G. Postiglione, G. Natale, G. Griffini, M. Levi, S. Turri, Compos. Part A: Appl. Sci. Manufac. 76, 110 (2015)
J. Zhang, B. Yang, F. Fu, F. You, X. Dong, M. Dai, Appl. Sci. 7, 20 (2017)
D. Zhang, B. Chi, B. Li, Z. Gao, Y. Du, J. Guo, J. Wei, Synth. Met. 217, 79 (2016)
Y.P. Mamunya, V.V. Davydenko, P. Pissis, E.V. Lebedev, Eur. Polymer J. 38, 1887 (2002)
A.S. Luyt, J.A. Molefi, H. Krump, Polym. Degrad. Stab. 91, 1629 (2006)
L. Yang, F. Liu, H. Xia, X. Qian, K. Shen, J. Zhang, Carbon 49, 3274 (2011)
B. Li, Y.-C. Zhang, Z.-M. Li, S.-N. Li, X.-N. Zhang, J. Phys. Chem. B 114, 689 (2010)
Z. Han, A. Fina, Prog. Polym. Sci. 36, 914 (2011)
B. Mortazavi, F. Hassouna, A. Laachachi, A. Rajabpour, S. Ahzi, D. Chapron, V. Toniazzo, D. Ruch, Thermochim. Acta 552, 106 (2013)
S.K. Das, N. Putra, P. Thiesen, W. Roetzel, J. Heat Transfer 125, 567 (2003)
I. Balberg, Carbon 40, 139 (2002)
S. Kirkpatrick, Rev. Mod. Phys. 45, 574 (1973)
T. Ota, M. Fukushima, Y. Ishigure, H. Unuma, M. Takahashi, Y. Hikichi, H. Suzuki, J. Mater. Sci. Lett. 16, 1182 (1997)
S.K. Bhattacharya, A.C.D. Chaklader, Polymer-Plastics Technol. and Eng. 19, 21 (1982)
K.S. Deepa, S. Kumari Nisha, P. Parameswaran, M.T. Sebastian, J. James, Appl. Phys. Lett. 94, 142902 (2009)
A. Rybak, G. Boiteux, F. Melis, G. Seytre, Compos. Sci. and Technol. 70, 410 (2010)
K. Miyasaka, K. Watanabe, E. Jojima, H. Aida, M. Sumita, K. Ishikawa, J. Mater. Sci. 17, 1610 (1982)
A. Kuriata, A. Sikorski, J. Mol. Model. 21, 56 (2015)
A. Dufresne, M. Paillet, J.L. Putaux, R. Canet, F. Carmona, P. Delhaes, S. Cui, J. Mater. Sci. 37, 3915 (2002)
V.S. Mironov, M. Park, C. Choe, J. Kim, S. Lim, H. Ko, J. Appl. Polym. Sci. 84, 2040 (2002)
W. Zhang, A.A. Dehghani-Sanij, R.S. Blackburn, J. Mater. Sci. 42, 3408 (2007)
Z.-D. Xiang, T. Chen, Z.-M. Li, X.-C. Bian, Macromol. Mater. Eng. 294, 91 (2009)
J. Vilc̆áková, P. Sáha, V. Kr̆esálek, O. Quadrat, Synth. Met. 113, 83 (2000)
C.-L. Dai, Sens. Actuators B 122, 375 (2007)
E. Terzic, C.R. Nagarajah, M. Alamgir, Eng. Appl. Artif. Intell. 23, 614 (2010)
W.H. Ko, Q. Wang, Sens. and Actuators A: Phys. 75, 242 (1999)
A.O. Salazar, W. Dunford, R. Stephan, E. Watanabe, IEEE Trans. Magn. 26, 2541 (1990)
W. Qu, C. Wenzel, G. Gerlach, Sens. and Actuators A: Phys. 77, 14 (1999)
Acknowledgements
The authors are grateful for financial support from Warsaw University of Technology, Faculty of Mechatronics, Institute of Metrology and Biomedical Engineering and Foundation for Polish Science project nr First TEAM/2016-1/7.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Podsiadły, B., Skalski, A., Wałpuski, B. et al. Heterophase materials for fused filament fabrication of structural electronics. J Mater Sci: Mater Electron 30, 1236–1245 (2019). https://doi.org/10.1007/s10854-018-0391-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10854-018-0391-4