Abstract
The highly cross-linked thermosetting polymers used as adhesives and as the matrices of fibre composites for the construction of lightweight vehicles are very brittle, and finding effective toughening solutions for such engineering applications is a long-standing problem. An anhydride-cured thermosetting epoxy polymer has been modified by the addition of different wt% of silica nanoparticles, core–shell rubber particles and hybrids with equal wt% of both. The fracture energy was measured at ambient and low temperature (− 40 °C and − 80 °C) to understand the brittle fracture behaviour. The fracture and toughening mechanisms were identified by scanning electron microscopy of the fracture surfaces. Analytical models were used to predict the modulus and fracture energy; the predictions agreed very well with the measured values. Toughening using silica nanoparticles is especially efficient at low particle contents. This shows how epoxies can be toughened successfully for use in industrial and transport applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Epoxies are thermosetting polymers which are used as adhesives, coatings and matrices of fibre-reinforced composites. They exhibit many useful properties such as a high modulus, high service temperature and no creep due to their highly cross-linked structure. However, this microstructure makes epoxies extremely brittle, and they have a poor resistance to the initiation and propagation of cracks from the defects which are naturally present. In service, the epoxy will experience static, cyclic or impact loading. Due to this brittle nature, the resultant stresses will cause further damage or propagation of existing cracks, which will greatly affect the lifetime of the component and may lead to catastrophic failure [1,2,3]. It is difficult to detect cracks in adhesively-bonded and fibre-composite structures, as the critical flaw size is very small due to their brittle nature, so the epoxies must be modified to prevent premature failure [1,2,3]. They are used in safety-critical structural applications, as they enable lightweight construction and promote fuel efficiency, for example in the construction of aircraft, cars and ships [4, 5]. It is thus essential to increase the toughness of epoxies.
The addition of a rubber [6,7,8], thermoplastic [9, 10] or block copolymer phase [11] which is soluble in the resin but phase-separates during curing of the epoxy is commonly used to toughen epoxy polymers. Among these, a very successful approach has been the addition of carboxyl-terminated butadiene acrylonitrile (CTBN) rubber which phase-separates into micron-sized particles during curing [12]. Thermoplastics such as polyethersulfone and polyetherimide have also been used [13,14,15]. Recently, different forms of rubber modifiers such as block copolymers have been used, and these can form complex microstructures [16]. The microstructure produced is dependent on the concentration used and the curing conditions (e.g. temperature, time, rate). Such modifications initiate multiple toughening mechanisms which absorb energy and increase toughness. These modifications can be very effective, resulting in tough thermoset materials, but they can lower significantly the glass transition temperature, Tg, and degrade the other properties if there is not complete phase separation [14, 15]. They also greatly increase the viscosity of the epoxy resin, which makes processing and manufacturing using the modified materials much more difficult and expensive.
An effective alternative to these phase-separating modifiers is to use pre-formed particles such as rubber [8], thermoplastic [14] or ceramic [17] particles which will increase the toughness without reducing the Tg of the epoxy polymer. Such rubber particles are generally core–shell particles, with a soft rubbery core surrounded by a harder shell of polymethylmethacrylate [18]. The toughening mechanisms have been identified as shear band yielding and plastic void growth after cavitation of the rubbery cores of the particles [16]. However, at low temperatures the rubber particles become much harder to cavitate due to their increased modulus, and so any toughening effect may be lost. Pre-formed thermoplastic particles such as polyamide [19, 20] can be used in toughening of epoxy. Ceramic particles such as boron nitride and silicon nitride can increase the toughness of epoxy polymers while also increasing the modulus [17]. The toughening mechanisms have been identified as shear band yielding and plastic void growth after debonding of the ceramic particles. Although these mechanisms absorb energy and increase toughness, the toughening effect is generally less than that of pre-formed rubber particles [16]. Although the toughening effects of these particles have been studied, most of the work only covers a few selected weight percentages, so can only assume there is a linear increase in toughness for the weight percentages that are not covered [1, 21, 22]. At low concentrations, the toughness can increase rapidly as there is a large volume of matrix able to undergo the toughening mechanisms, so it may be more cost-effective to use small concentrations of such particles.
Moreover, combining small concentrations of particles may be more effective than using a large concentration of a single particle type, as a synergy may be observed between soft and hard particles, especially when combining relatively small and large particles (e.g. silica nanoparticles and micron-sized rubber particles) [23]. This is because the toughening mechanisms activated by large (micron size) and small (nanometre size) particles are different. For larger particles, the main toughening mechanisms are crack pinning, deflection and debonding (for hard particles) or cavitation (for soft particles) with void growth and shear yielding [24]. Crack pinning and deflection would not occur for very small particles, as these mechanisms require that the diameter of particle is larger than the crack opening displacement at the crack tip [24, 25]. Therefore, the toughening mechanisms found when using nanoparticles are debonding followed by void growth and shear yielding [21, 26].
The properties and toughness of epoxy polymers are known to be affected by temperature, especially at low temperatures, which they can experience in automotive, aerospace and cryogenic applications [27, 28]. Therefore, it is necessary to test epoxy polymers at both ambient and low temperature, and to understand their fracture behaviour under these different conditions. There is more concern about low temperature performance than elevated temperature, as the epoxy is further from its glass transition temperature. Further, when particulate tougheners are added, it is essential to know whether the toughening mechanisms which are observed at ambient temperature are still operative and are as effective, at low temperatures.
It is expected that more brittle failure will occur when epoxy is tested at low temperatures [27], but no major changes are reported on the fracture surfaces and with the toughening mechanisms [28]. Mechanical testing at low temperature is not commonly performed for particle-modified epoxy polymers, but is more common for particle-modified epoxy composite laminates [29]. The addition of particles increases the fracture energy of the material, but the effect at low temperature is not always clear [28, 29]. This can be due to the different mechanisms which occur in the composite, such as variations in the fibre to matrix adhesion, in addition to the fracture in the matrix [28, 30, 31]. Testing the epoxy polymer allows characterisation without the influences from fibre interactions, confirming the effectiveness of the particle-reinforced epoxy at low temperature.
A typical epoxy polymer is considered in the present work. The effect on the fracture energy of the addition of silica and core–shell rubber (CSR) particles, both individually and when combined to form a hybrid, especially at low wt%, is studied. The room temperature results are compared with tests performed at low temperature. The toughening mechanisms are identified using scanning electron microscopy, and their relative contributions predicted using an analytical model. Understanding the failure mechanisms of these particle-modified epoxies helps in designing the best formulation for the conditions of application to prevent failure. This will enable lightweight, fuel-efficient and safer structures to be produced for transport applications.
Materials
Epoxy polymer
An anhydride-cured epoxy polymer was used. The epoxy resin was Araldite LY 556 (Huntsman Advanced Materials, Belgium), which is a diglycidyl ether of bisphenol A (DGEBA) with an epoxy equivalent weight (EEW) of 185 g/mol and a density of 1.175 g/ml. The hardener was Albidur HE-600 (Evonik, Germany), which is an accelerated methylhexahydrophthalic acid anhydride with an anhydride equivalent weight (AEW) of 170 g/mol and a density of 1.08 g/ml. These were used at a stoichiometric ratio of 1:1.09 of resin/hardener by weight. When cured at 165 °C, the epoxy polymer has a glass transition temperature, Tg, of 143 °C, as measured using differential scanning calorimetry (DSC) [26].
Silica nanoparticles
The silica nanoparticles used were Nanopox F400 (Evonik, Germany), which is a masterbatch of 40 wt% of silica nanoparticles in DGEBA and has a density of 1.4 g/ml [32]. The silica nanoparticles have a mean diameter of 20 nm [32]. The concentrations of silica nanoparticles used were chosen to be between 0.5 wt% and the maximum possible concentration of 25.4 wt% that can be used while maintaining the same stoichiometry (Table 1).
Core–shell rubber particles
The core–shell rubber (CSR) particles used were Paraloid EXL-2300G (Rohm and Haas, UK). These are an all-acrylic core–shell impact modifier based on butyl acrylate rubber [33], which are intended to improve the toughness, elongation at break and fatigue resistance of epoxy resins [34]. The particles were supplied in powder form with a density of 1.1 g/ml. They were sieved into three sizes: > 106 μm, between 106 μm and 38 μm, and < 38 μm. The intermediate fraction of between 106 μm and 38 μm was used in this work. These particles were found to be not individual particles but agglomerates of smaller particles, as will be discussed later on. Specimens containing between 0.5 wt% and the maximum concentration of 10 wt% of CSR were produced (Table 1), as 10 wt% was the highest possible content which was suitable for mixing the CSR particles into the epoxy, due to the increased viscosity.
Core–shell rubber/silica hybrid
The hybrid formulations used equal contents of silica nanoparticles and core–shell rubber particles mixed into the epoxy, for example the 1 wt% hybrid contains 1 wt% of silica and 1 wt% of CSR (Table 1). A maximum hybrid concentration of 10 wt% CSR and 10 wt% of silica was used, as this was the highest possible wt% from which plates could be cast due to the high viscosity of the hybrid-modified resin.
Experimental procedure
Epoxy plate preparation
Plates of epoxy were cast in release-coated metal moulds. Single-edge notch bending (SENB) specimens were machined from 6-mm-thick cast plates, and tensile specimens were machined from 3-mm-thick plates.
To manufacture the plates, all parts of the metal moulds were cleaned using acetone and then coated with release agent (Frekote 700-NC from Loctite, UK). The moulds were clamped firmly and preheated to 60 °C in a fan oven. The epoxy resin, modifiers and hardener were stirred using an RZR overhead mixer (Heidolph, Germany) at 90 rpm for 15 min. The mixture was degassed at 60 °C in a vacuum oven until the air bubbles were drawn out, and then poured into the preheated moulds. The moulds were placed into the fan oven, and the temperature was ramped at 1 °C/min to 95 °C, held for 1 h, then ramped at 1 °C/min to 165 °C, and held for 2 h. The moulds were allowed to cool in the oven, and the cast plates removed.
Tensile test procedure
Dumbbell geometry specimens, of type 1BA according to the ISO 527 standard [35], were machined from the 3-mm-thick cast plates using a table-mounted router (Festool OF200 EB).
The tests were performed in tension at room temperature and at a displacement rate of 1 mm/min using a universal testing machine (3369 from Instron, UK). The strain in the gauge length was measured using a clip-on extensometer, model 2620-601 (Instron, UK). The Young’s modulus, E, was calculated from the slope of the stress versus strain curve. The modulus was calculated by using linear regression of the experimental data over an interval from a strain of 0.025% to 0.075% as recommended by the Standard [35].
Room-temperature fracture test procedure
Single-edge notch bending (SENB) samples were machined from the cast plates. The samples were 6 mm in thickness, 12 mm in width and 60 mm in length according to the ISO 13586 standard [36]. Six specimens were prepared for each formulation. For each specimen, a 4-mm-deep notch was machined and a natural crack was made by tapping a liquid nitrogen-chilled razor blade into the notch. Test specimens would be rejected if the cracks produced were not at least four times the length of the notch tip radius or if the crack length was 10% more than 6 mm [36].
The SENB tests were performed at a constant displacement rate of 10 mm/min using an Instron 3369 universal testing machine. The maximum load was recorded, and the linear elastic fracture mechanics (LEFM) method was used to calculate the fracture energy.
The fracture toughness, Kc, can be calculated using [36]:
where Pc is the load at crack growth initiation, B is the specimen thickness, W is the specimen width and
where x = a/W, and where a is the crack length.
The fracture energy can be calculated from the fracture toughness by the LEFM method [36] using:
where v is the Poisson’s ratio and E is the measured tensile Young’s modulus. For epoxies, the value of Poisson’s ratio is commonly taken as v = 0.35 [21, 37].
Low-temperature fracture test procedure
Low-temperature fracture tests were performed at − 40 °C and − 80 °C. The SENB test setup was placed in a temperature chamber which was cooled by injecting controlled quantities of cold nitrogen gas, from a supply of liquid nitrogen, into the chamber. The SENB specimens were placed inside the chamber for 5 min to reach the same temperature as the environment before testing. Tests were performed at the quasi-static rate of 10 mm/min, as used for the ambient temperature tests. After one test had finished, the next test was performed only after the chamber temperature had returned to the set level, to ensure that all the tests were performed under the same conditions.
The fracture toughness was calculated using the same method as at room temperature. The values were converted to the fracture energy using the tensile modulus measured at room temperature, as the variation in modulus with temperature over this range is known to be relatively small [36].
Scanning electron microscopy
Scanning electron microscopy (SEM) was used to investigate the fracture surfaces of the SENB specimens after testing. This allowed the microstructure and the dispersion of particles to be identified, as well as the toughening mechanisms that they initiated.
The broken SENB samples were cut to a thickness of about 2 mm and attached to a sample holder using conductive tape. Electrical conductivity of the specimens was ensured by applying a line of silver paint on the side of the specimens, to provide conductivity between the fracture surface and the sample holder. For the high-magnification images, a conductive coating was sputtered onto the surface of the specimens to prevent charging using an EMI TECH K575X coater at 120 mA for 1 min. Field emission gun scanning electron microscopy (FEG-SEM) was performed using a LEO Gemini 125 (Carl Zeiss, Germany). An accelerating voltage of 5 kV was used for imaging. For the low-magnification images, gold was sputtered onto the surfaces using an Agar Automatic Sputter Coater. Scanning electron microscopy was performed using an S-3400 N microscope (Hitachi High Technologies, UK), using an accelerating voltage of 10 kV.
Results
Introduction
The results from tensile testing will be discussed first, as the tensile modulus is also required for the LEFM method used to calculate the fracture energy from the measured data for the SENB tests. The results from the room-temperature and the low-temperature SENB tests are then presented. In all cases, the values from the unmodified epoxy, silica-modified, CSR-modified and hybrid-modified (silica plus CSR) formulations are presented. Finally, representative scanning electron microscopy (SEM) images of the SENB fracture surfaces of the epoxy modified with each particle type (silica, CSR and hybrid) are shown, and the fracture behaviour of the materials and the toughening mechanisms are discussed.
Tensile tests
Unmodified epoxy
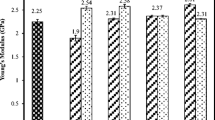
A Young’s modulus of 3.14 GPa was measured for the control epoxy (Table 2), which is identical to the value reported by Masania et al. [38] for this epoxy polymer.
Silica-modified epoxy
When silica nanoparticles were added to the epoxy, the modulus generally increased with the increased amount of particles added in (Table 2). This is as expected because silica has a much higher modulus, of 70 GPa [39], compared to that of the epoxy (3.14 GPa). The significance of the increases in modulus will be discussed with the results of the analytical modelling in the “Tensile modulus prediction” section. Tensile strength information is given in Table 3, and shows that the tensile strength is independent of the silica nanoparticle wt%, as expected due to the small size of the particles.
Core–shell rubber-modified epoxy
The addition of CSR particles increased the Young’s modulus of the epoxy up to 5 wt%, where a value of 3.90 GPa was measured (Table 2). It may be expected that the addition of the CSR particles would reduce the Young’s modulus of the specimens, because the rubber core will have a much lower modulus than that of the epoxy. However, the small increases in the modulus values indicate that the PMMA shell has a higher modulus compared to the epoxy and this causes the overall increase.
There was a significant reduction in the modulus value when the concentration of CSR was increased from 5 wt% to 10 wt%. This is due to agglomeration of the CSR particles, as could be seen on the fracture surfaces, which had a different appearance compared to the other wt% of CSR, and as will be discussed below with the results from the SEM imaging (“Core–shell rubber-modified epoxy” section). This indicates that the optimum concentration of CSR particles is below 10 wt%. The tensile strength (Table 3) reduces with increasing wt% of CSR due to the relatively large size of the particles, which act as defects and cause premature failure of the epoxy.
Silica/core–shell rubber-modified epoxy
The hybrids containing equal wt% of silica and core–shell rubber particles did not show significant changes in their tensile properties compared to the addition of silica only (Table 2). The increases were within the experimental error, confirming that the addition of CSR only gives a relatively small increase in modulus due to the presence of the PMMA shells. The use of 10 wt% of CSR in the hybrid gave a decrease in the modulus, which is likely to be due to agglomeration as for the epoxy with 10 wt% of CSR only.
Room-temperature fracture tests
Unmodified epoxy
For the control epoxy, a fracture energy of Gc = 68 J/m2 was measured using SENB tests at room temperature (Table 4). This agrees within experimental error with the value of 77 J/m2 quoted in the literature for this epoxy by Hsieh et al. [21]. This confirms that the unmodified epoxy is very brittle.
Silica-modified epoxy
When the 20-nm silica nanoparticles were added to the epoxy, there was an approximately linear increase in fracture energy as the wt% of silica increases up to 15 wt% (Table 4). However, at low silica contents, the increase in fracture energy is greater than linear, indicating that the silica nanoparticles are more effective at toughening at low contents. The significant increase at low silica content is of interest, as this has not been reported in previous work where the smallest content of silica nanoparticles used was 4 wt%, e.g. [21, 37, 40], and this will be discussed further with the results of the predictive modelling. At 15 wt% of silica and above, the fracture energy values reach a plateau at approximately 220 J/m2 (Fig. 1). These values agree well with those quoted in the literature [21, 37].
Core–shell rubber-modified epoxy
The addition of CSR particles to the epoxy gives a small increase in fracture energy to 96 J/m2 (Table 4). However, there is a notable plateau as the fracture energy barely increases when the wt% of CSR particles is increased, and a maximum fracture energy of 108 J/m2 was measured using 10 wt% of CSR (Fig. 2). Thus, the increases in fracture energy values for the intermediate wt% of CSR were not significant. Some agglomeration of the CSR particles occurs, which may reduce the toughening effect.
The CSR particles are not individual particles but are aggregates of much smaller particles (of about 300 nm in diameter). As these particles are relatively small, they will be relatively difficult to cavitate [41]. If they are poorly bonded to other particles in the aggregate, then the triaxial stresses within the plastic zone may be insufficient to cause cavitation and hence some of the potential toughening mechanisms are not activated. The small particles are not surrounded by epoxy, so the toughening mechanisms which rely on deformation of the epoxy can be expected to not be fully operative. Thus, the toughening effect is smaller than might be expected for core–shell rubber particles.
Silica/core–shell rubber-modified epoxy
There was a steady increase in fracture energy when the wt% of silica/CSR particles added into the epoxy increases (Fig. 3). The hybrid with 10 wt% of silica and CSR particles showed the largest improvement in fracture energy, but no synergy was found, i.e. there was no extra increase due to the addition of both types of particles. The agglomeration observed for the CSR-modified epoxies was also seen for the silica/CSR hybrid specimens, and this could explain why no synergy occurs. Indeed, the hybrids show similar fracture properties as when using one type of particle and this suggests that this combination of particles does not have a significant effect in improving the fracture energy of the epoxy.
Low-temperature fracture tests
Unmodified epoxy
The low-temperature SENB tests gave higher fracture energy values than at room temperature for the unmodified epoxy, and the values were higher when the temperature was lower; see Figs. 1, 2 and 3. At room temperature, an average fracture energy of 68 J/m2 was measured, increasing to 93 J/m2 at − 40 °C and 126 J/m2 at − 80 °C.
Silica-modified epoxy
For the silica-modified epoxy, the results of the low-temperature SENB tests are shown in Fig. 1. There was a significant increase in the measured fracture energy at all wt% of silica when tested at − 80 °C compared to the room-temperature tests. The increase was more significant with a high wt% of silica nanoparticles, as a nearly 50% increase in fracture energy was measured (e.g. for 25.4 wt% of silica the room-temperature fracture energy is 223 J/m2, compared with 349 J/m2 at − 80 °C). At − 40 °C, there was no significant difference in the fracture energies compared to the room-temperature values (Fig. 1) as the standard deviations overlap.
Core–shell rubber-modified epoxy
The results of the low-temperature SENB tests of the CSR-modified epoxy are shown in Fig. 2. The fracture energy is approximately doubled for most of the specimens tested at − 80 °C when compared to the room-temperature tests. There was an increasing trend in fracture energy when the wt% of particles increased. This trend was also seen for the tests performed at − 40 °C, but the fracture energy values were very similar to the room-temperature results for all wt%. There was a plateau when the wt% of CSR particles added in was high (at 10 wt%). This suggests that the high wt% use of CSR is not the optimum for toughening and that using a medium-to-lower wt% (2–5 wt%) would be most appropriate, as increasing the wt% further has no additional toughening effect. This indicates that the agglomeration which occurs at 10 wt% also influences the Gc value.
Silica/core–shell rubber-modified epoxy
The trend for an increase in fracture energy with increase in wt% of particles used was notable in the hybrid silica/CSR specimens for all temperature conditions (Fig. 3). However, the magnitude of the increase in fracture energy for the low-temperature tests was not as significant as with the use of only one type of particle. The fracture energy values were similar to those using CSR only, which were smaller than the silica results. The optimum amount of hybrid particles at low temperature is 10 wt% (i.e. 10 wt% of CSR plus 10 wt% of silica), as this concentration gave the highest fracture energy.
Summary
At room temperature, the fracture energy increases with the increase in wt% of particles, and no synergy was found with the use of hybrid silica/CSR particles.
At low temperature, the lower temperature (− 80 °C) gave higher fracture energy values for most specimens. This trend of increasing fracture energy with increasing wt% of particles is clearer and more significant when compared to room-temperature results. This showed that the effect of toughening was more significant when the materials experienced more brittle failure at lower temperatures [31, 42, 43].
The measured fracture energies are compared with analytical modelling predictions [21, 37, 44] in the “Analytical modelling” section.
Fractography
Unmodified epoxy
The fracture surfaces of the SENB unmodified epoxy specimens tested at room temperature were compared with the low-temperature fracture surfaces, and no significant differences were found between the different conditions. The surfaces were relatively smooth, with river lines parallel to the direction of local crack propagation, indicating that little energy is absorbed during fracture. A scanning electron microscope image of the fracture surface of the unmodified epoxy at room temperature is shown in Fig. 4.
Silica-modified epoxy
SEM images of the fracture surfaces of the silica-modified epoxy are shown in Fig. 5. Individual silica nanoparticles can be seen, and some possible voids can also be found in some images; see Fig. 5c for example. With silica particles of 20 nm in diameter, the voids formed by debonding of the epoxy from the silica followed by plastic void growth would be expected to be about 35 nm in diameter. This is because the void will grow until the circumferential strain is equal to the strain to failure measures from plane strain compression tests. Thus, the void grows until the void diameter = particle diameter x (1 + strain to failure), where the strain to failure measured in plane strain compression is 0.75 [21]. The smallest voids found in Fig. 4a were 33 nm in diameter, indicating that the observed voids were formed by debonding and void growth.
Similar results were found for the samples containing 5, 10, 15 and 25.4 wt% of silica nanoparticles. Some particles can be seen on the fracture surfaces, with some debonding and void growth of particles (Fig. 5a–c). When the wt% of particles was low, the surfaces appear relatively brittle and smooth as expected due to the low toughness. When the wt% of particles used was high, more particles can be seen on the fracture surfaces. The particles initiate toughening mechanisms and hence increase the roughness of the surface, so at high wt% the surfaces become very rough.
Core–shell rubber-modified epoxy
SEM images of the fracture surfaces of the CSR-modified epoxies are shown in Fig. 6. The CSR particles were distinct from the epoxy matrix at low wt%, as the epoxy is smooth and brittle and the CSR particle aggregates appear as light-coloured rough patches through which the crack propagates. At high wt%, the surface becomes much rougher and it is harder to distinguish the matrix from the CSR particle aggregates. Some agglomeration of the CSR particles can be seen on the fracture surfaces; see Fig. 6b for example.
The CSR particles are aggregates, typically 50 μm in diameter, of small CSR particles which are about 300 nm in diameter, as shown at higher magnification in Fig. 7. These small (primary) CSR particles cavitated during fracture to leave a void within the shell, as indicated by the dark circles within the light rings in Fig. 7b.
The aggregates of CSR particles were not observed to debond from the epoxy matrix, as no dark ring that would indicate a cavity formed by debonding was present around the aggregates; see Figs. 6 and 7a. Although the aggregates are much larger than the diameter of the plastic zone, evidence of toughening mechanisms such as crack pinning or crack deflection was not observed on the fracture surfaces as the crack propagated through the aggregates.
Silica/core–shell rubber hybrid-modified epoxy
SEM images of fracture surfaces of the silica/CSR hybrid-modified epoxy are shown in Fig. 8, and a higher-magnification image is shown in Fig. 9. The agglomerates of CSR particles can be readily identified in the silica/CSR hybrid-modified epoxy images, but it is much harder to identify the silica nanoparticles due to their small size and the roughness of the fracture surfaces. River lines are present on the surfaces (see Fig. 8b for example) which are typical for crack propagation in brittle polymers due to the crack being slowed when it propagates through an aggregate of CSR particles.
Fractography summary
The main toughening mechanisms identified using SEM in the silica-modified epoxy were debonding of the silica nanoparticles and subsequent void growth of the epoxy polymer. For the CSR-modified epoxy, particle cavitation was the main toughening mechanism, followed by void growth of the epoxy. A synergy effect was not found with the addition of silica/CSR hybrid particles, but the toughening mechanisms identified for the single particle-modified epoxies were also observed for the hybrids. Shear band yielding has been observed extensively in previous studies [21, 38, 45] using this epoxy and with the addition of the same silica nanoparticles, so it can be readily concluded that shear band yielding will also occur in the present work.
Analytical modelling
Introduction
Analytical models were used to predict the modulus and fracture energy of the modified epoxies. This method also identifies the effect of relative contributions of the different particles in hybrid systems, as well as the presence of any synergistic effect. The Halpin–Tsai model [21, 26, 37] was used to predict the tensile modulus of the materials, and the Huang and Kinloch model [21, 26, 37] was used to predict the fracture energy increase from the observed toughening mechanisms.
Tensile modulus prediction
The Halpin–Tsai model
The Halpin–Tsai model predicts the modulus, E, of a particle-modified material using [46]:
where Eu is the Young’s modulus of the matrix, vf is the volume fraction of particles, ζ is the Halpin–Tsai geometry factor, which is equal to 2 for spherical particles [21, 26, 37], and η can be written as:
where Ep is the modulus of the particles (70 GPa for the silica nanoparticles) and Eu is the modulus of the unmodified epoxy (3.14 GPa, as measured in the present work). The hybrid-modified epoxy predictions assume that the modulus for the hybrid-modified epoxy is equal to the sum of the increases due to the addition of each particle type.
Silica-modified epoxy modulus
The predicted modulus values of the silica-modified epoxies are shown in Fig. 10. Most of the predicted modulus values agree very closely to the measured values. There was a linear increase in modulus in the predictions when the wt% of silica nanoparticles increased, and the gradient of the linear increase was very similar to that measured experimentally. This shows that the Halpin–Tsai model works well for the silica-modified epoxy. It also confirms that the assumption that the modulus of the silica nanoparticles is equal to that of bulk silica (i.e. Ep = 70 GPa) [39] is reasonable.
Core–shell rubber-modified epoxy modulus
As the effective modulus of the CSR particles is unknown, this value was back-calculated from fitting to the experimental results at low CSR contents, and a value of Ep = 8.0 GPa was obtained. The predicted modulus values of the CSR-modified epoxy are shown in Fig. 11. The agreement becomes poor when the wt% of particles is increased, and there is a reduction in the measured modulus at 10 wt% of CSR, which is due to clustering of the particles. (Note that 10 wt% was the highest possible wt% of CSR that can be added to the resin as the viscosity became too high at larger CSR contents.) The predicted value suggests that a higher modulus could be obtained with a better distribution of particles at 10 wt% CSR.
Although the rubber core of the CSR particles will have a low modulus when compared to the epoxy, the modulus of the CSR-modified epoxy increases with wt%. This indicates that a stiffer shell is present, and the PMMA shell of the CSR particles has a modulus higher than that of the epoxy.
Hybrid-modified epoxy modulus
The predicted modulus values for the silica/CSR hybrid-modified epoxy are shown in Fig. 12. The hybrid predictions were made by adding the modulus increase contributed from the predictions for each of the two particle types. A similar pattern of results was found in the hybrid-modified epoxy predictions compared to the individual particles when compared to the experimental results, with reasonable agreement at low particle contents. There is also a drop in the modulus for the 10 wt% silica/CSR hybrid specimens, as was observed for the 10 wt% CSR specimens due to the presence of agglomerates.
Summary
The predicted modulus values generally agreed extremely well with the experimental findings. The silica-modified epoxy predictions agreed best with the experimental results. The modulus of the CSR-modified epoxy was expected to be lower than the modulus of the unmodified epoxy, because the modulus of rubber is lower than epoxy. However, the PMMA shell of the CSR particles increases the modulus, and hence slightly increased modulus values were found for the CSR-modified epoxy. This pattern continues for the silica/CSR hybrid-modified epoxy. Where a drop in the modulus was measured, when using 10 wt% of CSR, this was observed to be due to clustering of the particles.
Fracture energy prediction
The Huang and Kinloch model
The fracture energies of the modified epoxies can be predicted using the Huang and Kinloch model, which considers that the contributions from the various toughening mechanisms can be added to the fracture energy of the unmodified epoxy. The overall fracture energy can be written [47] as:
where Gu is the fracture energy of the unmodified epoxy and Ψ is the sum of the overall toughening contributions from the particles.
Considering the toughening mechanisms, shear band yielding occurs when particles are added to this epoxy, as shown by Hsieh et al. [21]. This is the case for both the silica nanoparticles and the core–shell rubber particles. For rubber-modified epoxies, the rubber particles may cavitate to create voids, which then increase in diameter by plastic deformation of the epoxy [48]. For silica-modified epoxies, the particles can debond to create voids, which then grow by plastic deformation of the epoxy [49]. These processes absorb energy and hence increase the toughness.
Fracture energy representation
There will be a contribution to Ψ from each of the identified toughening mechanisms. The increase in fracture energy due to shear banding is ΔGs, the contribution from debonding (or cavitation) of particles is ΔGdb, and that from plastic void growth is ΔGv [50]. Hence:
Debonding occurs for hard particles, while cavitation occurs for soft particles [37], but both processes create a void which is then able to grow. However, it has been shown that debonding or cavitation does not contribute significantly to the energy absorption [37] and hence can be ignored, i.e. ΔGdb = 0 J/m2. Therefore, Eq. 7 becomes [47]:
The contributions of shear band yielding and void growth can be calculated using the equations [47, 50] below.
Contribution from shear band yielding
The fracture energy contribution of shear band yielding, ΔGs, is given [37, 47] by:
where vf is the volume fraction of particles, σycu is the compressive yield stress, γfu is the compressive failure strain of the unmodified polymer (measured from plane strain compression tests) and [47, 50]:
where rp is the radius of the particles, and the radius of the plastic zone, ry, is given by:
where Ksp is the maximum stress concentration around a particle, µm = 0.2 is a material constant, and rpzu is the radius of plastic deformation zone of the unmodified epoxy, as discussed below. The value of Ksp is a function of the volume fraction of particles, vf, and can be expressed [37] as:
The values of the compressive yield stress, σycu, and the compressive failure strain, γfu, are taken from Hsieh et al. [21] (Table 5).
Contribution from plastic void growth
The fracture energy contribution from plastic void growth, ΔGv, is given [37, 47] by:
where vfv is the volume fraction of voids, vf is the volume fraction of particles, µm is a material constant, σycu is the compressive yield stress of the unmodified polymer and rpzu is the radius of plastic zone at fracture. The stress concentration factor for voids, Kv, depends on the volume fraction of particles, vf, and can be expressed [37] as:
The values required for the modelling are quoted in Table 5.
It has been reported that generally 100% of the rubber particles cavitate, but cavitation is easier for soft and large particles, so small particles or those with a stiffer rubber core may not cavitate [24].
For silica-modified epoxies, previous work has shown that if debonding does occur, not all of the silica nanoparticles will undergo debonding. Experimental measurements have shown that between 10 and 15% of the silica nanoparticles debond [21, 51]. This has been confirmed by theoretical work by Bray et al. [51] which showed that debonding is highly affected by the distances between particles. This work showed that once a silica particle debonds then its nearest neighbours can no longer debond due to the changes in the stress state around the particles. The theoretical prediction is that only 1/7 of the randomly dispersed nanoparticles would be able to debond [21, 51]. Thus, only 14.3% of the silica nanoparticles will be able to undergo debonding and subsequent void growth.
Three different cases are therefore modelled in the present work:
-
1.
100% of particles show plastic void growth
-
2.
14.3% of particles show plastic void growth
-
3.
Shear band yielding only
For the silica-modified epoxy in the present work, the toughening mechanisms of shear band yielding and plastic void growth of the epoxy polymer after particle debonding are expected to result [52].
It is very difficult to measure the volume fraction of voids from SEM of the fracture surfaces, especially for the silica nanoparticles, due to the small diameter of the particles. However, it is possible to predict the void diameter, and hence the volume fraction of voids, vfv, can be calculated by assuming that a void will grow until the circumferential strain equals the failure strain measured from plane strain compression tests of the unmodified epoxy. The predicted radius of a void is given by [51]:
where \( \gamma_{\text{fu}} \) is the failure strain measured in the plane strain compression test and \( r_{\text{p}} \) is the particle radius. This makes the analytical modelling truly predictive. If the volume fraction of voids was measured from the fracture surfaces, then the fracture tests would need to be performed before the modelling can be done, so the results are not properly predictive.
Plastic zone size
Localised plastic deformation is often the main energy dissipation mechanism in brittle materials. With the use of linear elastic fracture mechanics (LEFM), the radius of the plane strain plastic deformation zone is required for the prediction of the fracture energy using the equations above and can be found from the equations below [53, 54].
For the unmodified epoxy, the radius of the plane strain plastic deformation zone, rpzu, is given by:
where Eu is the modulus, Gcu is the fracture energy, v is the Poisson’s ratio and σytu is the tensile yield stress of the unmodified epoxy.
For the nanoparticle-modified epoxy, the radius of the zone is given by:
where \( \mu_{\text{m}} \) is the coefficient of increase in shear yield stress with hydrostatic pressure, which for epoxy is between 0.175 and 0.225. The value of Kvm depends on the volume fraction of particles, vf, and can be expressed as [55]:
The parameters used in the equations are listed in Table 5.
Silica-modified epoxy fracture energy
The fracture energy predictions for the silica-modified epoxy are compared with the measured values in Fig. 13. The 14.3% of void growth with shear predictions agree best with the experimental results when compared with the other assumptions used, which confirms that shear band yielding does occur although it cannot be observed using the scanning electron microscope. Note that the 100% void growth predictions are not shown in Fig. 13 as they greatly overestimate the fracture energy, as expected. The measured values agree very well with those by Hsieh et al. [37]. The predictions from the present work are slightly lower than those from Hsieh et al. due to the lower measured fracture energy of the unmodified epoxy.
The measured increase in fracture energy per wt% of silica added is the greatest at low silica contents, indicating that the silica nanoparticles are most effective at toughening when the well-dispersed particles are surrounded by a significant volume of epoxy which is able to deform plastically and absorb energy. The significant increase at low silica content is of interest, as this has not been reported in previous work where the smallest content of silica nanoparticles used was 4 wt%, e.g. [21, 37, 40]. Fractography has identified the toughening mechanisms for silica-modified epoxy as shear band yielding plus debonding and void growth, supported by finite element modelling which has shown that only 1 in 7 (i.e. 14.3%) of the silica nanoparticles will debond [51]. However, the experimental data lie above the predictions for 14.3% of void growth with shear (Fig. 13), suggesting that when the silica nanoparticles are widely spaced, more than 14.3% may undergo debonding and void growth. Bray et al. [51] calculated that 14.3% of the particles would be expected to undergo debonding when the silica content was high, using 20 wt% of silica for their modelling work. They showed that once one particle debonds, the particles close to the void created would not debond, but that when the particles are well separated debonding will occur, which implies that at low silica contents more (or all) of the silica particles would be expected to debond. Inspection of the relative energies quoted [51] shows that when the epoxy contains 2.5 wt% of silica nanoparticles, the energy required to debond a particle is unaffected by whether other particles have debonded or not. It would therefore be expected that the experimental data for 1 wt% and 2 wt% of silica nanoparticles would agree well with predictions assuming shear band yielding plus debonding and void growth of 100% of the particles. These predictions are shown in Fig. 13, and the agreement is very good. This confirms that at low silica contents all of the particles undergo debonding and void growth, and hence the toughening effect is much more pronounced.
Core–shell rubber-modified epoxy fracture energy
The CSR particles were identified to be composed of aggregates of smaller CSR particles (Fig. 7a), as discussed above. The large aggregates of CSR were not observed to debond from the epoxy matrix, as no dark ring that would indicate a cavity formed by debonding was present around the aggregates; see Figs. 6 and 7a. Indeed, as the large aggregates are approximately 50 μm in diameter they are much larger than the diameter of the plastic zone (which is 5.2 μm for the unmodified epoxy, as calculated using Eq. 16). However, the small CSR particles were observed to undergo cavitation, as shown by the holes within the particle shells on the SEM images of the fracture surfaces. Although void growth may occur, the energy dissipated is relatively low, because the individual CSR primary particles are not surrounded by epoxy polymer and hence the energy dissipated by plastic void growth is much smaller than for well-dispersed particles, e.g. Giannakopoulos et al. [47].
The experimental results show a steep increase in fracture energy when using a small CSR content, and the toughness then remains approximately constant within the experimental error with increasing wt% of CSR. At the higher CSR contents used, the experimental data lie between the predictions for shear band yielding only and those for 14.3% of void growth with shear (Fig. 14). Note that the 100% void growth predictions are not shown in the graph as they are significantly higher than the experimental results. This indicates that the CSR particles are relatively ineffective at toughening, but that some energy is dissipated via the void growth mechanism.
Silica/CSR hybrid-modified epoxy fracture energy
The fracture energy predictions for the silica/CSR hybrid-modified epoxy are shown in Fig. 15. The fracture energy values for the hybrids of silica and CSR were calculated using the sum of the increases in the results of the two particles used, as there was equal wt% of each particle type used in the epoxy. Note that the 100% void growth predictions are not shown in the graph as they are significantly higher than the experimental results. The measured fracture energies are lower than those for the silica-modified epoxy and lie between the predictions for shear band yielding only and those for 14.3% of void growth only (Fig. 15). This indicates that there is no synergy between the particle types for the silica/CSR hybrid-modified epoxy. Indeed, the addition of the CSR particles to the silica-modified epoxy reduces the fracture energy values rather than increasing them. Thus, it can be concluded that the size ratio between the agglomerates of CSR particles and the silica nanoparticles is too large for a synergistic effect, which is seen when micron-sized CTBN particles are used with the silica nanoparticles, as shown in Hsieh et al. [37] and Kinloch et al. [40].
Summary
The fracture energy predictions from the Huang and Kinloch model, based on the identified toughening mechanisms, agree well with the experimental results. For the silica-modified epoxy, the predictions for 14.3% of void growth with shear yielding fit best with the experimental results and concur with the previous studies, e.g. [37]. The experimental data for the CSR-modified epoxy were found to lie between the predictions for shear band yielding only and those for 14.3% of void growth with shear, showing that the CSR particles were relatively ineffective. Further, there is no synergy between the particle types for the silica/CSR hybrid-modified epoxy as the size ratio between the agglomerates of CSR particles and the silica nanoparticles appears to be too large for a synergistic effect. For the silica-modified epoxy, the increase in fracture energy per wt% of silica added is the greatest at low silica contents, confirming that more than 14.3% of the particles undergo debonding and void growth at low silica contents, and hence the toughening effect is much more pronounced.
Conclusions
An anhydride-cured thermosetting epoxy polymer was modified by the addition of different wt% of silica nanoparticles, core–shell rubber particles and the hybrids of both with equal wt%. The modulus was measured at room temperature. Their fracture behaviour was compared at different temperatures (ambient, − 40 °C and − 80 °C) to investigate the toughening effect at low temperatures. Scanning electron microscopy was used to identify the fracture and toughening mechanisms. Analytical models were used to predict the modulus and fracture energy, and these values were compared with the experimental results.
A modulus of 3.14 GPa was measured for the unmodified epoxy. The addition of silica nanoparticles increased the modulus of the epoxy. Although CSR would be expected to reduce the modulus, the PMMA shell on the CSR particles increases its modulus; hence, higher modulus values were found in the CSR-modified epoxy. The use of hybrid silica/core–shell rubber particles only shows a small increase in the modulus.
Room-temperature SENB provided fracture energy values without brittle failure problem; toughening effect is found especially at intermediate wt% of particles used. Toughening effect is more significant when specimens are tested at low temperature; higher fracture energy values are found when the test temperature is lower. Most of the results under brittle failure from low-temperature SENB test had higher standard deviations due to difficulties in performing tests at specific low-temperature conditions required.
The fracture surfaces from the room-temperature SENB tests were compared with those from the low-temperature tests, and no significant differences were found. Scanning electron microscopy identified debonding of the silica nanoparticles and cavitation of the CSR particles, followed by plastic void growth of the epoxy matrix.
The observed toughening mechanisms were modelled analytically. The measured fracture energies for the silica-modified epoxy agreed well with the predictions assuming debonding and void growth for 14.3% of the particles plus shear band yielding. The agreement between the predictions and the measured values for the CSR-modified and hybrid-modified epoxies was less good, as the aggregated nature of the CSR particles meant that they absorbed less energy than the dispersed particles. It was shown that the silica nanoparticles are most efficient at toughening at low concentrations, when all of the silica particles can undergo debonding and void growth. This indicates that is the most efficient for small particle contents, hence the toughness plateaus at higher particle volume fractions.
References
Xiao C, Tan Y, Yang X, Xu T, Wang L, Qi Z (2018) Mechanical properties and strengthening mechanism of epoxy resin reinforced with nano-SiO2 particles and multi-walled carbon nanotubes. Chem Phys Lett 695:34–43
Liu H-Y, Wang G-T, Mai Y-W, Zeng Y (2011) On fracture toughness of nano-particle modified epoxy. Compos B Eng 42(8):2170–2175
Saraç İ, Adin H, Temiz Ş (2018) Experimental determination of the static and fatigue strength of the adhesive joints bonded by epoxy adhesive including different particles. Compos B Eng 155:92–103
Mallick PK (2010) 8—joining for lightweight vehicles. In: Mallick PK (ed) Materials, design and manufacturing for lightweight vehicles. Woodhead Publishing, Cambridge, pp 275–308
Sadek MM (ed) (1988) Industrial applications of adhesive bonding. Elsevier Applied Science Publishers, Barking
Ricciardi MR, Papa I, Langella A, Langella T, Lopresto V, Antonucci V (2018) Mechanical properties of glass fibre composites based on nitrile rubber toughened modified epoxy resin. Compos B Eng 139:259–267
Yahyaie H, Ebrahimi M, Tahami HV, Mafi ER (2013) Toughening mechanisms of rubber modified thin film epoxy resins. Prog Organ Coat 76(1):286–292
Sobrinho LL, Calado VMA, Bastian FL (2012) Effects of rubber addition to an epoxy resin and its fiber glass-reinforced composite. Polym Compos 33(2):295–305
Hourston DJ (1997) Toughening of epoxy resins with thermoplastics: 3. An investigation into the effects of composition on the properties of epoxy resin blends. Polym Int 42(4):349–355
Wu Z, Yi X-S, Wilkinson A (2017) Interlaminar fracture toughness of carbon fibre/RTM6-2 composites toughened with thermoplastic-coated fabric reinforcement. Compos B Eng 130:192–199
Wang J, Xue Z, Li Y, Li G, Wang Y, Zhong W-H, Yang X (2018) Synergistically effects of copolymer and core-shell particles for toughening epoxy. Polymer 140:39–46
Wise CW, Cook WD, Goodwin AA (2000) CTBN rubber phase precipitation in model epoxy resins. Polymer 41(12):4625–4633
Paluvai NRMS, Nayak SK (2014) Synthesis and modifications of epoxy resins and their composites: a review. Polym Plast Technol Eng 53(16):1723–1758
Hourston DJ, Lane JM (1992) The toughening of epoxy resins with thermoplastics: 1. Trifunctional epoxy resin-polyetherimide blends. Polymer 33(7):1379–1383
Jiang M, Liu Y, Cheng C, Zhou J, Liu B, Yu M, Zhang H (2018) Enhanced mechanical and thermal properties of monocomponent high performance epoxy resin by blending with hydroxyl terminated polyethersulfone. Polym Test 69:302–309
Bagheri R, Marouf BT, Pearson RA (2009) Rubber-toughened epoxies: a critical review. Polym Rev 49(3):201–225
Rybak A, Gaska K, Kapusta C, Toche F, Salles V (2017) Epoxy composites with ceramic core–shell fillers for thermal management in electrical devices. Polym Adv Technol 28(12):1676–1682
Quan D, Ivankovic A (2015) Effect of core–shell rubber (CSR) nano-particles on mechanical properties and fracture toughness of an epoxy polymer. Polymer 66:16–28
Kishi H, Uesawa K, Matsuda S, Murakami A (2005) Adhesive strength and mechanisms of epoxy resins toughened with pre-formed thermoplastic polymer particles. J Adhes Sci Technol 19(15):1277–1290
Espuche E, Girodet C, Sautereau H, Chabert B, Ganga R, Valot E (1996) Influence of the addition of thermoplastic preformed particles on the properties of an epoxy/anhydride network. J Mater Sci 31(11):2997–3002. https://doi.org/10.1007/BF00356014
Hsieh TH, Kinloch AJ, Masania K, Taylor AC, Sprenger S (2010) The mechanisms and mechanics of the toughening of epoxy polymers modified with silica nanoparticles. Polymer 51(26):6284–6294. https://doi.org/10.1016/j.polymer.2010.10.048
Imanaka M, Takeuchi Y, Nakamura Y, Nishimura A, Iida T (2001) Fracture toughness of spherical silica-filled epoxy adhesives. Int J Adhes Adhes 21(5):389–396
Manjunatha CM, Jagannathan N, Padmalatha K, Taylor AC, Kinloch AJ (2012) The fatigue and fracture behavior of micron-rubber and nano-silica particles modified epoxy polymer. Int J Nanosci 11(03):1240002. https://doi.org/10.1142/S0219581X12400029
Kinloch AJ (1990) Adhesion and adhesives: science and technology. Chapman and Hall, London
Mohammed RD, Johnsen BB, Kinloch AJ, Taylor AC, Sprenger S (2008) Toughening mechanisms of nanoparticle-modified epoxy polymers. In: NSTI nanotech 2008, Vol 1, technical proceedings. CRC Press-Taylor & Francis Group, Boca Raton
Johnsen BB, Kinloch AJ, Mohammed RD, Taylor AC, Sprenger S (2007) Toughening mechanisms of nanoparticle-modified epoxy polymers. Polymer 48(2):530–541. https://doi.org/10.1016/j.polymer.2006.11.038
Coronado P, Argüelles A, Viña J, Mollón V, Viña I (2012) Influence of temperature on a carbon–fibre epoxy composite subjected to static and fatigue loading under mode-I delamination. Int J Solids Struct 49(21):2934–2940
Coronado P, Argüelles A, Viña J, Viña I (2014) Influence of low temperatures on the phenomenon of delamination of mode I fracture in carbon-fibre/epoxy composites under fatigue loading. Compos Struct 112:188–193
Kalarikkal SG, Sankar BV, Ifju PG (2005) Effect of cryogenic temperature on the fracture toughness of graphite/epoxy composites. J Eng Mater Technol 128(2):151–157
Shindo Y, Inamoto A, Narita F, Horiguchi K (2006) Mode I fatigue delamination growth in GFRP woven laminates at low temperatures. Eng Fract Mech 73(14):2080–2090
Budhe S, Banea MD, de Barros S, da Silva LFM (2017) An updated review of adhesively bonded joints in composite materials. Int J Adhes Adhes 72:30–42
Evonik (2018) Nanopox F products technical bulletin. Evonik Industries, Geesthacht
Dow, Paraloid EXL-2300/3300 (2001), Rohm and Haas, UK
Paraloid EXL product site, Dow. https://www.dow.com/en-us/product-search/paraloidexl Accessed 24 March 2019
BS-EN-ISO-527-1 (1996) Plastics — determination of tensile properties — part 1: general principles. BSI, London
BS-ISO-13586 (2000) Plastics - determination of fracture toughness (GIC and KIC). Linear elastic fracture mechanics (LEFM) approach. BSI, London
Hsieh TH, Kinloch AJ, Masania K, Sohn Lee J, Taylor AC, Sprenger S (2010) The toughness of epoxy polymers and fibre composites modified with rubber microparticles and silica nanoparticles. J Mater Sci 45(5):1193–1210. https://doi.org/10.1007/s10853-009-4064-9
Masania K, Taylor AC, Kinloch AJ, Sprenger S (2009) The fracture of nanosilica and rubber toughened epoxy fibre composites. In: Proceedings of the annual conference of the Adhesion Society, Savannah USA
Pascoe KJ (1978) An introduction to the properties of engineering materials, 3rd edn. Van Nostrand Reinhold, London
Kinloch A, Mohammed R, Taylor A, Eger C, Sprenger S, Egan D (2005) The effect of silica nano particles and rubber particles on the toughness of multiphase thermosetting epoxy polymers. J Mater Sci 40(18):5083–5086. https://doi.org/10.1007/s10853-005-7261-1
Guild FJ, Kinloch AJ, Taylor AC (2010) Particle cavitation in rubber toughened epoxies: the role of particle size. J Mater Sci 45(14):3882–3894. https://doi.org/10.1007/s10853-010-4447-y
Charalambous G, Allegri G, Hallett SR (2015) Temperature effects on mixed mode I/II delamination under quasi-static and fatigue loading of a carbon/epoxy composite. Compos A Appl Sci Manuf 77:75–86
Shindo Y, Takeda T, Narita F, Saito N, Watanabe S, Sanada K (2009) Delamination growth mechanisms in woven glass fiber reinforced polymer composites under mode II fatigue loading at cryogenic temperatures. Compos Sci Technol 69(11):1904–1911
Huang Y, Kinloch AJ (1992) Modelling of the toughening mechanisms in rubber-modified epoxy polymers—part I finite element analysis studies. J Mater Sci 27(10):2753–2762. https://doi.org/10.1007/BF00540702
Chong HM (2015) Toughening mechanisms of block copolymer and graphene nanoplatelet modified epoxy polymers. PhD thesis, Imperial College London
Halpin JC, Kardos JL (1976) Halpin-Tsai equations: a review. Polym Eng Sci 16(5):344–352
Giannakopoulos G, Masania K, Taylor AC (2011) Toughening of epoxy using core–shell particles. J Mater Sci 46(2):327–338. https://doi.org/10.1007/s10853-010-4816-6
Chen J, Kinloch AJ, Sprenger S, Taylor AC (2013) The mechanical properties and toughening mechanisms of an epoxy polymer modified with polysiloxane-based core-shell particles. Polymer 54(16):4276–4289. https://doi.org/10.1016/j.polymer.2013.06.009
Hsieh T-H (2011) Properties and toughening of silica nanoparticle- and carbon nanotube-modified epoxy polymers. PhD thesis, Imperial College London
Huang Y, Kinloch AJ (1992) Modelling of the toughening mechanisms in rubber-modified epoxy polymers—part II A quantitative description of the microstructure-fracture property relationships. J Mater Sci 27(10):2763–2769. https://doi.org/10.1007/BF00540702
Bray DJ, Dittanet P, Guild FJ, Kinloch AJ, Masania K, Pearson RA, Taylor AC (2013) The modelling of the toughening of epoxy polymers via silica nanoparticles: the effects of volume fraction and particle size. Polymer 54(26):7022–7032. https://doi.org/10.1016/j.polymer.2013.10.034
Adachi T, Osaki M, Araki W, Kwon S-C (2008) Fracture toughness of nano- and micro-spherical silica-particle-filled epoxy composites. Acta Mater 56(9):2101–2109
Dittanet P, Pearson RA (2013) Effect of bimodal particle size distributions on the toughening mechanisms in silica nanoparticle filled epoxy resin. Polymer 54(7):1832–1845
Dittanet P, Pearson RA (2012) Effect of silica nanoparticle size on toughening mechanisms of filled epoxy. Polymer 53(9):1890–1905
Johnsen BB, Kinloch AJ, Taylor AC (2005) Toughness of syndiotactic polystyrene/epoxy polymer blends: microstructure and toughening mechanisms. Polymer 46(18):7352–7369. https://doi.org/10.1016/j.polymer.2005.05.151
Acknowledgements
The authors would also like to thank Evonik, Germany, and Rohm and Haas, UK, for supplying materials. Some of the equipment used was provided by Dr. Taylor’s Royal Society Mercer Junior Award for Innovation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tsang, W.L., Taylor, A.C. Fracture and toughening mechanisms of silica- and core–shell rubber-toughened epoxy at ambient and low temperature. J Mater Sci 54, 13938–13958 (2019). https://doi.org/10.1007/s10853-019-03893-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10853-019-03893-y