Introduction

Age hardenable aluminum alloys with the main solutes being Si and Mg (6xxx series) find increasing applications within a wide range of sectors, e.g., in automotive industry [1] as car body parts as well as for architectural and structural applications [2] such as fences or flooring. Al–Mg–Si alloys obtain their maximum hardness by prolonged storage at elevated temperatures, a process referred to as artificial aging. During artificial aging, precipitates grow within the Al matrix, serving to harden the material. Although this heat treatment methods have been known for a long time [3, 4], the details of the precipitation sequence prior to formation of the final equilibrium phase β are still point of discussions [5, 6]. A generally agreed model is the following precipitation sequence [7]:

$$ {\hbox {SSSS}} \rightarrow {\hbox {Si-, Mg- clusters}} \rightarrow \beta '' \rightarrow \beta '/ {\hbox {U}}_1/ {\hbox {U}}_2/ {\hbox {B}}' \rightarrow \beta $$

Here, SSSS denotes the supersaturated solid solution and β″, β′, U1, U2, and B′ are metastable precipitates prior to the equilibrium phase β [7]. While β″ precipitates are coherent to the Al matrix, β′, U1 and U2 precipitates are semi-coherent [8] and β precipitates are incoherent [9,10,11]. Due to their coherence, β″ precipitates give the major contribution to the age hardening of the alloy; consequently, they are predominant in the peak-aged microstructure [12]. The number density of β″ precipitates, and thus, the maximum achievable hardness is strongly influenced by the parameters of the temperature treatment and the corresponding nucleation, i.e., initial clustering stages. For example, aging at 210 °C results in lower hardness due to a reduced number density of β″ precipitates compared to aging at 180 °C [13]. Furthermore, prolonged room temperature storage before artificial aging can have a negative effect on the formation of β″ precipitates [14]. Hence, for tailoring the hardening response and further material properties of aluminum alloys, it is inevitable to obtain a detailed understanding of the initial clustering stages as well as of the further steps of the precipitation sequence.

In particular, the observation of initial clusters is challenging due to several facts. Early clusters usually only involve few atoms, and moreover, these processes take place on very short timescales. Furthermore, the distinct clustering stages are complex and often overlapping in time. Common methods for the study of precipitation processes are atom probe tomography (APT), transmission electron microscopy (TEM), or differential scanning calorimetry (DSC). However, these methods encounter several difficulties in the case of the investigation of Al alloys: Initial clustering stages, consisting of a few atoms, are on the lower limit or even below the detectability of APT [15]. The similar electronic structure of Mg, Si and Al results in a very low contrast in TEM imaging; thus, early clustering stages can hardly be resolved. The quantitative analysis of non-isothermal DSC is difficult due to the complex precipitation process [16, 17] while for isothermal DSC the detection limit of the heat flow is easily reached.

Yet another technique namely dilatometry can monitor the length change of a sample in situ during artificial aging. The applicability of this technique for the observation of precipitation processes has been demonstrated on steels and special alloys [18,19,20]. Still, length changes during aging in the most aluminum alloys, especially in AW6060, are very small which can be a problem for most of today's commercially available dilatometers [21]. Our self-developed high-precision dilatometer already proved being capable of monitoring these small length changes during isothermal, in situ aging of AW6060 [13]. Nevertheless, the length change only reacts to the precipitation process after longer aging times (from ≈ 1000 s onwards), this requires a complementary technique which is suitable to monitor also very early clustering stages.

A powerful tool to investigate precipitation processes in light alloys is positron annihilation lifetime spectroscopy (PLS) [22]. Positrons are sensitive to the free volume of precipitates, allowing to register changes in microstructure as for example transitions from coherent to semi- or incoherent precipitates. The greatest benefit of this method, however, is that even small clusters and precipitates, that do not cause additional free volume, act as an attractive potential for positrons. This is due to the fact that typical alloying elements show higher positron affinities than the Al matrix [11, 23, 24]. Thus, positrons are capable of sensing the very early clustering stages after seconds of aging, but also structural changes after several hours of aging as for example the transition from β″ to β′ . In recent years, several groups studied the formation of precipitates during age hardening of Al alloys by means of positron annihilation spectroscopy. The group of Banhart conducted in situ PAS measurements in combination with electrical resistivity, DSC and hardness measurements on Al–Mg–Si alloys mostly during natural aging [25,26,27]. These studies included only few \(e^{+}\)-lifetime data points measured at room temperature after artificial aging [28]. Therefore, the results are only valid for artificial aging effects superimposed by natural secondary aging. Furthermore, Staab et al. conducted comprehensive studies concerning lightweight alloys analyzed by PAS. The main aspect of these measurements was the natural aging of lightweight alloys including copper additions studied by lifetime spectroscopy applying different temperatures during the measurement [29, 30]. The novelty in this study now is positron lifetime spectroscopy combined with high-precision dilatometry to analyze explicitly artificial aging of the commercial Al alloy AW6060 at 180 and 210  °C. In addition to the enormous accuracy of the applied dilatometer, the positron spectrometer setup includes the possibility to cool down the sample to temperatures far below room temperature, allowing to freeze the system in its defined aging state during the data acquisition times, which for precise data analysis are longer than the short initial clustering times. This novel and unique joint application of dilatometry and \(e^+\) spectroscopy is the ideal technique for the experimental observation of the atomistic precipitation processes in lightweight alloys, allowing a comprehensive analysis of the precipitation sequence within different time scales and temperature regimes.

Experimental

The material of interest in this study was a commercial-grade AW6060 Al alloy, in a T6 stateFootnote 1 in the as-received condition. All investigated samples were obtained from the same low-alloyed batch and were rich in magnesium (0.65 at.% Mg, 0.52 at.% Si). Prior to any aging experiments, all samples were solution heat-treated at (540 ± 1) °C for 30 min and subsequently quenched to room temperature.

A sketch of the heat treatment applied to the PLS samples is shown in Fig. 1. After solution heat treatment and quenching, the PLS samples were kept at room temperature for 4 min before artificial aging in a dry box at (180 ± 1) °C or (210 ± 1) °C for a defined period of time (between 10 and 1.14 × 106 s). To achieve a consistent heating and isothermal annealing throughout the experiment, the finely ground samples were put onto an isothermal aluminum plate (335 × 60 × 10 mm3) inside the dry box. Consequently, it became possible to estimate the heat-up time under the assumption that the cooling effect on the aluminum plate can be neglectedFootnote 2. To prevent secondary natural aging, the samples were cooled to liquid nitrogen temperatures immediately after artificial aging.

Figure 1
figure 1

Schematic sketch of the heat treatment of the AW6060 samples prior to positron annihilation lifetime spectroscopy (PLS)

Full size image

For the positron lifetime measurements, pairs of square shaped samples (1.5 × 10 × 10 mm3) with identical heat treatment were used. These identical samples were removed from the liquid nitrogen bath, and a \(^{22}\)Na source (encapsulated in aluminum foil) was sandwiched between them. The source-sample sandwich arrangement was transferred to a helium cryostat and cooled to − 73 °C. The sample handling time between removal from the liquid nitrogen bath until reaching subzero temperatures in the helium cryostat of the lifetime spectrometer was approximately 1 min. The positron lifetime measurements were taken using a digital positron lifetime spectrometer obtaining a full width at half maximum of the time resolution function of 163 ps. Each lifetime spectrum contained more than \(10^6\) counts and was analyzed after background and source correction using the program PALSFit [31]. Note that each positron lifetime data point stems from one separate pair of samples, the two platelets of each pair being treated identically. Thus, in total the present study is based on more than 70 sample pairs.

In addition to positron lifetime spectroscopy, in situ dilatometry was performed as a complementary method applying a self-developed high-stability laser dilatometer with an incremental length resolution of 20 pm [32]. The samples for dilatometry measurements were solution heat-treated and quenched inside the dilatometer. For quenching to room temperature, a He gas stream was applied. Four minutes after quenching, the samples were artificially aged at 180 and 210 °C, respectively. For a detailed description of the measurement procedure, the reader is referred to Ref. [13]. For additional characterization, Brinell hardness was measured with an EMCO-TEST DuraJet hardness tester, using the Brinell method. The measurements were taken at room temperature immediately after the artificial aging in the dry box. Each hardness value is a mean of five measurements, obtained from one square-based sample (4 × 10 × 10 mm3). To be consistent with \(e^{+}\) annihilation measurements, samples for hardness measurements were kept at room temperature for 4 min after solution heat treatment and prior to artificial aging.

Results and discussion

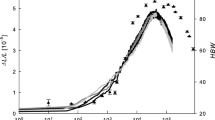
Three main steps are identified in the precipitation process from the comparison of the PLS data with the relative length change and the well known hardness response during aging at 180 °C (Fig. 2a), and 210 °C (Fig. 2b). In the first step (time span A: 10–100 s for 180 °C and 10–1200 s for 210 °C), both aging temperatures reveal the same characteristics in the positron annihilation data. The positron lifetime spectra are best fitted using a two-component analysis with the components \(\tau _0\) and \(\tau _1\) and the corresponding relative intensities \(I_0=1-I_1\) and \(I_1\). The shorter component \(\tau _0\) characterizes \(e^+\) annihilation from the free state (see “Quenched sample” section) and the longer component \(\tau _1\) is due to \(e^+\) annihilation from a defect-trapped state as specified in more detail below. \(\tau _1\) decreases from 227 ps to about 214 ps as soon as the samples are heated to the artificial aging temperatures and it stays almost constant with proceeding aging time (see Fig. 3a). While \(\tau _1\) does not vary within time span A the corresponding intensity \(I_1\) shows a slight decrease until ≈ 30 s (≈ 102 s) for 180 °C (210 °C) of aging temperature and then increases again until it reaches 100% at the end of time span A (see Fig. 3c). From this point onwards (time span B plus C), the most reasonable fit of the lifetime spectra is obtained by using only one lifetime component.

Figure 2
figure 2

Mean positron lifetime \(\tau _{\mathrm{mean}}\) (a 180 °C, blue circles; b 210 °C, red circles), relative length change \(\varDelta L/L\) (black line) and the corresponding hardness values HBW (green triangles) during artificial aging. The gray cross represents the mean positron lifetime of the as-quenched sample (AQ)

Full size image

Time span B is characterized by the constant mean \(e^{+}\) lifetime \(\tau _{\mathrm{mean}}= I_0\tau _0 + I_1\tau _1\), which is the case for artificial aging at 180 °C up to 104 s (Fig. 2a). Contrary, during aging at 210 °C the value for \(\tau _{\mathrm{mean}}\) increases continuously from 1000 s onwards (Fig. 2b). The underlying precipitation processes correspond to time span C of the sequence as outlined below.

The length change as well as the hardness continuously increases from 102 to 103 s onwards for 180 and 210 °C of aging temperature, respectively. Within interval C, the hardness and dilatometry values reach their maximum and subsequently decrease again for both aging temperatures. As soon as time span C is also reached for 180 °C of aging temperature (104 s, Fig. 2), PLS data show the same monotonous increase as observed for 210 °C already after 102 s of aging. Toward the end of time span C, the value of \(\tau _{\mathrm{mean}}\) shows no tendency of levelling off. It should be pointed out once more that each PLS data point in the measuring sequence corresponds to a different set of sample pair. Therefore, the very small scattering of the data reflects the remarkable statistical reliability and reproducibility of the experimental results.

The following discussion is separated into four parts: the analysis of the quenched sample as well as the analysis of the time spans A, B and C, corresponding to the three main precipitation steps for 180 and 210 °C.

Quenched sample

For the quenched sample, with corresponding data displayed as gray crosses in Figs. 2 and 3, the positron lifetime spectrum can be best described with two lifetime components. This is consistent with an incomplete positron trapping during the first 5 min of natural aging as also observed by Klobes et al. [29]. This is reasonable as the quenched samples were exposed to room temperature for 4 min prior to the start of the positron annihilation measurements.

Figure 3
figure 3

Results of the positron lifetime spectroscopy measured on Al–Mg–Si upon aging at 180 °C (blue circles) and 210 °C (red triangles) in dependence of the artificial aging time. a Long lifetime component (\(\tau _{1}\)). Note that for time spans B and C, \(\tau _{1}\) is equal to \(\tau _{\mathrm{mean}}\) (see Fig. 2), b calculated bulk lifetime (\(\tau _{b}\)) and c intensity \(I_{1}\) of lifetime component \(\tau _{1}\). The gray crosses (AQ, left-scale axis) represent the as-quenched sample. The lines are for guiding the eyes

Full size image

The obtained shorter lifetime component \(\tau _0=46\) ps arises from \(e^{+}-e^{-}\) annihilations within the bulk of the alloy; \(\tau _0\) is reduced due to the presence of defects [33]. It should be noted that the bulk lifetime \(\tau _{b}=(I_0/\tau _0 + I_1/\tau _1)^{-1}\) of 179 ps (see Fig. 3b), which is calculated according to the simple two-state trapping model, is somewhat higher than that in pure Al (\(\tau _{b_{Al}}=163\) ps [34]). The longer lifetime component of the quenched sample \(\tau _1=230\) ps (Fig. 3a) is lower than the lifetime of a positron in an Al vacancy (\(\tau _{V_{Al}}=248\) ps, even if a solute is attached to it [25]), although after 4 min of natural aging a sufficient amount of vacancies is still present in the alloy [35]. On the other hand, the value of \(\tau _1\) is higher than the positron lifetime in solute clusters (210–220 ps [26]). Such clusters already form during quenching or within the first minutes at room temperature after quenching [36, 37] and also act as an attractive potential to positrons [11, 23, 24]. The positron lifetime within clusters and within vacancies cannot be resolved separately. Therefore, \(\tau _1\) of the quenched sample is a trapping rate averaged mean value of two \(e^+\) lifetimes, one corresponding to \(e^+\) annihilations within vacancies, the second one corresponding to annihilation within clusters.

Time span A: dissolution of natural aging clusters and formation of artificial aging clusters

The first main step of the precipitation process upon artificial aging (time span A) is characterized by two-component fits of the corresponding lifetime spectra. The short lifetime component (\(\tau _0 \le 105\) ps, for all samples) is attributed to annihilations within the bulk of the alloy (see Fig. 3b for the calculated bulk lifetime).

The decrease of \(\tau _{1}\) with the onset of aging can be explained by annealing out of vacancies, as it was observed for natural aging, but on a longer timescale [35]. Although vacancies anneal out, the intensity of \(\tau _{1}\) increases after 10 s of artificial aging (see Fig. 3c). This indicates that new positron traps, i.e., clusters, are formed simultaneously. For aging times between 10 s and the end of time span A, the lifetime component \(\tau _{1}\) stays almost constant around a value of \(\tau _{1}=214\) ps, which is in the range of the lifetime reported in the literature for positrons within clusters [26]. The corresponding intensity \(I_1\), i.e., the amount of trapped positrons, shows a slight decrease until ≈ 30 s (102 s) for 180 °C (210 °C) of aging temperature.

A decrease in the amount of trapped positrons after the initial increase appears odd at first sight as artificial aging should result in a continuous growth of the number density of clusters. However, the samples were kept at room temperature for 4 min before artificial aging, which is a sufficient amount of time for the formation of natural aging clusters [29]. Previous studies showed that natural aging clusters differ from clusters formed by artificial aging [38]. Thus, while artificial aging clusters continue to grow in number density, smaller natural aging clusters dissolve [16, 39]. As long as the dissolution of natural aging clusters is the dominant process this leads to a decrease in the value of \(I_1\). Consequently, more positrons annihilate in the bulk of the material, lowering the mean positron lifetime (see Fig. 2a, b).

For artificial aging times longer than 30 s (180 °C) and 100 s (210 °C), \(I_{1}\) increases again, i.e., the formation of artificial aging clusters dominates over the dissolution of natural aging clusters. At the end of time span A, all positrons are trapped within solute clusters; the optimum fit of the lifetime spectra is received using only one lifetime component from this point onwards.

Even if the overall trends of the positron lifetime data are similar for both aging temperatures in time span A, a remarkable difference can be observed. The decrease of \(I_1\) is more pronounced and shifted to higher aging times in the case of 210 °C. This reflects a lower number density of artificial aging clusters for 210 °C compared to 180 °C, owing to a reduced cluster nucleation rate at the higher aging temperatures [40]

Time span B: growth of β″ precipitates

In time span B, the positron lifetime analysis reveals a single lifetime component; saturation trapping of positrons into previously formed clusters occurs. This defines a lower limit of the cluster concentration C according to the condition \(\sigma \times C \gg \frac{1}{\tau _b}\) required for \(e^+\) saturation trapping, where \(\sigma \) denotes the specific trapping rate of the positrons. The cluster number density N after a comparable aging step (170 °C, 1200 s) has been determined to \(N=4.4\times 10^{23}\) m\(^{-3}\) by atom probe characterization. In fact, this number density is compatible with saturation trapping of \(e^+\) taking into account typical values for the specific \(e^+\) trapping rate \(\sigma \).

An ideal complementary technique in this regime of \(e^+\) saturation trapping is dilatometry. In this time span, dilatometry shows a length increase, indicating a continuation of the precipitation process. An increase in length change corresponds to a predominant contribution of coherent β″ precipitates while a decrease would correspond to the predominant contribution of semi-coherent β′ precipitates [13]. Thus, clusters keep growing in size and eventually transform into β″ precipitates. This is also confirmed by the increase in hardness in this time span (see Fig. 2a) as it is well known that the strengthening process is mainly governed by β″ precipitates [36, 41].

Although, from dilatometry and hardness measurements, it is derived that clusters start to transform into β″ precipitates, the positron lifetime stays constant in time span B at 180 °C (see Fig. 3a). This shows that clusters and β″ precipitates have a similar defect-related free volume size which is in line with the fact that both the clusters and the β″ precipitates are coherent with the Al matrix.

For an aging temperature of 210 °C, no region of constant \(\tau _1\) can be observed. A period of continuously increasing \(\tau _1\) directly follows after time span A, as it will be discussed in the following section.

Time span C: transformation of β″ to β′ precipitates

Within time span C, the single positron lifetime component \(\tau _1\) continuously increases for both artificial aging temperatures. This now indicates the onset of the formation of β′ precipitates with an enhanced defect-related free volume associated with the incoherent interfaces. In fact, as an increasing fraction of coherent β″ precipitates transforms to semi-coherent β′ precipitates, the lifetime component \(\tau _1\) has to be considered as an average value of the lifetime of e\(^+\) annihilating within β″ precipitates (\(\tau _{\beta ''}\)) and those that annihilate within β′ precipitates (\(\tau _{\beta '}\)), i.e.,:

$$ \tau _1= \frac{\sigma _{\beta ''} C_{\beta ''} \tau _{\beta ''} + \sigma _{\beta '} C_{\beta '} \tau _{\beta '}}{\sigma _{\beta ''} C_{\beta ''} + \sigma _{\beta '} C_{\beta '}}. $$
(1)

Due to the semi-coherent structure of β′ precipitates, the value for \(\tau _{\beta '}\) is higher than for \(\tau _{\beta ''}\). Within time span C the concentration \(C_{\beta '}\) of semi-coherent precipitates increases, which leads to an increase of the e\(^{+}\) lifetime \(\tau _1\) (see Eq. 1). Even if \(C_{\beta ''}\) decreases, the condition for saturation trapping (here: (\(\sigma _{\beta ''} \times C_{\beta ''} + \sigma _{\beta '} \times C_{\beta '} ) \gg \frac{1}{\tau _b} \)) is still valid.

The fact that for the higher aging temperature of 210 °C \(\tau _1\) increases right after time span A shows that β″ precipitates transform earlier into β′ precipitates compared to 180 °C.

This difference in the temporal sequence of the precipitation process is also shown by the shift of the maximum in the \(\frac{\varDelta L}{L}\)-curve and hardness curve toward lower times (compare Fig. 2a, b). For both aging temperatures, the hardness and the length change continue to increase until reaching their maxima corresponding to the formation of β″ precipitates. For aging times longer than 3.7 × 104 s (1.2 × 104 s) at a temperature of 180 °C (210 °C), the hardness decreases just as the length change in the sample does indicating that the contribution of β′ to the overall precipitates starts to dominate.

It is important to point out, however, that the positron lifetime monitors the formation of β′ precipitates already at the beginning of time span C by its continuous increase. In this sense, positron data give more conclusive and earlier hints on the formation of β′ precipitates than dilatometry and hardness. Only by the combination with dilatometry and hardness measurements, it can be decisively concluded that the processes of β″ and β′ formation proceed simultaneously.

Summary and conclusion

The atomistic processes during artificial aging at distinct temperatures of a commercial Al alloy are analyzed using positron lifetime spectroscopy (PLS) and dilatometry accompanied by hardness measurements. According to the positron annihilation characteristics, the precipitation process can be divided into three time regimes, labeled as time spans A, B, C (corresponding to up to 1 min, up to 1 h, and more than 1 h for 180 °C, respectively).

Within the first period of aging (time span A), cluster number densities as well as the sizes of these clusters are below the detection limit of dilatometry or hardness. Only the sensitivity of \(e^+\) annihilation spectroscopy enables to monitor these early stages of the precipitation process. The variations of the intensity of the positron lifetime indicate a competing process of the dissolution of natural aging clusters and the concurrent formation of artificial aging clusters. This behavior is more pronounced in the case of 210 °C due to a lower cluster nucleation rate. With preceding aging times, artificial aging clusters grow in number density and eventually transform into β″ precipitates (time span B) as evidenced by an increase in length change and hardness. The clusters and β″ precipitates are characterized, however, by a similar defect-related free volume size as shown by the constant \(e^{+}\) lifetime in this regime.

For long aging times (time span C), the defect-related free volume increases for both aging temperatures supporting the results of dilatometry and hardness according to which in this regime β″ precipitates transform into semi-coherent β′ precipitates.

The present study demonstrates that the information on the precipitation process is accessible only by the unique joint application of the two complementary methods of positron annihilation and dilatometry. For the analysis of the early clustering stages, only PLS is sensitive enough, while for longer aging times only by the assistance of dilatometry the final conclusive hint on the transformation of precipitates is obtained.