Abstract
In the attempt to improve mathematical thinking for safeguarding our future societal needs, there is a worldwide tendency in schools to start training mathematical and arithmetical operations at an earlier age in children’s development. Recent theoretical developments and empirical research have pointed to alternative ways of approaching early mathematical thinking. In these latter approaches, mathematical development in the early developmental stages is seen as an emerging process in the context of children’s own activities that contributes to meaningful learning and stimulation of children’s cultural identity (Bildung approach). The discussion between the training approach versus the ‘Bildung’ approach is still intemperately going on. In this article, some outcomes of a research programme (based at the Free University Amsterdam) are discussed that present empirical studies and their theoretical background (cultural–historical theory, elaborated in an educational concept called ‘Developmental Education’) that demonstrates the promising potentials of promoting mathematical thinking through supporting young children’s appropriation of schematic representations and notations in the context of play.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Mathematics education in the knowledge society
Over the past decades, the global community has rapidly changed into a knowledge society, which has become increasingly dependent on the distribution and exchange of commodities and services for its production, innovation and social welfare. However, the functioning of the distributed means is also to a great extent dependent on the quality of understanding that goes with these means. Hence, the implementation of the knowledge society necessarily requires a distribution and exchange of understandings, which enable people to apply these means creatively in new situations.
A deep analysis of the assumptions of the knowledge society goes far beyond the intentions of this article. Nevertheless, a few of these assumptions need to be mentioned when we are interested in evaluating the implications of the knowledge society for (mathematics) education. Some basic assumptions of the knowledge society and economy are the following:
-
▪ knowledge can be coded and recoded in different symbolic means;
-
▪ knowledge is transferrable over situations and conditions;
-
▪ worldwide availability of codified knowledge and information is necessary for the functioning of the knowledge society (e.g., with the help of the world wide web);
-
▪ mathematics and natural sciences are particularly important for upholding the technological innovations that are deemed essential for the knowledge society and its economy.
Educational policy makers often have interpreted these assumptions as educational requirements, emphasising effective teaching of important subject matter and mastery of knowledge in operational form. On the other hand, educationalists (like Hargreaves, 2003) also have warned against strictly following the technocratic seductions of the knowledge society and have argued for approaches that put the identity formation of the individual in the centre of the educational obligations. In this view, a knowledge society will benefit most from critical, creative and well-informed citizens, which combine subject matter understandings with social interest and a democratic disposition. In these discussions, we can see a return of the old discussions between teaching as training cultural operations for application in relevant work situations versus teaching for identity formation and participation in cultural practises (‘Bildung’).
In the area of modern educational policy, the discussion about ‘training’ versus ‘Bildung’ has regained acute relevance with respect to mathematics education. In the Netherlands, for example, the so-called ‘realistic’ approach to mathematics education in primary and secondary education (that has dominated mathematics education for the past 30 years) is currently fiercely contested by people who propagate more direct teaching for the mastery of basic operations (algorithmic addition, subtraction, multiplication, division, etc.) and mathematical facts (see for example van de Craats, 2009). On a world-wide scale, this type of discussion is not exceptional (see for example the Math Wars in the US).
In this article, I want to contribute to this debate by arguing that teaching for understanding (as in a Bildung approach) and mastery of operations are not by definition incompatible. More particularly, I will discuss a developmental approach to mathematics education of young children on the basis of theoretical ideas and empirical evidence that provide arguments for the possible integration of the focus on understanding and operational mastery. I assume that much depends on how mathematics education was guided in the early stages of child development at school and which mathematical strategies and tools the child appropriates as a basis for meaningful mathematics learning and mastery of basic operations.
On the basis of research findings from a research programme ‘Developmental Education in the school context’ (based at the Free University Amsterdam), the article demonstrates how mathematical learning can be fostered in the early years of development at school age. In the following section, I will first present the main tenets of the approach based on the cultural–historical theory of Vygotsky. On this theoretical basis, it will be argued that understanding and mastery can be integrated on the basis of promoting authenticated actions that form the basis for identity development. From this point of view, I will point out that actions with numbers can be carried out in a meaningful way in the context of children’s play which can lead to operations with numbers that do make sense for these children and adults. Furthermore, I will review observational and quasi-experimental studies that give some insight into the emergence of symbolic representations and notation in the context of play with the help of adults and that provide us with evidence of the powerful role of these symbolic means for the learning and mastery of mathematical operations.
2 A developmental approach to mathematics education
In our research in the Netherlands, we address the problem of school learning from a cultural–historical point of view, based on the ideas of Vygotsky/Leont’ev (see for example, van Oers, 1990, 1996a, 2006). Since the early 1990s, we developed in collaboration with curriculum developers, teacher trainers and teachers an educational concept based on the cultural–historical theory that is successfully being implemented in a growing number of schools in the Netherlands. We call this concept ‘Developmental Education’Footnote 1. Within these schools, we study children’s development in different subject matter areas, including the development of mathematical thinking.
From this cultural–historical point of view, human development is conceived of as a process that can be described as development of cultural activities, with the help of cultural tools (Vygotsky, 1978). Nowadays, the approach is mostly referred to as the cultural–historical activity theory. Within this perspective, learning is seen as a process of qualitative change of actions that may take place when people participate in meaningful cultural activities and receive guidance for improving or appropriating actions. According to Vygotsky (1978, p. 19–30), actions receive their content and structure through the use of cultural tools. In the cultural–historical theory of Vygotsky, tools are conceived of as a special type of objects (including instruments, words and symbols) that can be used in actions for the transformation, stabilisation or regulation of other objects. A special category of tools, according to Vygotsky, are the signs as they structure human actions in cultural ways.
Most of the time, learning is connected to the employment of new or innovated tools (e.g., concepts) or to improvements in the use of already available tools for the solution of problems or accomplishments of tasks within the activities that constitute the context of actions. When a young child, for example, has learned how to count by using counting words in correct order, he or she can solve a specific type of problems. The improvement of this verbal counting tool with the employment of, for example, the number line, broadens this child’s capacity for problem solving with a range of new abilities, like estimating, comparing numbers, addition, subtraction and maybe even multiplication. The appropriation of this new tool (number line) qualitatively changes the structure of the child’s action in that it becomes more conceptual, more generalised and finally, maybe even abbreviated into perfectly mastered operations.
Over the past century, numbers of studies conducted all over the world have further specified the conditions for learning within the assumptions of the cultural–historical approach (see for example van Oers, Wardekker, Elbers & van der Veer, 2008). Five of them seem to be of particular importance for the understanding of mathematical learning:
-
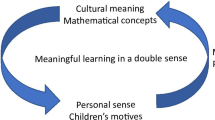
Meaningful learning: Following Leont’ev (1975), there are basically two levels of meaning in human action that need to be taken into account for the promotion of development through learning. On the one hand, we have the cultural meaning (of actions, objects, goals, tools/symbols). This is the value that a cultural community attributes to this action (etc.); it is the standard meaning one finds in textbooks or dictionaries. On the other hand, we have personal meaning (sense) that relates to the personal values a person attributes to these actions (etc.) given his motives. Personal sense is often expressed in interests, specific attitudes or dispositions. Such meaningful learning particularly is supposed to contribute to (identity) development. In order to be meaningful and to be stimulating for development, learning necessarily should be meaningful in this double sense: including both a cultural and a personal dimension at the same time. The cultural dimension of learning relates to timely provision of relevant cultural tools to pupils. Personal meaning, on the other hand, relates to involvement of pupils in practises that make sense to them, wherein they can participate and are being encouraged to reflect on the situations, the tasks at hand and how they can be addressed. Meaningful learning in this double sense is supposed to contribute to identity development (‘Bildung’), rather than to mere training of specific operations (which is inclined to focus exclusively on cultural meaning). Especially in the case where cultural meaning and personal meaning merge, identity is created between outer (mechanical) performance of actions (operations) and the intrinsic meaning (objective) of the activity. Identity formation can be conceived now as a process of creating personal sense in the performance of cultural actions by connecting performed actions with the intrinsic motive behind an activity: the one who does is identical to the one who intends. Mechanically mastering performance of specific actions does not necessarily or automatically relate to the intrinsic meaning of an activity and does not, as a result, contribute to identity formation. To put it once more in other words: identity formation is based on the education of authenticated actions in the context of cultural practises.
-
Participation in cultural practises: meaningful learning is always embedded in cultural practises that make sense to the participants. The practises that can be chosen for educational purposes can be of various types. In addition to school as an institutional practise especially invented for educational purposes, learning can also take place in real or simulated forms of practises that relate to societal roles (like shop owner, doctor, artist, carpenter, scientist etc.). The developmental outcome of the learning processes in each of these practises strongly depends on the format of the activity that takes place within that practise. Each format is characterised by the number, nature and status of the rules, by the level of involvement of the participants, by the degrees of freedom that are allowed to the participants in their choice of objects, actions, tools, goals or obedience to the rules (van Oers, 2009).
-
Help of more knowledgeable others: these others (e.g., adults) are important for the provision of cultural tools and for the supervision of their use within the practise. Davydov (e.g., 1996) gave a dominant role to the adult in teaching mathematics within a school context. He propagated the provision of generalised models for the improvement of mathematical actions. However, from an educational point of view, one may also question Davydov’s approach for being too restrictive with regard to the pupils’ degrees of freedom and for limiting the level of personal meaning (see for example the critique of Freudenthal, 1979a and b).
-
Leading activity: the nature of participation and the ability to benefit from help depend on a participant’s developmental level. Cultural–historical scholars (see Elkonin, 1972; Karpov, 2005) characterise the ontogenetic process in terms of prominent activities that are best fit to the motives of the pupil and that imply actions that children can perform with the help from others and which stimulate children’s development to a higher level of functioning. During the period of primary school, children’s developmental process can be characterised by the leading activities of play and intentional learning. Put differently, cultural–historical theory maintains that young children (until the age of 7/8) will learn optimally when their learning is embedded in playful activities (Elkonin, 1972; Karpov, 2005). After the age of (about) eight, children prefer to be involved in activities that support and stimulate intentional learning of cultural facts and understandings (Davydov, 1996).
-
Communication: the role of communication is central to all learning in each developmental period, but it is related to the basic motive that dominates this period’s leading activity. The development of mathematical thinking is basically a process of constructing means (and their correlated rules) for communicating with oneself and others about mathematical objects (like numbers, relations, functions etc.). A strong argument supporting this view is recently given by Anna Sfard (2008). In her view, thinking should be conceived of as a form of communication, which in human beings implies a property of recursive self-reference. It is this property of self-reference which lays the foundation for the possibility of discursive construction and transformation of mathematical objects and for the development of mathematical practises and education.
In our own research programme, we empirically tested the question whether directly providing mathematical models would yield different learning outcomes than educational processes that ascribe a more constructive role to pupils. In ten grade seven classes of primary schools (N = 239; age of pupils 10–11 years), we investigated mathematics lessons on fractions and graphs in which pupils in a collaborative process with peers and the teacher constructed models that could be used for their understanding and application of fractions. The instruction process could be characterised as guided co-construction. In advance of the study, the teachers involved were trained in how to interact with students in order to improve the students’ models by focussed questioning. The teaching–learning process started out from problems that engaged pupils and the students were invited to make schematic drawings of their solutions collaboratively (in small groups). During the lessons, the teachers clarified the rules for model construction and model use when necessary. However, the teachers also allowed the pupils enough freedom to construct, compare and try out their own tentative models. The teachers also controlled the modelling with a view to correct representation of the subject matter and if necessary, the teacher prompted the students to compare their models with conventional subject matter models of fractions.
Compared to control groups that received the models in a ready-made form from the teacher, the experimental (guided co-construction) groups turned out to perform significantly better on post-tests with regard to transfer of their understandings to new problems. The data were statistically analysed with regression analyses. The effect sizes, as defined by Cohen (1988), were calculated for mathematical performance on fractions and for transfer separately. As expressed in the post test and the transfer test, the total effect sizes are 0.40 and 0.63, respectively. These are moderate effects. However, if we estimate the net effect size for the transfer test—by taking into account the effect of the intervention already expressed in the post-test and correcting for scale differences between both scales—the effect size for differences on the transfer test shrinks to 0.23. This net effect size (over and above the effect size of the post-test) can be regarded as a small but significant effect (van Dijk, van Oers & Terwel, 2003; Terwel, van Oers, van Dijk & van den Eeden, 2009).
This outcome supports the assumption that meaningful learning (in the double sense of the word) can yield significant learning outcomes that can be applied in new situations which may eventually contribute to autonomous participation of pupils in cultural practises (i.e., to ‘Bildung’). As such, our developmental education approach may be taken to contribute to the realisation of the aims of the knowledge society, particularly in its need for transferable mathematics understandings.
In addition to these studies with older pupils, we also focused on questions related to the younger child, in order to find out how the early process of mathematical development can be fostered within preschool or early school contexts (children aged three to eight). We believe that the child’s view of mathematics and the development of their mathematical attitude might be strongly related to the quality of their first contacts with mathematics as a cultural discipline. In the following sections, I shall describe how young children can get engaged in mathematical activities in the context of a play-based curriculum and review a number of empirical studies that were conducted in order to examine our theoretical assumptions in this regard.
3 Early enculturation: the case of mathematics in play
Mathematics is a cultural activity that emerged somewhere in man’s cultural history and went through a rich and remarkable cultural–historical development to end up in the multi-faceted and highly sophisticated discipline as we know it today. Without trying to define the essence of mathematics, we can say that its evolution strongly depended on the construction of symbolic tools for problem solving, as well as on a permanent intentional self-reflection of mathematicians on their own activities. As explained by Duval (2006), mathematical objects are only accessible through symbolic representations and can only be understood as transformations of such semiotic representations. This is important for the early stages of mathematical development as well. Young children are not born with these ready-made symbolic tools and do not yet possess the habit of intentional self-reflection either. The capacity of reflection is based on the mastery of language and communication and starts developing only later in life through intensive communications with other people. Hence, we actually cannot maintain that very young children (1 to 3 years old) perform mathematical actions, even when they may carry out actions that we, as encultured adults, may recognise as mathematical. As long as these actions are not intentionally and reflectively carried out, we cannot say that children perform mathematical actions. Of course, neurological evidence may point towards brain structures that make animals and young children sensitive to special types of actions that may be dubbed mathematical from the outside (see for example Dehaene, 1997), but this still does not mean that these creatures are performing mathematically in the psychological sense of the word.
How, then, can mathematics ever take off in ontological development? Where does the mathematical dimension in development come from? Is it just imposed on children? Vygotsky’s theory of children’s early development might provide us with the beginning of an answer. In his view it is the interaction between young children and more knowledgeable others that creates the conditions for the emergence of mathematical actions, when external meanings (e.g., mathematical meanings) are interactively assigned to children’s actions. According to Vygotsky (1984, p. 226–227), young children adopt cultural actions precisely because the spontaneous actions are taken as cultural forms by the adults and reacted to accordingly. Vygotsky describes this process in three steps. Initially, the child may perform unintentionally on the basis of covert intentions or intuitively, an action or utter a word or sentence, which may be taken in some cases as ‘mathematical’ by the adult or more knowledgeable peers. Only when the adult reacts in a mathematical way to this action, for example by giving the action a mathematical name or showing one of its mathematical implications, does the child’s action begin to gain mathematical meaning, especially, when this is noticed by the child himself. In due time, through participation in such interactions, the child may acknowledge the cultural (mathematical) meaning of this reaction and finally, of his own actions as well. Similarly, we can suppose that the emergence of mathematical actions and concepts in young children’s activities is at first essentially dependent on the adults’ cultural reaction to the child’s actions and utterances. The emergence of mathematical thinking is ‘projected’ into the child’s mind in the process of cultural interactions with others, wherein the mathematical meanings of children’s actions are negotiated with the help of (transformations of) symbolic means.
These developmental principles are employed in our Developmental Education curriculum. In addition to this three-step dynamic of the emergence of meaning described in the previous paragraph, we also take into account the developmental dimension of children’s actions. According to Vygotsky (1978; see also Elkonin, 1972, who developed this theory further), the leading activity of young children from the age of (about three) is to be characterised as play activity. Hence, the early years curriculum is basically a play-based curriculum which means that children’s learning should always be embedded in children’s imitative participation in meaningful cultural practises. The format of these activities is such that children are allowed a high degree of freedom with regard to how they want to carry out or elaborate the rule-governed activity. In school, for instance, children are involved in role play settings, like playing supermarket, museum, railway station, travel agency, post office, construction worker, etc. In the context of these activities the young children encounter problems and tasks that they can try to solve with available means (which may look mathematics-like) or just on the basis of pragmatic intuitions. In the way the teacher acknowledges the children’s (spontaneous) actions, he may lay a foundation for the beginning of mathematical thinking. Let me give one example that I observed once in one of our classrooms:
In a constructive activity, two children (5 year olds) were building a castle for the King the teacher has read about. During their building activity the children encountered a problem when they ran out of one type of long blocks. After some trials, one of the children, without further comment, used two smaller blocks (together of the same length as the long block) and continued building. The teacher noticed it and verbalised the action of the child: ‘Very good, you replaced this long one for two smaller ones!’ The teacher discussed the situation and once again demonstrated that the long one had the same length as two small ones. Then the boys continued building. Initially, every time they needed a longer one, they said to each other (or even to themselves!): ‘we can replace a long one for two smaller ones’. At a later moment they also ran out of these small blocks and began trying a number of other blocks (even smaller), sometimes noticing: ‘no these are not the same’.
By explicitly naming the boys’ actions, an explicit and intentional thinking process was started with regard to division and equivalence. It is the action of the teacher that articulated this mathematical relationship and maybe set out the beginning of a new train of thought.
In our approach, we use these starting points for promoting mathematical development in young children (in our educational system, we are talking now of children from the age of 4 years old until 8). For reasons of brevity, I summarise the early years curriculum in our Developmental Education approach in the following points (related to the principles laid out above, see also van Oers, 1999a, b, 2001, 2003, 2004, 2009):
-
▪ children’s learning is embedded in a play-based curriculum: in the context of manipulative or role play, some of the children’s actions are articulated by the teacher and if possible imbued with mathematical meaning in the communication between teacher and child; with respect to didactics, the curriculum is fairly consistent with the starting points of realistic mathematics education (see for example, Goffree, 1993; Freudenthal, 1991);
-
▪ in the role-play activities, children imitate cultural practises (like supermarket, barbershop, travel agency, restaurant, etc.), which form contexts for (mathematical) learning;
-
▪ learning is closely related to learning to communicate, i.e., to appropriating means for communication over specific objects in particular practises (e.g., in the context of the post office, children learn to communicate in culturally acceptable ways about money, stamps, prices, numbers, trading, etc.);
-
▪ The role of the adult is essential for the development of children’s ability to participate in specific cultural contexts and for promoting development of cultural activities or for development into the direction of a new leading activity. That is to say that a teacher is always looking for meaningful teaching opportunities in the context of play that contributes to children’s ability for participation and that opens new ways of thinking and learning (see for example Karpov, 2005; van Oers, 1999b).
Two findings from our research on the play-based curriculum approach in Developmental Education must be mentioned here, as they are relevant for our present argument:
-
(1)
In a longitudinal study, we followed a class of young children (N = 34) from grade 2 through 4 (ages 5–7) that followed a play-based curriculum and worked on numbers when necessary in the children’s play. With respect to their mathematical learning (measured by a Dutch standardised test for numerical achievement in young children), we could establish that children from our play-based curriculum systematically scored above the national norm for numerical abilities for those age ranges (in the last test in grade 4, the score was equal to the national norm—see van Oers, 2003), without having been trained on these operations in special lessons. We can plausibly assume that a play-based curriculum creates good conditions for early numerical learning.
-
(2)
Starting out from practises that make sense for young children, an expert teacher can stimulate the evolution of activities in different directions (by articulating specific aspects), get children involved in new activities on that aspect and finally, end up in subject matter activities that look highly structured but still have meaningful relationships with the original activity. For example: In a role-play in a shoe-shop, children spontaneously started putting on shoes and trying which of the shoes was their size. The teacher used this to direct the children’s attention to measures and to comparing and estimating different sizes. Which of these shoes would fit your Daddy? This activity led to grouping shoes in different categories, to selling shoes and finally, to the activity of a book keeper who monitors the stock of the shop (selling and buying). This last activity (role-play of the stock keeper) was transformed by the teacher into a game for the older children (grade 4) of selling and buying shoes which were represented by numbers on cards. From an outsider point of view, children were doing just adding and subtracting (as can be found in any primary grade curriculum), but in our case, the actions remained meaningful for the children as they were still a part of their shoe shop play. So it is important to note that activities can evolve into new activities that may include ‘pure’ arithmetic as well (see van Oers, 1998, for further description).
As relatively small scale and sometimes only observational studies, the investigations gave preliminary indications for the value of a play-based curriculum for the promotion of mathematical thinking. We decided, however, that a deeper understanding was needed as to the kind of tools that could be used by young children in the development of their mathematical thinking to find out how such tools could be introduced in the context of their play activities and to determine what the benefits would be for the children’s mathematical development. Further observational studies were set up in order to get more insight in the processes that take place in the early stages of mathematical development. On the basis of observational studies (van Oers, 1994, 1996b), we found that the use of schematic representations in the context of play was a meaningful and accessible activity for young children in play. As schematic representations are representations of (spatial or conceptual) transformations and relationships between different objects, we assumed that this might be a meaningful basis for further formalised mathematical operations that are also based on transformations (see Duval, 2006). A quasi-experimental study (pre-test–post-test control group design) was set up in order to test our assumptions of the value of schematising in the context of play for the development of mathematical thinking. This and other empirical studies are reviewed below.
4 Learning to make symbolic representations
As noted before, an important condition for the emergence of mathematical thinking in the early years is the adults’ act of articulating spontaneous actions of the child and—if appropriate—assigning mathematical meaning to it. However, many opportunities to promote the beginnings of mathematical thinking are missed in practise, particularly with regard to children’s spontaneous actions of mark making, which are often discounted as ‘just scribbling’ or ‘drawing’. It cannot be excluded that some of that scribbling originates from children’s inclination to be active (or what the developmental psychologist Karl Bühler once named as ‘Funktionslust’). Conversations and close observations of children’s activities, however, have revealed that many of those scribbles and drawings have clear communicative intentions for the child. In earlier case-studies (see for example van Oers, 1997), we could observe children who added symbols (like words or numbers) to their drawings in order to make sure that they were understood properly by an observer. In these cases, the drawing had a clear communicative intention for the children and they tried to optimise this communicative function by transforming the drawing with the help of new symbols.
In my own observational studies in early years classrooms, I could witness children experimenting with graphic marks in order to find (best) ways to communicate meanings to others (see for example van Oers, 1996b). In a construction play, one 4-year-old child obviously wanted to communicate about her construction plan on how many blocks should be used in a wall. She started with a mark that looked like the conventional form of four (4), but finally she ended up with just marking four little circles. On different occasions in my observational studies, I could see that children also use (and appeal to) imagination in order to express their intentions. One boy was drawing the railway track that he made with his friend. He started drawing the sleepers (ties) between the rails, but after a while he stopped and said ‘It is too much to draw them all. It just goes on like this’. So the observers of his drawing had to imagine the follow-up of these sleepers. I have called this ‘the etcetera-function’ of imagination (van Oers, 2005). The operation of this function seems very common in children’s imaginative play and the construction of communicative marks. As this etcetera-aspect is also an important aspect of abstractions, we can see here the beginnings of abstract thought, which is also present in mathematical concepts and models (think about the number line that also does not explicitly represent all numbers or the notion of mathematical function). Not paying attention to these events (related to children’s graphical marking) means that educators may neglect important and stimulating early events for the promotion of mathematical thinking.
In many other play situations, researchers and teachers have observed children making scribbles that did not immediately make sense to outsiders. Important work in this area is done by Hughes (1986) and Munn (1998), showing that preschoolers already have different symbolic means for communication of mathematical aspects of their world. Hughes (1986) particularly argued that the children’s problems in mathematical learning is often caused by teachers’ neglect of children’s notations and by the imposition of new formal mathematical symbols (like numbers or operators) on children that they should use for the accomplishment of arithmetical school tasks. This causes a gap between the children’s personal understandings (expressed in personal symbols) and the formal arithmetic that is difficult to overcome by many children, according to Hughes. For these children, there is no way of transforming their personal notations into new mathematical ones.
In practise, however (both at school and at home), children’s graphical marks are often discarded without any follow-up. The interesting work of the English researcher Maulfry WorthingtonFootnote 2 has collected an overwhelming number of examples of young children’s spontaneous graphical mark making in the context of play and clarified them with interpretations (see Carruthers & Worthington, 2006). In my view, the following conclusions seem to be plausible from this work:
-
▪ Many of these ‘scribbles’ do have meanings for the child, some of them can be interpreted as mathematical in the sense that they seem to refer to number, quantity, or changes of quantity (in adult terms: addition, subtraction);
-
▪ By using these marks, children manifest communicative intentions;
-
▪ Sometimes, children improve their marks for communicative reasons;
-
▪ The role of the adult is very important for the articulation of these marks and for the assignment of a shared (mathematical) meaning to them.
Worthington is now carrying out a systematic study of the mark making process of young nursery school children (3- and 4-year-olds) in the context of their imaginative play, which may bring to the fore the dynamics of these processes of development of initial spontaneous marking of children into evident (or even conventional) mathematical symbols. Although the details of these processes are not yet clear, these studies, in my view, indeed point in the direction of a process of interactional mathematical meaning construction between children, their peers and adults, wherein mathematical meanings gradually emerge as functional tools for communication about specific aspects of the children’s situations or activities. Looking at the process from the standpoint of activity theory, we can see that meaning in the double sense (see above) is created in children in a process of guided co-construction. Consequently, we have reason to assume that this will finally yield meaningful mathematical symbols that may turn out to be more functional for the development of mathematical thinking than conventional symbols imposed onto the child’s mind (see also for example Hughes’ 1986 argument).
In a longitudinal study, Poland investigated the ways young children (5-year-olds) learn to refer to aspects of structure and change in the context of their play and how early years teachers can support the invention of means for communicating about these aspects (see Poland, 2007; Poland, van Oers & Terwel, 2009). Elaborating my previous studies on schematising in young children (see van Oers, 1994, 1996b, 2002), Poland could demonstrate that teachers can actively help young children to make structured symbolic representations (like schemes, maps, diagrams, pictograms, construction plans, brief instructions, etc.) that could be used for communicative purposes and for the organisation of real world activities or practises. Schematic representations were provoked by teachers within the children’s play by asking questions or doing suggestions about drawing a situation and sometimes step by step transforming these drawings into more parsimonious pictures that exposed only the necessary information. In conversations with children, the teachers reflected with the children on the schematic representations in order to find out if the ‘drawing’ was clear enough and included everything that was needed. It should be noted here that the provocation of schematising was never an isolated instruction but always an invitation to ‘make a picture’ (‘make a plan, a schema, a graph’) that had to be functional and meaningful in the context of the ongoing play.
The children’s actual drawing abilities are taken as a starting point for schematising. In grade two (5-year-old children), teachers participated in children’s role play (like playing a market place) and stimulated children with questions that basically required schematic representations (of the type mentioned above). Interactively, they assisted children to make first static schematisations (representations of a situation, or status quo, like a construction plan or a map of the play ground), later the schematisations evolved into dynamic representations referring to change, transformation, etc. It can be argued that dynamic representations are fundamental for the development of mathematical thinking (see van Oers & Poland, 2007). Dynamic representations typically include representation of transformations, change and movements and focus children’s attention to relations and transformations (both within and between schematic representations). The general acquaintance with the nature of different forms of transformations, presumably prepares the child for building an understanding of transformations in a symbolic world, such as mathematics, that is essentially constituted by the formation of mathematical objects with the help of semiotic transformations (Duval, 2006).
Poland tested the hypothesis that the appropriation of the ability of making (dynamic) representations would have a positive effect on the development of mathematical thinking in grade three (6-year-olds). Using a quasi-experimental design (pre-test and post-test in three experimental and three control schools; N = 137; all Developmental Education schools), she worked with experimental schools for a whole year in grade 2 (on average 5-years-olds). All schools were working with a play-based curriculum, but the experimental schools were assisted in introducing schematising whenever possible and relevant in a meaningful way in children’s play. At the beginning of the experiment, there was a slightly and significantly higher performance of the control children with regard to early mathematical abilities (like counting).
Children in the experimental schools frequently produced schematic representations (like maps, construction plans, symbolic signs, etc.) and reflected on the meaning of these representations with the help of the teacher. At the end of grade 2, pupils in the experimental group outperformed the pupils on schematising. But that was not our final goal because that would have been a trivial result (pupils who never learned nor practised schematising will obviously not demonstrate high abilities on such tasks). Poland did the final test in grade three (6-year-olds) in the context of these pupils’ mathematics development, using an ordinary standardised arithmetic test. She followed both the experimental and control pupils in their mathematics performances in the next year (grade three). The main results of her study can be summarised as follows:
-
▪ In a play-based curriculum, it is possible to assist young children in developing (static and dynamic) schematising abilities in a meaningful way;
-
▪ Playful learning of schematising abilities is an important prerequisite for early mathematics learning that brings about significantly better performances in the experimental groups on mathematising and arithmetic a year later, when compared to a control group. The critical tests for evaluating the schematising activities for the development of mathematical thinking were standardised tests for assessing the pupils’ proficiency in carrying out arithmetical operations. The effect size of the statistical difference between the experimental and control group was 1.4, which is an average effect according to Cohen (1988).
-
▪ However, when meaningful schematising is not continued and practised, the advantage of the experimental pupils disappeared in 6 months, as was manifest on a delayed post-test.
In this large scale longitudinal experiment, we could produce positive evidence for the potential of the play-based curriculum, particularly with regard to the promotion of mathematical thinking through the development of meaningful schematising in young children.
5 Conclusion
The studies that we did over the past 15 years in the development of early mathematical thinking (both observational case studies and large-scale quasi-experimental studies) all converge towards an important conclusion. The emergence of mathematical thinking in young children is a culturally guided process, wherein mathematical meaning can be assigned to (spontaneous) actions of the child. These actions can be further developed through collaborative problem solving with more knowledgeable others in the context of activities that make sense to the children.
By starting out from the children’s own schematic representations and helping them to improve these representations for the use of mathematical purposes, children are personally involved in the construction of mathematical means (schemas, diagrams, etc.). Consequently, they learn to carry out mathematical actions with the help of these means as authenticated actions of themselves. As was explained above, authenticated actions are a sign of identity formation in the context of cultural practises. In all reviewed studies, the focus of educational processes was primarily on children’s own initial understanding of the situations in the play activity and of the problems arising in that context. The teachers’ help, as conceived in Developmental Education, focused on improving the child’s ability to participate in the mathematical activity. The improvement of authenticated actions, based on schematic representations, led to practising these actions on a number of occasions and supported the process of automatisation as required for the performance of operations. Although there is still a lot to be investigated more profoundly in order to get a clear picture of the details of this process, it appears that the emphasis on understanding by dynamic schematising and the formation of authenticated mathematical actions (integrating both conventional mathematical meaning and personal sense) is a fruitful basis for the learning of authenticated mathematical operations. The results, however, also suggest that the focus on dynamic schematising (with its emphasis on symbolically representing transformations) has to be maintained during the following years as the benefits of schematising may easily disappear as compared to a training approach to the mastery of mathematical operations.
In the Developmental Education approach (based on a cultural historical framework), teachers are able to get engaged in interactions with children in the context of play to articulate children’s own graphical marks and to rouse the needs for special tools that support communication about distinct aspects of reality. In our research, we have been able to demonstrate the promising effects of this playful way of guiding the emergence of mathematical symbolising by relating it to higher achievements in the next higher grade of primary school. This lays a foundation for assuming that the focus on understanding (based on spontaneous actions and dynamic schematising) indeed can lead to higher performance in the mastery of operations. This can be seen as a sign of integration of performance and personal meaning, i.e., of the development of a mathematical identity (as defined previously). Many aspects of this dynamical process, though, have to be detailed further in future research.
Finally, it ought to be repeated here that teachers in the Developmental Education schools never imposed mathematical knowledge or operations on the children or trained them for the mastery of isolated mathematical operations. Where schematising and automatisation activities took place (like in the shoe-shop example above), this was carried out in a meaningful context that evolved out of children’s play. For the future of the upcoming knowledge society, it can be maintained that training of mathematical operations in young children is probably less productive than a ‘Bildung’ approach that aims at developing meaningful (authenticated) operations as derivatives of meaningfully emerging mathematical notions. The Developmental Education approach has proven to be a useful theoretical framework for teachers. It can assist teachers in appropriating the teaching abilities for engaging in the mathematical interactions with pupils which support the emergence of these pupils’ mathematical thinking on the basis of their (spontaneous) actions in the context of their play.
Notes
There are strong parallels between de ‘Developmental Education Approach’ in the domain of mathematics education and the Realistic Mathematics Approach as developed by the Freudenthal Institute in the Netherlands. Coming from different backgrounds (pedagogical psychology and mathematical didactics, respectively), they nevertheless share the strong conviction that (mathematical) learning is based on human activity, depends on the construction and use of cultural tools and is guided by reflective communication. Actually, both approaches share an interactive history since the 1970s. Despite these agreements, the two approaches show prominent differences as well. It is, however, far beyond the scope of this article to detail all communalities and differences.
Currently doing her dissertation research at the Free University in Amsterdam.
References
Carruthers, E., & Worthington, M. (2006). Children’s mathematics: Making marks, making meaning (2nd ed.). London: Paul Chapman Publishing.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, NJ: Lawrence Erlbaum.
Davydov, V. V. (1996). Teorija razvivajuščiego ubučenija [Theory of developmental education]. Moscow: Intor.
Dehaene, S. (1997). The number sense. How the mind creates mathematics. London: Penguin.
Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61, 103–131.
Elkonin, D. B. (1972). Toward the problem of stages in the mental development of the child. Soviet Psychology, 10, 225–251.
Freudenthal, H. (1979a). Lessen van Sovjet rekenonderwijskunde [Lessons of Soviet mathematics educational science]. Pedagogische Studiën, 56, 17–25.
Freudenthal, H. (1979b). Structuur van de wiskunde en wiskundige structuren: een onderwijskundige analyse [Structure of mathematics and mathematical structures: An analysis from an educational science point of view]. Pedagogische Studiën, 56, 51–61.
Freudenthal, H. (1991). Revisiting mathematics education. (China lectures). Dordrecht: Kluwer.
Goffree, F. (1993). Kleuterwiskunde [Young children’s mathematics]. Groningen: Wolters-Noordhoff.
Hargreaves, A. (2003). Teaching in the knowledge society. Education in the age of insecurity. New York: Teachers College Press.
Hughes, M. (1986). Children and number. London: Blackwell.
Karpov, Y. V. (2005). The neo-Vygotskian approach to child development. Cambridge: Cambridge University Press.
Leont’ev, A. N. (1975). Dejatel’nost, soznanie, ličnost’ [Activity, consciousness, personality]. Moscow: Politizdat.
Munn, P. (1998). Symbolic function in preschoolers. In C. Donland (Ed.), The developement of mathematical skills (pp. 47–71). Hove: Psychology Press.
Poland, M. (2007). The treasures of schematising: The effects of schematising in early childhood on the learning processes and outcomes in later mathematical understanding. (Dissertation). Enschede: Ipskamp.
Poland, M., van Oers, B., & Terwel, J. (2009). Schematising activities in early childhood Education. Educational Research and Evaluation, 15(3), 305–321.
Sfard, A. (2008). Thinking as communicating: Human development, the growth of discourses, and mathematizing. Cambridge: Cambridge University Press.
Terwel, J., van Oers, B., van Dijk, I., & van den Eeden, P. (2009). Are representations to be provided or generated in primary mathematics education? Effects on transfer. Education Research and Evaluation, 15(1), 25–44.
van de Craats, J. (2009). TIMSS 2007—Feiten en meningen [TIMMS 2007—Facts and opinions]. http://staff.science.uva.nl/~craats/TIMSS2007NL.pdf
van Dijk, I. M., van Oers, B., & Terwel, J. (2003). Providing or designing? Constructing models as a strategy for working with contextual problems in primary maths education. Learning and Instruction, 13(1), 53–72.
van Oers, B. (1990). The development of mathematical thinking in school: a comparison of the action-psychological and information-processing approaches. International Journal of Educational Research, 14(1), 51–66.
van Oers, B. (1994). Semiotic activity of young children in play: The construction and use of schematic representations. European Early Childhood Education Research Journal, 2(1), 19–34.
van Oers, B. (1996a). Learning mathematics as a meaningful activity. In L. Steffe, P. Nesher, P. Cobb, G. Goldin, & B. Greer (Eds.), Theories of mathematical learning (pp. 91–115). Hillsdale, NJ: Lawrence Erlbaum Associates.
van Oers, B. (1996b). Are you sure? The promotion of mathematical thinking in the play activities of young children. European Early Childhood Education Research Journal, 4(1), 71–89.
van Oers, B. (1997). The narrative nature of young children’s iconic representations: some evidence and implications. International Journal of Early Years Education, 5(3), 237–246.
van Oers, B. (1998). The fallacy of decontextualisation. Mind, Culture, and Activity, 5(2), 135–142.
van Oers, B. (1999a). Auf dem Wege zu einem spielorientierten Curriculum [Towards a play-oriented curiculum]. Theorie und Praxis der Sozialpädagogik, 35, 27–30.
van Oers, B. (1999b). Teaching opportunities in play. In M. Hedegaard & J. Lompscher (Eds.), Learning activity and development (pp. 268–289). Aarhus: University Press.
van Oers, B. (2001). Sprachliche Bildung: Pädagogische Verantwortung für frühe Lernprozesse. [Language Education. Pedagogical justification for Early learning processes]. In H. Colberg-Schrader, D. Engelhard, D. Höltershinken, K. Neumann, & T. H. Sprey-Wessing (Eds.), Kinder in Tageseinrichtungen. Ein Handbuch für Erzieherinnen, Vol. 15 (pp. 729–739). Seelze-Velber: Kallmeyer.
van Oers, B. (2002). The Mathematization of young children’s language. In K. Gravemeijer, R. Lehrer, B. van Oers, & L. Verschaffel (Eds.), Symbolizing and modeling in mathematics education (pp. 29–57). Dordrecht: Kluwer.
van Oers, B. (2003). Learning resources in the context of play. Promoting effective learning in early childhood. European Early Childhood Education Research Journal, 11(1), 7–26.
van Oers, B. (2004). Mathematisches Denken bei Vorschulkindern [Mathematical thinking in preschool children]. In W. E. Fthenakis & P. Oberhuemer (Eds.), Frühpädagogik international. Bildungsqualität im Blickpunkt (pp. 313–330). Wiesbaden: VS Verlag für Sozialwissenschaften.
van Oers, B. (2005). The potentials of imagination. Inquiry, 24(4), 5–18.
van Oers, B. (2006). An activity theory approach to the formation of mathematical cognition: developing topics through predication in a mathematical community. In J. Maaß & W. Schlöglmann (Eds.), New mathematics education research and practice. Rotterdam: Sense Publisher.
van Oers, B. (2009). Developmental education: Improving participation in cultural practices. In M. Fleer, M. Hedegaard, & J. Tudge (Eds.), Childhood studies and the impact of globalization: Policies and practices at global and local levels- World Yearbook of Education 2009 (pp. 293–317). New York: Routledge.
van Oers, B., & Poland, M. (2007). Schematising activities as a means for young children to think abstractly. Mathematics Education Research Journal, 19(2), 10–22.
van Oers, B., Wardekker, W., Elbers, E., & van der Veer, R. (Eds.) (2008). The transformation of learning. Advances in cultural-historical activity theory. Cambridge: Cambridge University Press.
Vygotsky, L. S. (1978). Mind in society: The development of higher psychological processes. Cambridge, Mass: Harvard University Press.
Vygotsky, L. S. (1984). Pedologija podrostka [Pedology of the child]. Moscow: Pedagogika.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
van Oers, B. Emergent mathematical thinking in the context of play. Educ Stud Math 74, 23–37 (2010). https://doi.org/10.1007/s10649-009-9225-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-009-9225-x