Abstract
Intensity-duration-frequency (IDF) curves, commonly used in stormwater infrastructure design to represent characteristics of extreme rainfall, are gradually being updated to reflect expected changes in rainfall under climate change. The modeling choices used for updating lead to large uncertainties; however, it is unclear how much these uncertainties affect the design and cost of stormwater systems. This study investigates how the choice of spatial resolution of the regional climate model (RCM) ensemble and the spatial adjustment technique affect climate-corrected IDF curves and resulting stormwater infrastructure designs in 34 US cities for the period 2020 to 2099. In most cities, IDF values are significantly different between three spatial adjustment techniques and two RCM spatial resolutions. These differences have the potential to alter the size of stormwater systems designed using these choices and affect the results of climate impact modeling more broadly. The largest change in the engineering decision results when the design storm is selected from the upper bounds of the uncertainty distribution of the IDF curve, which changes the stormwater pipe design size by five increments in some cases, nearly doubling the cost. State and local agencies can help reduce some of this variability by setting guidelines, such as avoiding the use of the upper bound of the future uncertainty range as a design storm and instead accounting for uncertainty by tracking infrastructure performance over time and preparing for adaptation using a resilience plan.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Increases in the intensity of rainfall events as a result of climate change are a major threat to infrastructure systems, especially stormwater infrastructure systems and the transportations systems they protect. Higher rainfall intensities lead to more severe storms, with expected increases in damages related to residential, street, and flash flooding (Mailhot and Duchesne 2009; Arnbjerg-Nielsen et al. 2013; Willems et al. 2013). The largest increases are expected in shorter duration events (less than a day) (Westra et al. 2014; Kuo et al. 2015) with hourly extreme precipitation events expected to increase by as much as 400% in North America (Prein et al. 2016b). A major concern is how these changes will affect the function of stormwater systems that have been designed using assumptions that future rainfall will be similar to past rainfall (i.e., the assumption of a stationary climate). These systems are designed to carry or store a specific intensity of rainfall called the “design storm,” which is a precipitation “event” characterized by its probability of occurrence (return period) and its duration. Rainfall intensities and their associated probabilities are standardized in practice in the form of intensity-duration-frequency (IDF) curves (Bonnin et al. 2006; PennDOT 2011; CSA Standards 2012). Updating standardized precipitation information to reflect changes in rainfall is necessary in order to ensure all communities have the information they will need to make good choices in rehabilitation and protection of their infrastructure.
IDF curves can be updated using climate change projections (Cook et al. 2017), such as output from regional climate models (RCMs), which increase the spatial resolution and accuracy of trends from coarse resolution general circulation models (GCMs) through improved land-atmosphere interactions (Teichmann et al. 2013; Cannon et al. 2015). RCMs are especially useful to the urban drainage engineering and planning communities because they are available at a sub-daily timestep, which is important to capture localized rainfall-runoff interactions (Durrans et al. 1999; Cowpertwait et al. 2007; Cook et al. 2017). However, RCMs have been shown to deviate from the observed correlation structure of sub-daily rainfall (Gregersen et al. 2013), and as a result, must be spatially corrected using statistical methods, referred to as model output statistics (MOS), that adjust RCMs to obtain precipitation values at point scales (Maraun et al. 2010). Unfortunately, these models also rarely agree on the magnitude of future change, a phenomenon classified as “uncertainty” in model results (Walker et al. 2013). Uncertainty can be inherited from GCMs due to factors such as internal variability, modeling assumptions, and greenhouse gas emissions scenarios (Kirtman et al. 2013), and can also arise from the spatial resolution of the RCM used in impact assessment (Leung and Qian 2003; Rauscher et al. 2010, 2016; Prein et al. 2016a; Mendoza et al. 2016; Karmacharya et al. 2017) and the MOS technique used in downscaling (Tryhorn and DeGaetano 2011; Gudmundsson et al. 2012; Bürger et al. 2013; Chen et al. 2013; Srivastav et al. 2014a; Sunyer et al. 2014; Cannon et al. 2015).
Uncertainty inherited from GCMs is usually addressed by using an ensemble of multiple models (Carter et al. 2007), but uncertainty from downscaling methods or spatial resolutions is often overlooked in practice. This is concerning because variation introduced due to different spatial resolutions and downscaling methods can surpass variation from the choice of climate model alone (Bürger et al. 2013; Sarr et al. 2015; Mandal et al. 2016a; Mendoza et al. 2016). Finer scale RCMs (i.e., 25 km or less) have been shown to better represent daily precipitation averages, extremes, and spatial distributions than coarser scale models (i.e., 50 km) (Leung and Qian 2003; Rauscher et al. 2010, 2016; Prein et al. 2016a; Karmacharya et al. 2017); however, coarser models are still being used because it is unclear if these findings are true for new RCM datasets that emerge. Numerous and potentially outdated MOS techniques are also being used for IDF curve updating because of the complexity and variability of findings across regions. This complicates the interpretation of results because different methods can lead to differences in the direction of change in precipitation, even when the same climate model is used (DeGaetano and Castellano 2017; Hassanzadeh et al. 2019).
Due to the complexity of considering multiple downscaling methods or multiple spatial resolutions, it is more likely that, in practice, stakeholders or government agencies would choose only one of each. As a result of this uncertainty, most engineering standards have been updated with different ad hoc approaches and available information. These types of inconsistencies have the potential to considerably alter engineering decisions and the level of protection afforded by the infrastructure. During the current design process, engineers calculate the actual stormwater pipe size required for the expected rainfall, and then choose a standardized pipe size increment (PennDOT 2015), which is closest to, but not below, the actual required pipe size. For example, the required pipe size diameter might be estimated to be 487 mm, and the designer chooses the closest available standardized increment size of 525 mm. It is possible that this additional capacity acts as a safety margin that in some cases will outweigh the uncertainties in downscaling or spatial resolution choices, leading to no change in pipe size dimensions under different choices. However, it is also possible that increases to design storms prescribed by climate models lead to oversized design configurations that are cost and space prohibitive. These uncertainties need to be investigated before updated IDF curves can be used with confidence to inform design.
In the present work, we investigate how the choice of climate model spatial resolution and the MOS technique for spatial adjustment alter rainfall predictions and uncertainty in sub-daily IDF curves. Using a newly available RCM dataset from NA-CORDEX, we first provide general trends in expected changes to the 1-h and 24-h storm for 34 cities across the USA. We then demonstrate how the uncertainty from the choice of MOS technique and RCM spatial resolution would alter the selection of design storm from these curves, as well as the dimensions and cost of a stormwater pipe for a sewer shed the size of four city blocks. Based on these findings, we provide a set of recommendations and best practices for practitioners.
2 Data and approach
We developed IDF curves in the present work using the annual maximum series (AMS) from observed rainfall and RCM simulations for 34 cities in the USA, five durations (1, 3, 6, 12, and 24 h), and six return periods (2, 5, 10, 25, 50, and 100 years). Section 2.1 presents the observed data and cities used to create the climate-corrected IDF curves. Section 2.2 describes the methods and RCM simulations used in this process, including the two RCM spatial resolutions, the three spatial adjustment techniques, and the analyses used to assess and bound uncertainty. The final sub-section (2.3) describes the post-processing steps used to assess implications of the modeling choices.
2.1 Selected cities and observed data
We identified cities that are representative of the US climate zones using Bukovsky climate regions, which are smaller and more hydrologically uniform than NOAA climate regions (Bukovsky 2012; Bukovsky et al. 2019). We prioritized cities with populations greater than 100,000 and continuous hourly observed data records from 1950 to 2014. We extracted hourly precipitation observations from 34 cities (two per climate region) from the NOAA National Center for Environmental Information (NOAA 2016) data repository. Data gaps in Detroit, Memphis, Seattle, and Birmingham were supplemented with data from the nearest station that had data for the missing time period. Section S1.1 in the Supplementary Information (SI) provides more details about the observed data. Figure 1 presents historical rainfall characteristics of the 34 US cities evaluated in this study. The 1-h 25-year storm was estimated for the period 1954 to 2013 using methods described in Section 2.2.
2.2 Development of updated sub-daily IDF curves
In order to calculate the expected change in extreme rainfall, we created IDF curves for historical (1954–2013) and future (2020–2099) time periods. We created historical curves by fitting the generalized extreme value (GEV) distribution (Coles 2001) to the annual maximum series (AMS) of rainfall in each city with maximum likelihood estimation (MLE) (Scholz 1980). We fit independent GEV distributions to each duration of AMS, which we aggregated to the desired temporal resolution using sliding maxima (van Montfort 1990). We also calculated GEV parameters corresponding to the confidence intervals using the standard error of the coefficient estimate (MathWorks 2019). We then extracted return levels, or rainfall depths, for a specific return period and confidence interval using the relationship to the GEV distribution parameters shown in Eq. 1. The confidence intervals for each return level correspond to the respective CI estimate of the three parameters.
where zp(d, CI) is the return level for a specific duration, d; confidence interval, CI; and probability of exceedance in any year, p; μ, σ, and ξ are the location, scale, and shape parameters of the GEV distribution, respectively, for a specific CI (Coles 2001). The intensity is calculated by dividing zp by the duration.
For future IDF curves, we modified this process to incorporate trends from RCM simulations, discussed in Section 2.2.2. We used an 80-year future time period (2020–2099) because it represents the full range of expected precipitation in the future and had the lowest uncertainty range when compared to shorter time period lengths, but not a considerably different mid-point. We fit a stationary GEV distribution to the entire time period instead of fitting a non-stationary GEV. Finding a robust, non-stationary trend in the GEV parameters was not possible at each location, and adding a trend in some locations adds additional uncertainty to an already uncertain process (Serinaldi and Kilsby 2015).
There are several additional choices required to develop updated IDF curves, including the selection of (i) the climate model ensemble, (ii) the spatial resolution of this ensemble, (iii) the spatial adjustment technique used to incorporate trends from the climate models into the IDF curves, and (iv) the procedure used to bound the uncertainty range from the GEV distribution and the climate model ensemble. Findings related to the choice of spatial resolution and spatial adjustment technique are discussed in Section 3. However, preliminary analysis indicated that findings related to the other choices were not significant enough to warrant additional consideration.
2.2.1 Regional climate model simulations
Choice of climate models
This analysis uses hourly rainfall time series from RCMs from the North American Coordinated Regional Downscaling Experiment (NA-CORDEX) project (Mearns et al. 2017). We used NA-CORDEX RCMs, which are driven using boundary conditions from CMIP5 GCMs (Taylor et al. 2011), because they are currently the only source of climate model output available at an hourly time step over a continuous 150-year period (1950–2100). The computational resource requirements of running these models at the hourly time step restricts the available RCM-GCM combinations, and only three combinations were available at the two spatial resolutions analyzed in this study (50 km and 25 km): RegCM4 driven by MPI-ESM-LR, WRF driven by MPI-ESM-LR, and WRF driven by GFDL-ESM2M. These simulations used only one greenhouse gas concentration trajectory, RCP 8.5 (Riahi et al. 2011). With 3 RCM-GCM combinations and two spatial resolutions, a total of 6 climate simulations were used in this analysis.
The limited number of simulations used in this study does have the potential to reduce the uncertainty range of the IDF curves relative to the large number of available climate simulations at the daily level. However, the NA-CORDEX experiment accounted for this by using GCMs with a wide range of climate sensitivity. MPI predicts a 3.6 °C rise for a doubling of atmospheric CO2 concentrations, while GFDL predicts a 2.4 °C increase. Thus, we prefer to use the smaller number of available simulations at the hourly time step primarily because the temporal downscaling step required for urban drainage studies is carried out in a consistent manner, upstream of the impacts analysis, using the same physically based equations within the RCM that are already considered as an uncertainty contribution. Furthermore, since the observed and climate model data are at the same temporal resolution (hourly), the IDF curve adjustment process is simplified because the same techniques can be applied to both observed and climate data. Although these hourly outputs are usually parameterized and sometimes inconsistent with realistic conditions, temporal downscaling methods employed after the climate modeling step are also not a panacea. These methods add another layer of uncertainty because they range in complexity and are based on historical relationships between sub-daily and daily rainfall patterns that may not be applicable in a changing climate. Ultimately, the choice between these two procedures is a trade-off that depends on preference, and like other choices evaluated in this paper, has not been standardized by any regulatory body evaluating climate impacts. An investigation into the impacts of this choice warrants additional attention, but is beyond the scope of this study.
Climate model data collection and processing
For each city, we extracted the rainfall time series from the RCM grid cell whose centroid was closest to the location of the NOAA weather station in the city (coordinates are provided in Table S1). Best practices for impact analyses usually recommend using the 9 or 25 grid cells surrounding each station. We chose to use a single grid cell because including values from adjacent grid cells increases uncertainty and makes it difficult to distinguish the differences in uncertainty due to modeling assumptions that are the focus of the study. This choice has the potential to alter the future uncertainty range by ± 10% (results for the raw RCM data are shown in SI Section S1.2).
Because model physics or data processing errors can lead to potentially unrealistic rainfall values, we further processed the RCM simulation data after extraction to eliminate historical hourly intensities greater than the historical maximum rainfall and future hourly maximum intensities more than five times greater than the next highest value. This processing resulted in truncation of less than 0.002% of values.
2.2.2 Choice of climate model spatial resolution
To evaluate the effects of spatial resolution, the RCM ensemble includes simulations using a 25-km and a 50-km grid cell. Finer resolution RCM simulations have been shown to better capture historical rainfall magnitude and spatial distributions; however, decreasing the spatial resolution by half increases the computational resource requirements by at least a factor of eight. The goal of this comparison is, first, to inform the climate modeling community whether the choice of climate model spatial resolution leads to a significant difference in the prediction of extreme rainfall at the sub-daily to daily time step, and second, to inform the engineering and impact modeling communities whether these differences could lead to different infrastructure decisions. The 25-year storm is used in this work as the basis for evaluation of the two different spatial resolutions.
2.2.3 Choice of spatial adjustment (MOS) technique
In addition to the choice of climate model spatial resolution, the choice of spatial downscaling or MOS technique used to incorporate RCM simulations into IDF curves has the potential to considerably alter future rainfall projections. To create climate-corrected IDF curves, many apply MOS techniques to the continuous rainfall time series as the first step in the process, through bias correction (Cannon et al. 2015; Kuo et al. 2015; Kueh and Kuok 2016), weather typing (Mandal et al. 2016b), or weather generators (Wilks and Wilby 1999). The extreme rainfall events extracted from these continuous series (i.e., the annual maximum or partial duration series) can also be adjusted, e.g., through quantile mapping (Srivastav et al. 2014b), genetic programming (Hassanzadeh et al. 2013), or historical analogs (Castellano and DeGaetano 2016). Finally, the intensity of rainfall (return level), evaluated after the GEV is fit to the extreme events, can also be adjusted, usually using a change factor that is a ratio calculated from historical and future climate model return levels (Forsee and Ahmad 2011; Zhu et al. 2012; Cook et al. 2017).
The goal of the MOS technique comparison in this analysis is not to evaluate the performance of each method, but instead to understand how different methods can influence the relative dimensions and cost of stormwater infrastructure projects. As a result, we selected a simplified method from each category that represents the strengths and weaknesses of each general approach. The first method, called Kernel Density Distribution Mapping (KDDM) (McGinnis et al. 2015), is a form of non-parametric quantile mapping that bias-corrects and spatially adjusts the continuous RCM time series to match observations. The relationship between the observed and historical climate model time series is defined by fitting a transfer function (spline) between their empirical CDFs (calculated using kernel density estimation and the trapezoid rule (Cook 2018)).
The second method, similar to the Equidistance Quantile Matching Method technique in Solaiman and Simonovic (2011), referred to as Parametric AMS Mapping (PAM), uses parametric quantile mapping to adjust the annual maximum series of the RCMs. The gridded AMS are spatially adjusted by finding their equivalent return level within the inverse GEV CDF of the observed AMS.
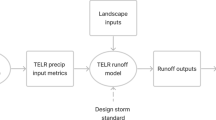
The final method, referred to as the change factor (CF) method, uses areal reduction factors to adjust the observed rainfall depth up or down depending on the change between the historical and future climate model simulations, as seen in Cook et al. (2017) and Mailhot et al. (2007). Figure 2 presents an overview of the sequence of steps required for each adjustment method; a detailed description of the equations and processes used for each method are provided in SI Section S2.
2.2.4 Estimating and bounding the future uncertainty range
Each future rainfall intensity, estimated with a particular MOS technique, RCM-GCM simulation, and spatial resolution (referred to henceforth as a “modeling combination”), has its own uncertainty range due to GEV distribution parameter uncertainty. In order for the results to be easier to interpret, especially for engineering and public stakeholders, it is sometimes desirable to distill the uncertainty ranges from multiple combinations into one range for each duration and return period. To do so, a total of 7 rainfall intensities, associated with the 1, 10, 25, 50, 75, 90, and 99% confidence intervals of the GEV fit of each modeling combination, were calculated for each return period and duration. We then merged these values for multiple modeling combinations together and estimated confidence intervals of this larger range using z-scores.
2.3 Post-processing of updated IDF values
2.3.1 Testing for statistical significance
We evaluated statistically significant differences between various rainfall intensities using the two-sided Kolmogorov-Smirnov (K-S) test (p = 0.01), which tests whether two samples come from the same distribution. The first test compared observed rainfall intensities to future intensities by comparing the observed range between the 90% and 10% CIs to the future ensemble containing all MOS and spatial resolution combinations. The second test evaluated differences in future rainfall intensities resulting from different MOS techniques: each ensemble for a single MOS technique containing all spatial resolutions and RCM combinations was compared to the equivalent ensembles for the other two MOS techniques. The final test compared future rainfall intensities from the two climate model spatial resolutions. In this case, the 50-km ensemble containing all RCM-GCM combinations for each MOS technique was compared to the equivalent 25-km ensemble.
2.3.2 Illustrative stormwater infrastructure design example
We used a design example of a storm sewer pipe sized large enough to contain the 25-year storm to evaluate how different sources of uncertainty may affect standard stormwater infrastructure sizing in many states (Lopez-Cantu and Samaras 2018). We calculated peak discharge using the rational method, with c = 0.65 for a moderately urbanized neighborhood (McCuen 2005), A = 4 ha (10 acres), and i = 1 h, assuming a 1-h time of concentration for the small watershed. We calculated pipe diameters using Manning’s equation with n = 0.013 for ordinary concrete lining and common parameters of s = 0.005, and kn = 1. We rounded the resulting diameters up to the nearest standard US pipe size: 18, 21, 24, 27, 30, 36, and 42 in. (equivalent to 450, 525, 600, 675, 750, 900, and 1050 mm). Using city-specific unit cost data from RS-means (RS Means 2019), we calculated pipe cost for a 1000-ft (305 m) pipe. This length is approximately equal to the length of road spanning four city blocks, an area approximately equal to 4 ha (10 acres).
3 Results and discussion
3.1 General trends
This section provides an overview of the general findings relating to how IDF values are expected to change in the future for different regions. Figure 3 presents the percent change in the 25-year storm in the future (2020–2099) relative to the observed period (1954–2013) for the 1-h (teal) and 24-h (dark blue) durations. All RCM-GCM simulations, spatial resolutions, and spatial adjustment techniques were combined into a single uncertainty range for engineering (see Section 2.2.4), shown as box plots in the bottom of the figure.
Percent change in the 25-year storm from observed period (1953–2013) to future period (2020–2099) for two durations, 1-h (teal) and 24-h (dark blue). In the top figure, marker type shows direction of trend, marker size shows magnitude of median change, and a plus sign (+) signifies that the median future surpasses the observed 90% CI. Hollow markers signify that the change is not significant (p = 0.01). The bottom figure shows uncertainty associated with median values. The box extends to the 25th and 75the quantile and whiskers extend to the 5th and 95th quantiles (equivalent to the 10 and 90% CI). Gray shading represents the historical 10% and 90% CI, and the tan band represents a change of ± 25% from the historical median
In more than half the cities, the median hourly and daily storms are expected to change by less than 25% (small- and medium-sized triangles). However, the uncertainty and distribution surrounding these numbers is wide because it incorporates uncertainty related to the GEV distribution parameters, climate models and their spatial resolutions, and MOS techniques. Because of this uncertainty, the K-S test null hypothesis was rejected (p = 0.01) in most cities for both durations, meaning that the observed and future values cannot be proven to come from the same distribution (e.g., they are significantly different). Some cities, especially those in the Western USA along the Rocky Mountains, did not show a significant change because the historical range (shown as a gray bar) was wide enough to include many of the values in the future range.
These findings suggest that it seems reasonable in some cases to apply a uniform climate factor of safety (e.g., of 25%) to the observed intensity, or to use the observed 90% confidence interval to account for future change. In the cities where the median change is smaller than 25%, this is still acceptable because it could account for additional uncertainty related to the modeling techniques. However, in cities where the median future change surpasses 25% (cities with the largest triangles), or surpasses the historical 90% confidence interval (cities with plus signs), using a 25% climate safety factor or the historical 90% CI would underestimate the future change. Given that the uncertainty of future rainfall predictions is high, these safety factors could still be used as long as the engineer is willing to accept the risks associated with under-design. To balance risks and maintain reasonable performance, all infrastructure systems will need to be monitored in order to understand when redesign or adaptation is needed (Olsen 2015; Kim et al. 2017; Doss-Gollin et al. 2018; Gilrein et al. 2019).
System monitoring at the hourly or sub-hourly time interval is crucial. This is because in about two thirds of cities analyzed, the shorter, hourly storms are expected to change more than the longer, daily storms. Median values and uncertainty also tend to be higher for these hourly storms, especially along the Western and Eastern coasts. The higher uncertainty relative to the daily storm is attributed to certain climate models predicting very extreme hourly events that shift the distribution higher. These intense hourly bursts, often surrounded by periods of little to no rainfall, are smoothed out during aggregation to the daily level, which is why the daily storm is sometimes shown to change by a smaller amount. In regions with higher expected increases in hourly storms, using a daily monitoring interval or design storm may not be adequate; engineers and planners should make sure that their site configuration can account for short, high-intensity bursts.
3.2 Influence of spatial resolution on future IDF values
In the previous section, both climate model resolutions (25 and 50 km) were included in the results. This section instead evaluates how the predicted precipitation intensity for the future would change if one resolution were chosen over another, and whether these differences are significantly different from each other. The null hypothesis that the two samples come from the same distribution was nearly always rejected, meaning that the two spatial resolutions almost always produce statistically significantly different results. Figure 4 presents these results for the 25-year return period across all durations (x-axis). The blue bars represent the average number of cities (for the three methods) where the 50-km ensemble produced significantly higher rainfall depths, while the orange bars show the number of cities where the 25-km ensemble produced higher values. The gray bars show the number of cities where the difference was not significant. The error bars represent the range for the three MOS techniques.
The rainfall intensity is nearly always significantly different between the two spatial resolutions; however, neither resolution consistently produces more (or less) rainfall. In about 70% of cities, the 50-km ensemble predicts a higher intensity for the 1-h duration, but the 25-km ensemble leads to a higher intensity in about 60% of cities for the 24-h storm. This behavior is unexpected because we found that the magnitude of the hourly distribution of the 25-km models tended to be considerably higher than the 50-km distribution, as expected based on previous studies (Leung and Qian 2003; Rauscher et al. 2010). However, in some cities, one or more of the 50-km climate models produced higher 1-h storms, which raised the median 1-h intensity for the entire 50-km ensemble. The daily intensities were not higher because cumulative daily rainfall was usually higher in the 25-km models. In other cities, this switch happened for a different reason. The relative difference between past and future 25-km models was smaller than the 50-km models for the 1-h duration, but larger for the 24-h duration. Despite intensities of higher magnitude, the 25-km models had a smaller relative change from the past, which caused the adjusted intensities to be lower than 50-km intensities for the 1-h duration.
These results show that one spatial resolution does not always produce higher values than another. Generally, finer resolutions have been shown previously to better represent daily extreme rainfall patterns and spatial distributions (Leung and Qian 2003; Prein et al. 2016a; Karmacharya et al. 2017). Our conclusions are similar to these findings. The finer resolution models (25 km) used in this analysis produced hourly values that were more consistent with real-world tendencies. The higher magnitude of the annual maximum series was closer in value to the observed AMS. Unlike the 50-km, the 25-km distribution did not produce unrealistic rainfall events that were several times greater than the next largest intensity. As a result, the 25-km AMS distribution was smoother, and the GEV parameters converged faster. Finally, in some of the 50-km runs, the historical AMS were greater than the future AMS for certain quantiles. This can lead to problems with bias correction and GEV fit. As a result, when updating IDF curves, we recommend that states, localities, or engineers use the finest spatial resolution available that is appropriate for the desired design application when selecting from RCM simulations with sufficient length and output frequency to sample extreme events well.
3.3 Influence of MOS technique on change in 25-year storm and pipe size
Some of the uncertainty discussed in the previous section results from differences in the MOS techniques (see Section 2.2.3). This section evaluates how much results for future rainfall differ between the three MOS techniques, whether these differences are statistically significant, and whether they would alter the size of a stormwater pipe designed using one method over another. This design example is oversimplified and likely would not be used in practice; however, the simplicity of this design process is desirable because the example is only intended to test sensitivity of the design storm, keeping all other watershed characteristics constant. Figure 5 presents the range (across the three MOS techniques) in the median percent change of the 1-h 25-year storm. The circles to the right of the main panel represent the change in pipe size (in mm) that would result from using the future value from each MOS technique relative to the observed design storm. Cities are ordered by median change from lowest (top) to highest (bottom).
Range in percent change in the median 1-h 25-year design storm across MOS techniques, KDDM (purple), PAM (green), and CF (orange). Marker type shows statistical significance (or lack of) between techniques. Circles show step change in pipe size from observed 1-h 25-year storm for a 4-ha watershed. Cities are ordered from top to bottom based on lowest to highest median future percent change
Consistent with other studies (e.g., Tryhorn and DeGaetano 2011; Gudmundsson et al. 2012; Bürger et al. 2013; Srivastav et al. 2014a; Sunyer et al. 2014), our findings show that selecting a different MOS technique can lead to considerable, and sometimes significant, differences in the expected percent change in rainfall. On average for the 34 cities, the median predicted change between MOS techniques differs by more than 20 percentage points, and can differ by nearly 100 percentage points. In cities with more extreme rainfall, like Jacksonville, a 20% difference in the median change equates to a difference in the design storm of more than 1 cm of rainfall. In 15 of the cities, the differences are large enough to alter the distribution and lead to statistically significant (p = 0.01) differences between MOS techniques. In nearly all cities where the differences are statistically significant and in some cities where they are not, the uncertainty in the median change would alter the engineering decision. In nearly half of cities, the pipe size changes by one or more increments (75 mm). These findings confirm that uncertainty related to climate models or spatial correction techniques can affect impact modeling results as well as the size and cost of infrastructure designed for climate resilience.
These results also show that different MOS techniques act differently in each city, even when the same climate model ensemble is used. In other words, one technique does not systematically bias the rainfall values to be higher or lower. This is because each technique alters the rainfall distribution in a different way, e.g., parametrically or using a ratio, and these differences can considerably change the unstable extreme value distribution, and thus, the relative magnitude of future rainfall intensities. These inconsistent results make the case for standardizing MOS techniques in all IDF studies nationally; however, since rainfall patterns vary by city, it is unlikely that the same MOS technique can be used in every US city or region.
As a result, stakeholders should select the technique that works best for their region, based on general guidelines. For instance, Cannon et al. (2015) propose that precipitation values should be detrended before they are used in quantile mapping. Furthermore, parametric mapping functions should be used with caution; there are instances in this research when abnormally high rainstorms in the climate model can lead to unrealistically large values of rainfall when aggregated to the 24-h duration. If these large storms are not removed from the prediction, the parametric mapping method will lead to unrealistic future results. Generally, non-parametric MOS techniques that adjust the observed time series to reflect future change tend to outperform parametric bias-correction techniques (Gudmundsson et al. 2012).
3.4 Influence of uncertainty from all choices on stormwater infrastructure decisions
As the previous sections show, the choice of spatial resolution and MOS technique both contribute considerable uncertainty to the range of updated IDF values. An additional source of uncertainty that has not yet been discussed is the selection of the design storm value within this uncertainty range. Instead of using the median intensity, as was done in the previous analysis, municipalities or engineers may wish to increase their level of protection by selecting a higher bound within the future uncertainty range (e.g., the 90% CI). Selecting a value farther away from the median has the potential to magnify inconsistencies between the modeling choices. Figure 6 highlights this fact for three different cities: New York (left), El Paso (middle), and Minneapolis (right). The figure shows the pipe diameters for a 4-ha watershed that would result from using different choices for the design storm, including (i) the median or 90% CI of the future range (line type), (ii) the 25-km or 50-km spatial resolution (colors), or (iii) one of three MOS techniques discussed previously (rows). Monetary values represent the cost per foot of pipe for each diameter and city.
Resulting pipe diameters (mm) for a 4-ha, moderately urbanized (c = 0.65) watershed in three selected cities (New York, El Paso, and Minneapolis as columns). Diameters vary depending on the time period, historical (gray) or future (colored); climate model spatial resolution, 25-km (orange) or 50-km (blue); MOS spatial correction technique (rows); or selection within the uncertainty range, mid-point (solid lines) or upper bound (dashed lines). Cost values are in USD/ft of concrete pipe for each diameter
Using the 90% CI of the future uncertainty range instead of the median may provide some additional protection in the future; however, the amount of protection varies by location and modeling choice. In El Paso, using the 90% CI from either MOS technique or spatial resolution (dashed lines) leads to an increase of one or two pipe sizes from the median future design storm (solid lines). This is a reasonable safety factor if stakeholders are willing to spend $10 to $36 more per foot of pipe to avoid overflows. However, in New York and Minneapolis, choosing the future 90% CI of could increase the pipe size by up to five increments, compared to the median future design storm. This choice would nearly double the unit cost of the pipe in these cities, which equates to paying an additional $8200 to $8500 for a concrete pipe spanning four city blocks. While this would increase protection, this considerable expansion may be unreasonable due to budget constraints, underground size restrictions, or flow velocity thresholds. If pipes are too large, then low flow velocities may not reach self-cleansing thresholds, leading to buildup of sediment and potential corrosion in the pipes (DeZellar and Maier 1980; Cook et al. 2018).
When compounded by uncertain modeling choices, the use of the upper bound of the future uncertainty range leads to design decisions that are inconsistent, not reproducible, and potentially costly. Due to these factors, more research is needed to ensure consistency of future uncertainty ranges. In the meantime, we recommend avoiding the use of the 90% CI of the future uncertainty range for design. If additional protection is desired, designers should instead use the median storm from a higher return period. Median values are less volatile, more reproducible, and easier to understand for stakeholders.
Despite the volatility and uncertainty of the higher confidence intervals of the future range, we cannot completely disregard these values because they could occur. The selected design value or infrastructure size may not directly account for the upper bound, but communities and practitioners should be aware that these values are plausible, and have a resilience plan in place if they do occur. Since many existing stormwater infrastructure systems in the USA were designed for a given level of risk and are currently underperforming in many areas (Lopez-Cantu and Samaras 2018; Wright et al. 2019), this plan should describe actions for upcoming replacement cycles and future adaption. For instance, when a new pipe is installed, designers could ensure that there is enough space to install a bigger pipe in the future, or to modify the pipe in some way to address the flow challenges described.
4 Summary and conclusions
The goal of this study is to evaluate how the choices of climate model spatial resolution and spatial adjustment technique alter rainfall predictions and uncertainty in updated IDF curves and stormwater infrastructure decisions made using these curves. There is considerable uncertainty in updated IDF curves as a result of these choices, as well as from the uncertainty in estimating statistical distribution parameters. The rainfall intensity is often significantly different between the two spatial resolutions and three spatial adjustment techniques, and none of the methods or spatial resolutions consistently bias results in one direction. These differences have the potential to alter the size of a stormwater pipe designed using these modeling choices, showing that these uncertainties from modeling choices affect resilience strategies and impact modeling. These modeling choices lead to the largest changes in the engineering decision when the design storm is selected from the upper bounds of the uncertainty distribution. In some cities, using the 90% confidence interval of the future uncertainty range instead of the median value changes the stormwater pipe diameter size by 5 increments, nearly doubling the cost of the pipe.
In order to reduce some of this variability, impact modelers will need to be more consistent in their modeling choices to ensure that engineers are accounting for the same type of uncertainty in design. State and local agencies can help this process by setting guidelines for resilient stormwater infrastructure designs. One suggested guideline would be to choose finer resolution climate simulations over coarser simulations, because they have been shown in this and other analyses to be more consistent with real-world rainfall patterns. Another guideline for design engineers would be to avoid using the upper bound of the future uncertainty range as a design storm, and instead rely on the median of the next highest return period if additional protection is desired. Unfortunately, it is still unclear which spatial adjustment technique is best suited for IDF curve updating, and the most appropriate method is likely to vary by region. Municipalities will need to identify best practices for their community, and in the absence of standardized guidelines, impact modelers will need to make a choice and be transparent about variability using uncertainty metrics like those in Mandal et al. (2016a).
As many other studies have said, there is unfortunately not a “one size fits all” solution and engineers using updated IDF curves should understand this in order to inform stakeholders that performance of infrastructure may vary over time. Unfortunately, no matter what size of infrastructure is selected, it is likely to experience increased variability and increases in short-duration, high-intensity rain storms. Tracking performance over time for both green and gray infrastructure, and using adaptable design principles will ensure communities are prepared for many future states (Cook et al. 2019). For instance, if a larger pipe size is selected, municipalities should plan to flush pipes during periods of drought, whereas smaller pipe sizes will likely need distributed green infrastructure placed upstream in order to send flows into pipes more slowly. To ensure approaches like these are implemented, communities should consider documenting them in a resilience plan.
This study highlights how different modeling choices could alter stormwater infrastructure decisions, but there are several limitations and future research needs. Only a limited number of climate models, emissions scenarios, and modeling techniques were used, which may not represent the full range of uncertainty in the future. Additionally, these findings only consider one procedure for estimating runoff for one type of stormwater infrastructure. Other studies have found that uncertainty introduced due to hydrologic models is non-negligible, but smaller than uncertainty introduced from climate models (Prudhomme and Davies 2009a, 2009b). Nonetheless, more research is needed to understand how significant these uncertainties are with respect to other sources of variability in engineering design, such as land use change, and how to manage these combined uncertainties in many types of green and gray stormwater infrastructure. Furthermore, the approach used in this study to combine parameter uncertainty from the GEV distribution with uncertainty from climate models and downscaling techniques was relatively simple and other techniques, such as jack-knifing (Kay et al. 2009; Shao and Tu 2012), may have defined different confidence intervals. In order to achieve consistent and reliable confidence intervals for IDF curves, a framework similar to Wilby and Harris (2006) should be developed to distill parameter uncertainty and climate uncertainty into a useable and consistent future uncertainty range for the engineering community.
References
Arnbjerg-Nielsen K, Willems P, Olsson J et al (2013) Impacts of climate change on rainfall extremes and urban drainage systems: a review. Water Sci Technol J Int Assoc Water Pollut Res 68. https://doi.org/10.2166/wst.2013.251
Bonnin GM, Martin D, Lin B, et al (2006) NOAA Atlas 14: Precipitation-Frequency Atlas of the United States, volume 2, Version 3.0
Bukovsky M (2012) Masks for the Bukovsky regionalization of North America, Regional Integrated Sciences Collective. Inst Math Appl Geosci Natl Cent Atmospheric Res Boulder CO Downloaded 07–03
Bukovsky M, Thompson JA, Mearns LO (2019) Weighting a regional climate model ensemble: does it make a difference? Can it make a difference? Clim Res 77:23–43
Bürger G, Sobie S, Cannon A et al (2013) Downscaling extremes: an intercomparison of multiple methods for future climate. J Clim 26:3429–3449
Cannon AJ, Sobie SR, Murdock TQ (2015) Bias correction of GCM precipitation by quantile mapping: how well do methods preserve changes in quantiles and extremes? J Clim 28:6938–6959
Carter T, Alfsen K, Barrow E, et al (2007) IPCC-TGICA: general guidelines on the use of scenario data for climate impact and adaptation assessment (TGICA), version 2
Castellano CM, DeGaetano AT (2016) A multi-step approach for downscaling daily precipitation extremes from historical analogues. Int J Climatol 36:1797–1807. https://doi.org/10.1002/joc.4460
Chen J, Brissette FP, Chaumont D, Braun M (2013) Performance and uncertainty evaluation of empirical downscaling methods in quantifying the climate change impacts on hydrology over two North American river basins. J Hydrol 479:200–214. https://doi.org/10.1016/j.jhydrol.2012.11.062
Coles S (2001) An introduction to statistical modeling of extreme values, 1st edn. Springer-Verlag London, London
Cook LM (2018) Using climate change projections to increase the resilience of stormwater infrastructure designs under uncertainty. Carnegie Mellon University
Cook LM, Anderson CJ, Samaras C (2017) Framework for incorporating downscaled climate output into existing engineering methods: application to precipitation frequency curves. J Infrastruct Syst:23. https://doi.org/10.1061/(ASCE)IS.1943-555X.0000382
Cook LM, Samaras C, VanBriesen JM (2018) A mathematical model to plan for long-term effects of water conservation choices on dry weather wastewater flows and concentrations. J Environ Manag 206:684–697. https://doi.org/10.1016/j.jenvman.2017.10.013
Cook LM, VanBriesen JM, & Samaras C (2019). Using rainfall measures to evaluate hydrologic performance of green infrastructure systems under climate change. Sustain Resilient Infrastruct:1–25. https://doi.org/10.1080/23789689.2019.1681819
Cowpertwait P, Isham V, Onof C (2007) Point process models of rainfall: developments for fine-scale structure. The Royal Society, pp:2569–2587
DeGaetano AT, Castellano CM (2017) Future projections of extreme precipitation intensity-duration-frequency curves for climate adaptation planning in New York state. Clim Serv 5:23–35. https://doi.org/10.1016/j.cliser.2017.03.003
DeZellar JT, Maier WJ (1980) Effects of water conservation on sanitary sewer and wastewater treatment plant. J Water Pollut Control 52
Doss-Gollin J, Farnham DJ, Steinschneider S, Lall U (2018) Robust adaptation to multi-scale climate variability. Earths Future
Durrans SR, Burian SJ, Nix SJ et al (1999) Polynomial-based disaggregation of hourly rainfall for continuous hydrologic simulation. JAWRA J Am Water Resour Assoc 35:1213–1221. https://doi.org/10.1111/j.1752-1688.1999.tb04208.x
Forsee W, Ahmad S (2011) Evaluating urban storm-water infrastructure design in response to projected climate change. J Hydrol Eng 16:865–873. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000383
Gilrein EJ, Carvalhaes TM, Markolf SA et al (2019) Concepts and practices for transforming infrastructure from rigid to adaptable. Sustain Resilient Infrastruct:1–22
Gregersen IB, Sørup HJD, Madsen H et al (2013) Assessing future climatic changes of rainfall extremes at small spatio-temporal scales. Clim Chang 118:783–797
Gudmundsson L, Bremnes JB, Haugen JE, Engen-Skaugen T (2012) Technical note: downscaling RCM precipitation to the station scale using statistical transformations–a comparison of methods. Hydrol Earth Syst Sci 16:3383–3390
Hassanzadeh E, Nazemi A, Elshorbagy A (2013) Quantile-based downscaling of precipitation using genetic programming: application to IDF curves in Saskatoon. J Hydrol Eng 19:943–955. https://doi.org/10.1061/(ASCE)HE.1943-5584.0000854
Hassanzadeh E, Nazemi A, Adamowski J et al (2019) Quantile-based downscaling of rainfall extremes: notes on methodological functionality, associated uncertainty and application in practice. Adv Water Resour 131:103371. https://doi.org/10.1016/j.advwatres.2019.07.001
Karmacharya J, Jones R, Moufouma-Okia W, New M (2017) Evaluation of the added value of a high-resolution regional climate model simulation of the South Asian summer monsoon climatology. Int J Climatol 37:3630–3643. https://doi.org/10.1002/joc.4944
Kay A, Davies H, Bell V, Jones R (2009) Comparison of uncertainty sources for climate change impacts: flood frequency in England. Clim Chang 92:41–63
Kim Y, Eisenberg DA, Bondank EN et al (2017) Fail-safe and safe-to-fail adaptation: decision-making for urban flooding under climate change. Clim Chang. https://doi.org/10.1007/s10584-017-2090-1
Kirtman B, Power SB, Adedoyin JA et al (2013) Near-term climate change: projections and predictability. In: Stocker TF, Qin D, Plattner G-K et al (eds) Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp 953–1028
Kueh S, Kuok K (2016) Precipitation downscaling using the artificial neural network BatNN and development of future rainfall intensity-duration-frequency curves. Clim Res 68:73–89
Kuo C-C, Gan T, Gizaw M (2015) Potential impact of climate change on intensity duration frequency curves of Central Alberta. Clim Chang:1–15. https://doi.org/10.1007/s10584-015-1347-9
Leung LR, Qian Y (2003) The sensitivity of precipitation and snowpack simulations to model resolution via nesting in regions of complex terrain. J Hydrometeorol 4:1025–1043. https://doi.org/10.1175/1525-7541(2003)004<1025:TSOPAS>2.0.CO;2
Lopez-Cantu T, Samaras C (2018) Temporal and spatial evaluation of stormwater engineering standards reveals risks and priorities across the United States. Environ Res Lett. https://doi.org/10.1088/1748-9326/aac696
Mailhot A, Duchesne S (2009) Design criteria of urban drainage infrastructures under climate change. J Water Resour Plan Manag 136:201–208. https://doi.org/10.1061/(ASCE)WR.1943-5452.0000023
Mailhot A, Duchesne S, Caya D, Talbot G (2007) Assessment of future change in intensity–duration–frequency (IDF) curves for Southern Quebec using the Canadian regional climate model (CRCM). J Hydrol 347:197–210
Mandal S, Breach PA, Simonovic SP (2016a) Uncertainty in precipitation projection under changing climate conditions: a regional case study. Am J Clim Change 5:116
Mandal S, Srivastav RK, Simonovic SP (2016b) Use of beta regression for statistical downscaling of precipitation in the Campbell River basin, British Columbia, Canada. J Hydrol 538:49–62. https://doi.org/10.1016/j.jhydrol.2016.04.009
Maraun D, Wetterhall F, Ireson AM et al (2010) Precipitation downscaling under climate change: recent developments to bridge the gap between dynamical models and the end user. Rev Geophys 48. https://doi.org/10.1029/2009RG000314
MathWorks (2019) Coefficient standard errors and confidence intervals. In: Documentation. https://www.mathworks.com/help/stats/coefficient-standard-errors-and-confidence-intervals.html?lang=en. Accessed 7 Mar 2019
McCuen RH (2005) Hydrologic analysis and design, 3rd edn. Pearson Prentice Hall
McGinnis S, Nychka D, Mearns LO (2015) A new distribution mapping technique for climate model bias correction. In: Lakshmanan V, Gilleland E, McGovern A, Tingley M (eds) Machine learning and data mining approaches to climate science. Springer, Berlin, pp 91–99
Mearns LO, McGinnis S, Korytina D, et al (2017) The NA-CORDEX dataset, version 1.0. NCAR Climate Data Gateway, Boulder, CO
Mendoza PA, Mizukami N, Ikeda K et al (2016) Effects of different regional climate model resolution and forcing scales on projected hydrologic changes. J Hydrol 541:1003–1019. https://doi.org/10.1016/j.jhydrol.2016.08.010
NOAA (2016) National Centers for Environmental Information. http://www.ncdc.noaa.gov/
Olsen J (ed) (2015) Adapting infrastructure and civil engineering practice to a changing climate
PennDOT (2011) Chapter 7, Appendix A: field manual for Pennsylvania design rainfall intensity charts from NOAA Atlas 14 Version 3 Data. In: PennDOT Drainage Manual 2010 Edition. Pennsylvania Department of Transportation, Harrisburg, PA, pp 1–40
PennDOT (2015) Chapter 13, Storm drainage systems. In: PennDOT Drainage Manual 2015 Edition. Pennsylvania Department of Transportation, Harrisburg, PA, pp 13–25
Prein AF, Gobiet A, Truhetz H et al (2016a) Precipitation in the EURO-CORDEX 0.11 degree and 0.44 degree simulations: high resolution, high benefits? Clim Dyn 46:383–412. https://doi.org/10.1007/s00382-015-2589-y
Prein AF, Rasmussen RM, Ikeda K et al (2016b) The future intensification of hourly precipitation extremes. Nat Clim Chang 7:48
Prudhomme C, Davies H (2009a) Assessing uncertainties in climate change impact analyses on the river flow regimes in the UK. Part 1: baseline climate. Clim Chang 93:177–195. https://doi.org/10.1007/s10584-008-9464-3
Prudhomme C, Davies H (2009b) Assessing uncertainties in climate change impact analyses on the river flow regimes in the UK. Part 2: future climate. Clim Chang 93:197–222
Rauscher SA, Coppola E, Piani C, Giorgi F (2010) Resolution effects on regional climate model simulations of seasonal precipitation over Europe. Clim Dyn 35:685–711. https://doi.org/10.1007/s00382-009-0607-7
Rauscher SA, O’Brien TA, Piani C et al (2016) A multimodel intercomparison of resolution effects on precipitation: simulations and theory. Clim Dyn 47:2205–2218. https://doi.org/10.1007/s00382-015-2959-5
Riahi K, Rao S, Krey V et al (2011) RCP 8.5—a scenario of comparatively high greenhouse gas emissions. Clim Chang 109:33. https://doi.org/10.1007/s10584-011-0149-y
RS Means (2019) RS Means Online Construction Estimating Software: 2019 Design Professional’s package CD. Gordian, Rockland, MA
Sarr MA, Seidou O, Tramblay Y, El Adlouni S (2015) Comparison of downscaling methods for mean and extreme precipitation in Senegal. J Hydrol Reg Stud 4:369–385. https://doi.org/10.1016/j.ejrh.2015.06.005
Scholz FW (1980) Towards a unified definition of maximum likelihood. Can J Stat 8:193–203. https://doi.org/10.2307/3315231
Serinaldi F, Kilsby CG (2015) Stationarity is undead: uncertainty dominates the distribution of extremes. Adv Water Resour 77:17–36. https://doi.org/10.1016/j.advwatres.2014.12.013
Shao J, Tu D (2012) In: Springer Science & Business Media (ed) The jackknife and bootstrap, Berlin
Solaiman TA, Simonovic SP (2011) Development of probability based intensity-duration-frequency curves under climate change. Water Resour Res Rep 34:1–93
Srivastav RK, Schardong A, Simonovic SP (2014a) Equidistance quantile matching method for updating IDFCurves under climate change. Water Resour Manag 28:2539–2562
Srivastav RK, Schardong A, Simonovic SP (2014b) Equidistance quantile matching method for updating IDFCurves under climate change. Water Resour Manag 28:2539–2562. https://doi.org/10.1007/s11269-014-0626-y
CSA Standards (2012) Development, interpretation, and use of rainfall intensity-duration-frequency (IDF) information: guideline for Canadian water resources practitiioners. Canadian Standards Association, Ontario, Canada
Sunyer MA, Gregersen IB, Madsen H et al (2014) Comparison of different statistical downscaling methods to estimate changes in hourly extreme precipitation using RCM projections from ENSEMBLES. Int J Climatol 35. https://doi.org/10.1002/joc.4138
Taylor KE, Stouffer RJ, Meehl GA (2011) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Teichmann C, Eggert B, Elizalde A et al (2013) How does a regional climate model modify the projected climate change signal of the driving GCM: a study over different CORDEX regions using REMO. Atmosphere 4:214–236
Tryhorn L, DeGaetano A (2011) A comparison of techniques for downscaling extreme precipitation over the Northeastern United States. Int J Climatol 31:1975–1989
van Montfort MA (1990) Sliding maxima. J Hydrol 118:77–85
Walker WE, Lempert RJ, Kwakkel JH (2013) Deep uncertainty. In: Encyclopedia of Operations Research and Management Science. Springer, Berlin, pp 395–402
Westra S, Fowler H, Evans J et al (2014) Future changes to the intensity and frequency of short-duration extreme rainfall. Rev Geophys 52:522–555
Wilby RL, Harris I (2006) A framework for assessing uncertainties in climate change impacts: low-flow scenarios for the River Thames, UK. Water Resour Res 42:n/a-n/a. https://doi.org/10.1029/2005WR004065
Wilks DS, Wilby RL (1999) The weather generation game: a review of stochastic weather models. Prog Phys Geogr 23:329–357. https://doi.org/10.1177/030913339902300302
Willems P, Olsson J, Arnbjerg-Nielsen K et al (2013) Climate change impacts on rainfall extremes and urban drainage: a state-of-the-art review. Geophys Res Abstr 15
Wright DB, Bosma CD, Lopez-Cantu T (2019) US hydrologic design standards insufficient due to large increases in frequency of rainfall extremes. Geophys Res Lett
Zhu J, Forsee W, Schumer R, Gautam M (2012) Future projections and uncertainty assessment of extreme rainfall intensity in the United States from an ensemble of climate models. Clim Chang 118:469–485. https://doi.org/10.1007/s10584-012-0639-6
Acknowledgments
This research was sponsored by the National Science Foundation (NSF) (NSF Collaborative Award Number CMMI 1635638/1635686). The authors acknowledge the World Climate Research Programme’s Working Group on Regional Climate, and the Working Group on Coupled Modelling, former coordinating body of CORDEX and responsible panel for CMIP5, and also thank the climate modeling groups (Melissa Bukovsky at NCAR and Hsin-I Chang at University of Arizona) for producing and making available their model output. We acknowledge additional data, resources, and support from researchers involved in the NA-CORDEX project, including Linda Mearns, Melissa Bukovsky, and Daniel Korytina. We also thank Andrew Thompson for pipe cost data collection and Jeanne VanBriesen, Mitchell Small, Xiaoju Chen, and Tania Lopez-Cantu for their feedback that significantly improved the quality of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
ESM 1
(DOCX 1697 kb)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cook, L.M., McGinnis, S. & Samaras, C. The effect of modeling choices on updating intensity-duration-frequency curves and stormwater infrastructure designs for climate change. Climatic Change 159, 289–308 (2020). https://doi.org/10.1007/s10584-019-02649-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-019-02649-6