1 Introduction

Microfluidic devices such as microchannels, microreactors, and micromixers have attracted wide attention from industry and academia. Because of their advantages such as small amounts of sample and reagent, less time consumption, low cost and high throughput, their usage is expected to be expanded in the fields of micro total analysis systems (µTAS) and lab-on-a-chip systems (Nguyen and Wu 2005; Hessel et al. 2005). Among the microfluidic devices, the efficient liquid–liquid mixing of micromixers plays an important role in various fields such as chemical synthesis, drug delivery, and life science. Due to the small dimensions of micromixers, flow in microchannel is generally laminar flow and the mixing is dominated by molecular diffusion. Since the molecular diffusion is a very slow process, micromixers depending on molecular diffusion solely require long channel length and are not efficient to complete mixing rapidly. Therefore, micromixers need another way to enhance mixing.

Micromixers can be classified into two types based on their mechanisms to enhance mixing; active and passive mixers. Active micromixers perturb the flow by external sources including ultrasonic vibration (Yang et al. 2000), acoustic (Zhu and Kim 1998) and bubble-induced vibrations (Liu et al. 2002). Although active micromixers can improve mixing efficiency, most of them are complex to fabricate and operate (Deng et al. 2014; Wang et al. 2003). On the other hand, passive micromixers do not require an external actuator and they enhance mixing by changing their geometries to generate convection. Then, the interface between fluids is stretched and folded, and efficient mixing is achieved. Several types of passive micromixers have been studied to date. Liu et al. (2000) proposed a three-dimensional serpentine micromixer and experimentally showed it is capable of improving the mixing. Buchegger et al. (2011) developed a micromixer which laminated different fluids and achieved very fast and uniform mixing. Zhang et al. (2011) proposed and investigated a planar zigzag microchannel with different flow rates. Their goal is to increase the contact surface area of fluids to enhance mixing. Another simple method for efficient mixing is to attach obstacles on the micromixer. Wang et al. (2002) proposed a Y-micromixer equipped with several round obstacles and compared the mixing efficiency and pressure drop through numerical simulation by changing the number and the layout of the obstacles. Alam et al. (2014) extended the strategy to compare the mixing performance with different obstruction shapes (e.g., diamond and hexagonal). Hsiao et al. (2014) and Borgohain et al. (2018) investigated a microchannel with winglet pairs and they confirmed that mixing is enhanced by the longitudinal vortices generated after the winglet pairs. Stroock et al. (2002a, b) developed a novel type of T-shaped micromixer with patterned grooves on the bottom of the channel, which is well known and called the staggered herringbone mixer (SHM) and the slanted groove mixer (SGM). The property of SHM is widely studied by both experiment (Williams et al. 2008) and simulation (Yang et al. 2005; Lynn and Dandy 2007; Kang et al. 2008; Liu et al. 2004).

Most of the numerical studies focus on clarifying the flow field generated by SHM, and it is still a minor study to optimize SHM. Ansari and Kim (2007a, b) and Cortes-Quiroz et al. (2009, 2010) conducted shape optimization of SHM. Both of them employed surrogate models to approximate the objective functions and successfully found the optimal micromixer. For the sake of simplicity, their optimization simplified the model by unifying the geometries such as width, length, and mounting angle of each groove. Moreover, the number of grooves on the channel was fixed during the optimization. In other words, the topology of the channel was fixed and the topological influence has not been investigated yet.

Topology optimization is the most flexible structural optimization method, which can modify connectivity of an object independently of its predefined topology in contrast to sizing and shape optimization that keep their topology during the optimization. Topology optimization has been applied to a variety of engineering optimization problems (Bendsøe and Sigmund 2004; Sigmund and Maute 2013; Deaton and Grandhi 2014). Although the topology optimization methods for structural design have matured in the past few decades, the application to flow problems is still limited due to the non-linearity of the governing equations. The first application to flow problems was relatively late among the applications of topology optimization. It was performed for the Stokes flow by Borrvall and Petersson (2003). Since then, several types of fluid topology optimization methods have been proposed; slow incompressible flows and slightly compressible flow with low to moderate Reynolds number (Evgrafov 2006; Gersborg-Hansen et al. 2005; Guest and Prévost 2006). However, most studies in the literature aim to minimize power dissipation of flow channels. Recently, a few other papers considering interesting and useful fluid problems have been published. Kondoh and his colleagues proposed a topology optimization problem to minimize the drag force and to maximize the lift force of an object put in a flow field (Kondoh et al. 2012). Besides, Lin et al. (2015) conducted fluid topology optimization of fluid diodes. They maximized the diodicity which is defined as the ratio of pressure drop of reverse flow and forward flow.

Topology optimization often contains a large design space due to a high degree of freedom for shape and topology representation (i.e., the number of design variables is often equal to the number of elements in the finite element mesh) (Guest and Smith Genut 2010). Thus, conventional topology optimization generally has employed the gradient-based method according to the sensitivity of an objective function to explore the optimal solution and has been developed based on this approach. However, the gradient-based method tends to get stuck to poor local optima rather than the global optimum (Sigmund and Petersson 1998; Kaminakis and Stavroulakis 2012; Ortmann and Schumacher 2013). On the other hand, Evolutionary Algorithm (EA) such as Genetic Algorithm (GA) is one of the metaheuristic optimization methods which are more possible to explore the global optimum. However, GA requires numerous function evaluations to realize population-based multipoint simultaneous exploration. Thus, GA is not efficient to solve the optimization problems with expensive calculations and requires impractical computational cost (i.e., large population and many generations) to obtain competitive solutions. In this case, surrogate models are effective to reduce computational cost required for function evaluation. This model approximates the response of each objective or constraint function to design variables in an algebraic expression. The model is derived from several sample points with real values of the objective or constraint function given by expensive numerical simulations. Thus, it can promptly give estimates of function values at arbitrary design variable values.

Topology optimization of micromixers has been conducted by Andreasen et al. (2009) and Deng et al. (2012) using the gradient-based method and they showed the optimal micromixers with grooves, which were quite similar to SHM and SGM. Their optima seem plausible but there is still a potential to find better local optima since they employed a gradient-based method despite several studies (Wang et al. 2002; Cortes-Quiroz et al. 2009), reporting that the mixing efficiency is a multi-modal (quite non-convex) function. As mentioned above, since the gradient-based method tends to get stuck to local optima particularly in non-convex optimization problems, a metaheuristic method such as GA is required to be employed to explore the whole objective space.

This study aims to propose a topology optimization method for passive micromixer using genetic algorithm. As reported in the previous studies (Yang et al. 2005; Lynn and Dandy 2007), the asymmetrical structures of the grooves on the channel bottom such as slanted grooves play a significant role to enhance mixing. Thus, this study proposes a novel method to represent grooves using a graph theory. Then, we consider two types of grooves attached on the bottom of the channel to the outer side (hereinafter called the convex grooves) or to the inner side (hereinafter called the concave grooves). Since GA is a population-based exploration method, the population must cover the search space entirely. Thus, we consider three optimization cases which differ in handling the grooves for the convex groove problem at first. Then, based on the knowledge extracted from three cases of the convex groove problem, the concave groove problem is implemented. Finally, the obtained optima in each case are investigated to understand comprehensive characteristics of grooves for mixing.

The rest of the paper is organized as follows. In Sect. 2, we introduce numerical methods including groove representation method using the graph theory, computational fluid dynamics (CFD) method and optimization methods such as GA and the Kriging surrogate model. Section 3 presents the definition of the objective function to quantify the mixing performance and four optimization problems; three convex groove problems and one concave groove problem. Section 4 presents the results and discussions of each case. In Sect. 4, we also perform a sensitivity analysis of selected important variables on the best solutions found by GA in each case to validate they are competitive local optima and to take a closer look at their relation to the mixing performance. Finally, concluding remarks are given in Sect. 5.

2 Numerical methodologies

2.1 Graph theoretical representation

The authors have proposed a topology optimization method using a surrogate-assisted genetic algorithm for single and multi-objective optimization of two-dimensional heatsinks (Yoshimura et al. 2017a). In Yoshimura et al. (2017a), the flow channel was represented by the level-set function interpolated by several scattered control points in the design domain. We defined the level-set function as the implicit function obtained by solving a partial differential equation in the entire design domain.

In the present study, the representation method should be capable of inserting or removing the grooves on the design domain with relatively a small number of design variables. Since a groove is put as a cuboid on the design domain, the top and the bottom of the groove can be regarded as the superposition of the step-function, which is a discontinuous function. Thus, it might be difficult to employ the interpolation-based representation methods which assume the material distribution following an implicit function, which is usually a continuous function, and are often used in non-gradient-based topology optimization (Guirguis et al. 2015; Yoshimura et al. 2017a). Hence, this study proposes a novel representation method for fluid problem inspired by the graph theory. In the context of topology optimization, the graph-theoretical representation is often applied in truss structures to represent the structure with a small number of design variables to the extent that genetic algorithm can handle (Kaveh and Kalatjari 2003; Lyu and Saitou 2005; Tang et al. 2005; Giger and Ermanni 2006, Su et al. 2011). In the truss structures, each bar element is represented as an edge of the graph.

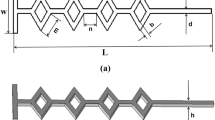
This study represents a graph G (V, E), where V is a finite and nonempty set of vertices, and E is a set of undirected edges denoted by the adjacency matrix A, where the element in the i-th row and the j-th column is denoted as aij. Here, aij = 1 if the i-th vertex is adjacent to the j-th vertex, otherwise aij = 0. In this study, a graph consisting of 3 × 3 = 9 vertices is considered. Figure 1 shows an example of the graph and the corresponding grooves on the micromixer expressed by the following equation:

Fig. 1
figure 1

A graph (left) and the corresponding grooves on the bottom of a micromixer (right). For sake of visibility, the right figure is displayed upside down

Full size image
$$V=\left\{ {v1,~v2,~v3,~v4,~v5,~v6,~v7,~v8,~v9} \right\},$$
(1)
$$E={\text{~}}\left\{ {\left( {v1,v5} \right),~\left( {v3,v5} \right),~\left( {v4,v8} \right),(v6,v8)} \right\}.$$

The design variables correspond to each element of the adjacency matrix A = aij \((1\hspace{0.17em}\le \hspace{0.17em}i\hspace{0.17em}<\hspace{0.17em}j\hspace{0.17em}\le \hspace{0.17em}9)\) and dimensions of the grooves (stated in Sect. 3 in more details).

2.2 Surface data generation

To generate mesh for numerical simulation, we need to construct an STL file consisting of a list of triangular facet data in each case. Since an object to be optimized changes topologically during the optimization, the STL file should be constructed automatically, efficiently, and precisely. This study employs the Delaunay triangulation (Chew 1989). Delaunay triangulation is the most popular and well-studied method for automatic mesh generation of complex domains. Although the two-dimensional Delaunay triangulation method is matured, the three-dimensional Delaunay triangulation still has several difficulties. One of the most significant drawbacks of the original Delaunay triangulation is convexity (i.e., the surface with non-convex region cannot be represented by the original triangulation) as illustrated in Fig. 2 (left). To solve this issue and recover the true boundary, several methods are developed such as the introduction of Steiner points (Liu et al. 2014) and node insertion (George et al. 1991). Although these methods show a promising effect in boundary recovery, they need the true boundary data a priori, which is not available in the present study. Thus, this study develops a simpler boundary recovery method to construct hundreds of different STL files quickly without conducting additional steps which require inserting additional points or moving existing points.

Fig. 2
figure 2

Delaunay triangulation of a slanted groove mixer. The boundary obtained using original Delaunay triangulation (left) and the true boundary obtained by removing unnecessary outer tetrahedra (right). For sake of visibility, both figures are displayed upside down

Full size image

Since the present modified Delaunay triangulation is an ad hoc method specialized in the current problem, we do not describe the method in detail (see our preliminary work (Yoshimura et al. 2017b) if necessary). The essence of the modified Delaunay triangulation is to introduce a unique number to each node. Based on these numbers, we can distinguish whether a tetrahedron is inside or outside of the true wall boundary.

2.3 CFD methodology

In this study, the mixture model provided by the commercial finite volume CFD package ANSYS Fluent17.2 is used to simulate flow fields and to analyze mixing of the micromixer. The governing equations are the continuity equation, the Navier–Stokes equations, and the convection–diffusion equation given as follows:

$$\nabla \cdot u=0,$$
(2)
$$\frac{{\partial u}}{{\partial t}}+\left( {u \cdot \nabla } \right)u= - \frac{1}{\rho }\nabla p+\nu {\nabla ^2}u,$$
(3)
$$\frac{{\partial c}}{{\partial t}}+u \cdot \nabla c=D{\nabla ^2}c,$$
(4)

where u is the fluid velocity, ρ is the density, ν is the kinetic viscosity, p is the fluid pressure, t is the time, \(\nabla\) is the gradient operator, c is the concentration, and D is the diffusion coefficient.

The SIMPLE algorithm is used for pressure–velocity coupling. The second-order upwind scheme is used for velocity and PRESTO! scheme is adopted for pressure (ANSYS, Inc. 2016). It is important to note that a high order scheme for volume fraction should be employed to capture the fluid interface precisely, and the QUICK scheme is adopted in the present study. Based on the STL file generated by the Delaunay triangulation stated in Sect. 2.2, the unstructured tetrahedral meshes are generated using the Mixed-Element Grid Generator in three Dimensions (MEGG3D) (Ito and Nakahashi 2004). To obtain the mesh-independent results, a sensitivity analysis for mesh size is conducted beforehand and the mesh size where mixing performance converges is found. In this study, the spacing length of the mesh cells is set to 6.25 µm.

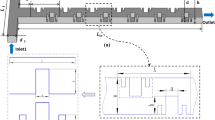
The geometry of a micromixer is illustrated in Fig. 3. In Fig. 3, the design domain corresponds to the first cycle of the green region and the geometry of the second cycle is assumed to be the same as that of the first cycle. In this study, according to the review on the parameters of micromixers reported by Cortes-Quiroz et al. (2009), the geometries of the micromixer are defined as follows; the height h is 80 µm, the width w is 200 µm, the length l is 1 mm, and the ratio lcycle/la is 2.5. It is important to note that although this study employs relatively short length of the micromixer to save the computational cost, the authors believe that the current length is sufficient to evaluate the performance of the micromixer for the optimization since most previous studies on the optimizations of micromixers (Ansari and Kim 2007a, b; Cortes-Quiroz et al. 2009, 2010; Deng et al. 2012) employed periodic design domain and confirmed a significant effect of mixing at an early stage (l ~ 1 mm) on the entire mixing performance. Thus, this study focuses on the mixing on the primary stage (for the sake of completeness, the longer channels with more cycles until the mixing is completed are investigated in the next section to verify that the mixing performance trend on more cycles does not change). As working fluids, this study employs water (liquid) and ethanol (liquid) with the properties shown in Table 1. The flow is assumed as viscous, isothermal (300 K), and incompressible.

Fig. 3
figure 3

The geometry of micromixer

Full size image
Table 1 Properties of working fluids
Full size table

The Reynolds number and the Péclet number based on the height of the channel are set to 1 and 1.2 × 103, respectively. The inlet of the microchannel is equally divided into two regions as illustrated in Fig. 3. 100% water is assigned to the blue region, 100% ethanol is assigned to the red region. The flow velocity is set to 1.8 cm/s uniformly at the inlet for both fluids and set as the Neumann boundary condition at the outlet. The pressure is set as the Neumann condition at the inlet and set as the Dirichlet condition (zero pressure) at the outlet. Along the wall, the no-slip boundary condition is imposed.

2.4 Optimization methodology

The genetic algorithm mimics the evolution of organisms, which selects individuals from the current generation as parents, generates new individuals as children by the crossover and mutation of the parents, and inherits better individuals to the next generation. In this study, the Non-dominated Sorting Genetic Algorithm II (NSGA-II) proposed by Deb et al. (2002) is employed for exploration because this algorithm is effective and widespread employed for many optimization problems including topology optimization problems (Cortes-Quiroz et al. 2009, 2010; Hamza et al. 2013; Garcia-Lopez et al. 2013; Guirguis et al. 2015; Yoshimura et al. 2017a,b). Since the improvement of a genetic algorithm is beyond the scope of this paper, the detailed procedure of NSGA-II is not stated here (see (Deb et al. 2002) for its details).

Although GA is capable of finding the global optimum, it requires numerous function evaluations to realize population-based multipoint simultaneous exploration. To save the computational cost for function evaluation, the Kriging surrogate model (Jones et al. 1998) can be employed together with GA. The Kriging model is based on Bayesian statistics, and can adapt well to nonlinear functions. In addition, the Kriging model estimates not only the function values themselves but also their uncertainties. Based on these uncertainties, the expected improvement (EI) of an objective function, which may be achieved a better optimum on the Kriging model by adding a new sample point, is estimated. In a single-objective optimization problem where y(x) is minimized, the improvement value I(x) and its expected value E[I(x)] are defined as in the following equations:

$$I\left( {\varvec{x}} \right)=\left\{ {\begin{array}{ll} {\left[ {{y_{{\text{min}}}} - y} \right]} \\ 0 \end{array}} \right.{\text{~~~~~~~~~~~~~}}\begin{array}{*{20}{c}} {{\text{if}}~y<~{y_{{\text{min}}}}} \\ {{\text{otherwise}}} \end{array},$$
(5)
$$E\left[ {I\left( {\varvec{x}} \right)} \right]=\mathop \int \limits_{{ - \infty }}^{{{y_{{\text{min}}}}}} \left( {{y_{{\text{min}}}} - y} \right)\phi \left( y \right)dy,$$
(6)

where ϕ is the probability density function denoted by N[\(\widehat{y}\left(\varvec{x}\right), {s}^{2}\left(\varvec{x}\right)\)]. Here, \(\widehat{y}\left(\varvec{x}\right)\) is the estimation of y(x) and s2(x) is the mean square error at point x indicating the uncertainty of the estimated value. Maximizing the EI instead of the original objective function, the location of an additional sample point is determined for updating the Kriging model. Adding new samples to the Kriging model based on EI iteratively, these samples are expected to reach the global optimum under the uncertainty of the Kriging model. This procedure is called Efficient Global Optimization (EGO) proposed by Jones et al. (1998) and widely employed for optimization. Note that ensuring the structural connectivity during the optimization is often a bottleneck to apply genetic algorithm for topology optimization (Deaton and Grandhi 2014). However, in the present problem, the topological change of the design domain does not affect the connectivity of the main channel.

3 Optimization problems

In this section, the problem definitions for each case study are stated. First of all, the objective function to evaluate the mixing performance is stated. In all cases, the standard deviation of concentration at the outlet of micromixer defined by the following equation is calculated:

$$\sigma =\sqrt {\frac{1}{N}\mathop \sum \limits_{{i=1}}^{N} {{({c_i} - {c_\infty })}^2}} ,$$
(7)

where ci is the concentration distribution of one fluid at the i-th cell on the outlet, \({c}_{\infty }\) is the mean concentration on the outlet, and N is the number of cells at the outlet. The standard deviation is 0.5 at the inlet and 0.4766 if the micromixer does not have a groove (i.e., mixing occurs due to diffusion only). The optimization problems are defined to minimize Eq. (7) as the objective function subject to the limitation on the number of grooves (stated later) for initial samples of the Kriging model in each case. The constraint is imposed only on the initial samples whereas the number of grooves is unlimited during the exploration.

The optimization procedure is expressed in the flowchart of Fig. 4. In each case, 100 initial sample points, which are generated randomly, are used to construct the Kriging model. The optimization is conducted based on the EGO framework. The Kriging model approximates the objective function (Eq. 7) and NSGA-II maximizes the EI value (Eq. 6) instead of the original objective function to determine the location of an additional sample point. The optimization iteration stops when the EI value is less than a prescribed threshold, which is set to \(1\hspace{0.17em}\times \hspace{0.17em}{10}^{-3}\) in Cases 1–3 and \(1\hspace{0.17em}\times \hspace{0.17em}{10}^{-2}\) in Case 4, or the topology of the design domain is not changed for three iterations.

Fig. 4
figure 4

The procedure of optimization

Full size image

As stated in Sect. 2.1, the input design variables are converted to graphs through the adjacency matrix. In general, the elements of the adjacency matrix are binary (i.e., aij = 1, if the edge is active, otherwise aij = 0). However, to implement EGO framework, the design variables are needed to be treated as real numbers.

The graph-theoretical representation enables us to represent numerous types of topology. For example, in the current problem, the 3 × 3 graph shown in Fig. 1 has 36 potential edges in the ground structure. When the number of edges is 10, the number of possible groove configurations is 36C10 = 254,186,856. Thus, it is obviously impractical to evaluate all configurations. The same problem has been reported by Kawamoto et al. (2004). In their work, they attempted to explore the global optimum of the truss structure represented by the graph theory with enumeration. However, they reported that a limitation to the number of edges must be employed, or the total computation time could amount to more than 100 years. Moreover, they also reported that the limitation does not always prevent global exploration since there are many poor configurations. It is worth noting that we must decide the array of the graph carefully to balance the flexibility of the structure represented by the graph and the efficiency of the exploration by GA. Here, 3 × 3 graph shown in Fig. 1 is deemed to be sufficient to investigate the optimal configurations because of the following three reasons. (1) Simpler graphs (e.g., 2 × 3) can only represent slanted grooves and cannot represent herringbone. (2) More complex graphs (e.g., 3 × 4) can be replicated by the present graph using periodic configuration. In this study, we focus on finding superior structures (topologies) in addition to the SGM or the SHM using the GA since the optima reported in previous studies on topology optimization for micromixers using gradient-based methods are still very similar to these well-studied structures. (3) The number of design variables is dominated by the adjacency matrix of the graph. Since the adjacency matrix of an undirected graph is a symmetric matrix and we can ignore its diagonal components, the number of design variables derived from the adjacency matrix is (n2 − n)/2, where n is the number of the total vertices. In other words, the number of variables increases approximately with the square of the number of vertices. In this study, since the Kriging model is employed to reduce the computational cost for the function evaluation (CFD simulation), the accuracy of the model is critical for efficient exploration. It is well-known that the cost of training a metamodel with more than 50 variables is prohibitive (Han et al. 2017).

As stated in Sect. 1, at first, we conduct the following three cases with the convex grooves on the design domain illustrated in Fig. 3a to deal with the following two issues: (1) how to treat the design variables as continuous values, and (2) the appropriate constraint to confine the design space.

Case. 1 The first case imitates the binary adjacency matrix. The number of design variables in Case 1 is 29 in total. First, two design variables are given to represent the groove width/channel width wg/w, and the groove depth/channel height d/h, in the range of [0.1, 0.4]. Then, 27 design variables are given to represent the adjacency matrix. The adjacency matrix for the 3 × 3 graph has 36 elements and 9 of them correspond to the edges parallel to the flow such as a14 and a25. Since the preliminary simulation revealed that these 9 elements do not contribute to the efficient mixing, the remaining 27 elements are considered as the design variables in the present study. 27 design variables are given in the range of [0, 1] and a threshold is introduced to classify whether the element is active or not. In this study, the threshold is set to 0.2 such that a groove is activated when the value of its corresponding element of the adjacency matrix is larger than 0.2. Moreover, this case limits the number of grooves to 4 for the initial samples of the Kriging model. Again note that to achieve the global exploration, this limitation is not imposed on the solutions searched by GA.

Case. 2 The second case treats the input variables as the width of each groove directly. The number of design variables in this case is 28 in total. First, one design variable denotes d/h in the range of [0.1, 0.4]. Then, 27 design variables are given to represent the adjacency matrix in the range of [0, 0.4]. This case sets the threshold to 0.1 for 27 design variables such that a groove is activated when the value of its corresponding element of the adjacency matrix is larger than 0.1. The values of these 27 design variables work as the weights of the adjacency matrix and each of them represents the ratio of the groove width to the channel width. In other words, the evident difference between Cases 1 and 2 is that Case 1 unifies the width of grooves by one design variable (wg/w), whereas Case 2 can consider different width on each groove. To the best of our knowledge, although several studies have conducted the parametric study or shape optimization of SHM and SGM, the micromixers considered in those work assumed the same groove width and the combination of the different width has not been investigated yet.

Case. 3 The third case is a minor change of Case 2. Case 3 treats the design variables in the same way as in Case 2. However, the limitation on the number of edges for initial samples increases to 6 in Case 3, whereas that is 4 in Case 2. Case 3 is considered to investigate the influence of the number of edges for initial samples and the proper limitation to achieve the efficient exploration by GA.

Based on the results and discussions of aforementioned three cases, we implement the additional fourth case with the concave grooves on the design domain illustrated in Fig. 3b.

Case. 4 The fourth case considers the micromixer with the concave grooves. Case 4 treats the design variables in the same way as Cases 2 and 3. Thus, the number of design variables in Case 4 is 28. Although the range of the design variables corresponding to the elements of the adjacency matrix is [0, 0.4] which is the same as that in the previous cases, the range of the design variable corresponding to the ratio of the groove height to the channel height hg/h differs from that in Cases 1–3. The range of hg/h is decided based on the discussion by Deng et al. (2012). Deng et al. (2012) reported that when hg/h > 0.8, it required mesh refinement and led to more computational cost due to the thin top layer. We have confirmed the same issue and the thin top layer generated when hg/h > 0.8 prevents the Delaunay triangulation from the accurate boundary recovery. Thus, the range of hg/h is defined as [0.1, 0.8]. The limitation on the number of edges for initial samples is set to 6 as in Case 3 (the reason for this decision will be described in the next section).

In summary, the case studies in the present paper are compared in Table 2.

Table 2 Comparison of Cases 1–4
Full size table

4 Results and discussion

4.1 Result (case 1)

First, in Case 1, the Kriging model is updated 15 times. As reported in the previous studies, the objective function is a multi-modal function (i.e., there are several micromixers whose objective function values are quite close but with different topology). Figure 5 shows the bottom of the micromixer with the grooves of the representative additional samples. Moreover, for illustrative purposes, the corresponding graphs composing one cycle are also shown in Fig. 5. Figure 6 shows the flow fields at several cross-sections along the x-direction of the best solution among the additional sample points. In addition, their objective function values are shown in Table 3.

Fig. 5
figure 5

Case 1: the representative micromixers in the additional samples. The configurations of grooves (left) and the graphs of one cycle (right)

Full size image
Fig. 6
figure 6

Case 1: the phase contours of the best solution

Full size image
Table 3 Case 1: objective function values of the representative micromixers in the additional samples
Full size table

As shown in Fig. 5, each local optimum mainly consists of slanted grooves. Moreover, Fig. 6a displays that the groove a34 is occupied by water, which is illustrated in blue, and transports the water into the ethanol side. Then, as shown in Fig. 6b, the fluid interface is distorted by the helical flows and the efficient mixing is achieved. Besides, GA reveals that large d/h is favorable and the objective function value is not sensitive to the structural changes on the design domain if d/h is less than 0.3. It is worthwhile to note that, in Case 1, due to the threshold for the design variables composing the adjacency matrix and the pseudo-binary treatment for them, the sensitivity of the design variables to the mixing performance is weakened and several unimportant grooves often appear during the optimization (e.g., a12 in 8th sample). In most cases, these grooves prevent the efficient exploration by GA and lead to slow convergence. To tackle with this issue, the continuous treatment for all of the design variables as implemented in Cases 2 and 3 is performed.

4.2 Result (case 2)

Second, in Case 2, the Kriging model is updated 10 times. In this case, GA confirms that the objective function is a multi-modal function as well as in Case 1. Figure 7 shows the bottom of the micromixer with the grooves and their corresponding graphs of the representative additional samples. The objective function values are shown in Table 4.

Fig. 7
figure 7

Case 2: the representative micromixers in the additional samples. The configurations of grooves (left) and the graphs of one cycle (right)

Full size image
Table 4 Case 2: objective function values of the representative micromixers in the additional samples
Full size table

As well as in Case 1, the asymmetric configurations consisting of the oblique grooves are obtained during the optimization in Case 2. As shown in Fig. 7, GA finds that an N-shaped configuration (a34, a37, and a67) and a V-shaped configuration (a34 and a37) are the dominant topologies. Since these configurations are crossing from one side to the other side, they transport water (blue region) to the ethanol side (red region) more efficiently than one thick groove (e.g., a34 in Case 1). As shown in Fig. 8a, b, the grooves are occupied by water and the fluid interface is distorted as well as in Case 1. Although Case 2 converges faster than Case 1 and the significant topologies are revealed, the objective function value of the best solution found in Case 2 is slightly worse than that found in Case 1. Although fast convergence is achieved by the continuous treatment for design variables, we attribute the slightly inferior solution to the limitation on the number of grooves. In other words, the constraint is too strict and prevents the global exploration and thus Case 3 with a loosened constraint is implemented.

Fig. 8
figure 8

Case 2: the phase contours of the best solution

Full size image

4.3 Result (case 3)

In Case 3, the Kriging model is updated 22 times. Since Case 3 is allowed to represent grooves more flexibly (up to 6 grooves), there are various micromixers in the initial samples compared with Cases 1 and 2. Figure 9 shows the configurations and the corresponding graphs of the representative micromixers in the additional samples. The objective function values are shown in Table 5.

Fig. 9
figure 9

Case 3: the representative micromixers in the additional samples. The configurations of grooves (left) and the graphs of one cycle (right)

Full size image
Table 5 Case 3: objective function values of the representative micromixers in the additional samples
Full size table

As shown in Fig. 9, the obtained optima are composed of complex configurations in addition to the V-shaped grooves. These intricate configurations play a further role in addition to the transportation of fluids observed in Cases 1 and 2. For illustrative purpose, the region of 5th and 6th cross-sections of Fig. 10a is zoomed up in Fig. 10b and the same region of Fig. 10c is also zoomed up in Fig. 10d. In contrast to the interface distorted to the arch shape in Cases 1 and 2, the interface shown in Fig. 10b is distorted more complicated, and Fig. 10d shows the interface is not only distorted but also split. It is well known that splitting the fluid repeatedly is efficient to enhance mixing. Indeed, the solution obtained in Case 3 is superior to the solutions obtained in the previous cases.

Fig. 10
figure 10

Case 3: the phase contours of the best solution

Full size image

Despite its superior optimum, it is worth mentioning slow convergence of Case 3. As stated in Sect. 3, we terminate the update of the Kriging model when either the EI value or the topology of the design domain is converged. Cases 1 and 2 are considered to converge relatively early since the dominant topologies often lead to early convergence, namely, they are misleading in terms of the global exploration. However, since the initial samples of the Kriging model in Case 3 contain various topologies than those of Cases 1 and 2, it is less likely to get stuck to early convergence. Therefore, GA could globally explore the optimum on the multi-modal objective function, and consequently, the convergence was delayed. Moreover, it is important to note that the number of grooves of the best and other local optima is 4–6. Hence, if the limitation on the number of grooves is 4, GA is not possible to explore the entire objective space and may be more likely to converge to inferior local optima. On the other hand, if the constraint is set to more than 8, the configurations of the grooves are less asymmetric and we cannot expect such structures to improve the mixing performance. Based on the discussion stated above, the constraint on the number of grooves for Case 4, the concave groove problem, is decided to 6.

4.4 Result (case 4)

Finally, Case 4 with the concave grooves is conducted. In Case 4, the Kriging model is updated 10 times. Note that since the value range of the objective function in Case 4 is relatively broader than that in the convex groove problems, the Kriging model is constructed based on the exponential value of the raw data. Figure 11 shows the configurations of the representative local optima and their corresponding graphs. The objective function values are shown in Table 6.

Fig. 11
figure 11

Case 4: the representative micromixers in the additional samples. The configurations of grooves (left) and the graphs of one cycle (right)

Full size image
Table 6 Case 4: objective function values of the representative micromixers in the additional samples
Full size table

As tabulated in Table 6, the objective function values in Case 4 are much better than those of Cases 1, 2, and 3. According to Fig. 11, the half lateral grooves (e.g., a12, a78) often appear in solutions and hg/h takes its maximum value (0.8). Figure 12 explains these differences from previous cases. As shown in Fig. 12, the fluid interface is strongly stretched and folded by the concave grooves. At first, the interface is asymmetrically stretched to ethanol side by the grooves a12 and a29 (second and third cross-sections of Fig. 12a). Then, the groove a49 stretches the interface again to the water side and the interface is folded (fourth cross-section of Fig. 12a). The flow passes the second cycle with this state and is stretched and folded again. The half lateral groove plays a key role to trigger the asymmetric stretching and this explains why 5th sample with a56 in addition to a12 and a78 is superior to other local optima.

Fig. 12
figure 12

Case 4: the phase contours of the best solution

Full size image

Note that, although the reader may think that micromixers with the concave groove are totally superior to those with convex grooves, it is not surprising that the pressure loss of Case 4 is nearly 20 times larger than that of Cases 1, 2, and 3. Since the pressure loss is an essential factor in practical operation, considering the constraint imposing admissible pressure loss would be necessary in the future. Through the comparison between convex and concave grooves in this study, one can choose an appropriate mixer based on their purpose and acceptable cost. The mixer with convex grooves is possible to enhance mixing with lower pressure drop while it needs much longer channel length (possibly more than 10 cycles verified in subsection 4.6). On the other hand, the mixer with concave grooves is possible to complete mixing in a very short channel length at the cost of high pressure drop.

4.5 Sensitivity analysis

As performed in the above cases, GA is capable of exploring the multi-modal objective space and finding several competitive local optima. However, the solutions found by GA are not guaranteed as local optima. Hence, finally we conduct a sensitivity analysis for the best solutions of Cases 1–4 to prove that these solutions are competitive local optima. The sensitivity analysis is performed under the following conditions: (1) the tested parameters are the sizing parameters (e.g., height or depth of grooves) and the activated elements of the adjacency matrix (the design variables whose value is larger than a prescribed threshold), (2) the perturbation to the i-th variable xi is given by an independent uniform random number in the range of [− 0.1xi, 0.1xi], (3) we accept the topological change due to the perturbation (e.g., a groove will disappear when the perturbed value is less than the threshold), and (4) the sensitivity analysis must be conducted in the original design space (when a perturbed variable value is larger than the upper limit of the variable, the variable value is fixed to the upper limit). In each case, 15 samples with perturbation are evaluated by ANSYS Fluent and compared with the obtained best solution (hereinafter called nominal). The results of the sensitivity analysis are shown in Figs. 13, 14, 15 and 16 and their objective function values are tabulated in Tables 7, 8, 9 and 10. Note that Fig. 13 (Case 1) shows only width and depth of the grooves since the width of the grooves is unified and the values of the elements of the adjacency matrix do not affect the dimension.

Fig. 13
figure 13

Case 1: influence of active design variables on mixing performance

Full size image
Fig. 14
figure 14

Case 2: influence of active design variables on mixing performance

Full size image
Fig. 15
figure 15

Case 3: influence of active design variables on mixing performance

Full size image
Fig. 16
figure 16

Case 4: influence of active design variables on mixing performance

Full size image
Table 7 Case 1: result of the sensitivity analysis. Comparison of perturbed samples and nominal solution (8th sample)
Full size table
Table 8 Case 2: result of the sensitivity analysis. Comparison of perturbed samples and nominal solution (3rd sample)
Full size table
Table 9 Case 3: result of the sensitivity analysis. Comparison of perturbed samples and nominal solution (20th sample)
Full size table
Table 10 Case 4: result of the sensitivity analysis. Comparison of perturbed samples and nominal solution (5th sample)
Full size table

Tables 7, 8, 9 and 10 show that the sensitivity analyses find several slightly superior solutions in all cases. To clarify the effects of the parameters, we further compare the perturbed variables with those of the nominal solution. Figures 13, 14, 15 and 16 compare the design variables and the objective function values of the 15 samples and the nominal solution used in each analysis. In Figs. 13, 14 and 15 (convex groove cases), we can observe that the samples with better objective function values than that of the nominal have deeper or at least one wider groove. In contrast to the subtle difference from the nominal solutions in Figs. 13, 14, 15 and 16 (concave groove case) shows that the objective function values change dramatically with the perturbation on the variables. In particular, there is a strong negative correlation between the height of the grooves and the objective function values (higher height leads to lower objective function value (better performance)). This may suggest that the performance of the concave groove is very sensitive to the subtle perturbation and the requirement of the robust design optimization from the viewpoint of practical application.

The sensitivity analyses to Cases 1–4 reveal that the solutions obtained by GA are quite close to local optima (on the order of 0.1% difference from nominal). We conclude that the exploration by GA can provide competitive solutions such that we can extract the specific fluid motions to improve the mixing performance.

4.6 Verification of the mixing performance trend in more groove cycles

As stated in Sect. 2.3, this study employs a relatively short channel with 2 groove cycles to reduce the computational cost. In this subsection, we conduct an additional numerical simulation for a channel with more cycles until the mixing is completed and verify that the trend of mixing performance enhanced by grooves does not change between the two lengths of cycles. It is important to note that we focus on the concave grooves (Case 4) and the verification for the convex grooves (Cases 1–3) is left for the future research because (1) we deem it is difficult to discuss the difference among local optima just based on CFD, although the mixing performance trend among local optima shown in Tables 3, 4 and 5 are quite close and its weak trend does not change even with a longer channel with 10 cycles (not shown here), and (2) the purpose of the current work is to clarify several qualitative characteristics to enhance mixing by grooves. The convex grooves enhance mixing by the transportation of fluid to other side by slanted grooves and the splitting of the interface by intricate groove structures. We think that it may be difficult to compare these characteristics quantitatively (i.e., we do not have a proper criterion to evaluate how intricate the structure is), whereas the mixing performance of concave grooves is improved by stretching and folding and the number of half lateral grooves plays a key role. In other words, the difference on mixing performance among local optima of Case 4 can be compared quantitatively.

First, the best local optimum called nominal in Sect. 4.5 is extended to 10 cycles and its mixing performance is evaluated by ANSYS Fluent. The geometry of the long mixer and its phase contour are shown in Fig. 17. As shown in Fig. 17b, the mixing is completed in an early stage (the mixing criterion is 2.686 × 10− 8 on the outlet after the 10th cycle). Since it is not effective to compare the mixing performance after the mixing is completed, we focus on the point (after the 4th cycle) where the mixing is about to be completed as indicated by the arrow in Fig. 17b.

Fig. 17
figure 17

Geometry and phase contour of the best optimum in Case 4 with 10 groove cycles

Full size image

Table 11 compares the mixing performance of the local optima of Case 4. Although the mixing is already about to be completed and the difference becomes weaker than that on 2 cycles, the trend of mixing performance among the optima still holds. The simulation on this subsection confirms that the validity of the optimization results with 2 groove cycles and the effectiveness of the proposed micromixer which is possible to complete mixing with less than 1.8 mm length compared with the optimized SHM which requires nearly 4 mm length (Ansari and Kim 2007b).

Table 11 Comparison of mixing performance of local optima of Case 4 after the 4th cycle
Full size table

5 Concluding remarks

A new approach for topology optimization of passive micromixers using graph-theoretical representation and surrogate-assisted genetic algorithm was proposed. This study focused on passive mixing enhanced by grooves on the bottom of the micromixers. This study revealed the following three aspects: (1) how the combination of grooves with different width affects the mixing performance, (2) how the user-defined constraint on the number of grooves affects the exploration performance of GA, and (3) the difference of mixing characteristics between the convex and the concave grooves.

In the convex groove cases, three types of optimization problems were considered. The first case treated the adjacency matrix as pseudo-binary and suggested that the design variables should be treated as continuous values for the efficient exploration by GA. The second case treated the design variables as continuous values and grooves with the different width can appear in the micromixer. GA also explored several local optima and revealed the dominant topologies which facilitate efficient mixing. However, as proved in Case 3, these topologies may be misleading and more loose constraint for the number of grooves should be employed. The third case loosened the limitation for the number of grooves to investigate the design space more widely. As a result, GA found more complex configurations which enhance mixing further by splitting the interface of fluids. The best optimum found in Case 3 was superior to those in Cases 1 and 2.

In the fourth case, the concave grooves were employed. The mixing performance in Case 4 was much superior to that in the convex groove problems. The high grooves and the combination of an oblique groove and a half lateral groove (i.e., a groove from one side to the center of the channel such as a12) were preferable to enhance mixing. The interface was stretched and folded repeatedly in the micromixer and the efficient mixing was achieved in short length. Although the mixing performance in Case 4 was much superior to that in Cases 1–3 (convex grooves), it also showed quite high pressure drop (i.e., it requires higher input energy for mixing). Therefore, future work should include a prescribed pressure drop into the optimization as a constraint to balance the pressure drop and the mixing performance. We hope that the comparison in this work will provide more options on selecting the types of micromixers for the researchers in the community based on their purpose and acceptable cost.

The sensitivity analysis was performed for each case to prove that the solutions found by GA were competitive local optima. The analyses showed that the solutions were sufficiently in the vicinity of local optima and the exploration by GA was capable of exploring the multi-modal objective space.

The approach proposed in the present study offered a novel aspect on application of GA to fluid topology optimization and revealed specific fluid motions in the passive micromixers. For more practical design of passive micromixer, since the performance of the micromixers is quite sensitive to the geometric perturbation as suggested by the sensitivity analysis, conducting the robust design optimization is a topic of ongoing work.