Abstract
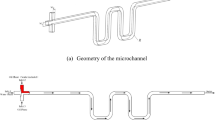
This numerical study was conducted to analyze and understand the parameters that affect the mixing performance of droplet-based flow in sinusoidal microfluidic channels. Finite element analysis was used for modeling fluid flow and droplet formation inside the microchannels via tracking interface between the two heterogeneous fluids along with multiple particle trajectories inside a droplet. The solutions of multiphase fluid flow and particle trajectories were coupled with each other so that drag on every single particle changed in every time step. To solve fluid motion in multiphase flow, level set method was used. Parametric study was repeated for different channel dimensions and different sinusoidal channel profiles. These results were compared with mixing in droplets inside a straight microchannel. Additionally, tracking of multiple particles inside a droplet was performed to simulate the circulating flow profile inside the droplets. Based on the calculation of the dispersion length, particle trajectories, and velocities inside droplets, it is concluded that having smaller channel geometries increases the mixing performance inside the droplet. This also shows that droplet-based fluid flow in microchannels is very suitable for performing chemical reactions inside droplets as it will occur faster. Moreover, narrower and sinusoidal microchannels showed better dispersion length difference compared to straight and wider microchannels.











Similar content being viewed by others
Abbreviations
- \({d}_{{\text {effective}}}\) :
-
Effective droplet diameter
- \({F}_{{\text {drag}}}\) :
-
Drag force on spherical particle
- \({F}_{{\text {st}}}\) :
-
Surface tension force
- h :
-
Length of the droplet
- u :
-
Flow velocity
- \({u}_{{\text {rel}}}\) :
-
Relative velocity of particle
- t :
-
Time
- \({t}_{{\text {corr.}}}\) :
-
Corresponding time for maximum dispersion length occurrence
- P:
-
Pressure
- P1:
-
Particle 1
- P2:
-
Particle 2
- r:
-
Particle radius
- \({r}_{{\text {i}}}\) :
-
Inner radius of sinusoidal channel
- \({r}_{{\text {c}}}\) :
-
Central radius of sinusoidal channel
- \({r}_{{\text {o}}}\) :
-
Outer radius of sinusoidal channel
- \({l}_{{\text {diff,3D}}}\) :
-
Three-dimensional dispersion length
- \({l}_{{\text {diff,max}}}\) :
-
Maximum dispersion length difference between particles
- \(\phi\) :
-
Level set function
- \(\epsilon , \gamma\) :
-
Numerical stabilization parameters of level set function
- \(\rho\) :
-
Density
- \(\mu\) :
-
Dynamic viscosity
References
Bashir S, Rees JM, Zimmerman WB (2011) Simulations of microfluidic droplet formation using the two-phase level set method. Chem Eng Sci 66:4733–4741
Bringer MR, Gerdts CJ, Song H, Tice JD, Ismagilov RF (2004) Microfluidic systems for chemical kinetics that rely on chaotic mixing in droplets. Philos Trans R Soc Lond Ser A 362(1818):1087–1104
Bruss H (1992) Viscous fingering in miscible displacements: Unification of effects of viscosity contrast, anisotropic dispersion, and velocity dependence of dispersion on nonlinear finger propagation. Phys Fluids A 4(11):2348–2359
Bruss H (2008) Theoretical microfluidics. Oxford University Press, New York
Chabreyrie R, Vainchtein D, Chandre C, Singh P, Aubry N (2009) Robustness of tuned mixing within a droplet for digital microfluidics. Mech Res Commun 36:130–136
Chabreyrie R, Vainchtein D, Chandre C, Singh P, Aubry N (2010) Using resonances to control chaotic mixing within a translating and rotating droplet. Commun Nonlinear Sci Numer Simulat 15:2124–2132
Chung C, Hyun Ahn K, Lee SJ (2009) Numerical study on the dynamics of droplet passing through a cylinder obstruction in confined microchannel flow. J Non-Newton Fluid Mech 162:38–44
Deshpande KB, Zimmerman WB (2006) Simulation of interfacial mass transfer by droplet dynamics using the level set method. Chem Eng Sci 61:6486–6498
Deshpande KB, Zimmerman WB (2006) Simulations of mass transfer limited reaction in a moving droplet to study transport limited characteristics. Chem Eng Sci 61:6424–6441
Dogana H, Nasb S, Muradoglu M (2009) Mixing of miscible liquids in gas-segmented serpentine channels. Int J Multiph Flow 35(12):1149–1158
Erdem EY, Cheng JC, Doyle FM, Pisano AP (2014) Multi-temperature zone, droplet-based microreactor for increased temperature control in nanoparticle synthesis. Small 10(6):1076–1080
Fries DM, Waelchli S, von Rohr PR (2008) Gas-liquid two-phase flow in meandering microchannels. Chem Eng J 135(1):S37–S45
Huebner AM, Abell C, Huck WTS, Baroud CN, Hollfelder F (2011) Monitoring a reaction at submillisecond resolution in picoliter volumes. Anal Chem 83:1462–1468
Jiang L, Zeng Y, Zhou H, Qu JY, Yao S (2012) Visualizing millisecond chaotic mixing dynamics in microdroplets: a direct comparison of experiment and simulation. Biomicrofluidics 6:012810
Lee W, Son G (2013) Numerical study of obstacle configuration for droplet splitting in a microchannel. Comput Fluids 84:130–136
Maddala J, Rengaswamy R (2014) Design of multi-functional microfluidic ladder networks to passively control droplet spacing using genetic algorithms. Comput Chem Eng 60:413–425
Naher S, Orpen D, Brabazon D, Poulsen CR, Morshed MM (2011) Effect of micro-channel geometry on fluid flow and mixing. Simul Model Pract Theory 19:1088–1095
Song H, Bringer MR, Tice JD, Gerdts CJ, Ismagilov RF (2003) Experimental test of scaling of mixing by chaotic advection in droplets moving through microfluidic channels. Appl Phys Lett 83(12):4664–4666
Song H, Tice JD, Ismagilov RF (2003) A microfluidic system for controlling reaction networks in time. Angew Chem Int Ed 42(7):768–772
Srisa-Art M, deMello AJ, Edel JB (2008) Fluorescence lifetime imaging of mixing dynamics in continuous-flow microdroplet reactors. Phys Rev Lett 101(1):014502
Stroock AD, Dertinger SK, Ajdari A, Mezic I, Stone HA, Whitesides GM (2002) Chaotic mixer for microchannels. Science 295(5555):647–651
Sussman M, Puckett EG (2000) A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows. J Comput Phys 162:301–337
Tice JD, Song H, Lyon AD, Ismagilov RF (2009) Formation of droplets and mixing in multiphase microfluidics at low values of the Reynolds and the capillary numbers. Langmuir 19:9127–9133
van der Graaf S, Nisisako T, Schroen CGPH, van der Sman RGM, Boom RM (2006) Lattice Boltzmann simulations of droplet formation in a T-shaped microchannel. Langmuir 22:4144–4152
Wanga J, Yua D, Jinga H, Tao J (2014) Hydrodynamic control of droplets coalescence in microfluidic devices to fabricate two-dimensional anisotropic particles through boundary element method. Chem Eng Res Des 92:2223–2230
Wu L, Tsutahara M, Kim LS, Ha M (2008) Three-dimensional lattice Boltzmann simulations of droplet formation in a cross-junction microchannel. Int J Multiph Flow 34:852–864
Wu CY, Tsai RT (2013) Fluid mixing via multidirectional vortices in converging–diverging meandering microchannels with semi-elliptical side walls. Chem Eng J 217:320–328
Yan Y, Guo D, Wen SZ (2012) Numerical simulation of junction point pressure during droplet formation in a microfluidic T-junction. Chem Eng Sci 84:591–601
Zaidi AA, Tsuji T, Tanaka T (2012) A new relation of drag force for high Stokes number monodisperse spheres by direct numerical simulation. Adv Powder Technol 25:1860–1871
Zimmerman WB (2006) Multiphysics modelling with finite element methods, vol 18. World Scientific Series on Stability, Vibration and Control of Systems, Singapore
Zimmerman WB, Homsy GM (1991) Nonlinear viscous fingering in miscible displacement with anisotropic dispersion. Phys Fluids A 3(8):1859–1872
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Özkan, A., Erdem, E.Y. Numerical analysis of mixing performance in sinusoidal microchannels based on particle motion in droplets. Microfluid Nanofluid 19, 1101–1108 (2015). https://doi.org/10.1007/s10404-015-1628-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10404-015-1628-7