Abstract
Social network data is typically made available in a graph format, where users and their relations are represented by vertices and edges, respectively. In doing so, social graphs need to be anonymised to resist various privacy attacks. Among these, the so-called active attacks, where an adversary has the ability to enrol sybil accounts in the social network, have proven difficult to counteract. In this article, we provide an anonymisation technique that successfully thwarts active attacks while causing low structural perturbation. We achieve this goal by introducing \((k, \Gamma _{G,\ell })\)-adjacency anonymity: a privacy property based on \((k,\ell )\)-anonymity that alleviates the computational burden suffered by anonymisation algorithms based on \((k,\ell )\)-anonymity and relaxes some of its assumptions on the adversary capabilities. We show that the proposed method is efficient and establish tight bounds on the number of modifications that it performs on the original graph. Experimental results on real-life and randomly generated graphs show that when compared to methods based on \((k,\ell )\)-anonymity, the new method continues to provide protection from equally capable active attackers while introducing a much smaller number of changes in the graph structure.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Online social networks (OSNs) have become the most successful digital application of our time. Over two billion personsFootnote 1 regularly use some OSN to interact with friends, share information, etc. As a result of this, massive amounts of information about personal relationships, consumption patterns, personal preferences, and more, are generated every day. An important part of this information is encoded in the form of social graphs. In a social graph, a vertex corresponds to a person (a user of the OSN), whereas edges represent relations between individuals. Personal information, such as name and e-mail address, is usually associated with vertices as attributes. Edges can also have associated attributes.
This massive amount of information is enormously valuable. OSNs themselves analyse this data in order to determine the advertisements they show to their users, filter out information that they consider not to be relevant, etc. As data holders, the OSN can effectively access the totality of the available data. However, third parties, such as social scientists, market researchers and public institutions, are also interested in accessing and analysing part of this information for conducting population studies, assessing the effect of communication campaigns, surveying public opinion and many other purposes. In order to enable these studies, it is necessary that OSN administrators release samples of their social graphs. However, despite the usefulness of the studies that can be conducted on the released data, the sensitive nature of the information encoded in social graphs raises serious privacy concerns.
In releasing a social graph for analysis, an indispensable first step for preserving user privacy is to remove all personally identifiable information from its vertices and edges. However, as shown by Narayanan and Shmatikov [21], even a graph with no identifying attributes can leak sensitive information, since some structural properties (e.g. the degree and neighbours of a vertex) can be unique to certain users. A re-identification attack seeks to leverage some knowledge about a set of users, the victims, to re-identify them after the graph is released. For example, an adversary who knows the number of friends of a victim can later re-identify her in the released graph if such value happens to be unique. Once a set of users is re-identified, the attacker can learn sensitive information, such as the existence of relations between two users or the affiliation of some of them to a community.
According to the means by which adversaries obtain the knowledge used to re-identify the victims, they are classified as passive or active [1]. On the one hand, a passive adversary relies on existing information, obtainable from publicly available sources, such as other OSNs, but does not attempt to purposely alter the structure of the network. On the other hand, an active adversary creates a set of accounts in the network and links them to other users, in such a manner that each victim is induced to uniquely satisfy some structural property allowing the adversary to re-identify all the victims after publication of the graph.
A common approach in counteracting re-identification attacks is to transform the original graph into another (similar) graph that satisfies a given privacy property. In this approach, the original graph is first stripped of any vertex and edge attributes, obtaining a pseudonymised graph, which is isomorphic to the original graph, but user information is replaced by uninformative, randomly generated labels. Then, a series of vertex/edge additions and removals are performed until the privacy property is satisfied. To that end, a number of privacy properties, based on the well-known notion of k-anonymity [27, 29], have been proposed. The first such property proposed for counteracting passive attacks was k-degree anonymity [14], which protects social graphs from adversaries that know the degrees of the victim vertices. Liu and Terzi [14] provided an efficient algorithm for obtaining k-degree anonymous graphs with a reasonable utility preservation, and later authors have proposed utility-oriented improvements on this type of methods [2, 3, 7, 15, 16, 25, 26, 32]. Additionally, new privacy properties, for example k-neighbourhood anonymity [35], that account for stronger passive attacks have been proposed. Each new property in this family accounts for increasing amounts of structural knowledge. The strongest among them is k-automorphism anonymity [37], which subsumes the rest. In all cases, every strengthening of the attacker model has come at the cost of obtaining anonymisation methods that alter the graph structure to a larger extent [37].
Regarding active attacks, a single privacy property, named \((k,\ell )\)-anonymity [30], has been proposed for quantifying the resistance of a graph to this type of attack. This property suffers from similar issues as k-automorphism anonymity; both are remarkably hard to evaluate and enforce. Indeed, current transformation approaches aiming at \((k,\ell )\)-anonymity [18] considerably affect the structure of the original graph. As we will discuss in the following sections, some aspects of this measure can be better tailored to serve as the basis for anonymisation methods.
The goal of this article is to explore further into the problem of counteracting active attacks on social graphs via edge set transformations with low structural perturbation. Taking \((k,\ell )\)-anonymity as our starting point, we focus on two main issues. First, it is computationally expensive to evaluate \((k,\ell )\)-anonymity and to use it as the basis for anonymisation methods. Second, \((k,\ell )\)-anonymity seems to overestimate the capabilities of active attackers. It assumes that the adversary is able to determine the exact distances between attacker nodes and arbitrary nodes in the network, which is infeasible in practice. This is evidenced by current active attacks [1, 23, 24], which are based on the neighbour relation between the victims and the attacker nodes.
Summary of contributions:
-
We first identify an important limitation of \((k,\ell )\)-anonymity that has been overlooked so far and makes it computationally expensive to use \((k,\ell )\)-anonymity as the privacy goal for perturbation-based anonymisation techniques, as we illustrate in Sect. 3 and validate in Sect. 6. As a fix for this limitation, we propose a new privacy property called \((k, \Gamma _{G,\ell })\)-anonymity (Sect. 3).
-
Secondly, we introduce the notion of \((k,\ell )\)-adjacency anonymity, a well-motivated relaxation of the adversary capabilities assumed by \((k,\ell )\)-anonymity (Sect. 4). Adjacency anonymity considers that the adversary only has prior knowledge about the vicinity of the sybil nodes, rather than about the whole graph as assumed by Trujillo-Rasua and Yero [30] and Mauw et al. [18]. Conceptually, \((k,\ell )\)-adjacency anonymity relates to \((k,\ell )\)-anonymity as k-neighbourhood relates to k-automorphism. By combining the two notions introduced in Sects. 3 and 4, we obtain the new privacy property \((k, \Gamma _{G,\ell })\)-adjacency anonymity.
-
We show that there exist efficient graph transformations towards \((k, \Gamma _{G,1})\)-adjacency anonymity for large values of k (Sect. 5), while previous anonymisation techniques [18] can only guarantee \((k, \ell )\)-anonymity for some \(k>1\) or some \(\ell >1\).
-
Finally, we perform experiments on real-life and randomly generated graphs (Sect. 6) to show that \((k, \Gamma _{G,1})\)-adjacency anonymous graphs can be obtained with low impact on the structure of the original graph. Our experiments also confirm that \((k, \Gamma _{G,1})\)-adjacency anonymous graphs are as resistant to some known active attacks as \((k,\ell )\)-anonymous graphs obtained by existing methods.
2 Related work
Several graph-oriented notions of k-anonymity have been proposed. As we mentioned above, Liu and Terzi [14] considered an adversary who knows the degree of the victim node. They defined the notion of k-degree anonymity, which is satisfied if for every vertex of the graph there exist \(k-1\) other vertices with the same degree. Liu and Terzi devised a simple and efficient algorithm to transform a graph into a k-degree anonymous graph. The authors also show that the utility of the graph is at least partly kept, because the average path length and the exponent of the power-law distribution of the original graph are preserved. Further improvements of this type of methods, aiming for increased utility levels, have been proposed [2, 3, 7, 15, 16, 25, 26, 32].
A privacy notion that is strictly stronger than k-degree anonymity is k-neighbourhood anonymity [35]. This property requires that for every vertex v in the graph, there exist at least \(k-1\) other vertices \(v_1,...,v_{k-1}\) such that the subgraph induced by v’s neighbours is isomorphic to the subgraph induced by \(v_i\)’s neighbours, for every \(i \in \{1, \ldots , k-1\}\). It is simple to see that every k-neighbourhood anonymous graph is \(k'\)-degree anonymous for some \(k'\ge k\). The notion of k-neighbourhood anonymity was later extended to account for l-diversity [36], imposing the additional constraint that, in every k-neighbourhood anonymous equivalence class of the vertex set, at most 1 / l members were originally associated with a particular sensitive label. Finally, a privacy notion strictly stronger than k-neighbourhood anonymity is that of k-automorphism anonymity [37]. A graph G is said to be k-automorphic if there exist \(k-1\) different automorphisms \(\varphi _1, \ldots , \varphi _{k-1}\) of G such that \(\varphi _i(v)\ne \varphi _j(v)\) for every \(v\in V(G)\) and every pair \(\varphi _i, \varphi _j\), \(1\le i<j\le k-1\). Alternative formulations of this privacy notion were presented independently as k-symmetry [33] and k-isomorphism [6]. A particularity of the latter is that it forces the creation of a disconnected graph with k connected components, which are pairwise isomorphic. A natural trade-off between the strength of the privacy notions and the amount of structural disruption caused by the anonymisation methods based on them has been empirically demonstrated by Zou et al. [37].
As we mentioned above, Backstrom et al. [1] were the first to show the impact of active attacks in social networks. They introduced the attack methodology, of which the walk-based attack used in Sect. 6 is an instance, consisting in planting a uniquely identifiable and efficiently retrievable attacker subgraph and creating unique fingerprints for the victims determined by their links to the attacker subgraph. A combination of active and passive strategies was introduced in Peng et al. [23, 24]. Their attack relies on a small set of sybil nodes to re-identify an initial set of victims, and then uses the information from an auxiliary, non-anonymised graph, to iteratively re-identify neighbours of previously re-identified victims.
To the best of our knowledge, \((k, \ell )\)-anonymity [30] has been until now the only privacy property tailored to measure the resistance of social graphs to active attacks. Likewise, a single algorithm, that of Mauw et al. [18], has been proposed specifically for protecting graphs from active attacks. This method uses the notion of \((k, \ell )\)-anonymity, but does not guarantee anonymity for k larger than 2, and in doing so it may add a proportionally large number of edges to the original graph. We remedy both issues in this article.
The work presented in this paper, along with those mentioned above, falls into one of the two main approaches of privacy-preserving social graph publication, namely that of publishing a new, anonymised version of the original graph. The other approach consists in generating a randomised model of the graph and using it to answer queries about the graph structure.
For example, Hay et al. [10] create a new, generalised graph where every vertex represents at least k vertices of the original graph. This graph is complete, and every generalised edge is weighted with the probability of an edge existing (in the original graph) between a pair of vertices randomly taken from each generalised vertex. Every time a query is posed, they use the generalised graph as a generative model, from which a random graph is sampled, and then answer the query on this random graph. The main problem with this approach, pointed out by Zou et al. [37], is that different generated graphs can dramatically differ from each other, even when repeatedly answering the same query. A related idea is applied by Sun et al. [28], who create a new graph where every original vertex can be represented by several new vertices. Another somewhat-related approach is presented by Mittal et al. [20] and Liu and Mittal [13]. Instead of creating a generalised graph, they create a new graph with the same vertex set and a randomly generated edge set. This graph is then used for answering neighbourhood queries. A fundamental difference between the work by Mittal et al. [20] and Liu and Mittal [13] and the ones previously discussed in this paper is that the former addresses a setting where vertex ids are public and only the existence of edges between vertices has to be kept private. In randomisation-based approaches, privacy is generally measured in terms of the increase in the adversary’s inference power after releasing each chunk of data. For example, Mittal et al. [20] and Liu and Mittal [13] measure the difference between the probabilities of the adversary correctly determining the existence of a set of edges before and after a (noisy) neighbourhood query is answered.
3 Revisiting \((k, \ell )\)-anonymity
In this section, we review the notion of \((k, \ell )\)-anonymity and observe a fundamental limitation of this privacy property that makes it difficult to be used in perturbation-based privacy-preserving techniques. We define a revised privacy notion, called \((k, \Gamma _{G,\ell })\)-anonymity, to alleviate this limitation.
3.1 Active attacks
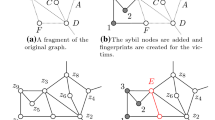
An active adversary relies on the ability to register several (fake) accounts to the network. Such accounts are called sybil accounts or sybil nodes, depending on whether one refers to the social network account or the social graph vertex. Prior to the publication of the social graph, the active attacker adds a set of sybil accounts to the network (e.g. nodes 1, 2, 3 and 4 in Fig. 1b). The sybil accounts establish links between themselves and also with the victims (e.g. users F and G in Fig. 1b). At this stage, the attacker only knows about the edges incident to the sybil nodes. Thus, she is unaware of the edge linking F and G.
After the publication of the pseudonymised social graph, the attacker first searches for the subgraph induced by the sybil nodes. Victims connected to the sybil subgraph can be re-identified by using the neighbour relation between sybil nodes and victims. For example, the non-sybil nodes connected to 1 and 4 in Fig. 1d must be F and G, respectively. This allows the adversary to acquire knowledge that was supposed to remain private, such as the existence of a link between F and G.
From a practical point of view, active attacks require the ability to create new accounts in the social network, which is trivial, and remain unnoticed by sybil detection techniques such as those described by Yu [34]. From a theoretical point of view, an active attack relies on creating a uniquely identifiable attacker subgraph, which requires the subgraph induced by the sybil nodes to be isomorphic to no other subgraph in the network. Backstrom et al. [1] described the properties of the attacker subgraph that guarantee uniqueness (with high probability) and showed that in most networks, \(\log n\) sybil nodes, where n is the number of vertices, are sufficient for creating an attacker subgraph that compromises any vertex and goes unnoticed to sybil detection methods.
Effectively determining whether a social graph is vulnerable to an active attack is a necessary step towards developing a mitigation strategy against it. For example, the complete graph \(K_n\) satisfies that for every proper subgraph S, there exists another subgraph \(S'\) that is isomorphic to S. This property obviously makes an active attack unfeasible in a complete graph. However, determining the actual resistance of an arbitrary graph to active attacks is not trivial. A first step in this direction was given by Trujillo-Rasua and Yero [30], who introduced the privacy measure \((k, \ell )\)-anonymity, which we describe in detail next.
3.2 \((k, \ell )\)-anonymity
Let \(G=(V,E)\) be an arbitrary pseudonymised graph. Throughout this paper, we will treat V as a set of randomly generated labels bearing no relation with the original identities of the network users. We will also assume that the elements of V can be traversed in some fixed (but arbitrary) total order \(\preceq \) and will denote an ordered subset of vertices \((S,\preceq )\), \(S\subseteq V\), simply as \(S=\{v_1,v_2,\ldots ,v_t\}\), where \(v_i\in S\) for \(i\in \{1,\ldots ,t\}\) and \(v_1 \preceq v_2 \preceq \cdots \preceq v_t\). Whether the notation refers to sets or ordered sets will be clear from the context.
Given an ordered set of sybil nodes \(S = \{ s_1, \ldots , s_t \}\) in G, Trujillo-Rasua and Yero [30] proposed to model the adversary knowledge about a vertex \(u \in V\) using her distances to the sybil nodes. To that end, they use the vector
where the distance \(d_G(u,v)\) is computed as the number of edges in a shortest path joining u and v. This vector is referred to as the metric representation of u with respect to S.
An active attacker is assumed to be able to re-identify those vertices having unique metric representations with respect to the set of sybil nodes under her control. In consequence, the data owner must ensure that every vertex in the published graph is undistinguishable from at least a minimum number of other vertices. This property is captured in the proposal of Trujillo-Rasua and Yero [30] by the notion of k-antiresolving set, which is enunciated as follows.
Definition 3.1
(k-antiresolving set) Let \(G=(V,E)\) be a non-trivial graph. A set \(S\subseteq V\) is a k-antiresolving set of G if k is the largest positive integer such that, for every \(v\in V(G)\setminus S\), there exist vertices \(w_1,w_2,\ldots ,w_{k-1}\in V(G)\setminus S\) such that \(v,w_1,w_2,\ldots ,w_{k-1}\) are pairwise different and
Note that if the set S of sybil nodes is forced to be k-antiresolving, then for every victim node v, there are at least \(k-1\) other nodes that cannot be distinguished from v by only inspecting their metric representations with respect to S. The notion of \((k,\ell )\)-anonymity was introduced by Trujillo-Rasua and Yero [30] to quantify the privacy of a social graph in the presence of active attackers by considering that every set of vertices up to a given cardinality may potentially be a set of sybil nodes. The formal definition of \((k,\ell )\)-anonymity relies on the parameter k-metric antidimension. The k-metric antidimension of a graph G is the minimum cardinality of any k-antiresolving set of G.
Definition 3.2
(\((k,\ell )\)-anonymity) A graph G is said to satisfy \((k,\ell )\)-anonymity if k is the smallest positive integer such that the k-metric antidimension of G is smaller than or equal to \(\ell \).
From a privacy perspective, if a graph satisfies \((k, \ell )\)-anonymity, an attacker with the capacity to enrol, and successfully retrieve, up to \(\ell \) sybil nodes in the graph would still be incapable of distinguishing any vertex from at least \(k-1\) other vertices. Certainly, a graph satisfying \((k, \ell )\)-anonymity for \(k>1\) effectively resists active attacks when performed by at most \(\ell \) sybil nodes. However, even the simplest of the privacy goals, namely transforming a (1, 1)-anonymous graph into a \((k, \ell )\)-anonymous graph for some \(k > 1\) or some \(\ell > 1\), has not been accomplished without significantly disrupting the graph structure [18]. Our observation is that \((k,\ell )\)-anonymity, although suitable to quantify resistance against active attacks, cannot be applied straightforwardly to privacy-preserving transformation of social graphs.
3.3 A limitation of \((k, \ell )\)-anonymity
Privacy measures based on k-anonymity all rely on the same basic principle: every user should belong to one or more anonymity sets of size at least k, where an anonymity set is a collection of indistinguishable objects with respect to a given adversary. In \((k, \ell )\)-anonymity, given a graph \(G = (V, E)\) and a subset \(S \subseteq V\) with \(|S| \le \ell \), the set of anonymity sets defined by S is the set of equivalence classes in \(V \setminus S\) with respect to the equivalence relation
We use \([u]_{S}\) to denote the equivalence class, i.e. the anonymity set, of a vertex u with respect to \(R_{G,S}\). Next, we formalise the relation between anonymity sets and \((k, \ell )\)-anonymity, making it explicit that a necessary condition for a graph to satisfy \((k, \ell )\)-anonymity is that the cardinality of all anonymity sets of each user must be at least k.
Observation 3.1
A graph \(G = (V,E)\) satisfies \((k,\ell )\)-anonymity if and only if k is the largest positive integer such that for every subset of vertices \(S \subseteq V\) with \(|S| \le \ell \) and every vertex \(u \in V \setminus S\), it holds that \(|[u]_{S}| \ge k\).
Most privacy properties define a single anonymity set for each user. For example, k-degree anonymity considers an adversary that knows the number of links of the victims. Thus, the anonymity set of a vertex u in k-degree anonymity is the (unique) set containing all vertices with the same degree as u. In \((k, \ell )\)-anonymity, however, every user may belong to a number of anonymity sets that exponentially grows with \(\ell \).
The drawback of considering many anonymity sets for each user in a privacy property is twofold. First, the computational complexity of determining whether the property is satisfied increases with the number of anonymity sets. This problem has already been investigated by Chatterjee et al. [4], who showed that the k-metric antidimension problem used in \((k, \ell )\)-anonymity is NP-Hard. Second, a graph transformation approach should take into account that increasing the size of the anonymity set of a user u with respect to a subset of vertices S may decrease the size of the anonymity set of the same user with respect to a different subset \(S'\). We illustrate this second drawback through the example in Fig. 2.
The graph G in Fig. 2 is (1, 1)-anonymous, as the anonymity set of \(v_1\) with respect to \(\{v_3\}\) is \(\{v_1\}\). Likewise, the anonymity set of \(v_3\) with respect to \(\{v_1\}\) is \(\{v_3\}\). Thus, any transformation of G aiming to achieve (2, 1)-anonymity should necessarily increase the cardinality of those two anonymity sets. That goal is achieved in the graph \(G'\) shown in the figure. However, in this graph the cardinality of the anonymity set of \(v_2\) with respect to \(\{v_4\}\), and vice versa, has dropped from 3 in G to 1 in \(G'\). Therefore, according to \((k, \ell )\)-anonymity, \(G'\) is an unsuccessful anonymisation of G. We argue that in the example above, \(G'\) should actually be considered as a successful anonymisation of G, as it transforms all 1-antiresolving sets of G, i.e. the ones that originally posed a privacy threat, into 3-antiresolving sets. We elaborate on this idea in what follows.
3.4 \((k,\Gamma _{G,\ell })\)-anonymity
We introduce the rationale that the probability of success of an adversary does not increase after perturbation. In fact, the first stage of an active attack (see Fig. 1b for reference) can only be considered successful if the attacker managed to make her set of sybil nodes a 1-antiresolving set of the original graph. Otherwise, the attacker will have more than one victim associated with the same fingerprint. In this circumstance, metric representations alone do not allow her to unambiguously assign the identity of any of those victims to any vertex of the graph after publication. For example, in Fig. 2, even though \(\{v_2\}\) is a 1-antiresolving set of \(G'\), the re-identification probability of an adversary leveraging this set of sybil nodes in G is at most 1 / 3 after the publication of \(G'\), because \(\{v_2\}\) is a 3-antiresolving set of G.
According to this rationale, we will consider that those vertex subsets that are \(k'\)-antiresolving, with \(k'\ge k\), in the original graph, are not the result of a successful first stage of an active attack. In consequence, we will focus on protecting the published graph from the remaining vertex subsets. With this idea in mind, the goal of the remainder of this section is to establish a theoretical framework that allows to disregard subsets of vertices with low re-identification power in the original graph. Because \((k,\ell )\)-anonymity does not allow to model such a conditional protection, we first introduce a parametrisable privacy notion and then derive from it an instance that will allow us to model the desired conditional privacy protection.
Definition 3.3
(\((k,\Gamma )\)-anonymity) Let G be a non-trivial graph and let \(\Gamma \subseteq {\mathcal {P}}(V(G))\) be a family of subsets of V(G). The graph G satisfies \((k,\Gamma )\)-anonymity if every \(S\in \Gamma \) is a \(k'\)-antiresolving set of G, with \(k'\ge k\).
Clearly, \((k,\ell )\)-anonymity is an instance of \((k,\Gamma )\)-anonymity, where \(\Gamma =\{S\ :\ S\subseteq V(G),\)\(|S|\le \ell \}\). More importantly, \((k,\Gamma )\)-anonymity allows us to determine whether a graph \(G'\), obtained by a series of perturbations on an initial graph G, reduces the threat potential of those attacker subgraphs in G with high probability of re-identification. We do so by instantiating \((k,\Gamma )\)-anonymity with a concrete interpretation of \(\Gamma \), denoted \(\Gamma _{G,\ell }\), which contains all subgraphs in G of cardinality up to \(\ell \) that are \(k'\)-antiresolving sets in G with \(k' < k\). That is to say, given the privacy parameter k, the set \(\Gamma _{G,\ell }\) accounts for all potential attacker subgraphs whose probability of re-identification is not guaranteed to be at most \(\frac{1}{k}\). This instantiation is formally defined as follows.
Definition 3.4
(\((k, \Gamma _{G,\ell })\)-anonymity) Let \(G=(V,E)\) be a non-trivial graph and let \(G'=(V,E')\) be the result of a series of perturbations on G. The graph \(G'\) is said to satisfy \((k, \Gamma _{G,\ell })\)-anonymity if it satisfies \((k,\Gamma )\)-anonymity for
According to this definition, it is sufficient to reduce the re-identification power of those vertex sets that originally are \(k'\)-antiresolving sets with \(k'<k\), by enforcing the condition that these sets are \(k''\)-antiresolving, with \(k''\ge k\), in the final graph. In particular, if a perturbed graph \(G'\) satisfies \((k,\ell )\)-anonymity, then it satisfies \((k, \Gamma _{G,\ell })\)-anonymity regardless of the original graph G. The converse is not true, as exemplified in Fig. 3. In the figure, the sets \(\{v_2\}\) and \(\{v_3\}\) are 1-antiresolving sets of \(G_1\). Since both sets are 2-antiresolving sets of \(G_2\) and \(G_3\), we have that \(G_2\) and \(G_3\) satisfy \((2,\Gamma _{G_1,1})\)-anonymity. Moreover, the sets \(\{v_1\}\) and \(\{v_4\}\) are 2-antiresolving sets of \(G_2\), so this graph also satisfies (2, 1)-anonymity. On the contrary, \(G_3\) is not (2, 1)-anonymous, as \(\{v_1\}\) and \(\{v_4\}\) are 1-antiresolving sets of this graph.
As we will show in Sect. 6, the notion of \((k, \Gamma _{G,\ell })\)-anonymity can be used to create variations of existing graph perturbation methods based on \((k, \ell )\)-anonymity that introduce a smaller number of modifications in the original graph, while providing the same level of protection against active attacks. As a final remark, note that we refer to \((k, \Gamma _{G,\ell })\)-anonymity as a conditional privacy property. We do so because the privacy level of the perturbed graph is measured in terms of the initial threats present in the original graph. This is consistent with previous uses of the terminology conditional privacy in microdata anonymisation [5, 9], to reflect the fact that the privacy of a dataset is measured in terms of the a priori adversary knowledge.
4 Adjacency anonymity
In this section, we continue analysing \((k,\ell )\)-anonymity in terms of the structural properties it requires on a graph. We observe that \((k,\ell )\)-anonymity assumes that the adversary knows every distance from the sybil nodes to other vertices of the graph. This makes it difficult for a graph to satisfy \((k, \ell )\)-anonymity even for small values of k or \(\ell \). For example, even-order cycles are regular and one may expect the users to be hidden behind the symmetry of the graph. However, as shown by Mauw et al. [18], we have that no even-order cycle satisfies (k, 1)-anonymity for any value of k greater than 1, because for any vertex u and its antipodal vertex v, we have \(|[v]_{\{u\}}|=1\), so \(\{u\}\) is a 1-antiresolving set.
By examining current active attacks [1, 23, 24], we observe that none is able to handle arbitrary distances from the attacker nodes to the victims. In fact, they all rely on the neighbour relation rather than on shortest paths. We argue that this is not only a characteristic of existing attacks, but rather a fundamental limitation of active adversaries. It seems unrealistic to expect that the adversary can keep control of arbitrary distance values. Accordingly, we propose \((k, \ell )\)-adjacency anonymity, which is based on a weaker, yet more realistic, adversarial model.
In a manner analogous to the definition of antiresolving sets, we use standard concepts from graph theory to represent an adversary whose knowledge about the victims consists of whether they are neighbours, or not, of each of the sybil nodes. The concept is known as adjacency representation, introduced by Jannesari and Omoomi [11], and defined as follows.
Definition 4.1
(Adjacency representation) Given a graph \(G=(V,E)\), an ordered set \(S = \{s_1, \ldots , s_t\} \subseteq V\) and a vertex \(u \in V\), the adjacency representation of u with respect to S is the vector \(a_G(u\ |\ S ) = (a_G(s_1,u), \ldots , a_G(s_t,u))\) where the function \(a_G:V \times V \rightarrow \mathbb {N}\) is defined by:
Note that \(a_G(u,v)=\min \{2,d_G(u,v)\}\) for every \(u,v\in V(G)\). Now, we will adapt the notion of a k-antiresolving set in order to account for the new type of adversary.
Definition 4.2
(k-adjacency antiresolving set) Let \(G=(V,E)\) be a non-trivial graph. A set \(S\subseteq V\) is a k-adjacency antiresolving set of G if k is the largest positive integer such that, for every \(v\in V\setminus S\), there exist vertices \(w_1,w_2,\ldots ,w_{k-1}\) such that \(v,w_1,w_2,\ldots ,w_{k-1}\) are pairwise different and
To illustrate the difference between k-adjacency antiresolving sets and k-antiresolving sets, consider again the case of even-order cycles discussed above. As we saw, every vertex u in an even-order cycle satisfies that \(\{u\}\) is a 1-antiresolving set. However, if the order of the cycle is \(n\ge 6\), then \(\{u\}\) is a 2-adjacency antiresolving set, since it has exactly 2 neighbours and \(n-3>2\) non-neighbours. In order to measure a graph’s increased resistance to an adversary that leverages adjacency representations, we enunciate the notions of \((k,\ell )\)-adjacency anonymity and \((k, \Gamma _{G,\ell })\)-adjacency anonymity, which relax the notions of \((k,\ell )\)-anonymity and \((k, \Gamma _{G,\ell })\)-anonymity, respectively. As above, we enunciate both properties as instances of a parametrisable notion called \((k,\Gamma )\)-adjacency anonymity.
Definition 4.3
(\((k,\Gamma )\)-adjacency anonymity) Let G be a non-trivial graph and let \(\Gamma \subseteq {\mathcal {P}}(V(G))\) be a family of subsets of V(G). The graph G satisfies \((k,\Gamma )\)-adjacency anonymity if every \(S\in \Gamma \) is a \(k'\)-adjacency antiresolving set of G, with \(k'\ge k\).
Definition 4.4
(\((k,\ell )\)-adjacency anonymity) A graph G is said to satisfy \((k,\ell )\)-adjacency anonymity if it satisfies \((k,\Gamma )\)-adjacency anonymity for \(\Gamma =\{S\ :\ S\subseteq V(G),\)\(|S|\le \ell \}\).
At a conceptual level, \((k, \ell )\)-adjacency anonymity has some aspects in common with k-neighbourhood anonymity [35], as both consider an adversary provided with a neighbourhood relation. Adjacency anonymity, however, requires indistinguishability with respect to several specific subsets of vertices, while such constraint is not imposed by k-neighbourhood anonymity.
Definition 4.5
(\((k, \Gamma _{G,\ell })\)-adjacency anonymity) Let \(G=(V,E)\) be a non-trivial graph and let \(G'=(V,E')\) be the result of a series of perturbations on G. The graph \(G'\) is said to satisfy \((k, \Gamma _{G,\ell })\)-adjacency anonymity if it satisfies \((k,\Gamma )\)-adjacency anonymity for
The notion of \((k, \Gamma _{G,\ell })\)-adjacency anonymity will be the basis for the anonymisation algorithm that we will introduce in the next section.
5 An anonymisation method based on \((k, \Gamma _{G,1})\)-adjacency anonymity
In order to showcase the usefulness of the new privacy properties, in this section we present a method for enforcing \((k, \Gamma _{G,1})\)-adjacency anonymity, which is based on edge additions and removals. We highlight two features of this method. Firstly, it allows to increase the privacy of a graph G of order n up to satisfying \((k,\Gamma _{G,1})\)-adjacency anonymity for any \(k\in \left[ 2,\left\lfloor \frac{n-1}{2}\right\rfloor \right] \). Secondly, this privacy level is achieved with a minimum number of graph edits.
5.1 General notation
Before proceeding, we introduce some notation that will be used throughout this section. In a graph G, the open neighbourhood of a vertex \(u\in V(G)\), denoted by \(N_G(u)\), is the set \(N_G(u)=\{v\in V(G)\mid (u,v)\in E(G)\}\), whereas the closed neighbourhood of u in G is the set \(N_G[u]=\{u\}\cup N_G(u)\). Similarly, for a set \(S\subseteq V(G)\), we define \(N_G(S)=\cup _{v\in S}N_G(v)\setminus S\) and \(N_G[S]=\cup _{v\in S}N_G[v]\). The degree of a vertex u, denoted by \(\delta _G(u)\), is its number of neighbours, i.e. \(\delta _G(u)=|N_G(u)|\). In a graph G of order n, we will refer to vertices of degree 0 and \(n-1\) as isolated and dominant vertices, respectively. For a graph \(G=(V,E)\) and a subset S of vertices of G, we will denote by \(\langle S \rangle _G\) the subgraph of G induced by S, that is \(\langle S \rangle _G=(S,E\cap (S\times S))\). If there is no ambiguity, we will drop the graph-specific subindices and simply write N(u), \(\delta (u)\), etc. Also recall that for a graph \(G=(V,E)\) and a set \(S\subseteq V\), \(R_{G,S}\) is the equivalence relation such that two vertices u and v satisfy \((u,v)\in R_{G,S}\) if and only if \(u,v\in V\setminus S\) and \(a_G(u\;|\;S)=a_G(v\;|\;S)\). Moreover, we will use the notation \(\mathcal {A}_{G,S}\) for the set of equivalence classes induced in \(V\setminus S\) by the relation \(R_{G,S}\). It is simple to see that S is a \((\min _{A\in \mathcal {A}_{G,S}}|A|)\)-adjacency antiresolving set of G.
5.2 The anonymisation method
Consider a \((k_0,1)\)-adjacency anonymous graph G of order n. We will analyse the modifications necessary to turn G into a \((k, \Gamma _{G,1})\)-adjacency anonymous graph \(G'\), with \(k>k_0\). First, the following result characterises the values of k for which such a transformation may be of interest.
Proposition 5.1
Let G be a non-complete, non-empty graph of order n satisfying (k, 1)-adjacency anonymity. Then, \(k\le \left\lfloor \frac{n-1}{2}\right\rfloor \).
Proof
Let \(G=(V,E)\) be a non-complete, non-empty graph of order n satisfying (k, 1)-adjacency anonymity. Suppose, for the purpose of contradiction, that \(k>\left\lfloor \frac{n-1}{2}\right\rfloor \). Let \(v\in V\) be a vertex of G satisfying \(\delta (v)\notin \{0,n-1\}\). The existence of such a vertex is guaranteed by the fact that the graph is neither complete nor empty. We have that \(\mathcal {A}_{G,\{v\}}=\{N_G(v), V\setminus N_G[v]\}\). If \(\delta (v)\le \left\lfloor \frac{n-1}{2}\right\rfloor \), then \(\{v\}\) is a \(k'\)-adjacency antiresolving set of G with \(k'<k\), which is a contradiction. On the other hand, if \(\delta (v)>\left\lfloor \frac{n-1}{2}\right\rfloor \), then \(|V\setminus N_G[v]|\le \left\lfloor \frac{n-1}{2}\right\rfloor \), which again means that \(\{v\}\) is a \(k'\)-adjacency antiresolving set of G with \(k'<k\), a contradiction. Therefore, we have that \(k\le \left\lfloor \frac{n-1}{2}\right\rfloor \).\(\square \)
In the light of Proposition 5.1, aiming for values of k above \(\left\lfloor \frac{n-1}{2}\right\rfloor \) is of little practical interest, since complete and empty graphs are not useful for analysis. Thus, in what follows we will focus on the values of k in the interval \(\left[ 2,\left\lfloor \frac{n-1}{2}\right\rfloor \right] \). Now, the following result enunciates the conditions that must be enforced in order to transform a graph \(G=(V,E)\) into a graph \(G'=(V,E')\) satisfying \((k, \Gamma _{G,1})\)-adjacency anonymity for some lower-bounded value of k.
Theorem 5.1
Let \(G=(V,E)\) be a non-trivial graph and let \(G'=(V,E')\) be a graph obtained from G by edge additions and removals. Let k be a positive integer satisfying \(1\le k\le |V|-1\). Then, the graph \(G'\) satisfies \((k', \Gamma _{G,1})\)-adjacency anonymity with \(k'\ge k\) if and only if every vertex \(v\in V\) such that \(1\le \delta _G(v)<k\) or \(|V|-k-1<\delta _G(v)\le |V|-2\) satisfies one of the following conditions:
-
(i)
\(\delta _{G'}(v)=0\)
-
(ii)
\(\delta _{G'}(v)=|V|-1\)
-
(iii)
\(k\le \delta _{G'}(v)\le |V|-k-1\)
Proof
Let \(v\in V\) be a vertex such that \(\{v\}\) is a \(k'\)-adjacency antiresolving set of G with \(k'<k\). If \(\delta _{G'}(v)=0\) or \(\delta _{G'}(v)=|V|-1\), we have that \(\mathcal {A}_{G',\{v\}}=\{V\setminus \{v\}\}\), so the set \(\{v\}\) is a \((|V|-1)\)-adjacency antiresolving set of \(G'\). Recall that according to the premises of the theorem, \(|V|-1\ge k\). Now we address the case where \(k\le \delta _{G'}(v)\le |V|-k-1\). Here, we have that \(\mathcal {A}_{G',\{v\}}=\{N_{G'}(v), V\setminus N_{G'}[v]\}\), so the set \(\{v\}\) is a \((\min \{\delta _{G'}(v),|V|-\delta _{G'}(v)-1\})\)-adjacency antiresolving set of \(G'\). Since \(\delta _{G'}(v)\ge k\) and \(|V|-\delta _{G'}(v)-1\ge k\), we have that \(\{v\}\) is a \(k''\)-antiresolving set of \(G'\) with \(k''\ge k\). In conclusion, \(G'\) satisfies \((k', \Gamma _{G,1})\)-adjacency anonymity with \(k'\ge k\).
To conclude our proof, let us now assume that there exists a vertex \(v\in V\) such that \(\{v\}\) is a \(k'\)-adjacency antiresolving set of G with \(k'<k\) and either \(1\le \delta _{G'}(v)<k\) or \(|V|-k-1<\delta _{G'}(v)\le |V|-2\). In both cases, we have that \(\mathcal {A}_{G',\{v\}}=\{N_{G'}(v), V\setminus N_{G'}[v]\}\). Since either \(|N_{G'}(v)|<k\) or \(|V\setminus N_{G'}[v]|<k\), we have that \(G'\) does not satisfy \((k'', \Gamma _{G,1})\)-adjacency anonymity for any \(k''\ge k\).\(\square \)
Our anonymisation method is based on Theorem 5.1. It receives as input a \((k_0,1)\)-adjacency anonymous graph \(G=(V,E)\) and an integer k such that \(k_0 < k \le \left\lfloor \frac{|V|-1}{2}\right\rfloor \) and efficiently obtains a \((k, \Gamma _{G,1})\)-adjacency anonymous graph \(G'=(V,E')\). As we mentioned above, the method works by performing a series of edge additions and removals upon G, as outlined in Algorithm 5.1 (Edit-Graph).
Algorithm 5.1
Given a \((k_0,1)\)-adjacency anonymous graph \(G=(V,E)\) and an integer \(k\in \left[ k_0+1,\left\lfloor \frac{|V|-1}{2}\right\rfloor \right] \), Edit-Graph provides a \((k, \Gamma _{G,1})\)-adjacency anonymous graph \(G'=(V,E')\).

In Algorithm Edit-Graph, the sets L and H are initialised with the vertices whose degrees in G are, respectively, smaller and greater than required for the privacy requirement to be satisfied (without being isolated nor dominant vertices). Then, by adding or removing edges, these vertices are forced to satisfy condition (iii) of Theorem 5.1. Note that, at step 12, when updating L, if the degree of an originally isolated vertex x has increased as a result of some edge addition, it is not included in L. This is so even if \(1\le \delta _{G'}(x)<k\), because \(\{x\}\notin \Gamma _{G,1}\). An analogous criterion is applied at step 19 to any originally dominant vertex if its degree decreases after an edge removal. The rationale behind the loop in steps 7 to 12 is to first add as many edges as possible between pairs of vertices from L, since every addition of this type contributes to both vertices getting closer to satisfy the required condition. When such additions are no longer possible, we then add edges linking a vertex \(u\in L\) and a vertex \(v\notin L\) whose degree is as small as possible, so the degree of vertices from H is only increased if there is no vertex in \(V\setminus H\) to which u can be linked. An analogous idea is applied in steps 14 to 19 to first remove edges joining pairs of vertices from H, then edges joining a vertex from H to another vertex, with the particularity that step 17 takes care of not making the degree of a vertex in \(L_0\) decrease again. For the values of k that we are considering, at least the edge addition and removal described in steps 10 and 17, respectively, are always possible. These operations are efficiently performed by maintaining the elements of V sorted by their degree and updating the ordering when necessary.
5.2.1 Complexity and optimality analysis
We first analyse the number of modifications performed by the algorithm. The best scenario occurs when all edge additions are done according to step 8, and all edge removals are done according to step 15, as shown in the following results.
Theorem 5.2
Let \(G=(V,E)\) be a \((k_0,1)\)-adjacency anonymous social graph and let \(k\in \left[ k_0+1,\left\lfloor \frac{|V|-1}{2}\right\rfloor \right] \). The number t of edges added by steps 7 to 12 of Algorithm Edit-Graph satisfies
Proof
Due to its length, we develop this proof in Appendix A.\(\square \)
The lower and upper bounds provided in Theorem 5.2 are tight, as exemplified in Fig. 4a, b, respectively.
Two examples where the number of edges added by steps 7 to 12 of Algorithm Edit-Graph (for \(k=2\)) reaches the a lower and b upper bounds of the inequalities in Eq. 2. In both cases, dashed lines indicate the edges added by the algorithm
The next result describes the number \(t'\) of edges removed by steps 14 to 19 of Algorithm Edit-Graph.
Theorem 5.3
Let \(G=(V,E)\) be a \((k_0,1)\)-adjacency anonymous social graph and let \(k\in \left[ k_0+1,\left\lfloor \frac{|V|-1}{2}\right\rfloor \right] \). Let \(G_t\) be the graph obtained from G after executing steps 7 to 12 of Algorithm Edit-Graph. The number \(t'\) of edges removed by steps 14 to 19 of Algorithm Edit-Graph satisfies
and
Proof
As in the previous case, we develop this proof in Appendix B.\(\square \)
The worst-case computational complexity of Algorithm Edit-Graph on a graph G of order n is \(\mathcal {O}(n^2)\), because every pair of vertices \(u,v\in V(G)\times V(G)\), \(u\ne v\), is susceptible of being evaluated once, either as a possible edge addition in steps 7 to 12, or as a possible edge removal in steps 14 to 19. However, in practice, especially for low-density graphs, steps 7 to 19 are performed in quasi-linear time, so the entire process is dominated by the \(\mathcal {O}(n\log n)\) complexity of step 2. This observation is relevant in view of the fact that real-life social graphs are characterised by having very low density. Additionally, in this scenario, and for the values of k that we are considering, steps 14 to 19 are very unlikely to be executed at all, because only a few vertices with very large degree exist.
Summarising. We have introduced in this section an anonymisation technique (Algorithm Edit-Graph) to transform social graphs into \((k, \Gamma _{G,1})\)-adjacency anonymous graphs for values of k up to \(\left\lfloor \frac{n-1}{2}\right\rfloor \), where n is the order of the graph. The proposed method is efficient and has theoretical tight bounds on the number of graph modifications it performs. Evaluating the actual perturbation of Algorithm Edit-Graph and the privacy offered by the resulting perturbed graphs is the aim of the next section.
6 Experiments
The purpose of the experiments reported in this section is to assess several aspects of our new proposals. First, we compare the effect of enforcing \((k,\Gamma _{G,\ell })\)-anonymity to that of enforcing \((k,\ell )\)-anonymity, in terms of privacy preservation and the number of graph edits performed. Additionally, we compare the methods based on these privacy notions to our Algorithm Edit-Graph, which is based on the notion of \((k,\Gamma _{G,\ell })\)-adjacency anonymity, and assess the effect of the value of k on the number of graph edits performed by Algorithm Edit-Graph. In these experiments, we consider an active attacker as the one evaluated by Mauw et al. [18], who has the ability to insert one sybil node into the graph. Then, to conclude our study, we assess the extent to which Algorithm Edit-Graph is able to provide protection from active attackers leveraging sets of sybil nodes larger than those covered by the theoretical privacy guarantee. The experiments were performed on the HPC platform of the University of Luxembourg [31].Footnote 2
6.1 Experimental setup
The core of our experiments are conducted on a large collection of randomly generated graphs. This collection is composed of 9.7 million graphs: 100,000 for each density value in the set \(\{0.03, 0.04, \ldots , 1\}\).Footnote 3 Each graph has 200 vertices, and its edge set is randomly generated in such a manner that the desired density value is met. The main reason for using such a collection is to obtain statistical information on the behaviour of the method for a large number of graphs. Moreover, considering a wide range of density values is interesting in view of the well-established fact that social networks show a tendency to undergo a densification process over time [12].
In order to complement the results obtained on randomly generated graphs, we additionally use for our evaluation three real-life social graphs. The first one was obtained in 2012 from 10 so-called ego-networks in Facebook [19]. An ego-network is the subgraph induced by the set of nodes representing all friends of a given user. The second social graph, which is commonly referred to as the Panzarasa graph, after one of its creators [22], was collected in 2004 from an online community of students at the University of California. In the Panzarasa graph, edges represent messages sent between students. A pair of users is considered to be connected if they exchanged at least one message in either direction. The original Panzarasa graph is directed and contains loops (users were allowed to send messages to themselves) and six isolated vertices. Before applying our methods to this graph, we removed edge orientation, loops and isolated vertices. Finally, the third social graph was obtained in 2012 from a collection of e-mail messages between members of Universitat Rovira i Virgili (URV), Spain [8]. As described by the authors, for the construction of the graph, group messages with more than 50 recipients were ignored, and edges were only added for pairs of users that sent messages to each other. Additionally, isolated vertices and connected components of order 2 were also eliminated from the final graph.
The Facebook graph has 4039 vertices, whereas the Panzarasa graph has 1893 and the URV graph has 1133. For every experiment using these graphs, we made 1000 runs, in each of which a different set of victims was randomly chosen, and the final results were averaged over these runs.
The chosen attack is the walk-based attack proposed by Backstrom et al. [1]. Let \(S=\{x_1,\ldots ,x_n\}\) be the set of sybil nodes enrolled by the adversary, and let \(T=\{y_1,\ldots , y_m\}\) be the set of victims. The walk-based attack creates a unique fingerprint for each victim \(y_i \in T\) by randomly selecting a subset \(N_i \subseteq S\) such that \(N_i \ne N_j\) for every pair of different \(i,j\in \{1, \ldots , m\}\), and connecting \(y_i\) to every \(x\in N_i\). In order to make the subgraph induced by the set of sybil nodes uniquely retrievable with high probability, the attack first adds all edges \((x_i,x_{i+1})\), \(1\le i \le n-1\), and then every other pair of sybil nodes is linked by an edge with probability \(\frac{1}{2}\).
Let \(G=(V,E)\) be an original graph; \(G'=(V\cup S,E\cup E')\), with \(E'\subseteq S\times (V\cup S)\), the graph obtained after simulating the action of the attacker; and \(G''=(V(G'), (E(G')\cup A)\setminus B)\), with \(A\subseteq (V(G')\times V(G')\setminus E(G'))\) and \(B\subseteq E(G')\), the result of applying a perturbation method on \(G'\). The probability of success for the walk-based attack is computed by the following formula [18]:
where \(\mathcal {X}\) contains all ordered subsets X of \(V(G')\) such that \(\langle X \rangle _{G''}\cong \langle S \rangle _{G'}\), \(V_{i,X}\) contains all vertices \(v\in V(G')\) that satisfy \(a_{G''}(v\ |\ X)=a_{G'}(y_i\ |\ S)\), and
6.2 Comparison of the privacy properties
We compare three perturbation-based social graph anonymisation methods, one of which is based on the original notion of \((k,\ell )\)-anonymity and the other two on the new privacy notions introduced in this paper: \((k,\Gamma _{G,\ell })\)-anonymity and \((k,\Gamma _{G,\ell })\)-adjacency anonymity.
The first method was introduced by Mauw et al. [18]. It transforms a (1, 1)-anonymous graph into a graph that satisfies \((k,\ell )\)-anonymity for some \(k>1\) or some \(\ell >1\). This method works by iteratively adding edges to the original graph. At each step, the method finds a 1-antiresolving set \(\{v\}\) and modifies the graph by adding an edge that induces an odd-order cycle in an eccentricity path of v. The method ends when no unitary 1-antiresolving sets are found. As discussed by Mauw et al. [18], a problem faced by this method is that an edge addition may cause other unitary vertex sets to become 1-antiresolving, which in turn causes the algorithm to add more edges to ensure that the privacy guarantee is satisfied.
The second method is a variation on the previous one, aiming to transform a (1, 1)-anonymous graph G into a graph \(G'\) satisfying \((k, \Gamma _{G,1})\)-anonymity for some \(k>1\). The modified method differs from the original method given by Mauw et al. [18] in two aspects:
-
1.
At each iteration step, a set \(\{v\}\) is selected such that it is 1-antiresolving in both the current and the original graph. In the original method, \(\{v\}\) is required to be a 1-antiresolving set of the current graph, even if it was k-antiresolving, with \(k>1\), in the original graph.
-
2.
The iteration stops when every 1-antiresolving set \(\{v\}\) of the original graph is k-antiresolving in the current graph with \(k>1\). In the original method, the iteration stops when the current graph has no unitary 1-antiresolving sets, including those that were originally k-antiresolving with \(k>1\).
Finally, the third method in consideration is our algorithm Edit-Graph, with \(k=2\), which guarantees the perturbed graph to be \((2,\Gamma _{G,1})\)-adjacency anonymous. We ran the three methods on the randomly generated graph collection described above. A walk-based attack leveraging one sybil node is simulated on each graph, and for each combination of a perturbation method and a density value, we computed the average of the values obtained for the success probability of the attack and the number of modifications performed, over the corresponding 100,000 graphs. For the first two methods, the number of modifications is the number of added edges, whereas for algorithm Edit-Graph it is the sum of the number of added edges (steps 7–12) and the number of removed edges (steps 14–19). An analogous experiment was run on the Facebook, Panzarasa and URV graphs.
The first relevant result from this experiment is that after perturbing the graphs with each of the three methods, the success probability of the walk-based attack with one sybil node is zero in all cases. This fact had already been reported for the first method in the work of Mauw et al. [18]. Here, we highlight the fact that the other two methods display the same behaviour, which shows that the notions of conditional privacy introduced by \((k,\Gamma _{G,\ell })\)-anonymity and \((k,\Gamma _{G,\ell })\)-adjacency anonymity are able to provide a level of protection against the walk-based attack (or similar neighbourhood-based attacks) that is at least as good as the one provided by \((k,\ell )\)-anonymity.
Average number of modifications done in randomly generated graphs by the methods enforcing \((k,\ell )\)-anonymity for some \(k>1\) or some \(\ell >1\) [18], \((k,\Gamma _{G,1})\)-anonymity with \(k>1\) (our variation on the method from [18]) and \((2,\Gamma _{G,1})\)-adjacency anonymity. (Alg. Edit-Graph with \(k=2\))
The advantages of using the new privacy properties become clear when we compare the average number of modifications introduced on the original graphs by each method, as depicted in Fig. 5 and Table 1. As can be observed in Fig. 5, the number of modifications performed by the method based on \((k, \Gamma _{G,\ell })\)-anonymity is at most the same as those performed by the method based on \((k,\ell )\)-anonymity. Moreover, for several density values, it is up to five times smaller. It is worth noting that the largest differences occur for small density values, which are typically observed in real-world social graphs. In our opinion, the most important conclusion that can be extracted from Fig. 5 is that adjusting the adversary model to a more realistic view of the capabilities of active adversaries allows for a considerable reduction of the number of necessary perturbations. This is due to the fact that the privacy notions based on the metric representation tend to “over-protect” vertices that appear as re-identifiable, but really are not. Methods based on \((k,\Gamma _{G,\ell })\)-adjacency anonymity do not take these unnecessary measures, thus altering the graph structure considerably less, as seen in the figure. From the analysis of Table 1, we can conclude that an analogous behaviour occurs in real-life graphs.
6.3 The effect of k in Algorithm Edit-Graph
In the previous section, we saw the number of modifications introduced by our Algorithm Edit-Graph for \(k=2\), as this is sufficient for comparing this algorithm with its two counterparts. Here, we go into more detail regarding the effect of rising the value of k on the number of modifications performed by the algorithm. To that end, Fig. 6 shows the average number of modifications performed on randomly generated graphs for \(k\in \{2,\ldots ,8\}\), whereas Table 2 shows the analogous values on real-life graphs.
The fact that larger values of k require the algorithm to perform more graph modifications is a direct consequence of the considered privacy property, so we will focus on other interesting facts that can be observed in Fig. 6. The smallest number of modifications is performed for intermediate density values. The reason for this behaviour is the fact that in these cases, almost no vertex corresponding to a legitimate user (that is, a non-sybil node) has a degree value in the intervals specified in Theorem 5.1, so the only modifications necessary tend to be the \(k-1\) edge additions necessary for rising the degree of the inserted sybil node to k. This is not the case for the smallest density values, where more edge additions may be necessary, and the largest density values, where edge removals are necessary to lower the degree of some vertices, whereas edge additions are necessary to rise the degree of the inserted sybil node.
To conclude, it is worth remarking that, in all the scenarios depicted in Fig. 6 and Table 2, the success probability of the walk-based attack with one sybil node continues to be zero.
Success probabilities of the walk-based attack, inserting one to eight sybil nodes, on randomly generated graphs for densities \(0.1, 0.2, \ldots , 1\). The seven rows in the bottom represent the results of the attack on graphs anonymised with Algorithm Edit-Graph, taking \(k\in \{2,\ldots ,8\}\). The two rows in the top represent the results of the attack on graphs anonymised with the method from Mauw et al. [18], and our variation on this method described in Sect. 6.2. For each cell’s RGB colour value, \(R = 255\cdot \Pr \), \(G = 0\) and \(B = 255\cdot (1-\Pr )\), where \(\Pr \) stands for the success probability of the attacks
6.4 Protection against attackers leveraging larger amounts of sybil nodes
It was pointed out by Mauw et al. [18] that graph perturbation methods aiming to enforce \((k,\ell )\)-anonymity for some \(k>1\) and \(\ell =1\) are to some extent able to thwart active attacks leveraging more than one sybil node. This was due to the fact that by altering the subgraph induced by the sybil nodes and/or the fingerprints of a subset of victims, the adversary is prevented from retrieving the set of sybil nodes, or correctly re-identifying the victims.
Here, we analyse to what extent Algorithm Edit-Graph shows an analogous behaviour. To that end, we simulated active attacks leveraging up to eight sybil nodes on the three real-life graphs and the random graphs of the collection with density values \(\{0.1,0.2,\ldots ,1\}\). Recall that according to Backstrom et al. [1], eight sybil nodes are sufficient for building a uniquely retrievable subgraph and re-identifying all vertices of a graph of order 200, as the ones in our collection. Then, we obtained nine anonymous versions of each resulting graph: seven of them by applying Algorithm Edit-Graph with \(k\in \{2,\ldots ,8\}\), and the other two by applying the method introduced by Mauw et al. [18], as well as the variation on this method described in Sect. 6.2. Figures 7 and 8 show the results of these experiments using colour matrices. The colour of each cell represents the averaged success probabilities of the attacks on the perturbed graphs. For each cell’s RGB colour value, R = \(255\cdot \Pr \), G = 0 and B = \(255\cdot (1-\Pr )\), where \(\Pr \) stands for the success probability of the attacks; that is, red cells (or cells with a prevailing red component) represent highly successful attacks, and prevailingly blue cells represent thwarted attacks.
From the analysis of both figures, the most important observation is that starting at values of k close to the number of sybil nodes, the success probability of the walk-based attack on \((k,\Gamma _{G,1})\)-adjacency anonymous graphs rapidly falls from values close to 1 to values close to 0. In other words, by increasing the value of k, a point is reached where attacks start to be successfully thwarted. This is a consequence of the manner in which edges between sybil nodes are generated in the attack, which makes all sybil nodes have very similar degrees. Thus, depending on the value of k, Algorithm Edit-Graph either modifies almost no sybil node’s degree, or it modifies almost all, in which case the attacker fails to retrieve the sybil subgraph. For small values of k, Algorithm Edit-Graph is less effective against attackers leveraging larger numbers of sybil nodes than the method by Mauw et al. [18], as well as its variant based on \((k,\Gamma _{G,\ell })\)-anonymity. This is a result of the smaller number of modifications introduced in the graph for satisfying \((2,\Gamma _{G,1})\)-adjacency anonymity for small values of k. For the same reason, as the value of k increases, Algorithm Edit-Graph becomes able to thwart attacks where the other methods are less effective, as illustrated by Fig. 7 (a, i, j) and Fig. 8.
Analysing Fig. 7 in more detail, we can observe that the behaviour of Algorithm Edit-Graph is negligibly affected by the original graph’s density, as illustrated by the considerably large similarity among the bottom seven rows of the colour matrices (a) to (j). The reason for this consistent behaviour lies in the fact that the algorithm’s ability to thwart the attack is a consequence of the density of the attacker subgraph being always slightly above 0.5, which in turn is a consequence of the specification of the attack, not of the density of the original graph.
Success probabilities of the walk-based attack, inserting one to eight sybil nodes, on the a Facebook, b Panzarasa and c URV graphs. The seven rows in the bottom represent the results of the attack on graphs anonymised with Algorithm Edit-Graph, taking \(k\in \{2,\ldots ,8\}\). The two rows in the top represent the results of the attack on graphs anonymised with the method from Mauw et al. [18], and our variation on this method described in Sect. 6.2. For each cell’s RGB colour value, R = \(255\cdot \Pr \), \(G = 0\) and \(B = 255\cdot (1-\Pr )\), where \(\Pr \) stands for the success probability of the attacks
Finally, comparing the colour matrices in Fig. 7 to those in Fig. 8, we can see that, for smaller numbers of sybils (up to three), our method is slightly more effective on the studied real-life graphs than on the randomly generated ones. While this observation is indeed positive, it is difficult to elucidate a clear reason for this behaviour. Also, as Fig. 8 shows, our method is slightly more effective on the Panzarasa and URV graphs than on the Facebook graph.
6.5 Summary of experimental results
The experiments described in this section show that when compared to \((k,\ell )\)-anonymity, the new notions of \((k, \Gamma _{G,\ell })\)-anonymity and \((k, \Gamma _{G,\ell })\)-adjacency anonymity allow to provide protection from equally capable active attackers while introducing a much smaller number of changes in the graph structure. Moreover, although the theoretical privacy guarantee offered by Algorithm Edit-Graph (\((k, \Gamma _{G,1})\)-adjacency anonymity) only concerns attackers with the ability to insert one sybil node in the network, the algorithm is also capable of thwarting attacks from more capable adversaries. Finally, we highlight that in terms of time complexity, the notion of \((k, \Gamma _{G,\ell })\)-adjacency anonymity allows to introduce more efficient algorithms. Recall that as we discussed in Sect. 5.2.1, the worst-case time complexity of Algorithm Edit-Graph on graphs of degree n is \(\mathcal {O}(n^2)\), whereas the complexity of the method proposed by Mauw et al. [18], as well as its variants proposed by Mauw et al. [17] and the one introduced in Sect. 6.2, is \(\mathcal {O}(n^4)\).
7 Concluding remarks
We have reassessed the notion of \((k,\ell )\)-anonymity, which quantifies the privacy level of a social graph in the presence of active adversaries. Firstly, we have introduced the notion of \((k, \Gamma _{G,\ell })\)-anonymity, which alleviates the computational cost of using \((k,\ell )\)-anonymity as the basis of anonymisation methods based on edge set perturbations. The new privacy property also allows us to reduce the amount of perturbation needed to protect a social graph from an active attack. Secondly, we have critically assessed one of the assumptions posed by \((k,\ell )\)-anonymity on the adversary capabilities. Judging that it is unrealistic to assume that an adversary will be able to know all distances between a set of sybil nodes and every other vertex of the social graph, we introduced the notion of adjacency anonymity, which accounts for adversaries who control the connection patterns with the neighbours of the sybil nodes. Finally, combining the two previous ideas, we have introduced a new privacy property: \((k, \Gamma _{G,\ell })\)-adjacency anonymity. Based on this new property, we proposed an efficient algorithm for transforming a graph G into a \((k, \Gamma _{G,1})\)-adjacency anonymous graph, for values of k up to \(\left\lfloor \frac{n-1}{2}\right\rfloor \), where n is the number of vertices of the graph. We have additionally determined tight bounds on the number of edits performed by this method. We conducted a series of experiments on three real-life social graphs and a collection of randomly generated graphs, which show that when compared to \((k,\ell )\)-anonymity, the new privacy notions continue to provide protection from equally capable active attackers while requiring a much smaller number of graph perturbations.
Notes
Source: statista.com.
The code and resources used in these experiments can be accessed at https://github.com/rolandotr/graph.
Although it is not a requirement of Algorithm Edit-Graph, the other two methods that we evaluate in these experiments require the original graph to be connected. We start with the density value 0.03 because there exist no connected graphs of order 200 and density 0.02 or 0.01.
References
Backstrom L, Dwork C, Kleinberg J (2007) Wherefore art thou r3579x?: anonymized social networks, hidden patterns, and structural steganography. In: Proceedings of the 16th international conference on World Wide Web, Banff, AB, Canada, May 2007, pp 181–190
Casas-Roma J, Herrera-Joancomartí J, Torra V (2013) An algorithm for \(k\)-degree anonymity on large networks. In: Proceedings of the 2013 IEEE/ACM international conference on advances in social networks analysis and mining, Niagara Falls, Canada, August 2013, pp 671–675
Casas-Roma J, Herrera-Joancomartí J, Torra V (2017) \(k\)-degree anonymity and edge selection: improving data utility in large networks. Knowl Inf Syst 50(2):447–474
Chatterjee T, DasGupta B, Mobasheri N, Srinivasan V, Yero I (2016) On the computational complexities of three privacy measures for large networks under active attack. CoRR, abs/1607.01438
Chen W, Cao Y, Wang H (2015) Conditional anonymity with non-probabilistic adversary. Inf Sci 324:32–43
Cheng J, Fu A, Liu J (2010) \(K\)-isomorphism: privacy preserving network publication against structural attacks. In: Proceedings of the 2010 ACM SIGMOD international conference on management of data, Indianapolis, IN, USA, June 2010, pp 459–470
Chester S, Kapron B, Ramesh G, Srivastava G, Thomo A, Venkatesh S (2013) Why Waldo befriended the dummy? \(k\)-anonymization of social networks with pseudo-nodes. Soc Netw Anal Min 3(3):381–399
Guimera R, Danon L, Diaz-Guilera A, Giralt F, Arenas A (2003) Self-similar community structure in a network of human interactions. Phys Rev E 68(6):065103
Halpern J, O’Neill K (2005) Anonymity and information hiding in multiagent systems. J Comput Secur 13(3):483–514
Hay M, Miklau G, Jensen D, Towsley D, Weis P (2008) Resisting structural re-identification in anonymized social networks. Proc VLDB Endow 1(1):102–114
Jannesari M, Omoomi B (2012) The metric dimension of the lexicographic product of graphs. Discrete Math 312(22):3349–3356
Leskovec J, Kleinberg J Faloutsos C (2005) Graphs over time: densification laws, shrinking diameters and possible explanations. In: Proceedings of the 11th ACM SIGKDD international conference on knowledge discovery in data mining, Chicago, IL, USA, August 2005, pp 177–187
Liu C, Mittal P (2016) Linkmirage: enabling privacy-preserving analytics on social relationships. In: Proceedings of NDSS 2016, San Diego, CA, USA
Liu K, Terzi E (2008) Towards identity anonymization on graphs. In: Proceedings of the 2008 ACM SIGMOD international conference on management of data, Vancouver, BC, Canada, June 2008, pp 93–106
Lu X, Song Y, Bressan S (2012) Fast identity anonymization on graphs. In: Liddle S, Schewe K, Tjoa A, Zhou X (eds) Database and expert systems applications, 23rd international conference, DEXA 2012, proceedings, Part I, Vienna, Austria, September 2012, pp 281–295
Ma T, Zhang Y, Cao J, Shen J, Tang M, Tian Y, Al-Dhelaan A, Al-Rodhaan M (2015) KDVEM: a \(k\)-degree anonymity with vertex and edge modification algorithm. Computing 97(12):1165–1184
Mauw S, Ramírez-Cruz Y, Trujillo-Rasua R (2018) Anonymising social graphs in the presence of active attackers. Trans Data Privacy 11(2):169–198
Mauw S, Trujillo-Rasua R, Xuan B (2016) Counteracting active attacks in social network graphs. In: Ranise S, Swarup V (eds) Data and applications security and privacy XXX, DBSec 2016. Trento, Italy, pp 233–248
Mcauley J, Leskovec J (2009) Discovering social circles in ego networks. ACM Trans Knowl Discov Data 8(1):4
Mittal P, Papamanthou C, Song D (2013) Preserving link privacy in social network based systems. In: Proceedings of NDSS 2013, San Diego, CA, USA
Narayanan A, Shmatikov V (2009) De-anonymizing social networks. In: Proceedings of the 30th IEEE symposium on security and privacy, Oakland, CA, USA, pp 173–187
Panzarasa P, Opsahl T, Carley K (2009) Patterns and dynamics of users’ behavior and interaction: network analysis of an online community. J Assoc Inf Sci Technol 60(5):911–932
Peng W, Li F, Zou X, Wu J (2012) Seed and grow: an attack against anonymized social networks. In: Proceedings of SECON 2012, Seoul, Korea, pp 587–595
Peng W, Li F, Zou X, Wu J (2014) A two-stage deanonymization attack against anonymized social networks. IEEE Trans Comput 63(2):290–303
Rousseau F, Casas-Roma J, Vazirgiannis M (2017) Community-preserving anonymization of graphs. Knowl Inf Syst 54(2):315–343
Salas J, Torra V (2015) Graphic sequences, distances and k-degree anonymity. Discrete Appl Math 188:25–31
Samarati P (2001) Protecting respondents’ identities in microdata release. IEEE Trans Knowl Data Eng 13(6):1010–1027
Sun Y, Yuan Y, Wang G, Cheng Y (2016) Splitting anonymization: a novel privacy-preserving approach of social network. Knowl Inf Syst 47(3):595–623
Sweeney L (2002) \(k\)-anonymity: a model for protecting privacy. Int J Uncertain Fuzziness Knowl-Based Syst 10(5):557–570
Trujillo-Rasua R, Yero I (2016) \(k\)-metric antidimension: a privacy measure for social graphs. Inf Sci 328:403–417
Varrette S, Bouvry P, Cartiaux H, Georgatos F (2014) Management of an academic HPC cluster: the UL experience. In: Proceedings of the 2014 international conference on high performance computing and simulation, Bologna, Italy, pp 959–967
Wang Y, Xie L, Zheng B, Lee K (2014) High utility \(k\)-anonymization for social network publishing. Knowl Inf Syst 41(3):697–725
Wu W, Xiao Y, Wang W, He Z, Wang Z (2010) \(K\)-symmetry model for identity anonymization in social networks. In: Proceedings of the 13th international conference on extending database technology, Lausanne, Switzerland, pp 111–122
Yu H (2011) Sybil defenses via social networks: a tutorial and survey. SIGACT News 42(3):80–101
Zhou B, Pei J (2008) Preserving privacy in social networks against neighborhood attacks. In: Proceedings of the 2008 IEEE 24th international conference on data engineering, Cancun, Mexico, pp 506–515
Zhou B, Pei J (2011) The \(k\)-anonymity and \(l\)-diversity approaches for privacy preservation in social networks against neighborhood attacks. Knowl Inf Syst 28(1):47–77
Zou L, Chen L, Özsu MT (2009) \(K\)-automorphism: a general framework for privacy preserving network publication. Proc VLDB Endow 2(1):946–957
Acknowledgements
The work reported in this paper was partially funded by Luxembourg’s Fonds National de la Recherche (FNR), via Grants C15/IS/10428112 (DIST) and C17/IS/11685812 (PrivDA).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proof of Theorem 5.2 (see page 14)
Theorem 5.2
Let \(G=(V,E)\) be a \((k_0,1)\)-adjacency anonymous social graph and let \(k\in \left[ k_0+1,\left\lfloor \frac{|V|-1}{2}\right\rfloor \right] \). The number t of edges added by steps 7 to 12 of Algorithm Edit-Graph satisfies
Proof
Let \(((u_1,v_1),(u_2,v_2),\ldots ,(u_t,v_t))\), with \((u_i,v_i)\in (V\times V)\setminus E\) for \(i\in \{1,\ldots ,t\}\), be the sequence of edges added to G by steps 7 to 12 of Algorithm Edit-Graph. Let \(E_0=E\) and \(E_i=E_{i-1}\cup \{(u_i,v_i)\}\), for \(i\in \{1,\ldots ,t\}\). Moreover, for every \(i\in \{0,\ldots ,t\}\), let \(G_i=(V,E_i)\) and \(L_i=\{v\in L:\;1\le \delta _{G_i}(v)<k\}\).
After adding the edge \((u_i,v_i)\), we have that \(\delta _{G_i}(u_i)=\delta _{G_{i-1}}(u_i)+1\) and \(\delta _{G_i}(v_i)=\delta _{G_{i-1}}(v_i)+1\), whereas \(\delta _{G_i}(x)=\delta _{G_{i-1}}(x)\) for every \(x\in V-\{u_i,v_i\}\).
We define the function
which specifies by how much the sum of the degrees of vertices from L needs to be increased for \(G_i\) to satisfy \((k, \Gamma _{G,1})\)-adjacency anonymity. Note that, by the definition of t, we have that \(missing(G_t)=0\). Moreover, \(missing(G_0)=\sum _{u\in V,\ 1\le \delta _G(u)<k}k-\delta _G(u)\). After adding the edge \((u_i,v_i)\), the following situations are possible:
-
1.
\(u_i,v_i\in L_{i-1}\). In this case, since two vertices from \(L_{i-1}\) have their degree increased by 1, we have that \(missing(G_i)=missing(G_{i-1})-2\).
-
2.
\(u_i\in L_{i-1}\) and \(v_i\notin L_{i-1}\), or vice versa. Here, \(missing(G_i)=missing(G_{i-1})-1\).
With the previous definitions in mind, we will address the proof of the left-hand inequality in Eq. 2. To that end, we will assume, for the purpose of contradiction, that
If \(missing(G_0)\) is even, we have that \(t<\frac{missing(G_0)}{2}\). Given that, in the best-case scenario, situation 1 above occurs at every iteration of the algorithm, we have
which is a contradiction.
In a similar manner, if \(missing(G_0)\) is odd, we have that \(t<\frac{missing(G_0)+1}{2}\). Here, in the best-case scenario, situation 1 above occurs in every iteration, except one, so
which is also a contradiction. Thus, we can conclude that
The right-hand inequality in Eq. 2 is trivial, given that at least one vertex has its degree increased by 1 at every iteration. The proof is thus complete.\(\square \)
Appendix B: Proof of Theorem 5.3 (see page 14)
Theorem 5.3
Let \(G=(V,E)\) be a \((k_0,1)\)-adjacency anonymous social graph and let \(k\in \left[ k_0+1,\left\lfloor \frac{|V|-1}{2}\right\rfloor \right] \). Let \(G_t\) be the graph obtained from G after executing steps 7 to 12 of Algorithm Edit-Graph. The number \(t'\) of edges removed by steps 14 to 19 of Algorithm Edit-Graph satisfies
and
Proof
We will follow a reasoning analogous to the one applied in the proof of Theorem 5.2. Let \(((u_1,v_1),(u_2,v_2),\ldots ,(u_{t'},v_{t'}))\), with \((u_i,v_i)\in E_t=E(G_t)\) for \(i\in \{1,\ldots ,t'\}\), be the sequence of edges removed from \(G_t\) by steps 14 to 19 of Algorithm Edit-Graph. Let \(E_{t+i}=E_{t+i-1}\setminus \{(u_i,v_i)\}\), for \(i\in \{1,\ldots ,t'\}\). Moreover, for every \(i\in \{1,\ldots ,t'\}\), let \(G_{t+i}=(V,E_{t+i})\) and \(H_i=\{v\in H:\;|V|-k-1<\delta _{G_{t+i}}(v)\le |V|-2\}\).
After removing the edge \((u_i,v_i)\), we obtain that \(\delta _{G_{t+i}}(u_i)=\delta _{G_{t+i-1}}(u_i)-1\) and \(\delta _{G_{t+i}}(v_i)=\delta _{G_{t+i-1}}(v_i)-1\), whereas \(\delta _{G_{t+i}}(x)=\delta _{G_{t-i-1}}(x)\) for every \(x\in V-\{u_i,v_i\}\).
Now we introduce the function
In a manner analogous to the proof of Theorem 5.2, we have that by definition \(excess(G_{t+t'})=0\) and
Additionally, after removing the edge \((u_i,v_i)\), the following situations are possible:
-
1.
\(u_i,v_i\in H_{i-1}\). In this case, since two vertices from \(H_{i-1}\) have their degree decreased by 1, we have that \(excess(G_{t+i})=excess(G_{t+i-1})-2\).
-
2.
\(u_i\in H_{i-1}\) and \(v_i\notin H_{i-1}\), or vice versa. Here, \(excess(G_{t+i})=excess(G_{t+i-1})-1\).
Now, to address the proof of the inequality in Eq. 3, we assume, for the purpose of contradiction, that
In consequence, if \(excess(G_t)\) is even, we have
which is a contradiction, whereas in the case that \(excess(G_t)\) is odd we have
which is also a contradiction, so we can conclude that Eq. 3 holds. As in Theorem 5.2, the upper bound (Eq. 4) is trivial.\(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mauw, S., Ramírez-Cruz, Y. & Trujillo-Rasua, R. Conditional adjacency anonymity in social graphs under active attacks. Knowl Inf Syst 61, 485–511 (2019). https://doi.org/10.1007/s10115-018-1283-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-018-1283-x