Abstract
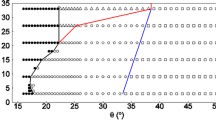
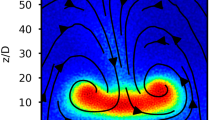
The discrete particle method (DPM) is used to model granular flows down an inclined chute with varying basal roughness, thickness and inclination. We observe three major regimes: arresting flows, steady uniform flows and accelerating flows. For flows over a smooth base, other (quasi-steady) regimes are observed: for small inclinations the flow can be highly energetic and strongly layered in depth; whereas, for large inclinations it can be non-uniform and oscillating. For steady uniform flows, depth profiles of density, velocity and stress are obtained using an improved coarse-graining method, which provides accurate statistics even at the base of the flow. A shallow-layer model for granular flows is completed with macro-scale closure relations obtained from micro-scale DPM simulations of steady flows. We obtain functional relations for effective basal friction, velocity shape factor, mean density, and the normal stress anisotropy as functions of layer thickness, flow velocity and basal roughness.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Akers B., Bokhove O.: Hydraulic flow through a contraction: multiple steady states. Phys. Fluids 20, 056601 (2008)
Allen, M.P., Tildesley, D.J. (eds): Computer Simulation of Liquids. Oxford University Press, Clarendon (1993)
Babic M.: Average balance equations for granular materials. Int. J. Eng. Sci. 35(5), 523–548 (1997)
Bagnold R.A.: Experiments on a gravity-free dispersion of large spheres in a Newtonian fluid under shear. Proc. R. Soc. A 255, 49–63 (1954)
Borzsonyi T., Ecke R.E.: Rapid granular flows on a rough incline: phase diagram, gas transition, and effects of air drag. Phys. Rev. E 74(6), 9 (2006)
Borzsonyi T., Ecke R.E.: Flow rule of dense granular flows down a rough incline. Phys. Rev. E 76(3), 10 (2007)
Bokhove O., Thornton A.R.: Shallow granular flows. In: Fernando, H.J. (eds) Handbook of Environmental Fluid Dynamics, Boca Raton, FL USA, ISBN:9781-43981-16691 (2012)
Cui X., Gray J.M.N.T., Johannesson T.: Deflecting dams and the formation of oblique shocks in snow avalanches at flateyri. J. Geophys. Res. 112, F04012 (2007)
Cundall P.A., Strack O.D.L.: A discrete numerical model for granular assemblies. Geotechnique 29, 47–65 (1979)
Daerr A., Douady S.: Two types of avalanche behaviour in granular media. Nature 399(6733), 241–243 (1999)
Denlinger R.P., Iverson R.M.: Flow of variably fluidized granular masses across three-dimensional terrain 2. Numerical predictions and experimental tests. J. Geophys. Res. 106(B1), 533–566 (2001)
Dalbey K., Patra A.K., Pitman E.B., Bursik M.I., Sheridan M.F.: Input uncertainty propagation methods and hazard mapping of geophysical mass flows. J. Geophys. Res. 113, B05203 (2008)
Forterre Y., Pouliquen O.: Long-surface-wave instability in dense granular flows. J. Fluid Mech. 486, 21–50 (2003)
Gray J.M.N.T., Cui X.: Weak, strong and detached oblique shocks in gravity driven granular free-surface flows. J. Fluid Mech. 579, 113–136 (2007)
Goujon C., Dalloz-Dubrujeaud B., Thomas N.: Bidisperse granular avalanches on inlined planes: a rich variety of behaviors. Eur. Phys. J. E. 23(2), 199–215 (2007)
Grigorian S.S., Eglit M.E., Yakimov Y.L.: New statement and solution of the problem of the motion of snow avalances. Physics of Snow, Avalanches and Glaciers, Tr Vysokogornogo Geofizich Inst. 12, 104–113 (1967)
Goldhirsch I.: Stress, stress asymmetry and couple stress: from discrete particles to continuous fields. Granul. Matter 12(3), 239–252 (2010)
Goujon C., Thomas N., Dalloz-Dubrujeaud B.: Monodisperse dry granular flows on inclined planes; role of roughness. Eur. Phys. J. E. 11, 147–157 (2003)
Gray J.M.N.T., Tai Y.C., Noelle S.: Shock waves, dead zones and particle-free regions in rapid granular free surface flows. J. Fluid Mech. 491, 161–181 (2003)
Gray J.M.N.T., Wieland M., Hutter K.: Free surface flow of cohesionless granular avalanches over complex basal topography. Proc. R. Soc. A 455, 1841–1874 (1999)
Hákonardóttir K.M., Hogg A.J.: Oblique shocks in rapid granular flows. Phys. Fluids 17, 077101 (2005)
Hutter K., Siegel M., Savage S.B., Nohguchi Y.: Two-dimensional spreading of a granular avalanche down an inclined plane. 1. Theory. Acta Mech. 100(1–2), 37–68 (1993)
Irving J.H., Kirkwood J.G.: The statistical mechanical theory of transport processes. J. Chem. Phys. 18, 817 (1950)
Iverson R.M.: The physics of debris flows. Rev. Geophys. 35, 245–296 (1997)
Jenkins J.T., Berzi D.: Dense inclined flows of inelastic spheres: tests of an extension of kinetic theory. Granul. Matter 12, 151–158 (2010)
Jenkins, J.T.: Hydraulic theory for a debris flow supported on a collisional shear layer. In: Proceedings of International Congress on Hydraulics Research IAHR, Tokyo, pp. 1–12 103307 (1993)
Jenkins J.T.: Dense shearing flows of inelastic disks. Phys. Fluids 18, 103307 (2006)
Jenkins J.T.: Dense inclined flows of inelastic spheres. Granul. Matter 10, 47–52 (2007)
Kulikovskii A.G., Eglit M.E.: Two-dimensional problem of the motion of a snow avalanche along a slope with smoothly changing properties. Prikladnaya Matematika i Mekhanika 37(5), 837–848 (1973)
Louge, M.Y., Keast, S.C.: On dense granular flows down flat frictional inclines. Phys. Fluids 13(5), 1213 (2001)
Luding, S., Lätzel, M., Volk, W., Diebels, S., Herrmann, H.J.: From discrete element simulations to a continuum model. Comput. Meth. Appl. Mech. Eng. 191, 21–28 (2001)
Louge, M.Y.: Model for dense granular fows down bumpy inclines. Phys. Rev. E 67, 061303 (2003)
Luding S.: Micro-macro models for anisotropic granular media. In: Vermeer, P.A., Ehlers, W., Herrmann, H.J., Ramm, E. (eds) Micro-Macro Models for Anisotropic Granular Media, pp. 195–206. A.A. Balkema, Leiden (2004)
Luding S.: Introduction to discrete element methods: basics of contact force models and how to perform the micro-marco transition to continuum theory. Eur. J. Environ. Civ. Eng. 12(7–8), 785–826 (2008)
Luding S.: From molecular dynamics and particle simulations towards constitutive relations for continuum theory. In: Koren, B., Vuik, K. (eds) Advanced Computational Methods in Science and Engineering Lecture Notes in Computational Science and Engineering, Springer, New York, NY (2009)
MiDi G.D.R.: On dense granular flows. Eur. Phys. J. E. 14, 341–365 (2004)
Pesch, L., Bell, A., Sollie, W.H., Ambati, V.R., Bokhove, O., Van der Vegt, J.J.W.: hpGEM a software framework for discontinous galerkin finite element methods. ACM Trans. Math. Softw. 33(4), Article No 23 (2007)
Pouliquen O., Forterre Y.: Friction law for dense granular flows: application to the motion of a mass down a rough inlined plane. J. Fluid Mech. 453, 131–151 (2002)
Pouliquen O., Forterre Y.: A non-local rheology for dense granular flows. Phys. Eng. Sci. 367(1909), 5091–5107 (2009)
Pouliquen O.: Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11(3), 542–548 (1999)
Shen S., Atluri S.N.: Atomic-level stress calculation and continuum molecular system equivalence. Comput. Model. Eng. Sci. 6(1), 91–104 (2004)
Silbert, L.E., Ertas, D., Grest, G.S., Halsey, D., Levine, T.C., Plimpton, S.J.: Granular flow down an inclined plane: Bagnold scaling and rheology. Phys. Rev. E. 64, 051302 (2001)
Silbert, L.E., Grest, G.S., Plimpton, D. Levine, J.W.: Boundary effects and self-organization in dense granular ows. Phys. Fluids 14(8), 2637–2646 (2002)
Schofield P., Henderson J.R.: Statistical mechanics of inhomogenous fluids. Proc. R. Soc. 379, 231–246 (1982)
Savage S.B., Hutter K.: The motion of a finite mass of material down a rough incline. J. Fluid Mech. 199, 177–215 (1989)
Silbert L.E., Landry J.W., Grest G.S.: Granular flow down a rough inclined plane: transition between thin and thick piles. Phys. Fluids 15(1), 1–10 (2003)
Todd B.D., Evans D.J., Daivis P.J.: Pressure tensor for inhomogeneous fluids. Phys. Rev. E 52(2), 1627–1638 (1995)
Taberlet N., Richard P., Jenkins J.T., Delannay R.: Density inversion in rapid granular flows: the supported regime. Eur. Phys. J. E Soft Matter Biol. Phy. 22(1), 17–24 (2007)
Vreman A.W., Al-Tarazi M., Kuipers A.M., VanSint Annaland M., Bokhove O.: Supercritical shallow granular flow through a contraction: experiment, theory and simulation. J. Fluid Mech. 578, 233–269 (2007)
Weinan E., Engquist B., Li X., Ren W., Vanden-Eijnden E.: Heterogeneous multiscale methods: a review. Commun. Comput. Phys. 2(3), 367–450 (2007)
Williams R., Stinton A.J., Sheridan M.F.: Evaluation of the Titan 2D two-phase flow model using an actual event: Case study of the Vazcún valley lahar. J. Volcan. Geotherm. Res. 177, 760–766 (2008)
Weinhart, T., Thornton, A.R., Luding, S., Bokhove, O.: From discrete particles to continuum fields near a boundary. Granul. Matter Special volume for Goldhirsch. pp. 1–69. ISSN:1434-5021. ISBN:10035-012-0317-4 (2012)
Acknowledgments
The authors would like to thank the Institute of Mechanics, Processes and Control, Twente (IMPACT) for the primary financial support of this work as part of the research program “Superdispersed multiphase flows”. The DPM simulations performed for this paper are undertaken in Mercury-DPM, which was initially developed within this IMPACT program. It is primarily developed by T. Weinhart, A. R. Thornton and D. Krijgsman as a joint project between the Multi ScaleMechanics (Mechanical Engineering) and the Mathematics of Computational Science (Applied Mathematics) groups at theUniversity of Twente. We also thank the NWO VICI grant 10828 and the DFG project SPP1482 B12 for financial support.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Weinhart, T., Thornton, A.R., Luding, S. et al. Closure relations for shallow granular flows from particle simulations. Granular Matter 14, 531–552 (2012). https://doi.org/10.1007/s10035-012-0355-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10035-012-0355-y