Skip to main content
SpringerLink
Log in

Nonlinear free vibration analysis of generic coupled induced strain actuated piezo-laminated beams

  • Originalarbeiten/Originals
  • Published:
Forschung im Ingenieurwesen Aims and scope Submit manuscript

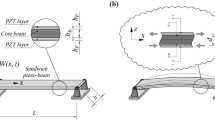
Abstract

Piezo-laminated thin beams have been analyzed with induced strain actuation using Kirchhoff’s hypothesis and von Kármán strain displacement relations. Extremizing the Lagrangian of the system derives the governing nonlinear partial differential equations for the beam. Eliminating the in-plane displacement, an integro-partial differential equation of motion is obtained in terms of the transverse displacement. A deflection function that satisfies the simply supported boundary conditions is assumed to get the system equation as a nonlinear second order ordinary differential equation in time, which is of Duffing’s type. The solution of the problem is obtained through exact integration. Results are presented for frequency and amplitude for surface bonded PZT-5A layer in composite beams with various stacking sequences.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bailey T, Hubbard JE (1985) Distributed Piezoelectric-Polymer Active Vibration Control of a Cantilever Beam. J Guidance Control Dynamics 8(5):605–611

    Article  MATH  Google Scholar 

  2. Crawley EF, Anderson EH (1990) Detailed Models of Piezo-ceramic Actuation of Beams. J Intell Mater Syst Struct 1:4–25

    Article  Google Scholar 

  3. Crawley EF, de Luis J (1987) Use of Piezoelectric Actuation as Elements of Intelligent Structures. AIAA J 25(10):1373–1385

    Article  Google Scholar 

  4. Im S, Atluri SN (1989) Effects of Piezo Actuator on a Finitely Deformed Beam Subjected to General Loading. AIAA J 27(12):1801–1807

    Article  MATH  Google Scholar 

  5. Crawley EF, Lazarus KB (1989) Induced Strain Actuation of Isotropic and Anisotropic Plates. AIAA J 29(6):944–951

    Article  Google Scholar 

  6. Chandra R, Chopra I (1993) Structural Modeling of Composite Beams with Induced-Strain Actuators. AIAA J 31(9):1692–1701

    Article  MATH  Google Scholar 

  7. Thornburgh R, Chattopadhay A, Ghoshal (2004) A Transient Vibration of Smart Structures using a Coupled Piezoelectric-Mechanical. Theory J Sound Vib 274:53–72

    Article  Google Scholar 

  8. Zhou YH, Wang J (2004) Vibration Control of Piezoelectric Beam-type Plates with Geometrically Nonlinear Deformation. Int J Nonlinear Mech 39:909–920

    Article  MATH  MathSciNet  Google Scholar 

  9. Waisman H, Abramovich H (2002) Active Stiffening of Laminated Composite Beam Using Piezoelectric Actuators. Composite Struct 58:109–120

    Article  Google Scholar 

  10. Thakkar D, Ganguli R (2004) Dynamic Response of Rotating Beams with Piezoceramic Actuation. J Sound Vib 270:729–753

    Article  Google Scholar 

  11. Thakkar D, Ganguli R (2006) Use of Single Crystal and Soft Piezo-Ceramics for alleviation of Flow Separation Induced Vibration in Smart Helicopter Rotor. Smart Mater Struct 15:331–341

    Article  Google Scholar 

  12. Thakkar D, Ganguli R (2006) Single-Crystal Piezo-ceramic Actuation for Dynamic Stall Suppression. Sens Actuators A 128:151–157

    Article  Google Scholar 

  13. Thakkar D, Ganguli R (2004) Helicopter Vibration Reduction in Forward Flight with Induced Shear Based Piezoceramic Actuation. Smart Mater Struct 30:599–608

    Article  Google Scholar 

  14. Librescu L (1975) Elastostatics and Kinetics of Anisotropic and Heterogeneous Shell-Type Structures. Noordhoff International Publishing, Leyden, Netherlands

    MATH  Google Scholar 

  15. Chia CY (1980) Non-linear Analysis of Plates. McGraw Hill, New York

    Google Scholar 

  16. Pillai SRR, Nageswara Rao B (1991) Improved Solution for the Nonlinear Vibration of Simply Supported Rectangular Cross-Ply Plates. J Sound Vib 150(3):517–519

    Article  Google Scholar 

  17. Nageswara Rao B, Pillai SRR (1992) Nonlinear Vibrations of a Simply Supported Rectangular Anti-symmetric Cross-ply Plate with Immovable Edges. J Sound Vib 152(3):568–572

    Article  MATH  Google Scholar 

  18. Srinivasan P (1995) Nonlinear Mechanical Vibrations. New Age International (P) Ltd. (Formerly Wiley Eastern), New Delhi

    Google Scholar 

  19. Abramowitz M, Stegun IA (1972) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables. US Department of Commerce, U.S. Government Printing office, Washington, D.C. 20402

    MATH  Google Scholar 

  20. Woinowsky-Krieger S (1950) The Effect of an Axial Force on the Vibration of Hinged Bars. Trans ASME J Appl Mech 72:35–36

    MathSciNet  Google Scholar 

  21. Dumir PC, Bhaskar A (1988) Some Erroneous Finite Element Formulations of Nonlinear Vibrations of Beams and Thin Plates. J Sound Vib 123:517–527

    Article  Google Scholar 

  22. Sarma BS, Varadan TK, Prathap G (1988) On Various Formulations of Large Amplitude Free Vibrations of Beams. Comput Struct 29:959–966

    Article  MATH  Google Scholar 

  23. Singh G, Sharma AK, Venkateswara Rao G (1990) Large Amplitude Free Vibrations of Beams – A Discussion on Various Formulations and Assumptions. J Sound Vib 142:77–85

    Article  Google Scholar 

  24. Singh G, Venkateswara Rao G, Iyengar NG R (1990) Reinvestigation of Large Amplitude Free Vibrations of Beams using Finite Elements. J Sound Vib 143:351–355

    Article  Google Scholar 

  25. Pillai SRR, Nageswara Rao B (1992) On nonlinear free Vibrations of Simply Supported Uniform Beams. J Sound Vib 159:527–531

    Article  MATH  Google Scholar 

  26. Nageswara Rao B (1992) Large-Amplitude Free Vibrations of Simply Supported Uniform Beams with Immovable Ends. J Sound Vib 155(3):523–527

    Article  MathSciNet  Google Scholar 

  27. Kapania RK, Raciti S (1989) Nonlinear Vibrations of Unsymmetrically Laminated Beams. AIAA J 27(2):201–210

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Technology, 208016, Kanpur, India

    K. Jayakumar & D. Yadav

  2. Structural Analysis and Testing Group, Vikram Sarabhai Space Centre, 695 022, Trivandrum, India

    B. Nageswara Rao

Authors
  1. K. Jayakumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. Yadav
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. B. Nageswara Rao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to B. Nageswara Rao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jayakumar, K., Yadav, D. & Rao, B.N. Nonlinear free vibration analysis of generic coupled induced strain actuated piezo-laminated beams . Forsch Ingenieurwes 72, 153–162 (2008). https://doi.org/10.1007/s10010-008-0077-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10010-008-0077-9

Keywords

Search

Navigation