Abstract
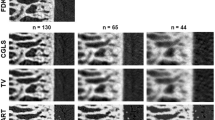
This study aimed at assessing the feasibility of a discrete algebraic reconstruction technique (DART) to be used in in vivo small animal bone studies. The advantage of discrete tomography is the possibility to reduce the amount of X-ray projection images, which makes scans faster and implies also a significant reduction of radiation dose, without compromising the reconstruction results. Bone studies are ideal for being performed with discrete tomography, due to the relatively small number of attenuation coefficients contained in the image [namely three: background (air), soft tissue and bone]. In this paper, a validation is made by comparing trabecular bone morphometric parameters calculated from images obtained by using DART and the commonly used standard filtered back-projection (FBP). Female rats were divided into an ovariectomized (OVX) and a sham-operated group. In vivo micro-CT scanning of the tibia was done at baseline and at 2, 4, 8 and 12 weeks after surgery. The cross-section images were reconstructed using first the full set of projection images and afterwards reducing them in number to a quarter and one-sixth (248, 62, 42 projection images, respectively). For both reconstruction methods, similar changes in morphometric parameters were observed over time: bone loss for OVX and bone growth for sham-operated rats, although for DART the actual values were systematically higher (bone volume fraction) or lower (structure model index) compared to FBP, depending on the morphometric parameter. The DART algorithm was, however, more robust when using fewer projection images, where the standard FBP reconstruction was more prone to noise, showing a significantly bigger deviation from the morphometric parameters obtained using all projection images. This study supports the use of DART as a potential alternative method to FBP in X-ray micro-CT animal studies, in particular, when the number of projections has to be drastically minimized, which directly reduces scanning time and dose.





Similar content being viewed by others
References
Perilli E, Le V, Ma B, Salmon P, Reynolds K, Fazzalari NL (2010) Detecting early bone changes using in vivo micro-CT in ovariectomized, zolendronic acid-treated, and sham-operated rats. Osteoporos Int 21:1371–1382
Mohan G, Perilli E, Kuliwaba JS, Humphries JM, Parkinson IH, Fazzalari NL (2011) Application of in vivo micro-computed tomography in the temporal characterization of subchondral bone architecture in a rat model of low-dose monosodium iodoacetate-induced osteoarthritis. Arthritis Res Ther 13:R210. doi:10.1186/ar3543
Perilli E, Cantley M, Marino V, Crotti T, Smith M, Haynes D, Dharmapatni A (2015) Quantifying not only bone loss, but also soft tissue swelling, in a murine inflammatory arthritis model using micro-computed tomography. Scand J Immunol 81:142–150
Van Bael S, Chai YC, Truscello S, Moesen M, Kerckhofs G, Van Oosterwyck H, Kruth JP, Schrooten J (2012) The effect of pore geometry on the in vitro biological behavior of human periosteum-derived cells seeded on selective laser-melted Ti6Al4 V bone scaffolds. Acta Biomater 8:2824–2834. doi:10.1016/j.actbio.2012.04.001
Wong HM, Yeung KWK, Lam KO, Tam V, Chu PK, Luk KDK, Cheung KMC (2010) A biodegradable polymer-based coating to control the performance of magnesium alloy orthopaedic implants. Biomaterials 31:2084–2096. doi:10.1016/j.biomaterials.2009.11.111
Feldkamp L, Davis L, Kress J (1984) Practical cone-beam algorithm. J Opt Soc Am A 1:612–619
Herman G (1980) Image reconstruction from projections: the fundamentals of computerized tomography. Academic press, New York
Batenburg KJ, Sijbers J (2011) DART: a practical reconstruction algorithm for discrete tomography. IEEE Trans Image Process 20:2542–2553. doi:10.1109/TIP.2011.2131661
Bals S, Batenburg KJ, Liang D, Lebedev O, Van Tendeloo G, Aerts A, Martens JA, Kirschhock CE (2009) Quantitative three-dimensional modeling of zeotile through discrete electron tomography. J Am Chem Soc 131:4769–4773. doi:10.1021/ja8089125
Batenburg KJ, Bals S, Sijbers J, Kübel C, Midgley PA, Hernandez JC, Kaiser U, Encina ER, Coronado EA, Van Tendeloo G (2009) 3D imaging of nanomaterials by discrete tomography. Ultramicroscopy 109:730–740
Batenburg KJ, Sijbers J, Poulsen HF, Knudsen E (2010) DART: a robust algorithm for fast reconstruction of three-dimensional grain maps. Journal of Applied Crystalography 43:1464–1473
van Aarle W, Van Gompel G, Batenburg KJ, Van de Casteele E, Sijbers J (2010) A 3-dimensional discrete tomography approach for superresolution micro-CT images: application to foams. In: The first international conference on image formation in X-ray computed tomography 45–48
Van Gompel G, Batenburg KJ, Van de Casteele E, van Aarle W, Sijbers J (2010) A discrete tomography approach for superresolution micro-CT images: application to bone. In: IEEE International Symposium on Biomedical Imaging: From Nano to Macro, pp 816–819. doi:10.1109/ISBI.2010.5490111
Palenstijn WJ, Batenburg KJ, Sijbers J (2013) The ASTRA tomography toolbox. In: 13th International Conference on Computational and Mathematical Methods in Science and Engineering
van Aarle W, Palenstijn WJ, De Beenhouwer J, Altantzis T, Bals S, Batenburg KJ, Sijbers J (2015) The ASTRA Toolbox: a platform for advanced algorithm development in electron tomography. Ultramicroscopy. doi:10.1016/j.ultramic.2015.05.002
van Aarle W, Palenstijn WJ, Cant J, Janssens E, Bleichrodt F, Dabravolski A, De Beenhouwer J, Batenburg KJ, Sijbers J (2016) Fast and flexible X-ray tomography using the ASTRA toolbox. Opt Express 24:25129–25147
Batenburg KJ, Sijbers J (2009) Optimal threshold selection for tomogram segmentation by projection distance minimization. IEEE Trans Med Imaging 28:676–686
Zaiontz C (2015) Real statistics using Excel. http://www.real-statistics.com. Accessed 29 Dec 2016
Perilli E, Baruffaldi F, Bisi MC, Cristofolini L, Cappello A (2006) A physical phantom for the calibration of three-dimensional X-ray microtomography examination. J Microsc 222:124–134
Palenstijn WJ, Batenburg KJ, Sijbers J (2011) Performance improvements for iterative electron tomography reconstruction using graphics processing units (GPUs). J Struct Biol 176:250–253. doi:10.1016/j.jsb.2011.07.017
Roelandts T, Batenburg KJ, den Dekker AJ, Sijbers J (2014) The reconstructed residual error: a novel segmentation evaluation measure for reconstructed images in tomography. Comput Vis Image Underst 126:28–37
Acknowledgements
Funding for the experimental data used in this work was provided by a grant from the Australian Research Council (DP0663271). This work was supported by the Research Foundation–Flanders (FWO, Belgium) through project funding G0F9117 N and S004217 N, and by the University of Antwerp (TOP BOF project 26824).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there are no conflicts of interest to disclose.
Additional information
E. Van de Casteele and E. Perilli contributed equally to this work.
About this article
Cite this article
Van de Casteele , E., Perilli, E., Van Aarle, W. et al. Discrete tomography in an in vivo small animal bone study. J Bone Miner Metab 36, 40–53 (2018). https://doi.org/10.1007/s00774-017-0815-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00774-017-0815-x