Abstract
In this work, a theory is developed for unifying large classes of nonlinear discrete-time dynamical systems obeying a superposition of a weighted maximum or minimum type. The state vectors and input–output signals evolve on nonlinear spaces which we call complete weighted lattices and include as special cases the nonlinear vector spaces of minimax algebra. Their algebraic structure has a polygonal geometry. Some of the special cases unified include max-plus, max-product, and probabilistic dynamical systems. We study problems of representation in state and input–output spaces using lattice monotone operators, state and output responses using nonlinear convolutions, solving nonlinear matrix equations using lattice adjunctions, stability, and controllability. We outline applications in state-space modeling of nonlinear filtering; dynamic programming (Viterbi algorithm) and shortest paths (distance maps); fuzzy Markov chains; and tracking audiovisual salient events in multimodal information streams using generalized hidden Markov models with control inputs.




Similar content being viewed by others
Notes
As explained in [31, 32], the adjunction is related to a concept in poset and lattice theory called ‘Galois connection.’ In [31, 59] an adjunction pair is denoted as \(({\large \varepsilon },{\large \delta })\), but in this paper we prefer to reverse the positions of its two operators, so that it agrees with the structure of a residuation pair \((\psi , {\psi }^\sharp )\).
Minimax algebra [21] has been based on bands (idempotent semigroups) and belts (idempotent presemirings), whereas max-plus algebra and its application to DES [2, 15, 20, 28] is based on dioids (canonically ordered semirings). In [21], a semilattice is called a commutative band and a lattice is called band with duality. Further, a belt is a semilattice-ordered semigroup, and a belt with duality [21] is a pair of two idempotent predioids [28] whose ‘additions’ are dual and form a lattice. Adding to a belt
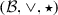 identity elements for
identity elements for  and \(\vee \), the latter of which is also an absorbing null for
and \(\vee \), the latter of which is also an absorbing null for  , creates an idempotent dioid [2, 20, 28]. More general (including nonidempotent) dioids are studied in [28]. Finally, belts that are groups under the ‘multiplication’
, creates an idempotent dioid [2, 20, 28]. More general (including nonidempotent) dioids are studied in [28]. Finally, belts that are groups under the ‘multiplication’  and as lattices have global bounds are called blogs (bounded lattice-ordered groups) in [21].
and as lattices have global bounds are called blogs (bounded lattice-ordered groups) in [21].In every clodum and clog, we have a pair of dual ‘additions’ and a pair of dual ‘multiplications.’ However, for brevity, we assign them shorter names that contain only one ‘addition’ (max) and one ‘multiplication,’ e.g., ‘max-plus clog’.
It is simply a matter a convention that we selected to call \(\wedge \) and
 as ‘dual addition and multiplication’ (instead of \(\vee \) and
as ‘dual addition and multiplication’ (instead of \(\vee \) and  ).
).In this paper, as ‘scalars’ we use numbers from \(\overline{\mathbb {R}}\) or its subsets, but the general definition of a weighted lattice allows for an arbitrary clodum as the set of ‘scalars.’
Despite its notation [15, 21], \(\varvec{M}^*\) is not the elementwise conjugate of the matrix \(\varvec{M}\) but is obtained via transposition and elementwise conjugation of \(\varvec{M}\). To avoid the above ambiguity, we prefer the terminology ‘adjoint’ which is based on some conceptual similarities with the adjoint of a linear operator in Hilbert spaces [21].
Although the main results [15] of max-plus eigenvalue analysis in the max-plus semiring assume all scalars \(< +\infty \), in the more general max-
 eigenvalue analysis over a clodum we allow scalars to equal \(\top \); this has direct applications for cloda \(\mathcal {K}=[0,1]\) in fuzzy systems, like the max–min clodum, where \(1=e=\top \).
eigenvalue analysis over a clodum we allow scalars to equal \(\top \); this has direct applications for cloda \(\mathcal {K}=[0,1]\) in fuzzy systems, like the max–min clodum, where \(1=e=\top \).For the max-plus clog \((\overline{\mathbb {R}},\vee ,\wedge ,+)\) the mean of a cycle \(\varvec{\sigma }\) is given by \(w(\varvec{\sigma }) / \ell (\varvec{\sigma })\), for the max-product clog \(([0,\infty ],\vee ,\wedge ,\times )\) it is given by \(w(\varvec{\sigma })^{1 / \ell (\varvec{\sigma })}\), whereas for the max–min clodum \(([0,1],\vee ,\wedge ,\min ,\max )\) the cycle mean is simply \(w\varvec{\sigma }\).
References
Avrachenkov KE, Sanchez E (2002) Fuzzy Markov chains and decision-making. Fuzzy Optim Decis Mak 1:143–159
Baccelli F, Cohen G, Olsder GJ, Quadrat J-P (1992) Synchronization and linearity: an algebra for discrete event systems (web edition, 2001). Wiley, New York
Bellman R, Karush W (1961) On a new functional transform in analysis: the maximum transform. Bull Am Math Soc 67:501–503
Bellman R, Karush W (1963) On the maximum transform. J Math Anal Appl 6:67–74
Bertsekas DP (2012) Dynamic programming and optimal control. Athena Scientific, Belmont (vol. I, 3rd ed., vol. II, 4th ed.)
Birkhoff G (1967) Lattice theory. American Mathematical Society, Providence, RI
Bishop CM (2006) Pattern recognition and machine learning. Springer, Berlin
Bloch I, Maitre H (1995) Fuzzy mathematical morphologies: a comparative study. Pattern Recognit 9(28):1341–1387
Blyth TS (2005) Lattices and ordered algebraic structures. Springer, Berlin
Blyth TS, Janowitz MF (1972) Residuation theory. Pergamon Press, Oxford
Borgefors G (1984) Distance transformations in arbitrary dimensions. Comput Vis Graph Image Process 27:321–345
Brockett RW (1970) Finite-dimensional linear systems. Wiley, New York
Brockett RW (1994) Language driven hybrid systems. In: Proceedings of 33rd conference on decision and control
Brogan WL (1974) Modern control theory. Quantum Publishers, New York
Butkovič P (2010) Max-linear systems: theory and algorithms. Springer, Berlin
Cassandras CG, Lafortune S (1999) Introduction to discrete event systems. Kluwer, Dordrecht
Charisopoulos V, Maragos P (2017) Morphological perceptrons: geometry and training algorithms. In: Proceedings international symposium on mathematical morphology (ISMM-2017), Fontainebleau, France
Cohen G, Dubois D, Quadrat JP, Viot M (1985) A linear system theoretic view of discrete event processes and its use for performance evaluation in manufacturing. IEEE Trans Autom Control 30:210–220
Cohen G, Gaubert S, Quadrat JP (2004) Duality and separation theorems in idempotent semimodules. Linear Alegbra Appl 379:395–422
Cohen G, Moller P, Quadrat JP, Viot M (1989) Algebraic tools for the performance evaluation of discrete event systems. Proc IEEE 77:39–58
Cuninghame-Green R (1979) Minimax algebra. Springer, Berlin
Cuninghame-Green RA, Butkovic P (2003) The equation Ax=By over (max, +). Theor Comput Sci 293:3–12
Doustmohammadi A, Kamen EW (1995) Direct generation of event-timing equations for generalized flow shop systems. In: Modeling, simulation, and control technologies for manufacturing, volume 2596 of proceedings of SPIE, pp 50–62
Evangelopoulos G, Zlatintsi A, Potamianos A, Maragos P, Rapantzikos K, Skoumas G, Avrithis Y (2013) Multimodal saliency and fusion for movie summarization based on aural, visual, and textual attention. IEEE Trans Multim 15(7):1553–1568
Felzenszwalb PF, Huttenlocher DP (2004) Distance transforms of sampled functions. Technical Report TR2004-1963, Cornell University
Gaubert S, Katz RD (2007) The Minkowski theorem for max-plus convex sets. Linear Alegbra Appl 421:356–369
Gazarik MJ, Kamen EW (1999) Reachability and observability of linear systems over max-plus. Kybernetika 35(1):2–12
Gondran M, Minoux M (2008) Graphs, dioids and semirings: new models and algorithms. Springer, Berlin
Hardouin L, Cottenceau B, Lhommeau M, Le Corronc E (2009) Interval systems over idempotent semiring. Linear Alegbra Appl 431(5–7):855–862
Heidergott B, Olsder GJ, van der Woude J (2006) Max plus at work: modeling and analysis of synchronized systems: a course on max-plus algebra and its applications. Princeton University Press, Princeton
Heijmans HJAM (1994) Morphological image operators. Academic Press, Boston
Heijmans HJAM, Ronse C (1990) The algebraic basis of mathematical morphology. Part I: dilations and erosions. Comput Vis Graph Image Process 50:245–295
Ho Y-C (ed) (1992) Discrete event dynamic systems: analyzing complexity and performance in the modern world. IEEE Press, New York
Hori T, Nakamura A (2013) Speech recognition algorithms using weighted finite-state transducers. Morgan & Claypool, San Rafael
Kaburlasos VG, Petridis V (2000) Fuzzy lattice neurocomputing (FLN) models. Neural Netw 13:1145–1169
Kailath T (1980) Linear systems. Prentice-Hall, Englewood Cliffs
Kamen EW (1993) An equation-based approach to the control of discrete even systems with applications to manufacturing. In: Proceedings of international conference on control theory and its applications, Jerusalem, Israel
Kamen EW, Doustmohammadi A (1994) Modeling and stability of production lines based on arrival-to-departure delays. In: Proceedings 33rd conference on decision and control
Klir GJ, Yuan B (1995) Fuzzy sets and fuzzy logic: theory and applications. Prentice-Hall, Englewood Cliffs
Lahaye S, Boimond J-L, Hardouin L (2004) Linear periodic systems over dioids. Discrete Event Dyn Syst 14:133–152
Litvinov GL, Maslov VP, Shpiz GB (2001) Idempotent functional analysis: an algebraic approach. Math Notes 69(5):696–729
Litvinov GL, Sobolevskii AN (2001) Idempotent interval analysis and optimization problems. Reliab Comput 7(5):353–377
Lucet Y (2010) What shape is your conjugate? A survey of computational convex analysis and its applications. SIAM Rev 52(3):505–542
Maragos P (1994) Morphological systems: slope transforms and max–min difference and differential equations. Signal Process 38:57–77
Maragos P (2005) Lattice image processing: a unification of morphological and fuzzy algebraic systems. J Math Imaging Vis 22:333–353
Maragos P (2013) Representations for morphological image operators and analogies with linear operators. In: Hawkes PW (ed) Advances in imaging and electron physics, vol 177. Academic Press, London, pp 45–187
Maragos P, Koutras P (2015) Max-product dynamical systems and applications to audio-visual salient event detection in videos. In: Proceedings IEEE international conference on acoustics speech and signal processing (ICASSP)
Maragos P, Schafer RW (1990) Morphological systems for multidimensional signal processing. Proc IEEE 78:690–710
Maragos P, Stamou G, Tzafestas SG (2000) A lattice control model of fuzzy dynamical systems in state-space. In: Goutsias J, Vincent L, Bloomberg D (eds) Mathematical morphology and its application to image and signal processing. Kluwer, Dordrecht
Maslov VP (1987) On a new superposition principle for optimization problems. Uspekhi Mat Nauk [Russ Math Surv] 42(3):39–48
McEneaney WM (2006) Max-plus methods for nonlinear control and estimation. Birkhauser, Boston
Mohri M, Pereira F, Ripley M (2002) Weighted finite-state transducers in speech recognition. Comput Speech Lang 16:69–88
Oppenheim AV, Schafer RW (1989) Discrete-time signal processing. Prentice-Hall, Englewood Cliffs, NJ
Pearl J (1988) Probabilistic reasoning in intelligent systems: networks of plausible inference. Morgan Kaufman Publishers, Los Altos
Rabiner L, Juang B-H (1993) Fundamentals of speech recognition. Prentice-Hall, Englewood Cliffs
Ritter GX, Sussner P, Diaz de Leon JL (1998) Morphological associative memories. IEEE Trans Neural Netw 9(2):281–293
Ritter GX, Urcid G (2003) Lattice algebra approach to single-neuron computation. IEEE Trans Neural Netw 14(2):282–295
Rockafellar RT (1970) Convex analysis. Princeton University Press, Princeton
Serra J (ed) (1988) Image analysis and mathematical morphology, volume 2: theoretical advances. Academic Press, London
Sternberg SR (1986) Grayscale morphology. Comput Vis Graph Image Process 35:333–355
Tsitsiklis JN (1995) Efficient algorithms for globally optimal trajectories. IEEE Trans Autom Control 40(9):1528–1538
van den Boom TJJ, De Schutter B (2012) Modeling and control of switching max-plus-linear systems with random and deterministic switching. Discrete Event Dyn Syst 22:293–332
Verbeek P, Dorst L, Verwer B, Groen F (1986) Collision avoidance and path finding through constrained distance transformation in robot state space. In: Proceedings of international conference on intelligent autonomous systems, Amsterdam
Verdu S, Poor HV (1987) Abstract dynamic programming models under commutativity conditions. SIAM J Control Optim 25(4):990–1006
Wagneur E (1991) Moduloids and pseudomodules–1. Dimension theory. Discrete Math 98:57–73
Yang P-F, Maragos P (1995) Min–max classifiers: learnability, design and application. Pattern Recognit 28(6):879–899
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the project “COGNIMUSE” under the “ARISTEIA” Action of the Operational Program Education and Lifelong Learning and was co-funded by the European Social Fund and Greek National Resources. It was also partially supported by the European Union under the projects MOBOT with Grant FP7-600796 and BabyRobot with Grant H2020-687831.
Rights and permissions
About this article
Cite this article
Maragos, P. Dynamical systems on weighted lattices: general theory. Math. Control Signals Syst. 29, 21 (2017). https://doi.org/10.1007/s00498-017-0207-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00498-017-0207-8





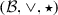 identity elements for
identity elements for  and
and  , creates an idempotent dioid [
, creates an idempotent dioid [ and as lattices have global bounds are called blogs (bounded lattice-ordered groups) in [
and as lattices have global bounds are called blogs (bounded lattice-ordered groups) in [ as ‘dual addition and multiplication’ (instead of
as ‘dual addition and multiplication’ (instead of  ).
). eigenvalue analysis over a clodum we allow scalars to equal
eigenvalue analysis over a clodum we allow scalars to equal  independent columns (rows). In [
independent columns (rows). In [