Tackling random fields non-linearities with unsupervised clustering of polynomial chaos expansion in latent space: application to global sensitivity analysis of river flooding

Abstract

A surrogate model is developed to accurately approximate a two-dimensional hydrodynamics numerical solver in order to conduct a reduced-cost variance-based global sensitivity analysis of the hydraulic state. The impact of uncertainties in river bottom friction and boundary conditions on the simulated water depth is analyzed for quasi-unsteady flows. An autoencoder technique adapted to non-linear variable dimension reduction is used to reduce the multi-dimensional model output so that the formulation of the surrogate remains computationally parsimonious. In addition, following the divide-and-conquer principle, a mixture of local polynomial chaos expansions is proposed to deal with non-linearity in the hydraulic state with respect to uncertain inputs. Machine learning techniques are used to automatically partition the input space into clusters that are not affected by non-linearities and support accurate surrogates. This combined strategy is applied to a reach of the Garonne River where river and floodplains dynamics are simulated by the numerical solver Telemac-2D. The merits of this strategy are highlighted when the flood front reaches regions where the topography features a strong gradient and where, consequently, strong non-linearities occur between the water depth and friction as well as hydrologic input forcing. By applying this strategy, the $Q_2$ metric improves by 90% compared to a classical polynomial chaos expansion surrogate, resulting in a much more reliable sensitivity analysis. This is particularly important in floodplain areas where human and economic activities are at stake.

1 Introduction

1.1 Flood monitoring

According to the World Health Organization (WHO), in Europe, floods are the most common natural hazard leading to emergencies, causing extensive damage, disruption and health effects (WHO 2017). Over the last 20 years, flood events have been recorded in 49 of the 53 member states. Estimates from WHO Regional Office for Europe, based on data from the international disaster database (EM-DAT), indicate that approximately 400 floods have caused the deaths of more than 2000 people, affected 8.7 millions others, and generated a loss of at least 72 billion euros over 2000–2014 (Guha-Sapir et al. 2015). The magnitude of the physical and human costs of such events can be reduced if adequate emergency prevention, preparedness, response, and recovery measures are implemented in a sustainable and timely manner (WMO 2013). Resilient and proactive health systems that anticipate needs and challenges are more likely to reduce risks and respond effectively during emergencies, thereby saving lives and alleviating human suffering. In this sense, several measures have been taken by governments and environmental organizations to minimize these effects (EFAS 2017), including the assessment and mapping of flood and tsunami health risks in order to indicate areas at highest risk, identify and analyze capacities for flood risk prevention, preparedness, response, and recovery with respect to the assessed flood risk, determine recommended actions for flood health emergency risk management, and assess resources and identify priorities for action.

The climate community estimates that about 1.3 billion people will be affected by flooding by 2050 due to climate change, increase in population density, and global degradation of environmental conditions (Arnell and Gosling 2016). It is increasingly clear that climate change has detectably influenced several water-related variables that contribute to floods, such as rainfall and snow melt. As global warming contributes to exacerbating sea level rise and extreme weather, floods are expected to grow by approximately 45% by the end of this century (Kulp and Strauss 2019). Thus, it is crucial to understand, assess, and anticipate flood events.

Flood monitoring benefits from world wide efforts by international programs dedicated to Earth observation from space, such as Copernicus, as well as from space agencies that support missions, such as Sentinel, or Surface Water Ocean Topography (SWOT) designed to study the topography of oceans and continental bodies of water (Biancamaria et al. 2016). In spite of the increasing volume, resolution, and precision of remote sensing water surface elevation observations, the prediction of flood events requires the use of reliable and robust numerical hydrodynamic models.

In France, the forecasting and vigilance of hydrological events likely to generate floods is ensured by Service de Prévision des Crues (SPC) whose action is coordinated by Service central d’hydrométéorologie et d’appui à la prévision des inondations (SCHAPI) of the Ministry of the Ecological Transition. The SPC/SCHAPI network works in partnership with Météo-France, which provides it with the meteorological variables (observations and forecasts) necessary to drive their hydrodynamic models.

1.2 Hydrodynamic numerical solvers

River hydrodynamic models are used to predict river water depth and discharge from which flood risk can be assessed. These predictions provide a Decision Support System (DSS) (Daupras et al. 2015) with informed hydraulic parameters and variables (water depth, discharge, and velocity) along with their evolution in the future for lead-times that range from a couple of hours to a couple of days depending on the dynamics of the catchment. $\text{DSS}$ are thus able to manage flood risk and eventually issue alerts for protective actions. Several research projects and concerted actions have been funded on the subject of river flood monitoring. For instance, the Hydrologic Ensemble Prediction EXperiment (HEPEX) aims to develop and demonstrate new hydrologic forecasting technologies and to facilitate the implementation of beneficial technologies into the operational environment (Schaake et al. 2006). The European Flood Awareness System (EFAS), initiated in 2003 (Thielen et al. 2009), seeks to improve flood preparedness in transnational European river basins by providing medium-range deterministic and probabilistic flood forecasting information, from 3 to 10 days in advance, to national hydro-meteorological services, e.g., SPC and SCHAPI.

Hydrodynamic numerical models are generally based on a deterministic approach that solves the Shallow Water Equations (SWE) derived from the free surface Navier-Stokes equations (de Saint-Venant 1871; Sohr 2001) and are prone to uncertainties. The uncertainty in the water depth and discharge field computed with a hydrodynamic solver is due to uncertainty in simplifying assumptions with respect to physics, particularly with respect to the flow dimension, approximate knowledge of hydraulic parameters, and imperfect description of forcing and geographical data. Uncertainty quantification aims to quantify and rank the major sources of uncertainties, thus allowing for a better informed and, eventually, improved hydraulic forecast.

1.3 Surrogate models for sensitivity analysis

Global Sensitivity Analysis (GSA) consists in studying how the uncertainty in the output of a model (numerical or otherwise) can be apportioned to the different sources of uncertainty in the model input (Saltelli 2002; Razavi et al. 2021). The aim of $\text{GSA}$ is to identify and rank the parameters that contribute mostly to the variability of the output of a model, also called a Quantity of Interest (QoI). It thus identifies which source of uncertainty should be reduced to most efficiently reduce uncertainty in the simulated $\text{QoI}$. A popular approach for sensitivity analysis is based on the decomposition of the output variance as the sum of the contributions associated with each input parameter and their combinations from which Sobol sensitivity indices are computed (Archer et al. 1997; Saltelli 2010). Extensions of those indices exist in the case of functional output (De Lozzo and Marrel 2017). This approach thus relies on sampling the uncertainties in the input space and the propagation of uncertainties through the model. $\text{Monte Carlo (MC)}$ simulation is the most common technique used for sampling and Sobol indices computation (Sobol’ 2001). However, its convergence is slow as it scales inversely to the square root of the $\text{MC}$ sample size and its cost becomes prohibitive for computationally expensive models such as $\text{two-dimensional (2D)}$ hydrodynamic solvers, especially in the context of real-time forecasting. To overcome this limitation, surrogate models may be used in place of the direct solver (Razavi et al. 2012). A surrogate model is a cheap-to-evaluate and parsimonious data-driven emulator of a reference model. This reference model can be seen as a black box that only provides a limited number of evaluations or observations. Thus, its output is known only at a few selected input points by means of a design of experiments. Then, the surrogate model seeks to approximate the reference model from this sparse input-output dataset. A variety of approximation techniques have been developed and applied as surrogates, such as linear regression models (Haldar and Mahadevan 1999), multidimensional scaling (Kruskal and Wish 1978), splines (Friedman 1991), Gaussian process (Rasmussen and Williams 2006), radial basis functions (Buhmann 2003), polynomial chaos expansions (Ghanem and Spanos 1991; El Garroussi et al. 2019), and artificial neural networks (Kasiviswanathan and Sudheer 2013). Some of them can interpolate the learning input-output dataset, e.g., Gaussian process regression, whereas others are designed to model the relationship between a $\text{QoI}$ and sources of random uncertainty, e.g., polynomial chaos expansions.

The surrogate model based on $\text{Polynomial Chaos Expansion (PCE)}$ (Lucor et al. 2004; Le Maître and Kino 2010) has proven useful in a wide range of applications, providing a low-cost yet accurate meta-model to estimate sensitivity indices (Sudret 2008; Crestaux et al. 2009). This surrogate model relies on the decomposition of the output random variable onto an orthonormal basis of polynomial functions. The polynomial coefficients are obtained either by using intrusive methods requiring access to the analytical code behind the numerical solver (e.g., Galerkin projection) or non-intrusive methods that rely on a learning database using the numerical solver as a black box (e.g., least square approximation). For steady flow in 1D and $\text{2D}$, Roy et al. (2018), Goutal et al. (2018), and El Garroussi et al. (2020) show that the $\text{PCE}$ surrogate model succeeds in representing the response in water depth to uncertainties in river bottom friction and upstream discharge, allowing for an efficient computation of Sobol indices, water depth $\text{Probability Density Function (PDF)}$, and water depth error covariance matrix over a reach of the Garonne River in southwest France.

However, $\text{PCE}$ surrogates tend to struggle when applied to problems that feature non-polynomial non-linearities (Li and Ghanem 1998) or stochastic discontinuities that may occur for time-varying processes (Najm 2009). Indeed, for unsteady flow with a $\text{2D}$ hydrodynamic model, strong non-linearities in the water depth response to changes in bottom friction and upstream discharge may occur when water overflows the minor bed of the river; especially near dikes and in areas where bathymetry features strong spatial gradients. These non-linearities tend to exacerbate in unsteady regime, when the flood front, characterized by a non-zero velocity and a zero water depth, enters a previously dry floodplain domain. In this context, classical $\text{PCE}$ meta-modeling is no longer adequate (Le Maître 2004; El Garroussi et al. 2020). Different approaches with varying degrees of complexity have been proposed in the literature to address the issue of $\text{PCE}$ meta-modeling in the presence of non-linearities. Examples include multi-resolution/multi-element polynomial chaos expansions (Le Maître et al. 2004; Wan and Karniadakis 2005), regression trees (Torre et al. 2019; Choubin et al. 2019; Marelli et al. 2021), multivariate adaptive regression splines (Friedman 1991; Dertimanis et al. 2018), among others. They rely on the idea of partitioning the input parameter space into (often disjoint) sub-spaces followed by the use of intrusive or non-intrusive methods to estimate $\text{PCE}$ coefficients. The surrogate model strategy should also be compatible with the dimension of the numerical solver output. Indeed, for functional output discretized over a mesh grid, the construction of a surrogate per mesh node would be computationally expensive, and could potentially lead to inconsistency as spatial coherence of the signal simulated field is not accounted for. The dimension of the model output should thus be reduced before the meta-modeling algorithm is applied (Bellman and Kalaba 1961; Lataniotis et al. 2020; El Garroussi et al. 2019). Dimension reduction stands in the transformation of high-dimension data into a meaningful representation of reduced dimension. On one hand, linear strategies, such as $\text{Principal Component Analysis (PCA)}$ (Wold et al. 1987), linear discriminant analysis (Izenman 2008), factor analysis (Yong and Pearce 2013), and 3-way tables (Cichocki et al. 2009) are often used. On the other hand, kernel PCA (Schölkopf et al. 1997), Laplacian eigenmap (Belkin and Niyogi 2003), locally linear embedding (Roweis and Saul 2000), isomap (Tenenbaum et al. 2000), and $\text{AutoEncoder (AE)}$ (Wang et al. 2016) are used to deal with non-linearities within data.

1.4 Objective and outline

In this paper, a surrogate model is developed to represent the $\text{2D}$ water depth field over the river and floodplain of the Garonne river, with respect to bottom friction and discharge. The surrogate model strategy aims to overcome the limitations of the classical $\text{PCE}$ approach from El Garroussi et al. (2020), which provides a poorly predictive surrogate model in the presence of non-linearities for a transient flow. Both $\text{PCA}$ and $\text{AE}$ algorithms are investigated to reduce the dimension of the hydraulic output field so that the computational cost of the surrogate construction remains parsimonious. A $\text{Mixture of Polynomial Chaos Expansion (MPCE)}$ approach is then implemented in the reduced space. $\text{Machine Learning (ML)}$ techniques are used to partition the input space into disjoint clusters that are not affected by non-linearities and support an accurate $\text{PCE}$ surrogate. The overall strategy, further denoted as $\text{reduced Mixture of Polynomial Chaos Expansions (rMPCE)}$, allows to take advantage of the advances made in $\text{PCE}$ surrogate modeling for local regression as well as in $\text{ML}$ for dimension reduction and clustering. The resulting surrogate is used to carry out a $\text{GSA}$ in order to rank the sources of uncertainty with a variance-based sensitivity analysis in the presence of non-linearities and at a parsimonious computational cost. The $\text{rMPCE}$ approach and its application for the computation of Sobol indices for a reach of the Garonne river is presented.

The paper is organized as follows. Section 2 provides a brief overview of uncertainty in hydraulics. Section 3 presents the methods for dimension reduction, clustering and classification, and polynomial chaos for the mixture of experts surrogate. It also presents metrics to assess the validity of the surrogate and the formulation of Sobol indices. Results are presented in Sect. 4, illustrating the capability of the $\text{rMPCE}$ to deal with both high-dimension and complex non-linear processes. Finally, concluding remarks, limitations, and perspectives are given in Sect. 5.

Fig. 1

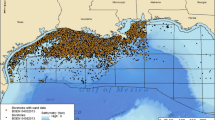
Satellite image of the Garonne river (southwest France) 50 km reach between Tonneins (upstream) and La Réole (downstream) on which the mesh is overlaid. Inset at the bottom left is a zoom of the mesh on the Garonne in Marmande regions. The red circles indicate monitoring stations and the blue arrow indicates the flow direction

2 Uncertainty quantification for hydraulic modeling

2.1 The Garonne catchment

The study area extends over a 50 km reach of the Garonne river (southwest France) from Tonneins (upstream) to the confluence with the rivers Lot and La Réole (downstream) (see Fig. 1). It has a population of nearly 40,000 mainly concentrated in Tonneins and Marmande. This part of the valley is identified as an area at high risk of flooding (Lang and Coeur 2014). Significant floods have affected this territory, such as the floods of December 1981 and February 2003, to a lesser extent January 2014, and more recently January 2021. Significant floods occurred also in June 1875, March 1930, and February 1952. The climate in the Marmande area is a degraded oceanic climate. Due to the downstream situation of the territory of Marmande, floods can occur at any season and with various origins (oceanic, Pyrenean, Mediterranean, Cévenol). Their characteristics are very different from one season to another, but the threats they represent remain very important. This part of the valley was equipped in the nineteenth century with infrastructure to protect the Garonne floodplain from flooding events. A system of longitudinal dykes and weirs was progressively constructed after the 1875 flood in order to protect floodplains and organize submersion and flood retention areas. Protections on the Garonne river form a system of successive storage areas for the floodplain beyond the dikes. This configuration is similar to the characteristic of other managed rivers such as the Rhone and the Loire. The $\text{QoI}$ for the study is the water depth simulated over the river bed and the floodplain using the bi-dimension numerical model presented in Sect. 2.2. The uncertainties in the model parameters and forcing as well as in the model outputs are described in Sect. 2.3.

2.2 2D hydraulic modeling

The $\text{Shallow Water Equations (SWE)}$ (de Saint-Venant 1871) are commonly used in environmental hydrodynamics modeling. They are derived from the Navier-Stokes equations (Sohr 2001) and based on the assumption that the horizontal length scale is significantly greater than the vertical scale, implying that vertical velocities are negligible, vertical pressure gradients are hydrostatic, and horizontal pressure gradients are due to displacement of the free surface. $\text{SWE}$ express mass and momentum conservation averaged in the vertical dimension. The non-conservative form of the equations is written in terms of the water depth h and the horizontal components $u_x$ and $u_y$ of the velocity $\overrightarrow{u}$ in Cartesian coordinates (Hervouet 2007a):

$$\begin{aligned}&\text{Continuity:} \frac{\partial h}{\partial t} + \overrightarrow{u}.\overrightarrow{\text{grad}}\; h + h\; \text{div}\overrightarrow{u} =0 \end{aligned}$$

(1a)

$$\begin{aligned}&\text{Momentum along } x: \frac{\partial u_x}{\partial t} + \overrightarrow{u}.\overrightarrow{\text{grad}}\; u_x \nonumber \\&\qquad = -g\frac{\partial H}{\partial x} + F_x + \text{div}\left( \nu _e\overrightarrow{\text{grad}}\; u_x\right) \end{aligned}$$

(1b)

$$\begin{aligned}&\text{Momentum along } y: \frac{\partial u_y}{\partial t} + \overrightarrow{u}.\overrightarrow{\text{grad}}\; u_y \nonumber \\&\qquad = -g\frac{\partial H}{\partial y} + F_y + \text{div}\left( {\nu }_{e}\overrightarrow{\text{grad}}\;u_y\right) \end{aligned}$$

(1c)

where $\overrightarrow{\text{grad}}$ and $\text{div}$ are the gradient and divergence operators, with:

$$\begin{aligned} \left\{ \begin{array}{r c l} F _ {x} = - \frac{g}{{K_{\text{s}}} ^ {2}} \frac{u_x \sqrt{u_x^2+u_y^2}}{{h} ^ {\frac{4}{3}}} - \frac{1}{\rho _ {\text{w}}} \frac{\partial {P} _ {\text{atm}}}{\partial x} + \frac{1}{h} \frac{{\rho } _ {\text{air}}}{{\rho } _ {\text{w}}}{C_{\text{D}}}{u} _ {\text{w} , x} \sqrt{{u} _ {\text{w} , x} ^ {2} + {u} _ {\text{w} , y} ^ {2}} \\ F _ {y} = - \frac{g}{{K_{\text{s}}} ^ {2}} \frac{u_y \sqrt{u_x^2+u_y^2}}{{h} ^ {\frac{4}{3}}} - \frac{1}{\rho _ {\text{w}}} \frac{\partial {P} _ {\text{atm}}}{\partial y} + \frac{1}{h} \frac{{\rho } _ {\text{air}}}{{\rho } _ {\text{w}}}{C_{\text{D}}}{u} _ {\text{w} , y} \sqrt{{u} _ {\text{w} , x} ^ {2} + {u} _ {\text{w} , y} ^ {2}} \end{array} \right. \end{aligned}$$

and:

• $\rho _{\text{w}}$/$\rho _{\text{air}}$ [kg m$^{{-3}}$] is the water/air density;

• $P_{\text{atm}}$ [Pa] is the atmospheric pressure;

• $u_{\text{w},x}$ and $u_{\text{w},y}$ [m s$^{{-1}}$] are the horizontal wind velocity components;

• $C_{\text{D}}$ [-] is the wind influence coefficient;

• $K_{\text{s}}$ [$\text{m}^{1/3}\,\text{s}^{-1}$] is the river bed and floodplain friction coefficient, using the Strickler formulation (Bernardara et al. 2010; Strickler 1981);

• $F_x$ and $F_y$ [m s$^{{-2}}$] are the horizontal components of external forces (friction, wind and atmospheric forces),

• h [m] is the water depth;

• $H=h+z_{\text{B}}$ [m] is the water level with $z_{\text{B}}$ the bottom level;

• $u_x$ and $u_y$ [m s$^{{-1}}$] are the horizontal components of velocity;

• $\nu _e$ [m$^{{2}}$ s$^{{-1}}$] is the water diffusion coefficient; and

• g [m $\text{s}^2$] is the standard gravity.

To solve the system of $\text{SWE}$ (1), initial conditions $h(x,y,t=0)=h_0(x,y)$, $u_x(x,y,t=0)=u_{x,0}(x,y)$ and $u_y(x,y,t=0)=u_{y,0}(x,y)$ are provided along with boundary conditions (BC) at the surface, the bottom, and at upstream and downstream frontiers: $h(x_{\text{BC}}, y_{\text{BC}}, t) = h_{\text{BC}}(t)$.

Due to the presence of non-linear terms in $\text{SWE}$, a closed-form solution of those equations is not available, except for very simplified cases. Therefore, they are discretized in space/time and their dynamic is numerically integrated using various schemes, e.g., method of characteristics (Chintu 1986), (discontinuous) Galerkin method (Eskilsson and Sherwin 2004), finite-element method (Hervouet 2007b), and finite-volume method (Anastasiou and Chan 1997), among others.

In this study, the $\text{Telemac-2D (T2D)}$¹ solver (Galland et al. 1991) based on a finite-element method is used (Hervouet 2007b). The equations are solved over a triangular mesh (see Fig. 1) featuring about 41,000 nodes, refined in the river bed and near the dykes. The discharge at Tonneins is imposed as the upstream boundary condition where the state-discharge rating curve at La Réole is imposed as the downstream boundary condition. A quasi-unsteady state is considered, which refers to the convergence to a steady state. Indeed, the upstream discharge is set as a ramp starting from the initial condition value (1500 $\text{m}^3\,\text{s}^{-1}$) linearly increasing to a constant $Q_{\text{up}}$ (denoted Q for simplicity in the following). Each T2D transient simulation is integrated over 3 days (53 time steps of 5000 s) so that a steady flow associated to Q is prescribed over the entire area at the end of Day 3.

The Strickler friction coefficient $K_{\text{s}}$ is uniformly defined over four areas as displayed in Fig. 2. The friction coefficient values result from a calibration procedure over a set of non-over flowing events. These are set, respectively, to 45, 38, and 40 $\text{m}^{1/3}\,\text{s}^{-1}$over upstream, middle and downstream parts of the river bed and 17 $\text{m}^{1/3}\,\text{s}^{-1}$over the floodplain. More details on the Garonne river $\text{T2D}$ model are given in Besnard and Goutal (2011).

Fig. 2

Position of the five uncertain hydraulic variables over the study area: upstream discharge $Q_{\text{up}}$, floodplain bottom friction $K_{\text{s},1}$, upstream, middle, and downstream river bed bottom friction $K_{\text{s},2}$, $K_{\text{s},3}$, and $K_{\text{s},4}$, respectively

2.3 Hydraulic uncertainty quantification

Typically, uncertainties are classified in two groups: epistemic uncertainty, resulting from incomplete knowledge of the correct settings of the model’s parameters, and aleatory uncertainty, resulting from the incomplete knowledge of the true value of the physical system and usually linked to the aleatory nature of the physics. In this study, both epistemic and aleatory uncertainties are considered by investigating the effect of uncertainties in friction coefficients and in the upstream discharge forcing on water depth for the transient flow simulated with $\text{T2D}$.

Indeed, the small number of discharge and water depth measurements limits the spatial description and calibration of the friction in the river bed and the floodplain, leading to discontinuous values between friction areas. The $K_{\text{s}}$ coefficients setting is indeed prone to uncertainty related to the zoning assumption, the calibration procedure, and the set of calibration events. This uncertainty is more significant in the floodplain area where there is no observing station. The limited number of measurements also yields errors in upstream inflow to the river as it relies on the use of a rating curve, usually extrapolated for high flow, to translate the inflow from the measured water depth.

In the $\text{GSA}$ sampling, the uncertainties in the friction coefficients and inflow are assumed to be independent. This assumption brings significant simplification with respect to reality where friction depends on water level. Yet it allows for a simplified description and calibration of friction coefficients, given the density of the observing network.

Classically, according expert knowledge, the friction coefficient is contained in an interval bounded by physical values depending on the roughness of soil material (Vazquez 2006; Goutal et al. 2018). Consequently, using the principle of maximum entropy (Shore and Johnson 1980), the distribution of the bounded Strickler friction coefficient is uniform. The boundaries of the uniform distribution are arbitrarily chosen $\pm 5$ from the calibrated value (Besnard and Goutal 2011) for the main channel roughness, as shown in Table 1. The Strickler friction coefficient of the floodplain is characterized by high uncertainty due to different land cover; therefore, the support of its distribution is wider and the boundaries have been chosen based on expert judgment. It should be noted that small Strickler’s coefficient values are considered to account for the presence of vegetation or urban areas in the floodplain.

The upstream discharge is estimated using an extrapolation of discharge frequency curves at high probabilities (75 %) of occurrence of floods with a return period of two years. Confidence intervals on the extrapolated value can be derived. In that case, when the mean value (discharge of the two-year return period) and the standard deviation (extrapolated from the confidence intervals) are known, the maximum entropy distribution is Gaussian (Shore and Johnson 1980). The upstream discharge is, therefore, assumed to follow a Gaussian distribution centered on its biennial value at Tonneins (3300 $\text{m}^{3}\,\text{s}^{-1}$), with a standard deviation of 1100 $\text{m}^{3}\,\text{s}^{-1}$. Moreover, to avoid unrealistic values, the $\text{PDF}$ is truncated at 600 $\text{m}^{3}\,\text{s}^{-1}$, corresponding to the annual mean discharge, and 6000 $\text{m}^{3}\,\text{s}^{-1}$, corresponding to the vicennial flood at Tonneins. The characteristics of the uncertain model inputs distributions are summarized in Table 1.

Table 1 Distribution of input variable uncertainties

3 Uncertainty propagation using reduced mixture of polynomial chaos expansions

3.1 Introduction to the rMPCE strategy

This section proposes a $\text{reduced Mixture of Polynomial Chaos Expansions (rMPCE)}$. This advanced surrogate model strategy aims to predict a $\text{2D}$ output field subject to non-linearities with respect to sub-divided input space variables. This strategy features an output reduction stage and a local regression stage via clustering and classification. These stages are detailed in the following after a general presentation of the strategy.

The direct model in denoted by ${\mathscr {M}}$. It computes a $p$ length real output $\mathbf{y}=\left( y_1,\ldots ,y_{p}\right)$ from a $d$ length real input $\mathbf{x}=\left( x_1,\ldots ,x_{d}\right)$. The learning set consists of n (input, output) samples, a.k.a., evaluations, snapshots, or observations, is denoted $\left\{ \mathbf{x}^{(i)},\mathbf{y}^{(i)}\right\} _{i\in {\mathscr {L}}}$ , where ${\mathscr {L}}=\{1,\ldots ,n\}$ is the set of indices of the n learning samples. The corresponding learning input matrix is denoted $\mathbf{X}$ with $[\mathbf{X}]_{ij} = x_j^{(i)}$ and the learning output matrix is denoted $\mathbf{Y}$ with $[\mathbf{Y}]_{ij} = y_j^{(i)}$. Lastly, underline is reserved for random variables (e.g., $\underline{u}$ or $\underline{U}$) while vectors and matrices are written in bold and in lower case (e.g., ${\mathbf{x}}$) and upper case (e.g., ${\mathbf{X}}$), respectively.

Transposed to the test case, these elements are defined as follows. The vector of upstream inflow and spatially defined friction coefficients $\mathbf{x}= (Q, K_{\text{s}})$ is denoted $\underline{\mathbf{x}}$ when treated as a random variable. $\mathbf{y}= \left( h_1,\ldots ,h_p\right)$ is the $\text{2D}$ water depth field at the $\text{T2D}$ simulation time step of interest T, discretized over a mesh of size p and denoted $\underline{\mathbf{y}}$ when treated as a random variable. The time step of interest corresponds to the flood’ s rising part; it occurs 1 day, 2 h, 21 min and 20 s after the beginning of the studied flood. At this simulation time, the classical $\text{PCE}$ leads to poor results (El Garroussi et al. 2020). Without loss of generality, the proposed strategy remains applicable for all time steps.

The $\text{rMPCE}$ strategy is a two-stage process as illustrated in Fig. 3:

• 1. an offline learning stage that builds the model from a learning database,

• 2. an online prediction stage that evaluates the model to issue a prediction.

Moreover, the hyper-parameters of the surrogate model can be optimized in an outer loop around the learning stage in order to increase its accuracy measured on a validation database.

The learning stage developed in algorithm 1 features four main steps:

• 1. Reduction of the output variable dimension from $p$ to ${\tilde{p}}<p$: the original space of dimension $p$ is replaced with a latent space of dimension ${\tilde{p}}$ built from the learning output matrix $\mathbf{Y}$. The learning output matrix $\mathbf{Y}\in {\mathscr {M}}_{n,p}({\mathbb {R}})$ is then replaced with the reduced learning output matrix ${\tilde{\mathbf{Y}}}\in {\mathscr {M}}_{n,{\tilde{p}}}({\mathbb {R}})$, which is computationally easier to handle. This reduction step is called encoding while the reverse is called decoding and maps from the latent space ${\mathbb {R}}^{{\tilde{p}}}$ to the original one ${\mathbb {R}}^{p}$.

• 2. Unsupervised clustering of the n learning output data into K groups, a.k.a., clusters: the reduced learning output matrix ${\tilde{\mathbf{Y}}}$ is split into K local reduced learning output matrix ${\tilde{\mathbf{Y}}}^{(k)}\in {\mathscr {M}}_{n_k,{\tilde{p}}}({\mathbb {R}}),~k\in \{1,\ldots ,K\}$, where the $n_k$ observations in ${\tilde{\mathbf{Y}}}^{(k)}$ share common patterns; ${\mathscr {L}}_k\subset {\mathscr {L}}$ is the sub-set of the learning indices of the samples belonging to the kth cluster, with $\cup _{k=1}^K {\mathscr {L}}_k = {\mathscr {L}}$ and ${\mathscr {L}}_k\cap {\mathscr {L}}_{k'}=\emptyset$ for any $k'\ne k$.

• 3. Classification of the input space into K subspaces, based on the clustering results:

  • This step defines the boundaries of separation between the different classes within the input space.

  • This step provides a classifier taking a $\mathbf{x}$ as input and returning its degree of membership $C_k(\mathbf{x})$ to the kth class, with $C_k(\mathbf{x})\ge 0$ and $\sum _{k=1}^KC_k(\mathbf{x})=1$ by construction.

• 4. Construction of a $\text{2D}$-functional output $\text{PCE}$ surrogate for each cluster; e.g., for the kth cluster:

  • The dimension of the local output matrix $\mathbf{Y}^{(k)}=\left( y_j^{(i)}\right) _{\begin{array}{c} i\in {\mathscr {L}}_k\\ 1\le j \le p \end{array}}$ related to the kth cluster is reduced from $p$ to ${\tilde{p}}$ and denoted $\widetilde{\mathbf{Y}^{(k)}}$.

  • A multi-output $\text{PCE}$ is built from the local learning input matrix $\mathbf{X}^{(k)}=\left( x_j^{(i)}\right) _{\begin{array}{c} i\in {\mathscr {L}}_k\\ 1\le j \le d \end{array}}$ and the reduced local output matrix $\widetilde{\mathbf{Y}^{(k)}}$.

  • The local surrogate model maps from the input space to the local latent space and requires a decoding step to go back to the original local output space.

The prediction phase predicts the water depth ${\hat{\mathbf{y}}}$ of a given input $\mathbf{x}$. First, the degree of membership to the K classes is computed from the classifier: $C_1(\mathbf{x}),\ldots ,C_K(\mathbf{x})$. Then, the local $\text{PCE}$ models are evaluated at $\mathbf{x}$. Lastly, the global prediction in the latent space is a convex combination of the local ones:

$$\hat{\tilde{\mathbf{y}}}=\sum_{k=1}^KC_k(\mathbf{x})\text{PCE}_k(\mathbf{x})$$

and $\hat{{\tilde{\mathbf{y}}}}$ is expanded to the original output space, resulting in the prediction ${\hat{\mathbf{y}}}$.

The current study is limited to hard classification, where a single class is attached to a given $\mathbf{x}$. This implies that $C_k:{\mathbb {R}}^d\rightarrow \{0,1\}$ instead of $C_k:{\mathbb {R}}^d\rightarrow [0,1]$. This results in the evaluation of a single local $\text{PCE}$; more precisely, the one indexed by ${\hat{k}}\in \{k:~C_k(\mathbf{x})=1\}$.

Fig. 3

Flowchart of the $\text{rMPCE}$ surrogate model: learning phase (left hand side) and prediction phase (right hand side)

Fig. 4

Output space dimension reduction consists of encoding the output variable into a reduced dimension space, called the latent space. The initial water depth vector is reconstructed as the reduced space vector is decoded onto the original output space

3.2 Dimension reduction

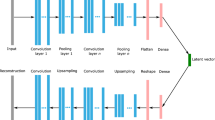
In spite of recent advances that propose to estimate the $\text{PCE}$ coefficients on a sparse grid (Eldred and Burkardt 2009) or with basis adaptive methods (Li and Ghanem 1998), the formulation of a surrogate model remains computationally expensive, especially when the dimension of the output is large. A common strategy applied here, is to build a surrogate model in a reduced output space, evaluating it for an input value, and then projecting its output value onto the original output space. In this study, two dimension reduction methods are investigated: $\text{PCA}$ and $\text{AE}$. Both methods are applied on $\mathbf{Y}\in {\mathscr {M}}_{n,p}({\mathbb {R}})$, the matrix of the n evaluations of the $p$-length output $\mathbf{y}$ as illustrated in Fig. 3.

In this study, the output $\mathbf{y}$ is the water depth field discretized over the $\text{T2D}$ unstructured mesh over the Garonne area. The output matrix $\mathbf{Y}$ is encoded onto a reduced latent space (see Fig. 4) as the matrix of the n evaluations of the ${\tilde{p}}$-length reduced output ${\tilde{\mathbf{y}}}$, ${\tilde{\mathbf{Y}}}\in {\mathscr {M}}_{n,{\tilde{p}}}({\mathbb {R}})$, and is further used for the clustering stage. Moreover, any element of the latent space can be decoded onto the original output space. In particular, the initial matrix $\mathbf{Y}$ can be reconstructed, with some loss of information quantifying the performance of the reduction dimension technique.

3.2.1 Principal components analysis

$\text{PCA}$ (Wold et al. 1987; Abdi and Williams 2010) is a popular data processing and dimension reduction technique with numerous applications in hydraulics (El Garroussi et al. 2019; Noori et al. 2010). $\text{PCA}$ seeks an orthogonal latent space spanned by the space directions of greatest variance, expressed as linear combinations of the original variables. $\text{PCA}$ can be computed via the $\text{Singular Value Decomposition (SVD)}$ (Abdi and Williams 2010) of the matrix $\mathbf{Y}\in {\mathscr {M}}_{n,p}({\mathbb {R}})$.

The $\text{SVD}$ of $\mathbf{Y}$ reads $\mathbf{Y}= {\mathbf{U}}{\mathbf{D}}{\mathbf{V}}^\top$, where ${\mathbf{U}}$ is an $n\times n$ orthogonal matrix, ${\mathbf{V}}$ is a $p\times p$ orthogonal matrix, and ${\mathbf{D}}$ is a rectangular diagonal matrix with non-negative real numbers on the diagonal. Columns of ${\mathbf{U}}{\mathbf{D}}$ are called principal components (PCs) and form an orthonormal basis in which the n samples $\mathbf{y}^{(1)},\ldots ,\mathbf{y}^{(n)}$ are linearly uncorrelated. Then, the projection of the latter on the ${\tilde{p}}\le p$ first PCs reads: ${\tilde{\mathbf{Y}}}=[{\mathbf{U}}]_{:,1:{\tilde{p}}}[{\mathbf{D}}]_{1:{\tilde{p}},1:{\tilde{p}}}\in {\mathscr {M}}_{n,{\tilde{p}}}({\mathbb {R}})$, thus reducing the output data dimension from $p$ to ${\tilde{p}}$. The column of V displays the corresponding weights associated to the PCs and any observation ${\tilde{\mathbf{y}}}$ in the latent space can be projected onto the original space: $\mathbf{y}=\left[ {\mathbf{V}}^\top \right] _{1:p,1:{\tilde{p}}}{\tilde{\mathbf{y}}}$.

$\text{PCA}$ allows summarizing data when the interesting patterns increase the variance of projections onto orthogonal components. But $\text{PCA}$ also has limitations that are developed in Lever et al. (2017): the underlying structure of the data must be linear, patterns that are highly correlated may be unresolved because all modes are uncorrelated, and the goal is to maximize variance and not necessarily to find clusters.

3.2.2 Autoencoder

In order to deal with non-linear structure in the data matrix $\mathbf{Y}$, the use of an $\text{AE}$ (Hinton and Salakhutdinov 2006; van der Maaten et al. 2007) for dimension reduction was investigated. It relies on an unsupervised artificial neural network that encodes a variable of dimension $p$ into a latent variable of dimension ${\tilde{p}}\le p$ and decodes this latent one to a recovered variable of dimension $p$, as close as possible to the original. The latent space is often called a bottleneck because of the particular shape of this neural network, illustrated in Fig. 4. In this paper, an $\text{AE}$ with a symmetrical architecture (Nowlan and Hinton 1992) was used in order to reduce the number of parameters to be optimized in the network; it is based on encoder-decoder weight sharing. Steps needed for encoding and decoding are presented in Algorithms 3 and  4, respectively. An $\ell$-depth encoder maps $\mathbf{y}\in {\mathbb {R}}^{p}$ onto the latent space ${\mathbb {R}}^{{\tilde{p}}}$ using $\ell$ successive encoding transformations:

$$\begin{aligned} \forall l\in \{1,\ldots ,\ell \},~ \varvec{\varphi }_l = \sigma _l\left( {\mathbf{w}}_l\varvec{\varphi }_{l-1}+\varvec{b}_l\right) \in {\mathbb {R}}^{p_l} \end{aligned}$$

with $\varvec{\varphi }_0 = \mathbf{y}$. ${\mathbf{w}}_l\in {\mathscr {M}}_{p_l,p_{l-1}}({\mathbb {R}})$ is a matrix of weight parameters, $\varvec{b}_l\in {\mathbb {R}}^{p_l}$ is a vector of bias parameters, and $\sigma _l:{\mathbb {R}}^{p_l}\mapsto {\mathbb {R}}^{p_l}$ is an activation function. The $\ell$ successive layers are of decreasing dimension: $p=p_0> p_l> \ldots > p_\ell ={\tilde{p}}$.

Then, the decoder maps the latent variable $\varvec{\varphi }_{\ell }\in {\mathbb {R}}^{{\tilde{p}}}$ onto the original space, using $\ell$ successive decoding transformations using the transposes of the encoder weight matrices as weight matrices for the decoder:

$$\begin{aligned} \forall l\in \{1,\ldots ,\ell \},~\varvec{\varphi }_{\ell +l} = \sigma _{\ell -l}\left( {\mathbf{w}}_{\ell -l+1}^T\varvec{\varphi }_{\ell +l-1}+\varvec{b}_{\ell +l}\right) \in {\mathbb {R}}^{p_{\ell -l}}. \end{aligned}$$

with $\sigma _0$ being the identity function.

Thus, an autoencoder $\phi _{\ell }=\phi _{\text{d},\ell }\circ \phi _{\text{e},\ell }$ is a sequence of $2\ell$ transformations, the first $\ell$ performing an encoding $\phi _{\text{e},\ell }:{\mathbb {R}}^{p}\mapsto {\mathbb {R}}^{{\tilde{p}}}$ and the next $\ell$ a decoding $\phi _{\text{d},\ell }:{\mathbb {R}}^{{\tilde{p}}}\mapsto {\mathbb {R}}^{p}$. The learning phase seeks the weights and biases minimizing the error $\Vert \phi _{\ell }(\mathbf{Y})-\mathbf{Y}\Vert _2^2$ while the use phase expands the dimension of a vector ${\tilde{\mathbf{y}}}\in {\mathbb {R}}^{{\tilde{p}}}$ with the decoding function: $\phi _{\text{d},\ell }({\tilde{\mathbf{y}}})\in {\mathbb {R}}^{p}$. These weights and biases are usually initialized randomly and updated during training through the gradient backpropagation technique (Amari 1993).

3.3 Clustering and classification tools

Clustering is an unsupervised learning process that classifies data for which variables are observed via labels by using similarity measures. This approach is widely used for the purposes of data visualization, data compression, data denoising, or to better understand the correlations present in the data. In the present work, clustering methods are applied to the matrix ${\tilde{\mathbf{Y}}}$ resulting from the output dimension reduction stage as shown in Fig. 3. It seeks to group the n dimension-reduced observations $\left\{ {\tilde{\mathbf{y}}}^{(1)},\ldots ,{\tilde{\mathbf{y}}}^{(n)}\right\}$ into K clusters and create the corresponding sub-sets of learning indices ${\mathscr {L}}_1, \dots , {\mathscr {L}}_K$, with $\cup _{k=1}^K{\mathscr {L}}_k={\mathscr {L}}$ and ${\mathscr {L}}_k\cap {\mathscr {L}}_{k'}=\emptyset$ if $k\ne k'$. The kth cluster is associated with the label k, also known as the index or class. Then, these labels are mapped to the input space, here upstream forcing and bottom friction, to train a classifier $\mathbf{x}\rightarrow \left( C_1(\mathbf{x}),\ldots ,C_K(\mathbf{x})\right)$ mapping from ${\mathbb {R}}^{d}$ to $[0,1]^K$ to identify the boundaries between these clusters in the input space and to give the degree of membership of an input $\mathbf{x}$ to each of the corresponding classes. In the case of hard classification, only one class is associated to the input $\mathbf{x}$ and so the classifier maps from ${\mathbb {R}}^{d}$ to $\{0,1\}^K$.

3.3.1 Clustering

Formally, clustering involves partitioning the set of observations ${\mathscr {L}}$ into K disjoint sets ${\mathscr {L}}_1, \dots , {\mathscr {L}}_K$ by returning labels indicating the index of the class of membership of each observation. Both k-means (Likas et al. 2003) and Gaussian mixture models (Mclachlan and Basford 1988) clustering algorithms are investigated in this paper. Both require prescribing the number of clusters K. The latter can either be prescribed manually based on the user’s knowledge or estimated from a selection criteria such as the silhouette criterion (Rousseeuw 1987) that evaluates the separation distance between the resulting clusters. For a given observation indexed by i, belonging to the kth cluster, the silhouette criterion reads:

$$\begin{aligned} s_k(i) = \frac{b_k(i) - a_k(i)}{\max (a_k(i), b_k(i))} \end{aligned}$$

(2)

where:

• $a_k(i)=\frac{1}{|{\mathscr {L}}_k|- 1}\sum _{j \in {\mathscr {L}}_k, j \ne i} d(i,j)$ is the average distance of the ith observation to all other observations in the kth cluster, with $d(i,j)=\left\| {\tilde{\mathbf{y}}}^{(i)}-{\tilde{\mathbf{y}}}^{(j)}\right\| _2$,

• $b_k(i)=\min _{l \ne k} \frac{1}{|{\mathscr {L}}_l|} \sum _{j \in {\mathscr {L}}_l} d(i,j)$ is the smallest mean distance of the ith observation to all observations in any other cluster, of which i is not a member,

• $|{\mathscr {S}}|$ is the cardinal number of the set ${\mathscr {S}}$.

Therefore, if i has been properly assigned, then the score $s_k$ is equal to 1. A score of 0 means that clusters are overlapping, and a score less than 0 means that i was assigned to the wrong cluster.

The k-means algorithm partitions the n observations into K clusters in which each observation belongs to the cluster with the nearest mean. It seeks to minimize the variance within the clusters:

$$\begin{aligned} \mathop {\text{argmin}}\limits _{{\mathscr {L}}_1,\ldots ,{\mathscr {L}}_K} \sum _{k=1}^{K}\sum _{i \in {\mathscr {L}}_k} \left\| {\tilde{\mathbf{y}}}^{(i)}-\varvec{\mu }_k\right\| _2, \end{aligned}$$

(3)

where $\varvec{\mu }_k=|{\mathscr {L}}_k|^{-1}\sum _{i\in {\mathscr {L}}_k}{\tilde{\mathbf{y}}}^{(i)}$ is the empirical mean of ${\tilde{\mathbf{y}}}$ in cluster ${\mathscr {L}}_k$.

Given an initial set of K means $\varvec{\mu }_1^{(1)},...,\varvec{\mu }_K^{(1)}$, the algorithm iterates the two following steps, presented at iteration t, until convergence:

• Assignment step: assign each observation to the cluster with the nearest mean, i.e., $\forall k\in \{1,\ldots ,K\}$:

  $$\begin{aligned} {\mathscr {L}}_k^{(t)}= & {} \left\{ i: i\in {\mathscr {L}}\left| \right. \forall j\in \{1,\ldots ,K\},~ \left\| {\tilde{\mathbf{y}}}^{(i)} - \varvec{\mu }_k^{(t)}\right\| _2 \right. \\\le & {} \left. \left\| {\tilde{\mathbf{y}}}^{(i)} - \varvec{\mu }_j^{(t)}\right\| _2 \right\} . \end{aligned}$$

• Update step: recalculate means for observations assigned to each cluster, i.e., $\forall k\in \{1,\ldots ,K\}$:

  $$\begin{aligned} \varvec{\mu }_k^{(t+1)} = \frac{1}{\left| {\mathscr {L}}_k^{(t)}\right| } \sum _{i \in {\mathscr {L}}_k^{(t)}} {\tilde{\mathbf{y}}}^{(i)}. \end{aligned}$$

Because k-means struggles with clusters of varying density and with outliers, a clustering algorithm based on mixture of distributions was investigated here.

The Gaussian Mixture Model (GMM) relies on the assumption that the empirical distribution of the n observed vectors ${\tilde{\mathbf{y}}}^{(1)},\ldots ,{\tilde{\mathbf{y}}}^{(n)}$ is close to a mixture of K Gaussian distributions. Then, each observation is associated to the most likely Gaussian distributions, which then defines its cluster. The $\text{GMM}$ is a mixture of K multivariate normal distributions. The kth distribution is characterized by its mean $\varvec{\mu }_k$, covariance matrix $\varvec{\varSigma }_k$, and weight $\omega _k$. The $\text{PDF}$ of this $\text{GMM}$ reads:

$$\begin{aligned} \pi ({\tilde{\mathbf{y}}}) = \sum _{k=1}^K \omega _k\pi _{{\mathscr {G}}}({\tilde{\mathbf{y}}};\varvec{\mu }_k,\varvec{\varSigma }_k), \end{aligned}$$

(4)

where $\pi _{{\mathscr {G}}}({\tilde{\mathbf{y}}};\varvec{\mu },\varvec{\varSigma })=\frac{1}{(2\pi )^{{\tilde{p}}/2}\Vert \varvec{\varSigma }\Vert ^{1/2}}\exp \left( -\frac{1}{2}\left( {\tilde{\mathbf{y}}}-\varvec{\mu }\right) ^\top \varvec{\varSigma }^{-1}\left( {\tilde{\mathbf{y}}}-\varvec{\mu }\right) \right)$ is the $\text{PDF}$ of the Gaussian distribution with mean $\varvec{\mu }$ and covariance matrix $\varvec{\varSigma }$.

The $\text{GMM}$ parameters $\left\{ \omega _k,\varvec{\mu }_k,\varvec{\varSigma }_k\right\} _{1\le k\le K}$ are estimated iteratively using an Expectation Maximization algorithm (Moon 1996; Bettebghor et al. 2011) until convergence of the likelihood. The expectation of the posterior probability $\lambda _k$ of belonging to cluster ${\mathscr {L}}_k$ can be expressed with Bayes’ theorem:

$$\begin{aligned} \lambda _k({\tilde{\mathbf{y}}}) = \frac{ \omega _k\pi _{{\mathscr {G}}} \left( {\tilde{\mathbf{y}}};\varvec{\mu }_k,\varvec{\varSigma }_k\right) }{\sum _{j=1}^K\omega _j\pi _{{\mathscr {G}}} \left( {\tilde{\mathbf{y}}};\varvec{\mu }_j,\varvec{\varSigma }_j\right) }. \end{aligned}$$

This is the E-step, where E stands for Expectation. Then, the mixture parameters $\varvec{\mu }_k$ and $\varvec{\varSigma }_k$ can be re-estimated by maximizing $\pi _{{\mathscr {G}}}({\tilde{\mathbf{y}}};\varvec{\mu }_k,\varvec{\varSigma }_k)$:

$$\begin{aligned} \varvec{\mu }_k= & {} \frac{\sum _{i\in {\mathscr {L}}} \lambda _k\left( {\tilde{\mathbf{y}}}^{(i)}\right) {\tilde{\mathbf{y}}}^{(i)}}{\sum _{j\in {\mathscr {L}}} \lambda _k\left( {\tilde{\mathbf{y}}}^{(j)}\right) },~~~~ \\ \varvec{\varSigma }_k= & {} \frac{\sum _{i\in {\mathscr {L}}}\lambda _k\left( {\tilde{\mathbf{y}}}^{(i)}\right) \left( {\tilde{\mathbf{y}}}^{(i)}-\varvec{\mu }_k\right) \left( {\tilde{\mathbf{y}}}^{(i)} - \varvec{\mu }_k\right) ^\top }{\sum _{j\in {\mathscr {L}}}\lambda _k\left( {\tilde{\mathbf{y}}}^{(j)}\right) },\\ \omega _k= & {} \frac{1}{n}\sum _{i\in {\mathscr {L}}}\lambda _k\left( {\tilde{\mathbf{y}}}^{(i)}\right) . \end{aligned}$$

This is the M-step, where M stands for Maximization. The cluster of each observation i can be determined using Eq .4.

Contrary to the k-means grouping, the $\text{GMM}$ grouping can be either soft or hard. Soft grouping means that each observation i is assigned to each cluster in a weighted manner while hard grouping means that each observation i belongs to only one cluster. In this study, a hard splitting is considered: any point ${\tilde{\mathbf{y}}}$ is assigned to cluster $\arg \max _k \pi _{{\mathscr {G}}}({\tilde{\mathbf{y}}};\varvec{\mu }_k,\varvec{\varSigma }_k)$.

The clustering assigns each of the n learning observations a label among $\{1,\ldots ,K\}$. The classification uses these labels to draw the boundaries between classes in the input space.

3.3.2 Classification

Classification is a supervised learning process based on labels and derived from the clustering that groups observations into classes with respect to their labels, and identifies the boundaries between these classes.

The clustering has annotated each of the n learning observations with a label. According to these labels, the input variable, here, the liquid boundary condition and the friction of the river bottom $\mathbf{x}^{(i)} =\left[ Q^{(i)}, K_{\text{s}}^{(i)}\right]$, is associated to $k$th cluster. The degree of membership of $\mathbf{x}^{(i)}$ to the kth cluster is written through the corresponding variable $c_i$, such as $c_i = k$.

Here, a multi-class classification algorithm is considered: support vector machines (Cortes and Vapnik 1995).

Support Vector Machines (SVM) aim at solving classification problems by finding good decision boundaries between two classes within the input space. For multi-class classification ($K > 2$), the same principle is used. The multi-class problem is broken down to multiple binary classification cases called one-vs-one. $\text{SVM}$ proceed to find the decision boundaries in two steps:

• Mapping step: Input data are mapped to a new high-dimension representation (target representation space) where the classification problem becomes simpler and where the decision boundary can be expressed as a hyperplane.

• Maximizing the margin step: The separation hyperplane (decision boundary) is computed by maximizing the distance between the hyperplane and the closest data points from each class.

Because the mapping step is often computationally intractable, a “kernel trick”  (Vapnik 1995; Scholkopf et al. 1999) is used. It is based on a kernel function k that maps any two input data $\left\{ \mathbf{x}^{(i)}, \mathbf{x}^{(j)}\right\}$ to the distance between these data in the target representation space, completely bypassing the explicit computation of the new representation. The kernel trick is also used to develop non-linear generalization of the $\text{SVM}$. Let ${\mathscr {H}}$ be a k-kernels space. A general $\text{SVM}$ is a discriminator of the form $D(\mathbf{x}) = c_i(f(\mathbf{x}) + b)$ where $f \in {\mathscr {H}}$ and $b \in {\mathbb {R}}$ are given by solving the general problem for a given $C \ge 0$:

$$\begin{aligned} \left\{ \begin{array}{lll} \min _{f \in {\mathscr {H}}, b \in {\mathbb {R}}} \ \frac{1}{2} \Vert f\Vert _{{\mathscr {H}}}^2 + C \sum _{i=1}^{n}\zeta _i , \\ c_i\left( f(\mathbf{x}^{(i)}\right) + b) \ge 1 - \zeta _i, \;\ \forall i \in \{1,\ldots ,n\}, \\ 0 \le \zeta _i, \;\ \forall i \in \{1,\ldots ,n\}. \end{array} \right. \end{aligned}$$

(5)

where $\zeta _i$ model the potential errors when the margin constraint is not verified. The decision functions of the following form are obtained:

$$\begin{aligned} f(\mathbf{x}) = \sum _{i \in {\mathscr {A}}} \alpha _i c_i k\left( \mathbf{x}, \mathbf{x}^{(i)}\right) \end{aligned}$$

(6)

where ${\mathscr {A}}$ is the constraints set and $\alpha _i$ are solutions of the following quadratic programming problem:

$$\begin{aligned} \left\{ \begin{array}{lll} \min _{{\alpha } \in {\mathbb {R}}^n} \ \frac{1}{2} \sum _{i, j=1}^{n}\alpha _i \alpha _j c_i c_j k\left( \mathbf{x}^{(i)}, \mathbf{x}^{(j)}\right) - \sum _{i=1}^n \alpha _i , \\ 0 \le \alpha _i \le C, \; \forall i \in \{1,\ldots ,n\}, \\ \sum _{i=1}^{n}\alpha _i c_i = 0. \end{array} \right. \end{aligned}$$

(7)

The main advantage of the $\text{SVM}$ algorithm is its capability to deal with a wide variety of classification problems including high-dimension and non-linearly separable problems. One of its major drawbacks is that it requires many parameters to set correctly (under Scikit learn library (Pedregosa et al. 2011)) to attain good classification results.

3.4 Polynomial chaos expansions

The $\text{PCE}$ surrogate model is built within each of the K classes in parallel (see Fig. 3).

Let us consider the construction of a $\text{PCE}$ within a single class and a computational model of interest ${\mathscr {M}}: {\mathscr {D}}_{x} \subset {\mathbb {R}}^{d} \mapsto {\mathbb {R}}$, taking the vector $\mathbf{x}=(x_1,\ldots ,x_{d})\in {\mathscr {D}}_{x}$ as input and returning $\mathbf{y}\in {\mathbb {R}}^{p}$ as output: $\mathbf{y}:={\mathscr {M}}(\mathbf{x})$. In the following, for the sake of simplicity, $\mathbf{y}$ is assumed to be a scalar ($p=1$). In the case of a vectorial response ($p>1$), the following derivations hold component-wise.

In uncertainty quantification, the deterministic input vector $\mathbf{x}$ is replaced by the associated random variable $\underline{\mathbf{x}}= \left( \underline{x}_1,\ldots ,\underline{x}_{d}\right)$ and $\underline{\mathbf{y}}= {\mathscr {M}}(\underline{\mathbf{x}})$ is in turn a random variable. $\underline{\mathbf{x}}$ is defined over the probability space $({\mathscr {D}}_{\mathbf{x}}, {\mathscr {F}}, {\mathbb {P}})$ and $f_{\underline{\mathbf{x}}}$ is its joint $\text{PDF}$. We seek to quantify the uncertainty in $\underline{\mathbf{y}}$ due to uncertainty in $\underline{x}_1,\ldots ,\underline{x}_{d}$. We assume that the random input variables are independent so as to comply with the assumption required for the polynomial chaos expansion theory. We also consider that the scalar output $\underline{y}$ is a second order random variable, i.e, ${\mathbb {E}}\left[ \underline{y}^2\right] < +\infty$.

Under the previous assumptions, the random variable $\underline{y}$ can be expressed as a generalized polynomial chaos expansion (Xiu and Karniadakis 2002; Soize and Ghanem 2004):

$$\begin{aligned} \underline{y}= \sum _{\alpha \in {\mathbb {N}}^{d}} \gamma _\alpha \psi _\alpha ( \underline{\mathbf{x}} ), \end{aligned}$$

(8)

where $\psi _\alpha (\mathbf{x}) = {\prod _{i=1}^{d}\psi _{i,\alpha _i}(x_i)}$ is a tensor product of univariate orthonormal polynomials, i.e. ${\mathbb {E}}\left[ \psi _{i,j}(\underline{x}_i)\psi _{i,k}(\underline{x}_i)\right] =\int _{D_{x_i}}\psi _{i,j}(x_i)\psi _{i,k}(x_i)f_{\underline{x}_i}(x_i)dx_i=\delta _{jk}$. $\gamma _\alpha$ is the deterministic coefficient associated with $\psi _{\alpha }$. ${\alpha } = (\alpha _1, ..., \alpha _d)$ is the multi-index vector with $\alpha _i$ the degree of the univariate polynomial $\psi _{i,\alpha _i}$ and $\gamma _{\alpha _i}=\left\langle \underline{y}, \psi _{\alpha _i}^i(\underline{\mathbf{x}})\right\rangle =\int _{D_{x_i}}\psi _{i,\alpha _i}(x_i) {\mathscr {M}}(\mathbf{x})f_{\underline{x}_i}(x_i)dx_i$.

Xiu and Karniadakis (2002) show the set of polynomials that provides an optimal basis for the different continuous probability distributions of the input variable $\underline{\mathbf{x}}$. It is derived from the family of hyper-geometric orthogonal polynomials known as the Askey scheme (Dongbin and Karniadakis 2003). The optimality of these basis selections derives from orthogonality with respect to weighting functions that correspond to the $\text{PDF}$s of the continuous distributions when placed in a standard form. For instance, when $\underline{x}_i$ is a standard uniform (resp. standard normal) random variable, the corresponding basis comprises orthonormal Legendre (resp. Hermite) polynomials (Abramowitz et al. 1988).

3.4.1 Truncated polynomial chaos expansion

In practice, it is not tractable to use an infinite series expansion. An approximate representation is obtained with a truncation:

$$\begin{aligned} {\mathscr {M}}_{{\mathscr {A}}}(\underline{\mathbf{x}})= \sum _{\alpha \in {\mathscr {A}}}\gamma _\alpha \psi _\alpha (\underline{\mathbf{x}}), \end{aligned}$$

(9)

with ${\mathscr {A}} \in {\mathbb {N}}^{d}$ the truncation set of size m, i.e., $\gamma _{{\mathscr {A}}}=\left( \gamma _{\alpha }\right) _{\alpha \in {\mathscr {A}}}\in {\mathbb {R}}^m$ and $\epsilon _{{\mathscr {A}}}(\underline{\mathbf{x}})=\sum _{\alpha \in {\mathbb {N}}^{d}\setminus {\mathscr {A}}} \gamma _\alpha \psi _\alpha (\underline{\mathbf{x}})$ the truncation-induced error. Blatman and Sudret (2011) introduced a hyperbolic truncation scheme that selects all polynomials satisfying the following criterion:

$$\begin{aligned} {\mathscr {A}}_{q}^{d,P} = \left\{ \alpha \in {\mathbb {N}}^{d}: \Vert \alpha \Vert _q = \left( \sum _{i=1}^{d}\alpha _i^q \right) ^{\frac{1}{q}} \le P \right\} , \end{aligned}$$

with P being the highest total polynomial degree and $0 < q \le 1$ being the parameter determining the hyperbolic truncation surface. To further reduce the number of candidate polynomials, one can additionally apply a low-rank truncation scheme that reads (Sudret 2015):

$$\begin{aligned} {\mathscr {A}}_{q}^{d,P,r} = \left\{ \alpha \in {\mathbb {N}}^{d}: \Vert \alpha \Vert _0 = \sum _{i=1}^{d} \mathbb {1}_{\alpha _i > 0} \le r, \Vert \alpha \Vert _q \le P \right\} , \end{aligned}$$

where $\Vert \alpha \Vert _0$ is the rank of the multivariate polynomial $\psi _\alpha$, defined as the total number of non-zero components $\alpha _i, i = 1,...,d$. In this study, the prescribed rank r is chosen as a small integer value, e.g., $r = 2,3$  (Mai et al. 2016) and the polynomial degree P is varied from 2 to 9, and the value retained is the one that minimizes the prediction error.

3.4.2 Estimation of coefficients

The computation of the coefficients $\gamma _{\alpha }$ in Eq. 9 can be conducted by means of intrusive (i.e, Galerkin scheme) or non-intrusive approaches (e.g., stochastic collocation, projection, regression methods) (Blatman et al. 2007). In this paper, we consider a standard regression method based on the minimization of a mean squared learning error (Baudin et al. 2017). In practice, the coefficients are obtained by minimizing an empirical mean over a learning database:

$$\begin{aligned} \hat{\varvec{\gamma }}_{{\mathscr {A}}} = \mathop {\text{argmin}}\limits _{\varvec{\gamma }_{{\mathscr {A}}} \in {\mathbb {R}}^m} \sum _{i\in {\mathscr {L}}}\left( {\mathscr {M}}\left( \mathbf{x}^{(i)}\right) - \sum _{\alpha \in {\mathscr {A}}} \varvec{\gamma }_\alpha \psi _\alpha \left( \mathbf{x}^{(i)}\right) \right) ^2, \end{aligned}$$

(10)

where $\left\{ \mathbf{x}^{(i)}, i \in {\mathscr {L}}\right\}$ is a $\text{Design Of Experiment (DOE)}$ obtained with a random sampling of the input random vector. For that purpose, the computational model ${\mathscr {M}}$ is integrated for each point of the $\text{DOE}$, yielding the learning output matrix $\mathbf{Y}$. Equation 10 basically represents the problem of estimating the parameters of a linear regression model, for which the least squares solution reads $\hat{\varvec{\gamma }}_{{\mathscr {A}}} = \left( {\mathbf{A}}^T.{\mathbf{A}} \right) ^{-1}{\mathbf{A}}^T\mathbf{Y}$, where ${\mathbf{A}}= \left( \psi _j\left( \mathbf{x}^{(i)}\right) \right) _{\begin{array}{c} i\in {\mathscr {L}}\\ 1\le j\le m \end{array}}$ is the information matrix containing the evaluation of the polynomial basis functions over the $\text{DOE}$. Hence, the approximated output variable ${\hat{\underline{y}}}$ can be expressed as follows:

$$\begin{aligned} {\hat{\underline{y}}} = \sum _{\alpha \in {\mathscr {A}}} {\hat{\gamma }}_\alpha \psi _\alpha ( \underline{\mathbf{x}} ). \end{aligned}$$

(11)

At the prediction phase, only the $\text{PCE}$ related to the class to which the new observation belongs is evaluated (hard evaluation).

3.5 Surrogate model validation metrics

In the present study, two standard metrics are used to measure the quality of the $\text{rMPCE}$ surrogate model at T: the $Q_2$ predictive coefficient and the $\text{Root Mean Squared Error (RMSE)}$. The validation is carried out over an (input, output) validation database ${\mathscr {D}}_v$ of size $n_v$.

3.5.1 Predictive coefficient

At the kth mesh node, the $Q_2$ predictive coefficient is defined as:

$$\begin{aligned} Q_{2,k} = 1 - \frac{\text{MSE}_k({\mathscr {D}}_v)}{\text{MSE}_k({\mathscr {D}}_v;\text{mean})}, \end{aligned}$$

(12)

where $\text{MSE}_k({\mathscr {D}}_v) = {n_v}^{-1}\sum _{i = 1}^{{n_v}}\left( \underline{y}^{(n+i)}_k - {\hat{\underline{y}}}^{(n+i)}_k\right) ^2$

and $\text{MSE}_k({\mathscr {D}}_v; \text{mean}) = n_v^{-1}\sum _{i = 1}^{n_v}\left( \underline{y}^{(n+i)}_k - {\overline{\underline{y}}}_k\right) ^2$ is the MSE of the averaging model returning the mean of the learning outputs whatever the input parameter value.

The global counterpart of $\text{MSE}({\mathscr {D}}_v; \text{mean})$ is computed spatially by averaging over the p elements of the output vector:

$$\begin{aligned} \text{MSE}({\mathscr {D}}_v; \text{mean}) = p^{-1}\sum _{k=1}^p\text{MSE}_k({\mathscr {D}}_v; \text{mean}). \end{aligned}$$

Thus, the global counterpart of $Q_{2}$ is:

$$\begin{aligned} Q_{2} = 1 - \frac{\text{MSE}({\mathscr {D}}_v)}{\text{MSE}({\mathscr {D}}_v;\text{mean})}. \end{aligned}$$

(13)

The predictive coefficient measures the performance of the surrogate model with respect to the data average. When $Q_2$ is lower than (resp. equal to) zero, the surrogate is worse than (resp. equal to) the learning output values average. When $Q_2$ is equal to one, the surrogate interpolates the validation database. In practice, the surrogate is deemed appropriate when $Q_2$ is greater than 0.8. The predictive coefficient is also found under the name of Nash-Sutcliffe model efficiency coefficient in the hydrological literature, where it assesses the predictive capacity of the simulated discharge over a time window with respect to observed discharges (Nash and Sutcliffe 1970).

3.5.2 Root Mean Squared Error

The $\text{RMSE}$ is used to measure the accuracy of the model and should be equal to 0 when the model is perfect. At the kth given mesh node, it is defined as the square root of the mean squared errors (MSE), measuring the squared distance between the surrogate model and the reference model:

$$\begin{aligned} \text{RMSE}_k({\mathscr {D}}_v)=\sqrt{\text{MSE}_k({\mathscr {D}}_v)}. \end{aligned}$$

(14)

Their global counterpart are: $\text{MSE}({\mathscr {D}}_v)=p^{-1}\sum _{k=1}^p\text{MSE}_k({\mathscr {D}}_v)$

and $\text{RMSE}({\mathscr {D}}_v)=\sqrt{\text{MSE}({\mathscr {D}}_v)}$.

3.6 Sensitivity analysis

Sensitivity analysis aims to investigate how the different uncertain input variables $\underline{x}_1,\ldots ,\underline{x}_{d}$ influence the output variable $\underline{\mathbf{y}}={\mathscr {M}}(\underline{\mathbf{x}})$ over the whole uncertain input space. ${\mathscr {M}}$ either stands for the direct solver or for its surrogate. The overall objective is to identify which input parameters contribute the most to the uncertainty in the output and to order them accordingly. For the sake of simplicity, we focus on a mono-dimensional output variable $\underline{y}$. The model output uncertainty can be represented by its variance ${\mathbb {V}}[\underline{y}]$ to be explained on the basis of the uncertain input variables and their interactions. This is the purpose of the Sobol methodology (Sobol 1993; Saltelli 2010; Iooss and Lemaître 2015; Razavi et al. 2021), valid when $\underline{x}_1,\ldots ,\underline{x}_{d}$ are independent and when $\underline{y}$ is a second-order random variable, i.e, ${\mathbb {E}}\left[ \underline{y}^2\right] < \infty$. This technique decomposes the total output variance ${\mathbb {V}}\left[ \underline{y}\right]$ into $2^d-1$ elementary contributions:

$$\begin{aligned} {\mathbb {V}}\left[ \underline{y}\right] = \sum _{i \in I_d} V_i + \sum _{\begin{array}{c} i,j \in I_d \\ j>i \end{array}} V_{i,j}+ \ldots + V_{1, 2, \ldots , d} =\sum _{u\subseteq I_d} V_u \end{aligned}$$

where:

• $I_d=\{1,\ldots ,d\}$;

• $V_i={\mathbb {V}}\left[ {\mathbb {E}}\left[ \underline{y}|\underline{x}_i\right] \right]$ is the contribution of $\underline{x}_i$ alone;

• $V_{i,j}={\mathbb {V}}\left[ {\mathbb {E}}\left[ \underline{y}|\underline{x}_i, \underline{x}_j\right] \right] -V_i-V_j$ is the contribution of the $x_i$ in interaction with $\underline{x}_j$;

• and so on.

In practice, interest is focused on standardized versions of these contributions:

$$\begin{aligned} \sum _{i \in I_d} S_i + \sum _{\begin{array}{c} i,j \in I_d \\ j>i \end{array}} S_{i,j}+ \ldots + S_{1, 2, \ldots , d} =\sum _{u\subseteq I_d} S_u \end{aligned}$$

where $S_u=\frac{V_u}{{\mathbb {V}}\left[ \underline{y}\right] }$ is the Sobol index related to the interaction between the uncertain input variables $\underline{x}_i,~i\in u$. $S_u$ is the part of ${\mathbb {V}}\left[ \underline{y}\right]$ explained by this interaction. All these indices add up to 1 and, thus, represent proportions of output variance. Most of the time, Sobol study is conducted on:

• the first-order indices, $S_1,\ldots ,S_d$, where $S_i$ represents the part of ${\mathbb {V}}[\underline{y}]$ explained by $\underline{x}_i$ only; and

• the total-order indices, $S_1^T,\ldots ,S_d^T$, where $S_i^T=\sum _{\begin{array}{c} u\subseteq I_d\\ u\ni i \end{array}}S_i$ gathers all contributions related to $\underline{x}_i$.

When the difference between $S_i$ and $S_i^T$ is significant, this means that there are interactions between $\underline{x}_i$ and other uncertain input variables explaining ${\mathbb {V}}[\underline{y}]$. In this case, it is common to look at the value of the second-order indices $S_{i,1},\ldots ,S_{i,d}$ and so on. Conversely, $S_i^T\approx S_i$ leads to the conclusion that there is no interaction between $\underline{x}_i$ and another variable explaining ${\mathbb {V}}[\underline{y}]$. Consistently, $\sum _{i}{S_i} = 1$ if there is no interaction between the input parameters.

4 Application to the study case

4.1 Strategy and experimental settings

The $\text{rMPCE}$ strategy results at T are compared to those of a classical $\text{PCE}$ strategy. Different choices for dimension reduction, clustering, and regression are investigated. For this purpose, two databases are generated in this study with an optimized Latin Hypercube Sampling (LHS)  (Damblin et al. 2013) for the uncertain input variables whom $\text{PDF}$s are described in Table 1:

• a learning database of 1000 T2D evaluations to build and fit the surrogate model; and

• a validation database of 500 T2D evaluations to evaluate the accuracy of the surrogate model.

4.2 Computational environment

CERFACS’s cluster, Nemo, has been used to run $\text{T2D}$ simulations. The Nemo cluster includes 6912 cores distributed in 288 compute nodes. The ECU power peak is 277 Tflop/s. The computational cost of $\text{T2D}$ solver is reduced thanks to the parallel computing (single simulation lasts 6 min using 24 processors instead of 20 min using one processor). $\text{GSA}$ based on a large set of $\text{T2D}$ simulations is too costly. Hence the need for surrogate model formulation.

The rMPCE surrogate model proposed in this study is based on algorithms from different Python libraries. The first step uses $\text{AE}$ from Keras Tensorflow (Géron 2017) with a graphics processing unit (GPU) support Python package to reduce the dimension of the output space. The second step of this algorithm involves clustering and classifying data using a $\text{GMM}$ and $\text{SVM}$ algorithms from the Scikit-Learn library (Pedregosa et al. 2011). In the final step, the algorithm constructs a local regression model within the cluster; for this purpose, $\text{PCE}$ of the OpenTURNS library (Baudin et al. 2017) is used.

The meta-model learning stage (see Algorithm 1) is moderately costly: the tuning of the $\text{AE}$ parameters takes about 3 h and the construction of the $\text{PCE}$ takes about 15 min. The computational cost of the prediction stage is then drastically reduced, e.g., predicting 500 simulations takes 470 s.

Fig. 5

Evolution of the $\text{RMSE}$ computed between the real water depth (learning database) and the one reconstructed with the $\text{PCA}$ inverse method in solid blue line and the $\text{AE}$ decoder in dashed blue line, and of the reconstructed output variance for the $\text{PCA}$ in solid red line, according to the latent space dimension ${\tilde{p}}$

4.3 Results

4.3.1 Output dimension reduction

Dimension reduction results for $\text{PCA}$ and $\text{AE}$ are presented in Fig. 5. The size of the latent space ${\tilde{p}}$ is plotted along the x-axis, the left y-axis represents the $\text{RMSE}$ (quadratic error between initial and reconstructed water level field) in meters for $\text{PCA}$ (solid blue line) and $\text{AE}$ (dotted blue line), and the right y-axis represents the cumulated explained variance for the $\text{PCA}$. Different neural network architectures were tested in order to minimize the $\text{RMSE}$ metric. The resulting neural network is compiled with mean squared error loss and Adam optimizer (Zhang 2018) with 0.001 learning rate and the default Keras parameters. The number of training epochs is set to 200 while the batch size for the training cycle is set to 50. The size of the input is set to 41,416 neurons corresponding to the number of features in the database.

Fig. 6

Spatialized maximum absolute error computed between a simulated water depth (one simulation from the learning database) and its reconstruction using $\text{PCA}$ inverse method with 37 principal components. In zoom, the bathymetry profile along the horizontal section including the point with the maximum reconstruction error

For $\text{PCA}$, the $\text{RMSE}$ decreases exponentially from 9 to 3.82 centimeters as the number of principal components in the latent space increases from 1 to 50. For 26 components, 98% of the variance of the water depth is explained and the $\text{RMSE}$ is about 4 centimeters. For a small number of components, $\text{AE}$ leads to a larger $\text{RMSE}$ than $\text{PCA}$: 27 centimeters against 9 centimeters for a single component. Beyond 24 components, $\text{AE}$ leads to a smaller $\text{RMSE}$ than $\text{PCA}$: 1.27 centimeter against 3.82 centimeters for 50 components. A latent space spanned over 37 components offers a good compromise between accuracy and computational cost for both methods. Despite the fact that $\text{AE}$ is relatively expensive compared to $\text{PCA}$ (2 h against 3 min), it allows to account for non-linearities in areas with strong gradient bathymetry, mainly in ditches and downstream of dikes. Indeed, the maximum absolute error for water depth reconstructed from the $\text{PCA}$ displayed in Fig. 6 reaches 3 meters in a mesh node located in a ditch for a selected simulation, while the maximum absolute error for water depth reconstructed from $\text{AE}$ remains smaller than 1 centimeter. Therefore, in the following, dimension reduction is achieved using the more accurate $\text{AE}$ technique.

Fig. 7

Silhouette plot for various clusters of the output learning variable resulting from k-means (top pannels) and $\text{GMM}$ (bottom panels) clustering methods setting the number of clusters to K = 2,3,4 (from left to right)

4.3.2 Clustering and classification

Figure 7 displays the silhouette criterion defined in Eq. 2 for both k-means (top panels) and $\text{GMM}$ (bottom panels) clustering methods, setting the number of clusters to $K=2,3,4$ (from left to right). The silhouette criterion $s_k(i)$ is plotted along the x-axis for each observation i. The observation labels are indicated along the y-axis and arranged by the color-coded cluster number. The red vertical line indicates the average silhouette criterion computed among all observations and all clusters. This figure displays the quality of the clustering as well as the size of the resulting clusters. When $K=2$ and $K=4$, the size of the clusters are heterogeneous with silhouette values $s_k(i)$ smaller than the mean value. $K=3$ provides homogeneous clusters with satisfying silhouette values for all clusters. In the following, the three classes resulting from the $\text{GMM}$ classification are kept.

A hydraulic analysis of the clusters shows that the first cluster gathers medium-flow simulations where the flow submerges the dikes and barely propagates in the floodplain. The second cluster characterizes high-flow simulations where the flow significantly propagates in the floodplain and the third cluster characterizes low flow simulations where the flow is confined in the river bed.

Fig. 8

First two modes in each of the three resulting $\text{GMM}$ classes (learning database)

The first (top panels) and second $\text{AE}$ modes (bottom panels) for each cluster (with $K=3$) are shown in Fig. 8. In cluster 1, the first mode represents the mean flow dynamics while the second mode represents the flow obstacles. In cluster 2, the first mode corresponds to the maximum extent of the water while the second mode highlights the influence areas of upstream and downstream boundary conditions. In cluster 3, the first mode could be interpreted as the maximum flow extent and the second mode as a versus upstream-downstream flow.

4.3.3 Regression

Figure 9 displays the predictive coefficient when the flood occurs, computed between the validation database and a classical $\text{PCE}$ prediction on the left panel and between the validation database and the $\text{rMPCE}$ prediction on the right panel. The areas where $Q_2$ is close to 0 are indicated in yellow and it clearly appears that $\text{rMPCE}$ provides a far more predictive surrogate than classical $\text{PCE}$.

Fig. 9

Spatialized predictive coefficient computed between the validation database and the surrogate prediction at T: classical $\text{PCE}$ (left) and ${\text{rMPCE}}$ (right)

The classical $\text{PCE}$ poorly predicts 6625 nodes ($Q_2 < 0.8$) out of the 41,416 mesh nodes, mostly located in the floodplain where the response in water depth to change in friction and in inflow is non-linear (Fig. 9 left panel). The $\text{rMPCE}$ leads to a significant improvement for 90% of these poorly predicted nodes (564 nodes remain with $Q_2 < 0.8$) as illustrated in Fig. 9 (right panel).

Given these two maps, the contribution of the $\text{rMPCE}$ strategy is significant for a good prediction of the water height in the floodplain where human and economic stakes are predominant. A zoom on the diagnostic of the $\text{rMPCE}$ strategy for poorly predicted nodes ($Q_2 < 0.8$) raises the contribution of the loop on the polynomial degree P to quality prediction improvement. The $Q_2$ resulting from setting the same P for the different classes in $\text{rMPCE}$ (uniform $\text{rMPCE}$) is plotted as a dotted blue line in Fig. 10. P equal to 4 for the local $\text{PCE}$s of the three classes returns a value of $Q_2$ equal to 0.64, which is physically unsatisfactory. P greater than 4 leads to an over-fitting of the model to the learning data and a lower value leads to an under-fitting.

Fig. 10

Evolution of the predictive coefficient $Q_2$ of $\text{rMPCE}$ (solid red line) in which the polynomial degree has been optimized within each class and of uniform $\text{rMPCE}$ (solid blue line with cross marker), resulting from setting the same polynomial degree for the different classes

The $Q_2$ resulting from the polynomial degree optimization loop (varying the polynomial degree P between 2 and 9) for $\text{PCE}$ in each of the three classes is plotted as a dashed red line. The first class, mostly defined by medium flows, requires a P equal to 5 in order to approximate properly the water depth while the second class, characterized by high flows, requires a P equal to 4 and the third class, corresponding to low flows, requires a P equal to 3. This suggests that the physics in the first class is complex and requires to increase P, whereas the physics in the third class is rather simple as the optimal P for this class is equal to 3. Thus, the $\text{PCE}$ polynomial degree optimization loop allows obtaining a good approximation of the modes representing the water depth following dynamics within each class.

Fig. 11

Sobol indices of the hydraulic input variables estimated using Saltelli’s method based on $\text{rMPCE}$ for the simulated water depth at time T = 95,000 s. First-order indices are plotted on the left panels and total order on the right panels for $K_{\text{s},1}$ (floodplain), $K_{\text{s},2}$ (upstream river bed), $K_{\text{s},3}$ (middle river bed), $K_{\text{s},4}$ (downstream river bed), and Q (upstream forcing) from top to bottom

4.3.4 Sensitivity analysis

The variance-based $\text{GSA}$ in this study is based on Saltelli’s method for the estimation of Sobol indices using the $\text{rMPCE}$ surrogate model. The main goal of $\text{GSA}$ is to rank the uncertain parameters according to their influence on the variance of the $\text{QoI}$, here, the water depth $\text{2D}$ field. Figure 11 displays the first-order (left panels) and total order (right panels) Sobol indices for the four Strickler friction coefficients and discharge (from top to bottom) at time T. Analysis of the first order Sobol indices reveals the large influence of the discharge as this uncertain variable explains about 80% of the water depth variance on the overall domain. The Strickler friction coefficient associated to the floodplain area influences by 9% the water depth variance upstream and in some dyked areas. The influence of the Strickler coefficients associated with the river bed remains weak or slightly significant in a few places; for example, $K_{\text{s},4}$ influences the water depth variance by 82% locally in a dyked zone downstream of the river.

The analysis of the total Sobol indices indicates that while the friction coefficients have a low first order Sobol index, they are not negligible as they have a significant influence through their interactions with other variables. Yet, the discharge remains by far the most influencing variable when it interacts with the other variables as shown in the right-bottom plot. It should be noted that the $\text{GSA}$ results depend on the hypothesis on the input random variables distributions. For instance, the significant influence of the floodplain Strickler friction coefficient compared to that of the river bed coefficients may be due to the large uncertainty translated by the large range of $K_{\text{s},1}$’s uniform distribution.

5 Conclusions, limitations, and future research

5.1 Conclusions

In this paper, an $\text{rMPCE}$ surrogate model is used to conduct a $\text{GSA}$ in order to rank the sources of uncertainty with a variance-based sensitivity analysis in the presence of non-linearities and at a parsimonious computational cost. The $\text{rMPCE}$ strategy is based on a mixture of a polynomial chaos expansions implemented in a reduced output space and into clusters where non-linearities between input and output remain small. It is used to approximate the $\text{2D}$ water depth simulated using the $\text{T2D}$ numerical solver. The uncertain input space contains five scalars and the uncertain output space is a $\text{2D}$ discretized field of large dimension (about 41,000 mesh nodes). This strategy is illustrated when the flood front enters the floodplain, causing non-linearities between inflow, friction and the water field, especially in regions of strong bathymetry gradient.

The first step of the $\text{rMPCE}$ strategy involves compressing the water depth data. To this end, the $\text{PCA}$ and $\text{AE}$ methods were compared. $\text{PCA}$ is a simple linear transformation on the input space to directions of maximum variation while $\text{AE}$ is an advanced technique that minimizes the reconstruction loss. The $\text{AE}$ technique yielded more accurate results as it was able to deal with non-linearities in the output field.

The second step of the $\text{rMPCE}$ strategy involves grouping the reduced data with similar patterns into classes. After comparing the silhouette coefficient derived from the k-means and $\text{GMM}$ methods, three classes were considered based on the $\text{GMM}$, leading to three different hydraulic behaviors. The third step consists of defining the boundaries between these classes within the input space using the $\text{SVM}$ algorithm. It appears that the boundaries were mostly driven by the discharge variable.

The last step of the $\text{rMPCE}$ strategy is to construct a local optimized $\text{PCE}$ within each class. It was shown that the resulting surrogate model simulates properly the water depth over the study area and improves the prediction by 90% compared to the one given by a classical $\text{PCE}$. Indeed, $\text{PCE}$ was successful in predicting water depth for over 83% of the grid points, mostly in the river bed. However, it fails to predict water depth in the floodplains where non-linearities occur. In these regions, $\text{rMPCE}$ was able to deal with non-linearities and provide good prediction for 98% of the grid points.

Sobol indices were then estimated using the $\text{rMPCE}$ surrogate model. It was shown that the water depth over the considered study area is predominantly controlled by the upstream discharge except for the left bank side of the upstream which is influenced by the Strickler friction coefficient of the floodplain. The total Sobol indices of the three Strickler friction coefficients related to the river bed indicate that despite the fact that those variables have a low first-order Sobol index in all domain, they are not negligible as they influence the water depth through interactions with the other variables. It has also been emphasized that those results depend on the description of the input variables $\text{PDF}$.

5.2 Limitations

In practice, tuning the $\text{AE}$ hyper-parameters, such as the number of layers and the number of neurons per layer, remains difficult (van der Maaten et al. 2007). One way to overcome this limitation is to consider an existing architecture that was proven successful for a similar problem, or training the $\text{AE}$ directly from the $\text{PCA}$ response given that the $\text{AE}$ may be considered as a non-linear extension of $\text{PCA}$, or using pre-training methods allowing for a layer-by-layer learning (Makhzani and Frey 2015).

Due to time constraints, the model has not been tested for the case where all time steps are taken into account in one batch. Eventually, this could reduce the non-linearities present, in particular for the dimension reduction step.

The assumption for the description of the PDF for the Strickler coefficients could be revisited. An ensemble of coupled sediment-hydrology simulations could be generated in order to investigate how the topography evolves with the flow and consequently the friction evolves.

The assumption of independence of the input variables, Strickler’s friction coefficient and upstream discharge, can be reviewed. In this sense, a sensitivity analysis could be conducted by considering the Shapely indices (Iooss and Prieur 2017).

5.3 Future research

As a perspective, first, the proposed surrogate modeling strategy should be applied to all time steps of the hydraulic simulation and to the computation of the time-varying Sobol indices. Also, numerical improvement could be reached with the analytical computation of Sobol indices from the local polynomial coefficients instead of their stochastic estimation with the Saltelli method with the $\text{rMPCE}$ surrogate as implemented here. Additionally, the mixture strategy could also be revisited with kernel based-clustering methods that could take into account the non-linearities, an adaptive re-sampling in clusters with a small predictive coefficient, and a weighted sum of the predictions from the local models using frequentist model averaging or Bayesian model averaging. A local mesh refinement in areas where the predictive coefficient of $\text{rMPCE}$ remains small could be investigated. This would lead to further improvement relying on multi-fidelity approaches.

Another perspective would be to improve the rMPCE to simulate the hydraulic state on another time window than the one used for training in order to better meet the needs of data assimilation, typically when we go from one assimilation cycle to another. In this sense, a possible approach would be to combine rMPCE with NARX (Mai et al. 2016) to simulate the dynamics from one time step to another.

A major perspective for this work is to extend the uncertain input space. To begin with, the input space could include time-varying upstream forcing in order to simulate realistic flood events. It could also include a spatially refined friction field, potentially resulting from calibration with a densified, remotely sensed observation network. In both cases, the dimension of the input space should also be reduced, for instance, using the dimension reduction techniques applied here for the output space dimension reduction.

Finally, the resulting surrogate model can be used in the context of data assimilation. Indeed, the computation of the Sobol indices allows the identification of variables that should be included in the control vector. Then, the surrogate model could be used in place of the direct numerical solver for a low-cost stochastic estimation of the background covariance matrix in ensemble-based data assimilation algorithms. The assimilation of in-situ and remote-sensing water level data with a parsimonious ensemble-based algorithm paves the way for the improvement of forecasted water depth and discharge in an operational framework.