Abstract
Arctic sea-ice area and volume have substantially decreased since the beginning of the satellite era. Concurrently, the poleward heat transport from the North Atlantic Ocean into the Arctic has increased, partly contributing to the loss of sea ice. Increasing the horizontal resolution of general circulation models (GCMs) improves their ability to represent the complex interplay of processes at high latitudes. Here, we investigate the impact of model resolution on Arctic sea ice and Atlantic Ocean heat transport (OHT) by using five different state-of-the-art coupled GCMs (12 model configurations in total) that include dynamic representations of the ocean, atmosphere and sea ice. The models participate in the High Resolution Model Intercomparison Project (HighResMIP) of the sixth phase of the Coupled Model Intercomparison Project (CMIP6). Model results over the period 1950–2014 are compared to different observational datasets. In the models studied, a finer ocean resolution drives lower Arctic sea-ice area and volume and generally enhances Atlantic OHT. The representation of ocean surface characteristics, such as sea-surface temperature (SST) and velocity, is greatly improved by using a finer ocean resolution. This study highlights a clear anticorrelation at interannual time scales between Arctic sea ice (area and volume) and Atlantic OHT north of \(60\,^\circ \hbox {N}\) in the models studied. However, the strength of this relationship is not systematically impacted by model resolution. The higher the latitude to compute OHT, the stronger the relationship between sea-ice area/volume and OHT. Sea ice in the Barents/Kara and Greenland–Iceland–Norwegian (GIN) Seas is more strongly connected to Atlantic OHT than other Arctic seas.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The recent accelerated loss of Arctic sea ice is undeniable, with declines in ice area and thickness during all months of the year and a progressive transition from multi-year to first-year ice (Vaughan et al. 2013; Notz and Stroeve 2016; Barber et al. 2017; Petty et al. 2018). The annual mean Arctic sea-ice area has decreased by \(\sim 2\) million \(\hbox {km}^2\) from 1979 to 2016 (Onarheim et al. 2018), i.e. an average loss of \(\sim 53000~\hbox {km}^2~\hbox {a}^{-1}\), but sea-ice area displays strong regional and seasonal expressions. The perennial ice-covered seas (i.e. East Siberian, Chukchi, Beaufort, Laptev, and Kara) constitute the largest contributors to sea-ice loss in summer, while sea-ice loss in winter is dominated by the seasonally ice-covered seas located farther south (i.e. Barents, Okhotsk, Greenland, and Baffin), which are almost entirely ice-free in summer (Onarheim et al. 2018). Despite the uncertainty among the different thickness observational datasets (Zygmuntowska et al. 2014), sea ice in the Central Arctic has significantly thinned since 1975 (Lindsay and Schweiger 2015; Kwok 2018).
Multiple mechanisms have contributed to the recent loss of Arctic sea ice, including anthropogenic global warming (Notz et al. 2016), changes in large-scale atmospheric circulation (Döscher et al. 2014) and ocean heat transport (OHT, Carmack et al. 2015), combined with powerful climate feedbacks acting in the Arctic (Goosse et al. 2018; Massonnet et al. 2018). A number of studies show that Arctic sea ice in the Atlantic sector (Barents, Kara, and Laptev Seas) is strongly influenced by Atlantic OHT (e.g. Sando et al. 2010; Arthun et al. 2012; Ivanov et al. 2012; Polyakov et al. 2017). Arthun et al. (2012) suggest that the recent observed sea-ice reduction in the Barents Sea occurred concurrently with an increase in Atlantic OHT due to both strengthening and warming of the oceanic inflow. Ivanov et al. (2012) also identify such a link between increased OHT and reduced Arctic sea ice in the western Nansen Basin, located north of Barents Sea, between Svalbard and Severnaya Zemlya. They show that the location of specific zones with thinner ice and lower ice concentration mirrors the pathway of the Fram Strait branch of the Atlantic Water. Polyakov et al. (2017) provide observational evidence that the ‘atlantification’ is also responsible for sea-ice loss in the eastern Eurasian Basin. They argue that the recent increased penetration of Atlantic Water into the eastern Eurasian Basin, associated with stratification weakening and pycnocline warming, has led to a greater upward Atlantic Water heat flux to the ocean surface and a consequent reduction of ice growth in winter.
From a modeling perspective, Mahlstein and Knutti (2011) show that coupled general circulation models (GCMs) from the Coupled Model Intercomparison Project phase 3 (CMIP3) with the strongest northward OHT have the smallest September Arctic sea-ice extent and thickness. They suggest that improving the representation of OHT in GCMs (e.g. by using finer resolution) would lead to a smaller inter-model spread in the projections of the Arctic climate system. Koenigk and Brodeau (2014) confirm the leading role of OHT in the current Barents Sea ice reduction through bottom melt using the EC-Earth model. However, their results do not indicate a clear impact of OHT on the Central Arctic sea ice. Three CMIP5 model outputs show that the increased OHT at the Barents Sea Opening (BSO) results in ice area reduction in the Barents Sea, while the enhanced OHT at Fram Strait influences sea-ice area variability in the Central Arctic via bottom melting (Sando et al. 2014a). A CMIP5 multi-model analysis suggests that enhanced Atlantic OHT has played a leading role in the recent observed decline in winter Barents sea-ice area (Li et al. 2017). Burgard and Notz (2017) analyze changes in the energy budget of the Arctic Ocean coming from 26 CMIP5 models and find that the Arctic warming between 1961 and 2099 is driven by the net atmospheric surface flux in 11 models and by the meridional ocean heat flux in 11 models. This study shows a significant negative correlation between the Atlantic meridional ocean heat flux and Arctic sea-ice area across the models. The links between OHT and Arctic sea ice are further confirmed by a study using 40 Community Earth System Model Large Ensemble (CESM-LE) members (Auclair and Tremblay 2018), in which \(80\%\) of the rapid ice declines are correlated to increased OHT (mainly at the BSO and Bering Strait). The CESM-LE members further show that OHT in the Barents Sea is a major source of internal Arctic winter sea-ice variability and predictability (Arthun et al. 2019) and that the local contribution of internal variability strongly depends on the month and Arctic region analyzed (England et al. 2019).
The impact of model resolution on OHT has been analyzed in several studies. Roberts et al. (2016) run the HadGEM3-GC2 model with two different configurations (60 km in the atmosphere and \(0.25^\circ\) in the ocean; 25 km in the atmosphere and \(1/12^\circ\) in the ocean) and show that a higher ocean resolution leads to stronger warm boundary currents, which results in higher sea-surface temperature (SST) and increased upward latent heat flux from the ocean to the atmosphere, thus providing a higher OHT. Similarly, Hewitt et al. (2016) and Roberts et al. (2018) find that poleward OHT increases with higher ocean resolution, but does not change significantly with finer atmosphere resolution, for their respective models (HadGEM3-GC2 and ECMWF-IFS, respectively). Grist et al. (2018) also find that a higher ocean resolution leads to higher Atlantic OHT in a multi-model comparison including three coupled GCMs with ocean resolutions ranging from \(1^\circ\) to \(1/12^\circ\). Other analyses reveal an improvement in OHT in the Barents Sea when GCMs are regionally downscaled to a resolution of \(\sim ~10~\hbox {km}\) (Sando et al. 2014b). The effect of resolution on Arctic sea ice has received less attention, but the study of Kirtman et al. (2012) shows that the use of a higher ocean resolution in the Community Climate System Model version 3.5 (CCSM3.5), from \(1.2^\circ\) to \(0.1^\circ\), results in ocean surface warming, especially in the Arctic and regions of strong ocean fronts. This warming is associated with a reduction of Arctic sea ice. The impact of model resolution on the relationships between Arctic sea ice and Atlantic OHT has not been investigated in detail yet.
Here, we provide the first detailed analysis of the horizontal resolution effect on Arctic sea ice, Atlantic OHT and relationships between both quantities. To this end, we use the outputs of five coupled GCMs (12 model configurations in total) that follow the protocol of the High Resolution Model Intercomparison Project (HighResMIP; Haarsma et al. 2016) and participate in the EU Horizon 2020 PRIMAVERA project (PRocess-based climate sIMulation: AdVances in high-resolution modelling and European climate Risk Assessment, https://www.primavera-h2020.eu/). It is important to note that only two model configurations in this study benefit from several member runs, which limits the assessment of internal variability. The goal of the present study is to quantify the impact of model resolution on Arctic sea-ice area and volume, then on North Atlantic OHT, and finally on the links between both Arctic sea ice and Atlantic OHT. Section 2 presents the model outputs and reference products (observations and reanalyses) used in this study. Section 3 provides our results in terms of Arctic sea ice, North Atlantic OHT and links between the two. Section 4 discusses the impact of model resolution, the impact of OHT on Arctic sea ice and some issues inherent to a multi-model analysis on resolution dependence. Finally, our conclusions are presented in Sect. 5.
2 Methodology
2.1 Models
Model outputs come from HighResMIP (Haarsma et al. 2016), which is one of the CMIP6-endorsed Model Intercomparison Projects (MIPs). HighResMIP is the first climate multi-model approach dedicated to the systematic investigation of the role of horizontal resolution. We mainly use the model outputs of coupled historical runs (referred to as ‘hist-1950’ in HighResMIP), in order to compare our results to observations. We also analyze the outputs of coupled control runs (‘control-1950’ in HighResMIP, using a constant atmospheric forcing corresponding to the year 1950) and compare them to historical runs. This allows one to check whether the results obtained depend on the forcing or not. Both hist-1950 and control-1950 runs start in 1950 at the end of a 30–50-year spin-up and are integrated for 65 years (until 2014). Five different GCMs (12 model configurations in total), representing the atmosphere, ocean and sea ice, are considered in this study. Each model has a ‘low’ and a ‘high’ (or ‘medium’) resolution configuration, and two of these models also have an ‘intermediate’ resolution configuration. In the following text, when we use the word ‘resolution’ without specifying whether it is atmosphere or ocean resolution, we mean atmosphere and ocean resolutions combined. Our study is limited by the number of ensemble members available: only two model configurations have different members (see text below). Thus, a clear assessment of internal variability is not possible in the context of this analysis. A summary of model characteristics is given in Table 1.
The first model is the Global Coupled 3.1 configuration of the Hadley Centre Global Environmental Model 3 (HadGEM3-GC3.1; Williams et al. 2018), hereafter referred to as HadGEM3. It is formed by the Global Atmosphere 7.1 (GA7.1), Global Land 7.0 (GL7.0), Global Ocean 6.0 (GO6.0, Storkey et al. 2018) and Global Sea Ice 8.1 (GSI8.1) components. The atmosphere and land components are based on the Unified Model (UM; Cullen 1993) and Joint UK Land Environment Simulator (JULES; Best et al. 2011), respectively. The ocean component is version 3.6 of the Nucleus for European Modelling of the Ocean (NEMO, Madec 2016), consisting of a hydrostatic, finite-difference, primitive-equation general circulation model. It is coupled to version 5.1 of the Los Alamos sea-ice model (CICE; Hunke et al. 2015). We use three different HadGEM3 configurations having different horizontal resolutions. The first configuration, HadGEM3-LL, uses the N96 atmosphere grid (nominal resolution of 250 km, i.e. 135 km at \(50^\circ \hbox {N}\)) and ORCA1 tripolar ocean grid (resolution of \(1^\circ\)). The second configuration, HadGEM3-MM, runs with the N216 atmosphere grid (nominal resolution of 100 km, i.e. 60 km at \(50^\circ \hbox {N}\)) and ORCA025 ocean grid (resolution of \(0.25^\circ\)). The third configuration, HadGEM3-HM, uses the N512 atmosphere grid (nominal resolution of 50 km, i.e. 25 km at \(50^\circ \hbox {N}\)) and the same ocean resolution as HadGEM3-MM (\(0.25^\circ\)). A few parameters change between the three configurations, but stay limited to resolution-dependent parameterizations (Table 1). One of the main differences is the albedo of snow on sea ice, which is smaller by \(2\%\) in HadGEM3-LL compared to HadGEM3-MM and HadGEM3-HM due to overestimation of Arctic sea-ice area and volume at low resolution compared to observations (Kuhlbrodt et al. 2018).
The second model is the European Centre for Medium-Range Weather Forecasts Integrated Forecast System (ECMWF-IFS) cycle 43r1 (Roberts et al. 2018). The atmospheric component of the ECMWF-IFS model is a hydrostatic, semi-Lagrangian, semi-implicit dynamical-core model using a cubic octahedral reduced Gaussian (Tco) grid. The land surface component is the Hydrology Tiled ECMWF Scheme of Surface Exchanges over Land (HTESSEL; Balsamo et al. 2009). The ocean and sea ice components are based on version 3.4 of NEMO and version 2 of the Louvain-la-Neuve Sea-Ice Model (LIM2; Fichefet and Morales Maqueda 1997), respectively. In this study, we use three configurations of the ECMWF-IFS model run at different horizontal resolutions. The low-resolution configuration, referred to as ECMWF-LR, uses the Tco199 atmosphere grid (nominal resolution of 50 km) and ORCA1 ocean grid. The high-resolution configuration, named ECMWF-HR, uses the Tco399 atmosphere grid (nominal resolution of 25 km) and ORCA025 ocean grid. The intermediate-resolution configuration, ECMWF-MR, has the same atmosphere resolution as ECMWF-LR (Tco199) and the same ocean resolution as ECMWF-HR (ORCA025). All three configurations are configured to be as close as possible to each other with differences limited to resolution-dependent parameterizations (Table 1). Six members are available for ECMWF-LR and four members for ECMWF-HR (see Roberts et al. 2018 for further details). In the present study, we present the results of the ensemble means of both ECMWF-LR and ECMWF-HR, except in Figs. 7, 8, 9 and 10, where we show results from the first member of these configurations.
The third model is version 1.1 of the Alfred Wegener Institute Climate Model (AWI-CM; Sidorenko et al. 2015; Rackow et al. 2018). It is made up of version 6.3 of the European Centre/Hamburg (ECHAM6.3) atmospheric model and version 1.4 of the Finite Element Sea ice-Ocean Model (FESOM; Wang et al. 2014; Sein et al. 2016). ECHAM is a spectral model and includes the land surface model JSBACH (Stevens et al. 2013). The FESOM ocean-sea ice component employs an unstructured mesh, which allows using enhanced horizontal resolution in dynamically active regions while keeping a coarse-resolution setup otherwise. Two model configurations of AWI-CM at different horizontal resolutions are used in the present study. The first configuration, AWI-LR, uses the T63 atmosphere grid (nominal resolution of 250 km, i.e. 129 km at \(50^\circ \hbox {N}\)) and an ocean mesh with resolution varying from 24 km to 110 km (\(\sim 90\) km in the vicinity of the Gulf Stream and \(\sim 25\) km in the Arctic). The second configuration, AWI-HR, uses the T127 atmosphere grid (nominal resolution of 100 km, i.e. 67 km at \(50^\circ \hbox {N}\)) and an ocean mesh varying from 10 to 60 km, with a refined resolution in key ocean straits (\(\sim 10\) km in the vicinity of the Gulf Stream and \(\sim 25\) km in the Arctic). Details on the two ocean meshes are in Sein et al. (2016). Beside the resolution, small differences (e.g. model time step) exist between both configurations and are noted in Table 1.
The fourth model is version 2 of the Euro-Mediterranean Centre on Climate Change Climate Model (CMCC-CM2; Cherchi et al. 2018). It is composed of version 4 of the Community Atmosphere Model (CAM; Neale et al. 2013), NEMO3.6 for the ocean, CICE4.0 for sea ice, and version 4.5 of the Community Land Model (CLM, Oleson et al. 2013). Two configurations of CMCC-CM2 are employed in this analysis. They both make use of the same ocean resolution (ORCA025, i.e. \(0.25^\circ\)). The first configuration, CMCC-HR4, has a resolution of \(1^\circ\) in the atmosphere (64 km at \(50^\circ \hbox {N}\)), while the second configuration, CMCC-VHR4, has a resolution of \(0.25^\circ\) (18 km at \(50^\circ \hbox {N}\)). No other difference exists between the two configurations.
The fifth model is version 1.2 of the Max Planck Institute Earth System Model (MPI-ESM, Müller et al. 2018). The ECHAM6.3 atmospheric component is coupled to version 1.6.3 of the Max Planck Institute Ocean Model (MPIOM, Jungclaus et al. 2013). MPIOM is a free-surface ocean-sea ice model that solves the primitive equations with the hydrostatic and Boussinesq approximations. The two model configurations of MPI-ESM used in this study employ the same ocean model grid, i.e. the \(0.4^\circ\) tripolar grid (TP04). They differ by their atmosphere resolution: the low-resolution configuration, MPI-HR, uses the T127 grid (nominal resolution of 100 km, i.e. 67 km at \(50^\circ \hbox {N}\)), while the high-resolution configuration, MPI-XR, runs on the T255 grid (nominal resolution of 50 km, i.e. 34 km at \(50^\circ \hbox {N}\)). Beside the atmosphere horizontal resolution, the only difference between both configurations is the atmosphere model time step (Table 1).
For the five models used here, we retrieve monthly mean sea-ice concentration (‘siconc’ CMIP6 variable), equivalent sea-ice thickness (‘sivol’; i.e. mean sea-ice volume per grid-cell area), SST (‘tos’), zonal and meridional components of ocean velocity (‘uo’ and ‘vo’), ocean potential temperature (‘thetao’), Atlantic OHT, as well as grid-cell area. The OHT in HadGEM3, CMCC-CM2 and MPI-ESM simulations is computed online (‘hfbasin’ CMIP6 variable). For AWI-CM and ECMWF-IFS, OHT is not available as a model output, so it is computed offline. For AWI-CM, OHT is the sum of the heat transport computed from the total heat flux applied at the ocean surface (atmosphere/ocean exchanges) and the transport derived from the vertically integrated heat tendencies (ocean accumulation, release of heat). For ECMWF-IFS, OHT is computed from monthly mean products of meridional velocity and potential temperature of the ocean (which take the sub-monthly eddy variability into account). All model outputs represent the total OHT as they include both the time-mean and transient (eddy) contributions.
It is important to note that we compute Arctic sea-ice area (and not sea-ice extent) in this study, due to uncertainties in modeled sea-ice extent arising from the grid geometry (Notz 2014). We retrieve this quantity from sea-ice concentration and area of model grid cells. Sea-ice volume is computed from equivalent sea-ice thickness (‘sivol’) and area of grid cells.
2.2 Reference products
Several observational and reanalysis datasets are used in the present analysis in order to evaluate model results.
For sea-ice concentration, the second version of the global sea-ice concentration climate data record (OSI-450) from the European Organisation for the Exploitation of Meteorological Satellites Ocean Sea Ice Satellite Application Facility (EUMETSAT OSI SAF 2017) is used (Lavergne et al. 2019). This dataset covers the period from 1979 to 2015 and is derived from passive microwave data from Scanning Multichannel Microwave Radiometer (SMMR), Special Sensor Microwave/Imager (SSM/I) and Special Sensor Microwave Imager Sounder (SSMIS). In our study, we use the data from 1979 to 2014 to be consistent with HighResMIP model outputs. The OSI SAF algorithm to retrieve sea-ice concentration from brightness temperature is a hybrid method combining an algorithm that is tuned to perform better over open-water and low-concentration conditions and an algorithm that is tuned to perform better over closed-ice and high-concentration conditions (Lavergne et al. 2019). The spatial resolution of this dataset is 25 km and its accuracy for sea-ice retrieval in the Northern Hemisphere is \(5\%\) (EUMETSAT OSI SAF 2017). We compute the monthly mean concentration from daily data.
For sea-ice thickness, we use the Ice, Cloud, and land Elevation Satellite (ICESat) gridded data at a spatial resolution of 25 km (Kwok et al. 2009). This satellite altimeter provides sea-ice freeboard height, from which sea-ice thickness is derived based on spatially varying snow depth (from the ECMWF snowfall accumulation fields) and densities of ice (constant), snow (seasonal behavior) and water (constant). The coverage period is limited to the months of October–November and February–March from 2003 to 2008. The mean absolute uncertainty of this dataset is 0.21 m in October–November and 0.28 m in February–March (Zygmuntowska et al. 2014).
Monthly mean sea-ice thickness from the Pan-Arctic Ice-Ocean Modeling and Assimilation System (PIOMAS) is also considered for the period 1979–2014. PIOMAS is a coupled ocean and sea-ice model with capability of assimilating daily sea-ice concentration and SST. It is based on the Parallel Ocean Program (POP) coupled to a multi-category thickness and enthalpy distribution (TED) sea-ice model (Zhang and Rothrock 2003). The model is driven by daily National Centers for Environmental Prediction / National Center for Atmospheric Research (NCEP/NCAR) reanalysis surface forcing fields. The mean horizontal resolution in the Arctic is 22 km. PIOMAS data agree well with ICESat ice thickness retrievals over the Central Arctic with a mean difference lower than 0.1 m (Schweiger et al. 2011). However, the trend in ice thickness varies by about \(40\hbox {-}50\%\) depending on the atmospheric forcing used to drive the model (Lindsay et al. 2014) and care needs to be taken when using this product (Chevallier et al. 2017).
For the poleward Atlantic OHT, we use annual mean estimates from Trenberth and Caron (2001) that cover the period from February 1985 to April 1989. These estimates are computed on a \(2.8^\circ\) grid by combining top-of-the-atmosphere (TOA) radiation data from the Earth Radiation Budget Experiment (ERBE) with NCEP/NCAR reanalysis. They show a relatively good agreement compared to direct measurements of Atlantic OHT. The more recent estimates from Trenberth and Fasullo (2017) are also used and cover the period 2000–2014 on a \(1^\circ\) grid. They are based on TOA radiation data from Clouds and the Earth’s Radiant Energy System (CERES), ECMWF Interim Re-Analysis (ERA-Interim) and ocean heat content from Ocean ReAnalysis Pilot v5 (ORAP5) reanalysis. In addition, we use OHT estimates derived from the Rapid Climate Change-Meridional Overturning Circulation and Heatflux Array (RAPID-MOCHA; Johns et al. 2011). The RAPID-MOCHA array is an observing system deployed at \(26.5^\circ \hbox {N}\), near the latitude of maximum Atlantic OHT. This array allows to provide continuous measurements from April 2004. We also use direct hydrographic measurements of Atlantic OHT coming from different expeditions (\(30^\circ \hbox {S}\), \(11^\circ \hbox {S}\), \(8^\circ \hbox {N}\), \(14^\circ \hbox {N}\), \(24^\circ \hbox {N}\), \(57^\circ \hbox {N}\)) and reported in Fig. 1 of Grist et al. (2018). Finally, we use OHT estimates at the BSO (71.5–73.5\(^\circ \hbox {N}\), \(20^\circ \hbox {E}\)) derived from hydrographic data and current meter moorings coming from the Institute of Marine Research (IMR, Norway). These data were kindly provided by R. Ingvaldsen and span the period from 1997 to 2017.
For SST, we use version 2 of the National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation Sea Surface Temperature (OI SST) analysis. These data are provided at a spatial resolution of \(0.25^{\circ }\) and a temporal resolution of one day, from September 1981 to present. In our study, we compute monthly mean SST from daily data and we use data from 1982 to 2014 to be consistent with model outputs. The OI SST analysis combines Advanced Very High Resolution Radiometer (AVHRR) satellite data and in-situ observations from ships and buoys on a regular global grid following the procedure described in Reynolds et al. (2007). Daytime and nighttime satellite observations are adjusted to the daily average of in-situ (ships and buoys) data. All satellite data are bias adjusted relative to seven days of in-situ data using a spatially smoothed 7-day in situ SST average.
We finally retrieve the ocean surface absolute geostrophic velocities (zonal and meridional components) provided by the Sea Level Thematic Assembly Centre (SL TAC) through the Copernicus Marine Environment Monitoring Service (CMEMS). We use the reprocessed gridded daily data provided at a spatial resolution of \(0.25^{\circ }\). In our study, we compute monthly means over the period 1993–2016. This is a multi-mission altimeter data processing system (Jason-3, Sentinel-3A, HY-2A, Saral/AltiKa, Cryosat-2, Jason-2, Jason-1, T/P, ENVISAT, GFO, ERS1/2), where all missions are homogenized with respect to the reference OSTM/Jason-2 mission. These altimeter data are in relatively good agreement with in-situ observations of the North Atlantic Current (Roessler et al. 2015) and the Norwegian Atlantic Slope Current (Skagseth et al. 2004). Errors in geostrophic currents from this dataset range between 5 and \(15~\hbox {cm}~\hbox {s}^{-1}\) depending on the ocean surface variability (Pujol 2017).
3 Results
3.1 Arctic sea ice
Figures 1 and 2 show monthly mean Arctic sea-ice area and volume, respectively, averaged over 1979–2014. This period is chosen to be comparable to observations, but key results are independent of the chosen period. For all of the models used in this study, we find a year-round decrease of Arctic sea-ice area and volume with finer ocean resolution (comparing HadGEM3-LL with HadGEM3-MM/HM, ECMWF-LR with ECMWF-MR/HR, and AWI-LR with AWI-HR). This decrease is especially pronounced for ECMWF-IFS, i.e. \(-\,23\%\) to \(-\,30\%\) in area (Table 2) and \(-\,36\) to \(-\,49\%\) in volume (Table 3) over the whole period. The change in sea-ice area and volume is less clear with changing atmosphere resolution. For HadGEM3, increasing the atmosphere resolution from 100 (HadGEM3-MM) to 50 km (HadGEM3-HM) leads to lower sea-ice area and volume (Figs. 1, 2). However, sea-ice area and volume increase with finer atmosphere resolution for ECMWF-IFS (from 50 km in ECMWF-MR to 25 km in ECMWF-HR) and CMCC-CM2 (from 100 km in CMCC-HR4 to 25 km in CMCC-VHR4). For MPI-ESM, sea-ice area generally increases with higher atmosphere resolution, although the increase is relatively small and not significant over the whole time period (Fig. 1, Table 2), while sea-ice volume decreases (Fig. 2, Table 3). Thus, the implication from this sample of models is that a finer ocean resolution leads to reduced Arctic sea-ice area and volume, while the impact of atmosphere resolution is less clear. This point will be further discussed in Sect. 4.1.
Both HadGEM3 and ECMWF-IFS models generally overestimate sea-ice area and volume during all months compared to OSI SAF (Fig. 1) and PIOMAS (Fig. 2), respectively, with an unrealistically high volume for the ECMWF-LR configuration. For HadGEM3 and ECMWF-IFS, using a finer ocean resolution provides results in better agreement with both sea-ice area from OSI SAF (Fig. 1) and sea-ice volume from PIOMAS (Fig. 2). ECMWF-MR is very close to the observed sea-ice area, and HadGEM3-HM is in good agreement with the sea-ice volume from PIOMAS. The situation is not as clear-cut for AWI-CM, CMCC-CM2 and MPI-ESM models. Both AWI-CM configurations overestimate sea-ice area in winter and underestimate it in summer compared to observations. The finer resolution (AWI-HR) is closer to OSI SAF sea-ice area during December-May, and farther away the rest of the year compared to AWI-LR (Fig. 1). CMCC-HR4 underestimates sea-ice area, while CMCC-VHR4 stays within the bounds of interannual variability of OSI SAF (Fig. 1). MPI-ESM sea-ice area agrees with OSI SAF within the bounds of interannual variability in winter and underestimates this quantity in summer. The finer resolution of MPI-ESM (MPI-XR) is closer to OSI SAF in terms of sea-ice area from November to March and June, and farther away the rest of the year compared to MPI-HR (Fig. 1). Both AWI-CM and MPI-ESM slightly underestimate sea-ice volume compared to PIOMAS, with the coarser resolutions of these two models being closer to PIOMAS during the whole year (Fig. 2). CMCC-HR4 slightly overestimates the sea-ice volume from reanalysis, while CMCC-VHR4 clearly has too high ice volume (Fig. 2).
Despite these model biases, all five models can reproduce the general behavior of the mean seasonal cycles of Arctic sea-ice area and volume compared to OSI SAF observations (Fig. 1) and PIOMAS reanalysis (Fig. 2), respectively, with a maximum in March for area and April for volume, and a minimum in August-September for area and September for volume. All HadGEM3, AWI-CM and MPI-ESM configurations, as well as the low resolution of ECMWF-IFS, overestimate the amplitude of the mean seasonal cycles of Arctic sea-ice area and volume compared to OSI SAF observations (Fig. 1) and PIOMAS reanalysis (Fig. 2), respectively. The two higher resolutions of ECMWF-IFS and the two CMCC-CM2 configurations underestimate these cycles. Using a finer resolution has different implications on the amplitude of the seasonal cycles of sea-ice area and volume for the different models. For HadGEM3, the amplitude decreases and is in better agreement with observations/reanalysis at finer ocean resolution. For ECMWF-IFS, the amplitude also decreases with finer ocean resolution, but the coarser resolution (ECMWF-LR) has an amplitude of sea-ice area that is closer to observations, while the amplitude of sea-ice volume is closer to PIOMAS with the finer resolutions (ECMWF-MR/HR). For AWI-CM, the amplitude stays relatively similar between both ocean resolutions. For CMCC-CM2, the amplitude slightly increases and is in better agreement with observations with finer atmosphere resolution. For MPI-ESM, the amplitude increases with finer atmosphere resolution, and the coarser resolution has an amplitude closer to observations.
In agreement with OSI SAF observations and PIOMAS reanalysis, the trends in Arctic sea-ice area and volume over 1979–2014 are significantly negative (\(5\%\) level) for all models and all months (Figs. 3 and 4). Compared to observations and reanalysis, the trends in sea-ice area and volume of HadGEM3-LL, ECMWF-LR and MPI-HR are generally more negative than the observed and reanalysis trends. On the contrary, the trends in area and volume of HadGEM3-HM, ECMWF-MR, ECMWF-HR, AWI-LR and MPI-XR are generally less negative than the observed and reanalysis trends. The two CMCC-CM2 configurations have trends in sea-ice volume that are more negative than PIOMAS during the whole year, while they have trends in sea-ice area that are less negative than OSI SAF in summer. AWI-HR has a trend in sea-ice volume that is less negative than PIOMAS. For all models, the trends in sea-ice area and volume are less negative with finer ocean resolution, with the exception of AWI-CM for which the trend in sea-ice area becomes more negative with finer resolution. As for mean values, the impact of atmosphere resolution on trends in area and volume is not clear, with less negative trends for HadGEM3 (comparing HadGEM3-MM and HadGEM3-HM) and MPI-ESM, and more negative trends for ECMWF-IFS (comparing ECMWF-MR and ECMWF-HR) and CMCC-CM2 (Figs. 3 and 4). The higher resolution configurations do not necessarily have sea-ice area and volume trends in closer agreement with observations and reanalysis. Comparing the mean sea-ice volume (Fig. 1) and the trend in sea-ice volume (Fig. 3), we find that models with lower mean sea-ice volume generally have less negative trends in sea-ice volume. This can be explained by the ice growth-thickness feedback, i.e. models with thinner sea ice have larger ice-growth rates, partly limiting sea-ice melting (Bitz and Roe 2004). Thus, models with thinner sea ice, such as the higher ocean resolution versions of the models used here, have a slower loss of ice volume, which would explain the reduced negative trends at finer ocean resolution.
March Arctic sea-ice thickness averaged over 1982–2014 (1982–2010 for AWI-LR and AWI-HR). Black and red contour lines show March and September sea-ice edges (where sea-ice concentration is \(15\%\)), respectively. Results from (a–h, j–k) HighResMIP hist-1950 model outputs, i PIOMAS sea-ice thickness and OSI SAF sea-ice concentration, and l ICESat sea-ice thickness. Sea-ice thickness from ICESat is averaged over the months of February to April from 2003 to 2008
Latitudinal transect of Atlantic Ocean heat transport (OHT) averaged over 1950–2014 for all HighResMIP hist-1950 model configurations used in this study (1951–2013 for AWI-CM and 1951–2014 for HadGEM3). We also plot OHT estimates from Trenberth and Caron (2001) (TC2001) and Trenberth and Fasullo (2017) (TF2017), averaged over 1985–1989 and 2000–2014 respectively, as well as hydrographic measurements (with associated error uncertainty) as in Grist et al. (2018). An inset map of the North Atlantic region is shown in the upper left corner
Mean March sea-ice thickness decreases with finer ocean resolution in all regions of the Arctic for ECMWF-IFS and AWI-CM, while it stays relatively similar for HadGEM3 (Fig. 5). With finer atmosphere resolution, the mean March thickness decreases for MPI-ESM and increases for CMCC-CM2 (Fig. 5). These results are valid for all months of the year, as summarized in Table 4. Compared to ICESat observations (Fig. 5l) and PIOMAS reanalysis (Fig. 5i), HadGEM3, ECMWF-IFS and CMCC-CM2 configurations overestimate the mean sea-ice thickness, while AWI-CM and MPI-ESM underestimate it. The highly overestimated thickness from ECMWF-LR (Fig. 5b) combined with too high sea-ice area (Fig. 1) lead to the unrealistically high sea-ice volume of this model configuration (Fig. 2). The biases in Arctic sea ice simulated by ECMWF-LR are partly explained by excessive ice growth due to negative biases in longwave and shortwave cloud radiative forcings over the Arctic (Roberts et al. 2018).
The location of the Arctic sea-ice edge (defined as the isoline where sea-ice concentration is \(15\%\)) is generally better represented at finer resolution with ECMWF-IFS, HadGEM3 and CMCC-VHR4 compared to OSI SAF observations (Fig. 5). In the low-resolution configurations of ECMWF-IFS (Fig. 5b) and HadGEM3 (Fig. 5a), the sea-ice edge typically extends too far south in both Bering and Labrador Seas. The situation is more nuanced for AWI-CM and MPI-ESM, with an improvement at finer resolution in some cases (e.g. March sea-ice edge in Bering Sea in AWI-HR, Fig. 5f) and a worsening in other cases (e.g. September sea-ice edge in AWI-HR, Fig. 5f).
All the results of this section are based on historical runs (hist-1950). When we use control runs (control-1950), HadGEM3, ECMWF-IFS and AWI-CM also exhibit lower sea-ice area and volume with finer ocean resolution, while MPI-ESM has higher sea-ice area with higher resolution, in a similar way as for hist-1950 runs. Thus, control-1950 runs confirm our results based on hist-1950 runs. The fact that control-1950 and hist-1950 runs provide similar results means that our findings are independent of the presence of time-evolving external climate forcings.
In the models studied, the main impacts of model resolution on Arctic sea ice (area, volume, thickness, edge) are summarized below:
-
sea-ice area and volume decrease with finer ocean resolution, while the impact of atmosphere resolution is less clear (Figs. 1, 2, Tables 2, 3);
-
a finer ocean resolution leads to improved sea-ice area and volume compared to observations and reanalysis for HadGEM3 and ECMWF-IFS (Figs. 1, 2);
-
a finer resolution leads to worsened sea-ice volume compared to reanalysis for AWI-CM, CMCC-CM2 and MPI-ESM (Fig. 2);
-
a finer ocean resolution leads to a decrease in the amplitude of mean seasonal cycles of sea-ice area and volume for HadGEM3 and ECMWF-IFS and no change for AWI-CM (Figs. 1 and 2);
-
the trends in sea-ice area and volume are less negative with finer ocean resolution (except the trend in sea-ice area of AWI-CM) (Figs. 3, 4);
-
the mean sea-ice thickness clearly decreases with finer ocean resolution for ECMWF-IFS and AWI-CM, while it stays relatively similar for HadGEM3 (Fig. 5, Table 4);
-
the location of the sea-ice edge is better represented at finer resolution with ECMWF-IFS, HadGEM3 and CMCC-CM2 (Fig. 5);
-
the results from control runs (control-1950) are comparable to historical runs (hist-1950).
3.2 North Atlantic OHT
Figure 6 presents the mean northward OHT in the Atlantic averaged over 1950–2014. For all model configurations, the latitudinal variation of OHT follows the observed profiles (hydrographic measurements and estimates), but the OHT is generally underestimated by models between \(20^\circ \hbox {S}\) and \(30^\circ \hbox {N}\) and overestimated at higher latitudes. OHT model underestimation at low latitudes and overestimation at high latitudes reflects insufficient heat loss to the atmosphere between these two latitudes. The insufficient North Atlantic heat loss in models is an important topic of research, which may be partially addressed as resolution increases to eddy-resolving scale (Roberts et al. 2016).
Enhanced ocean resolution implies increased poleward OHT at all latitudes for HadGEM3 and ECMWF-IFS (Fig. 6), in closer agreement with the OHT estimates from Trenberth and Fasullo (2017). The two AWI-CM configurations follow each other closely, although the OHT is globally higher at finer resolution (especially around \(24^\circ \hbox {N}\) and \(45^\circ \hbox {N}\)). A finer atmosphere resolution leads to higher Altantic OHT for HadGEM3 and CMCC-CM2 (although CMCC-VHR4 has lower OHT at high latitudes compared to CMCC-HR4), lower OHT for MPI-ESM, and almost no change for ECMWF-IFS (Fig. 6). Note that recent studies show that HadGEM3-GC2 (Hewitt et al. 2016) and ECMWF-IFS (Roberts et al. 2018) present smaller differences in OHT when only the atmosphere resolution is varied compared to ocean resolution.
Most model configurations underestimate the mean OHT observational estimate of \(1.21 \pm 0.34\) petawatts (PW) from the RAPID-MOCHA array (\(26.5^\circ \hbox {N}\) in the Atlantic Ocean), averaged over 2005-2014 (Table 5). A finer ocean resolution brings the models in better agreement with these observations (from HadGEM3-LL to HadGEM3-MM/HM; from ECMWF-LR to ECMWF-MR/HR; from AWI-LR to AWI-HR). A finer atmosphere resolution has different implications, with higher OHT at \(26.5^\circ \hbox {N}\) for HadGEM3 (from HadGEM3-MM to HadGEM3-HM), ECMWF-IFS (from ECMWF-LR to ECMWF-MR) and CMCC-CM2, and lower OHT at \(26.5^\circ \hbox {N}\) for MPI-ESM. Compared to the mean observed OHT at the BSO of \(49 \pm 21\) terawatts (TW; averaged over 1998–2014), HadGEM3 and ECMWF-IFS clearly underestimate the observed value at low ocean resolution (\(1^\circ\)) and are in relatively good agreement with observations at finer ocean resolution (\(0.25^\circ\)) (Table 5). Increasing the atmosphere resolution does not lead to an improvement of OHT at the BSO compared to observations for HadGEM3 and ECMWF-IFS, while it does for CMCC-CM2 and MPI-ESM.
Overall, trends in Atlantic OHT at \(50^\circ \hbox {N}\), \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\) from 1979 to 2014 decrease with finer ocean resolution (Table 6). The situation is more nuanced with atmosphere resolution, with a decreasing trend with resolution for HadGEM3 and MPI-ESM and an increasing trend for ECMWF-IFS and CMCC-CM2. However, the trend in OHT at \(50^\circ \hbox {N}\) is significant (\(5\%\) level) only for 6 model configurations (out of 12) and the OHT trend at \(60^\circ \hbox {N}\) is significant only for 2 model configurations (Table 6). Furthermore, note that trends at \(50^\circ \hbox {N}\) are mostly negative. On the contrary, most model configurations show a significant positive trend in OHT at \(70^\circ \hbox {N}\) (Table 6). For HadGEM3-MM and HadGEM3-HM, the OHT trend at \(70^\circ \hbox {N}\) is not significant but positive. These positive OHT trends at \(70^\circ \hbox {N}\) coincide with the negative trends in Arctic sea-ice area (Fig. 3) and volume (Fig. 4) over the same time period (1979–2014), highlighting the link between OHT at sufficiently high latitude (\(70^\circ \hbox {N}\) in our case) on the one hand and Arctic sea-ice area and volume on the other hand. The only model configuration for which the trend in OHT at \(70^\circ \hbox {N}\) is negative is ECMWF-MR, but it is not significant (Table 6). Note that this specific model configuration presents the least negative trends in sea-ice area (Fig. 3) and volume (Fig. 4). In summary, a finer ocean resolution generally results in less positive trends in OHT at \(70^\circ \hbox {N}\) (Table 6) and less negative trends in Arctic sea-ice area (Fig. 3) and volume (Fig. 4).
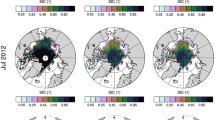
Spatial analysis of SST, ocean surface velocity and sea-ice edge provides insight into the potential links between OHT and Arctic sea ice. More specifically, the mean SST in the North Atlantic Ocean (especially between 40 and \(70^\circ \hbox {N}\)) increases with finer ocean resolution, as illustrated by HadGEM3 (Fig. 7a, d, j), ECMWF-IFS (Fig. 7b, e, k) and AWI-CM (Fig. 7c, f, l). The role of atmosphere resolution is again more complex: for example, for MPI-ESM, the mean SST decreases with finer atmosphere resolution (Fig. 7g, h, m). The impact of resolution on sea-surface velocity is even more explicit, with an overall intensification and better position of the North Atlantic currents with finer ocean resolution for HadGEM3, ECMWF-IFS and AWI-CM, while the velocity decreases with MPI-ESM (Fig. 8). In Figs. 7 and 8, we only show the March SST and surface velocity fields (averaged over 1982–2014), respectively, but these statements are valid for all months of the year. The higher SST and ocean surface velocity of HadGEM3-MM and ECMWF-HR (compared to HadGEM3-LL and ECMWF-LR, respectively) lead to a retreated sea-ice edge in the North Atlantic Ocean (Figs. 7d, e and 8d, e, compared to Figs. 7a, b and 8a, b, respectively). On the contrary, the lower SST and surface velocity of MPI-XR compared to MPI-HR results in a sea-ice edge located farther south (Figs. 7h, 8h, compared to Figs. 7g and 8g, respectively). Compared to observed SST and ocean surface velocity, the enhanced ocean resolution clearly improves the model results (Figs. 7, 8, Table 7). Especially, we note that an eddy-permitting ocean resolution (\(\sim 0.25^\circ\)) provides SST and ocean surface velocity in better agreement with observations compared to a coarser resolution, with a clear model underestimation of these two fields with an ocean resolution of \(\sim 1^\circ\). Note that further improvements are expected at higher ocean resolution (i.e. \(1/12^\circ\) or higher), which would allow to resolve ocean Rossby radius at mid and high latitudes and coastal regions.
The complex ocean surface circulation of specific regions, such as the Barents Sea, is better represented with refined model ocean resolution down to \(0.25^\circ\) or with a variable-resolution mesh (Fig. 9). As the ocean resolution increases, a detailed path of the surface circulation emerges in Barents Sea, and the currents intensify. This is especially clear for the HadGEM3 and ECMWF-IFS models. Surface velocity field at \(1^\circ\) ocean resolution is very weak, reaching only few cm \(\hbox {s}^{-1}\) in HadGEM3-LL (Fig. 9a) and ECMWF-LR (Fig. 9b). At \(0.25^\circ\) ocean resolution (HadGEM3-MM, ECMWF-HR; Fig. 9d,e), the surface current paths are clearly identified. In particular, the Norwegian Atlantic Current, flowing poleward, splits into two distinct branches: one part flows eastward through the BSO and the other continues toward Fram Strait (as West Spitsbergen Current). Within the Barents Sea, we clearly distinguish the main counterclockwise circulation and the current system between Frans Josef Land and Novaya Zemlya. The position of the sea-ice edge retreats northward as the model resolution is refined for ECMWF-IFS (Fig. 9b,e), in line with a stronger surface current flowing through the BSO. For AWI-CM, the surface velocity increases with finer resolution (Fig. 9c,f), despite the fact that AWI-LR and AWI-HR have approximately the same ocean resolution in the Barents Sea (\(\sim 25\) km). A detailed study of the AWI-CM model shows that AWI-LR overestimates the convection in Greenland–Iceland–Norwegian (GIN) Seas, which in turn reduces the Atlantic water inflow into the Barents Sea (Sein et al. 2018). For MPI-ESM, the ice edge extends farther south with finer resolution as the surface velocity decreases (Fig. 9g,h).
The spatial details of sea-ice concentration in the Barents Sea are better captured with a sufficiently high resolution for HadGEM3 and ECMWF-IFS (Fig. 10). HadGEM3-LL has a very sharp gradient in sea-ice concentration from the western to eastern Barents Sea (Fig. 10a) compared to observations (Fig. 10i), while HadGEM3-MM has a smoother and more realistic pattern (Fig. 10d). ECMWF-LR clearly overestimates sea-ice concentration in the whole Barents Sea (Fig. 10b), while ECMWF-HR is much closer to observations (Fig. 10e). For AWI-CM, the mean sea-ice concentration in the Barents Sea computed from AWI-LR is closer to observations compared to AWI-HR, which has slightly more ice than AWI-LR (Fig. 10c, f). However, the ocean resolution in this region is relatively similar between both configurations; therefore, differences might be due to other factors (e.g. stronger ocean currents in AWI-HR compared to AWI-LR, Fig. 9c, f). The two MPI-ESM configurations do not differ substantially in terms of sea-ice concentration in the Barents Sea, despite some differences west of Svalbard and off Novaya Zemlya coast (Fig. 10g, h).
As for Arctic sea ice (Sect. 3.1), the results of this section are based on historical runs (hist-1950). The use of control runs (control-1950) leads to similar results, i.e. a finer ocean resolution results in higher poleward OHT from the North Atlantic Ocean (not shown).
In the models studied, the main effects of model resolution on North Atlantic OHT and related fields (SST and ocean surface velocity) are summarized below:
-
enhanced ocean resolution implies increased poleward OHT, while the role of atmosphere resolution is less clear (Fig. 6, Table 5);
-
trends in Atlantic OHT at \(50^\circ \hbox {N}\), \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\) decrease with finer resolution, with a significant positive trend in OHT at \(70^\circ \hbox {N}\) for most model configurations (Table 6);
-
the mean SST and ocean surface velocity in the North Atlantic Ocean increase with finer ocean resolution (Figs. 7 and 8, Table 7);
-
the complex ocean surface circulation of the Barents Sea requires an ocean resolution of at least \(0.25^\circ\) or a variable-resolution mesh for a distinct and continuous depiction of the currents (Fig. 9);
-
sea-ice concentration in the Barents Sea is better represented at \(0.25^\circ\) ocean resolution compared to \(1^\circ\) with HadGEM3 and ECMWF-IFS (Fig. 10);
-
these key results are also valid when using control runs instead of historical runs.
3.3 Arctic sea ice and Atlantic OHT
The results from Sects. 3.1 and 3.2 show that: (1) in HadGEM3, ECMWF-IFS and AWI-CM, enhanced ocean resolution leads to increased poleward Atlantic OHT and decreased Arctic sea-ice area and volume; (2) in CMCC-CM2, a finer atmosphere resolution results in higher Atlantic OHT from \(20^\circ \hbox {S}\) to \(60^\circ \hbox {N}\) and slightly lower OHT from \(60^\circ \hbox {N}\) to the North Pole, as well as higher sea-ice area and volume; (3) in MPI-ESM, enhanced atmosphere resolution leads to decreased poleward OHT in the North Atlantic, increased Arctic sea-ice area and reduced sea-ice volume; (4) in HadGEM3, higher atmosphere resolution results in enhanced OHT and lower sea-ice area and volume; (5) in ECMWF-IFS, the impact of atmosphere resolution on OHT is low, while sea-ice area and volume increase with finer atmosphere resolution. In this section, we further analyze the links between Arctic sea ice (area and volume) and poleward Atlantic OHT.
March sea-surface temperature (SST) in the North Atlantic Ocean averaged over 1982–2014 (1982–2013 for AWI-LR and AWI-HR). The white contour line shows the March sea-ice edge (where sea-ice concentration is \(15\%\)). Results from (a–h) HighResMIP hist-1950 model outputs (first member for ECMWF-LR and ECMWF-HR) and i observations (OI SST for SST and OSI SAF for sea-ice concentration). Difference in March SST between the high- and low-resolution configurations of j HadGEM3, k ECMWF-IFS, l AWI-CM, and m MPI-ESM
March sea-surface velocity in the North Atlantic Ocean averaged over 1982–2014 (1982–2010 for AWI-LR and AWI-HR, 1993–2016 for observation). The blue contour line shows the March sea-ice edge (where sea-ice concentration is \(15\%\)). Results from a–h HighResMIP hist-1950 model outputs (first member for ECMWF-LR and ECMWF-HR) and i satellite observations (multi-mission for ocean velocity and OSI SAF for sea-ice concentration)
March sea-surface velocity in Barents Sea averaged over 1982–2014 (1982–2010 for AWI-LR and AWI-HR, 1993–2016 for observation). The blue contour line shows the March sea-ice edge (where sea-ice concentration is \(15\%\)). Results from a–h HighResMIP hist-1950 model outputs (first member for ECMWF-LR and ECMWF-HR) and i satellite observations (multi-mission for ocean velocity and OSI SAF for sea-ice concentration)
March sea-ice concentration in Barents Sea averaged over 1982–2014 (1982-2013 for AWI-LR and AWI-HR). The white contour lines show sea-surface temperature (SST, \(^\circ \hbox {C}\)) with a \(2^\circ \hbox {C}\) spacing. Results from a–h HighResMIP hist-1950 model outputs (first member for ECMWF-LR and ECMWF-HR) and i satellite observations (OSI SAF for sea-ice concentration and OI SST for SST)
Regression slopes (\(a_{SIA/OHT}\)) between detrended monthly mean Arctic sea-ice area and detrended annual mean Atlantic OHT at \(50^\circ \hbox {N}\) (solid black curves), \(60^\circ \hbox {N}\) (solid blue curves) and \(70^\circ \hbox {N}\) (solid red curves) for the different HighResMIP model configurations used in this study (1950–2014) and for each month of the year. Significant slopes (\(5\%\) level) are marked by dots, while not significant slopes are marked by crosses
Regression slopes (\(a_{SIV/OHT}\)) between detrended monthly mean Arctic sea-ice volume and detrended annual mean Atlantic OHT at \(50^\circ \hbox {N}\) (solid black curves), \(60^\circ \hbox {N}\) (solid blue curves) and \(70^\circ \hbox {N}\) (solid red curves) for the different HighResMIP model configurations used in this study (1950–2014) and for each month of the year. Significant slopes (\(5\%\) level) are marked by dots, while not significant slopes are marked by crosses
The relationship between monthly mean Arctic sea-ice area and annual mean North Atlantic OHT is investigated by regressing the first variable against the second one for each month over 1950–2014. In order to isolate the relationships associated with interannual variability, we remove the trends from both variables before regressing the variables against each other. Atlantic OHT is computed at \(50^\circ \hbox {N}\), \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\). This diagnostic thus provides the loss (or gain) in Arctic sea-ice area per PW of poleward Atlantic OHT. Figure 11 presents a synthesis of these regression slopes for 10 out of the 12 model configurations (we do not show results from ECMWF-MR and HadGEM3-HM for clarity) and each month of the year. This clearly highlights that the slopes are overall negative when OHT is computed at \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\), meaning that sea-ice area generally decreases with increasing OHT (although the slopes can be positive for some model configurations during some months, e.g. CMCC-HR4 with OHT at \(60^\circ \hbox {N}\) in February-April). Furthermore, in general, the higher the latitude to compute OHT, the more negative the slopes, meaning that on average there is a greater change in sea-ice area per unit change in OHT (except for MPI-ESM in summer-autumn). This is especially obvious for HadGEM3 and ECMWF-IFS, with a loss in sea-ice area per PW of OHT at \(70^\circ \hbox {N}\) of \(\sim\)5-10 million \(\hbox {km}^2\) for HadGEM3-LL (Fig. 11a), \(\sim\)10-15 million \(\hbox {km}^2\) for HadGEM3-MM (Fig. 11b), \(\sim\)30-40 million \(\hbox {km}^2\) for ECMWF-LR (Fig. 11c) and \(\sim\)20 million \(\hbox {km}^2\) for ECMWF-HR (Fig. 11d).
Similar conclusions are generally drawn when we regress monthly mean Arctic sea-ice volume (instead of area) against Atlantic OHT (Fig. 12). The loss in sea-ice volume per PW of OHT at \(70^\circ \hbox {N}\) is \(\sim\)20,000 \(\hbox {km}^3\) for HadGEM3-LL (Fig. 12a), \(\sim\)20,000–30,000 \(\hbox {km}^3\) for HadGEM3-MM (Fig. 12b), \(\sim\)150,000–200,000 \(\hbox {km}^3\) for ECMWF-LR (Fig. 12c), \(\sim\)70,000 \(\hbox {km}^3\) for ECMWF-HR (Fig. 12d), \(\sim\)20,000–40,000 \(\hbox {km}^3\) for AWI-LR (Fig. 12e), mostly not significant for AWI-HR (Fig. 12f), \(\sim\)30,000–40,000 \(\hbox {km}^3\) for CMCC-HR4 (Fig. 12g), and not significant for CMCC-VHR4 (Fig. 12h), MPI-HR (Fig. 12i) and MPI-XR (Fig. 12j), although the slopes are generally negative for AWI-HR, CMCC-VHR4 and MPI-HR. While a clear correlation between Arctic sea-ice area/volume and OHT is found, these relationships do not appear to systematically change with resolution (Figs. 11 and 12).
We also compute sea-ice area in seven specific Arctic sectors, following the methodology of Koenigk et al. (2016), and we regress these sea-ice areas against the annual mean Atlantic OHT, in order to check whether some sectors have a stronger signal than others. As the regression slope between the total Arctic sea-ice area and OHT is generally more negative in winter and when OHT is computed at \(70^\circ \hbox {N}\) compared to more southern latitudes (Fig. 11), we focus on the relationship between March sea-ice area and OHT at \(70^\circ \hbox {N}\). Results from the ECMWF-HR configuration are presented in Fig. 13 to illustrate the analysis, with each dot representing March sea-ice area against annual mean OHT at \(70^\circ \hbox {N}\) for each year of the period 1950–2014. A clear anticorrelation between March sea-ice area and OHT at \(70^\circ \hbox {N}\) is found for the total Arctic (Fig. 13a), Barents/Kara Seas (Fig. 13f) and GIN Seas (Fig. 13h), with sea-ice losses of 18.3 million \(\hbox {km}^2~\hbox {PW}^{-1}\), 5.6 million \(\hbox {km}^2~\hbox {PW}^{-1}\) and 8.2 million \(\hbox {km}^2~\hbox {PW}^{-1}\), respectively. This indicates a strong potential influence of the North Atlantic OHT on the total Arctic sea-ice area, and especially in the regions closely connected to the North Atlantic (i.e. Barents/Kara and GIN Seas).
The previous result is generally valid for all other model configurations. Figure 14 shows the regression slopes of March Arctic sea-ice area against annual mean OHT computed at \(70^\circ \hbox {N}\) for the different Arctic regions and all model configurations. This shows that the area-OHT regression slopes are significantly negative in all model configurations for the total Arctic (Fig. 14a, except AWI-LR and CMCC-HR4), Barents/Kara Seas (Fig. 14f, except MPI-XR) and GIN Seas (Fig. 14h, except CMCC-HR4). For the total Arctic and these two specific sectors, no clear impact of resolution is found, beside the fact that the sensitivity of Arctic sea-ice area to OHT is slightly higher at finer ocean resolution for HadGEM3 and AWI-CM. For the other Arctic regions, results are more contrasted, with no consensus across models and much lower regression slopes. If we regress sea-ice area against OHT at \(50^\circ \hbox {N}\), no clear correlation is found for any of the Arctic regions. With OHT computed at \(60^\circ \hbox {N}\), the anticorrelation between sea-ice area and OHT is stronger for the total Arctic, GIN Seas and Labrador Sea/Baffin Bay.
The results of this section are based on historical runs (hist-1950). The use of control runs (control-1950) leads to relatively similar results, which confirms our findings related to the relationships between Arctic sea ice and OHT. In particular, area-OHT and volume-OHT regression slopes are generally negative. Also, the higher the latitude to compute OHT, the more negative the slopes, with an order of magnitude similar to historical runs. Finally, for control runs, we find no clear impact of model resolution on the intensity of the relationship between Arctic sea-ice area/volume and Atlantic OHT, similarly to historical runs. Therefore, the agreement between hist-1950 and control-1950 runs allows to rule out the possibility that Arctic sea-ice area/volume and OHT are correlated due to anthropogenic global warming. In that way, control-1950 runs allow highlighting that a mechanistic link exists between the two variables.
Scatter plots of detrended March sea-ice area (\(\hbox {Area}_{03}\)) against detrended annual mean Atlantic OHT computed at \(70^\circ \hbox {N}\) (\(\hbox {OHT}_{70N}\)) in ECMWF-HR for a the whole Arctic and b–h seven specific Arctic regions (GIN stands for Greenland–Iceland–Norwegian). All yearly values between 1950 and 2014 are plotted. Correlation coefficients R and regression slopes a (with their respective p-value and standard deviation) are indicated in the upper/lower right corner of each panel
Regression slopes (\(a_{SIA/OHT}\)) between detrended March Arctic sea-ice area and detrended annual mean Atlantic OHT at \(70^\circ \hbox {N}\) (computed over 1950–2014) for a the whole Arctic and b–h seven specific Arctic regions (GIN stands for Greenland–Iceland–Norwegian). The X axis shows the 12 model configurations used, with the first letter indicating the model (H: HadGEM3; E: ECMWF-IFS; A: AWI-CM; C: CMCC-CM2; M: MPI-ESM). The black line on top of each bar indicates the standard deviation of these slopes
In the models studied, the main results related to the links between Arctic sea ice and North Atlantic OHT are summarized below:
-
regression slopes of sea-ice area/volume against poleward OHT are generally negative when OHT is computed at \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\), meaning that an increase in OHT leads to a loss of sea-ice area and volume (Figs. 11, 12);
-
the higher the latitude to compute OHT, the more negative the regression slopes, suggesting a stronger connection between the northern North Atlantic OHT and Arctic sea ice (Figs. 11, 12);
-
area-OHT regression slopes are overall significantly negative in all model configurations for the total Arctic, Barents/Kara Seas and GIN Seas when OHT is computed at \(70^\circ \hbox {N}\) (Figs. 13, 14), suggesting these are regions where the sea ice-OHT connection is strongest;
-
these key results are also valid when using control runs instead of historical runs, highlighting that a mechanistic link exists between Arctic sea-ice area/volume and OHT.
4 Discussion
4.1 Impact of model resolution
In the models studied, we find reduced Arctic sea-ice area (Fig. 1, Table 2) and volume (Fig. 2, Table 3) as well as enhanced poleward Atlantic OHT (Fig. 6, Table 5) with finer ocean resolution (HadGEM3, ECMWF-IFS and AWI-CM). Changing the atmosphere resolution only has different consequences on sea ice and OHT depending on the model used, as demonstrated in Sects. 3.1 and 3.2. In particular, an increased atmosphere resolution leads to higher OHT and reduced sea-ice area/volume in HadGEM3, higher OHT and increased area/volume in CMCC-CM2, lower OHT, increased area and decreased volume in MPI-ESM, and finally almost no change in OHT and increased area/volume in ECMWF-IFS. Thus, we argue that the impacts of ocean resolution on Atlantic OHT and Arctic sea ice are robust, while the impacts of atmosphere resolution are less clear. This hypothesis is confirmed by previous modeling studies that we describe hereafter.
Hewitt et al. (2016) and Roberts et al. (2018) find that poleward OHT increases with finer ocean resolution, but does not change significantly with finer atmosphere resolution, for their respective models (HadGEM3-GC2 and ECMWF-IFS, respectively). Hewitt et al. (2016) use four different HadGEM3-GC2 configurations with different atmosphere and ocean resolutions as well as coupling frequencies. They show that enhanced ocean resolution results in reduced SST biases, improved OHT, and deeper and stronger overturning circulation. Roberts et al. (2018) analyze the same three ECMWF-IFS configurations as the ones we use in this study. They show that all three configurations present a negative SST bias in the North Atlantic and excessive Arctic sea ice, which are both improved when using higher ocean resolution, probably due to a better representation of OHT. The use of the intermediate ECMWF-MR configuration in their study allows them to show that changes in ocean resolution affect more the mean climate state than changes in atmosphere resolution.
Grist et al. (2018) also find that the ocean resolution is the key resolution affecting Atlantic OHT in a multi-model comparison including three coupled GCMs. They show that an increase in ocean resolution from \(1^\circ\) to \(0.25^\circ\) considerably strengthens the Atlantic OHT and leads to higher SST and latent heat loss. In contrast, increasing the atmosphere resolution only has much lower impact on OHT compared to the ocean resolution, due to a compensation between regional changes in the shortwave radiative input to the ocean and increased latent heat loss. Increasing both the ocean and atmosphere resolutions leads to changes in OHT similar to those obtained by increasing the ocean resolution only. In our study, we analyze models that use ocean resolutions in the same range as in Grist et al. (2018), but the main difference is that these models follow the same coordinated protocol (HighResMIP). Therefore, our study confirms the previous findings of a robust impact of ocean resolution on OHT and Arctic sea ice compared to atmosphere resolution.
The way ocean resolution affects OHT is strongly linked to the modeling of boundary currents, such as the Gulf Stream. Roberts et al. (2016) show that a finer ocean resolution results in stronger warm boundary currents in HadGEM3-GC2, which leads to higher SST and increased upward latent heat flux from the ocean to the atmosphere, thus providing a higher OHT. In our study, we also find that finer ocean resolution leads to stronger warm boundary currents in the North Atlantic (Fig. 8) and higher SST (Fig. 7), resulting in enhanced poleward Atlantic OHT (Fig. 6). Ocean surface velocity fields clearly demonstrate the increase in the intensity of the main currents, such as the Gulf Stream and North Atlantic Current, when ocean resolution increases (Fig. 8). An ocean resolution of \(1^\circ\) is clearly too coarse to resolve the Rossby radius of deformation at mid-latitudes.
The reduced Arctic sea-ice area and volume at finer ocean resolution are probably driven by the higher poleward Atlantic OHT. This is especially evident for HadGEM3 and ECMWF-IFS, for which the sea-ice edge retreats northward with higher ocean resolution due to enhanced SST (Fig. 7) and surface currents (Fig. 8). Moreover, trends in OHT at 70°N (Table 6) generally become less positive and trends in Arctic sea-ice area (Fig. 3) and volume (Fig. 4) are generally less negative with finer ocean resolution, suggesting a tight link between both trends. Further modeling studies are needed to investigate in details the impact of enhanced Atlantic OHT on reduced Arctic sea-ice area and volume.
4.2 Impact of ocean heat transport on Arctic sea ice
Beside the impact of model resolution on Arctic sea ice and Atlantic OHT, our results show that sea-ice area/volume and OHT are strongly linked. Several studies show that OHT exerts a strong influence on sea ice by bringing warm water that melts the ice in some specific Arctic regions, especially in the Atlantic sector (e.g. Arthun et al. 2012; Ivanov et al. 2012; Polyakov et al. 2017). In our study, we confirm that the link between Arctic sea ice and North Atlantic OHT is strong (Sect. 3.3). For example, it is clear that higher Atlantic OHT at \(70^\circ \hbox {N}\) is associated with lower Arctic sea-ice area for the whole Arctic Ocean and especially in specific peripheral seas, such as Barents/Kara Seas and GIN Seas (Figs. 11, 13, 14). This is also the case when taking sea-ice volume instead of sea-ice area, although with weaker correlation (Fig. 12).
The OHT-sea ice relationship is stronger when OHT is computed at higher latitude (i.e. \(70^\circ \hbox {N}\)) (Fig. 11). This is probably due to the fact that most of the ocean heat that reaches \(70^\circ \hbox {N}\) goes then into the Arctic Ocean. The OHT-sea ice relationship is weaker when OHT is taken farther south. At \(60^\circ \hbox {N}\), part of the Atlantic Water can still recirculate into the Atlantic Ocean without entering the Nordic Seas (Daniault et al. 2016; Holliday et al. 2018), although the OHT-sea ice relationship is also generally present in all model configurations at this latitude (Fig. 11). At \(50^\circ \hbox {N}\), the re-circulation is even greater than at \(60^\circ \hbox {N}\), resulting in relatively weak OHT-sea ice correlations. Therefore, the latitude at which OHT is computed needs to be high enough in order to have an impact on Arctic sea ice. Note that OHT at \(70^\circ \hbox {N}\) linearly increases with OHT at \(60^\circ \hbox {N}\). This is expected as the Atlantic Meridional Overturning Circulation (AMOC) displays coherence over significant latitude ranges north and south of 40\(^\circ\)N (Bingham et al. 2007). In addition, the marked decline in the strength of the OHT-sea ice connection between \(60^\circ \hbox {N}\) and \(50^\circ \hbox {N}\) (Fig. 11) reflects the fact that a large and variable amount of heat transported north at \(50^\circ \hbox {N}\) is transferred to the atmosphere between \(50^\circ \hbox {N}\) and \(60^\circ \hbox {N}\).
Our study extends the model intercomparison from Mahlstein and Knutti (2011) by including coupled GCMs at different ocean resolutions. While Mahlstein and Knutti (2011) analyze the CMIP3 outputs, for which the ocean resolution is typically coarser than \(\sim 1^\circ\), here we consider an ocean grid typically ranging from \(\sim 0.25^\circ\) to \(1^\circ\). Mahlstein and Knutti (2011) find a correlation of \(R\) = − 0.72 between OHT computed at \(60^\circ \hbox {N}\) and September Arctic sea-ice extent using CMIP3 model results. They suggest that finer model resolution might improve Arctic climate model projections by providing a more accurate OHT. In our study, we show that a finer ocean resolution enhances OHT and thus results in reduced Arctic sea-ice area and volume, in better agreement with observations for ECMWF-IFS and HadGEM3.
Our analysis also corroborates the findings from Li et al. (2017), who identify a significant anti-correlation between trends in winter Barents sea-ice extent and trends in OHT at the BSO across the CMIP5 models. They also find a weak correlation between trends in winter Barents sea-ice extent and trends in global mean surface air temperature, suggesting a leading role of the enhanced Atlantic OHT in the winter Barents sea-ice extent decline. Our study goes beyond the analysis of Li et al. (2017) by investigating the impact of resolution on the OHT-sea ice relationship in several Arctic regions.
The study of Burgard and Notz (2017) indicates a significant negative correlation between the mean Atlantic meridional ocean heat flux (OHF) and mean sea-ice area across 26 CMIP5 models, in agreement with our study. 15 models used in their analysis show an increase in the cumulated energy anomaly from the meridional OHF over the period 1961-2099, while 9 models provide a decrease in this quantity and the OHF is relatively constant in two models, with all models having a negative trend in Arctic sea-ice area over that time period. This suggests that for the 9 models showing a decrease in OHF, there is a positive correlation between ocean heat flux and sea-ice area. However, Burgard and Notz (2017) consider a much longer period than we do here, by including not only historical CMIP5 simulations, but also RCP4.5 simulations up to the end of the 21st century. The OHF decrease in the 9 models mentioned above appears only during the projection simulations (around 2010-2040). Thus, a potential source of difference between our analysis and their study is the fact that the Arctic regions dominating the anti-correlation between sea-ice area and OHT in our study (e.g. Barents/Kara and GIN Seas) could be ice free during the projection phase of Burgard and Notz (2017). Furthermore, the methodological approach of Burgard and Notz (2017) for computing OHF differs from ours in several aspects, including the latitude at which the OHF is computed (\(66^\circ \hbox {N}\) in their analysis) and the statistical analysis of the relationship between OHF and sea-ice area. For the latter aspect, they do not detrend OHF and sea-ice area when comparing both quantities together, and they consider annual mean OHF and annual mean sea-ice area, while we correlate annual mean OHT and monthly mean sea-ice area for all months of the year. Therefore, we think that all these methodological differences between Burgard and Notz (2017) and our study make it difficult to perform a direct and meaningful comparison.
Our results are in line with the analysis of Auclair and Tremblay (2018), who use 40 CESM-LE members with a nominal resolution of \(1^\circ\) in all climate components (atmosphere, ocean, land, sea ice). They define a rapid sea-ice decline as a period of at least 4 years for which the trend in the 5-year running mean minimum sea-ice extent is lower than \(-\,0.3\) million \(\hbox {km}^2\,\hbox {a}^{-1}\). All members present at least one rapid sea-ice decline, and \(80\%\) of these rapid declines are correlated to OHT anomalies, mainly those of the BSO and Bering Strait. In their study, they find that changes in OHT cause rapid sea-ice declines when the sea-ice extent is large enough to cover the continental shelves and that the atmosphere is the main driver when the initial sea-ice extent only covers the deep basins. By using 40 members, they are able to confirm the robustness of CESM-LE results.
Finally, the relationships between Arctic sea-ice area/volume and OHT are confirmed by control runs. This supports the hypothesis that these correlations cannot be caused by the anthropogenic global warming signal.
4.3 Issues associated with a multi-model analysis on resolution dependence
Below we identify four issues inherent with a multi-model analysis on resolution dependence.
First, part of the differences observed between two configurations of the same model is due to the change in resolution, but another part is due to different values of model parameters and the specific parameterizations used in the different configurations (Table 1). Some of these differences are unavoidable. For example, the Gent and McWilliams (1990) parameterization is necessary at low resolution to represent eddies and is switched off at higher resolution (typically around 25-50 km). Furthermore, models need to adapt the eddy viscosity as a function of their resolution. The model time step also needs to decrease at finer resolution. Beside model resolution, differences between model configurations are thus limited to model-dependent parameterizations and time step. Note that the primary goal of PRIMAVERA and HighResMIP is to specifically test the role of horizontal resolution by running the same models at different resolutions and only changing the parameters that are known function of resolution. The combination of limited differences in tuning parameters between model configurations (other than the resolution) and agreement with previous studies (e.g. Hewitt et al. 2016; Roberts et al. 2016, 2018; Grist et al. 2018) indicates that our findings are robust for the models studied.
Second, the limited number of ensemble members for the models used in this analysis does not allow us to perform a full assessment of internal variability. However, for ECMWF-LR and ECMWF-HR, we have 6 and 4 members, respectively. This is probably not sufficient to assess the full spectrum of internal variability for these two model configurations, but results show that the anti-correlation between sea-ice area and OHT is a robust feature across all members of these two configurations (not shown), which strengthens our findings related to sea ice-OHT interactions.
Additionally, under the HighResMIP framework, adopted in this paper, a short spin-up of 30–50 years is implemented, which may affect the results, especially the historical runs (hist-1950). To address this issue, parallel control runs (control-1950) have been examined to check the impacts of model drift and forcing on the results. For our analysis, we note that our key results are overall similar when using historical and control runs. We also identify that the trends in sea-ice area and volume are significantly different in historical runs compared to control runs, so that the impact of model drift is smaller than the impact of the forcing.
Finally, the computation of ocean areas based on the model masks between the two configurations of the same model sometimes reveals non-negligible differences. If we compute the ocean area north of \(40^\circ \hbox {N}\) (40–45 million \(\hbox {km}^2\)), the inter-configuration differences stay relatively small when the ocean grid is used (i.e. \(-\,0.2\%\) between HadGEM3-MM and HadGEM3-LL and \(-\,1.4\%\) between ECMWF-HR and ECMWF-LR). However, if the atmosphere grid is used, the differences are larger. Arctic sea-ice area from HadGEM3 and AWI-CM models is computed on the atmosphere grid since sea-ice concentration is provided on this grid. The difference in ocean area north of \(40^\circ \hbox {N}\) is \(+3.9\%\) between HadGEM3-MM and HadGEM3-LL, and \(-\,3.8\%\) between AWI-HR and AWI-LR, when the atmosphere grid is used. This has to be considered when interpreting the difference in Arctic sea-ice area of \(-\,8\%\) between HadGEM3-MM and HadGEM3-LL, and \(-\,14\%\) between AWI-HR and AWI-LR (Table 2). Therefore, the increased ocean area in HadGEM3-MM compared to HadGEM3-LL probably weakens the effect of sea-ice area reduction due to resolution, while the decreased ocean area in AWI-HR compared to AWI-LR probably amplifies this reduction. These different oceanic areas do not, however, affect the OHT-sea ice regression slopes.
5 Conclusions
This paper presents the first model intercomparison regarding the impact of horizontal resolution on both Arctic sea ice and Atlantic OHT arising from HighResMIP in the framework of the EU Horizon 2020 PRIMAVERA project. We analyze the outputs from five different coupled GCMs, i.e. HadGEM3, ECMWF-IFS, AWI-CM, CMCC-CM2 and MPI-ESM, with each model using at least two different horizontal resolutions (in both the atmosphere and ocean for the three first models, and only in the atmosphere for the last two models).
We show that using a finer ocean resolution decreases both Arctic sea-ice area and volume in HadGEM3, ECMWF-IFS and AWI-CM, providing results in better agreement with observations and reanalysis for HadGEM3 and ECMWF-IFS. The mean sea-ice thickness clearly decreases with finer ocean resolution for ECMWF-IFS and AWI-CM, while it stays relatively similar for HadGEM3. Trends in Arctic sea-ice area and volume over 1979–2014 are less negative with finer ocean resolution (except the trend in sea-ice area of AWI-CM). The location of the Arctic sea-ice edge is better represented with finer ocean resolution. The impact of atmosphere resolution on sea ice is less clear and leads to different results depending on the model used.
The mean poleward Atlantic OHT increases with ocean resolution in HadGEM3, ECMWF-IFS and AWI-CM. Trends in Atlantic OHT at \(50^\circ \hbox {N}\), \(60^\circ \hbox {N}\) and \(70^\circ \hbox {N}\) decrease with finer ocean resolution. The majority of the model configurations used here show a significant positive trend of Atlantic OHT at \(70^\circ \hbox {N}\) over 1979–2014, in agreement with negative trends in Arctic sea-ice area and volume. Again, the impact of atmosphere resolution on OHT is not obvious.
The use of a finer ocean resolution allows to greatly improve the representation of SST and ocean surface velocity. These two quantities increase with finer ocean resolution, especially between \(40^\circ \hbox {N}\) and \(70^\circ \hbox {N}\). More specifically, we show that using a \(1^\circ\) ocean resolution is not sufficient to accurately model SST and sea-surface velocity. This is especially relevant when looking at specific Arctic sectors, such as the Barents Sea. The use of an ocean resolution of \(\sim 0.25^\circ\) allows to better represent the complex ocean circulation there.
While reduced Arctic sea-ice area and volume are strongly correlated to increased OHT north of \(60^\circ \hbox {N}\) in the models studied, these relationships do not systematically change with resolution. The higher the latitude to compute OHT, the stronger the anticorrelation between Arctic sea-ice area and OHT. The specific Arctic regions that are more directly influenced by Atlantic OHT are in the Atlantic sector of the Arctic Ocean, i.e. Barents/Kara Seas and GIN Seas, which first receive the warm Atlantic water inflow.
Finally, we encourage further studies on the role of model resolution on Arctic sea ice and North Atlantic OHT. As HighResMIP is still ongoing at the time of writing, more model outputs and analyses will be provided, which will give insights into our understanding of the impact of resolution. In particular, the inclusion of more ensemble members of the same model configuration will allow assessing the role of internal variability. These studies will allow reducing the uncertainties related to model projections of Arctic climate.
References
Arthun M, Eldevik T, Smedsrud LH, Skagseth O, Ingvaldsen RB (2012) Quantifying the influence of Atlantic heat on Barents Sea ice variability and retreat. J Clim 25:4736–4743. https://doi.org/10.1175/JCLI-D-11-00466.1
Arthun M, Eldevik T, Smedsrud LH (2019) The role of Atlantic heat transport in future Arctic winter sea ice loss. J Clim 32:3327–3341. https://doi.org/10.1175/JCLI-D-18-0750.1
Auclair G, Tremblay B (2018) The role of ocean heat transport in rapid sea ice declines in the Community Earth System Model Large Ensemble. J Geophys Res 123:8941–8957. https://doi.org/10.1029/2018JC014525
AWI (2018a) AWI-CM1.1HR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.AWI.AWI-CM-1-1-HR.hist-1950
AWI (2018b) AWI-CM1.1LR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.AWI.AWI-CM-1-1-LR.hist-1950
Balsamo G, Beljaars A, Scipal K, Viterbo P, van den Hurk B, Hirschi M, Betts AK (2009) A revised hydrology for the ECMWF model: verification from field site to terrestrial water storage and impact in the integrated forecast system. J Hydrometeorol 10:623–643. https://doi.org/10.1175/2008JHM1068.1
Barber DG, Meier WN, Gerland S, Mundy C, Holland M, Kern S, Li Z, Michel C, Perovich DK, Tamura T (2017) Arctic sea ice. In: Snow, water, ice and permafrost in the Arctic (SWIPA) 2017. Tech. rep., Arctic Monitoring and Assessment Programme (AMAP), Oslo, Norway
Best MJ, Pryor M, Clark DB, Rooney GG, Essery RLH, Ménard CB, Edwards JM, Hendry MA, Porson A, Gedney N, Mercado LM, Sitch S, Blyth E, Boucher O, Cox PM, Grimmond CSB, Harding RJ (2011) The Joint UK land environment simulator (JULES), model description, Part 1: energy and water fluxes. Geosci Model Dev 4(3):677–699. https://doi.org/10.5194/gmd-4-677-2011
Bingham RJ, Hughes CW, Roussenov V, Williams RG (2007) Meridional coherence of the North Atlantic meridional overturning circulation. Geophys Res Lett. https://doi.org/10.1029/2007GL031731
Bitz CM, Roe GH (2004) A mechanism for the high rate of sea ice thinning in the Arctic Ocean. J Clim 17:3623–3632
Burgard C, Notz D (2017) Drivers of Arctic Ocean warming in CMIP5 models. Geophys Res Lett 44:4263–4271. https://doi.org/10.1002/2016GL072342
Carmack E, Polyakov I, Padman L, Fer I, Hunke E, Hutchings J, Jackson J, Kelley K, Kwok R, Layton C, Melling H, Perovich D, Persson O, Ruddick B, Timmermans ML, Toole J, Ross T, Vavrus S, Winsor P (2015) Toward quantifying the increasing role of oceanic heat in sea ice loss in the new Arctic. Bull Am Meteorol Soc 96:2079–2105. https://doi.org/10.1175/BAMS-D-13-00177.1
Cherchi A, Fogli PG, Lovato T, Peano D, Iovino D, Gualdi S, Masina S, Scoccimarro E, Materia S, Bellucci A, Navarra A (2018) Global mean climate and main patterns of variability in the CMCC-CM2 coupled model. J Adv Model Earth Syst 11:185. https://doi.org/10.1029/2018MS001369
Chevallier M, Smith GC, Dupont F, Lemieux JF, Forget G, Fujii Y, Hernandez F, Msadek R, Andrew K, Peterson Storto A, Toyoda T, Valdivieso M, Vernieres G, Zuo H, Balmaseda M, Chang YS, Ferry N, Garric G, Haines K, Keeley S, Kovach RM, Kuragano T, Masina S, Tang Y, Tsujino H, Wang X (2017) Intercomparison of the Arctic sea ice cover in global ocean-sea ice reanalyses from the ORA-IP project. Clim Dyn 49(3):1107–1136. https://doi.org/10.1007/s00382-016-2985-y
CMCC (2018a) CMCC-CM2-HR4 model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.CMCC.CMCC-CM2-HR4.hist-1950
CMCC (2018b) CMCC CMCC-CM2-VHR4 model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.CMCC.CMCC-CM2-VHR4.hist-1950
Cullen MJP (1993) The unified forecast/climate model. Meteorol Mag 112(1449):81–94
Daniault N, Mercier H, Lherminier P, Sarafanov A, Falina A, Zunino P, Pérez FF, Rios AF, Ferron B, Huck T, Thierry V, Gladyshev S (2016) The northern North Atlantic Ocean mean circulation in the early 21st century. Prog Oceanogr 146:142–158. https://doi.org/10.1016/j.pocean.2016.06.007
Döscher R, Vihma T, Maksimovich E (2014) Recent advances in understanding the Arctic climate system state and change from a sea ice perspective: a review. Atmos Chem Phys 14:13,571–13,600. https://doi.org/10.5194/acp-14-13571-2014
ECMWF (2018a) ECMWF-IFS-HR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.ECMWF.ECMWF-IFS-HR.hist-1950
ECMWF (2018b) ECMWF-IFS-LR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.ECMWF.ECMWF-IFS-LR.hist-1950
ECMWF (2018c) ECMWF-IFS-MR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.ECMWF.ECMWF-IFS-MR.hist-1950
England M, Jahn A, Polvani L (2019) Non-uniform contribution of internal variability to recent Arctic sea ice loss. J Clim. https://doi.org/10.1175/JCLI-D-18-0864.1
EUMETSAT OSI SAF (2017) Global sea ice concentration climate data record 1979-2015 (v2.0, 2017)
Fichefet T, Maqueda MMA (1997) Sensitivity of a global sea ice model to the treatment of ice thermodynamics and dynamics. J Geophys Res 102:12609–12646
Gent PR, McWilliams JC (1990) Isopycnal mixing in ocean circulation models. J Phys Oceanogr 20:150–155. https://doi.org/10.1175/2011JCLI4083.1
Goosse H, Kay JE, Armour KC, Bodas-Salcedo A, Chepfer H, Docquier D, Jonko A, Kushner PJ, Lecomte O, Massonnet F, Park HS, Pithan F, Svensson G, Vancoppenolle M (2018) Quantifying climate feedbacks in polar regions. Nat Commun 9:1919. https://doi.org/10.1038/s41467-018-04173-0
Grist JP, Josey SA, New AL, Roberts MJ, Koenigk T, Iovino D (2018) Increasing Atlantic Ocean heat transport in the latest generation coupled ocean-atmosphere models: the role of air-sea interaction. J Geophys Res. https://doi.org/10.1029/2018JC014387
Haarsma RJ, Roberts MJ, Vidale PL, Senior CA, Bellucci A, Bao Q, Chang P, Corti S, Fuckar NS, Guemas V, von Hardenberg J, Hazeleger W, Kodama C, Koenigk T, Leung LR, Lu J, Luo JJ, Mao J, Mizielinski MS, Mizuta R, Nobre P, Satoh M, Scoccimarro E, Semmler T, Small J, von Storch JS (2016) High Resolution Model Intercomparison Project (HighResMIP v1.0) for CMIP6. Geosci Model Dev 9:4185–4208. https://doi.org/10.5194/gmd-9-4185-2016
Hewitt HT, Roberts MJ, Hyder P, Graham T, Rae J, Belcher SE, Bourdallé-Badie R, Copsey D, Coward A, Guiavarch C, Harris C, Hill R, Hirschi JJM, Madec G, Mizielinski MS, Neininger E, New AL, Rioual JC, Sinha B, Storkey D, Shelly A, Thorpe L, Wood RA (2016) The impact of resolving the Rossby radius at mid-latitudes in the ocean: results from a high-resolution version of the Met Office GC2 coupled model. Geosci Model Dev 9:3655–3670. https://doi.org/10.5194/gmd-9-3655-2016
Holliday NP, Bacon S, Cunningham SA, Li F, Mcdonagh EL (2018) Subpolar North Atlantic overturning and gyre-scale circulation in the summers of 2014 and 2016. J Geophys Res 123:4538–4559. https://doi.org/10.1029/2018JC013841
Hunke E, Lipscomb W, Turner A, Jeffery N, Elliott S (2015) CICE: the Los Alamos sea ice model, documentation and software user’s manual, Version 5.1. (Tech. Rep. LA-CC-06-012.). Tech. rep., Los Alamos National Laboratory
Ivanov VV, Alexeev VA, Repina I, Koldunov NV, Smirnov A (2012) Tracing Atlantic Water signature in the Arctic sea ice cover east of Svalbard. Adv Meteorol. https://doi.org/10.1155/2012/201818
Johns WE, Baringer MO, Beal LM, Cunningham SA, Kanzow T, Bryden HL, Hirschi JJM, Marotzke J, Meinen CS, Shaw B, Curry R (2011) Continuous, array-based estimates of Atlantic Ocean heat transport at 26.5 N. J Clim 24:2429–2449. https://doi.org/10.1175/2010JCLI3997.1
Jungclaus JH, Fischer N, Haak H, Lohmann K, Marotzke J, Matei D, Mikolajewicz U, Notz D, von Storch JS (2013) Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM): the ocean component of the MPI-Earth system model. J Adv Model Earth Syst 5:422–446. https://doi.org/10.1002/jame.20023
Kirtman BP, Bitz C, Bryan F, Collins W, Dennis J, Hearn N, Kinter JL, Loft R, Rousset C, Siqueira L, Stan C, Tomas R, Vertenstein M (2012) Impact of ocean model resolution on CCSM climate simulations. Clim Dyn 39:1303–1328. https://doi.org/10.1007/s00382-012-1500-3
Koenigk T, Brodeau L (2014) Ocean heat transport into the Arctic in the twentieth and twenty-first century in EC-Earth. Clim Dyn 42:3101–3120. https://doi.org/10.1007/s00382-013-1821-x
Koenigk T, Caian M, Nikulin G, Schimanke S (2016) Regional Arctic sea ice variations as predictor for winter climate conditions. Clim Dyn 46:317–337. https://doi.org/10.1007/s00382-015-2586-1
Kuhlbrodt T, Jones CG, Sellar A, Storkey D, Blockley E, Stringer M, Hill R, Graham T, Ridley J, Blaker A, Calvert D, Copsey D, Ellis R, Hewitt H, Hyder P, Ineson S, Mulcahy J, Siahaan A, Walton J (2018) The low-resolution version of HadGEM3 GC3.1: development and evaluation for global climate. J Adv Model Earth Syst 10:2865–2888. https://doi.org/10.1029/2018MS001370
Kwok R (2018) Arctic sea ice thickness, volume, and multiyear ice coverage: losses and coupled variability (1958–2018). Environ Res Lett 13(10):105005. https://doi.org/10.1088/1748-9326/aae3ec
Kwok R, Cunningham GF, Wensnahan M, Rigor I, Zwally HJ, Yi D (2009) Thinning and volume loss of the Arctic Ocean sea ice cover: 2003–2008. J Geophys Res. https://doi.org/10.1029/2009JC005312
Lavergne T, Sorensen AM, Kern S, Tonboe R, Notz D, Aaboe S, Bell L, Dybkjaer G, Eastwood S, Gabarro C, Heygster G, Killie MA, Kreiner MB, Lavelle J, Saldo R, Sandven S, Pedersen LT (2019) Version 2 of the EUMETSAT OSI SAF and ESA CCI sea-ice concentration climate data records. Cryosphere 13:49–78. https://doi.org/10.5194/tc-13-49-2019
Li D, Zhang R, Knutson TR (2017) On the discrepancy between observed and CMIP5 multi-model simulated Barents Sea winter sea ice decline. Nat Commun 8:14991. https://doi.org/10.1038/ncomms14991
Lindsay R, Schweiger A (2015) Arctic sea ice thickness loss determined using subsurface, aircraft, and satellite observations. Cryosphere 9:269–283. https://doi.org/10.5194/tc-9-269-2015
Lindsay R, Wensnahan M, Schweiger A, Zhang J (2014) Evaluation of seven different atmospheric reanalysis products in the Arctic. J Clim 27(7):2588–2606. https://doi.org/10.1175/JCLI-D-13-00014.1
Madec G (2016) NEMO ocean engine. Note du Pôle de modélisation, Institut Pierre-Simon Laplace (IPSL), France, No 27, ISSN No 1288-1619
Mahlstein I, Knutti R (2011) Ocean heat transport as a cause for model uncertainty in projected Arctic warming. J Clim 24:1451–1460. https://doi.org/10.1175/2010JCLI3713.1
Massonnet F, Vancoppenolle M, Goosse H, Docquier D, Fichefet T, Blanchard-Wrigglesworth E (2018) Arctic sea-ice change tied to its mean state through thermodynamic processes. Nat Clim Change 8:599–603. https://doi.org/10.1038/s41558-018-0204-z
MOHC (2018a) HadGEM3-GC31-HM model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.MOHC.HadGEM3-GC31-HM.hist-1950
MOHC (2018b) HadGEM3-GC31-LL model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.MOHC.HadGEM3-GC31-LL.hist-1950
MOHC (2018c) HadGEM3-GC31-MM model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.MOHC.HadGEM3-GC31-MM.hist-1950
MPI-M (2018) MPI-ESM1.2-HR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.MPI-M.MPI-ESM1-2-HR.hist-1950
MPI-M (2019) MPI-ESM1.2-XR model output prepared for CMIP6 HighResMIP hist-1950. Earth System Grid Federation. http://cera-www.dkrz.de/WDCC/meta/CMIP6/CMIP6.HighResMIP.MPI-M.MPI-ESM1-2-XR.hist-1950
Müller WA, Jungclaus JH, Mauritsen T, Baehr J, Bittner M, Budich R, Bunzel F, Esch M, Ghosh R, Haak H, Ilyina T, Kleine T, Kornblueh L, Li H, Modali K, Notz D, Pohlmann H, Roeckner E, Stemmler I, Tian F, Marotzke J (2018) A higher-resolution version of the Max Planck Institute Earth System Model (MPI-ESM1.2-HR). J Adv Model Earth Syst 10:1383–1413. https://doi.org/10.1029/2017MS001217
Neale RB, Richter J, Park S, Lauritzen PH, Vavrus SJ, Rasch PJ, Zhang M (2013) The mean climate of the Community Atmosphere Model (CAM4) in forced SST and fully coupled experiments. J Clim 26:5150–5168. https://doi.org/10.1029/2007GL031138
Notz D (2014) Sea-ice extent and its trend provide limited metrics of model performance. Cryosphere 8(1):229–243. https://doi.org/10.5194/tc-8-229-2014, http://www.the-cryosphere.net/8/229/2014/
Notz D, Stroeve J (2016) Observed Arctic sea-ice loss directly follows anthropogenic CO2 emission. Science 354(6313):747–750. https://doi.org/10.1126/science.aag2345
Notz D, Jahn A, Holland M, Hunke E, Massonnet F, Stroeve J, Tremblay B, Vancoppenolle M (2016) The CMIP6 Sea-Ice Model Intercomparison Project (SIMIP): understanding sea ice through climate-model simulations. Geosci Model Dev 9:3427–3446. https://doi.org/10.5194/gmd-9-3427-2016
Oleson KW, Lawrence DM, Bonan GB, Drewniak B, Huang M, Koven C, et al (2013) Technical description of version 4.5 of the Community Land Model (CLM). Tech. rep., NCAR Technical Note
Onarheim IH, Eldevik T, Smedsrud LH, Stroeve JC (2018) Seasonal and regional manifestation of Arctic sea ice loss. J Clim 31:4917–4932. https://doi.org/10.1175/JCLI-D-17-0427.1
Petty AA, Stroeve JC, Holland PR, Boisvert LN, Bliss AC, Kimura N, Meier WN (2018) The Arctic sea ice cover of 2016: a year of record-low highs and higher-than-expected lows. Cryosphere 12(2):433–452. https://doi.org/10.5194/tc-12-433-2018
Polyakov IV, Pnyushkov AV, Alkire MB, Ashik IM, Baumann TM, Carmack EC, Goszczko I, Guthrie J, Ivanov VV, Kanzow T, Krishfield R, Kwok R, Sundfjord A, Morison J, Rember R, Yulin A (2017) Greater role for Atlantic inflows on sea-ice loss in the Eurasian Basin of the Arctic Ocean. Science 356(6335):285–291. https://doi.org/10.1126/science.aai8204
Pujol MI (2017) Copernicus Marine Environment Monitoring Service: Sea Level TAC - DUACS products. Quality Information Document
Rackow T, Goessling HF, Jung T, Sidorenko D, Semmler T, Barbi D, Handorf D (2018) Towards multi-resolution global climate modeling with ECHAM6-FESOM. Part II: climate variability. Clim Dyn 50:2369–2394. https://doi.org/10.1007/s00382-016-3192-6
Reynolds RW, Smith TM, Liu C, Chelton DB, Casey KS, Schlax MG (2007) Daily high-resolution-blended analyses for sea surface temperature. J Clim 20:5473–5496. https://doi.org/10.1175/2007JCLI1824.1
Roberts CD, Senan R, Molteni F, Boussetta S, Mayer M, Keeley SPE (2018) Climate model configurations of the ECMWF Integrated Forecast System (ECMWF-IFS cycle 43r1) for HighResMIP. Geosci Model Dev 11:3681–3712. https://doi.org/10.5194/gmd-11-3681-2018
Roberts MJ, Hewitt HT, Hyder P, Ferreira D, Josey SA, Mizielinski M, Shelly A (2016) Impact of ocean resolution on coupled air-sea fluxes and large-scale climate. Geophys Res Lett 43:10430–10438. https://doi.org/10.1002/2016GL070559
Roessler A, Rhein M, Kieke D, Mertens C (2015) Long-term observations of North Atlantic Current transport at the gateway between western and eastern Atlantic. J Geophys Res 120:4003–4027. https://doi.org/10.1002/2014JC010662
Sando AB, Nilsen JEO, Gao Y, Lohmann K (2010) Importance of heat transport and local air-sea heat fluxes for Barents Sea climate variability. J Geophy Res 115(C07):013. https://doi.org/10.1029/2009JC005884
Sando AB, Gao Y, Langehaug R (2014a) Poleward ocean heat transports, sea ice processes, and Arctic sea ice variability in NorESM1-M simulations. J Geophys Res 119:2095–2108. https://doi.org/10.1002/2013JC009435
Sando AB, Melsom A, Budgell WP (2014b) Downscaling IPCC control run and future scenario with focus on the Barents Sea. Ocean Dyn 64:927–949. https://doi.org/10.1007/s10236-014-0731-8
Schweiger A, Lindsay R, Zhang J, Steele M, Stern H, Kwok R (2011) Uncertainty in modeled Arctic sea ice volume. J Geophys Res 116:C00D06. https://doi.org/10.1029/2011JC007084
Sein DV, Danilov S, Biastoch A, Durgadoo JV, Sidorenko D, Harig S, Wang Q (2016) Designing variable ocean model resolution based on the observed ocean variability. J Adv Model Earth Syst 8(2):904–916. https://doi.org/10.1002/2016MS000650
Sein DV, Koldunov NV, Danilov S, Sidorenko D, Wekerle C, Cabos W, Rackow T, Scholz P, Semmler T, Wang Q, Jung T (2018) The relative influence of atmospheric and oceanic model resolution on the circulation of the North Atlantic Ocean in a coupled climate model. J Adv Model Earth Syst 10:2026–2041. https://doi.org/10.1029/2018MS001327
Sidorenko D, Rackow T, Jung T, Semmler T, Barbi D, Danilov S, Dethloff K, Dorn W, Fieg K, Goessling HF, Handorf D, Harig S, Hiller W, Juricke S, Losch M, Schröter J, Sein DV, Wang Q (2015) Towards multi-resolution global climate modeling with ECHAM6-FESOM. Part I: model formulation and mean climate. Clim Dyn 44:757–780. https://doi.org/10.1007/s00382-014-2290-6
Skagseth O, Orvik KA, Furevik T (2004) Coherent variability of the Norwegian Atlantic Slope Current derived from TOPEX/ERS altimeter data. Geophys Res Lett. https://doi.org/10.1029/2004GL020057
Stevens B, Giorgetta M, Esch M, Mauritsen T, Crueger T, Rast S, Salzmann M, Schmidt H, Bader J, Block K, Brokopf R, Fast I, Kinne S, Kornblueh L, Lohmann U, Pincus R, Reichler T, Roeckner E (2013) Atmospheric component of the MPI-M earth system model: ECHAM6. J Adv Model Earth Syst 5:146–172. https://doi.org/10.1002/jame.20015
Storkey D, Blaker AT, Mathiot P, Megann A, Aksenov Y, Blockley EW, Calvert D, Graham T, Hewitt HT, Hyder P, Kuhlbrodt T, Rae JGL, Sinha B (2018) UK Global Ocean GO6 and GO7: a traceable hierarchy of model resolutions. Geosci Model Dev 11:3187–3213. https://doi.org/10.5194/gmd-11-3187-2018
Trenberth KE, Caron JM (2001) Estimates of meridional atmosphere and ocean heat transports. J Clim 14:3433–3443
Trenberth KE, Fasullo JT (2017) Atlantic meridional heat transports computed from balancing Earth energy locally. Geophys Res Lett 44:1919–1927. https://doi.org/10.1002/2016GL072475
Vaughan D, Comiso J, Allison I, Carrasco J, Kaser G, Kwok R, Mote P, Murray T, Paul F, Ren J, Rignot E, Solomina O, Steffen K, Zhang T (2013) Observations: cryosphere. In: Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker, T. F., D. Qin, G.-K. Plattner, M. Tignor, S. K. Allen, J. Boschung, A. Nauels, Y. Xia, V. Bex and P. M. Midgley (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
Wang Q, Danilov S, Sidorenko D, Timmermann R, Wekerle C, Wang X, Jung T, Schröter J (2014) The finite element sea ice-ocean model (FESOM) vol 1.4: formulation of an ocean general circulation model. Geosci Model Dev 7:663–693. https://doi.org/10.5194/gmd-7-663-2014
Williams KD, Copsey D, Blockleya EW, Bodas-Salcedo A, Calvert D, Comer R, Davis P, Graham T, Hewitt HT, Hill R, Hyder P, Ineson S, Johns TC, Keen AB, Lee RW, Megann A, Milton SF, Rae JGL, Roberts MJ, Scaife AA, Schiemann R, Storkey D, Thorpe L, Watterson IG, Walters DN, West A, Wood RA, Woollings T, Xavier PK (2018) The met office global coupled model 3.0 and 3.1 (GC3.0 and GC3.1) configurations. J Adv Model Earth Syst 10:357–380. https://doi.org/10.1002/2017MS001115
Zhang J, Rothrock DA (2003) Modeling global sea ice with a thickness and enthalpy distribution model in generalized curvilinear coordinates. Mon Weather Rev 131:845–861
Zygmuntowska M, Rampal P, Ivanova N, Smedsrud LH (2014) Uncertainties in Arctic sea ice thickness and volume: new estimates and implications for trends. Cryosphere 8:705–720. https://doi.org/10.5194/tc-8-705-2014
Acknowledgements
David Docquier, Jeremy P. Grist, Malcolm J. Roberts, Christopher D. Roberts, Dmitry V. Sein, Doroteaciro Iovino and Alessio Bellucci are funded by the EU Horizon 2020 PRIMAVERA project, grant agreement no. 641727. Jeremy P. Grist is also funded by ‘The North Atlantic Climate System Integrated Study: ACSIS’ programme (NE/N018044/1) of the Natural Environment Research Council of the UK. Malcolm J. Roberts is also supported by the Joint UK BEIS/Defra Met Office Hadley Centre Climate Programme (GA01101). Leandro Ponsoni is funded by the EU Horizon 2020 APPLICATE project, grant agreement no. 727862. François Massonnet is funded by the Fonds National de la Recherche Scientifique (FNRS, Belgium) and was funded by the Ministerio de Economía, Industria y Competitividad (MINECO, Spain). Dmitry V. Sein is also supported by the state assignment of FASO Russia (theme no. 0149-2019-0015). Computations have been performed on the JASMIN platform managed by the Centre for Environmental Data Archive (CEDA, UK), from which model data are available. We thank Jon Seddon (Met Office) for his enormous contribution in making the PRIMAVERA model data available. Computational resources have also been provided by the Deutsches Klimarechenzentrum (DKRZ). We thank Pierre-Yves Barriat (UCLouvain) for his help in using computing resources at UCLouvain. We also thank Eleftheria Exarchou and Javier Vegas-Vegidor (BSC) for their help in using CDFTOOLS on JASMIN. We acknowledge Kevin Trenberth and John Fasullo (NCAR) for providing their OHT estimates. We also thank Jan Hegewald (AWI) for his substantial contribution in running AWI-CM. We acknowledge Katja Lohmann (MPI) for information provided related to the MPI-ESM model. Data from the RAPID-MOCHA program are funded by the US National Science Foundation and UK Natural Environment Research Council and are freely available at www.rapid.ac.uk/rapidmoc and mocha.rsmas.miami.edu/mocha. We acknowledge Randi Ingvaldsen for providing observations of OHT at the Barents Sea Opening. We finally thank the editor Jean-Claude Duplessy and three anonymous reviewers for their very helpful comments during the revision of our paper.
Author information
Authors and Affiliations
Contributions
DD, TF and JPG designed the science plan. DD analyzed the model outputs, produced the figures and wrote the manuscript with the contribution from all co-authors. MJR, CDR, TS/DS/DVS and DI/AB provided insights about their respective models. TS and DS performed the OHT computations from AWI-CM, while CDR computed OHT from ECMWF-IFS. LP and FM provided useful comments to help improve the analysis.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Docquier, D., Grist, J.P., Roberts, M.J. et al. Impact of model resolution on Arctic sea ice and North Atlantic Ocean heat transport. Clim Dyn 53, 4989–5017 (2019). https://doi.org/10.1007/s00382-019-04840-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04840-y