Abstract
Two or more spatio-temporally co-located meteorological/climatological extremes (co-occurring extremes) place far greater stress on human and ecological systems than any single extreme could. This was observed during the California drought of 2011–2015 where multiple years of negative precipitation anomalies occurred simultaneously with positive temperature anomalies resulting in California’s worst drought on observational record. The large-scale drivers which modulate the occurrence of extremes in two or more variables remains largely unexplored. Using California wintertime (November–April) temperature and precipitation as a case study, we apply a novel, nonparametric conditional probability distribution method that allows for evaluation of complex, multivariate, and nonlinear relationships that exist among temperature, precipitation, and various indicators of large-scale climate variability and change. We find that multivariate variability and statistics of temperature and precipitation exhibit strong spatial variation across scales that are often treated as being homogeneous. Further, we demonstrate that the multivariate statistics of temperature and precipitation are highly non-stationary and therefore require more robust and sophisticated statistical techniques for accurate characterization. Of all the indicators of the large-scale climate conditions we studied, the dipole index explains the greatest fraction of multivariate variability in the co-occurrence of California wintertime extremes in temperature and precipitation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Single meteorological or climatological extremes have a strong and disproportionate impact on societies, ecological systems, and natural environments. However, the joint occurrence of two or more co-occurring extremes has the potential to negatively impact human and natural systems in ways far greater than any single event could (Leonard et al. 2014). For example, drought is commonly thought of as a result of only a lack of precipitation, i.e. meteorological drought. However, negative precipitation anomalies co-occurring with positive temperature anomalies can greatly exacerbate drought conditions due to the increased evapotranspirative demand placed on the system, i.e. agricultural drought (AghaKouchak et al. 2014; Diffenbaugh et al. 2015). Positive temperature anomalies coupled with high humidity can result in extreme heat index values, which can be detrimental to human health (Steadman 1979; Wehner et al. 2016). Flooding can result from both unusually intense precipitation events and unusually long-lived events; however, when unusually long-lived events are also unusually intense in terms of their precipitation rate, flooding can be abrupt and extreme, leading to loss of life, property damage, and severely compromised infrastructure. While much is known about heat extremes, drought extremes, and precipitation extremes individually, little is known about what controls their co-occurrence both regionally and globally.
Understanding what controls the co-occurrence of extremes, their natural variability, and how they have changed in past, present, and future climates is challenging in light of anthropogenic forcing and the lack of a historical analogue that could shed light on the climate response to such forcing. In addition to anthropogenic forcing, variability also arises naturally from the presence of large-scale, low-frequency atmosphere–ocean interactions known as teleconnections (Polade et al. 2013). These modes of variability are well-documented to have a detectable signature on climatological precipitation and temperature patterns and to modulate the occurrence of extremes (Cayan et al. 1999; Krichak et al. 2014). To date, few studies have focused on the role large-scale climate patterns play in driving and altering the probabilities for experiencing co-occurring extremes. Diffenbaugh et al. (2015) demonstrated that the occurrence of drought has been exacerbated by anthropogenic factors, specifically in California, USA, by increasing the probability that any given dry year(s) will coincide with warm years. AghaKouchak et al. (2014) showed that the return period for the hot and dry conditions that prevailed during the California winter of 2014 was dramatically increased by considering the joint probability of temperature and precipitation (AghaKouchak et al. 2014). While these and similar studies begin to address the role that large-scale climate conditions may play in modulating extremes and their joint occurrence, there has been no systematic study that addresses the role modes of variability play in altering the probabilities for experiencing co-occurring extremes. Further, previous studies (e.g. AghaKouchak et al. 2014) assume that the statistics of meteorological and climatological variables are stationary, meaning that the descriptive statistics of variables do not change over time. However, given the influence these modes of variability have on California’s hydroclimate and the significant alteration of the background state of the climate by human activities, it is reasonable to assume that climate statistics are not stationary (Serinaldi and Kilsby 2015). To account for nonstationarity in higher dimensional distributions Sarhadi et al. (2018) employ a vine copula approach to assess the change in risk of hot and dry conditions in CMIP5 models resulting from human activities, but do not consider the roles of natural modes of variability have on the bivariate distributions.
To address the highlighted gap in knowledge, we use California as a testbed for exploring the influence of natural variability and large-scale climate change on the multivariate statistics of temperature and precipitation. Specifically, we seek to understand the role teleconnections play in modulating the wintertime co-occurrence of extremes, while at the same time addressing the potential violation of data stationarity assumptions. We achieve this by directly estimating joint conditional probability density functions of temperature and precipitation, in two representative California regions, conditional on several indices of natural variability and climate change. Using this methodology, we seek to understand: (1) How the joint probability of California temperature and precipitation is modulated by several well-known teleconnections that potentially affect California’s climate, (2) How the strength of each climate mode varies regionally within California, and (3) the degree to which teleconnections modulate return intervals of co-occurring extremes in temperature and precipitation. Considering California’s rapidly increasing population and, hence, water demands, we place particular emphasis on understanding joint occurrences of wintertime extremes in high temperature and low precipitation anomalies, which greatly exacerbate drought conditions, as was observed in 2014. Quantifying the contributions from naturally occurring modes of variability is a key requirement for isolating and understanding the role anthropogenic forcing plays in modulating the pattern of occurrence of extremes and their co-occurrence. However, the goal here moving forward will be to document the roles various modes of natural variability have in the altering probabilities of co-occurring extremes in temperature and precipitation rather than to disentangle natural variation from anthropogenic forcing.
2 Methods
2.1 Data
For this study we employ NOAA’s, National Centers for Environmental Information, NCEI (formerly NCDC), temperature and precipitation datasets for California (Center USNCD 2016). The temperature and precipitation data consist of station data, averaged within regions known as climate divisions, geographically defined to encompass broadly similar regional climates. These data are averaged to monthly time periods and extend from 1895 to present. For each climate division in California we then temporally average these data across the wintertime, wet-season period, defined here to be the six month period extending from November through April the following calender year. We use the data extending from November, 1895 to April, 2017 resulting in 122 wet-season periods. To study California’s joint wintertime temperature and precipitation dependence on the large-scale state of the climate, we leverage five datasets. To study the El Niño Southern Oscillation (ENSO) dependence we use the Multivariate ENSO Index (MEI) (Wolter and Timlin 1993). Pacific Decadal Oscillation (PDO) dependence is modeled using the time series from NCEI (Center USNCD 2016), as originally derived by Mantua et al. (1997). The Atlantic Multidecadal Oscillation data is obtained from ESRL (Enfield et al. 2001). The North American winter “dipole index” (DPI) (Wang et al. 2014, 2015) is calculated from both twentieth century reanalysis (20CR) (Compo et al. 2011) and NCEP reanalysis II (Kanamitsu et al. 2002). We use the NCEP data to fill in the years 2015, 2016, 2017, which are missing from the 20CR data. We do this using a simple linear correlation between the two datasets and then use the linearly interpolated values. Integrated Vapor Transport (IVT) and 250 hPa temperature fields are calculated from the ERA-20C dataset (Poli et al. 2016). Finally, we consider the global mean temperature anomaly (GMTA) as reported by NOAA (Center USNCD 2016). These conditioning datasets are averaged over the same time period as the temperature and precipitation data. No temporal lags are considered in this analysis.
The large-scale modes of variability we chose for primary analysis in this study, specifically, ENSO, PDO, AMO, DPI, and GMTA, were based on a several factors. First, we wanted to use modes of variability that were generally well-established, well-studied, and well-known across a wide range of disciplines. Second, we wanted to represent independent modes of variability arising from different genesis mechanisms: ENSO, PDO, and AMO are largely SST forced modes affecting remote locations through atmospheric teleconnections, while DPI and GMTA are largely connected to atmospheric variations only. We do note however, that according to Newman et al. (2016), ENSO and PDO are likely not independent of each other and that DPI is also likely to have a connection to SSTAs in the West Pacific Warm Pool (Wang et al. 2014; Teng and Branstator 2017; Swain et al. 2017). Finally, considering the wide array of climate indices available (National Center for Atmospheric Research Staff 2019; National Oceanic and Atmospheric Administration 2019), we also used a pairplot (Fig. S11) to help identify independent and correlated modes.
To assess regional variation of each climate mode we choose to focus on two climate divisions representing the coastal latitudinal end-members of the state. CD1 represents the coastal northern most division and is sparely populated, heavily forested, and typified by a temperate rain-forest climate. CD6 represents the coastal southern most climate division and is densely populated, with large areas of urban sprawl, and is typified by a largely arid, Mediterranean climate surrounded by a dry desert environment.
2.2 Probability density estimation
A central goal of this study is to understand how the joint statistics of temperature and precipitation depend on various large-scale modes of variability and climate change: conditional probability density functions. To this end, we employ the method of O’Brien et al., fastKDE (O’Brien et al. 2014, 2016), which objectively and directly computes non-parametric kernel density estimates based on the self-consistent, unbiased, and optimal method of Bernacchia and Pigolotti (2011). We estimate conditional probability density functions (cPDFs) directly from trivariate probability density estimates and marginal density estimates as follows:
where R and T denotes precipitation and temperature respectively, and X is the conditioning variable: X\(\in\) (MEI, PDO, AMO, DPI, GMTA). Thus Eq. 1 is a trivariate function that gives the joint probability of co-occurring values of wintertime temperature and precipitation given the conditioning variable at a specific value. As such we are able to directly estimate the probability of co-occurring extreme winter temperature and precipitation as a function of indices of large-scale climate variability and change. Further, with this methodology we are able to explore the effects non-stationary in the data, with respect to the conditioning variables. This methodology allows us to uniquely isolate the influences of the given covariate on the joint distribution in a probabilistic framework (O’Brien et al. 2014). Error estimates on the cPDFs shown on panels d,e,i,j on all Figs. 1, 2, 3, 4 and 5 are derived from bootstrap resampling the data 5000 times and recalculating the cPDFs for each resampling. From the set of 5000 cPDFs, we calculate the 5th and 95th percentiles of the density estimates at each data value. The cPDFs on which we calculate the error estimates represent the PDFs associated with the P10/90 values of each mode of variability. We choose to compute the error on the P10/90 cPDFs such that we capture the end member behavior of the conditional distributions while at the same time retaining enough samples to be able to compute robust estimates of the conditional densities. The years associated with the respective modes of variability having winter averages less than (greater than) the P10 (P90) values are documented in Table S1.
3 Results
3.1 The ENSO conditional distributions
c The fastKDE estimate of temperature versus precipitation, calculated as the wintertime spatiotemporal averages over stations within California, USA, climate division 1 (filled dots), and conditioned on (as a continuous function of) the ENSO strength phase (MEI index). Dots show data points that went into the fastKDE estimate. The starred and hexagon points represent 2014 and 2017 respectively, each colored by the MEI value corresponding to that year. The colored, closed contours (the colored wireframe) depict the levels of constant probability corresponding to the 95th percentile from the conditional trivariate PDF. The thick colored line centered in c depicts the expected value of the trivariate distribution. For the points, the closed contours, and the mean line, colors correspond to the phase of ENSO, cool colors (low values of MEI) representing La Niña conditions and warm colors (high values of MEI) representing El Niño conditions. a The conditional marginal distribution of precipitation colored by the corresponding to the MEI value or ENSO phase. The black PDF shows the stationary distribution for twentieth century precipitation. b As in a, but for conditional PDFs and percentiles for temperature. d, e The precipitation (temperature) cPDFs corresponding to the 10th and 90th percentile values of the MEI index. Shading denotes the 5th and 95th percentiles of the bootstrapped cPDFs. Lines/regions drawn as dashes represent statistical insignificance at the 0.05 level. Lines/regions drawn as solid represent statistical significance at the 0.05 level. The vertical lines represent the expected value (mean) of the respective distributions where the shading indicates the 5th/95th percentiles of the expected values of the bootstrapped cPDFs. f–j As in a–e, but for temperature and precipitation data corresponding California climate division 6
The El Niño-Southern Oscillation (ENSO) is a well-documented, naturally occurring coupled ocean–atmosphere oscillation, which transitions between its warm/positive phase known as El Niño and its cool/negative phase known as La Niña. ENSO is known to affect global weather and climate on the seasonal to inter-annual timescales (Gershunov and Barnett 1998) and it has the ability to impact remote locations, such as California via teleconnections (Cayan et al. 1999). Cayan et al. (1999) considered median and 90th percentile precipitation, and showed increases in both percentiles for the El Niño phase over the southern half of California and no change for both percentiles over the northern portion of the state. Here, we consider the joint distribution of California wintertime temperature and precipitation using ENSO as a continuous conditioning variable. This methodology allows us to calculate the joint and marginal conditional distributions as a function of ENSO phase and strength thus controlling for the non-stationarity in the data introduced by ENSO forcing. Further, we break the temperature and precipitation data down by climate division to illustrate the regional differences ENSO has on joint temperature and precipitation relationships. Figure 1c, h show the cPDFs of wintertime temperature and precipitation for Climate Division 1 (CD1) and Climate division 6 (CD6) as a function of ENSO phase and strength as monitored by the MEI. Central to those panels are color coded hoops representing the 95th percentile of the trivariate conditional distributions. Each of the hoops correspond to the contour of constant probability containing 95% of the cPDF. Near the center of each panel is a single continuous curve, which tracks the expected value of each joint cPDF. Underlying the closed contours of constant probability, are the precipitation and temperature data as a scatter plot along the horizontal axis and vertical axis respectively and are the data that went into the cPDF estimation. In Fig. 1a, the conditional marginal precipitation density estimates are shown (i.e. estimates of the precipitation PDF as a function of ENSO), likewise, panel b shows the conditional marginal temperature density estimates. In both panels a and b, the cPDFs drawn in black represent the twentieth century distributions for each variable. In all panels the color of each density estimate and all data indicate the value of the MEI index on which the PDF was conditioned. The colors of the cPDFs track the phase of ENSO ranging from negative values (cool colors) representing La Nina conditions to positive values (warm colors) representing El Niño conditions.
Figure 1 shows the striking difference of how ENSO affects these two geographically distinct climate divisions. In both CD1 and CD6, the multivariate relationship between ENSO and winter temperature and precipitation is non-linear as seen in Fig. 1c, h by the multivariate conditional mean line drawn at the center of each panel. Despite many studies using linear techniques to describe ENSO and its teleconnections, the non-linearity observed here is expected due ENSO’s linkages to tropical deep convection, which has been documented in previous studies (Hoerling et al. 1997; Livezey et al. 1997; Gershunov 1998; Williams and Patricola 2018). Both CD1 and CD6 show an increase in temperature during the El Niño phase, statistically significant at the 0.05 confidence level. However, interestingly, CD1 experiences a slightly larger temperature increase than CD6 while also developing a strong left (cool/low-temp) skew during El Niño as seen in Fig. 1b, e. This means that while the majority of strong El Niño events result in very warm winters in northern California, there is also a substantial probability of experiencing very cold winters in northern California during strong El Niño events. This El Niño cold tail temperature skew is also observed at the daily timescale for the DJF period whereby the mean tends to warmer relative to La Niña, but with cold tail probabilities that rival those associated with La Niña (Guirguis et al. 2015). In addition to interpreting the mean of the bivariate distributions and the marginal distributions, additional information can be gleaned from the contours of the conditional bivariate distributions in panels c and h. The orientations of the conditional contours indicate the primary axes of variability associated with the respective phases of ENSO. For example, the major axis of the La Niña conditional closed contours (purple contours) for CD6 (panel h) shows a primarily negative orientation indicating that during La Niña, temperature and precipitation tend to be negatively correlated. However, the orientation of the major axis of the El Niño conditional closed contours (yellow contours) has shifted and is nearly horizontal, indicating that in general winter temperature and precipitation are not highly correlated during El Niño events. However, the outermost El Niño contour shows an inflated lobe in the upper left corner (panel h) indicating the occurrence of a winter characterized by a strong El Niño with high temperatures but anomalously low precipitation. That winter, indicated by the bright yellow dot in the upper left hand region of panel h is the winter of 2015–2016, in which the canonically strong El Ni no event failed to deliver even average precipitation to Southern California (L’Heureux et al. 2017). With the exception of 2015–2016 winter, the conditional El Niño contours show a positively sloping major axis indicating that overall, during El Niño events, winter temperature and precipitation are positively correlated.
With respect to wintertime precipitation, CD6 shows a large and statistically significant increase during the warm El Niño phase while CD1 shows only a modest, not statistically significant, increase, and only for the very strongest El Niño events. Moreover, the increases in mean precipitation for both CD1 and CD6 are occurring for very different reasons: CD1 experiences an increase in the mean due to a mode shift in the distribution while CD6 experiences an increase in the mean due to a disproportionate increase in the tail probabilities for experiencing extremely wet winters. The respective shape changes to the distributions are important observations as the societal and environmental risks and impacts from a disproportionate increase in the probability for extremes is not the same as an increase in the mean due to a uniform shifting of all probabilities. In other words, from a societal or environmental impacts perspective, not all shifts in the mean are created equal. Further, the respective changes to the precipitation distributions may happen for different physical reasons. In CD6, it has been shown that increases in the mean during the warm ENSO phase result from an increase in the daily rainfall rate (Feldl and Roe 2011; Gershunov 1998); however, this may not account for total shift in the mean due to the disproportionate increase in the tail probabilities at seasonal timescales. Similarly, what is the physical mechanism for the mode shift in precipitation as observed in CD1? The physical drivers of these changes will be explored in a future manuscript.
Comparing the precipitation marginals of CD1 and CD6 (Fig. 1a, f), qualitatively, the tails of the CD1 cPDFs are smooth and uniform while those of CD6 have an undulating character to them. This is something that can be noticed associated with the CD6 precipitation marginals throughout and is primarily due to two factors. (1) The precipitation variability in CD6 is inherently larger than in CD1, thus the estimates of the tails are less well-constrained/resolved for the equivalent number of samples. And (2), the underlying mechanics of the kernel density estimation method, fastKDE, rely on a Fourier transform of the data whereby the tails of kernels associated with data that are sparse (i.e. extreme values) can constructively interfere leading to undulations in those regions. The bootstrap error analysis we use, described in the methods section, is designed to quantify the uncertainty in the PDF associated with this phenomenon. By definition, every sample is included in the estimate of the cPDFs, however, the amount each sample contributes to the cPDF estimate is determined by the width of the optimally calculated kernel associated with the conditioning variable, here the ENSO index MEI. Specifically, the kernel used here has a width of approximately 3.5 MEI units, which spans a large portion of the data having a range of 4.5 MEI units. This means for the max MEI value of 2.7, the kernels associated with data less than MEI \(\approx 1.0\,(2.7 - 3.5/2)\) do not contribute much to the density at the max MEI value. This implies that at the max MEI value of 2.7, approximately only 20 data points are actively contributing to the density there. This example illustrates why we chose to use P10/90 values for our end-member analyses rather than min/max values, as we increase the number of kernels contributing to our estimates to approximately 90, which greatly increases the number of samples that inform our estimates. See O’Brien et al. (2016) for further details.
The starred and hexagon points mark 2014 and 2017 respectively. The coloring of both points indicate that both the very dry winter of 2014 and the very wet winter of 2017 occurred during ENSO neutral conditions, highlighting the substantial variability in winter precipitation in California not explained by ENSO. In fact, our results show that statewide, El Niño increases the expected (mean) precipitation from 486 to 520 mm, making the El Niño phase of ENSO only responsible for a modest 7% increase the expected statewide winter precipitation. This result is consistent with the satellite-based findings of Savtchenko et al. (2015). In addition, California obtains roughly 60% of its freshwater resources from snow melt runoff (Lauer 2011) and CD1 is home to the Salmon–Klamath–Trinity mountains, the primary snow melt source for Shasta and Trinity lakes, the second and third largest reservoirs, respectively, in northern California. As seen in Fig. 1a, CD1 experiences roughly the same wintertime precipitation regardless of ENSO phase; however, winter temperatures are much cooler during the La Niña phase, likely resulting in deeper snow packs, a lower snow line, and a delayed spring melt, thereby contributing to a more reliable water source for the dry summer months to follow. Thus for northern California, contrary to popular belief, from a water security and reliability perspective, La Niña winters may in fact actually be preferable.
3.2 The PDO conditional distributions
The Pacific Decadal Oscillation is a low frequency north Pacific ocean sea surface temperature pattern first described by Mantua et al. (1997). ENSO and PDO are not independent and recently it has become apparent that PDO may be directly forced by ENSO forcing (Newman et al. 2016). However, in terms of their respective effects on the climate system, specifically precipitation and temperature patterns, they each have unique and distinct effects (DeFlorio et al. 2013), despite their broadly similar SST patterns (see Figs. S1, S3). While ENSO has a direct physical causal pathway for affecting the climate system, the causal physical mechanisms by which the PDO affects temperature and precipitation patterns is less clear (Pierce 2002). However, more recently Meehl and Hu (2006) found that wind anomalies forced ocean Rossby waves, which sets the PDO decadal timescale, and are themselves linked to anomalous mid-latitude atmospheric circulations which in turn drive precipitation anomalies. Figure 2 shows the conditional distributions of temperature and precipitation as a continuous function of the PDO phase and strength. As with the ENSO distribution shown in Fig. 1, non-stationarity introduced into the data by PDO forcing is evident. With respect to the precipitation marginal distribution the overall effect of PDO (Fig. 2a) is larger than that of ENSO in northern California; however, the shift in the mean is still statistically insignificant at the 0.05 confidence level (Fig. 2a). In CD6 the contrast between the effects of PDO and ENSO are more stark. While ENSO results in a strong and statistically significant increase in mean precipitation resulting from an increased probability for experiencing extreme wet winters, the effects of PDO in CD6 shows a nonlinear, but ultimately zero correlation to changes in wintertime precipitation. This is not true for temperature. Both CD1 and CD6 show large, uniform, and statistically significant increases in wintertime temperature. For CD1 during the cool PDO phase, the probability of exceeding the 90th percentile of twentieth century temperature is near zero (P \(\approx\) 0.01) while during the warm phase that probability is over 20 times greater (P \(\approx\) 0.2). Correspondingly, the return period for experiencing very warm wintertime temperatures exceeding the 90th percentile decreases from a 1-in-100 year event during the cool phase to a 1-in-5 year event during the warm PDO phase. It should be noted however, that the PDO is not the only physical mechanism by which the return periods of temperature and precipitation are affected. The effect shown in Fig. 2 is the role PDO plays in affecting those statistics. The case is similar for CD6 though slightly less pronounced. The many implications for these changes in wintertime temperatures as a function of the PDO phase. During the positive phase of the PDO, elevated wintertime temperatures increase the snow line elevation, can produce more rain-on-snow events, decrease snow pack, and alter the peak runoff timing, all of which have a large impact on California’s water supply (McCabe and Dettinger 2002). Given the slow evolution of the PDO, the results here could provide a measure of predictability for inter-decadal precipitation and temperature forecasts for state water managers to better manage water supplies. However, interdecadal and seasonal variability may be the dominate control for extreme years as for both the very dry and warm winter of 2014 and the very wet winter of 2017, PDO was in near neutral conditions and consequently, likely did not play a major role in driving those extreme conditions. We note however, that the PDO may not be an independent mode of SST variability, but more a result of an integration of several modes of variability occurring across a range of temporal and spatial scales (Newman et al. 2016). Newman et al. (2016) show the PDO to likely be a result of ocean memory i.e. re-emergence, tropical forcing from ENSO, and the Aleutian Low, which were shown using lagged correlations to lead the PDO. Given that ENSO conditions were in near neutral conditions during the 2014/2017 extreme years, perhaps the Aleutian low, taken as a primary driver of PDO variability, could have played a larger role in driving those extreme years. To consider this possibility, we used the North Pacific Index (NPI) (Trenberth and Hurrell 1994), an often employed index to characterize the strength of the Aleutian low, as a conditioning variable for the temperature and precipitation distributions. The results indicate (figure not shown) that, as with ENSO, the Aleutian low was in near neutral conditions and as such, is not a likely driver for the extreme years of 2014/2017.
As in Fig. 1, however all distributions are conditional on the phase of the PDO. The coloring in all panels here represents the phase of the PDO where cool colors represent the negative (cool) phase and warm color represent the positive (warm) PDO phase
3.3 The AMO conditional distributions
The Atlantic Multidecadal Oscillation is a long-term warming and cooling of North Atlantic sea surface temperatures with a period of 60–70 years (Schlesinger and Ramankutty 1994; Kerr 2000). The warm phase of the AMO has been previously connected to increased drought conditions over the central U.S., increased rainfall in Florida, and a low-frequency modulation of ENSO (Enfield et al. 2001). Of interest here is what effect the AMO has on the multivariate statistics of wintertime temperature and precipitation in California. Mestas-Nuñez and Enfield (1999) showed that the AMO was inextricably linked to a warming of the North Pacific through an atmospheric bridge involving the Arctic Oscillation. Thus one plausible physical mechanism for the AMO to affect west coast weather statistics would be the warming of north Pacific acting as an enhanced moisture source for west coast storms thereby affecting the precipitation distribution and in turn the multivariate statistics. Also of interest, the composite SST pattern which captures AMO values at or exceeding the 90th percentile also shows a strong ENSO signal in the eastern Pacific. This appears to be driven primarily by the years 1998 and 2016 when both ENSO and AMO exceeded their respective 90th percentile thresholds (Fig. S5). Figure 3 shows the multivariate distributions of California CD1 and CD6 temperature and precipitation as a function of the AMO phase and strength. Northern California’s relationship with AMO is positive in both temperature and precipitation and close to linear in both variables. However, in southern California while temperature increases monotonically with AMO phase, precipitation increases linearly from cool to neutral conditions but then the relationship reverses and decreases linearly from neutral to warm AMO conditions. The behavior of the multivariate relationships may indeed be real (Fig. 3c, h); however, it is difficult to assert conclusively as the mean changes between the cool and warm phases of the AMO are not statistically at the 0.05 confidence level (Fig. 3d, e, i, j). California, taken as a whole (Fig. S6), shows a multivariate relationship with AMO more similar in character to how CD1 behaves. While there is slightly more non-linearity in the relationship, both temperature and precipitation increase monotonically as AMO transitions from its cool phase to its warm phase. However, again like both CD1 and CD6, the relationships between California temperature and precipitation are not significant at the 0.05 confidence level, suggesting that the AMO does not have an appreciable direct effect on California’s temperature and precipitation statistics. However, as described in previous literature (e.g. Levine et al. 2017a; Kang et al. 2014), the AMO may exert an indirect effect on California temperature and precipitation via the low-frequency modulation of ENSO variability and strength. In both the aforementioned studies, the AMO tended to suppress both ENSO variability and strength.
As in Fig. 1, however all distributions are conditional on the phase of the AMO. The coloring in all panels here represents the phase of the AMO where cool colors represent the negative (cool) phase and warm color represent the positive (warm) AMO phase
3.4 The DPI conditional distributions
The Dipole Index (DPI) described by Wang et al. (2014), characterizes a state of the atmosphere whereby, when in the positive phase, a persistent, quasi-stationary pattern produces deep troughing in the eastern U.S. and strong ridging over the western U.S. and eastern Pacific, which reverses in the negative phase (Wang et al. 2017, Fig. S7). During the winter of 2013–2014, the positive phase of this index reached an all-time high and resulted in record setting cold snaps in the Eastern U.S., while the U.S. west coast was simultaneously gripped by record setting drought conditions (Swain et al. 2014; Wolter et al. 2015). As in the previous plots, Fig. 4 shows the multivariate relationships of CD1 and CD6 temperature and precipitation. Most evident here is how highly non-stationary the data are as a function of the DPI. Panels a and c show a strong precipitation response to the DPI, whereby the expected value of precipitation for CD1 decreases from 1342 mm during the negative phase of the DPI to 801 mm during the positive phase of the DPI representing a drop of \(\sim\)40%. The change in mean expected precipitation between the two phases of the DPI is achieved through a uniform shifting of all probabilities as shown in Fig. 4a. Collectively the DPI explains \(\sim\)50% of the wintertime precipitation variance for CD1 and statewide and \(\sim\)36% for CD6, far greater than any other large-scale index we considered. The high explanatory power of the DPI makes it an obvious candidate to explore as a predictor variable. However, we refrain from assessing the potential predictability of the DPI and reserve that analysis for a future manuscript. Interestingly, for CD1 wintertime temperature, the strong ridging does not produce a statistically significant increase in temperature as one might expect (Fig. 4e). For the very wet winter of 2017 Fig. 6 shows CD1 received 1458 mm of precipitation, which is a \(\sim\)P90 event with respect to the 20th century distribution. However, when taking the 2017 DPI value of 360 into account, with respect to the conditional distribution at that DPI level, the winter of 2017 was only a \(\sim\)P75 event. In other words, the anomalous winter of 2017 was much more likely when considering the probability of occurrence with respect to the DPI conditional distributions. This suggests that there is a level of probabilistic predictability to the outcome of any given winter in California when monitoring/forecasting the state of the dipole circulation. Similarly, during the drought winter of 2014 CD1 received only 594 mm of precipitation, which is 56% of normal or equivalently a 8th percentile event. However, if one was to consider this event from the perspective of the corresponding conditional DPI distribution then the anomalous dry winter of 2014 is a 20th percentile event. So when considering the winter of 2014 with respect to a cPDF which takes into account the atmospheric circulation features present, what was an extreme event becomes more likely and thus more predictable. Taken together, Fig. 6 shows the how dramatically the probabilities change for experiencing either drought or deluge depending on the strength of the DPI.
As in Fig. 1, however all distributions are conditional on the strength of the dipole index. In all panels, the coloring corresponds to the strength of the dipole index where cool colors represent a weak dipole and warm colors represent a strong dipole, i.e. strong ridging in the western U.S. with a deep trough present over the eastern U.S.
Southern California, CD6, shows a similar strong and statistically significant (\(\hbox {p} \le 0.1\)) precipitation response to changing of phases of the DPI. During the negative phase of the DPI, the mean expected wintertime precipitation is 475 mm, while during the positive phase its only 290 mm. For CD6 the winter of 2017 resulted in 551 mm of precipitation. Shown in Fig. 4g, i, the probability of experiencing a winter of this magnitude or larger during the positive phase of the DPI is 0.014. However, during the negative phase of the DPI that probability increases to 0.36, representing an increase by a factor of 26. Correspondingly, the return period for experiencing the winter of 2017 during the positive phase of the DPI is a 1-in-70 year event while during the negative phase its a 1-in-3 year event. Unlike CD1, CD6 experiences a statistically significant (\(\hbox {p}\le 0.1\), significance test described in the “Methods” section) increase in temperature transitioning from the negative to the positive phase of the DPI.
Statewide, DPI causes California to experience statistically significant shifts in both mean wintertime temperature and precipitation (Fig. S8). While the twentieth century mean precipitation is 486 mm, during the positive phase of the DPI that decreases to 362 mm while during the negative phase it increases to 589 mm. The drought winter of 2014, statewide California received 262 mm of precipitation, which ranks as the sixth driest winter on record. With respect to the twentieth century distribution, this level of winter precipitation or lower only has a \(\sim 0.06\) probability of occurrence. However, when taking in to account the corresponding DPI level, the probability of experiencing a winter that dry increases by over a factor of 2 (\(\hbox {P}\approx 0.13\)). Similarly for the wet winter of 2017, statewide California received 744 mm of rain, making it the 7th wettest winter statewide. The probability of experiencing a winter this wet or wetter with respect to the twentieth century distribution is \(\sim 0.07\). However, taking into account the corresponding DPI index, that probability also increases by over a factor of 2.
3.5 The GMTA conditional distributions
One of the most prominent changes to the global climate from the early twentieth century to present is that of anthropogenically forced temperature rise (Intergovernmental Panel on Climate Change 2014). From the late 1800’s to present the earth has experienced nearly a \(1\,^{\circ }\hbox {C}\) rise in average temperature (Team 2018), (Fig. S9). Figure 5 shows the conditional multivariate distributions of wintertime temperature and precipitation as a function of the global mean temperature anomaly (GMTA) for CD1 and CD6. Cool colors represent periods with low GMTA occurring primarily in the late 19th century and early twentieth century. While warm colors represent periods with high GMTA occurring almost exclusively in the early twenty-first century. Not surprisingly, the relationship between global mean temperature and regional temperature in both climate divisions is positive and both exhibit statistically significant shifts. However, its notable that CD6 has experienced roughly twice the increase in wintertime regional temperatures as CD1 has for the same amount of global mean temperature rise as seen in Fig. 5e, j. This is also true of the JJA period (figure not shown) and therefore carries with it a significant increased risk for heat-related health issues in CD6 that is not present in CD1, which contains a large portion of California’s population. This highlights a critical aspect of climate change: the risks and negative impacts from a changing climate are not distributed evenly, globally, as well as regions as geographically limited as California. We hypothesize that the differential warming rates in CD6 versus CD1, as a function of global mean temperature rise, is driven by the urban heat island effect, as CD1 is primarily densely forested temperate rain forest, while CD6 is primarily an urbanized semi-arid Mediterranean environment. Exploring this hypothesis however is beyond the scope of this manuscript. Similarly, statewide, California has experienced a statistically significant increase in wintertime temperatures as a function of global mean temperature rise (Fig. S10). This increase in wintertime temperatures over the last century has significant consequences for California ranging from an earlier spring, shorter warmer winters, decreased snow pack to the disruption of ecological niches to sensitive native and endemic plants and animals (Stewart et al. 2005; Mote et al. 2005; Parmesan 2006). Another notable feature of Fig. 5e, j as well is an apparent reduction of wintertime temperature variance indicated by the contraction of the cPDFs transitioning from an early century cool climate to our present relatively warm climate. We tested whether the variance reduction was statistically significant and in this framework, it was not. However, that said, the effect may be real as several studies have documented and predict a decrease in wintertime midlatitude temperature variance with warming (Rhines et al. 2017; Holmes et al. 2016).
The dominant mode of historical natural variability is within the precipitation dimension. However, the conditional climate change signal in all cases is approximately orthogonal to the axis of natural variability (Fig 5c, h). Mahony and Cannon (2018) identified this behavior, departure intensification, in projections of future climate in CMIP5 models analyzing the climate change behavior of summertime temperature and precipitation. The univariate relationship between global mean temperature and precipitation is much more complicated than temperature and highly non-linear. Both CD1 and CD6 wintertime precipitation show a positive relationship with the GMTA early in the century. That is, early in the record both climate divisions trend toward warmer wetter winters. However, mid-century at a GMTA of \(\sim\) 0.15 \(^{\circ }\)C, the relationship reverses such that warmer winters become increasingly associated with drier winters. This is also true of California precipitation state wide. The combination of decreasing wintertime precipitation and warmer winter temperatures represents two trends which exacerbate each other whereby California receives less precipitation that falls as snow and snow that melts more quickly, ultimately having a large effect on California’s summertime water supply (Knowles et al. 2006; Cayan et al. 2001). Moreover, monotonically increasing wintertime temperatures increase summertime wildfire risks in a commensurate fashion (Yoon et al. 2015). This, combined with negative precipitation anomalies greatly exacerbates wildfire risk. To this point, in January 2018 the Thomas fire became the largest fire in California history burning nearly 300,000 acres causing nearly two billion dollars in damages (Cal Fire 2018b; Ding 2018). In the October–December period of 2017 preceding the Thomas fire, CD6 experienced its second lowest precipitation anomaly and highest temperature anomaly for that period, the co-occurrence of which, was likely at the root of the intensity of that fire. As a side-note, at the time of this writing, the Ranch fire (Mendocino complex) has now become the largest fire in state history charing over 450,000 acres of land (Cal Fire 2018a).
As in Fig. 1, however all distributions are conditional on the global mean temperature anomaly
4 Discussion
The conditional probability distribution functions (cPDF) for CD1 DPI corresponding to 2014 in yellow, 2017 in purple, and the full distribution of 20th century winter precipitation in black. The vertical lines in the corresponding colors represent the expected values of those distributions respectively. The region shaded in yellow represents the probability of getting a year as dry or dryer than 2014 according to the 2014 DPI cPDF. The purple shaded region represents the probability of getting a year as wet or wetter than 2017 according to the 2017 DPI cPDF. The hashed regions represent what those same probabilities would be if estimating them from the full PDF of twentieth century precipitation
We have applied the novel kernel density estimation method of O’Brien et al. (2014) to characterize the multivariate behavior of wintertime temperature and precipitation in California as a function of selected large-scale modes of climate variability. This methodology allows us to investigate the impacts and contributions of various large-scale climate conditions to altering the probabilities of co-occurring extremes as continuous variables as opposed to simple “on/off switches”. This is an important advancement in the understanding of how large-scale climate modes affect variability in temperature and precipitation and their joint behavior, as it is demonstrated that relationships observed are often non-linear and therefore cannot be well-described by linear correlation analysis typically employed in this area of climate research. Further, this methodology allows us to account for non-stationarity in the data regardless of what time scale that non-stationarity occurs on. For example, the PDO introduces non-stationarity into the data on the decadal timescale while ENSO introduces non-stationarity on the inter-annual timescale. Being able to account for this non-stationarity allows for a more robust and nuanced estimate of how the univariate and multivariate statistics vary as a function of each index.
Overall the relationships between ENSO and winter temperature and precipitation are non-linear, stronger in the southern California than in northern California, and statewide, only explain about 7% of the precipitation variance. Both CD1 and CD6 experience statistically significant increases in winter temperature during El Niño. However, the utility of this method demonstrates that, while the increases in mean temperature are roughly equal in CD1 and CD6, the full distributions themselves look very different. CD1 has a strong left (cool) skew that is not present in CD6 indicating that in CD1, some strong El Niño winters can be quite cold relative to the mean during that phase. The worst drought conditions in California occur when negative precipitation anomalies co-occur with positive temperature anomalies as happened in 2014. California winter temperature and precipitation, regionally and statewide, show an overall positive relationship with ENSO indicating that co-occurring extremes for drought conditions are not favored by this teleconnection. In general with ENSO, California winters are either wet and warm (El Niño) or cool and dry (La Niña). To verify that the MEI was accurately capturing ENSO’s teleconnection with California, we repeated the analysis with the commonly used Niño3.4 index (Rayner 2003). Not surprisingly, the relationships were nearly identical save for small variations in the shape of the multivariate distributions (figure not shown). Finally it is known that there are different flavors of ENSO, the most commonly known of which is the Modoki (Capotondi et al. 2015). To consider how this variation of El Niño differs in its teleconnection to California winter temperature and precipitation relative to its standard counterpart described by the MEI, we used the monthly Modoki index from JAMSTEC and repeated the analysis (Ashok et al. 2007; JAMSTEC 2018). Despite having a distinct spatial SST pattern, we find that overall, in CD1, CD6, and statewide, the Modoki teleconnection to temperature and precipitation exhibits very similar behavior to the standard El Niño.
Of the decadal-scale teleconnections, PDO has the greatest effect on California temperature and precipitation statistics. Although statewide, PDO is correlated with increased precipitation, which is primarily driven by regional correlations in northern California, no relationships statewide or regional are statistically significant at the 0.05 level. However, PDO may exert other effects on precipitation not reflected in Fig. 2 through its connection with ENSO. As shown by Newman et al. (2016) and by Fig. S11, PDO and ENSO are not independent. When PDO is in its warm phase, ENSO tends to sit at a higher background state, enhancing El Niños and suppressing La Niñas. The converse is also true, when PDO is in its cool phase, El Niños are suppressed and La Niñas enhanced. In addition, ENSO–PDO interactions are further documented by Gershunov and Barnett (1998) who showed that ENSO teleconnections to North American Climate via heavy daily precipitation frequency are also sensitive to the PDO phase. Statewide, and in both CD1 and CD6, PDO does exert a statistically significant effect on temperature raising expected mean statewide, CD1, and CD6 temperature by approximately 0.7 \(^\circ\)C, 1 \(^\circ\)C, and 0.5 \(^\circ\)C respectively during its positive warm phase. However, despite these increases in temperature, evidence seems to suggest that it is suppressed precipitation during the PDO cool phase that drives drought in the west (Meehl and Hu 2006; Cook et al. 2016). Less important for California climate is the AMO, which showed no statistically significant relationships to either temperature or precipitation. However, again like PDO, AMO may effect precipitation in California by modulation of ENSO teleconnections as there is some evidence to suggest that AMO tends to suppress ENSO variability and strength (Levine et al. 2017b; Kang et al. 2014).
Of all of the indices we studied, the DPI has the largest control over precipitation in California explaining \(\sim\) 50% of the variance statewide and in CD1 and \(\sim\) 36% in CD6. In addition, the DPI is the only index to show a positive correlation with temperature and a negative correlation with precipitation, thus making it the only large-scale index to increase the risk of experiencing co-occurring extremes in both suppressed precipitation and elevated temperatures, which together exacerbate drought conditions. Given that the DPI explains such a large fraction of the variance in California precipitation, it presents an opportunity to use the index and the associated conditional probability distributions shown in Fig. 6, as a tool for water supply forecasting and reservoir management. For example, reservoirs in California operate based on rule curves, which specify storage targets that provide a flood management pool in the winter months to accommodate increased inflow while increasing storage during the summer months to provide additional water supply during the summer months when the risk of high impact storms is virtually non-existent. These rule curves are derived from historical observations and risk analysis (Brekke et al. 2009). Recently, the idea of forecast informed reservoir operations (FIRO) has gained increased attention as a potential alternative to rule curves to provide additional water storage without diminishing the flood control capability the reservoirs provide (Jasperse et al. 2017). Leveraging the the cDPI distribution to provide longer range probability estimates of precipitation along with shorter range numerical weather prediction could further enhance reservoir operations for more efficient use of California’s water supply.
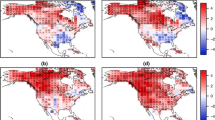
Wintertime (NDJFMA) integrated vapor transport (IVT) and 250 hPa temperature anomalies relative to twentieth century climatology for DPI P10 years (a, b) and DPI P90 years (c, d). All four panels have the corresponding 250 hPa geopotential height anomalies overlaid as contours drawn in black with dashed/solid contours indicating negative/positive anomalies with contour interval of 15 m
Figures 4 and 6 demonstrate the strong control the dipole circulation pattern has on California temperature and precipitation through statistical characterization. However, the physical processes which underlie and drive such changes to the respective conditional probability distributions are not uncovered by such analyses. To that end, Fig. 7 demonstrates the connection between the large-scale dipole circulation pattern and integrated vapor transport (IVT), which is strongly correlated with precipitation (Neiman et al. 2009; Rutz et al. 2014), and temperature anomalies at the seasonal timescale. Figure 7a shows the negative phase of the dipole pattern as indicated by the P10 DPI index relative to NDJFMA climatology. Panel a shows an enlarged and deepened Northeast Pacific trough with strengthened cyclonic flow that enhances and directs moisture transport to the Western U.S. via an Eastward extension of the storm track centered around \(40^{\circ }\hbox {N}\). Comparatively, panel c shows the positive phase of the dipole circulation (P90 years) the pattern is reversed, and the associated ridging and anticyclonic flow weakens the Pacific storm track and results in its termination over the Eastern Pacific before it reaches the U.S West coast resulting in reduced winter precipitation. The temperature signal for the negative and positive phases of the dipole circulation shown in panels b and d respectively are quite distinct. The negative/positive phase show confined narrow bands of circumglobal midlatitude cooling/warming. These features are suggestive signatures of jet acting as waveguides for the propagation of Rossby waves as described in Branstator et al. (2017). Taken together, Fig. 7c, d show how the positive phase of the dipole circulation results in the simultaneous occurrence of both reduced rainfall and increased temperatures during the boreal winter, the combination of which, can result in greatly exacerbated drought risk. While Fig. 4e indicates that the warming experienced in CD1 is not statistically significant, Fig. 7d shows that during the positive (ridging) phase of the dipole circulation, the midlatitude warming signal is both robust and circumglobal. The lack of statistical significance in the warming signal for CD1 could result from a signal-to-noise issue. We also note that wintertime Northeast Pacific anticyclonic circulation has been shown to induce an anomalous cold northerly flow along the west coast of North America (Favre and Gershunov 2006), which would serve to dampen the warming response typically associated with anticyclones during the boreal summer.
The dipole index depicts the amplification and attenuation of the wintertime stationary waves, the dominate wither circulation feature over North America. As such it contains no intrinsic information about the generation of the circulation regime. The dipole pattern the DPI measures can arise from various mechanisms and was the focus of many different studies, particularly with respect to the North American winter of 2013/14. That winter was characterized by drought across the west and record snow and cold over much of the east (Palmer 2014). It was at this time the DPI hit its highest level. The mechanisms of the dipole circulation are rooted in mid-latitude atmospheric internal dynamics however, it can be enhanced by tropical diabatic heating of the atmosphere and the resulting Rossby wave that forms. Teng and Branstator (2017), who refer to the dipole pattern as a circumglobal Rossby wave of wavenumber 5, found that while tropical heating anomalies are not necessary for formation of the dipole pattern, they do double the chance of them forming. Seager et al. (2015) and Wang and Schubert (2014) came to similar conclusions finding that while SST anomalies can cause ridging over the west coast, the magnitude of the observed ridging in 2011–2014 is not explained by SST anomalies alone suggesting the role of internal atmospheric variability or other forcings constructively interfering in contributing to the extreme ridging. We find using the twentieth century reanalysis and NCEP/NCAR reanalysis that the wintertime DPI has been increasing by 0.6 m/year (p < 0.001) and 0.7 m/year (p < 0.1) respectively, while Wang et al. (2014) showed that the variance in DJF DPI has been increasing as well. Using different metrics, Singh et al. (2016) also observed an amplification of the dipole pattern. This suggests that this type of circulation pattern is become stronger with time and is switching polarities more intensely and frequently. Practically, inferring from the DPI cPDFs in Fig. 6, this means an increasing frequency of dramatic shifts between very dry winters and very wet winters. This increase in precipitation volatility was found in an analysis of CMIP5 models to result from an increased frequency in the number of dry days per year in conjunction with an increase in rainfall intensity on days it does rain, thereby increasing the seasonal-scale precipitation variability (Polade et al. 2014, 2017). More recently, in an analysis of the LENS RCP8.5 ensemble, Swain et al. (2018) found a twenty-first century increase in both wet and dry extremes which results in a 25–100% increase in dry-to-wet precipitation events with little change in the mean. Further, in that study it was shown that relative to the preindustrial control runs, the pressure anomalies driving both wet and dry years at the end of the twenty-first century were more extreme suggesting the DPI characterizing these anomalous features would be correspondingly more extreme as well. Similarly, Wang and Schubert (2014) found in an analysis of 12 AMIP model runs, the distribution of geopotential heights in the latter half of the century relative to the first increased suggesting an increase in blocking events. However, in this same study, the corresponding precipitation PDF remained unchanged suggesting the decrease in precipitation from storm occurrences due to blocking was offset by an increase in precipitable water following Clausius–Clapeyron. Despite model-based evidence suggesting an increase in the frequency and strength of geopotential height anomalies and blocking, robust observational evidence is lacking and/or mixed (Barnes 2013; Barnes et al. 2014; Francis and Vavrus 2015; Screen and Simmonds 2013). However, the extent to which anthropogenic forcing plays a role in generating extreme geopotential height (GPH) anomalies is less clear. Swain et al. (2014) show that the occurrence of extreme geopotential heights exceeding the 99th percentile of preindustrial control runs increases by up to 670% in twentieth century CMIP5 simulations including both natural and anthropogenic forcing, no increases in extreme heights were found in simulations including only natural forcing. Similarly Wang et al. (2014) found an increase in sliding variance of the DPI present both in the 20CR reanalysis and CESM1-GHG simulations, however this signal was not present in the CESM1-NAT simulations suggesting a anthropogenic component to the increase in frequency of dipole pattern occurrences. Additionally, Williams et al. (2015) found that while precipitation is the primary driver of drought variability, anthropogenic warming accounted for 8–27% of the observed drought in 2012–2014 and 5–18% in 2014. While the physical mechanisms of how climate change may alter the strength and/or frequency of the dipole pattern, both in its cyclonic and anticyclonic configurations, several potential pathways exist. Arctic warming (Francis and Vavrus 2015; Cohen et al. 2014), Pacific SST anomalies (Seager and Henderson 2016; Watson et al. 2016; Swain et al. 2017), and sea-ice concentration and extent (Alexander et al. 2004; Sewall 2005), are all projected to change due to human activities over the twenty-first century and have roles in influencing mid-latitude weather patterns and large-scale circulations.
The Dipole circulation pattern is highly related to the Tropical/Northern Hemisphere (TNH) pattern (Mo and Livezey 1986). DJF correlations between the TNH and the DPI are extremely high with an r value of 0.87. The TNH is defined as the forth rotated EOF of 700 mb winter height anomalies and when correlated with rain gauge stations around the globe, finds its larges correlations with those stations in the maritime continent. This suggests that the TNH/DPI is likely related to convection generated gravity/Rossby waves originating in the warm-pool region. This would be consistent with the findings of Wang et al. (2014). Moreover, Mo and Livezey (1986) found that the TNH was associated with variability on timescales longer than a season, thus potentially partially explaining the extreme persistence of the ridge that formed over California during the winter of 2013/14.
Finally, we considered the effect the Arctic oscillation may have on the occurrence of joint extremes in California temperature and precipitation. Despite the attention the Arctic gets on modulating mid-latitude weather, when it comes to temperature and precipitation change in California, we obtained a null result (figure not shown). For CD1, CD6, and state wide averaged data, both temperature and precipitation showed little sensitivity to the phase of the Arctic oscillation.
5 Summary
We have implemented a novel, nonparametric conditional probability distribution method that allows evaluation of complex, multivariate, and nonlinear relationships that exist among temperature, precipitation, and various indicators of large-scale climate variability and change. We have shown that the multivariate statistics of temperature and precipitation are demonstrably non-stationary and therefore benefit from more sophisticated statistical techniques for accurate characterization. In addition, the multivariate variability and statistics of temperature and precipitation exhibit strong spatial variation across a region that is often treated as having homogeneous and stationary statistics (AghaKouchak et al. 2014). We find that inter annual-to-multi decadal modes of atmosphere-ocean variability in the Pacific and Atlantic explain modest amounts of variability in co-occurring extremes in California, at best. Despite the historic focus on ENSO as the main driver of precipitation variability in California, we find that ENSO only explains about 7% of the variability statewide. However, the dipole index, a measure of the strength and polarization of the mean-state circulation present over North America, accounts for a much larger fraction of precipitation variance, nearly 40% statewide. This suggests that a better understanding of the drivers and predictability of large-scale atmospheric variability is key to interannual—to decadal prediction of co-occurring hydroclimate extremes in the western U.S.
References
AghaKouchak A, Cheng L, Mazdiyasni O, Farahmand A (2014) Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys Res Lett 41(24):8847–8852. https://doi.org/10.1002/2014GL062308
Alexander MA, Bhatt US, Walsh JE, Timlin MS, Miller JS, Scott JD (2004) The atmospheric response to realistic Arctic Sea ice anomalies in an AGCM during winter. J Clim 17(5):890–905. https://doi.org/10.1175/1520-0442(2004)017<0890:TARTRA>2.0.CO;2
Ashok K, Behera SK, Rao SA, Weng H, Yamagata T (2007) El Niño Modoki and its possible teleconnection. J Geophys Res 112(C11):C11,007. https://doi.org/10.1029/2006JC003798
Barnes E (2013) Revisiting the evidence linking Arctic amplification to extreme weather in midlatitudes. Geophys Res Lett 40(17):4734–4739. https://doi.org/10.1002/grl.50880
Barnes EA, Dunn-Sigouin E, Masato G, Woollings T (2014) Exploring recent trends in Northern Hemisphere blocking. Geophys Res Lett 41(2):638–644. https://doi.org/10.1002/2013GL058745
Bernacchia A, Pigolotti S (2011) Self-consistent method for density estimation. J R Stat Soc B Stat Methodol 73(3):407–422. https://doi.org/10.1111/j.1467-9868.2011.00772.x. arXiv:0908.3856
Branstator G, Teng H, Branstator G, Teng H (2017) Tropospheric waveguide teleconnections and their seasonality. J Atmos Sci JAS-D-16-0305.1. https://doi.org/10.1175/JAS-D-16-0305.1
Brekke LD, Maurer EP, Anderson JD, Dettinger MD, Townsley ES, Harrison A, Pruitt T (2009) Assessing reservoir operations risk under climate change. Water Resour Res 45(4):1–16. https://doi.org/10.1029/2008WR006941
Cal Fire (2018a) Ranch Fire (Mendcino complex). http://www.fire.ca.gov/current_incidents/incidentdetails/Index/2175
Cal Fire (2018b) InciWeb. Thomas fire incident information. http://cdfdata.fire.ca.gov/incidents/incidents_details_info?incident_id=1922. Accessed 6 Aug 2018
Capotondi A, Wittenberg AT, Newman M, Di Lorenzo E, Yu JY, Braconnot P, Cole J, Dewitte B, Giese B, Guilyardi E, Jin FF, Karnauskas K, Kirtman B, Lee T, Schneider N, Xue Y, Yeh SW (2015) Understanding ENSO diversity. Bull Am Meteorol Soc 96(6):921–938. https://doi.org/10.1175/BAMS-D-13-00117.1
Cayan DR, Redmond KT, Riddle LG (1999) ENSO and hydrologic extremes in the western United States. J Clim 12(9):2881–2893. https://doi.org/10.1175/1520-0442(1999)012<2881:EAHEIT>2.0.CO;2
Cayan DR, Dettinger MD, Kammerdiener SA, Caprio JM, Peterson DH (2001) Changes in the onset of spring in the western United States. Bull Am Meteorol Soc 82(3):399–415. https://doi.org/10.1175/1520-0477(2001)082<0399:CITOOS>2.3.CO;2
Center USNCD (2016) National Climate Data Center NCDC climate data online. http://www7.ncdc.noaa.gov/CDO/CDODivisionalSelect.jsp
Cohen J, Screen JA, Furtado JC, Barlow M, Whittleston D, Coumou D, Francis J, Dethloff K, Entekhabi D, Overland J, Jones J (2014) Recent Arctic amplification and extreme mid-latitude weather. Nat Geosci 7(9):627–637. https://doi.org/10.1038/ngeo2234. http://www.nature.com/articles/ngeo2234. arXiv:1204.5445
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P, Brönnimann S, Brunet M, Crouthamel RI, Grant AN, Groisman PY, Jones PD, Kruk MC, Kruger AC, Marshall GJ, Maugeri M, Mok HY, Nordli Ø, Ross TF, Trigo RM, Wang XL, Woodruff SD, Worley SJ (2011) The twentieth century reanalysis project. Q J R Meteorol Soc 137(654):1–28. https://doi.org/10.1002/qj.776
Cook BI, Cook ER, Smerdon JE, Seager R, Williams AP, Coats S, Stahle DW, Díaz JV (2016) North American megadroughts in the common era: reconstructions and simulations. Wiley Interdiscip Rev Clim Change 7(3):411–432. https://doi.org/10.1002/wcc.394
DeFlorio MJ, Pierce DW, Cayan DR, Miller AJ (2013) Western U.S. extreme precipitation events and their relation to ENSO and PDO in CCSM4. J Clim 26(12):4231–4243. https://doi.org/10.1175/JCLI-D-12-00257.1
Diffenbaugh NS, Swain DL, Touma D (2015) Anthropogenic warming has increased drought risk in California. Proc Natl Acad Sci 112(13):3931–3936. https://doi.org/10.1073/pnas.1422385112
Ding A (2018) Charting the financial damage of the Thomas Fire. https://thebottomline.as.ucsb.edu/2018/04/charting-the-financial-damage-of-the-thomas-fire
Enfield DB, Mestas-Nuñez AM, Trimble PJ (2001) The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U.S. Geophys Res Lett 28(10):2077–2080. https://doi.org/10.1029/2000GL012745
Favre A, Gershunov A (2006) Extra-tropical cyclonic/anticyclonic activity in north-eastern Pacific and air temperature extremes in western North America. Clim Dyn 26(6):617–629. https://doi.org/10.1007/s00382-005-0101-9
Feldl N, Roe GH (2011) Climate variability and the shape of daily precipitation: a case study of ENSO and the American west. J Clim 24(10):2483–2499. https://doi.org/10.1175/2010JCLI3555.1
Francis JA, Vavrus SJ (2015) Evidence for a wavier jet stream in response to rapid Arctic warming. Environ Res Lett 10(1):014005. https://doi.org/10.1088/1748-9326/10/1/014005. http://stacks.iop.org/1748-9326/10/i=1/a=014005?key=crossref.74581076f734b2377ec8042d3aebe25d
Gershunov A (1998) ENSO influence on intraseasonal extreme rainfall and temperature frequencies in the contiguous United States: implications for long-range predictability. J Clim 11(12):3192–3203. https://doi.org/10.1175/1520-0442(1998)011<3192:EIOIER>2.0.CO;2
Gershunov A, Barnett TP (1998) Interdecadal modulation of ENSO teleconnections. Bull Am Meteorol Soc 79(12):2715–2725. https://doi.org/10.1175/1520-0477(1998)079<2715:IMOET>2.0.CO;2
Guirguis K, Gershunov A, Cayan DR (2015) Interannual variability in associations between seasonal climate, weather, and extremes: wintertime temperature over the southwestern United States. Environ Res Lett 10(12). https://doi.org/10.1088/1748-9326/10/12/124023
Hoerling MP, Kumar A, Zhong M (1997) El Niño, La Niña, and the nonlinearity of their teleconnections. J Clim 10(8):1769–1786. https://doi.org/10.1175/1520-0442(1997)010<1769:ENOLNA>2.0.CO;2
Holmes CR, Woollings T, Hawkins E, de Vries H (2016) Robust future changes in temperature variability under greenhouse gas forcing and the relationship with thermal advection. J Clim 29(6):2221–2236. https://doi.org/10.1175/JCLI-D-14-00735.1
Intergovernmental Panel on Climate Change (ed) (2014) Climate change 2013—the physical science basis. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781107415324. http://ebooks.cambridge.org/ref/id/CBO9781107415324
JAMSTEC (2018) Modoki index. http://www.jamstec.go.jp/frsgc/research/d1/iod/DATA/emi.monthly.txt
Jasperse J, Ralph M, Anderson M, Brekke LD, Dillabough M, Dettinger M, Haynes A, Hartman R, Jones C, Forbis J, Rutten P, Talbot C, Webb RH (2017) Preliminary viability assessment of Lake Mendocino forecast informed reservoir operations. In: Technical report, USGS. http://pubs.er.usgs.gov/publication/70192184
Kanamitsu M, Ebisuzaki W, Woollen J, Yang SK, Hnilo JJ, Fiorino M, Potter GL (2002) NCEP-DOE AMIP-II reanalysis (R-2). Bull Am Meteorol Soc 83(11):1631–1644. https://doi.org/10.1175/BAMS-83-11-1631
Kang IS, No Hh, Kucharski F (2014) ENSO amplitude modulation associated with the mean SST changes in the tropical central Pacific induced by Atlantic multidecadal oscillation. J Clim 27(20):7911–7920. https://doi.org/10.1175/JCLI-D-14-00018.1
Kerr RA (2000) A North Atlantic climate pacemaker for the centuries. Science 288(5473):1984–1985. https://doi.org/10.1126/science.288.5473.1984
Knowles N, Dettinger MD, Cayan DR (2006) Trends in snowfall versus rainfall in the western United States. J Clim 19(18):4545–4559. https://doi.org/10.1175/JCLI3850.1. arXiv:0504262v1
Krichak SO, Breitgand JS, Gualdi S, Feldstein SB (2014) Teleconnection-extreme precipitation relationships over the Mediterranean region. Theor Appl Climatol 117(3–4):679–692. https://doi.org/10.1007/s00704-013-1036-4
Lauer S (2011) Sierra Nevada water facts. In: Technical report, Water Education Foundation. http://www.sierranevadaconservancy.ca.gov/our-region/docs/sierrabookletfinal.pdf
Leonard M, Westra S, Phatak A, Lambert M, van den Hurk B, McInnes K, Risbey J, Schuster S, Jakob D, Stafford-Smith M (2014) A compound event framework for understanding extreme impacts. Wiley Interdiscip Rev Clim Change 5(1):113–128. https://doi.org/10.1002/wcc.252
Levine AFZ, McPhaden MJ, Frierson DMW (2017a) The impact of the AMO on multidecadal ENSO variability. Geophys Res Lett 44(8):3877–3886. https://doi.org/10.1002/2017GL072524
Levine AFZ, McPhaden MJ, Frierson DMW (2017b) The impact of the AMO on multidecadal ENSO variability. Geophys Res Lett 44(8):3877–3886. https://doi.org/10.1002/2017GL072524
L’Heureux ML, Takahashi K, Watkins AB, Barnston AG, Becker EJ, Di Liberto TE, Gamble F, Gottschalck J, Halpert MS, Huang B, Mosquera-Vásquez K, Wittenberg AT (2017) Observing and predicting the 2015/16 El Niño. Bull Am Meteorol Soc 98(7):1363–1382. https://doi.org/10.1175/BAMS-D-16-0009.1. arXiv:9812034
Livezey RE, Masutani M, Leetmaa A, Rui H, Ji M, Kumar A (1997) Teleconnective response of the Pacific-North American region atmosphere to large central equatorial Pacific SST anomalies. J Clim 10(8):1787–1820. https://doi.org/10.1175/1520-0442(1997)010<1787:TROTPN>2.0.CO;2
Mahony CR, Cannon AJ (2018) Wetter summers can intensify departures from natural variability in a warming climate. Nat Commun 9(1):783. https://doi.org/10.1038/s41467-018-03132-z. http://www.nature.com/articles/s41467-018-03132-z
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC (1997) A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Am Meteorol Soc 78(6):1069–1079. https://doi.org/10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2
McCabe GJ, Dettinger MD (2002) Primary modes and predictability of year-to-year snowpack variations in the western United States from teleconnections with Pacific Ocean climate. J Hydrometeorol 3(1):13–25. https://doi.org/10.1175/1525-7541(2002)003<0013:PMAPOY>2.0.CO;2
Meehl GA, Hu A (2006) Megadroughts in the Indian monsoon region and southwest North America and a mechanism for associated multidecadal Pacific Sea surface temperature anomalies. J Clim 19(9):1605–1623. https://doi.org/10.1175/JCLI3675.1
Mestas-Nuñez AM, Enfield DB (1999) Rotated global modes of non-ENSO sea surface temperature variability. J Clim 12(9):2734–2746. https://doi.org/10.1175/1520-0442(1999)012<2734:RGMONE>2.0.CO;2
Mo KC, Livezey RE (1986) Tropical-extratropical geopotential height teleconnections during the Northern Hemisphere winter. Mon Weather Rev 114(12):2488–2515. https://doi.org/10.1175/1520-0493(1986)114<2488:TEGHTD>2.0.CO;2
Mote PW, Hamlet AF, Clark MP, Lettenmaier DP (2005) Declining mountain snowpack in western North America. Bull Am Meteorol Soc 86(1):39–50. https://doi.org/10.1175/BAMS-86-1-39
National Center for Atmospheric Research Staff (2019) The climate data guide: overview: climate indices. https://climatedataguide.ucar.edu/climate-data/overview-climate-indices
National Oceanic and Atmospheric Administration, Earth System Research Laboratory PSD (2019) Climate indices: monthly atmospheric and ocean time-series. https://www.esrl.noaa.gov/psd/data/climateindices/list/
Neiman PJ, White AB, Ralph FM, Gottas DJ, Gutman SI (2009) A water vapour flux tool for precipitation forecasting. Proc Inst Civil Eng Water Manag 162(2):83–94. https://doi.org/10.1680/wama.2009.162.2.83
Newman M, Alexander MA, Ault TR, Cobb KM, Deser C, Di Lorenzo E, Mantua NJ, Miller AJ, Minobe S, Nakamura H, Schneider N, Vimont DJ, Phillips AS, Scott JD, Smith CA (2016) The Pacific decadal oscillation. Revisited. J Clim 29(12):4399–4427. https://doi.org/10.1175/JCLI-D-15-0508.1
O’Brien TA, Collins WD, Rauscher SA, Ringler TD (2014) Reducing the computational cost of the ECF using a nuFFT: a fast and objective probability density estimation method. Comput Stat Data Anal 79:222–234. https://doi.org/10.1016/j.csda.2014.06.002
O’Brien TA, Kashinath K, Cavanaugh NR, Collins WD, O’Brien JP (2016) A fast and objective multidimensional kernel density estimation method: FastKDE. Comput Stat Data Anal 101:148–160. https://doi.org/10.1016/j.csda.2016.02.014. http://linkinghub.elsevier.com/retrieve/pii/S0167947316300408
Palmer T (2014) Record-breaking winters and global climate change. Science 344(6186):803–804. https://doi.org/10.1126/science.1255147. http://science.sciencemag.org/content/344/6186/803.abstract
Parmesan C (2006) Ecological and evolutionary responses to recent climate change. Annu Re Ecol Evol Syst 37(1):637–669. https://doi.org/10.1146/annurev.ecolsys.37.091305.110100
Pierce DW (2002) The role of sea surface temperatures in interactions between ENSO and the North Pacific oscillation. J Clim 15(11):1295–1308. https://doi.org/10.1175/1520-0442(2002)015<1295:TROSST>2.0.CO;2
Polade SD, Gershunov A, Cayan DR, Dettinger MD, Pierce DW (2013) Natural climate variability and teleconnections to precipitation over the Pacific–North American region in CMIP3 and CMIP5 models. Geophys Res Lett 40(10):2296–2301. https://doi.org/10.1002/grl.50491
Polade SD, Pierce DW, Cayan DR, Gershunov A, Dettinger MD (2014) The key role of dry days in changing regional climate and precipitation regimes. Sci Rep 4:1–8. https://doi.org/10.1038/srep04364
Polade SD, Gershunov A, Cayan DR, Dettinger MD, Pierce DW (2017) Precipitation in a warming world: assessing projected hydro-climate changes in California and other Mediterranean climate regions. Sci Rep 7(1):1–10. https://doi.org/10.1038/s41598-017-11285-y
Poli P, Hersbach H, Dee DP, Berrisford P, Simmons AJ, Vitart F, Laloyaux P, Tan DG, Peubey C, Thépaut JN, Trémolet Y, Hólm EV, Bonavita M, Isaksen L, Fisher M (2016) ERA-20C: an atmospheric reanalysis of the twentieth century. J Clim 29(11):4083–4097. https://doi.org/10.1175/JCLI-D-15-0556.1
Rayner NA (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407. https://doi.org/10.1029/2002JD002670. http://www.ncbi.nlm.nih.gov/pubmed/509
Rhines A, McKinnon KA, Tingley MP, Huybers P (2017) Seasonally resolved distributional trends of North American temperatures show contraction of winter variability. J Clim 30(3):1139–1157. https://doi.org/10.1175/JCLI-D-16-0363.1
Rutz JJ, Steenburgh WJ, Ralph FM (2014) Climatological characteristics of atmospheric rivers and their inland penetration over the western United States. Mon Weather Rev 142(2):905–921. https://doi.org/10.1175/MWR-D-13-00168.1
Sarhadi A, Ausín MC, Wiper MP, Touma D, Diffenbaugh NS (2018) Multidimensional risk in a nonstationary climate: Joint probability of increasingly severe warm and dry conditions. Sci Adv 4(11):eaau3487. https://doi.org/10.1126/sciadv.aau3487
Savtchenko AK, Huffman G, Vollmer B (2015) Assessment of precipitation anomalies in California using TRMM and MERRA data. J Geophys Res Atmos 120(16):8206–8215. https://doi.org/10.1002/2015JD023573
Schlesinger ME, Ramankutty N (1994) An oscillation in the global climate system of period 65–70 years. Nature 367(6465):723–726. https://doi.org/10.1038/367723a0
Screen JA, Simmonds I (2013) Exploring links between Arctic amplification and mid-latitude weather. Geophys Res Lett 40(5):959–964. https://doi.org/10.1002/grl.50174
Seager R, Henderson N (2016) On the role of Tropical Ocean forcing of the persistent North American west coast ridge of winter 2013/14. J Clim 29(22):8027–8049. https://doi.org/10.1175/JCLI-D-16-0145.1
Seager R, Hoerling M, Schubert S, Wang H, Lyon B, Kumar A, Nakamura J, Henderson N (2015) Causes of the 2011–14 California drought. J Clim 28(18):6997–7024. https://doi.org/10.1175/JCLI-D-14-00860.1
Serinaldi F, Kilsby CG (2015) Stationarity is undead: uncertainty dominates the distribution of extremes. Adv Water Resour 77:17–36. https://doi.org/10.1016/j.advwatres.2014.12.013. https://linkinghub.elsevier.com/retrieve/pii/S0309170815000020
Sewall JO (2005) Precipitation shifts over western North America as a result of declining Arctic Sea ice cover: the coupled system response. Earth Interact 9(26):1–23. https://doi.org/10.1175/EI171.1
Singh D, Swain DL, Mankin JS, Horton DE, Thomas LN, Rajaratnam B, Diffenbaugh NS (2016) Recent amplification of the North American winter temperature dipole. J Geophys Res Atmos 121(17):9911–9928. https://doi.org/10.1002/2016JD025116
Steadman RG (1979) The assessment of sultriness. Part I: A temperature-humidity index based on human physiology and clothing science. J Appl Meteorol 18(7):861–873. https://doi.org/10.1175/1520-0450(1979)018<0861:TAOSPI>2.0.CO;2
Stewart IT, Cayan DR, Dettinger MD (2005) Changes toward earlier streamflow timing across western North America. J Clim 18(8):1136–1155. https://doi.org/10.1175/JCLI3321.1
Swain DL, Tsiang M, Haugen M, Singh D, Charland A, Rajaratnam B, Diffenbaugh NS (2014) The extraordinary California drought of 2013/2014: character, context, and the role of climate change (in “explaining extremes of 2013 from a climate perspective”). Bull Am MeteorOL Soc 95(9):S3–S7
Swain DL, Singh D, Horton DE, Mankin JS, Ballard TC, Diffenbaugh NS (2017) Remote linkages to anomalous winter atmospheric ridging over the northeastern Pacific. J Geophys Res Atmos 122(22):12,194–12,209. https://doi.org/10.1002/2017JD026575
Swain DL, Langenbrunner B, Neelin JD, Hall A (2018) Increasing precipitation volatility in twenty-first-century California. Nat Clim Change 8(5):427–433. https://doi.org/10.1038/s41558-018-0140-y. http://www.nature.com/articles/s41558-018-0140-y
Team G (2018) GISS surface temperature analysis (GISTEMP)
Teng H, Branstator G (2017) Causes of extreme ridges that induce California droughts. J Clim 30(4):1477–1492. https://doi.org/10.1175/JCLI-D-16-0524.1
Trenberth KE, Hurrell JW (1994) Decadal atmosphere-ocean variations in the Pacific. Clim Dyn 9(6):303–319. https://doi.org/10.1007/BF00204745. arXiv:0601117
Wang H, Schubert S (2014) Causes of the extreme dry conditions over California during early 2013 (in “explaining extremes of 2013 from a climate perspective”). Bull Am Meteorol Soc 95(9):S7–S11. https://doi.org/10.1175/1520-0477-95.9.S1.1
Wang SY, Hipps L, Gillies RR, Yoon JH (2014) Probable causes of the abnormal ridge accompanying the 2013–2014 California drought: ENSO precursor and anthropogenic warming footprint. Geophys Res Lett 41(9):3220–3226. https://doi.org/10.1002/2014GL059748
Wang SYS, Huang WR, Yoon JH (2015) The North American winter ‘dipole’ and extremes activity: a CMIP5 assessment. Atmos Sci Lett 16(3):338–345. https://doi.org/10.1002/asl2.565
Wang SYS, Yoon JH, Becker E, Gillies R (2017) California from drought to deluge. Nat Clim Change 7(7):465–468. https://doi.org/10.1038/nclimate3330
Watson PAG, Weisheimer A, Knight JR, Palmer TN (2016) The role of the tropical West Pacific in the extreme Northern Hemisphere winter of 2013/2014. J Geophys Res Atmos 121(4):1698–1714. https://doi.org/10.1002/2015JD024048
Wehner M, Stone D, Krishnan H, AchutaRao K, Castillo F (2016) The deadly combination of heat and humidity in India and Pakistan in summer 2015. Bull Am Meteorol Soc 97(12):S81–S86. https://doi.org/10.1175/BAMS-D-16-0145.1
Williams AP, Seager R, Abatzoglou JT, Cook BI, Smerdon JE, Cook ER (2015) Contribution of anthropogenic warming to California drought during 2012–2014. Geophys Res Lett 42(16):6819–6828. https://doi.org/10.1002/2015GL064924
Williams IN, Patricola CM (2018) Diversity of ENSO events unified by convective threshold sea surface temperature: a nonlinear ENSO index. Geophys Res Lett 45(17):9236–9244. https://doi.org/10.1029/2018GL079203
Wolter K, Timlin MS (1993) Monitoring ENSO in COADS with a seasonally adjusted principal component index
Wolter K, Hoerling M, Eischeid JK, van Oldenborgh GJ, Quan XW, Walsh JE, Chase TN, Dole R (2015) How unusual was the cold winter of 2013/14 in the upper midwesT? (in “explaining extremes of 2014 from a climate perspective”). Bull Am Meteorol Soc 96(12):S10–S14
Yoon JH, Kravitz B, Rasch PJ, Simon Wang SY, Gillies RR, Hipps L (2015) Extreme fire season in California: a glimpse into the future? Bull Am Meteorol Soc 96(12):S5–S9. https://doi.org/10.1175/BAMS-D-15-00114.1
Acknowledgements
The authors would like to thank three anonymous reviewers for their insightful and helpful comments that greatly improved the quality of this manuscript. This research was supported by the Director, Office of Science, Office of Biological and Environmental Research of the U.S. Department of Energy as part of their Regional and Global Climate Modeling Program (RGCM) under contract no. DE-AC02-05CH11231, and SYW is supported by DOE Grant DESC0016605.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
O’Brien, J.P., O’Brien, T.A., Patricola, C.M. et al. Metrics for understanding large-scale controls of multivariate temperature and precipitation variability. Clim Dyn 53, 3805–3823 (2019). https://doi.org/10.1007/s00382-019-04749-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04749-6