Abstract
The interdecadal Pacific Oscillation (IPO) represents the decadal mode of the El Niño-Southern Oscillation phenomenon. As such the IPO is one of the dominant modes of decadal climate variability on both sides of the Pacific Ocean basin. For this paper we utilized a newly developed tree-ring data network comprised of five multi-centennial Vietnamese cypress ring-width chronologies that range from around 11°N–23°N latitude. We combined these data with an average of tree-ring derived drought indices from the North American Drought Atlas over the south central USA, from a box that spans from 27.5°N–35.0°N, 85.0°–110.0°W and contains 55 gridpoints and more than 100 tree ring site chronologies, these 2 locations exhibit rainfall variations that are strongly, negatively correlated with each other and are representative of the influence of the IPO on terrestrial rainfall. The final reconstruction model, weighted most heavily on the three most southerly of the five Vietnamese cypress records, spans from 1350 to 2004, and explains nearly 57% of the variance in the original IPO data for the 5-month season of October–February. The reconstruction model passes all standard statistical tests using a split calibration-verification scheme. We reveal 15 positive and 15 negative phase shifts of the IPO prior to the period of instrumentation, suggesting that the IPO has been active for at least the past seven centuries with varying degrees of intensity. We compare our reconstruction with two related millennial records: the MacDonald and Case (Geophys Res Lett 32(8):L08703, 2005) tree ring-derived reconstruction of the Pacific Decadal Oscillation, and an ice core-derived reconstruction of the IPO from the Law Dome Ice core in Antarctica by Vance et al. (Geophys Res Lett 33(6):L06712, 2015). While there is good general agreement with the latter record, there are three key periods of the past where the two records are out of phase, and we explore the reasons for this disparity. Direct comparison with the related Tripole Index (TPI) shows weaker correlation, likely owing to the stronger relationship between our tree ring data and the equatorial Pacific region relative to the north and south regions of the Pacific that combine to comprise the TPI calculation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Interdecadal Pacific Oscillation, or IPO, is a term first used by Power et al. (1999) to define a trans-Pacific sea surface temperature anomaly (SSTA) pattern that reflects a Pacific wide manifestation of what Mantua et al. (1997) referred to as the Pacific Decadal Oscillation, or PDO. As is the case for the PDO, the IPO features relatively abrupt ‘shifts’ in the SSTA pattern across the Pacific Ocean that can persist for 2–3 decades. However, rather than the predominantly northern Pacific expression of the PDO, the IPO has a Pacific basin-wide, bi-hemispheric climate pattern with links to the Indian Ocean sector and ocean–atmosphere coupling (Power et al. 1999; Meehl and Hu 2006; Parker et al. 2007). The IPO and PDO are highly correlated, and phase changes of both are directly correlated with increased or decreased frequency of warm and cold phases of El Niño-Southern Oscillation phenomenon (ENSO), respectively (Verdon and Franks 2006). Negative phases reflect La Niña-like (cold) SSTA over the tropical Pacific, while positive phases appear El Niño-like (warm). Phase changes of both modes take place roughly every 20–30 years (Mantua et al. 1997; Power et al. 1999). The IPO’s influence extends from the Pacific to the Indian Ocean, southern Asia and Madagascar (D’Arrigo et al. 2006; Crueger et al. 2009; D’Arrigo and Ummenhofer 2015), to Australia (Power et al. 1999; Arblaster et al. 2001), and even Antarctica (Palmer et al. 2015; Vance et al. 2015; Meehl et al. 2016b). It has also been suggested that the IPO influences global temperature, as a recent hiatus in global warming was related to the late 1990s IPO phase change (Meehl et al. 2013, 2016a; England et al. 2014), and ensuing Indian Ocean heat content changes transmitted from the Pacific through the atmospheric and oceanic bridge (Lee et al. 2015; Nieves et al. 2015; Ummenhofer et al. 2017; Jin et al. 2018a, b).
Since the early twentieth century three IPO regime shifts (i.e., values of IPO that exceed ± 0.5) have been identified: a positive phase from 1922 to 43, followed by a negative phase from 1946 to 76, and another positive phase from 1978 to 98. Our ability to reconcile only three cycles of the IPO from the instrumental data limits studies of the long-term frequency, amplitude, and dominance of the IPO. Therefore paleo-proxy data from key regions of IPO influence must be analyzed for evidence of IPO variability prior to the period of instrumentation. In North America, Dai (2012) demonstrated that the IPO influences rainfall over the contiguous US, and in particular over western and south-central regions of the country. Over the southwestern US, decadal variations in rainfall are strongly in phase with the evolution of the IPO, with dry and wet periods linked to cold and warm phases, respectively (Dai 2012). Drought reconstructions by Cook et al. (2007) suggest that Medieval “mega” droughts over the American West were spatially coherent, widespread, and have no modern analog. Both the IPO and PDO have been linked to enhanced drought risk on both sides of the Pacific (Kiem and Franks 2004; McCabe et al. 2004), and while Medieval drought reigned across the North American West, mainland Southeast Asia (MSEA) appeared to have experienced one of its wettest periods on record (Buckley et al. 2010, 2014; Cook et al. 2010a). This inverse pattern between the North American West and MSEA during IPO phase shifts is clearly evident from the instrumental record (Meehl and Hu 2006), and paleoclimatic data from these two regions suggest that the IPO may have been active during Medieval times (Buckley et al. 2010, 2014).
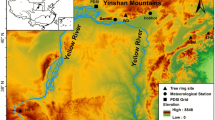
Few reconstructions of the IPO have been developed, in contrast to the PDO, which has several. For example (MacDonald and Case 2005) developed a millennial-length PDO reconstruction from North Pacific tree rings, while other reconstructions have been produced using North American (D’Arrigo et al. 2001) and east Asian (D’Arrigo et al. 2006; D’Arrigo and Ummenhofer 2015) tree rings and Pacific (Gedalof et al. 2002) and Indian Ocean (Crueger et al. 2009) corals, or multi-proxy combinations of some of these records (Verdon and Franks 2006). With the exception of the MacDonald and Case (2005) millennial-length PDO reconstruction, however, these records are relatively short and/or geographically restricted. Buckley et al. (2010, 2014) demonstrated the influence of the IPO over MSEA from a single cypress (Fokienia hodginsii) tree-ring record from southern Vietnam, with sufficient strength of signal to allow for a statistically robust 750-year reconstruction that explained around 41% of the variance of the instrumental record (due to it being derived from a single site, these authors didn’t seek to focus on this IPO reconstruction other than to note the strength of the IPO’s influence on the regional climate). More recently Vance et al. (2015) developed a 1000 year reconstruction of the IPO from the sea salt content contained in ice cores from Law Dome in East Antarctica, and they linked this record to hydroclimate changes over Australia, where positive phases are associated with aridity and negative phases with wetness. Here we produce a new record of IPO variability over the past nearly seven centuries, based on multiple sites from the two regions on opposite sides of the Pacific that are the most strongly, inversely influenced by the IPO–MSEA and the south-central region of North America, as shown in Fig. 1.
Locations of the Fokienia hodginsii (FH) core collections used for this study: 1 = Mu Cang Chai or MCFH (Sano et al. 2008); 2 = Pu Mat National Park or PMFH (this study); 3 = Quang Nam Protected Forest or QNFH (Buckley et al. 2017, 2018); 4 = Kon Tum region including Ka Kinh National Park or KKFH (this study); and 5 = Bidoup Nui Ba National Park or BDFH (Buckley et al. 2010)
2 Materials and methods
2.1 A Vietnamese cypress ring-width network
For this study we used three previously published, indexed ring-width records from F. hodginsii (of the family Cupressaceae, henceforth referred to as cypress), the most reliable long-lived dendroclimatic responder yet found from the Asian tropics. These records are the Mu Cang Chai F. hodginsii (MCFH) from northern (Sano et al. 2008, 2012), Quang Nam F. hodginsii (QNFH) from central (Buckley et al. 2017, 2018) and the Bidoup Nui Ba F. hodginsii (BDFH) from southern Vietnam (Buckley et al. 2010, 2014), respectively. The two new cypress tree-ring records are from Pu Mat National Park in the north (PMFH), and the Kon Tum area in central Vietnam (KKFH). Full details regarding the quality of the three published records can be found in the references noted, while a summary of the most pertinent statistics for all five sites are listed in Table 1, and their locations are shown in Fig. 1.
For all site collections we air dried and mounted all core samples with their transverse axes exposed, and then prepared each core surface with a series of progressively finer abrasive meshes (up to 1500 µm). This resulted in clearly visible cellular structures for each ring in order to ensure accurate identification of ring boundaries. All annual growth rings were then cross-dated using traditional visual and microscopy-based techniques, such as skeleton plotting (Stokes and Smiley 1968), prior to measurement. Measurements of the three published records were made with a resolution of 0.001 mm, using a Velmex sliding stage micrometer coupled with a computer running the capture program J2X developed by VoorTech Consulting. For the new collections, each dated core was scanned using an EPSON Perfection V850 Pro model scanner coupled with Silverfast imaging software in order to produce a high-resolution image (2400 dpi). These images were measured and analyzed with the software CooRecorder V8.1.1 and CDendro V8.1.1 from Cybis Dendrochronology (Larsson 2016), also with a resolution of 0.001 mm. Measurements in CooRecorder are made using a linear x, y coordinate system, where the boundary of each annual ring is marked with successive coordinate points, and the distance between each of those points is measured along the line of cells in sequence. CooRecorder’s companion program CDendro facilitated real time correlation analyses between sequential measurements from individual cores and master growth indices (i.e., multiple crossdated cores averaged together). Quality of the crossdating was further assessed and confirmed via the industry-standard program COFECHA (Holmes 1983).
Each ring-width time series (including the three previously published records) was detrended and normalized using the relatively new method of “signal free” standardization (Melvin et al. 2007; Briffa and Melvin 2011; Melvin and Briffa 2014), as used and described by Buckley et al. (2017, 2018) for the cypress site in central Vietnam (QNFH in Fig. 1). For this purpose, we used the program RCSig, a freeware program developed at the Lamont-Doherty Earth Observatory that is based on the commonly used program ARSTAN (Cook 1985). The signal free methodology is employed in order to retain as much mid-to-low frequency (MLF) variability as possible, while still removing trends that are unlikely to be related to the external forcing of climate.
2.2 North American Drought Atlas data
We extracted and averaged the gridded tree-ring reconstructed PDSI values from a region spanning from 27.5° to 35°N, 85°–110°W from the North American Drought Atlas, or NADA (Cook et al. 2004, 2010b), as represented by one of the two yellow boxes in Fig. 2. The PDSI data are reconstructed for the months of June–August (JJA) from a dense network of tree ring collections spread across the continent, and are interpolated to a 2.5° × 2.5° grid. We next averaged the 55 extrapolated PDSI gridpoints from within the 8.5° × 25° box described above, a region within which are more than 100 tree ring chronologies (Cook et al. 2004). The two yellow boxes in Fig. 2 mark the areas of highest correlation with the first PC scores from the five cypress records over MSEA and North America, respectively, and also represent the regions of highest correlation between rainfall and PDSI as shown by Meehl and Hu (2006, Fig. 9). As noted above, this region of North America is strongly related to IPO variability, and expresses a stable opposite-sign relationship with MSEA over the past several centuries.
The first PC of the 5-site Fokienia hodginsii network (a) vs. November–April Max T and SST (1900–2006), and b the NADA summer PDSI averaged gridbox (right) vs. February–May Max T and October–May SST (1900–2006). The temperature data is from the Berkeley earth surface temperature (BEST) records of mean, minimum and maximum temperature over land (Rohde et al. 2013), while the SST data is from NCDC extended reconstruction sea surface temperature data (ERSSTv5, Huang et al. 2017). The two yellow boxes highlight the two locations of strongest anti-correlation during IPO years as shown by Meehl and Hu (2006), and the regions used for reconstruction of the IPO
2.3 Climate data and indices
We obtained the IPO Index data from the Met Office Hadley Centre for Climate Change (2016: http://cola.gu.edu/c20c/.). Other data sets we used for comparison purposes for this study are the NCDC extended reconstruction sea surface temperature data (ERSSTv5, Huang et al. 2017), and the Berkeley earth surface temperature (BEST) records of mean, minimum and maximum temperature over land (Rohde et al. 2013), the CRU TS4.01 land surface temperature data (Harris et al. 2014), twentieth century reanalysis (1871–2011; Compo et al. 2011) and precipitation at 0.5° horizontal resolution from the Global Precipitation Climatology Centre (version 7; 1901–2013; Schneider et al. 2013). The common analysis period for the composite analyses was taken as 1901–2007. Moisture transport is calculated as the product of the zonal and meridional wind components and specific humidity at every level in the atmosphere and then vertically integrated from the surface to 500 hPa. We also obtained, for comparison purposes, the Tripole Index (TPI), which is based on the unfiltered ERSST data (Henley et al. 2015), and the Vance et al. (2015) reconstruction of the IPO based on ice core records from Law Dome in Antarctica.
2.4 Reconstructing IPO from tree rings and PDSI
We used the five Vietnam cypress records shown in Fig. 1 and highlighted in Table 1, and the average gridded PDSI values from the NADA indicated in Fig. 2 by the yellow box over North America, as predictors of IPO for our reconstruction model. In order to select our target season for reconstruction, point-by-point regression was used for each of the six variables with monthly IPO for a 24-month window that spans 2 full years (January–December for prior and current years, depicted in sequence as months 1–24 in Fig. 3). It is clear from Fig. 3 that the strength of the inverse correlation between Vietnam cypress growth and IPO increases from north to south, and is strongest for BDFH and KKFH, the two most southerly sites. In fact, there are no significant months of correlation with the northern PMFH index, and the weakest of the significant correlations are with MCFH. This is consistent with the reduced influence of the IPO on rainfall over northern Vietnam, as shown in Fig. 4. Composite analyses over Southeast Asia indicate severe deficit (surplus) of rainfall over the Maritime Continent and Vietnam, especially at the southern sites (Fig. 4a, e), during positive (negative) reconstructed IPO phases. This is due to a reduction (enhancement) of the East Asian winter monsoon, as shown by the anomalous moisture transport for positive (negative) IPO phases (Fig. 4c, g). The NADA gridbox data exhibits a near equally strong direct correlation to IPO that essentially mirrors the response for the Vietnamese cypress data, with anomalous wet (dry) conditions over the Southwest and Southeast US during positive (negative) IPO phases (Fig. 4b, f). Since the strongest correlation for both sets of data falls within the 5-month period of prior October to current February, this was the period we selected for reconstruction and composite analyses. For building our reconstruction we used the program PCReg, a principal components regression program that is freely available for download from the Lamont-Doherty Earth Observatory’s Tree Ring Laboratory. For a more complete description of the model used for reconstruction of the IPO, see the calibration and verification statistics presented in Table 2.
Climate response plots for the six time series used for this project vs. the full period (1872–2004) IPO data, as derived from program PCReg as described in the text. The locations of each of these sites are shown in Fig. 1: PMFH—Pu Mat Fokienia hodginsii tree ring index; MCFH—Mu Cang Chai Fokienia hodginsii index; NADA—the 55-gridbox average from the North American Drought Atlas; QNFH—Quang Nam Fokienia hodginsii tree ring index; KKFH—Kon Tum Fokienia hodginsii index; BDFH—Bidoup Nui Ba National Park Fokienia hodginsii tree ring index. The red dashed lines indicate the 95% confidence limits based on the point-by-point regression estimate for each month of IPO against annual growth for a 24-month dendroclimate window (from left to right—January of the prior year to December of the current year). For all but PMFH only months of significant correlations are shown. The ONDJF months were selected for climate reconstruction, as indicated by the red asterisks in each plot
Composite anomalies of precipitation (in mm/month) and vertically integrated moisture transport from the surface to 500 hPa (in kg m−1 s−1) for (left a, c, e and g) Southeast Asia and (right b, d, f and h) North America during (top) positive and (bottom) negative IPO phases in our reconstructed IPO index. The yellow circles in panels a and e mark the locations of the five Vietnamese tree ring records, and the NADA gridbox is highlighted by the black box in panels b and f
3 Results and discussion
The reconstruction of IPO we present here spans from 1350 to 2004 CE, and explains 56.7% of the variance of the instrumental data-derived IPO record (Table 2). It should be noted that the coefficient of efficiency statistic (CE) for verification on both halves of the record (Figs. 5, 6) is consistently positive for both 1st differenced and un-differenced data, and therefore indicates an acceptable amount of model fidelity as described in Cook and Kairiukstis (1990). The first differencing comparison is conducted to assure that correlation of trend in data is not driving the strength of the relationship, accentuating instead the high frequency variations of both datasets. It is noteworthy that correlations are strongest for 1st differenced data, indicating the robust nature of the year-to-year correlation between IPO and tree growth in both locations. While the CE statistic has no significance test per se, the test is particularly sensitive to the influence of outliers and therefore positive values for CE are indicative of model skill.
Calibration period (1872–1941) comparison between the actual values for the October–February IPO (blue) and the robust estimates (black-dashed) based on our regression model for the calibration period (1872–1941). The top plot is for undifferenced data and the bottom plots are for same data after first-differencing. Scatterplots on the right express the linear relationships between the same data as on the left. Full reconstruction details are included in Table 2
Same as for Fig. 5 but for the verification period (1941–2004) data
The full reconstruction is presented in Fig. 7, with the periods of positive and negative IPO phases highlighted. There are three modern phases of the IPO, as noted previously, and our record captures them all. However, the earliest instrumental positive phase (~ 1922–1942) is far less pronounced than the period from ~ 1900–1920 which represents one of the strongest positive IPO phases of the past seven centuries in our record, as is also the case for the TPI developed by Henley et al. (2015), but appears to be driven mostly by their Region 2 box over the equatorial Pacific (see the lower panel in their Fig. 2). This period is also strongly expressed in the Vance et al. (2015) reconstruction of IPO from Antarctica. Prior to the modern period we have identified what we consider 15 pronounced positive phases and 15 similarly pronounced negative phases of the IPO, in a predominantly alternating pattern. We calculated the shifts in IPO phase as changes in our 13-year low pass filtered data that exceed ± 0.5 and persist for more than 1 decade.
The unfiltered October–February IPO reconstruction from 1350 to 2004 (fine black line) based on tree ring data from Vietnam and tree ring derived PDSI regional average from North America (see Fig. 2). The thick red line shows the 13-year low-pass filtered version of the data, with the 15 positive and 15 negative pre-instrumental phases of the IPO highlighted by pink and blue bars, respectively. The red and blue dashed lines highlight the three modern positive and negative PDO phases, respectively as noted from the literature (i.e., positive 1922–1943; negative 1946–1976; positive 1978–1998). The two dashed black lines mark the threshold values of 0.5 above and below the mean. Some key droughts and pluvials as mentioned by Cook et al. (2010a) and Buckley et al. (2010, 2014) are denoted by the black lettering as follows: AD1 and AD2 refer to the Ankgor Droughts 1 and 2; KE encompasses the Kuwae Eruption of 1453 that Buckley et al. (2010) noted as the second wettest year of the BDFH record; MDD corresponds with the Ming Dynasty Drought from 1631 to 48 CE; UND is an unnamed drought of the late seventeenth century that is evident in all of the major Southeast Asia records; SPD is the Strange Parallels Drought; EID is the East India Drought; and VHD marks the period of the two Victorian Holocaust Droughts in 1877–78 and 1888–89, respectively. Note the extreme values for those individual years, following shortly after the largest value of the entire record (6.513) in 1865, marked by the red asterisk
One pressing question regarding the paleo history of the IPO relates to both its vigor and variance over the past millennium. It is clear from Fig. 7 that the vigor of the IPO during some periods of our reconstruction is more pronounced than others, and that there is an increasing trend in the variance through time. We therefore compiled some basic statistics in Tables 3, 4 and 5 of our IPO reconstruction as well as the Vance et al. (2015) IPO reconstruction (henceforth referred to as Vance-IPO). For our IPO reconstruction both the standard deviation and variance show an obvious increasing trend through time, attaining maximum values in the nineteenth century where three of the highest values of the entire record can be found (6.513 for the year 1865, 4.412 for 1878 and 5.872 for 1889). The latter two values occur during the two largest El Niño events of the instrumental record that triggered the so-named “Victorian Holocaust” droughts described by Davis (2002). Interestingly, while these individual years are markedly high the positive phase associated with them is not particularly strong. Much stronger periods of positive IPO are seen in the eighteenth century during periods defined by Cook et al. (2010b) and Buckley et al. (2010, 2014) as the Strange Parallels Drought (SPD) and the East Indian Drought (labeled SPD and EID, respectively in Fig. 7). The latter decade of the seventeenth century shows a moderately strong IPO positive phase during an unnamed drought (UND) that is evident across all of Southeast Asian (Buckley et al. 2017; Stevens et al. 2018). The negative phases of IPO in our reconstruction also exhibit greater strength in the eighteenth century, and two protracted events in the latter half of the nineteenth century, as discussed below.
3.1 A tumultuous eighteenth century for Southeast Asia
According to our reconstruction the eighteenth century exhibited perhaps the most vigorous IPO of the past 700 years, where values for the 13-year smoothed data exceed ± 1.5 for successive years and individual years within each phase exceed ± 3.0 for multiple years. The century began with a strong positive phase from ~ 1685–1705 (see below Sect. 3.2), a sharp negative phase from 1725 to 1740, a positive phase from 1740 to 1760, negative from 1770 to 1780, and strongly positive from 1780 to 1795. The three positive phases were coincident with some of the most societally significant periods of drought for the region over the past millennium (e.g., Buckley et al. 2007, 2010, 2014, 2017; Cook et al. 2010a; Hansen et al. 2017; Lieberman 2003; Lieberman and Buckley 2012; Sano et al. 2008). Tree ring records from Southeast Asia show that the transition from the seventeenth century into the eighteenth century experienced a 2-decades period of drought across most of the region—a drought that has drawn little attention but is among the most pronounced decadal droughts of the past several centuries (Stevens et al. 2018). We will refer to this drought as the Unnamed Drought or UND, as noted in Fig. 7. The SPD, so-named by Cook et al. (2010a) after Lieberman (2003), spanned much of the mid eighteenth century and occurred during the 1740–60 positive IPO phase, as shown from our reconstruction. Buckley et al. (2014) showed this to be a period of great societal upheaval across MSEA, when all of the regional polities collapsed (Lieberman 2003), and the Tay Son Uprising toppled the 350-year reign of the Le dynasty (Dutton 2006). Investigating the SPD in the MADA and a 1300-year climate model simulation, Hernandez et al. (2015) also found IPO-like SST across the Indo-Pacific, with equatorial Pacific SST during prolonged MSEA drought episodes more reminiscent of central-Pacific El Niño events than the canonical eastern Pacific SST. Following the SPD the IPO reverted to a negative phase (1770–80) before returning to the strongest positive phase of the entire reconstruction, spanning the years 1780–1795 during what Cook et al. (2010b) referred to as the East India Drought (EID). Buckley et al. (2014) describe the last few decades of the eighteenth century in terms of repeated, protracted, decadal periods of drought across much of South and Southeast Asia, leading to the Bengali Famine Drought (1769–73), and the East Indian Drought (1790–96). These two tragic events led to millions of deaths from starvation, over what was surely one of the most tumultuous times of the past millennium across the region.
3.2 Prior to the eighteenth century
The seventeenth century also experienced vigorous IPO activity, with two brief negative phases centered on 1640 and 1680, respectively, the latter only barely below the − 0.5 threshold from the mean. These two negative phases were preceded by an extended positive phase from 1605 to 1635. Of interest is a double-peaked positive phase that spanned from about 1685–1720, at a time of one of the driest periods over Southeast Asia as shown by several tree ring records (Buckley et al. 2010, 2017; Cook et al. 2010b; Stevens et al. 2018). The sixteenth and fifteenth centuries saw somewhat reduced strength of the IPO, with the exception of a major protracted negative phase from ~ 1435–1460 (labeled KE in Fig. 7). This is consistent with indications of a mid-century pluvial across southern MSEA (Buckley et al. 2010), whose PDSI reconstruction shows the second wettest year on record in 1453 following the eruption of Kuwae (Gao et al. 2006; Buckley et al. 2010; Anchukaitis et al. 2010). The period of the two so-named Angkor Droughts (Buckley et al. 2010; Cook et al. 2010a), in the mid fourteenth and early fifteenth centuries, respectively, show indications of positive IPO phasing, especially for AD1, though not as strongly expressed as in later events. These periods of drought, as shown by Buckley et al. (2014), were not accompanied by wet conditions in the American Southwest, which experienced simultaneous drought indicative of processes not related to ENSO/IPO variability.
3.3 Indo-Pacific climate anomalies during IPO phases
Composite analyses of the large-scale Indo-Pacific climate conditions during positive and negative phases of our reconstructed IPO during the instrumental period (1901–2007) reveal distinct teleconnection patterns. We not only see the out-of-phase relationship between hydroclimate in MSEA and the southern US, but strong precipitation anomalies in equatorial Africa and South America (Fig. 8a, e). Specifically, eastern (western) equatorial Africa experiences wet (dry) conditions during the positive IPO phase, while northern South America, including the Amazon basin and northeast Brazil, experience drought and anomalous wet conditions further to the south (Fig. 8a). These changes in hydroclimate are consistent with a shift in the zonal Walker circulation: the upward branch is associated with the anomalously warm SST in the eastern Pacific, while anomalous descending motion is suppressing convection over northern South America and the Indo Pacific Warm Pool (IPWP), while East Africa experiences enhanced moisture convergence and convection (Fig. 8a–d). The situation is reversed during the negative phase of the IPO that is characterized by cool SST in the equatorial eastern Pacific and moisture convergence over the IPWP and northern South America (Fig. 8e–h). Some of the IPO responses shown here for decadal timescales are reminiscent of the well-known teleconnections during ENSO events (cf. Ropelewski and Halpert 1987). Spatial patterns of precipitation linked to ENSO over mainland Southeast Asia are complex, vary with individual events, and exhibit a general pattern of decreased precipitation during warm-phase events (El Niño) and greater precipitation during cool-phase events (La Niña) (Räsänen et al. 2015). Yamoah et al. (2016) argue that NCEP reanalysis of strong El Niño years reveals a tripole pattern, exemplified by the TPI as defined by Henley et al. (2015). In this case a low-pressure cell forms during warm phases of ENSO and spans from Malaysia to southern China, thus creating a subordinate meridional circulation cell with the high-pressure cell over the IPWP.
It is noteworthy that the SST composites for our reconstructed IPO do not show much in the way of anomalies over the Indian Ocean sector. In contrast, D’Arrigo and Ummenhofer (2015) identified substantial Indian Ocean SSTAs during both PDO phases, based on their reconstructed May–September PDO from a Myanmar teak record. Several recent studies (e.g., Dong et al. 2016; Lee et al. 2015; Nieves et al. 2015; Ummenhofer et al. 2017; Jin et al. 2018a, b) also found significant IPO influences over the Indian Ocean. While some of the Indian Ocean response is expressed as a subsurface response, there is also a delay of several years with the IPO/PDO until the response makes its way into the Indian Ocean. This is especially true for anomalies transmitted through the oceanic bridge, since the atmospheric bridge through the Walker circulation is more immediate. For our reconstruction, we analyzed anomalies for the October–February period, and it is therefore plausible that other seasons (i.e., June–August or September–November) might be more directly comparable, and may explain the lack of Indian Ocean SST response in our reconstruction.
We compared our record to the Vance IPO record (Fig. 9) and we reveal generally strong agreement in spite of the vastly different nature of these two records. Vance et al. (2015) based their reconstruction on the salt record from an ice core from the Law Dome in Antarctica, and linked it to rainfall anomalies over eastern Australia. Their connection to the IPO through a mid latitude atmospheric teleconnection is more strongly linked to the TPI Region 3, which sits right over and to the east of Australia (Henley et al. 2015). While there are three distinct periods that are out-of-phase between our two records, centered on 1600, 1700 and 1810, respectively, there are periods that agree quite strongly with each other such as the entire fifteenth century. There is also a high degree of phasing between the three decadal out-of-phase periods noted above, indicating the likelihood that some external forcing acting on longer time scales may be influencing one or both records in differing ways. The Vance IPO record extends back to 1000 CE, while the record we present here extends back only to 1350. Therefore we compared the prior Buckley et al. (2010) IPO reconstruction, based only on the BDFH tree ring record, against Vance IPO in the bottom panel (b) of Fig. 9. Once again, there is good general, decadal-scale agreement between the two records, but a notable out-of-phase period centered around 1180 CE at the tail end of what Vance et al. (2015) describe as “an unprecedented century of aridity” over eastern Australia related to a positive IPO. It is clear that while both of our records are capturing real climate variability related to the IPO, there are regional climate factors that are at play that are not shared between our two records.
The top plot a shows the 13-year low-pass filtered Buckley October–February IPO reconstruction (solid red), against the IPO reconstruction of Vance et al. (2015, blue line) based on geochemical parameters from the Law Dome ice core in Antarctica. The two reconstructions show general agreement for much of the time, in spite of being derived in very different ways. While the three “modern” phase shifts (red and blue dashed lines) are recorded similarly, there are three key periods of negative IPO in the Vance record in the early 17th, early 18th and early nineteenth centuries that are distinctly out of phase, as denoted by the blue bars. The bottom plot b compares the earliest portion of the Vance IPO series (black line back to 1000 CE) with a prior IPO reconstruction by Buckley et al. (2010) based on the BDFH site only (dashed red line from 1350 back to 1057 CE). The large pink bar from 1102 to 1212 highlights the period of “an unprecedented century of aridity” in eastern Australia, related to a strong positive IPO, as described by Vance et al. (2015)
We present a stacked plot in Fig. 10 of the annually averaged TPI of Henley et al. (2015), the MacDonald and Case (2005) IPO reconstruction, the Vance-IPO reconstrutction and our own IPO reconstruction. The TPI is calculated as the difference between the SSTA averaged over a region of the central equatorial Pacific (their Region 2), and the average of the SSTA in the northwest and southwest Pacific sectors (25°N–45°N, 140°E–145°W; and 50°S–15°S, 150°E–160°W, respectively). For context the composite anomalies shown in Fig. 8d, h, indicate the areas of strongest SST response during the IPO positive and negative phases. While the TPI does show strong agreement with the PDO and the IPO, its calculation does not include regions that are included in the IPO calculations, such as the Indian Ocean sector, which is often uncoupled from the TPI regional SSTAs. Our IPO reconstruction is based on two terrestrial regions that are influenced by the Oceanic sectors as expressed through regional hydroclimate. It is therefore not surprising that the two records are not in better agreement. It appears that our IPO reconstruction is far more heavily influenced by the TPI Region 2 calculation used by Henley et al. (2015), as shown in their lower plot of Fig. 2. This region spans from 10°S–10°N, 170°E–90°W, which straddles the equatorial Pacific and is the region of highest correlation of PC 1 of the Vietnam cypress records as shown in Fig. 2. The Henley et al. (2015) Regions 1 and 3 fall for the most part outside the region of greatest influence for our cypress and NADA records. This is particularly the case for the NADA (Fig. 2b). It would therefore not be unexpected that our terrestrially derived records of IPO influence are at least in part capturing influences not shared by TPI, particularly the influence of the Indian Ocean sector as noted above.
Stacked plot comparing a the Tri Pole Index (TPI) developed by Henley et al. (2015); b the MacDonald and Case (2005) PDO reconstruction back to 1350; c the Vance et al. (2015) IPO reconstruction back to 1350; and d, our reconstruction of IPO. All data smoothed with a 13-year low pass filter, and gray bars highlight every other century
4 Conclusions
We produced a highly robust reconstruction of the IPO using tree-ring related data from both sides of the Pacific Ocean, from locations where hydroclimate dominates the tree ring signal and are anti-correlated with each other. The terrestrial hydrological imprint from these two regions is strongly dominated in turn by the IPO, and this enabled us to produce a reconstruction that captures nearly 57% of the variance of the IPO index. Our reconstruction indicates a consistently active IPO for at least the last 700 years with 15 positive and 15 negative phases displayed prior to the period of instrumentation. Our reconstruction is also in good general agreement with the Vance et al. (2015) IPO reconstruction developed from Antarctic ice core from the Law Dome, in spite of the very different proxy sources, procedures used, and regions involved in each reconstruction. In spite of the overall agreement, however, there are several key periods of discord between our two reconstructions that likely reflect climate drivers not related to ENSO/IPO, or reflect spatial instability of some components of the IPO influence. In particular, our reconstruction seems mostly influenced by the TPI Region 2 over the equatorial Pacific, while the Vance IPO record is likely more strongly influenced by TPI Region 3. Similarly, our reconstruction shows some discord with the TPI itself, likely owing to the very different spatial characteristics of the two records as discussed above. The record we present here shows a clear systematic increase in the variance of IPO over the past six centuries and ought to be a useful launching point for future research.
Change history
16 August 2019
In the Original publication of the article, a grant number was not included in the in acknowlegement section. The correct information is as follows.
References
Anchukaitis KJ, Buckley BM, Cook ER, Cook BI, D'Arrigo RD, Ammann CM (2010) Influence of volcanic eruptions on the climate of the Asian monsoon region. Geophys Res Lett 37(22):L22703. https://doi.org/10.1029/2010GL044843
Arblaster J, Meehl G, Moore A (2001) Interdecadal modulation of Australian rainfall. Clim Dyn 18(6):519–531. https://doi.org/10.1007/s00382-001-0191-y
Briffa KR, Melvin TM (2011) A closer look at regional curve standardization of tree-ring records: justification of the need, a warning of some pitfalls, and suggested improvements in its application. In: Dendroclimatology. Springer Netherlands, pp 113–145
Buckley BM, Palakit K, Duangsathaporn K, Sanguantham P, Prasomsin P (2007) Decadal scale droughts over northwestern Thailand over the past 448 years: links to the tropical Pacific and Indian Ocean sectors. Clim Dyn 29(1):63–71
Buckley BM, Anchukaitis KJ, Penny D, Fletcher R, Cook ER, Sano M, Le Canh Nam A, Wichienkeeo TT, Minh TM, Hong (2010) Climate as a contributing factor in the demise of Angkor, Cambodia. Proc Natl Acad Sci USA 107(15):6748–6752. https://doi.org/10.1073/pnas.0910827107
Buckley BM, Fletcher R, Wang S-YS, Zottoli B, Pottier C (2014) Monsoon extremes and society over the past millennium on mainland Southeast Asia. Quat Sci Rev 95(C):1–19. https://doi.org/10.1016/j.quascirev.2014.04.022
Buckley BM, Stahle DK, Luu HT, Wang S-Y, Nguyen TQT, Thomas P, Le C Nam, Ton TM, Bui TH, Nguyen VT (2017) Central Vietnam climate over the past five centuries from cypress tree rings. Clim Dyn 48(11–12):3707–3723
Buckley BM, Hansen KG, Griffin KL, Schmiege SS, Oelkers R, D’Arrigo RD, Stahle DK, Davi N, Nguyen TQT, Le CN, Wilson RJ (2018) Blue intensity from a tropical conifer’s annual rings for climate reconstruction: an ecophysiological perspective. Dendrochronologia 50:10–22
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P, Brönnimann S (2011) The twentieth century reanalysis project. Q J R Meteorol Soc 137(654):1–28
Cook ER (1985) A time series analysis approach to tree-ring standardization. Ph.D. Dissertation, University of Arizona, Tucson, p 171
Cook ER, Kairiukstis LA (eds) (1990) Methods of dendrochronology: applications in the environmental sciences. Springer Netherlands
Cook ER, Woodhouse CA, Eakin CM, Meko DM, Stahle DW (2004) Long-term aridity changes in the western United States. Science 306(5698):1015–1018. https://doi.org/10.1126/science.1102586
Cook ER, Seager R, Cane MA, Stahle DW (2007) North American drought: reconstructions, causes, and consequences. Earth Sci Rev 81(1–2):93–134. https://doi.org/10.1016/j.earscirev.2006.12.002
Cook ER, Anchukaitis KJ, Buckley BM, D’Arrigo RD, Jacoby GC, Wright WE (2010a) Asian monsoon failure and megadrought during the last millennium. Science 328(5977):486–489. https://doi.org/10.1126/science.1185188
Cook ER, Seager R, Heim RR Jr, Vose RS, Herweijer C, Woodhouse C (2010b) Megadroughts in North America: placing IPCC projections of hydroclimatic change in a long-term palaeoclimate context, edited by C. Caseldine, C. Turney, A. Long. J Quat Sci 25(1):48–61. https://doi.org/10.1002/jqs.1303
Crueger T, Zinke J, Pfeiffer M (2009) Patterns of Pacific decadal variability recorded by Indian Ocean corals. Int J Earth Sci (Geol Rundsch) 98(1):41–52. https://doi.org/10.1007/s00531-008-0324-1
D’Arrigo R, Ummenhofer CC (2015) The climate of Myanmar: evidence for effects of the Pacific Decadal Oscillation. Int J Climatol 35(4):634–640. https://doi.org/10.1002/joc.3995
D’Arrigo R, Villalba R, Wiles G (2001) Tree-ring estimates of Pacific decadal climate variability. Clim Dyn 18(3–4):219–224. https://doi.org/10.1007/s003820100177
D’Arrigo R, Wilson R, Palmer J, Krusic P, Curtis A, Sakulich J, Bijaksana S, Zulaikah S, Ngkoimani LO (2006) Monsoon drought over Java, Indonesia, during the past two centuries. Geophys Res Lett 33(4):L04709. https://doi.org/10.1029/2005GL025465
Dai A (2012) The influence of the inter-decadal Pacific oscillation on US precipitation during 1923–2010. Clim Dyn 41(3–4):633–646. https://doi.org/10.1007/s00382-012-1446-5
Davis M (2002) Late Victorian holocausts: El Niño famines and the making of the third world. Verso Books, Brooklyn
Dong L, Zhou T, Dai A, Song F, Wu B, Chen X (2016) The footprint of the inter-decadal Pacific oscillation in Indian Ocean sea surface temperatures. Sci Rep 6:21251. https://doi.org/10.1038/srep21251
Dutton GE (2006) The Tay Son uprising: society and rebellion in eighteenth-century Vietnam. University of Hawaii Press
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Sen Gupta A, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat Clim Change 4(3):222–227. https://doi.org/10.1038/nclimate2106
Gao C, Robock A, Self S, Witter JB, Steffenson JP, Clausen HB, Ammann C (2006) The 1452 or 1453 AD Kuwae eruption signal derived from multiple ice core records: Greatest volcanic sulfate event of the past 700 years. J Geophys Res Atmos 111(D12):D12107
Gedalof Z, Mantua NJ, Peterson DL (2002) A multi-century perspective of variability in the Pacific Decadal Oscillation: new insights from tree rings and coral. Geophys Res Lett 29(24):57-1-57–4. https://doi.org/10.1029/2002GL015824
Hansen KG, Buckley BM, Zottoli B, D’Arrigo RD, Van Truong V, Nguyen DT, Nguyen HX (2017) Discrete seasonal hydroclimate reconstructions over northern Vietnam for the past three and a half centuries. Clim Change 145(1–2):177–188
Harris I, Jones PD, Osborn TJ, Lister DH (2014) Updated high-resolution grids of monthly climatic observations—the CRU TS3.10 dataset. Int J Climatol 34:623–642. https://doi.org/10.1002/joc.3711
Henley BJ, Gergis J, Karoly DJ, Power SB, Kennedy J, Folland CK (2015) A Tripole Index for the Interdecadal Pacific Oscillation. Clim Dyn 45(11–12):3077–3090. https://doi.org/10.1007/s00382-015-2525-1
Hernandez M, Ummenhofer CC, Anchukaitis KJ (2015) Multi-scale drought and ocean-atmosphere variability in monsoon Asia. Environ Res Lett. https://doi.org/10.1088/1748-9326/10/7/074010
Holmes RL (1983) Computer assisted quality control. Tree-Ring Bull 43:69–78
Huang B, Thorne PW, Banzon VF, Boyer T, Chepurin G, Lawrimore JH, Menne MJ, Smith TM, Vose RS, Zhang HM (2017) Extended reconstructed sea surface temperature, version 5 (ERSSTv5): upgrades, validations, and intercomparisons. J Clim 30(20):8179–8205
Jin X, Kwon Y, Ummenhofer CC, Seo H, Kosaka Y, Wright JS (2018a) Distinct mechanisms of decadal subsurface heat content variations in the eastern and western indian ocean modulated by tropical Pacific SST. J Climate 31:7751–7769
Jin X, Kwon Y, Ummenhofer CC, Seo H, Schwarzkopf FU, Biastoch A, Böning CW, Wright JS (2018b) Influences of Pacific climate variability on decadal subsurface ocean heat content variations in the Indian Ocean. J Clim 31:4157–4174
Kiem AS, Franks SW (2004) Multi-decadal variability of drought risk, eastern Australia. Hydrol Process 18(11):2039–2050. https://doi.org/10.1002/hyp.1460
Larsson L-Å (2016) CDendro & CooRecorder program package for tree ring measurements and crossdating of the data, version 8.1.1. http://www.cybis.se/forfun/dendro
Lee S-K, Park W, Baringer MO, Gordon AL, Huber B, Liu Y (2015) Pacific origin of the abrupt increase in Indian Ocean heat content during the warming hiatus. Nat Geosci 8:445–450
Lieberman VB (2003) Strange parallels: Southeast Asia in global context, c 800-1830, vol 1. Cambridge University Press
Lieberman V, Buckley B (2012) The impact of climate on Southeast Asia, circa 950–1820: new findings. Mod Asian Stud 46(5):1049–1096
MacDonald GM, Case RA (2005) Variations in the Pacific Decadal Oscillation over the past millennium. Geophys Res Lett 32(8):L08703. https://doi.org/10.1029/2005GL022478
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC, Mantua NJ, Hare SR, Zhang Y, Francis RC (1997) A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Am Meteorol Soc 78(6):1069–1079. https://doi.org/10.1175/1520-0477(1997)078%3C1069:APICOW%3E2.0.CO;2
McCabe GJ, Palecki MA, Betancourt JL (2004) Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States. Proc Natl Acad Sci USA 101(12):4136–4141
Meehl G, Hu A (2006) Megadroughts in the Indian Monsoon Region and Southwest North America and a mechanism for associated multidecadal Pacific sea surface temperature anomalies. J Clim 19(9):1605–1623, https://doi.org/10.1175/JCLI3675.1
Meehl GA, Hu A, Arblaster JM, Fasullo J, Trenberth KE (2013) Externally forced and internally generated decadal climate variability associated with the interdecadal Pacific oscillation. J Clim 26(18):7298–7310. https://doi.org/10.1175/JCLI-D-12-00548.1
Meehl GA, Hu A, Santer BD, Xie SP (2016a) Contribution of the Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends. Nat Clim Change 6(11):1005
Meehl GA, Arblaster JM, Bitz CM, Chung CT, Teng H (2016b) Antarctic sea-ice expansion between 2000 and 2014 driven by tropical Pacific decadal climate variability. Nat Geosci 9(8):590–595
Melvin TM, Briffa KR (2014) CRUST: software for the implementation of regional chronology standardisation: Part 1. Signal-free RCS. Dendrochronologia 32(1):7–20. https://doi.org/10.1016/j.dendro.2013.06.002
Melvin TM, Briffa KR, Nicolussi K, Grabner M (2007) Time-varying-response smoothing. Dendrochronologia 25(1):65–69. https://doi.org/10.1016/j.dendro.2007.01.004
Nieves V, Willis JK, Patzert WC (2015) Recent hiatus caused by decadal shift in Indo-Pacific heating. Science 349:532–535
Palmer JG, Cook ER, Turney CSM, Allen K, Fenwick P, Cook BI, O’Donnell A, Lough J, Grierson P, Baker P (2015) Drought variability in the eastern Australia and New Zealand summer drought atlas (ANZDA, CE 1500–2012) modulated by the Interdecadal Pacific Oscillation. Environ Res Lett 10(12):1–12. https://doi.org/10.1088/1748-9326/10/12/124002
Parker D, Folland C, Scaife A, Knight J, Colman A, Baines P, Dong B (2007) Decadal to multidecadal variability and the climate change background. J Geophys Res 112(D18):D18115–D18118. https://doi.org/10.1029/2007JD008411
Power S, Casey T, Folland C, Colman A, Mehta V (1999) Inter-decadal modulation of the impact of ENSO on Australia. Clim Dyn 15(5):319–324. https://doi.org/10.1007/s003820050284
Räsänen TA, Lindgren V, Guillaume JHA, Buckley BM, Kummu M (2015) On the spatial and temporal variability of ENSO precipitation and drought teleconnection in mainland Southeast Asia. Clim Past Discuss 11(6):5307–5343. https://doi.org/10.5194/cpd-11-5307-2015
Rohde R, Muller RA, Jacobsen R, Muller E, Perlmutter S, Rosenfeld A, Wurtele J, Groom D, Wickham C (2013) A new estimate of the average earth surface land temperature spanning 1753 to 2011. Geoinfor Geostat Overview 1:1. https://doi.org/10.4172/gigs.1000101
Ropelewski CF, Halpert MS (1987) Global and regional scale precipitation patterns associated with the El Niño/Southern Oscillation. Mon Weather Rev 115:1606–1626
Sano M, Buckley BM, Sweda T (2008) Tree-ring based hydroclimate reconstruction over northern Vietnam from Fokienia hodginsii: eighteenth century mega-drought and tropical Pacific influence. Clim Dyn 33(2–3):331–340. https://doi.org/10.1007/s00382-008-0454-y
Sano M, Xu C, Nakatsuka T (2012) A 300-year Vietnam hydroclimate and ENSO variability record reconstructed from tree ring δ18O. J Geophys Res 117:D12115. https://doi.org/10.1029/2012JD017749
Schneider U, Becker A, Finger P, Meyer-Christoffer A, Ziese M, Rudolf B (2013) GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor Appl Climatol. https://doi.org/10.1007/s00704-013-0860-x
Stevens LR, Buckley BM, Kim S, Hill P, Doiron K (2018) Increased effective moisture in northern Vietnam during the Little Ice Age. Palaeogeogr Palaeoclimatol Palaeoecol 511:449–461
Stokes MA, Smiley TL (1968) An introduction to tree-ring dating. University of Chicago Press, Chicago
Ummenhofer CC, Biastoch A, Böning CW (2017) Multi-decadal Indian Ocean variability linked to the Pacific and implications for preconditioning Indian Ocean Dipole events. J Clim 30:1739–1751
Vance TR, Roberts JL, Plummer CT, Kiem AS, van Ommen T (2015) Interdecadal Pacific variability and eastern Australian megadroughts over the last millennium. Geophys Res Lett. https://doi.org/10.1002/(ISSN)1944-8007
Verdon DC, Franks SW (2006) Long-term behaviour of ENSO: interactions with the PDO over the past 400 years inferred from paleoclimate records. Geophys Res Lett 33(6):L06712. https://doi.org/10.1029/2005GL025052
Yamoah KA, Chabangborn A, Chawchai S, Schenk F, Wohlfarth B, Smittenberg RH (2016) A 2000-year leaf wax-based hydrogen isotope record from Southeast Asia suggests low frequency ENSO-like teleconnections on a centennial timescale. Quatern Sci Rev 148:44–53
Acknowledgements
Use of the following data sets is gratefully acknowledged: Global Precipitation Climatology Center data set by the German Weather Service (DWD) through http://gpcc.dwd.de, NOAA ERSST and TPI data provided by NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, through https://www.esrl.noaa.gov/psd and https://www.esrl.noaa.gov/psd/data/timeseries/IPOTPI; and the Twentieth Century Reanalysis Project supported by the US. DOE, Office of Science Innovative and Novel Computational Impact on Theory and Experiment program, Office of Biological and Environmental Research, and NOAA Climate Program Office. This research was funded by the National Science Foundation of the USA research Grants AGS 12-03818, AGS 13-03976, AGS 12-03704, AGS 13-04245, AGS 13-03976, AGS 16-02455 and AGS 16-02629, with additional funding from the Lamont-Doherty Earth Observatory’s Climate Center and Climate and Life initiatives. We are most grateful to our colleagues in Vietnam from Bidoup-Nui Ba National Park in Lam Dong Province and the Southern Institute of Ecology in HCMC for logistical help throughout the course of this project, along with the forest rangers and staff at the various site locations from which we sampled throughout Vietnam. We also extend our sincere thanks to Masaki Sano for the use of his Mu Cang Chai Fokienia hodginsii record. Lamont-Doherty Contribution no. 8295.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Buckley, B.M., Ummenhofer, C.C., D’Arrigo, R.D. et al. Interdecadal Pacific Oscillation reconstructed from trans-Pacific tree rings: 1350–2004 CE. Clim Dyn 53, 3181–3196 (2019). https://doi.org/10.1007/s00382-019-04694-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04694-4