Abstract
The reforecast of 11 models in the sub-seasonal to seasonal (S2S) prediction project has been analyzed to investigate the effects of the Madden–Julian Oscillation (MJO) on the prediction skill of winter 2-m air temperature (T2M) over China. Most of the S2S models have useful prediction skills (correlation skill ≥ 0.5) before pentads 3 and 4. ECMWF model can possess a good prediction skill for almost four pentads and perform the best among the 11 models. ECCC and ECMWF models have more reliable ensemble prediction and better ensemble strategies than the other models. All the models tend to have lower T2M prediction skill over the Tibetan Plateau than that over the other regions of China. Moreover, initial state and model resolution have important influences on S2S prediction skill. In most of the models at pentads 3 and 4, T2M prediction skill of forecast with MJO at initial time is significantly higher than that without over parts of China. However, the spatial distributions of the prediction skill differences due to MJO are not consistent among the 11 models. This indicates that there is an uncertainty of the effects of MJO on T2M prediction over China at pentads 3 and 4. Planetary-scale teleconnection pattern excited by MJO over the Northern Hemisphere is the possible reason for the effect of MJO on T2M prediction skill. Because most of the models can maintain this teleconnection pattern for 3–4 forecast pentads, MJO can affect the atmospheric circulation over China during this period, and improve the T2M prediction skill in the models. This finding suggests that the prediction of winter T2M over China initialized with MJO can be more skillful at pentads 3 and 4 than that without MJO in the initial conditions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Skillful climatic forecasts on sub-seasonal time scales (10–90 days) can provide practical information for the decisions in government and business activities that are vulnerable to sub-seasonal climatic variability (Dutton et al. 2013; White et al. 2017). All the time, sub-seasonal prediction is a hard nut to crack in the climate forecast systems, including both statistical and dynamical ones (Hudson et al. 2011; Vitart et al. 2012; Zhang et al. 2013). During the past decade, many efforts have been made to narrow the gap between medium-range weather and seasonal forecasts, especially in dynamical forecasts (Vitart 2014).
Although there are efforts under way to make sub-seasonal to seasonal (S2S) forecast in operation, it is still on its early stage of development (White et al. 2017). S2S time scale is an awkward time range for dynamical forecast (Lau and Waliser 2012). Prediction time is too long that numerical model loses most of the memory of the initial conditions, which are the primary prediction source for medium-range weather forecast (2 weeks; Lorenz 1975). In addition, the atmosphere during S2S period has less time to sufficiently respond to the slow evolving aspects of climatic system (sea surface temperature, sea ice, and soil moisture etc.), which are the major dependents of seasonal to inter-annual forecasts (von Neumann 1955). Recently, researchers found that the low-frequency processes in the climatic system are extremely valuable for S2S forecast (Fu et al. 2011; Zhang et al. 2014), and can provide useful information that strongly influences the lead time of S2S forecast (Waliser et al. 1999; Pegion and Sardeshmukh 2011).
The intra-seasonal oscillation in the atmosphere is one of the most important potential source of S2S predictability (Riddle et al. 2013; Hsu et al. 2015), especially the Madden–Julian Oscillation (MJO; Neena et al. 2014a). MJO can provide useful information for intra-seasonal forecast in tropics (Neena et al. 2014b; Zhu et al. 2015; Tippett et al. 2015). For example, the prediction skill of the MJO itself relates to the initial condition of MJO in both statistical and dynamical models (Jiang et al. 2008; Nasuno et al. 2013; Wu et al. 2016). When forecasts are initialized with active (inactive) MJO, models generally exhibit high (low) prediction skills (Kang and Kim 2010; Kang et al. 2014; Kim et al. 2014; Cavanaugh et al. 2015; Xiang et al. 2015). In addition, MJO also affects sub-seasonal prediction skill over extratropics. For example, Johnson et al. (2014) found that MJO contributes to the improvement of the forecast skill of the North American 2-m air temperature (T2M) during winter in the forecast of weeks 3 and 4. The forecast of 500-hPa geopotential height (H500) in extratropics is more skillful during MJO events than that during null MJO events (Jones et al. 2015). The linkage between MJO and the prediction skill of extratropical sub-seasonal climate is mainly due to the influence of MJO on extratropical climate through the teleconnection pattern triggered by the tropical convection associated with MJO (Cassou 2008; Lin and Brunet 2009; Zhou et al. 2011, 2016; Lee et al. 2011; Yoo et al. 2012; Garfinkel et al. 2014). Therefore, it is interesting to understand the relationship between MJO and the forecast skill of extratropical sub-seasonal climate in various numerical models to improve S2S prediction.
Among various projects that try to improve numerical weather and climate forecasts (e.g., Bougeault et al. 2010; Kirtman et al. 2014), the S2S project provides opportunities for the understanding and improvement of the sub-seasonal forecast skill of the present dynamical prediction systems in 11 operational meteorological centers around the world (http://www.s2sprediction.net). In addition, the S2S project supplies a considerable database for researchers to explore sub-seasonal variability (Vitart et al. 2017). Using this database, the prediction skill of numerical models in operational centers can be evaluated and compared, and thus the common and different features among these models can be further investigated. For example, recently, the forecast skill of winter MJO (Vitart 2017; Liu et al. 2017, 2018) and intra-seasonal variation of Asian summer monsoon (Jie et al. 2017) have been assessed through using the S2S project database. Furthermore, the S2S project presents an opportunity for the understanding of the relationship between MJO and model prediction skill in extratropics. In this study, using the S2S database, we focus on the prediction skills of T2M and the effects of MJO on the skills over China during extended boreal winter (November–March).
The structure of this paper is as follows. Section 2 introduces the data and method. Section 3 shows the prediction skills of the 11 models in the S2S project. The effects of MJO on the prediction skill of winter T2M over China and possible mechanism are provided in Sects. 4 and 5, respectively. At last, Sect. 6 will contain a summary and discussions.
2 Data and methods
2.1 Data
The 6-hourly T2M and H500 of ERA-Interim reanalysis during 1981–2016 are obtained from the ECMWF (http://apps.ecmwf.int/datasets/). The reanalyses with the horizontal resolutions of 1.5° × 1.5° and 2.5° × 2.5° are used. The daily bivariate MJO index of Wheeler and Hendon (2004) during 1981–2016 is provided by the Australian Bureau of Meteorology (http://www.bom.gov.au/climate/mjo/). The two components of MJO index (denoted by RMM1 and RMM2) are based on the first two empirical orthogonal functions of outgoing longwave radiation and 850- and 200-hPa zonal winds, with seasonal cycle and inter-annual variability being removed (see Wheeler and Hendon 2004 for details). The amplitude and phase of MJO are defined by \(A=\sqrt {RM{M_1}^{2}+RM{M_2}^{2}}\) and \(\theta =\arctan (RM{M_2}RM{M_1}^{{ - 1}})\), respectively.
The reforecast data of the S2S project is downloaded from ECMWF website (https://www.ecmwf.int/en/research/projects/s2s). The S2S project provides reforecasts of the 11 dynamical models from the operational centers around the world (Vitart et al. 2017). These centers include the Australian Bureau of Meteorology (BoM), the China Meteorological Administration (CMA), the Environment and Climate Change Canada (ECCC), the European Centre for Medium-Range Weather Forecasts (ECMWF), the Hydrometeorological Centre of Russia (HMCR), the Italy Institute of Atmospheric Sciences and Climate of the National Research Council (ISAC-CNR), the Japan Meteorological Agency (JMA), the Korea Meteorological Administration (KMA), the Météo-France/Centre National de Recherche Meteorologiques (Meteo-France), the US National Centers for Environmental Prediction (NCEP), and the UK Met Office (UKMO).
The ensemble sizes of these reforecasts are from 3 to 33 (Table 1). The reforecasts are conducted from daily to twice a month. Forecast times range from 31 to 62 days, and forecast period is from 20 to 32 years, during which the forecasts are available. The archived horizontal resolution of the reforecast data is 1.5° × 1.5°, except that it is 2.5° × 2.5° in BoM. Thus, reanalyses with two resolutions are used for evaluation. It is noted that those resolutions are different from the resolutions that are set for the running of models (Table 1). Since some centers have updated their reforecast, there are some differences between the reforecast data used in this study and that introduced by Vitart et al. (2017). For example, the ensemble size of ISAC-CNR reforecast used to be one, and now it is updated to five. The reforecast periods of some models have also been updated (e.g., KMA, ECCC, and UKMO). The reforecast periods are different among the 11 S2S models, and the common period of the reforecast among the 11 models is 1999–2010 (Table 1). In order to have an accurate model inter-comparison, the prediction skill during 1999–2010 for each model are checked during model evaluation (Sect. 3). However, for MJO’s effect on T2M prediction skill, we need as many samples as we could use, and thus we present the results during each model’s entire reforecast period in Sects. 4 and 5. This is mainly because some models (e.g., Meteo-France, KMA, JMA, and UKMO) have too few reforecasts during the common period 1999–2010, due to their low reforecast frequency (Table 1).
The ensemble mean of the reforecasts is obtained by averaging among the ensemble members of each model with equal weight. In order to remove seasonal cycle and synoptic variability, we subtract the climatology of seasonal cycle during the reforecast period for each model, and then average the reforecasts into pentads during their forecast time. Thus, the forecast times range from 6 to 12 pentads amongst the 11 models, and only the first 6 pentads are analyzed in the present study. It is noted that the climatology of seasonal cycle is calculated for every forecast time of each model, for example, the climatology at forecast day 1 is calculated only using the forecast data at day 1, and so on. Observed T2M, H500, RMM1, and RMM2, with seasonal cycle being removed, are also averaged into pentads. Because the reforecast period and frequency are different in the 11 models, the climatology of seasonal cycle for observations is also calculated according to the reforecast period and frequency of each model. At last, we obtain 11 sets of observed anomalies of T2M, H500, RMM1, and RMM2, which correspond to the 11 reforecasts of the S2S models. In this study, we mainly focus on the prediction skill of T2M over China during extended boreal winter (November–March). The correlation skill and root mean square error (RMSE) are computed between the anomalies of S2S reforecasts and observations to evaluate the model prediction skill of T2M.
2.2 Significant test
The significant test for the difference of prediction skill is conducted according to the Monte Carlo techniques (Ebisuzaki 1997; Zhou et al. 2011, 2016). For each model’s reforecast, the differences of T2M prediction skill between the forecast initialized with and without MJO are computed and denoted by Diff. After that, five steps are carried out to obtain the significance as follows.
-
1.
We randomly shuffle the MJO index by time during winter, but do not change the observed and reforecasted T2M. This manipulation generates a set of new randomly matched pairs between the MJO index and T2M.
-
2.
The initial times with MJO amplitude ≥ 1 and < 1 are picked out using the randomly shuffled MJO index.
-
3.
The differences of T2M prediction skills between the forecasts initialized with and without MJO based on the new-generated pairs are computed and denoted by Diffshuffle.
-
4.
We repeat the steps (1) to (3) for 1000 times.
-
5.
Finally, the probability (p value) of Diffshuffle ≥ Diff > 0 is calculated in each grid point.
The non-hypothesis is that there is no positive difference between prediction skill with and without MJO at initial time, which indicates Diff > 0 occurs by chance. Therefore, if the p value is smaller than 0.05, this means that the positive difference is significant at the 5% level and does not occur by chance. It is noted that the significance of Diff < 0 is not calculated.
3 Evaluation of T2M prediction skills of S2S models
The winter T2M prediction skill of the ensemble mean in the S2S models is evaluated over four regions in China (Fig. 1), including southern China (Reg1), western China (Reg2), central northern China (Reg3), and northeastern China (Reg4). T2M is averaged over each of those four regions for both observation and reforecast.
Figure 2 shows the T2M prediction skills of 11 S2S models during 1999–2010 over the four regions of China. Prediction skill is represented by the correlation coefficient between the anomalies of observed and forecasted T2M during winter. A skillful prediction is defined as that with a correlation coefficient greater than 0.5. In Fig. 2, the 11 S2S models can produce a skillful prediction of T2M for about three to four pentads over China, except that it is about two (two and a half) pentads in Reg1 in BoM (Reg2 in HMCR). In some models, such as BoM, HMCR, ISAC-CNR, Meteo-France, and JMA, the prediction skill in southern China (Reg1) is lower than that in the other three regions. The difference of prediction skill among Regs2–4 is generally negligible in the 11 models. ECMWF model has the highest skillful prediction at the first four pentads over China, and the other models have skill only up to pentads 3 or 4. Useful prediction skills of BoM, HMCR, and CMA are found before pentad 3 over China, which is shorter than in the other models. It is found that models with a higher prediction skill at the initial pentad (pentad 1) tend to have larger prediction skill during the first six forecast pentads. For example, the prediction skills of ECMWF and UKMO are higher than the skills of BoM, HMCR, and CMA at pentad 1. This leading advantage almost exists during the forecast time of pentads 2 to 6, which indicates that initial state can have important influence on S2S prediction skill. Moreover, the models of BoM, HMCR and CMA, which are run with coarse horizontal resolutions (Table 1), tend to have low prediction skills. Although the NCEP model also has a coarse horizontal resolution, its prediction skills are better than those three models.
Correlation skill (y-axis) of the 11 S2S models during the forecast time of the first six pentads (x-axis) of 1999–2010 for a Reg1, b Reg2, c Reg3, and d Reg4, respectively. Each line in a panel represents the prediction skill of a model, and legend is shown in panel a. The reference line with correlation skill of 0.5 is also drawn in each panel
The prediction skills of the 11 models with the same ensemble size are also examined and shown in Fig. 3. Figure 3 is the same as that of Fig. 2, but only the first three ensemble members are used to obtain the prediction skill. The results got from Fig. 3 are generally similar to that of Fig. 2. However, when the ensemble size is decreased to three, prediction skills decrease in the models that have large ensemble size, for example, the models of ECMWF, Meteo-France, and BoM. The HMCR model also has a large ensemble size of 15, but prediction skills do not change too much. When the ensemble size deceases to three, ECMWF model is not the only model with the highest prediction skill among the 11 models. The prediction skills in ECCC, UKMO, and KMA models are generally comparable to those of ECMWF model. This indicates that the leading advantage of ECMWF model’s prediction may also come from its ensemble generation strategy.
Same as Fig. 2, but only for the first three ensemble members of each model
Therefore, the RMSE of the ensemble mean of all members is compared against ensemble spread for each model during 1999–2010 in Fig. 4. The calculation of ensemble spread is based on the study by Fortin et al. (2014). If ensemble spread matches the RMSE of ensemble mean, ensemble prediction is considered to be reliable; otherwise, if ensemble spread is smaller (larger) than the RMSE, the ensemble is under-dispersive (over-dispersive), and the prediction is overconfident (underconfident; Warner 2010; Vitart 2017). Ensemble spread is almost linearly increasing with RMSE during the first six forecast pentads (Fig. 4) in the 11 models, except for that during the first two pentads in Meteo-France model. The ensemble spread has been compared with the RMSE over each region for each model. The ensemble spread is larger than RMSE in BoM, but ensemble spread is smaller than RMSE before pentad 4 in Reg1 and after pentad 2 in Reg3. Thus, ensemble predictions are generally underconfident in BoM. In ECCC, HMCR, KMA, CMA, ECMWF, ISAC-CNR, UKMO, JMA, and NCEP, ensemble spreads are smaller than RMSE, indicating overconfident ensemble predictions are in these models. In Meteo-France, ensemble predictions are overconfident before (underconfident after) pentad 4, except for the prediction of Meteo-France at pentad 1. Amongst the 11 S2S models, the ensemble spreads in ECCC and ECMWF are closer to the RMSE than the spread in the other models. This indicates that ECCC and ECMWF models have more reliable ensemble prediction than the other models, for which the ensemble generation strategies need to be improved.
RMSE (solid line) of ensemble mean and ensemble spread (dash line) of T2M of the 11 models during 1999–2010 in the S2S project, including a BoM, b ECCC, c HMCR, d KMA, e CMA, f ECMWF, g ISAC-CNR, h Meteo-France, i UKMO, j JMA, and k NCEP. Red, blue, orange, and green lines represent Regs1–4, respectively. The ensemble size (Ens. Size) of each model is provided in each panel
Figure 5 shows the prediction skill map of all the ensemble members for each model at forecast pentad 3 during winter of 1999–2010. In Fig. 5, the prediction skills in BoM, HMCR, and CMA (KMA, ECMWF, and UKMO) are smaller (higher) than the skills in the other models. In BoM, skillful prediction (≥ 0.5) are found over northeastern China, and the lowest prediction skills are found over southern China. In ECCC, skillful prediction are over southern Xinjiang, Sichuan, and northeastern China. In HMCR, skillful prediction can be located over northeastern China and southern Xinjiang, but smallest prediction skill are found over the Tibetan Plateau and northern Xinjiang. In KMA, skillful prediction are over western, southern and northeastern China. In CMA, good prediction skills are only found over northeastern China. In ECMWF, skillful prediction can be found over most part of China, except for part of the Tibetan Plateau. In ISAC-CNR, skillful prediction is over southern Xinjiang and northeastern China. In Meteo-France, skillful prediction is found over Xinjiang, the Yangtze River Valley, and northeastern China. The pattern of prediction skills in UKMO is quiet similar to that in KMA. In JMA, skillful prediction is over Xinjiang, the upper and middle reaches of the Yangtze River, and northeastern China. In NCEP, prediction skill pattern is similar to those of KMA and UKMO. Generally, most of the 11 models show bad (good) prediction skills over part of the Tibetan Plateau (northeastern China). Moreover, except for the Tibetan Plateau, in BoM, HMCR, ISAC-CNR, Meteo-France, and JMA, the prediction skills over southern China (Reg1) are generally smaller than the skills over the other regions (Regs2–4), which is consistent with those shown in Fig. 2.
Each model’s systematic error of T2M at forecast pentad 3 during November–March of 1999–2010 is shown in Fig. 6. The result at pentad 3 is shown because most of the models have skillful prediction before pentad 3. In Fig. 6, most of the 11 models present negative systematic error of T2M over China, except for ISAC-CNR. In BoM, positive systematic error is over part of southern China and part of northern China. In ECMWF and JMA, positive systematic error is also found over northwestern China. In the 11 models, the largest systematic error is found over the Tibetan Plateau, except that in ECCC the largest systematic error is over northern China. In order to check the relationship between systematic error and prediction skill, the spatial correlation between them are computed. The spatial correlations between the absolute value of systematic error (Fig. 6) and prediction skill (Fig. 5) are 0.02, 0.14, − 0.31, − 0.24, − 0.31, − 0.33, 0.03, − 0.25, − 0.19, 0.10, and − 0.20 for BoM, ECCC, HMCR, KMA, CMA, ECMWF, ISAC-CNR, Meteo-France, UKMO, JMA, and NCEP, respectively. These correlations are significantly negative at the 5% level basing on student’s t test, except for BoM, ECCC, ISAC-CNR, and JMA. This indicates that the high prediction skill relates to the low systematic error, but in BoM, ECCC, ISAC-CNR, and JMA, this relationship is weak and positive. Moreover, some common features can be identified between Figs. 5 and 6, for example, the lowest prediction skills and the highest systematic errors are both found over part of the Tibetan Plateau. However, it is still difficult to tell whether prediction skill is caused by systematic error. Therefore, the relationship between systematic error and prediction skill needs further studies.
Same as Fig. 4, but for systematic error
4 Effects of MJO on T2M prediction skills
Skillful predictions of T2M are generally before pentads 3 and 4 over China in most of the S2S models (Fig. 2). This section shows the prediction skills at pentads 3 and 4 over China during winter, as well as the effects of MJO on prediction skill. In the present study, we mainly conduct the comparison between the correlation prediction skills initialized with and without an active MJO (amplitude ≥ 1). It is noted that in this and next sections we present the results during each model’s entire reforecast period.
Figure 7 presents the scatter plots of the prediction skill in the four regions over China for each model at the forecast time of pentad 3. In Fig. 7, the prediction skills of the forecast initialized with (Y-axis) and without (X-axis) an active MJO are shown. A solid reference line with the slope of 1.0 in Fig. 7 indicates that the prediction skills with MJO are equal to those without MJO. Thus, when a marker is above (below) this reference line, the prediction skill with MJO is larger (smaller) than that without MJO. A solid marker indicates a significant difference. The effects of MJO at forecast initial time are different in each region over China among different models. In Reg1 (Fig. 7a), there are 8 of the 11 models show that the prediction skill of the forecast initialized with MJO is larger than that without MJO, including BoM, HMCR, CMA, ISAC-CNR, Meteo-France, NCEP, UKMO and ECMWF models. Among the 8 models, the differences of prediction skills are significant at the 5% level in Meteo-France and HMCR. The significant test is conducted according to the Monte Carlo technique introduced in Sect. 2. In the JMA, ECCC, and KMA models, prediction skills initialized with MJO are smaller than those without. In Reg2 (Fig. 7b), except for BoM, ECCC, Meteo-France, and ECMWF, all the models show higher prediction skill when there is a MJO at forecast initial time. The differences of prediction skill in NCEP, CMA, and HMCR are significant at the 5% level. In Reg3 (Fig. 7c), the same phenomenon is also identified that the prediction skill is higher when MJO is at initial time, except for the models of BoM and ECMWF. The NCEP, JMA, CMA, and ECCC models show significant skill differences. In Reg4 (Fig. 7d), all the models have higher prediction skill when the forecast is initialized with an MJO, except for HMCR, ISAC-CNR, and NCEP models. The differences in JMA and ECCC are significant. At pentad 4 (Fig. 8), the prediction skill drops below 0.5 for all the models, except that ECMWF model has the highest prediction skill among all the models, and is the only model that holds a skillful prediction of T2M over most part of China. In Regs1–4, there are 6, 7, 9, and 9 of the 11 models having a higher prediction skill with MJO at initial time than those without. Moreover, the differences of prediction skills are significant in NCEP and CMA over Reg1 (Fig. 8a), in NCEP and BoM in Reg2 (Fig. 8b), in NCEP and HMCR in Reg3 (Fig. 8c), and in ISAC-CNR, CMA, and HMCR in Reg4 (Fig. 8d). Generally, most of the S2S models at pentads 3 and 4 tend to have a higher prediction skill with MJO at initial time than without. This indicates that there is an impact of MJO on the S2S prediction skill of T2M over China during boreal winter.
Scatter plots for T2M prediction skill of each model at pentad 3 in a Reg1, b Reg2, c Reg3, and d Reg4. X-axis (Y-axis) represents the prediction skill of the forecast initialized without (with) an active MJO. Significant difference between prediction skill with and without MJO is indicated by a solid dot, and the rest are indicated by a multiple sign inside a hollow circle. The reference line with correlation skill of 0.5 is also provided in each panel (dash line)
Same as Fig. 7, but for pentad 4
Figures 9, 10 and 11 provide the spatial distribution of the prediction skill differences between the forecasts with and without MJO at initial time for forecast pentads 2–4, as well as their significance. The significant test is introduced in Sect. 2. In Figs. 9 and 10, solid (dash) lines represent positive (negative) differences. The differences between prediction skill with and without MJO at initial time are generally positive over most parts of China in the 11 S2S models at pentad 2 (Fig. 9). All of the 11 models generally show that there are significant positive differences over western China, except for Meteo-France. In JMA, KMA, and UKMO (ECCC and NCEP), the differences of prediction skills are also significant over southern China (northeastern China). The increase of the prediction skill due to the MJO is about 0.05–0.15 at pentad 2.
Differences of prediction skill at pentad 2 between the forecast initialized with and without an active MJO (contours). The differences ≥ 0 (< 0) are plotted with solid (dash) lines. The shaded areas are significant at the 5% level. The significant test is based on the Monte Carlo method (see the text for details). Each panel shows the differences of prediction skill for each model, and provides the model name at the left corner
Same as Fig. 9, but for pentad 3
Same as Fig. 9, but for pentad 4
At pentad 3 in Fig. 10, the differences of prediction skill between forecast initialized with and without MJO increase to 0.05–0.30. This indicates that the effects of MJO on prediction skill increase at pentad 3. Moreover, the areas with significant differences are different from those at pentad 2. In BoM, the positive differences are significant over the Tibetan Plateau and small part of southern China. In CMA, the significant positive differences are over almost the entire China, except for northeastern China. In ECCC, the differences are significantly positive over central northern and northeastern China, but negative over parts of southern and northwestern China. In ECMWF, the differences are significantly positive over the Tibetan Plateau, southern Xingjiang, and part of northeastern China, but negative over northern Xingjiang and part of eastern China. In HMCR, the significant positive areas are quite similar to those in CMA. In ISAC-CNR, significant positive differences are found over the Tibetan Plateau, but negative differences are found over part of eastern China. In JMA, almost the entire China has positive differences, but with significance over central northern and northeastern China. In KMA, significant positive differences are over parts of the Tibetan Plateau and central northern and eastern China, but negative differences are found over eastern China. In Meteo-France, significant positive differences are found over southern and central northern China, but the differences are negative over northwestern China. In NCEP, significant positive areas are over part of southern China, northwestern China, and central northern China, but negative areas are over most part of northeastern China. In UKMO, the differences are significantly positive over northwestern and central northern China. The results shown in Fig. 10 are consistent with those shown in Fig. 7.
At pentad 4 (Fig. 11), the results shown are similar to those shown in Figs. 9 and 10, but the impacts of MJO on prediction skill are stronger than the impacts at pentads 2. However, significant areas reduce over most part of China at pentad 4 for most of the models, except that the differences in CMA, HMCR, and NCEP are still significantly positive over most part of China. This means that the effects of MJO on the T2M prediction skill over China decrease at pentad 4 in most of the models. Figures 10 and 11 show that T2M forecast with MJO at initial time tends to have about 0.05–0.3 higher correlation prediction skills than that without MJO over China during winter. Moreover, the significant areas of prediction skill differences are not uniform among the 11 S2S models (Figs. 10, 11). This indicates that there are large uncertainties of the effects of MJO on T2M prediction skill over China during winter among the 11 S2S models at pentads 3 and 4.
Furthermore, the influence of MJO phases at initial time on the prediction skill over China is also investigated (figures not shown). However, each model shows various prediction skill differences in the eight phases of MJO, and the variation of skill differences with respect to MJO phases has less consistency among the 11 S2S models. Therefore, the effect of MJO phases on the T2M prediction skill is complex among the 11 models and need further investigation.
5 Possible mechanism
The possible linkage between MJO and prediction skill of T2M over China is the teleconnection induced by MJO over the Northern Hemisphere. Figures 12 and 13 present the MJO phase composites of H500 anomalies during the first four forecast pentads for observation and reforecasts. The compositions of three models on MJO phases 2 and 6 are shown as examples. Moreover, Figs. 12 and 13 only show the results of ECMWF, CMA, and ISAC-CNR as examples. In Figs. 14 and 15, bar charts will be presented as the summary of MJO teleconnection and its relationship with MJO’s effect on prediction skill.
Same as Fig. 8, but for MJO phase 6
a Percentage of the grids with significant differences of prediction skills between the forecast with and without initial MJO. The prediction skill is at pentad 3. The percentage is shown in bars and calculated over the region of 15°N–60°N and 70°E–140°E on each MJO phase for each model. The legend is also presented in penal (a). The average percentages during eight phases for the 11 models are plotted in line with each value marked by red dot. b Spatial correlations of MJO phase compositions of H500 between each model and observation at pentad 3. The correlations are shown in bars, and calculated over the region of 10°N–87.5°N and 0°–360°E on each phase of each model. Same as penal a, the average is shown in line. c Percentage of the phase composition grids of H500 that has the same sign and significance as the observation at pentad 3. The percentages are shown in bars and calculated over the region of 10°N–87.5°N and 0°–360°E on each phase of each model. The averages are also shown in line
Same as Fig. 14, but for pentad 4
In the observation on phase 2 at the initial time of forecast, MJO is with its convection center over the Indian Ocean (Wheeler and Hendon 2004). Teleconnection represented by significant anomalous H500 can be found over the Northern Hemisphere (Fig. 12a). Moreover, this teleconnection pattern varies with the forecast time from pentads 1 to 4 (Fig. 12a–d). In ECMWF (Fig. 12e–h), CMA (Fig. 12i–l), and ISAC-CNR (Fig. 12m–p) models, the evolution of the teleconnection patterns is generally consistent with observations (Fig. 12a–d). At pentad 4, the teleconnection patterns in the models start to be quite different from those in the observation (Fig. 12d). In Fig. 13, MJO is on phase 6 at initial time, while the convection center of MJO is over the western Pacific, and there is an inactive convection center of MJO over the Indian Ocean (Wheeler and Hendon 2004). We can derive similar conclusions from Fig. 13 as that presented in Fig. 12. In addition, in both Figs. 12 and 13, the MJO-triggered teleconnection pattern over the Northern Hemisphere generally lasts about four pentads in the models.
However, through H500 compositions on two phases in three models, we cannot find out the linkage between teleconnection and the effect of MJO on T2M prediction. Therefore, in Figs. 14a and 15a, we present the percentage of the grid points with the significant differences of T2M prediction skill between forecast with and without MJO over the region of 15°N–60°N and 70°E–140°E for each MJO phase in every model, denoted as Emjo. The prediction skill differences for each phase are obtained by using the similar method as presented in Figs. 11 and 12, but the differences are between forecasts with MJO at a phase and without MJO. This can generally quantitatively represent the effect of MJO on T2M prediction on each MJO phase in model. Figures 14b and 15b show the spatial correlation between the phase composition of H500 in observation and model over the Northern Hemisphere (10°N–87.5°N and 0°–360°E), denoted as Cspatial. In addition, the percentages of the phase composition grids of H500 that has the same sign and significance as the observation in the Northern Hemisphere are also shown in Figs. 14c and 15c, denoted as Hmjo. Both Cspatial and Hmjo represent how well the model can predict the MJO teleconnection pattern. However, compared to Cspatial, Hmjo can provide the agreement of both the significance and spatial pattern of H500 composition between observations and models. Now it is interesting to find that at pentad 3, the correlation between Emjo and Hmjo (Cspatial) is 0.45 (0.29), which is significant at the 5% level (sample size is 88). At pentad 4, the correlation between Emjo and Hmjo (Cspatial) is 0.32 (0.23), which is also significant at the 5% level. When average the values among the eight phases of each model, the lines in Figs. 14 and 15 can be obtained. The correlation between the averaged Emjo and Cspatial is 0.36 at pentad 3, which is not significant (sample size is 11), but is 0.75 between Emjo and Hmjo and significant at the 5% level. At pentad 4, the correlation between Emjo and Cspatial is 0.33 and not significant, but is 0.75 and significant between Emjo and Hmjo. These results indicate that the effect of MJO on T2M over China area is significantly related to the teleconnection pattern of MJO over the Northern Hemisphere.
Generally, among the 11 S2S models, if a model can well predict the teleconnection of MJO over the Northern Hemisphere, MJO can affect the atmospheric circulation over China, and then influences T2M. Thus, the MJO has impact on the prediction skill of T2M over China. If a model cannot predict the teleconnection pattern of MJO over the Northern Hemisphere, MJO has relatively less influence on T2M prediction skill over China. Therefore, improvements in the prediction of the MJO teleconnections could potentially improve the S2S forecast skill of T2M over China.
6 Summary and discussions
T2M prediction skill of ensemble forecast is evaluated over China during winter, based on the S2S database. Most of the 11 S2S models have the correlation prediction skill that is greater than 0.5 before pentads 3 and 4. The ECMWF model displays useful prediction skill for about four pentads over China, which is the best among the 11 S2S models. In contrast, BoM, HMCR, and CMA models can hold useful prediction skill for about three pentads only. All the models tend to have lower T2M prediction skill over part of the Tibetan Plateau than over the other regions of China, which may relate to the large systematic error over the Tibetan Plateau. Except for the Tibetan Plateau, the prediction skills in models from BoM, HMCR, ISAC-CNR, Meteo-France, and JMA are generally smaller than the skills over the other regions in China. This is probably because the T2M over southern China is affected by more factors than over northern China. Through evaluating T2M prediction skill, it is found that the initial state and model resolution also have important influence on the S2S prediction skill. Moreover, the leading advantage of ECMWF model’s prediction may benefit from its ensemble generation strategy. Amongst the 11 models, ECCC and ECMWF models have more reliable ensemble prediction and better ensemble strategies than the other models, in which the ensemble predictions are either overconfident or underconfident.
In most of the models, some parts of China at pentads 3 and 4 tend to have significant higher prediction skill when the forecasts are initialized with an active MJO. Therefore, MJO is an important factor that influences the prediction skill of T2M over China during winter. At pentad 2, the effects of MJO on prediction skill are weaker than the effects at pentads 3 and 4. This is probably because that the initial condition has stronger effect than MJO before the first two pentads. After pentad 2, the effects of the low-frequency processes in the atmosphere start to have more influences than the initial condition, such as MJO. In addition, the significant areas of prediction skill differences are not uniform among the 11 S2S models at pentads 3 and 4, which indicates the uncertainty of the effects of MJO on T2M prediction skill over China during winter. Most likely, this is because different models have different performances in both the predictions of MJO itself (Vitart 2017) and its teleconnection over extratropics. Moreover, the prediction skills of each S2S model vary with the eight phases of MJO, and the variation of prediction skills with respect to MJO phases has no consistency among the 11 S2S models.
The possible reason for the effect of MJO at initial forecast time on the prediction skill of T2M is that MJO can induce teleconnection over the Northern Hemisphere. Models that can (cannot) well predict the teleconnection can cause MJO may have more (less) influence on T2M prediction skill over China during winter. However, there are negative differences of the prediction skill in some of the S2S models. As pointed by Hendon et al. (2000), the reduced prediction skill at MJO active period is because MJO is the dominant mode of sub-seasonal variability, and failing to forecast it may detriment the prediction over both tropics and extratropics. Therefore, if a model fails to predict the MJO teleconnection patterns, it is likely to display lower prediction skill when an MJO is present in the initial conditions. As a result, the improvement of the prediction of MJO and its teleconnection over extratropics could potentially improve the prediction skill of T2M over China during winter. However, in the present study, the teleconnection of MJO over the Northern Hemisphere is partially analyzed, and further works are needed to evaluate the prediction skill of MJO teleconnection comprehensively.
Finally, this study may provide a practical suggestion for the selection of initial time of S2S forecast, especially for CMA, who has a particular interest in the prediction over China. In the present S2S forecast system, the initial time is chosen artificially, such as daily, weekly, or four times a month (Table 1). For S2S prediction, one may consider choosing the initial time based on MJO activity to improve the forecast skill at forecast pentads 3 and 4. MJO is sporadic, with episodes of cyclical activity interspersed with inactive periods, and the gap between two active MJO days ranges from 1 to 45 days in winter (Fig. 16). However, almost 90% of the gap days are smaller than 15 days (Fig. 16). Therefore, the selection of initial time of S2S forecast could be in the days with active MJO. For the days between longer gaps of MJO activity (> 15 days), initial time without MJO could be also used as complement to narrow the gaps between two forecasts. Furthermore, users of S2S forecast might consider the predictions with MJO at initial time to be more skillful than those without at forecast pentads 3 and 4.
References
Bougeault P, Toth Z, Bishop C, Brown B, Burridge D, Chen DH, Ebert B, Fuentes M, Hamill TM, Mylne K, Nicolau J, Paccagnella T, Park Y-Y, Parsons D, Raoult B, Schuster D, Dias PS, Swinbank R, Takeuchi Y, Tennant W, Wilson L, Worley S (2010) The THORPEX interactive grand global ensemble. Bull Am Meteorol Soc 91:1059–1072
Cassou C (2008) Intraseasonal interaction between the Madden–Julian Oscillation and the North Atlantic Oscillation. Nature 445:523–527
Cavanaugh NR, Allen T, Subramanian A, Mapes B, Seo H, Miller AJ (2015) The skill of atmospheric linear inverse models in hindcasting the Madden–Julian Oscillation. Clim Dyn 44:897–906
Dutton JA, James RP, Ross JD (2013) Calibration and combination of dynamical seasonal forecasts to enhance the value of predicted probabilities for managing risk. Clim Dyn 40:3089–3105
Ebisuzaki W (1997) A method to estimate the statistical significance of a correlation when the data are serially correlated. J Clim 10:2147–2153
Fortin V, Abaza M, Anctil F, Turcotte R (2014) Why should ensemble spread match the RMSE of the ensemble mean? J Hydrometeorol 15:1708–1713
Fu X, Wang B, Lee J-Y, Wang W, Li G (2011) Sensitivity of dynamical intraseasonal precition skills to different initail conditions. Mon Weather Rev 139:2572–2592
Garfinkel CI, Benedict JJ, Maloney ED (2014) Impact of the MJo on the boreal winter extratropical circulation. Geophys Res Lett 41:6055–6062
Hendon HH, Liebmann B, Newman M, Glick JD, Schemm JE (2000) Medium-Range forecast errors associated with active episodes of the Madden–Julian Oscillation. Mon Weather Rev 128:69–86
Hsu P-C, Li T, You L, Gao J, Ren H-L (2015) A spatial-temporal projection model for 10–30 day rainfall forecast in South China. Clim Dyn 44:1227–1244
Hudson D, Alves O, Hendon HH, Marshall AG (2011) Bridging the gap between weather and seasonal forecasting: intraseasonal forecasting for Australia. Q J R Meteorol Soc 137:673–689
Jiang X, Waliser DE, Wheeler MC, Jones C, Lee M-I, Schubert SD (2008) Assesing the skill of an all-season statistical forecast model for the Madden–Julian Oscillation. Mon Weather Rev 136:1940–1956
Jie W, Vitart F, Wu T, Liu X (2017) Simulations of the Asian summer monsoon in the sub-seasonal to seasonal prediction project (S2S) database. Q J R Meteorol Soc 143:2282–2295
Johnson NC, Collins DC, Feldstein SB, L’Heureux ML (2014) Skillful wintertime North American temperature forecasts out to 4 weeks based on the state of ENSO and the MJO. Wea Forecast 29:23–37
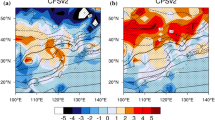
Jones C, Hazra A, Carvalho LMV (2015) The Madden–Julian Oscillation and boreal winter forecast skill: an analysis of NCEP CFSv2 reforecasts. J Clim 28:6297–6307
Kang I-S, Kim H-M (2010) Assessment of MJO predictability for boreal winter with various statistical and dynamical models. J Clim 23:2368–2378
Kang I-S, Jang P-H, Almazroui M (2014) Examiniation of multi-perturbation methods for ensemble prediction of the MJO during boreal summer. Clim Dyn 42:2627–2637
Kim H-M, Webster PJ, Toma VE, Kim D (2014) Predictability and prediction skill of the MJO in two operational forecating systems. J Clim 27:5364–5378
Kirtman BP, Min D, Infanti JM, Kinter JL III, Paolino DA, Zhang Q, ven den Dool H, Saha S, Mendez MP, Becker E, Peng P, Tripp P, Huang J, Dewitt DG, Tippett MK, Barnston AG, Li S, Rosati A, Schubert SD, Rienecker M, Suarez M, L ZE, Marshak J, Lim Y-K, Tribbia J, Pegion K, Merryfield WJ, Denis B, Wood EF (2014) The North American multimodel ensemble Phase-1 Seasonal-to-Interannual Prediction; Phase-2 toward Developing Intraseasonal Prediction. Bull Am Meteor Soc 95:585–601
Lau WK, M, Waliser DDE (2012) Intraseasonal variability in the atmosphere–ocean climate system (Second Edition). Springer, Berlin Heidelberg, 613 pp
Lee S, Gong T, Johnson N, Feldstein SB, Pollard D (2011) On the possible link between tropical convection and the Northern Hemisphere Arctic suface air temperature change between 1958 and 2001. J Clim 24:4350–4367
Lin H, Brunet G (2009) The influence of the Madden–Julian oscillation on Canadian wintertime surface air temperature. Mon Weather Rev 137:2250–2262
Liu X, Wu T, Yang S, Li T, Jie W, Zhang L, Wang Z, Liang X, Li Q, Cheng Y, Ren H, Fang Y, Nie S (2017) MJO prediction using the sub-seasonal to seasonal forecast model of Beijing Climate Center. Clim Dyn 48:3283–3307
Liu X, Li W, Wu T, Li T, Gu W, Bo Z, Yang B, Zhang L, Jie W (2018) Validity of parameter optimization in improving MJO simulation and prediction using the sub-seasonal to seasonal forecast model of Beijing Climate Center. Clim Dyn. https://doi.org/10.1007/s00382-018-4369-y (online)
Lorenz EN (1975) Climatic predictability. The physical basis of climate and climate modeling, GARP Publication Series, vol 16. World Meteorological Organization, pp 132–136
Nasuno T (2013) Forecast skill of Madden–Julian oscillation events in a global nonhydrostatic model during the CINDY2011/DYNAMO observation period. SOLA 9:69–73
Neena JM, Lee JY, Waliser D, Wang B (2014a) Predictability of the Madden–Julian Oscillation in the intraseasonal variability hindcast experiment (ISVHE). J Clim 27:4531–4543
Neena JM, Jiang X, Waliser D, Lee J-Y, Wang B (2014b) Eastern Pacific intraseasonal variability: Apredictability perspective. J Clim 27:8869–8883
Pegion K, Sardeshmukh PD (2011) Prospects for improving subseasonal predictions. Mon Weather Rev 139:3648–3666
Riddle EE, Stoner MB, Johnson NC, L’Heureux ML, Collins DC, Feldstein SB (2013) The impact of the MJO on clusters of wintertime circulation anomalies over the North American region. Clim Dyn 40:1749–1766
Tippett MK, Almazroui M, Kang I-S (2015) Extended-range forecasts of areal-averaged rainfall over Saudi Arabia. Wea Forecast 30:1090–1105
Vitart F (2014) Evolution of ECMWF sub-seasonal forecast skill scores. Q J R Meteorol Soc 140:1889–1899
Vitart F (2017) Madden–Julian Oscillation prediction and teleconnections in the S2S database. Q J R Meteorol Soc 143:2210–2220
Vitart F, Robertson AW, Anderson DLT (2012) Subseasonal to seasonal prediction project: bridging the gap between weather and climate. WMO Bull 61(2):23–28
Vitart F, Ardilouze C, Bounet A, Brookshaw A, Chen M, Codorean C, Deque M, Ferranti L, Fucile E, Fuentes M, Hendon H, Hodgson J, Kang H-S, Kumar A, Lin H, Liu G, Liu X, Malguzzi P, Mallas I, Manoussakis M, Mastrangelo D, Maclachlan C, Mclean P, Minami A, Mladek R, Nakazawa T, Najm S, Nie Y, Rixen M, Robertson AW, Ruti P, Sun C, Takaya Y, Tolstykh M, Venuti F, Waliser D, Woolnough S, Wu T, Won D-J, Xiao H, Zaripov R, Zhang L (2017) The subseasonal to seasonal (S2S) prediction project database. Bull Am Meteor Soc 98:163–173
von Neumann J (1955) Some remarks on the problem of forecasting climate fluctuations. Paper presented at Dynamics of Climate: The Proceedings of a Conference on the Application of Numerical Integration Techniques to the Problem of the General Circulation. Pergamon Press, Oxford, U.K. (published 1960)
Waliser DE, Jones C, Schemm J-KE, Graham NE (1999) A statistical extended-range tropical forecast model based on the slow evolution of the Madden–Julian Oscillation. J Clim 12:1918–1939
Warner TT (2010) Numerical weather and climate prediction. Cambridge University Press, Cambridge
Wheeler MC, Hendon HH (2004) An all-season real-time multivariate MJO index: development of an index for monitoring and prediction. Mon Weather Rev 132:1917–1932
White CJ, Carlsen H, Robertson AW, Klein RJT, Lazo JK, Kumar A, Vitart F, de Perez EC, Ray AJ, Murray V, Bharwani S, Macleod D, James R, Fleming L, Morse AP, Eggen B, Graham R, Kjellstrom E, Becker E, Pegion KV, Holbrook NJ, Mcevoy D, Depledge M, Perkins-Kirkpatrick S, Brown TJ, Street R, Jones L, Remenyi TA, Hodgson-Johnston I, Buontempo C, Lamb R, Meinke H, Arheimer B, Zebiak SE (2017) Potential applications of subseasonal-to-seasonal (S2S) predictions. Meteorol Appl 24:315–325
Wu J, Ren H-L, Zuo J, Zhao C, Chen L, Li Q (2016) MJO prediction skill, predictability, and teleconnection impacts in the Beijing Climate Center Atmospheric general circulation model. Dyn Atmos Oceans 75:78–90
Xiang B, Zhao M, Jiang X, Lin S-J, Li T, Fu X (2015) The 3–4 week MJO prediction skill in a GFDL coupled model. J Climate 28:5351–5364
Yoo C, Lee S, Feldstein B (2012) Arctic response to an MJO-like tropical heating in an idealized GCM. J Atmos Sci 69:2379–2393
Zhang C, Gottschalck J, Maloney ED, Moncrieff MW, Vitart F, Waliser DE, Wang B, Wheeler MC (2013) Cracking the MJO nut. Geophys Res Lett 40:1223–1230
Zhang P, Li G, Fu X, Liu Y, Li L (2014) Clustering of Tibetan Plateau Vortices by 10–30-day intraseasonal oscillation. Mon Weather Rev 142:290–300
Zhou Y, Thompson KR, Lu Y (2011) Mapping the relationship between Northern Hemisphere winter surface air temperature and the Madden–Julian Oscillation. Mon Weather Rev 139:2439–2454
Zhou Y, Lu Y, Yang B, Jiang J, Huang A, Zhao Y, La M, Yang Q (2016) On the relationship between the Madden–Julian Oscillation and 2 m air temperature over central Asia in boreal winter. J Geophys Res Atmos 121:13250–213272
Zhu Z, Li T, Hsu P-C, He J (2015) A spatial–temporal projection model for extened-range forecast in the tropics. Clim Dyn 45:1085–1098
Acknowledgements
This study is supported by the National Key R&D Program of China (Grant no. 2016YFA0602100). We also thanks the support from the National Natural Science Foundation of China (Grant nos. 41505056 and 41625019). Yang Zhou thanks the support from the Startup Foundation for Introducing Talent of NUIST. Finally, we thank the reviewers for their insightful and constructive comments.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhou, Y., Yang, B., Chen, H. et al. Effects of the Madden–Julian Oscillation on 2-m air temperature prediction over China during boreal winter in the S2S database. Clim Dyn 52, 6671–6689 (2019). https://doi.org/10.1007/s00382-018-4538-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4538-z