Abstract
The seasonal prediction skill and predictability of the Northern Hemisphere storm track anomalies in boreal winter (December–January–February, DJF) is examined using seasonal ensemble reforecasts for 1982–2009 from the ECMWF Integrated Forecast System at two different atmospheric resolutions in Project Minerva. It is found that the predictable signals of storm track variations are associated with the two leading EOF modes of ensemble-averaged DJF variances of the high-pass filtered daily meridional winds at 250-hPa level derived from each of the hindcast ensemble members. These two EOF modes are highly correlated both temporarily and spatially between two sets of reforecasts. The first mode (EOF1) mainly shows a latitudinal shift of the storm tracks over the central-eastern North Pacific and the North America continent. The second mode (EOF2) is primarily the pulsing signal exerting on the mean storm track background of the North Pacific. The model predictive skill is verified against observations. The first mode has higher prediction skills and larger skillful regions than the second one. In particular, the first predictable mode is generated by the ENSO-induced wave train, starting from tropical central Pacific and propagating to North America. The skillful region lies in the North Pacific to the west of California, corresponding to the southern lobe of EOF1. The second predictable mode is generated by the North Pacific Mode, which evokes a distinctive wave train, emanating from the tropical western Pacific and propagating northeastward. Its skillful region of the storm track prediction is confined to a small area of Canada western coastlines.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Storm tracks lie in mid-latitudes as latitudinally confined geographical locations of large 2–6 day variance in meteorological variables, featuring frequent passage of synoptic weather systems (e.g., extratropical cyclones) (Guo et al. 2017). The strength and position of the extratropical storm tracks vary on seasonal, interannual and decadal-to-centennial time scales (Stockdale et al. 2011; Chang et al. 2013). The interannual variability of the storm tracks exhibits intensity fluctuations (pulsing) near the climatological centers and meridional displacement of their positions (Lau 1988; Yang and Chang 2006, 2007). Using the gridded atmospheric reanalysis data, Wettstein and Wallace (2010) showed that the month-to-month variations associated with the pulsing and latitudinal shifting with respect to the climatological mean storm tracks can be represented respectively by the two empirical orthogonal function (EOF) leading modes of the monthly variances of the high-pass filtered daily winds at the upper tropospheric pressure levels (e.g., 300 hPa). Furthermore, Wettstein and Wallace (2010) and Athanasiadis et al. (2010) connect these low-frequency fluctuations of the storm track with the dominant patterns of the climate variability, such as the North Atlantic Oscillation (NAO) and the western Pacific (WP) and Pacific North America (PNA) patterns.
Applying the same methodology to the European Centre for Medium-range Weather Forecasts (ECMWF) atmospheric general circulation model (AGCM) and coupled NCAR Community Climate System (CCSM) simulations, Feng et al. (2018) examined the capability of the state-of-the-art climate models in simulating the major patterns of the storm track variability. Complementary to the observational studies (e.g., Wettstein and Wallace 2010), they demonstrated the associations of the model-produced anomalous storm track variations with the major patterns of the lower frequency atmospheric and oceanic variability. In particular, the two leading EOFs of storm track fluctuations over the North Atlantic (NA) section are largely associated with the internal atmospheric variability, while two leading EOF modes over the North Pacific (NP) basin stem from a combination of internal atmospheric variations and external forcing from the underlying sea surface temperature (SST) anomalies (e.g., Feng et al. 2018). Furthermore, the pulsing of the NP storm track is mainly associated with the North Pacific Mode (NPM) while the meridional displacement is more closely linked to the El Niño–Southern Oscillation (ENSO) cycle. These model results are consistent with previous findings that, during El Niño years, the Pacific storm track shifts equatorward and downstream (Straus and Shukla 1997; Zhang and Held 1999; Eichler and Higgins 2006), while it moves toward the opposite way during La Niña years (Yang et al. 2015).
The ENSO phenomenon is the strongest inter-annual climate variation and probably the most predictable one. Its connection with the Pacific storm tracks may have significant implication to the seasonal prediction of the latter. The predictability of the atmospheric internal variability is significantly shorter, generally within a month, but the atmospheric anomalies induced by the sustained underlying surface forcing can persist and thus be more predictable on seasonal time scales (Shukla 1981; Palmer et al. 2008). Since the storm track fluctuations over NP are strongly influenced by ENSO, we speculate a certain part of its variability may be predictable on seasonal time scales. The storm track activity is a source of regional extreme weather and climate events, with the characteristics of strong winds and heavy precipitation. Successfully predicting anomalous seasonal changes of storm track strength and position are therefore not only of scientific but also of practical interest. However, the predictability of the storm track variability is usually limited because the high-level atmospheric internal variability may impair the associations of the storm track activities with the oceanic forcing. In practice, a useful forecast strategy is to perform ensemble prediction, in which the ensemble forecast is remarkably more skillful than any individual forecast (Chen and Cane 2008). The large number of the ensemble members allows scientists to increase the signal-to-noise ratio and separate the SST-forced variability from the atmospheric internal variability. Recently, Yang et al. (2015) investigated the seasonal predictability of extratropical storm track variability using the 12-member ensemble prediction from the GFDL high-resolution climate prediction model. Applying the average predictability time (APT) method (Delsole et al. 2011) to the seasonal standard deviation of 24 h sea level pressure tendency, Yang et al. (2015) reveal that the first two leading components of extratropical storm track variability for both boreal winter (December–January–February; DJF) and summer (July–August–September; JAS) show predictive skill up to 9 months. The first predictable component is connected to the ENSO related spatial pattern, and the second one is attributed to the radiative forcing changes and oceanic multidecadal fluctuations.
In this paper, the prediction skill of the extratropical winter season (DJF) storm tracks, as well as the sources of their predictability, is examined using the coupled ECMWF model ensemble hindcast runs at two different atmospheric resolutions in project Minerva. We use a variable different from the one used by Yang et al. (2015) to represent the storm track predictability and applied a different method to examine its predictability. Our results are generally consistent with those from Yang et al. (2015) but also show some interesting differences. The remainder of this paper is structured as follows. Section 2 introduces data and model configuration. Section 3 evaluates the seasonal predictability of the Northern Hemisphere (NH) mid-latitude storm tracks. The potential mechanism for the storm track predictability is discussed in Sect. 4. The summary is provided in Sect. 5.
2 Data and model configuration
Since the large ensemble members are conducive to reducing the noise level, the existing ensemble hindcast from ECMWF coupled model in Project Minerva are adopted to study the NH mid-latitude storm track seasonal predictability. ERA-Interim reanalysis data are then used to validate the model fidelity.
Minerva is a collaborative project between the ECMWF and the Center for Ocean-Land-Atmosphere Studies (COLA) (e.g., Zhu et al. 2015). Its primary mission is to explore the impact of increased atmospheric resolution on model fidelity and prediction skill in a coupled, seamless framework. Seasonal hindcasts were carried out with a state-of-the-art coupled model, very similar to the ECMWF seasonal forecast system, version 4 (System 4) (Feng et al. 2017). The atmosphere component of the coupled system is an updated version of the ECMWF integrated Forecast System (IFS). The ocean component uses the Nucleus for European Modeling of the Ocean (NEMO), version 3.0 (Madec 2008). Its horizontal configuration adopts the ORCA1 grid (http://www.noc.soton.ac.uk/nemo/), with a horizontal resolution of approximately 1° (meridionally refined to 1/3° near the equator). Vertically, it has 42 levels, 18 of which are in the upper 200 m. IFS and NEMO are coupled every 3 h.
Ensemble hindcasts in Project Minerva were conducted with a vertical atmosphere resolution of hybrid 91 levels up to the top layer of 0.01 hPa and three different atmospheric horizontal resolutions: T319 (~ 62 km), T639 (~ 31 km), and T1279 (~ 16 km), but the oceanic horizontal resolution is fixed (Manganello et al. 2016). 7-month hindcasts at T319 (T639) have 51 (15) ensemble members, being carried out with observed initial conditions of May 1 during 1980–2011 and November 1 during 1980–2010 (Zhu et al. 2015). Another subset of cases was implemented with the IFS at T1279 only from 2000 to 2010/2011, because of the limit of computing resources. The initialization scheme for both IFS and NEMO is identical to that for the operational ECMWF System 4 (Molteni et al. 2011). For the consistency of ensemble member and period, we only use the first 15 ensemble members of the T319 and T639 simulations initialized on November 1. The variables we used from Minerva include the daily 250-hPa meridional wind, as well as seasonal (DJF) mean of the sea surface temperature (SST), precipitation, sea level pressure (SLP), and 250-hPa geopotential height. Extending the method in Wettstein and Wallace (2010), we use the seasonal variance of the high-pass filtered 250-hPa meridional wind component (vv250) as the storm-track indicator. The high-pass filter retains all periods shorter than 10 days, representative of baroclinic eddies. The digital filter used is similar to that used by, for example, Blackmon (1976), who retain periods of 2–6 days. Here the high frequency category extends up to periods of 10 days, in order to capture not only the growth and propagation of baroclinic waves, but their life cycle as well (Simmons and Hoskins 1976). For the ensemble hindcast, the storm track intensity is firstly evaluated for each ensemble member and the ensemble mean intensity is defined as the average for all ensemble members.
For verification, the same variables from ERA-Interim (e.g., the daily meridional wind at 250-hPa, as well as the monthly SST, precipitation, SLP, and 250-hPa geopotential height) are also used. ERA-Interim is an ECMWF re-analysis of the global atmosphere, starting from September 1979, continuously updated in real time. Its horizontal spectral resolution is T255 (~ 80 km) (Dee et al. 2011) and have been transformed to a regular 0.75° latitude × 0.75° longitude grid. Vertically, it is discretized on 60 levels from the surface up to 0.1-hPa-pressure level (Poli et al. 2010).
3 Modes of seasonal predictability and prediction skill
Before investigating the seasonal predictability of NH storm tracks, we first assess the fidelity of coupled ECMWF model in reproducing the DJF climatology of the storm tracks (Fig. 1). Generally speaking, the hindcasts with both resolutions (Fig. 1b, c) of the forecast system are able to capture the broad geographic features of observed NH storm track climatology (Fig. 1a), including the position of the two peaks centered around 45°N and zonally oriented over the North Pacific and North Atlantic basins. The model-produced intensities are quite realistic, though slight overestimations of the North Pacific storm track exist in both runs. Moreover, there are no significant differences in intensity between the low-resolution run (T319; Fig. 1b) and the high-resolution run (T639; Fig. 1c). This is consistent with the result in Feng et al. (2018) that the storm track simulation is not sensitive to the increase of the model resolution.
The first two leading EOF modes of Northern Hemisphere DJF mean vv250 from the ensemble hindcasts at T319 and T639 are shown in Fig. 2. It is interesting to see that the spatial patterns of the first two leading modes from the T319 runs are very similar to the corresponding ones from T639. In particular, EOF1s from T319 (Fig. 2a) and T639 (Fig. 2c) both show a dipole structure over the eastern North Pacific basin centered at 120°W, straddling the eastern part of the climatological location of the storm tracks with positive values in the Southern lobes and negative values in the Northern lobes, and extending downwind over the North America continent. This pattern suggests a meridional displacement of the North Pacific storm track position on its eastern side, as well as a downstream response from its climatological storm track center. In the North Atlantic, the T319 runs show a stronger enhancement of the storm track downstream of this climatological location (Fig. 2a) than the T639 runs do (Fig. 2b). The first leading mode explains ~ 40% of the variance in both resolution runs, which accounts for a significant amount of the total variance of the ensemble mean anomalies. EOF2s in both T319 (Fig. 2b) and T639 (Fig. 2d) are also analogous to each other, and they demonstrate a monopole pattern over the midlatitude North Pacific in the climatological location of the storm tracks, with weak lower latitude feedback in an opposite sign. Again, the T319 runs show a somewhat stronger downstream effect than the T639 runs do. The key feature of EOF2 lies in the North Pacific basin with a monopole center, indicative of the strengthening or weakening strengths recurrently exerting on the climatological-mean storm track. The second mode likewise explains a large amount of total variance with 19.4% at T319 and 17.4% at T639. From the above discussion, we can see that the dominant variability of these two predictable patterns is located in the North Pacific sector.
The EOF modes of an ensemble mean do not necessarily represent the predictable patterns by themselves. The basis for us to consider the two leading EOF modes of the ensemble-averaged vv250 field as the predictable patterns is the fact that both the spatial structures and time series of the leading EOF modes of the predicted ensemble means are highly consistent between two sets of seasonal hindcasts with different atmospheric resolutions (T319 and T639). Although these two forecast systems have the same dynamical core and nearly identical physical parameterizations, the difference of atmospheric resolutions generates large differences between corresponding ensemble members from the beginning of integrations. Therefore, the high consistency of the two leading EOF modes between the different ensemble-means testifies the robustness of these predicted patterns in these forecast systems and can be designated as the predictable modes of these seasonal hindcasts. In fact, higher EOF modes do not show such consistency between the two sets of the hindcasts and are unpredictable.
Previous studies have shown that, in some cases, the maximum signal-to-noise EOF (MSN EOF) analysis (e.g., Venzke et al. 1999; Huang 2004) is better than the conventional EOF in extracting the predictable patterns of an ensemble prediction (e.g., Hu and Huang 2007; Zhang et al. 2018). This is particularly true when the ensemble size is moderate and noise level is high. As a result, the ensemble mean still contains a considerable amount of residual noise. On the other hand, if the intrinsic predictability is high, moderate ensemble size may be sufficient (e.g., Kumar and Chen 2015). In this case, the leading conventional and MSN EOFs are similar to each other and the former is preferable because of its simplicity (e.g., Zhu et al. 2012; Shin et al. 2018). Given the consistency of the ensemble mean EOFs from the two forecast systems, we argue that they are adequate representations.
One should also note that these two predictable patterns from the hindcasts are quite different from those of the leading EOF modes derived from the ECMWF atmospheric simulations as shown in Figs. 1 and 2 of Feng et al. (2018) and the observed ones shown in Wettstein and Wallace (2010), where the leading modes of vv250 in the North Atlantic are also significant. This difference suggests that the variations of the North Atlantic storm tracks from the ECMWF atmospheric simulations are more strongly associated with atmospheric internal variability, which are much weakened by ensemble averaging of the hindcast runs. Ensemble mean hindcasts in this study suppress the atmospheric internal variability, achieving diminishing EOF modes of vv250 over the North Atlantic. Moreover, the DJF mean of storm track variability in this study would also cause differences from the monthly storm track variations in Feng et al. (2018).
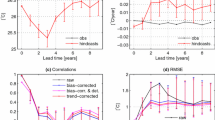
Further evidence for the predictable nature of the leading EOF modes of the ensemble storm track hindcasts can be seen from their principal components (PCs). The first two leading PCs are shown by solid thick lines in Fig. 3. It can be seen that these two PCs of the ensemble mean vv250 at T319 are highly correlated with the corresponding ones at T639, with the correlation coefficient of 0.94 for PC1s (solid thick blue and red lines in Fig. 3a), and 0.70 for PC2s (solid thick blue and red lines in Fig. 3b). The temporal coherence between two different resolution hindcasts confirms the predictable property of these two leading modes. The higher correlation coefficient of PC1 between the two sets of hindcasts suggests that the shifting of the storm track in the North Pacific (EOF1) has higher predictability than the pulsing (EOF2).
T319 PC1 (solid blue solid) and T639 PC1 (solid red solid) of the ensemble-averaged vv250, the projected time series of the ERA_Interim vv250 onto T319 EOF1 (blue cross) and onto T639 EOF1 (red cross), as well as the projected time series of T319 vv250 from individual simulations onto T319 EOF1 (blue dots) and the projected time series of T639 vv250 from individual simulations onto T639 EOF1 (blue dots) shown in (a) T319 PC2 (blue solid) and T639 PC2 (red solid) of the ensemble-averaged vv250, the projected time series of the ERA_Interim vv250 onto T319 EOF2 (blue cross) and onto T639 EOF2 (red cross), as well as the projected time series of T319 vv250 from individual simulations onto T319 EOF2 (blue dots) and the projected time series of T639 vv250 from individual simulations onto T639 EOF2 (blue dots) shown in (b) All vv250 in this figure are based on NH DJF mean
After establishing their predictability of the two ensemble hindcast EOF modes of the storm track variability, we further examine their predictive skills (i.e., consistency with observations) through an observation-based verification. Projecting the observed Northern Hemisphere DJF mean vv250 to the two leading EOF patterns from the hindcasts, we obtain their corresponding projected time series from the observations (cross marks in blue for EOF1 and red for EOF2 in Fig. 3), which are directly comparable with the corresponding PCs. In fact, the PC1 from T319 (thick blue line in Fig. 3a) and its corresponding projected time series from observation (blue cross marks) are generally in phase and close to each other, with a correlation of 0.79. The projected time series from individual ensemble members onto EOF1 of the ensemble-averaged NH DJF mean vv250 at T319 are also shown in Fig. 3a by blue dots. Overall, the observed projections (blue crosses) are well mingled with those projected with the ensemble members onto EOF1 (blue dots), suggesting that the ensemble predictions are reliable. Larger deviations of the observed projection from PC1 occur in the winters of 1990/91, 1991/92 and 2004/05 but the observed projects (blue crosses) are still within the spread range of the ensemble member projections (the blue dots) in these years. A very similar result is derived for the T639 hindcasts, with the PC1 (red curve)-observation (red crosses) correlation of 0.80.
The correlation between PC2 from T319 (thick blue line in Fig. 3b) and its corresponding projected time series from observation (blue cross marks) is 0.50. The corresponding correlation for T639 is 0.32. Physically, we speculate that the slightly lower skill score in T639 reflects the fact that the uncertainty is higher in this set of hindcasts because of its higher horizontal resolution. Simply using atmospheric initial states interpolated from a lower resolution reanalysis data, the T639 hindcasts may not initialize its active smaller scale features adequately, which may end up generating more noise to the larger scale variations. Overall, the correlation skills of PC2s are apparently lower than their counterparts for EOF1 but both still pass the 95% significance tests. In particular, both sets of hindcasts seem to catch the weakened storm track intensity during 1986–1988 and 1997–1998 (Fig. 3b). The projected time series from ensemble members at T319 show comparable spreads with those at T639 in both PC1 related panel (Fig. 3a) and PC2 related panels (Fig. 3b), implying the resolution change has no significant influence on the spreads of variability.
We further examine the model predictive skill in the framework of the observational patterns of the storm track variability. The four leading EOFs of the observed NH DJF mean vv250 are shown in Fig. 4. EOF1 (Fig. 4a) shows a main dipole pattern over the North Atlantic basin with some weak upstream pulsing of the North Pacific storm tracks. On the other hand, EOF2 (Fig. 4b) displays a dipole structure over the North Pacific, with some features over the eastern North Atlantic. EOF1 is apparently dominated by the meridional shift of the North Atlantic storm tracks while EOF2 (Fig. 4b) shows some resemblance to the meridional shift of the North Pacific storm tracks as depicted in the hindcast EOF1 shown in Fig. 2. EOF3 (Fig. 4c) and EOF4 (Fig. 4d) both present more complicated spatial structures that are harder to explain physically. These higher modes are included because they still account for substantial fractions of the total variance. Together, these four modes account for 48% of the total variance.
Clearly, the observed EOF modes contain both potentially unpredictable and predictable signals. The correlations between the four observed leading PCs and the two leading PCs of the hindcasts are conducted to reveal their connections. As discussed above, the hindcast PCs in T319 highly resembles the corresponding ones in T639, especially for PC1. For brevity, the PC correlations only between T319 ensemble mean and observations are presented in Table 1. The analysis shows the PC1 from the T319 ensemble mean vv250 is significantly correlated with the observed PCs 2–4, suggesting all of them contain predictable signals. However, the observed PC1 is correlated with PC2 of the hindcasts. The significant correlations between the hindcast PCs and those from observations are visually demonstrated in Fig. 5. In particular, the PC1 of hindcast vv250 and its significantly correlated PCs from observations are shown in Fig. 5a, while the PC2 from hindcasts and the PC1 from observations are shown in Fig. 5b.
The skillful region of the hindcasts is investigated by performing correlation analysis, along with regression analysis, between the observed NH DJF mean vv250 at each grid point and the PCs of the ensemble mean hindcast EOF modes. The skillful region related to the hindcast PC1 is shown in Fig. 6a. The correlation/regression structure shows the skillful region for the PC1 is located in North Pacific south of 30°N and centered around 120°W to the west of California, which bears certain resemblance to the southern lobe of the North Pacific anomalies of the EOF1 (Fig. 2a) although its northern lobe is not significantly shown. However, the hindcast PC2 has generally low prediction skills, with significant correlations with the observations only near the west coast of Canada (not shown).
Correlation coefficients (shaded) and regression coefficients (contours) between T319 PC1 and the observed vv250 in a, between observed PC2 and T319 vv250 in b, between observed PC3 and T319 vv250 in c, and between observed PC4 and T319 vv250 in d. Only values of correlation coefficients pass 95% significance level are shaded, and the regression coefficients are overlaid by contours. The observed vv250 are based on the NH DJF mean, and the simulated vv250 are based on the ensemble-averaged NH DJF mean. Correlations and regressions of vv250 to the PCs are carried out grid by grid
We also correlated the hindcast ensemble mean storm track variability (i.e., the ensemble mean vv250 field) with the observed PCs. The observed PC1 shows no significant correlations in large areas (not shown) possibly because its dominant dipole pattern over North Atlantic (Fig. 4a) is mainly atmospheric internal variability (Feng et al. 2018). On the other hand, the observed PC2, PC3, and PC4 each shows areas of the significant correlations with the ensemble mean vv250 field, especially over the North Pacific, consistent with their significant correlations with the hindcast PC1. The correlation between the observed PC2 and the NH DJF mean vv250 hindcasts (Fig. 6b) shows a dipole structure over the North Pacific, somewhat similar to the observed EOF2 (Fig. 4b) and the hindcast EOF1 (Fig. 2a). The correlation analysis based on the observed PC3 (Fig. 6c) exhibits a zonal band of moderate but statistically significant correlations near 30°N, extending from eastern North Pacific eastward into the European Continent. Some traces of such band is presented in hindcast EOF1 (Fig. 2a) and in observed EOF3 (Fig. 4c). The correlation pattern related to the observed PC4 also shows dipole structure over the North Pacific, as well as a statistically significant area over South Asia.
In summary, these hindcasts demonstrate considerable skill in predicting the downstream meridional shift of the winter storm track over the North Pacific, which is verifiable through the comparison with observations. On the other hand, the predicted pulsing of the storm track in the North Pacific, though demonstrating consistency between the two sets of hindcasts (i.e., potential predictability), is less verifiable from the observations.
4 Sources of seasonal predictability
Previous studies (e.g., Wettstein and Wallace 2010) have demonstrated that the storm track variations are closely associated with the dominant patterns of the climate variability, where their sources of seasonal predictability are likely located. To explore these potential sources of the predictability, correlation analyses between the two leading hindcast PCs and monthly mean anomalies of SST, SLP, 250 hPa geopotential height, and precipitation are discussed in this section. Because the two leading modes from the T319 run are significantly correlated both temporarily and spatially with their counterparts from the T639 run, the mechanisms are investigated only using the T319 run.
The correlation between the hindcast PC1 and the ensemble mean hindcast SST anomalies in DJF (Fig. 7a) show that the southward shifting of the storm track downstream in the North Pacific (Fig. 2a) is associated with the warm phase of ENSO (the El Niño), characterized by an east–west seesaw of the tropical SST warmer than normal in the central and eastern Pacific but colder than normal in the western Pacific, as well as warm SST anomalies in the tropical Indian Ocean. Correspondingly, the DJF precipitation correlation shows positive anomalies near the dateline on the equator and a southward shift of the ITCZ in the central and eastern Pacific (Fig. 7b). In addition, the SLP pattern presents positive anomalies in the western tropical Pacific and the Indian Oceans centered over the Maritime Continent, and the negative anomalies in the eastern equatorial Pacific (Fig. 7c). More important to the North Pacific storm track variations is the negative SLP anomalies centered near the North American coast and the positive SLP anomalies in the northern subtropical central-western Pacific. These features are associated with the tropical heating-induced teleconnections. Since the planetary wave train response is equivalent barotropic, it is more clearly shown in the 250-hPa geopotential height field, with a pair of symmetric highs over the central Pacific on both sides of the equator, a low off the North America coast and a high over northern North America (Fig. 7d). This pattern resembles a well-known ENSO-induced wave train, emanating from tropical central Pacific, passing the North Pacific, propagating to North America (e.g., Straus and Shukla 2002). The correlation study of Fig. 7 reaffirms the connections of ENSO forcing to storm track predictability documented in Yang et al. (2015).
Correlation coefficients between PC1 and SST in a, between PC1 and Precipitation in b, between PC1 and SLP in c, as well as between PC1 and 250-hPa geopotential height in d. PC1 is calculated from the ensemble-averaged T319 NH DJF mean vv250. Other variables are also based on the ensemble-averaged T319 NH DJF mean. Correlations of the related variables to PC1 are performed grid by grid
One should note that this ENSO-forced wave train bears some resemblance with the Pacific-North America (PNA) pattern, which has been demonstrated observationally by Wallace and Gutzler (1981) and Horel and Wallace (1981), analytically by Hoskins and Karoly (1981), and numerically by Blackmon et al. (1983). Wettstein and Wallace (2010) showed that the positive polarity of the PNA pattern is associated with an equatorward shift of the storm track with baroclinic wave activity strongest downstream of the shifted jet stream (their Fig. 13a). PNA-like patterns can either originate from the internal atmospheric variability or generated by the tropical atmospheric heat sources of the ENSO-induced SST anomalies. The spatial structures of internally generated and externally forced modes may also be slightly different, especially over the North America continent (Straus and Shukla 2002). However, the relationship between the shifted storm tracks and the tropically forced wave train in Fig. 7 is very similar to what have been shown in Wettstein and Wallace (2010). In our case, the large area of positive precipitation anomalies in the tropical central Pacific serves as the heat source of this wave train. One may notice that the anticyclones in the 250-hPa geopotential height, where the wave train starts (Fig. 7d), is located to the east of the heat source released by the positive anomalous precipitation (Fig. 7b). This is possibly caused by the nonlinear advection and the time-dependence nature of the vorticity source (Sardeshmukh and Hoskins 1985; Liu and Alexander 2007).
We have further carried out the correlations between the PC1 from T319 hindcasts and the observed DJF anomalies of these variables (Fig. 8) to validate the hindcast patterns described above. The spatial structures of the observation-based correlations are analogous to the corresponding ones from the hindcasts in Fig. 7, though with weaker coefficients. The weaker coefficients in the observed panels imply higher noise level. The higher magnitude of correlation coefficients in ensemble mean hindcasts can be explained as the ensemble average reduces the noise present in the individual runs, increasing the correlations in ensemble hindcasts (Krishnamurti et al. 2000; Palmer et al. 2000). On the other hand, the structure similarity of the corresponding correlation panels between Fig. 7 related to the ensemble mean hindcasts and Fig. 8 associated with observations suggests the model well reproduced the process that ENSO influences the meridional shift of mid-latitude storm tracks.
Correlation coefficients between T319 PC1 and observed SST in a, between T319 PC1 and observed precipitation in b, between T319 PC1 and observed SLP in c, as well as between T319 PC1 and observed 250-hPa geopotential height in d. T319 PC1 is calculated from the ensemble-averaged NH DJF mean vv250. The observed variables are also based on the NH DJF mean. Correlations of the observed fields to T319 PC1 are performed grid by grid
A similar correlation/regression analysis is carried out based on the PC2 of ensemble-averaged NH DJF mean vv250 from the T319 hindcasts. The correlation patterns between PC2 of hindcast vv250 and those ensemble mean variables from T319 hindcasts are shown as shadings in Fig. 9 while regression coefficients are overlaid as contours. The hindcast PC2 is positively correlated with the two patches of the SST anomalies, one along the East Asia coast and extending from northern Philippine to the dateline, and the other near the South America coast near the equator. It is also negatively correlated to two bands of the SST anomalies. One is in the Kuroshio extension from the western to central North Pacific, and the other in the western tropical Pacific (Fig. 9a). The areas of the SST anomalies are limited and their correlations to the hindcast PC2 are only marginally significant. However, the spatial structure of the SST anomalies bears certain resemblance to the North Pacific Mode as identified by Deser and Blackmon (1995) and Hartmann (2015, his Fig. 1c). Likewise, the statistically significant precipitation anomalies positively correlated with PC2 are limited in the eastern equatorial Pacific while the broader negatively correlated rainfall anomalies in the western and central equatorial Pacific do not pass the 95% significance test (Fig. 9b). However, both SLP (Fig. 9c) and 250-hPa geopotential height (Fig. 9d) anomalies seem to show a wave train starting from the tropical western-central tropical-to-subtropical Pacific, propagating northeastward to Greenland via central North Pacific and North America continent. This wave train shows similar atmospheric pattern to the one demonstrated in Fig. 3b, c (with opposite sign) in Hartmann (2015) as the atmospheric response to the NPM mode. The trajectory of this wave train is largely consistent with the enhanced storm track activities in a belt extending from the central North Pacific to the North Atlantic.
Correlation coefficients (shaded) and regression coefficients (contours) between PC2 and SST in a, between PC2 and Precipitation in b, between PC2 and SLP in c, as well as between PC2 and 250-hPa geopotential height in d. Only regions passing the 95% statistical significance test are shaded. PC2 is calculated from the ensemble-averaged T319 NH DJF mean vv250. Other variables are also based on the ensemble-averaged T319 NH DJF mean. Correlations of the related variables to PC2 are performed grid by grid
Generally speaking, the correlations of T319 PC2 to the observed variables are able to reproduce this relationship more or less, but with even a smaller significant area (Fig. 10). In particular, the incomplete NPM in Fig. 9a and the precipitation anomalies in Fig. 9b can be represented by the observed statistically significant SST anomalies (Fig. 10a) and precipitation anomalies (Fig. 10b), respectively. On the other hand, the NPM induced wave train can barely detected in the observed correlated SLP pattern (Fig. 10c) or 250 hPa geopotential height pattern (Fig. 10d). Only in a small area is the correlation significant. But the regression contours in the 250 hPa geopotential height filed (Fig. 10d) clearly show such a wave train of the atmospheric response to the NPM. This further confirms the source of the weaker predictability of EOF2 comes from the NPM.
Correlation coefficients between PC2 and observed SST in a, between PC2 and observed precipitation in b, between PC2 and observed SLP in c, as well as between PC2 and observed 250-hPa geopotential height in d. PC2 is calculated from the ensemble-averaged T319 NH DJF mean vv250. Observed variables are based on the ERA-Interim NH DJF mean. Correlations of the related variables to PC2 are performed grid by grid
5 Summary
We have examined the seasonal predictability of the extratropical NH DJF mean storm tracks using the ECMWF coupled model ensemble hindcast runs with two different atmospheric resolutions. In this analysis, we define the potentially predictable components of the winter storm track variations as the two leading EOFs of the DJF ensemble averaged vv250 from each member of the hindcasts initialized at November 1 for 1979–2012. These two modes are highly correlated both temporarily and spatially between the two sets of hindcasts at different horizontal resolution. EOF1 shows a latitudinal shift of the storm tracks over the central-east North Pacific, slight downstream of its climatological location, as well as a secondary center over the eastern North Atlantic. EOF2 is the pulsing signal exerting on the mean storm track background of the North Pacific, which also expands into the North America continent and the North Atlantic. The first mode explains around 40% of the total variance while the second one explains slightly less than 20%. Projection of observed vv250 data onto these two hindcast PCs further reveals the model has prediction skills associated with these two modes, with higher skills and larger skillful regions of EOF1 than EOF2. The skillful region for EOF1 lies in the North Pacific to the west California areas, which is the south lobe of the North Pacific dipole structure from observations. The skillful region for EOF2 is small and confined to the west coastlines of Canada. The correlation analysis between the observed leading PCs of vv250 and the model simulated vv250 further reveals that the predictable signals are contained in the four leading modes of the observed storm track EOF patterns.
Further analysis with respect to the hindcast ensemble mean DJF SST and atmospheric fields indicates that the most predictable component associated with the hindcast PC1 is physically evoked by the ENSO induced wave train resembling the PNA pattern. Generated by SST-induced atmospheric heating sources in the central equatorial Pacific, this wave train connected with EOF1 of simulated vv250 is emanating from tropical central Pacific, passing the North Pacific, propagating to North America. During the El Niño winter, the PNA generated southward shift of the jet stream also causes a southward shift of the North Pacific storm track. On the other hand, the other predictable component associated with the hindcast PC2 is generated by the NPM-induced wave train. This wave train shows a trajectory distinctive of the PNA, originating from the tropical West Pacific, propagating northwestward to the Greenland region. The heat source released from the negative precipitation anomalies for this wave train seems possibly to reside in the tropical western Pacific. The first storm track predictable component linked to ENSO cycle is consistent with those of Yang et al. (2015, see their Figs. 4, 12). The NPM connection of the second storm track predictable mode seems to be different from Yang et al.’s results and deserves attention in future studies.
References
Athanasiadis PJ, Wallace JM, Wettstein JJ (2010) Patterns of wintertime jet stream variability and their relation to the storm tracks. J Atmos Sci 67:1361–1381
Blackmon ML (1976) A climatological spectral study of the 500 mb geopotential height of the Northern Hemisphere. J Atmos Sci 33:1607_1623
Blackmon ML, Geisler JE, Pitcher EJ (1983) A general circulation model study of January climate anomaly patterns associated with interannual variation of equatorial Pacific sea surface temperatures. J Atmos Sci 40:1410–1425
Chang EKM, Guo Y, Xia X, Zheng M (2013) Storm-track activity in IPCC AR4/CMIP3 model simulations. J Clim 26:246–260. https://doi.org/10.1175/JCLI-D-11-00707.1
Chen D, Cane MA (2008) El Niño prediction and predictability. J Comput Phys 227:3625–3640
Dee DP et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597
DelSole T, Tippett MK, Shukla J (2011) A significant component of unforced multidecadal variability in the recent acceleration of global warming. J Clim 24(3):909–926
Deser C, Blackmon ML (1995) On the relationship between tropical and North Pacific sea-surface temperature variations. J Clim 8:1677–1680
Eichler T, Higgins W (2006) Climatology and ENSO-related variability of North American extratropical cyclone activity. J Clim 19:2076–2093
Feng X et al (2017) A multimodel analysis of the resolution influence on precipitation climatology in the Gulf Stream region. Clim Dyn 48:1685–1704
Feng X et al (2018) An examination of the Northern Hemisphere mid-latitude storm track interannual variability simulated by climate models—sensitivity to model resolution and coupling. Clim Dyn. https://doi.org/10.1007/s00382-018-4378-x
Guo Y et al (2017) Variations of Northern Hemisphere storm track and extratropical cyclone activity associated with the Madden–Julian oscillation. J Clim 30:4799–4818
Hartmann DL (2015) Pacific sea surface temperature and the winter of 2014. Geophys Res Lett 42:1894–1902. https://doi.org/10.1002/2015GL063083
Horel JD, Wallace JM (1981) Planetary scale atmospheric phenomena associated with the Southern Oscillation. Mon Weather Rev 109:813–829
Hoskins BJ, Karoly DJ (1981) The steady linear response of a spherical atmosphere to thermal and orographic forcing. J Atmos Sci 38:1179–1196
Hu ZZ, Huang B (2007) The predictive skill and the most predictable pattern in the tropical Atlantic: the effect of ENSO. Mon Weather Rev 135:1786–1806
Huang B (2004) Remotely forced variability in the tropical Atlantic Ocean. Clim Dyn 23:133–152
Krishnamurti TN, Kishtawal CM, Zhang Z, LaRow T, Bachiochi D, Williford E, Gadgil S, Surendran S (2000) Multimodel ensemble forecasts for weather and seasonal climate. J Clim 13:4196–4216
Kumar A, Chen M (2015) Inherent predictability, requirement on the ensemble size, and complementarity. Mon Weather Rev 143:3192–3203
Lau N-C (1988) Variability of the observed mid-latitude storm tracks in relation to low-frequency changes in the circulation pattern. J Atmos Sci 45:2718–2743, https://doi.org/10.1175/1520-0469(1988)045,2718:VOTOMS.2.0.CO;2
Liu Z, Alexander MA (2007) Atmospheric bridge, oceanic tunnel, and global climatic teleconnections. Rev Geophys 45:RG2005. https://doi.org/10.1029/2005RG000172
Madec G (2008) NEMO reference manual, ocean dynamics component: NEMO-OPA. Preliminary version. IPSL Note Pole Modél 27:91
Manganello JV et al (2016) Seasonal forecasts of tropical cyclone activity in a high-atmospheric-resolution coupled prediction system. J Clim 29:1179–1200, https://doi.org/10.1175/JCLI-D-15-0531.1
Molteni F et al (2011) The new ECMWF Seasonal Forecast System (System 4). In: ECMWF Technical Memoranda, No. 656, pp 49
Palmer TN, Brankovic C, Richardson DC (2000) A probability and decision model analysis of PROVOST seasonal multimodel ensemble integrations. Q J R Meteorol Soc 126:2013–2033
Palmer TN, Doblas-Reyes FJ, Weisheimer A, Rodwell MJ (2008) Toward seamless prediction: calibration of climate change projections using seasonal forecasts. Bull Am Meteorol Soc 89:459–470
Poli P, Healy SB, Dee DP (2010) Assimilation of global positioning system radio occultation data in the ECMWF ERA-Interim reanalysis. Q J R Meteorol Soc 136:1972–1990
Sardeshmukh PD, Hoskins BJ (1985) Vorticity balances in the tropics during the 1982–83 El Niño–Southern Oscillation event. Q J R Meteorol Soc 111:261–278
Shin CS, Huang B, Zhu J, Marx L, Kinter JL (2018) Improved seasonal predictive skill and enhanced predictability of the Asian summer monsoon rainfall following ENSO events in NCEP CFSv2 hindcasts. Clim Dyn 2018:1–22
Shukla J (1981) Dynamical predictability of monthly means. J Atmos Sci 38:2547–2572
Simmons AJ, Hoskins BJ (1976) The life cycles of some nonlinear baroclinic waves. J Atmos Sci 35:414–432
Stockdale TN et al (2011) ECMWF Seasonal Forecast System 3 and its prediction of sea surface temperature. Clim Dyn 37:455–471. https://doi.org/10.1007/s00382-010-0947-3
Straus DM, Shukla J (1997) Variations of mid-latitude transient dynamics associated with ENSO. J Atmos Sci 54:777–790
Straus DM, Shukla J (2002) Does ENSO force the PNA? J Clim 15:2340–2358
Venzke S, Allen MR, Sutton RT, Rowell DP (1999) The atmospheric response over the North Atlantic to decadal changes in sea surface temperatures. J Clim 12:2562–2584
Wallace JM, Gutzler DS (1981) Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon Weather Rev 109:784–812
Wettstein JJ, Wallace JM (2010) Observed patterns of month-to-month storm track variability and their relationship to the background flow. J Atmos Sci 67:1420–1437
Yang X, Chang EKM (2006) Variability of the Southern Hemisphere winter split flow: a case of two-way reinforcement between mean flow and eddy anomalies. J Atmos Sci 63:634–650. https://doi.org/10.1175/JAS3643.1
Yang X, Chang EKM (2007) Eddy–zonal flow feedback in the Southern Hemisphere winter and summer. J Atmos Sci 64:3091–3112. https://doi.org/10.1175/JAS4005.1
Yang X et al (2015) Seasonal predictability of extratropical storm tracks in GFDL’s high-resolution climate prediction model. J Clim 28:3592–3611
Zhang Y, Held IM (1999) A linear stochastic model of a GCM’s mid-latitude storm tracks. J Atmos Sci 56:3416–3435
Zhang T, Huang B, Yang S, Kinter JL (2018) Predictable patterns of the atmospheric low-level circulation over the Indo-Pacific Region in Project Minerva: seasonal dependence and intra ensemble variability. J Clim 31:8351–8379
Zhu J, Huang B, Balmaseda MA (2012) An ensemble estimation of the variability of upper-ocean heat content over the tropical Atlantic Ocean with multi-ocean reanalysis products. Clim Dyn 39:1001–1020
Zhu J et al (2015) ENSO prediction in Project Minerva: sensitivity to atmospheric horizontal resolution and ensemble size. J Clim 28:2080–2095
Acknowledgements
X. Feng, B. Huang, and D. Straus were supported by Grants from NSF (AGS-1338427), NOAA (NA14OAR4310160), and NASA (NNX14AM19G). X. Feng is also supported by the Institute for Basic Science (Project Code IBS-R028-D1), and B. Huang is supported by the NOAA MAPP Grant (NA17OAR4310144). We are grateful for project Minerva to provide hindcasts used in this study.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Feng, X., Huang, B. & Straus, D.M. Seasonal prediction skill and predictability of the Northern Hemisphere storm track variability in Project Minerva. Clim Dyn 52, 6427–6440 (2019). https://doi.org/10.1007/s00382-018-4520-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4520-9