Abstract
Potential increases in extreme rainfall induced hazards in a warming climate have motivated studies to link precipitation intensities to temperature. Increases exceeding the Clausius–Clapeyron (CC) rate of 6–7%/°C–1 are seen in short-duration, convective, high-percentile rainfall at mid latitudes, but the rates of change cease or revert at regionally variable threshold temperatures due to moisture limitations. It is unclear, however, what these findings mean in term of the actual risk of extreme precipitation on a regional to local scale. When conditioning precipitation intensities on local temperatures, key influences on the scaling relationship such as from the annual cycle and regional weather patterns need better understanding. Here we analyze these influences, using sub-hourly to daily precipitation data from a dense network of 189 stations in south-eastern Austria. We find that the temperature sensitivities in the mountainous western region are lower than in the eastern lowlands. This is due to the different weather patterns that cause extreme precipitation in these regions. Sub-hourly and hourly intensities intensify at super-CC and CC-rates, respectively, up to temperatures of about 17 °C. However, we also find that, because of the regional and seasonal variability of the precipitation intensities, a smaller scaling factor can imply a larger absolute change in intensity. Our insights underline that temperature precipitation scaling requires careful interpretation of the intent and setting of the study. When this is considered, conditional scaling factors can help to better understand which influences control the intensification of rainfall with temperature on a regional scale.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Hydro-meteorological hazards induced by extreme precipitation pose considerable risk to communities. Thus, statements on possible changes of extreme precipitation are delicate information for politicians, urban planners, farmers, and others who need to manage the risk from climate and weather extremes. However, knowledge gaps exist especially on regional to local scales due to the complex precipitation generating processes, the high natural variability of rainfall, and because data are often not available in sufficient resolution, length, or quality (Alexander 2016; Prein and Gobiet 2016; Contractor et al. 2015).
In recent years, an increasing number of studies has built on the physically based expectation that extreme precipitation intensity changes with temperature following the Clausius–Clapeyron (CC) equation, which describes the water holding capacity of the atmosphere. Thus, an increase in rainfall intensity of 6–7%/°C–1 (CC-rate) is expected, given constant relative humidity. The concept and recent developments have been reviewed by Westra et al. (2014) and O’Gorman (2015). Three major aspects can be summarized.
First, convective extreme precipitation intensities at sub-daily scales have been found to increase at rates up to about double the CC-rate in both observations and models over the mid-latitudes, whereas intensities on the daily scale and those associated with stratiform precipitation mostly increase at approximately the CC-rate (Ivancic and Shaw 2016; Ban et al. 2015; Berg and Haerter 2013; Lenderink and van Meijgaard 2009; Haerter and Berg 2009). The high scaling rates have been attributed to both a shift from stratiform to convective precipitation, and an intensification of the convective process itself (Moseley et al. 2016; Attema et al. 2014; Loriaux et al. 2013; Berg et al. 2013).
Second, a decline or reversal of extreme intensities takes place at regionally varying threshold temperatures when the environmental conditions shift from a moist to dry regime and suppress a further intensification of rainfall (Prein et al. 2017; Chan et al. 2016; Drobinski et al. 2016).
Third, connecting local temperature-precipitation relationships to global warming is controversial (IPCC 2013, p. 626) and the available studies differ in scope. Some analyze a single rain gauge (Formayer and Fritz 2016), others assess regional (e.g., Molnar et al. 2015; Wasko and Sharma 2015), or global station networks (e.g., Wang et al. 2017; O’Gorman 2015). Zhang et al. (2017) differentiate studies that detect long-term trends in precipitation intensities with global warming (e.g., Barbero et al. 2017), and studies that establish regional scaling relationships based on conditional quantiles (e.g., Drobinski et al. 2016). In the first case, thermodynamic effects and the Earth’s energy budget are considered to be the dominant factors. In the latter, the variable dynamic conditions throughout the annual cycle become increasingly influential. Furthermore, the cooling effect of precipitation on local temperatures might significantly influence the scaling rates especially for larger-scale precipitation events (Bao et al. 2017).
Here we analyze the variability of the temperature precipitation relationship at the regional to local scale, deliberately considering how the annual cycle and weather systems affect the sensitivity of the statistical scaling factors on the sub-hourly, the hourly and the daily scale. Thus the aim of this study is not to analyze trends in rainfall extremes, but to gain deeper insight into the controls of the spatio-temporal variability of scaling factors on a regional level and to address the implications for interpreting the results. We use sub-hourly rainfall data from a very dense regional station network over south-eastern Austria, filling a gap between the aforementioned single station studies and considerably sparser station networks on national scales.
The study region presents an interesting setting from both a climatological and a socio-economic viewpoint. The geographic location transitions from high Alpine terrain in the north-west of the region to lower-elevation forelands in the south-east, where a strong warming trend with a substantial increase in heat days has been observed over the last decades (Kabas et al. 2011). Moisture advection from the Mediterranean Sea and orographic lifting provide essential ingredients for extreme precipitation events on the southern Alpine slopes (Cassola et al. 2016; Panziera et al. 2015; Schicker et al. 2010; Sodemann and Zubler 2010) and lows over the Mediterranean moving northeastward ('Vb'-cyclone tracks) regularly result in excessive rain and large-scale flooding in the southern and south-eastern Alpine region (Volosciuk et al. 2016; Messmer et al. 2015; Hofstaetter and Chimani 2012).
Furthermore, small-scale flash flooding caused by local, short-term extremely intense convective rainfall has destroyed human livelihood in the past, where for the most destructive events, rainfall depths of 100–600 mm have been reconstructed (hydroConsult GmbH 2011; Schocklitsch 1914; Forchheimer 1913). One of the top three Central European one-day precipitation records occurred here (Munzar et al. 2011). The area is densely populated and the terrain favors debris flows and landslides. The local agriculture with vineyard and fruit cultivation is vulnerable to short-term extreme precipitation and hailstorms especially during the summer half year.
We assess the temperature sensitivity of the maximum (10-min) peak and maximum hourly rainfall intensity within observed rainfall events, as well as daily rainfall sums during the summer half year (April to October). The questions we strive to answer here are: (1) Which factors control the spatial and temporal variability seen in the temperature sensitivities on a regional scale? (2) How applicable and useful is the scaling approach on the regional to local scale considering regional climate variability? (3) What do scaling factors tell us about changes in absolute rainfall intensities?
The paper is structured as follows. The data and methods used are described in Sects. 2 and 3, respectively. We report and discuss the spatial, seasonal, and storm-type variability of scaling factors in Sects. 4.1 and 4.2, and link them to actual rainfall amounts in Sect. 4.3 to assess how the temperature sensitivities can be interpreted from a regional to local impact scale perspective. Concluding arguments are given in Sect. 5.
2 Data
Austrian south-eastern Alpine foreland region (red polygon) and precipitation measurement stations used in the analysis. Observations of additional atmospheric variables (temperature, humidity) are available for most stations operated by the Austrian meteorological service ZAMG (red). Stations operated by the Austrian hydrographic service AHYD (blue) provide precipitation data only
Our study area comprises the south-eastern Alpine foreland region of Austria south of the main Alpine ridge (Fig. 1). Southerly flow and weak gradient situations with convective precipitation during the summer months are the dominant patterns associated with extreme daily precipitation sums in the eastern part. In the southern- and westernmost part, the heaviest precipitation days occur during “Southern Stau” situations and peak in October (Seibert et al. 2006).
We use sub-daily precipitation data from 77 semi-automated weather stations of the Austrian meteorological service (ZAMG) and from 112 rain gauges provided by five provincial administrations of the Austrian hydrographic service (AHYD), both delivering 0.1 mm resolution in rainfall amount. This yields a total number of 189 stations, with record lengths from 1 to 58 years (median: 14 years), ending November 2014. The mean distance to the nearest neighboring station is \({\sim }\)6 km. 1–5 min aggregated precipitation at AHYD stations was summed up to match the 10 minute aggregated precipitation reported at ZAMG stations. The data are cut to our focus season defined as the period from 1st April to 31st October.
The average amount of missing data is 1.4%, with 15 stations reporting a higher fraction of over 15%. These 15 stations are not excluded from the analysis, because they are amongst the stations with the longest records (20 years on average) and a detailed inspection showed that periods of missing data are due to long coherent out-of-service periods. As no time series or trend analysis is done in this study, we decided to use all existing information on plausible events. Since previous quality control of the data varied with the provider, all station series were double-checked for data gaps and inconsistencies.
Extreme outliers (events exceeding the 99.95th percentile) were analyzed case-by-case and only removed from the statistical analysis if they could not be justified to be physically plausible. For this, we analyzed the rainfall records at the station where the event was recorded and at the five closest neighboring stations from 12 h before until 12 h after the event. We checked the records for suspicious values (e.g., 99 and similar, several identical values in a row, sudden breaks), and in addition investigated weather review reports issued by the ZAMG documenting exceptional rainfall events, and hydrographical year books issued by the Austrian Federal Ministry of Agriculture, Forestry, Environment and Water Management, which contain dates and record rainfall amounts, water levels and runoff at AHYD gauges. As a result, 41 out of 153 outlier events were excluded from the sample.
Because temperature measurements are not available for every precipitation station, the daily average and maximum temperature of the days of and preceding a precipitation event were interpolated for all station locations from the high quality 1 \(\times\) 1 km SPARTACUS (Hiebl and Frei 2016) and INCA (Haiden et al. 2010) gridded temperature data products (INCA to extend the SPARTACUS dataset from 2011 to 2014). We used inverse distance-weighted horizontal interpolation and a standard vertical temperature lapse rate (−6.5 K/km). Single station temperature time series used for validation showed very good agreement of the interpolated and directly observed temperatures, confirming the adequacy of this approach.
3 Methods
We estimate the temperature sensitivity of extreme precipitation on an event basis rather than from single observations. This has been done by several other authors (Wasko and Sharma 2015; Molnar et al. 2015; Gaál et al. 2014) and prevents double counting of dependent observations within the same storm. Note that this considers only the temporal dependence; if the same storm moves over more than one station, it repeatedly enters the sample.
We first define periods of continuous rainfall as rainfall events, where each dry interval separates two rainfall events. For each day, we save the number and duration of events, the total number of wet observations, the daily precipitation sum and rain rate (total sum divided by the number of wet observations). We consider only the highest 10-min amount as maximum peak intensity (MPI) and the highest hourly amount as maximum hour intensity (MHI). This way, we only pair each daily mean temperature once, while keeping the information on how concentrated or dispersed the total daily rainfall was distributed over the day.
In addition, we performed a circulation type classification (CTC) based on daily ERA-Interim data (1979–2016, Dee et al. 2011) over the Greater Alpine Region (40.5–51.57°N, 3.0–20.25°E), using the COST Action 733 CTC software (Philipp et al. 2016). We apply a principal component analysis and cluster analysis with 27 circulation types (CTs), which has been shown to perform best in explaining Alpine precipitation variability (Schiemann and Frei 2010). In addition to sea level pressure, we include data of convective available potential energy as indicator of atmospheric stability and seasonality, 700 hPa wind velocity to consider fast and slow moving systems, and 500 hPa geopotential.
Since we are primarily interested in summertime convective precipitation as well as in keeping samples large enough for robust statistical analyses, it is not expedient to continue with 27 CTs. Hence we classify each given day as either falling into a summer convective CT or not. This is done by visual inspection of the anomaly plots of the variables used, the frequency of occurrence, and precipitation anomalies of the CTs (using ZAMG GPARD-1 1 \(\times\) 1 km daily gridded precipitation data over Austria, Hofstätter et al. 2015).
Maximum hour and maximum peak intensities (MHI and MPI), as well as the daily precipitation sums (DPS) are paired with the daily mean temperature of the day of event onset (Tmean). Days with an average daily temperature below 5 °C were dismissed to exclude snow events. We alternatively calculated the temperature sensitivities for the daily rain rate, for the daily maximum temperature, as well as for the mean and maximum temperature of the day prior to event onset in order to exclude cooling due to the event itself, but the scaling results did not show significant differences to the results obtained from Tmean. Similar low sensitivities against some variation in temperature choice were found by Lenderink and van Meijgaard (2009) and Lepore et al. (2015).
We also calculated the scaling rates for dew point temperatures (dpT), as they are a more immediate indicator of the available moisture (Lenderink and Meijgaard 2010), and compared them to the results for Tmean. Data were only available for a reduced sample of ZAMG stations. The change rates for the 98th percentile were not significantly different for dpT as compared to Tmean, while the moderate intensities showed higher dpT sensitivities.
We calculate the scaling factors that describe the percentage change in precipitation intensity per degree of daily mean temperature using quantile regression. In contrast to ordinary least squares regression, quantile regression estimates the influence of the independent variable on a selected conditional quantile of the dependent variable instead of just on the mean (see, e.g., McMillen 2012). Quantile regression thus gives a more comprehensive picture of the influence of temperature on the distribution of precipitation intensities. We fit the quantile regression model for each event sample of interest to the logarithmic precipitation as a function of mean temperature, similar to Wasko et al. (2015),
where P is the event precipitation intensity (MHI, MPI, or DPS), q is the target quantile, and T the daily mean temperature of the event onset day. Based on the linear-slope regression coefficient \(\beta _{1}^{q}\) obtained from this fit, the scaling factor (SF) as the rate of change of precipitation with temperature is then estimated as
The significance of a regression coefficient \(\beta _{1}^{q_{e}}\), where \(q_{e}\) is the quantile of interest (e.g., the 98th percentile), is estimated to be most robust and distinct if it not only deviates from zero with 95% confidence, but if the 95% confidence interval of \(\beta _{1}^{q_{e}}\) does not overlap with the one of \(\beta _{1}^{q_{med}}\), where \(q_{med}\) is the median (50th percentile). The method is also more robust against outliers and allows a more straightforward reporting of the statistical uncertainties than the more common temperature binning approach (e.g., studies reviewed in Westra et al. 2014).
Quantile regression is a linear method, and therefore non-linearities in the data are not considered (which is also the case when a linear regression is fit to binned percentiles). However, in sensitivity tests, in which we cut off the data at different temperatures at the lower and higher ends of the temperature range, we found that the decrease of intensities at the highest temperatures primarily manifests itself in large uncertainty ranges in in these areas, while the overall scaling factor remains robust. This is due the smaller sample sizes at the highest temperatures. Thus, the uncertainty ranges deliver an important indicator of the robustness of the regression. To account for non-linearities in a more explicit way, we calculated the scaling rates in moving windows over the temperature range (see Sect. 4.3).
4 Results and discussion
4.1 Spatial variability and regional patterns of scaling factors
Scaling factors (SFs) of station event precipitation intensity with daily mean temperature for the 98th percentile. Results for the maximum peak intensities (MPI, top panel), maximum hourly intensities (MHI, center panel), and daily precipitation sums (DPS, lower panel) are shown. Plus symbols (+) indicate that the SF is sensitivity significantly different from zero, circles (o) indicate that the SFs of the 98th percentile is also significantly different from the 50th percentile (median). The size of the circle symbols indicates the length of the station record as summarized in the legend
Figure 2 and Table 1 show the 98th percentile station event scaling factors (SFs) for maximum peak intensity (MPI), maximum hour intensity (MHI), the daily precipitation sum (DPS), and the average rain rate (mm/h, Table 1 only) of the entire event sample.
With an average SF of 12%/°C, the MPIs increase with daily mean temperature at rates that exceed the CC-rate and that are significantly higher than those for moderate intensities (50th percentile) at the majority of the stations. The MHIs increase closer to the CC-rate at 9% on average, but a spatial partition emerges with higher/lower SFs in the eastern/western part of the study region, respectively. The higher sensitivity of the 10 min peak intensity compared to the hourly peak intensity is robust throughout our analysis. This is interesting, because even though most studies see scaling rates increase when the time scales decrease from daily to sub-hourly resolution, findings on super-CC scaling on the sub-hourly scale have been inconclusive (Molnar et al. 2015, and review by Westra et al. 2014). The SFs of the DPS show a bipolar pattern with SFs around 3% in the eastern part and negative SFs around –10% in the western part.
We calculated the station SFs for each summer month individually, for the MPI, MHI, DPS, and rain rates (not separately shown). We find that the MPI sensitivities generally show the most consistent scaling at CC-to-super-CC rates throughout the year, especially in the eastern region. In the west, super-CC scaling prevails, but several stations show non-significant or even negative scaling especially in April and October. For the MHI, positive scaling at approximately the CC-rate is consistent in the east, whereas in the west, the picture is inconclusive. Here, negative SFs prevail in April, rise towards CC-rates in September for almost all stations, and become negative again in October at several stations. The bipolar pattern of the SFs of the DPS is consistent throughout the year, although the transition from negative to positive SFs is located farther west in April, May, and June.
The regional and seasonal patterns of SFs indicate that regional scale temperature sensitivity depends on weather patterns and the climatology of the region. The eastern part of the study region is located at lower elevations and the average daily mean temperatures are higher than in the mountainous and high Alpine western part throughout the year. Climatologically, the days of heaviest precipitation in the eastern region are predominantly convective and occur during July and August under weak-pressure-gradient synoptic situations. In the south western part, the heaviest precipitation days culminate in October during ’Southern Stau’ conditions, when moist air masses from the Mediterranean are lifted at the Karavanks and Carnic Alps, often resulting in persistent and intense precipitation (Prettenthaler et al. 2010; Seibert et al. 2006).
This helps to explain the low and negative SFs in the south-western part of our study region, since in these situations, the moisture content of the advected air mass is driven by warm Mediterranean SSTs, while local temperatures are cooler especially in the fall season. In addition, the daily mean temperature during long and persistent rainfall events is likely to be more affected by the rainfall events itself than it is for short events (Bao et al. 2017). The eastern part is largely shielded from ’Southern Stau’ events, the highest extremes occur during shorter convective events during the warm summer months and are less affected by cooling effects due to the event itself, which can explain the higher SFs in this region.
It is apparent that despite the regional patterns, some neighboring stations show large differences in SFs. This underlines that deriving regional temperature sensitivities from a single station is problematic. Especially in mountainous regions, station altitude and temperature range could in part account for differences of scaling factors in nearby stations. However, in a simple linear regression analysis, we find no statistically significant influence of the station altitude on the SFs. We do find a weakly significant positive effect of the station temperature range on its MHI SF, explaining about 15% of the variability, but not on the MPI SF.
The spatial variability and pattern of scaling rates presented here are consistent with results from Molnar et al. (2015), who, for 59 rain gauges over Switzerland, found that stations in pre-Alpine areas show higher SFs than high Alpine regions and valleys. The analysis of the considerably denser rain gauge network used here robustly confirms the influence of regional weather patterns on SF in a mountainous region.
4.2 Seasonal and storm type patterns of scaling factors
Climatological precipitation over the Alpine area generally reaches its maximum in the warmer summer/fall season and its minimum in the cold winter season (Frei and Schär 1998). Scaling factors conditioned on the local absolute temperatures are therefore always governed by the annual cycle, and hence are of limited suitability to assess the effect of global warming on extreme precipitation intensities (see Zhang et al. 2017 for a more detailed discussion). Still, it is highly worthwhile to look at conditional SFs in order to quantify the extent to which the annual cycle and weather patterns govern the local temperature-scaling relationship and to assess under which temperature conditions intense rainfall is most likely to occur.
The previous section showed that rainfall intensities and temperatures are not spatially independent, and pooling all stations over the study region conceals higher scaling rates particularly in the east (see Fig. 3). We thus separate the western and eastern parts of the study region by the 15°E meridian. The mixing effect over diverging temperature ranges might also play a role in mountain regions due to the substantial vertical temperature gradients. However, we do not further account for these effects here.
As displayed in Fig. 3, MPIs show the highest scaling rates, ranging from 2–12%, with MHIs being 1–2% lower on average, while the DPS SFs are mostly negative. The MPI and MHI extreme intensities (98th percentile) increase faster with temperature than the moderate intensities (50th percentile) during May–September in the western region and during April–October in the eastern region. For the daily sums, the difference between the moderate and extreme daily sums is only significant in the eastern region. Here, the moderate daily sums decrease by 4–7%/°C, while the extreme daily sums only decrease at about 0–2%/°C.
Inspecting the distribution of rainfall events and temperature in the subsamples (not shown) helps to understand the variability driven by the differences in regional climatology as described above. A possible explanation for diverging scaling rates in moderate and extreme DPS is the concentrated nature of convective storms that dominate extreme precipitation in the east. When it rains on a hot summer day, it pours. The shorter and more concentrated a rainfall event, the less difference there is between the MPI, MHI, and the DPS. Hence, the DPS from extremely intense rainfall events do not decrease as significantly with temperature as the moderate DPS. in the western part, extreme DPS occur at cooler temperatures and events last longer. In addition, the rainfall sums are larger than in the east, and it is therefore harder to preserve high scaling rates (see Sect. 4.3 for discussion).
Furthermore, the MPI sensitivities are significantly lower in July and September. The analysis of the scatter plots of the underlying temperature-precipitation distributions in these months (not shown) indicate extremes that are higher and more evenly distributed over the temperature range than in other months. This is because the temperature range is shifted to the right and the extreme intensities decrease over the hottest temperatures. Moisture limitations might inhibit larger scaling factors at these temperatures (see Westra et al. 2014), however, data on relative humidity are only available for the ZAMG stations and cannot sufficiently prove this general assumption.
In addition to rainfall intensity, event duration is an important factor of the damage potential of extreme precipitation. Convective showers in the mid-latitudes are usually short and intense, whereas extreme stratiform precipitation events accumulate large sums at lower intensities over longer durations. Short events, however, occur frequently and under all weather conditions in our sample.
Monthly scaling factors in the east and west region (upper and lower row, respectively) for the 98th percentile of maximum peak intensities (MPI, red), maximum hour intensities (MHI, yellow), and daily precipitation sums (DPS, blue) on days with a total maximum of two wet hours (left), 2–5 wet hours (middle), and 5–24 wet hours (right). SFs for days under summer convective synoptic conditions are shown separately (dashed lines, Jun–Sep). The shaded areas denote the 95% confidence interval of the SFs
In order to assess whether the temperature sensitivity of summertime convective precipitation is different from other days, we separated those days from our sample that fall within a circulation type (CT) associated with convective conditions over the Alpine domain. Note that this is not a classification of the rainfall type in individual events, but of the large-scale synoptic situation over the Alps. In addition, the samples were conditioned on the total duration of non-zero rainfall (0.2–2, 2–5, 5–24 h), indicating the overall 'wetness' of the day when an event occurred. Figure 4 shows the results for the subsamples.
CC- to super-CC scaling is apparent on days with short rainfall events over the entire region. In the east, the SFs for MPI and DPS diverge in autumn, which is due to an increasing influence of events yielding high total sums at lower temperatures and rain rates. In the west, the proximity of MPI and DPS SFs indicate that both the daily sums and the peak intensities increase with temperature.
The convective CT sample isolates the hottest days during high summer. The temperature sensitivities during June, July, and August (JJA) are lower than for the other CTs. In the east region, daily mean temperatures reach up to 27 °C, while extreme rainfall intensities start to decline from \({\sim }\)24 °C upwards. In September, the mean temperatures generally do not exceed \({\sim }\)24 °C anymore and the higher SFs indicate a robust increase of extreme intensities in convective CTs. In the western region, daily mean temperatures in JJA rarely exceed \({\sim }\)24 °C. Extreme rainfall intensities, however, start to decline already at \({\sim }\)20 °C. This indicates that the reversal of extremes as described in, e.g., Prein et al. (2017) is location specific even on this regional scale.
On the wetter days in July, SFs during nonconvective-CTs are only about 2–3%/°C. Again, the distribution of temperature and precipitation suggests that Tmean in July rarely falls below 10 °C, and high precipitation intensities occur over the entire temperature range, decreasing at its high end, resulting in low SFs. This decrease of the highest intensities at the highest temperatures is less pronounced in June and September, and in addition, fewer extreme intensities are observed at cooler temperatures, which leads to a steeper increase and a higher SF. Further research on the synoptic patterns and atmospheric conditions that inhibit or foster the intensification of extreme intensities in the warmest summer months is needed to explain the differences in SFs.
4.3 How regional scaling factors relate to absolute rainfall intensities
Risk from extreme precipitation is either posed through high intensity rainfall over short times, causing sudden and small scale flash flooding, or through persistent precipitation leading to slower-onset but larger-scale flooding. We have shown that the temperature sensitivity of extreme precipitation, defined as the 98th percentile of event maximum intensities on the 10 minute, the hourly and the daily scale, vary with the station location, the time of the year, and the prevailing weather patterns. The magnitude of a scaling factor, however, does not provide any information on the magnitude of the actual rainfall intensity.
CC (blue) and super-CC (2CC, red) scaling rates, originating from the 50th (thin lines) and 98th (fat lines) percentile values calculated for the 5–7 °C daily Tmean bin. The panels show maximum peak intensities (MPI, top), maximum hour intensities (MHI, middle), and daily precipitation sums (DPS, bottom) on a log-scale (left ordinate) and linear scale (right ordinate); the legend box on top identifies the individual cases. Actual MPI, MHI, and DPS rainfall records over the SEA study region are shown as green dashed lines
Figure 5 shows four graphs of CC- and super-CC-rates for the MPI, MHI, and DPS 50th and 98th percentile, respectively. The graphs are initialized at the respective percentile value estimated for the 5–7 °C Tmean bin. By means of the highest observed rainfall intensities over the study area, we illustrate how the scaling rates relate to absolute amounts of precipitation intensity.
Whether a scaling rate implies a high absolute change in rainfall intensity depends on the magnitudes of the scaling rate, the rainfall intensity, and the temperature. For the 98th percentile MPI, a CC-rate can be perpetuated up to daily mean temperatures above 30 °C before traversing the threshold of the current record rainfall amount. The same holds true for a super-CC rate in the case of the much smaller 50th percentile MPI.
This changes drastically when either the absolute rainfall intensities increase, or the scaling factor is higher. For example, super-CC scaling in MPI from our graph (Fig. 5, top) would imply record intensities beyond daily mean temperature of \({\sim }\)16–17 °C. For scaling in the DPS (Fig. 5, bottom), the threshold temperatures to reach the record are \({\sim }\)16 °C for CC- and \({\sim }\)8 °C for super-CC scaling, respectively.
Furthermore, a low scaling factor in high rainfall intensities implies a larger absolute change than a high scaling factor in low rainfall intensities. Even though the scaling factors in the western region—or on days with long rainfall durations—are lower than they are in the eastern region—or on days with short rainfall events—, the extremes do significantly increase with temperature during the summer months. At around 20 °C, for example, a 4% increase in a long event MHI \({\sim }\)50 mm) implies an additional 2 mm per degree; at the same time, an 8% increase in a short event MHI \({\sim }\)20 mm) means an additional 1.6 mm per degree. That is, even though the MHI in longer and larger scale rainfall events scales lower, the flood risk might increase considerably if the event occurs in warmer temperature conditions.
Our findings also demonstrate that the change rate for a given percentile (e.g., 98th) should only be compared under consideration of the underlying temperature and precipitation data, because the actual percentile values may vary significantly, with major implications for the resulting scaling factor.
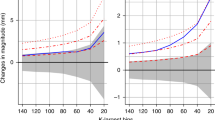
Absolute 98th percentile values (upper panels in both rows) of the maximum peak intensities (MPI, left, red), maximum hour intensities (MHI, middle, yellow), and daily precipitation sums (DPS, right, blue) for the east and west region. The lower panels in both rows show the corresponding scaling factors calculated over 7 °C moving windows (as indicated in the left panels). Note that the scales for the scaling factors vary for MPI, MHI, and DPS. Both percentiles and scaling factors are shown for summertime convective synoptic situations (dashed) and all other synoptic conditions (solid), with CC-rates shown as reference lines (black dashed)
Figure 6 shows a comparison of the actual 98th percentile values of rainfall intensity calculated for 2 °C bins containing at least 100 events. To visualize non-linear dependencies in the data and to get a better understanding how the SFs relate to the absolute rainfall intensities, we calculated the SFs for sub-samples using a 7 °C moving window over the range of daily mean temperatures. The window width of 7 °C yielded the most robust SFs when trading off the event sample size and a sufficiently large temperature spread over which the regression could be calculated. We find this approach more informative than splitting the event sample only once at the estimated threshold temperature at which the scaling turns from positive to negative (Wasko and Sharma 2015).
The illustrations of Fig. 6 summarize the findings of the spatial and seasonal analysis of the scaling factors and their relation to absolute rainfall. The temperature sensitivities are highest for the MPI, lower for the MHI, and lowest for the DPS. The highest SFs are seen between about 10–15 °C, after which they start to decline.
The temperature sensitivity under summertime convective conditions is lower than on other days until approx. 20 °C. These convective days are characterized by warmer temperatures and overall higher extreme precipitation intensities. Extreme convective precipitation in the generally cooler western region occurs at lower local daily mean temperatures than in the eastern region.
Orographic enhancement of convection in mountainous regions is one reason for the strong intensities at lower temperatures occurring in the western region. This is supported by recent regional climate models, which show that global warming likely intensifies Alpine summer convective precipitation (Giorgi et al. 2016). Generally, SFs are lower and extreme percentiles are higher in the western region. The 98th percentile MPIs start to decrease around 24 and 20 °C in the eastern and western regions, respectively. However, the data on events at the highest ends of the temperature distributions are too sparse to calculate robust percentiles and SFs.
The peak intensities of small scale, short convective showers, which contribute the largest share of events in this high temperature range, might be underrepresented in the data due to the limited spatial coverage of the observation network (Kann et al. 2015; Jones 2014), adding uncertainty to the analysis of the scaling relationship at these temperatures. It is likely that humidity constraints contribute to the inhibition of further intensification of the extreme intensities. Data on relative humidity, however, is only available for approx. one third of the stations and thus moisture conditions could not be robustly assessed. Data in the subsample for which humidity could be analyzed indicate lower relative humidity on days with the most extreme intensities as compared to days with moderate precipitation, pointing to a potential moisture limitation. However, further research is needed to test this assumption in our study region. Recent contributions to the literature by Loriaux et al. (2016a) and Loriaux et al. (2016b) demonstrate that considering relative humidity alone is not sufficient to explain the intensification of extreme precipitation. Through including atmospheric control factors such as large scale moisture convergence and atmospheric stability, they deliver valuable contributions to process understanding.
5 Summary and concluding remarks
We have analyzed the temperature sensitivities of extreme daily, hourly and sub-hourly (10-min) precipitation intensities of rainfall events over a dense network of 189 rain gauges in the south-eastern Alpine foreland region of Austria. Scaling factors conditioned on local temperatures require a different interpretation than scaling factors that assess the precipitation response to global warming, as seasonal weather patterns and the annual cycle outweigh the thermodynamic response. We looked at the spatial and seasonal patterns of the temperature sensitivities to assess these implications. Linking the scaling rates to actual changes in rainfall amounts enables new insights for the adequate interpretation of temperature sensitivity from an impact-perspective. We find several distinct aspects of scaling behavior over the study region.
First, the maximum 10-min peak intensities (MPI) significantly and strongly increase with temperature at super-CC rates at most of the stations, whereas peak hourly intensities (MHI) do so at weaker rates around the CC-rate, and daily precipitation sums (DPS) decrease with temperature.
Second, the temperature sensitivities are higher in the generally warmer eastern parts of the study region, where extreme precipitation is associated with short, convective rainfall events during summer and low gradient synoptic conditions with high shares of locally recycled moisture (Bisselink and Dolman 2008). Extremes here rarely occur in cold temperature conditions. In contrast, the scaling factors in the western part of the study region are lower. Extreme precipitation occurs when Mediterranean moisture is advected and lifted at the southern slopes of the Alps. Thus the moisture is not locally sourced, and local temperatures might be less indicative of the sensitivity (Zhang et al. 2017). Also, the cooling effect of large scale events might play a role here (Bao et al. 2017), as well as the orographic amplification of precipitation and generally cooler temperatures in the Alpine environment.
Third, the temperature sensitivities are higher for short duration rainfall as compared to long duration events in both regions. This implies that the peak event intensities on the hourly and sub-hourly scale in long rainfall events increase slower with temperature than peak event intensities in short rainfall events. An explanation for these differences is again the variability of weather patterns, but this time within the respective regions. Further research on how the temperature sensitivities look like in different weather types, might thus reveal valuable insight into the dynamic controls of the temperature precipitation scaling on a regional to local scale.
The salient seasonal and spatial variability in the scaling factors that we found underlines the difficulty to compare scaling factors among different studies. The confrontation with actual rainfall amounts showed that the sample size and the magnitude of a specific percentile are crucial parameters of a given rainfall change rate.
From a risk assessment perspective, it is furthermore important to note that a statistically defined extreme event can deviate from what is considered an extreme event in practice. For example, high scaling factors at low daily mean temperatures do not necessarily imply large absolute changes in precipitation intensity, while even moderate scaling factors at high temperatures may have substantial consequences in terms of accumulated rainfall.
It is often justifiably argued that the local temperature is not an appropriate choice for temperature precipitation scaling, since the moisture uptake often occurs in regions and at temperatures far away from the point of precipitation. Through taking into account these dynamic factors by isolating, e.g., weak gradient synoptic situations with mainly local moisture recycling from other events, regional temperature sensitivities can however deliver useful insights into how the thermodynamic and dynamic factors play together in controlling the change of precipitation intensities with temperature in specific seasons and regions.
References
Alexander LV (2016) Global observed long-term changes in temperature and precipitation extremes: a review of progress and limitations in IPCC assessments and beyond. Weather Clim Extrem 11:4–16. doi:10.1016/j.wace.2015.10.007
Attema JJ, Loriaux JM, Lenderink G (2014) Extreme precipitation response to climate perturbations in an atmospheric mesoscale model. Environ Res Lett 9(1):014003. doi:10.1088/1748-9326/9/1/014003
Ban N, Schmidli J, Schär C (2015) Heavy precipitation in a changing climate: Does short-term summer precipitation increase faster? Geophys Res Lett 42(4):1165–1172. doi:10.1002/2014GL062588
Bao J, Sherwood SC, Alexander LV, Evans JP (2017) Future increases in extreme precipitation exceed observed scaling rates. Nat Clim Change 7(2):128–132. doi:10.1038/nclimate3201
Barbero R, Fowler HJ, Lenderink G, Blenkinsop S (2017) Is the intensification of precipitation extremes with global warming better detected at hourly than daily resolutions? Geophys Res Lett 44(2):974983. doi:10.1002/2016GL071917
Berg P, Haerter JO (2013) Unexpected increase in precipitation intensity with temperature—a result of mixing of precipitation types? Atmos Res 119:56–61. doi:10.1016/j.atmosres.2011.05.012
Berg P, Moseley C, Haerter JO (2013) Strong increase in convective precipitation in response to higher temperatures. Nat Geosci 6(3):181–185. doi:10.1038/ngeo1731
Bisselink B, Dolman AJ (2008) Precipitation recycling: moisture sources over Europe using ERA-40 Data. J Hydrometeorol 9(5):1073–1083. doi:10.1175/2008JHM962.1
Cassola F, Ferrari F, Mazzino A, Miglietta MM (2016) The role of the sea on the flash floods events over Liguria (northwestern Italy). Geophys Res Lett 43(7):3534–3542. doi:10.1002/2016GL068265
Chan SC, Kendon EJ, Roberts NM, Fowler HJ, Blenkinsop S (2016) Downturn in scaling of UK extreme rainfall with temperature for future hottest days. Nat Geosci 9(1):24–28. doi:10.1038/ngeo2596
Contractor S, Alexander LV, Donat MG, Herold N (2015) How well do gridded datasets of observed daily precipitaion compare over Australia? Advances in Meteorology p 325718. doi:10.1155/2015/325718
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hölm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thëpaut JN, Vitart F (2011) The era-interim reanalysis: configuration and performance of the data assimilation system. Quart J R Meteorol Soc 137(656):553–597. doi:10.1002/qj.828
Drobinski P, Alonzo B, Bastin S, Da Silva N, Muller C (2016) Scaling of precipitation extremes with temperature in the French Mediterranean region: what explains the hook shape? J Geophys Res Atmos 121(7):3100–3119. doi:10.1002/2015JD023497
Drobinski P, Silva ND, Panthou G, Bastin S, Muller C, Ahrens B, Borga M, Conte D, Fosser G, Giorgi F, Güttler I, Kotroni V, Li L, Morin E, Önol B, Quintana-Segui P, Romera R, Torma CZ (2016) Scaling precipitation extremes with temperature in the Mediterranean: past climate assessment and projection in anthropogenic scenarios. Climate Dynamics pp 1–21, doi:10.1007/s00382-016-3083-x
Forchheimer P (1913) Der Wolkenbruch im Grazer Hügelland vom 16. Juli 1913. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften in Wien, mathematisch–naturw Klasse, Abt 2a 122:2100–2109
Formayer H, Fritz A (2016) Temperature dependency of hourly precipitation intensities—surface versus cloud layer temperature. Int J Climatol 37(1):1–10. doi:10.1002/joc.4678
Frei C, Schär C (1998) A precipitation climatology of the Alps from high-resolution rain-gauge observations. Int J Climatol 18(8):873–900. doi:10.1002/(SICI)1097-0088(19980630)18:8<873::AID-JOC255>3.0.CO;2-9
Gaál L, Molnar P, Szolgay J (2014) Selection of intense rainfall events based on intensity thresholds and lightning data in Switzerland. Hydrol Earth Syst Sci 18(5):1561–1573. doi:10.5194/hess-18-1561-2014
Giorgi F, Torma C, Coppola E, Ban N, Schar C, Somot S (2016) Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nature Geoscience 9(8):2016/07/11/online, DOI: 10.1038/NGEO2761, wOS:000382137900013
Haerter JO, Berg P (2009) Unexpected rise in extreme precipitation caused by a shift in rain type? Nat Geosci 2(6):372–373. doi:10.1038/ngeo523
Haiden T, Kann A, Wittmann C, Pistotnik G, Bica B, Gruber C (2010) The integrated nowcasting through comprehensive analysis (INCA) system and its validation over the eastern Alpine region. Weather Forecast 26(2):166–183. doi:10.1175/2010WAF2222451.1
Hiebl J, Frei C (2016) Daily temperature grids for Austria since 1961-concept, creation and applicability. Theor Appl Climatol 124(1–2):161–178. doi:10.1007/s00704-015-1411-4
Hofstaetter M, Chimani B (2012) Van Bebber’s cyclone tracks at 700 hPa in the Eastern Alps for 1961–2002 and their comparison to Circulation Type Classifications. Meteorologische Zeitschrift 21(5):459–473. doi:10.1127/0941-2948/2012/0473
Hofstätter M, Jacobeit J, Homann M, Lexer A, Chimani B, Philipp A, Beck C, Ganekind M (2015) WETRAX - Weather patterns, cyclone tracks and related precipitation extremes. Grossflächige Starkniederschläge im Klimawandel in Mitteleuropa. Projektendbericht, Geographica Augustana, p 19
hydroConsult GmbH (2011) Hochwasserdokumentation Wölzertal 7.7.2011. Tech. rep., Amt der Steiermärkischen Landesregierung FA19B
IPCC (2013) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. doi:10.1017/CBO9781107415324
Ivancic TJ, Shaw SB (2016) A U.S.-based analysis of the ability of the Clausius–Clapeyron relationship to explain changes in extreme rainfall with changing temperature. Journal of Geophysical Research: Atmospheres 121(7):30663078, doi:10.1002/2015JD024288
Jones JAA (2014) Global hydrology: processes, resources and environmental management. Routledge, London
Kabas T, Foelsche U, Kirchengast G (2011) Seasonal and annual trends of temperature and precipitation within 1951/1971–2007 in south-eastern Styria, Austria. Meteorologische Zeitschrift 20(3):277–289. doi:10.1127/0941-2948/2011/0233
Kann A, Meirold-Mautner I, Schmid F, Kirchengast G, Fuchsberger J, Meyer V, Tächler L, Bica B (2015) Evaluation of high-resolution precipitation analyses using a dense station network. Hydrol Earth Syst Sci 19(3):1547–1559. doi:10.5194/hess-19-1547-2015
Lenderink G, van Meijgaard E (2009) Unexpected rise in extreme precipitation caused by a shift in rain type? Nat Geosci 2(6):373–373. doi:10.1038/ngeo524
Lenderink G, Ev Meijgaard (2010) Linking increases in hourly precipitation extremes to atmospheric temperature and moisture changes. Environ Res Lett 5(2):025208. doi:10.1088/1748-9326/5/2/025208
Lepore C, Veneziano D, Molini A (2015) Temperature and CAPE dependence of rainfall extremes in the eastern United States. Geophys Res Lett 42(1):74–83. doi:10.1002/2014GL062247
Loriaux JM, Lenderink G, De Roode SR, Siebesma AP (2013) Understanding convective extreme precipitation scaling using observations and an entraining plume model. J Atmos Sci 70(11):3641–3655. doi:10.1175/JAS-D-12-0317.1
Loriaux JM, Lenderink G, Siebesma AP (2016a) Large-scale controls on extreme precipitation. J Clim 30(3):955–968. doi:10.1175/JCLI-D-16-0381.1
Loriaux JM, Lenderink G, Siebesma AP (2016b) Peak precipitation intensity in relation to atmospheric conditions and large-scale forcing at midlatitudes. J Geophys Res Atmos 121(10):5471–5487. doi:10.1002/2015JD024274
McMillen DP (2012) Quantile regression for spatial data. Springer-Verlag, Berlin
Messmer M, Gomez-Navarro JJ, Raible CC (2015) Climatology of Vb cyclones, physical mechanisms and their impact on extreme precipitation over Central Europe. Earth Syst Dyn 6(2):541–553. doi:10.5194/esd-6-541-2015
Molnar P, Fatichi S, Gaál L, Szolgay J, Burlando P (2015) Storm type effects on super Clausius–Clapeyron scaling of intense rainstorm properties with air temperature. Hydrol Earth Syst Sci 19(4):1753–1766. doi:10.5194/hess-19-1753-2015
Moseley C, Hohenegger C, Berg P, Haerter JO (2016) Intensification of convective extremes driven by cloud-cloud interaction. Nat Geosci 9(10):748–752. doi:10.1038/ngeo2789
Munzar J, Ondracek S, Auer I (2011) Central European one-day precipitation records. Moravian Geograph Rep 19(1):32–40
O’Gorman PA (2015) Precipitation extremes under climate change. Curr Clim Change Rep 1(2):49–59. doi:10.1007/s40641-015-0009-3
Panziera L, James CN, Germann U (2015) Mesoscale organization and structure of orographic precipitation producing flash floods in the Lago Maggiore region. Quart J R Meteorol Soc 141(686):224–248. doi:10.1002/qj.2351
Philipp A, Beck C, Huth R, Jacobeit J (2016) Development and comparison of circulation type classifications using the COST 733 dataset and software. Int J Climatol 36(7):2673–2691. doi:10.1002/joc.3920
Prein AF, Gobiet A (2016) Impacts of uncertainties in European gridded precipitation observations on regional climate analysis. Int J Climatol 37(1):305–327. doi:10.1002/joc.4706
Prein AF, Rasmussen RM, Ikeda K, Liu C, Clark MP, Holland GJ (2017) The future intensification of hourly precipitation extremes. Nat Clim Change 7(1):48–52. doi:10.1038/nclimate3168
Prettenthaler F, Podesser A, Pilger H (2010) Klimaatlas Steiermark. Periode 1971-2000. Eine anwenderorientierte Klimatographie. No. 4 in Studien zum Klimawandel in Österreich, ÖAW
Schicker I, Radanovics S, Seibert P (2010) Origin and transport of Mediterranean moisture and air. Atmos Chem Phys 10(11):5089–5105. doi:10.5194/acp-10-5089-2010
Schiemann R, Frei C (2010) How to quantify the resolution of surface climate by circulation types: an example for Alpine precipitation. Phys Chem Earth, Parts A/B/C 35(9–12):403–410. doi:10.1016/j.pce.2009.09.005
Schocklitsch A (1914) Die Hochwasserkatastrophe in Graz am 16. Juli 1913. Zeitschrift des Österreichischen Ingenieur- und Architekten-Vereines 27:511–518
Seibert P, Frank A, Formayer H (2006) Synoptic and regional patterns of heavy precipitation in Austria. Theor Appl Climatol 87(1–4):139–153. doi:10.1007/s00704-006-0198-8
Sodemann H, Zubler E (2010) Seasonal and inter-annual variability of the moisture sources for Alpine precipitation during 1995–2002. Int J Climatol 30(7):947–961. doi:10.1002/joc.1932
Volosciuk C, Maraun D, Semenov VA, Tilinina N, Gulev SK, Latif M (2016) Rising mediterranean sea surface temperatures amplify extreme summer precipitation in central Europe. Sci Rep 6:32450. doi:10.1038/srep32450
Wang G, Wang D, Trenberth KE, Erfanian A, Yu M, Bosilovich MG, Parr DT (2017) The peak structure and future changes of the relationships between extreme precipitation and temperature. Nat Clim Change 7(4):268–274. doi:10.1038/nclimate3239
Wasko C, Sharma A (2015) Steeper temporal distribution of rain intensity at higher temperatures within Australian storms. Nat Geosci 8(7):527–529. doi:10.1038/ngeo2456
Wasko C, Sharma A, Johnson F (2015) Does storm duration modulate the extreme precipitation-temperature scaling relationship? Geophysical Research Letters 42(20):2015GL066274. doi:10.1002/2015GL066274
Westra S, Fowler HJ, Evans JP, Alexander LV, Berg P, Johnson F, Kendon EJ, Lenderink G, Roberts NM (2014) Future changes to the intensity and frequency of short-duration extreme rainfall. Rev Geophys 52(3):522–555. doi:10.1002/2014RG000464
Zhang X, Zwiers FW, Li G, Wan H, Cannon AJ (2017) Complexity in estimating past and future extreme short-duration rainfall. Nat Geosci 10(4):255–259. doi:10.1038/ngeo2911
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF). The study was funded by the FWF-DK Climate Change of the Austrian Science Fund (FWF Doctoral Programme No. W 1256-G15; http://dk-climate-change.uni-graz.at). The interdisciplinary faculty and students of this doctoral programme are thanked for discussion and comments during the study and A. Prein, M. Tye (NCAR Boulder), and C. Unterberger for valuable comments on earlier versions of the manuscript. We thank the offices of the Austrian Hydrographic Service and the Austrian National Weather Service ZAMG for provision of the precipitation data and for complementary meteorological data.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schroeer, K., Kirchengast, G. Sensitivity of extreme precipitation to temperature: the variability of scaling factors from a regional to local perspective. Clim Dyn 50, 3981–3994 (2018). https://doi.org/10.1007/s00382-017-3857-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3857-9