Abstract
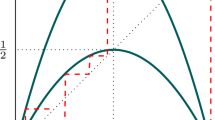
We consider a family \({\{T_{r}: [0, 1] \circlearrowleft \}_{r\in[0, 1]}}\) of Markov interval maps interpolating between the tent map \({T_{0}}\) and the Farey map \({T_{1}}\). Letting \({\mathcal{P}_{r}}\) denote the Perron–Frobenius operator of \({T_{r}}\), we show, for \({\beta \in [0, 1]}\) and \({\alpha \in (0, 1)}\), that the asymptotic behaviour of the iterates of \({\mathcal{P}_{r}}\) applied to observables with a singularity at \({\beta}\) of order \({\alpha}\) is dependent on the structure of the \({\omega}\)-limit set of \({\beta}\) with respect to \({T_{r}}\). The results presented here are some of the first to deal with convergence to equilibrium of observables with singularities.
Article PDF
Similar content being viewed by others
References
Aaronson, J.: An Introduction to Infinite Ergodic Theory. AMS Mathematical Surveys and Monographs, vol. 50 (1997)
Aaronson J.: An ergodic theorem with large normalising constants. Isr. J. Math. 38, 182–188 (1981)
Baladi V.: Positive Transfer Operators and Decay of Correlations. World Scientific, Singapore (2000)
Boyarsky A., Góra P.: Laws of Chaos: Invariant Measures and Dynamical Systems in One Dimension. Probability and Its Applications. Birkhäuser, Basel (1997)
Collet, P.: Some Ergodic Properties of Maps of the Interval, vol. 52. Dynamical systems (Temuco, 1991/1992), pp. 55–91, Travaux en Cours. Herman (1996)
Dajani, K., Kraaikamp, C.: Ergodic Theory of Numbers. The Carus Mathematical Monographs, vol. 29 (2002)
Dedecker J., Gouëzel S., Merlevède F.: Some almost sure results for unbounded functions of intermittent maps and their associated Markov chains. Ann. Inst. H. Poincaré Probab. Stat. 46(3), 796–821 (2010)
Doeblin W., Fortet R.: Sur des chaînes à liaisons complètes. Bull. Soc. Math. Fr. 65, 132–148 (1937)
Erickson K.: Strong renewal theorems with infinite mean. Trans. Am. Math. Soc. 151, 263–291 (1970)
Esposti M.D., Isola S., Knauf A.: Generalized Farey trees, transfer operators and phase transitions. Commun. Math. Phys. 275, 297–329 (2007)
Falconer K.J.: Fractal Geometry: Mathematical Foundations and Applications, 3th edn. Wiley, New York (2014)
Fiala, J., Kleban, P., Özlük, A.: The phase transition in statistical models defined on Farey fractions. J. Stat. Phys. 110, 73–86 (2003)
Fremlin D.H.: Measure Theory, vol. 2. Torres Fremlin, Colchester (2001)
Garsia A., Lamperti J.: A discrete renewal theorem with infinite mean. Comment. Math. Helv. 37, 221–234 (1962)
Giampieri M., Isola S.: A one-parameter family of analytic Markov maps with an intermittency transition. Discrete Contin. Dyn. Syst. 12(1), 115–136 (2005)
Gouëzel S.: Sharp polynomial estimates for the decay of correlations. Isr. J. Math. 139, 29–65 (2004)
Gouëzel S.: Berry–Esseen theorem and local limit theorem for non uniformly expanding maps. Ann. Inst. H. Poincaré Probab. Stat. 41(6), 997–1024 (2005)
Gouëzel, S.: Stable Laws for the Doubling Map. Unpublished, pp. 1–15 (2008)
Gouëzel S.: Correlation asymptotics from large deviations in dynamical systems with infinite measure. Colloq. Math. 125(2), 193–212 (2011)
Hofbauer F., Keller G.: Ergodic properties of invariant measures for piecewise monotonic transformations. Math. Z. 180, 119–140 (1982)
Hennion, H., Herveé, L.: Limit Theorems for Markov Chains and Stochastic Properties of Dynamical Systems by Quasi-Compactness. Lecture Notes in Mathematics, vol. 1766. Springer, New York (2001)
Ionescu-Tulcea C.T., Marinescu G.: Théorème ergodique pour des classes d’opérations non complètement continues. Ann. Math. 52(1), 140–147 (1950)
Kautzsch, J.: Renewal Theory for Operators in Banach Spaces. Diplomarbeit Universität Bremen (2011)
Kautzsch J., Kesseböhmer M., Samuel T., Stratmann B.O.: On the asymptotics of the \({\alpha}\)-Farey transfer operator. Nonlinearity 28, 143–166 (2015)
Keller G.: On the rate of convergence to equilibrium in one-dimensional systems. Commun. Math. Phys. 96, 181–193 (1984)
Kesseböhmer M., Kombrink S.: Fractal curvature measures and Minkowski content for self-conformal subsets of the real line. Adv. Math. 230, 2474–2512 (2012)
Kesseböhmer M., Munday S., Stratmann B.O.: Strong renewal theorems and Lyapunov spectra for \({\alpha}\)-Farey and \({\alpha}\)-Lüroth systems. Ergod. Theory Dyn. Syst. 32(3), 989–1017 (2012)
Kesseböhmer M., Slassi M.: A distribution limit law for the continued fraction digit sum. Math. Nachrichten 281(9), 1294–1306 (2008)
Kesseböhmer M., Stratmann B.O.: A multifractal analysis for Stern–Brocot intervals, continued fractions and Diophantine growth rates. J. Reine Angew. Math. 605, 133–163 (2007)
Kleban, P., Özlük, A.: A Farey fraction spin chain. Commun. Math. Phys. 203, 635–647 (1999)
Knauf A.: On a ferromagnetic spin chain. Commun. Math. Phys. 153, 77–115 (1993)
Knauf A.: The number-theoretical spin chain and the Riemann zeros. Commun. Math. Phys. 196, 703–731 (1998)
Lanford O.E., Ruedin L.: Statistical mechanical methods and continued fractions. Helv. Phys. Acta 69, 908–948 (1996)
Mayer D.H.: Continued fractions and related transformations. In: Bedford, T., Keane, M., Series, C. (eds.) Ergodic Theory, Symbolic Dynamics and Hyperbolic Spaces, Oxford University Press, Oxford (1991)
Melbourne I., Terhesiu D.: Operator renewal theory and mixing rates for dynamical systems with infinite measure. Invent. Math. 189, 61–110 (2012)
Pomeau Y., Manneville P.: Intermittency transition to turbulence in dissipative dynamical systems. Commun. Math. Phys. 74, 189–197 (1980)
Rychlik M.: Bounded variation and invariant measures. Stud. Math. LXXVI, 69–80 (1983)
Sarig O.: Subexponential decay of correlations. Invent. Math. 150, 629–653 (2002)
Schuster H.G.: Deterministic Chaos. VCH, New York (1988)
Thaler M.: The asymptotics of the Perron–Frobenius operator of a class of interval maps preserving infinite measure. Stud. Math. 143(2), 103–119 (2000)
Tyran-Kaminska M.: Weak convergence to Lévy stable processes in dynamical systems. Stoch. Dyn. 10(2), 263–289 (2010)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dmitry Dolgopyat.
The first two authors were supported by the German Research Foundation (DFG) grant Renewal Theory and Statistics of Rare Events in Infinite Ergodic Theory (Geschäftszeichen KE 1440/2-1).
Rights and permissions
About this article
Cite this article
Kautzsch, J., Kesseböhmer, M. & Samuel, T. On the Convergence to Equilibrium of Unbounded Observables Under a Family of Intermittent Interval Maps. Ann. Henri Poincaré 17, 2585–2621 (2016). https://doi.org/10.1007/s00023-015-0451-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00023-015-0451-8