Abstract
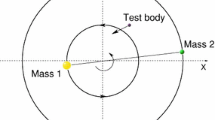
The present work investigates a mechanism of capturing processes in the restricted three-body problem. The work has been done in a set of variables which is close to Delaunay's elements but which allows for the transition from elliptic to hyperbolic orbits. The small denominator difficulty in the perturbation theory is overcome by embedding the small denominator in an analytic function through a suitable analytic continuation. The results indicate that motions in nearly parabolic orbits can become chaotic even though the model is deterministic. The theoretical results are compared with numerical results, showing an agreement of about one percent. Some possible applications to cometary orbits are also given.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Arnold, V.I., Usp. Mat. Nank.18, 9 (1963) [Russ. Math. Surv.18, (6), 85, (1963)].
Balescu, R.,Statistical Mechanics of Charged Particles, (Interscience, New York, 1963).
Bilo, e.H. and Van de Hulst, H.C.,Bull. Astron. Inst. Netherlands 15, 119 (1960).
Birkoff, G.D.,Dynamical Systems, (A.M.S. Publications, Providence, 1927).
Cary, J.R.,Phys. Rep. 79, 129 (1981).
Chirikov, B.V. and Vecheslavov, V.V., “Chaotic Dynamics of Comet Haley”, (Preprint 86-184, Institute of Nuclear Physics, Novosibirsk, 1986).
Deprit, A.,Celestial Mechanics 1, 12 (1969).
Dewar, R.L.,J. Phys. A9, 2043 (1976).
Escobal, P.,Methods of Orbit Determination (Krieger, New York, 1976).
Everhart, E.,Astron. J. 73, 1039 (1968).
Everhart, E.,Astron. J. 74, 735 (1969).
Everhart, E.,Astron. J. 75, 258 (1970).
Everhart, E.,Astron. J. 78, 329 (1973)
Gldberger, M. and Watson, r.,Collision Theory, (Wiley, New York, 1964).
Greence, J.M.,J. Math. Phys. 20, 1183 (1980).
Hori, G., Publications of the Astronomical Society of Japan18, 287 (1966).
Kolmogorov, A.N.,Dok. Akad. Nank. 98, 527 (1954). English translation: Los Alamos Scientific Laboratory Translation No. LA-TR-71-67.
Lighthill, J.,Proc. R. Soc. Lond. A407, 35 (1986).
Lyttleton, R.A. and Hammersley, J.M.,M. N. Roy. Astr. Soc. 127, 257 (1964).
Marsden, B.G.,Catalog of Cometary Orbits, International Astronomical Union, 1986.
Moser, J.,Nach. Akad. Wiss. Goettingen Math. Phys. K1. 2 1, 1 (1962).
Oort, J.H.,Bull. Astron. Inst. Neth. 11, 91 (1950).
Petrosky, T.Y.,Phys. Rev. A. 29, 2078 (1984).
Petrosky, T.Y.,Phys. Rev. A 32, 3716 (1985).
Petrosky, T.Y.,Phys. Lett. A117, 328 (1986).
Petrosky, T.Y. and I. Prigogine, PNAS (to appear, 1987).
Poincaré, H.,Les Methodes Nouvelles de la Mechanique Celeste, (Dover, New York, 1967; English translation NASA Technical Translton F-451.)
Prigogine, I.,Non-Equilibrium Statistical Mechanics, (Interscience, New York, 1962).
Prigogine, I., Grecos, A. and George, Cl.,Celestial Mechanics 16, 489 (1977).
Résibois, R. and I. Prigogine,Bull. Classe Sci., Acad. Roy. Belg.46, 53 (1960).
Strömgre, E.,Publ. KObs. No. 19 (1914).
Szebehely, V.,Theory of Orbits, (Academic Press, New York, 1967).
Whittaker, E.T.,A Treatise on the Analytical Dynamics of Particles and Rigid Bodies, 4th Edition. (Cambridge University Press, Cambridge, 1959).
Yabushita, S.,Astron. and Astrophys. 16, 471 (1972a).
Yabushita, S.,Astron. and Astrophys. 20, 205 (1972b).
Yabushita, S.,Mon. Not. R. Astr. Soc. 187, 445 (1979).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Petrosky, T.Y., Broucke, R. Area-preserving mappings and deterministic chaos for nearly parabolic motions. Celestial Mechanics 42, 53–79 (1987). https://doi.org/10.1007/BF01232948
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/BF01232948