Two-level moderated mediation models with single-level data and new measures of effect sizes

Abstract

This article proposes a two-level moderated mediation (2moME) model with single level data, and develops measures to quantify the moderated mediation (moME) effect sizes for both the conventional moME model and the 2moME model. A Bayesian approach is developed to estimate and test moME effects and the corresponding effect sizes (ES). Monte Carlo results indicate that (1) the 2moME model yields more accurate estimates of the parameters than the conventional moME model; (2) the 95% credibility interval following the 2moME model covers the moME effects and the ESs more accurately than that following the conventional moME model; and (3) statistical tests for the existence of the moME effects with the 2moME model are more reliable in controlling type I errors than those with the conventional moME model, especially under heteroscedasticity conditions. In addition, the developed measures of ES are more interpretable, and directly answer the questions regarding the extent to which a moderator can account for the change of the mediation effect between the predictor and the outcome variable through the mediator variable. An empirical example illustrates the application of the 2moME model and the ES measures.

Introduction

Mediation and moderation analyses are commonly used methods for studying the relationship between a predictor (X) and an outcome variable (Y) in social science research. To better understand the relationships among variables, there is an increasing demand for a more general theoretical framework that combines moderation and mediation analyses. Recently, statistical analysis of moderated mediation (moME) effects has become a powerful tool for scientists to investigate complex processes. The conceptual model of moME emphasizes that the question of interest is how the “mediation effect” of the predictor on the outcome variable via the mediation variable varies as the first-stage moderator variable or (and) the second-stage moderator variable changes. However, because the moderated mediation effect is treated as an interaction effect by including a product term of the predictor (or mediator) with the moderator in the conventional statistical model for moME analysis, it is difficult to distinguish the different roles of the predictor, mediator, and moderator in practice, which will be discussed further in later sections.

An effect size (ES) is a quantitative reflection of the magnitude of some phenomenon that is used for the purpose of addressing a question of interest (Kelley & Preacher, 2012). Routinely reporting ESs has been recommended as the primary solution to the issue of overemphasis on significance testing (American Education Research Association, 2006; Cumming, 2014; Funder et al., 2013; Pek & Flora, 2018; Rozeboom, 1960; Wilkinson, 1999). Therefore, appropriate ESs for measuring moME effects are very important in reporting and interpreting inferential results (Rights & Sterba, 2018). However, there does not exist an effective measure that allows us to answer the question regarding the extent to which the moderator variable (Z) moderates the indirect effect of X on Y via the mediator variable (M) in the moME model.

To distinguish the roles of the moderator, mediator, and predictor in the analysis of moME effect and to better match with the conceptual model, we first reformulate the conventional moME model and extend it to a two-level moME (2moME) model with single level data. The new model does not need the homoscedasticity assumptions required by the conventional model. Second, to fill the lack of interpretable measures of ESs in conducting moME analysis, we develop ES measures by quantifying the mediation-effect variance attributed to the moderator(s) for both the conventional moME and the 2moME models under different scenarios. Then, the 2moME model and measures of effect size will be estimated by the Bayesian method and examined via a simulation study. Next, the application of the new model and the ES measures of the moderated mediation effect will be illustrated with a real data example.

Mediation model and its effect size measures

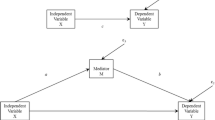
Mediation analysis studies the relationship between X and Y by introducing a mediator variable M. Mediation occurs when the effect of X on Y is transmitted through M (Fig. 1a). Statistically, the existence of a mediation effect can be done by testing whether or not the indirect path X→M→Y (i.e., the product a₀b₀) as shown in Fig. 1b (the bolded paths) is zero. The model in Fig. 1b can be written as

$$ {M}_i={d}_{M0}+{a}_0{X}_i+{e}_{Mi}, $$

(1)

$$ {Y}_i={d}_{Y0}+{c}_0{X}_i+{b}_0{M}_i+{e}_{Yi}, $$

(2)

where d_M0 and d_Y0 represent intercepts, a₀, b₀, and c₀ are regression coefficients¹, and e_Mi and e_Yi represent errors with means 0 and variances ${\sigma}_{eM}^2$ and ${\sigma}_{eY}^2$, respectively.

Fig. 1

Diagrams of the mediation model

By inserting Eq. (1) into Eq. (2), the combined equation becomes

$$ {\displaystyle \begin{array}{c}{Y}_i={d}_{Y0}+{c}_0{X}_i+{b}_0\left({d}_{M0}+{a}_0{X}_i+{e}_{Mi}\right)+{e}_{Yi}\\ {}\kern2.56em =\left({d}_{Y0}+{d}_{M0}{b}_0\right)+\left({c}_0+{a}_0{b}_0\right){X}_i+{b}_0{e}_{Mi}+{e}_{Yi}.\end{array}} $$

(3)

The mediation effect is evaluated by the product term a₀b₀ in Eq. (3). The Sobel test (Sobel, 1982) and the bootstrap methods (MacKinnon et al., 2004; Shrout & Bolger, 2002) are widely used for testing the hypothesis of null mediation effect, represented by a₀b₀=0.

When the null hypothesis does not hold, various ES measures have been proposed to quantify the size of the indirect effect in the context of mediation analysis, including the ratio of the indirect effect to the total effect, the ratio of the indirect effect to the direct effect (Alwin & Hauser, 1975; Sobel, 1982); standardized indirect effects (Alwin & Hauser, 1975; Cheung, 2009; MacKinnon, 2008; Preacher & Hayes, 2008); proportions of the variance of Y that can be attributed to the indirect effect of X on Y through M (de Heus, 2012; Fairchild et al., 2009; MacKinnon, 2008; Preacher & Kelley, 2011; Lachowicz et al., 2018). Reviews and more detailed discussions about the ES of indirect effects can be found in Preacher and Kelley (2011) and Lachowicz et al. (2018).

These ES measures for the indirect effect have many desirable properties. However, they were formulated based on the assumptions that both the error variance of M and Y are constants across individuals, called homoscedasticity. As we shall see, the moME model itself implies that the mediation effect varies across different values of the moderator variable(s). It is necessary to consider how to quantify the variation of the indirect effect attributed to the moderator(s) to advance the analysis of the moME effect.

Moderation model and its effect size measures

Moderated multiple regression model

The moderation effect describes the conditions under which the relationship between X and Y is related to a third variable Z, as shown in Fig. 2a for the conceptual model. Such a hypothesis is commonly tested using moderated multiple regression (MMR) (Aiken & West, 1991), and the statistical diagram of MMR is given in Fig. 2b. The MMR model can be written as

$$ {Y}_i={b}_0+{b}_1{X}_i+{b}_2{Z}_i+{b}_3{X}_i{Z}_i+{\varepsilon}_i, $$

(4)

where ε_i is assumed to have a zero mean and a constant variance (i.e., homoscedasticity assumption). A moderation effect is endorsed when the least squares (LS) estimate of b₃ is statistically significantly different from zero (the bolded path in Fig. 2b), and the conditional effect of X on Y is statistically defined as b₁+ b₃Z (Baron & Kenny, 1986).

Fig. 2

Diagrams of the moderation model

Several ES measures have been proposed to quantify the size of the moderation effect, which mainly include the difference of coefficients of determination ($\Delta {R}_Y^2$), ${f}_Y^2$, partial and semi-partial correlations, standardized regression coefficients (Smithson & Shou, 2017), and a few recently developed alternative measures (Dahlke & Sackett, 2018; Nye & Sackett, 2017; Smithson & Shou, 2017). The measure ΔR² can be expressed as

$$ \Delta {R}^2={R}_{int}^2-{R}_1^2, $$

(5)

where ${R}_{int}^2$ is the coefficient of determination for the multiple regression model in Eq. (4), and ${R}_1^2$ is the coefficient of determination when the interaction term XZ is removed from Eq. (4). For researchers conducting moderation analysis using the MMR model, reporting ΔR² is perceived as both necessary and informative to evaluate the additional contributions of the moderator variable (Aiken & West, 1991; Cohen, 1988; Cumming, 2014). It is generally accepted that ΔR² is a good measure of the importance of the moderator and is commonly reported in publications (Aguinis et al., 2005; Murphy & Russell, 2017). Clearly, the ΔR² in Eq. (5) measures the percentage of the variance of Y that is uniquely explained by the interaction term XZ. However, according to Fig. 2a, the interest of moderation analysis is how the regression coefficient of X on Y is affected by Z across individuals. The concept of moderation clearly distinguishes the role of the moderator from that of the predictor. In particular, the relationship between the predictor and the outcome variable is of primary interest, and the moderator affects this relationship. An interaction arises when considering the relationship among three or more variables, and it describes a situation in which the effect of one causal variable on the outcome variable depends on the state of a second causal variable (that is, when effects of the two causes are not additive). In practice, the roles of the variables can be determined substantively or by consulting the existing literature (Baron & Kenny, 1986; Kraemer et al., 2001; Kraemer et al., 2002; Kraemer et al., 2008), and the different roles also need to be clear when interpreting the effects of the predictor and the moderator variables. Kraemer et al. (2008) provided concrete steps to distinguish the predictor from the moderator. These steps emphasize that the moderator temporally precedes the independent variable. In conducting moderation analysis, what we are really interested in is how Z changes the effect of X on Y, rather than the effect of XZ on Y. Therefore, proper measures of moderation ES should reflect the degree for the moderator variable to alter the effect of X on Y, rather than the effect of XZ on Y. Unfortunately, most traditional measures of moderation ESs changed the concept of moderation to interaction. Because the moderator and the predictor variable are treated equally, they misrepresent the meaning of moderation ES (Liu & Yuan, 2021). In particular, ΔR² is simply the proportion of the total variance of Y uniquely explained by the interaction term XZ. These traditional measures do not match the concept of moderation effect. Moreover, when the homoscedasticity assumption is violated, the results of testing b₃=0 under the MMR model are unreliable, and the resulting F, t, or Welch’s t tests following the LS method are unable to control type I and type II errors (Long & Ervin, 2000). A review conducted by Aguinis et al. (1999) shows that approximately 50% of the literature using the MMR model with LS analysis clearly violated the constant-variance assumption. In fact, violations appear to be most likely for the MMR model (Aguinis & Pierce, 1998).

Two-level moderated regression model

A two-level moderated regression (2MMR) model with single-level data was proposed by Yuan et al. (2014). The model can be defined hierarchically using three equations:

Level 1:

$$ \kern6.00em {Y}_i={b}_{i0}+{b}_{i1}{X}_i+{\varepsilon}_i; $$

(6)

Level 2:

$$ \kern6.00em {b}_{i0}={\gamma}_{00}+{\gamma}_{01}{Z}_i+{u}_{i0}, $$

(7)

$$ \kern6.00em {b}_{i1}={\gamma}_{10}+{\gamma}_{11}{Z}_i+{u}_{i1}, $$

(8)

where b_i0 and b_i1 can vary across individuals and the moderator Z accounts for their changes; γ₀₀, γ₀₁, γ₁₀, and γ₁₁ are regression coefficients. Plugging Eqs. (7) and (8) into Eq. (6) gives us the combined form of the 2MMR model

$$ {Y}_i={\gamma}_{00}+{\gamma}_{01}{Z}_i+\left({\gamma}_{10}+{\gamma}_{11}{Z}_i+{u}_{i1}\right){X}_i+{\delta}_i. $$

(9)

Since single-level data do not have a nested structure to provide information to distinguish the error term ε_i from the level-2 residual u_i0, we combine them into δ_i = ε_i + u_i0 and continue to use σ² to denote the variance of δ_i for convenience, i.e., $\left(\begin{array}{c}{\delta}_i\\ {}{u}_{i1}\end{array}\right)\sim N\left(\left(\begin{array}{c}0\\ {}0\end{array}\right),\left(\begin{array}{cc}{\sigma}^2& {\tau}_{01}\\ {}{\tau}_{10}& {\tau}_{11}\end{array}\right)\right)$. Although δ_i and u_i1 are not necessarily independent for the 2MMR model, we make such an assumption for more accurate variance-parameter estimates in practice (see Yuan et al., 2014). Equation (9) implies that Y_i has two components of error, u_i1X_i and δ_i. For a given value of X, the error variance is $Var\left({u}_{i1}{X}_i+{\delta}_i|{X}_i={x}_i\right)={x}_i^2{\tau}_{11}+2{x}_i{\tau}_{01}+{\sigma}^2$, which explicitly accounts for violation of homoscedasticity generated by the moderation effect in practice. It is a natural phenomenon in human development that individuals differ more as age, level of education, years of experience, or other chronological variables increase (Yuan et al., 2014). Nelson and Dannefer (1992) reviewed 185 gerontological studies and found that a majority of the studies presenting data reported increases in variability with age. Bast and Reitsma (1998) found that individuals differ more in reading as they become older. Therefore, it is common for the variance of the outcome variable to increase with the value of the predictor. The model in Eq. (9) can effectively account for such empirical heteroscedasticity, and the 2MMR model is also a natural translation of the moderation effect in Fig. 2a.

The 2MMR model also represents a direct translation of the conceptual model of moderation effect into a statistical model. The level-1 model describes the effect of X on Y with random intercepts b_i0 and regression coefficient b_i1 due to individual differences. The level-2 model describes the effects of the moderator variables Z_i on the first level random coefficients. The parameter γ₁₁ captures the moderation effects of Z_i on X→Y. The 2MMR model highlights the interpretation of the moderation effect, that is, how the “varying effect” of X on Y (i.e., b_i1) is influenced by the moderator variables Z_i (level 2). The 2MMR model implies that the effect of X on Y varies across individuals. It is also in line with the person-oriented method (Sterba & Bauer, 2010).

The percentage of the variance of b_i1 explained by Z is naturally evaluated by

$$ {\rho}^2=\frac{\gamma_{11}^2 Var\left({Z}_i\right)}{\gamma_{11}^2 Var\left({Z}_i\right)+{\tau}_{11}}, $$

(10)

which was formally defined by Yuan et al. (2014). This ρ² allows us to directly answer the question of the extent to which Z moderates the effect of X on Y.

Although moderation analysis can advance our understanding of the underlying processes being investigated, a simple moderation model is often insufficient to explain the complicated relationships among variables. There is an increasing demand for a more general theoretical framework that combines mediation and moderation into a single model. The most commonly used one is the moME model (Edwards & Lambert, 2007; Hayes, 2018; MacKinnon, 2008; Muller et al., 2005; Wang & Preacher, 2015), in which the mediating process depends on a moderator variable Z. In this article, we will develop measures to answer the question as to what extent the moderator variable Z explains the variation of the mediation effect of M on the relationship of X to Y across individuals.

Moderated mediation model and its effect size measure

Moderated mediation occurs when the strength of an indirect effect depends on the value of a moderator variable (Preacher et al., 2007). Because the indirect effect in Fig. 1 is the product of two effects (the effect of X on M, and the effect of M on Y controlling for X), if one of these effects is moderated, then so too is the indirect effect. Several models have been proposed corresponding to moME effects under different scenarios (Hayes, 2015; Preacher et al., 2007; Wang & Preacher, 2015). Figure 3 shows four common scenarios of moMEs: first stage (the path of X on M) moME model (Fig. 3a), second stage (the path of M on Y) moME model (Fig. 3b), first stage and second stage moME models by one common moderator variable (Fig. 3c) or by two different moderator variables (Fig. 3d). The focused moderated mediation effects under different scenarios are marked with the bolded paths in Fig. 3.

Fig. 3

Four scenarios of the moderated mediation models

Let us focus on the model in Fig. 3d, because the other scenarios can be regarded as special cases of this model. The model in 3d is conventionally expressed as:

$$ {M}_i={d}_{M0}+{d}_{M1}{Z}_{i1}+{a}_0{X}_i+{a}_1{X}_i{Z}_{i1}+{e}_{Mi}, $$

(11)

$$ {Y}_i={d}_{Y0}+{d}_{Y1}{Z}_{i1}+{d}_{Y2}{Z}_{i2}+{b}_0{M}_i+{b}_1{M}_i{Z}_{i2}+{c}_0{X}_i+{c}_1{X}_i{Z}_{i1}+{c}_2{X}_i{Z}_{i2}+{e}_{Yi}, $$

(12)

where e_Mi and e_Yi are assumed to be independent and follow normal distributions with means zero and constant variances. If Z₁ moderates the relationship X → M and/or Z₂ moderates the relationship M → Y, then moME occurs. The conditional indirect effect given Z₁ = z₁ and Z₂ = z₂ can be expressed as

$$ moME=\left({a}_0+{a}_1{z}_1\right)\left({b}_0+{b}_1{z}_2\right). $$

(13)

Thus, the difference between two conditional indirect effects is

$$ {dif}_{me}=\left({a}_0+{a}_1{z}_{11}\right)\left({b}_0+{b}_1{z}_{21}\right)-\left({a}_0+{a}_1{z}_{12}\right)\left({b}_0+{b}_1{z}_{22}\right), $$

(14)

where z₁₁ and z₁₂ are two values of Z₁, and z₂₁ and z₂₂ are two values of Z₂. In practice, to detect whether Z₁ and/or Z₂ moderate the mediation effect ab, we need to test whether the mediation effects vary across different values of Z₁ and Z₂. The null hypothesis of the test is H₀: dif_me = 0. Preacher et al. (2007) discussed how to estimate and test moME using methods including the Sobel test, the second-order delta method, and the bootstrap method. For scenarios represented by Fig. 3a and b, Hayes (2015) described a confidence interval approach to convey the uncertainty in estimating the association between the moderator and the indirect effect. However, estimating the coefficients a₀ and a₁, b₀ and b₁ in Eqs. (11) and (12) by the LS method or using the default option in a statistical package relies on the homoscedasticity assumption of e_Mi and e_Yi, respectively. Testing the difference between mediation effects under different sets of moderator values (i.e., H₀: dif_me = 0) also relies on the homoscedasticity assumption of e_Mi and e_Yi. Violating this assumption often results in an inflated type II error rate. Violations of homoscedasticity are common in practice (Aguinis & Pierce, 1998; Alexander & DeShon, 1994).

As for measures of moderated mediation effects, the difference between two conditional indirect effects dif_me in Eq. (14) can be used to quantify the change of mediation effect. But dif_me changes with the selected values of the moderator variables. Thus, dif_me is not a measure of the overall moME effect, but a value for checking the existence of moME effect. While the index of moderated mediation (i.e., a₁b₀ or a₀b₁ ) proposed by Hayes (2015) can be used to quantify the overall effect of moME, it only applies to scenarios represented by Fig. 3a or b. In particular, it measures the effect of the interaction term XZ₁ or MZ₂ on Y, rather than the extent Z₁ and/or Z₂ moderate the indirect effect of X→M→Y. Therefore, it does not match the concept of moderated mediation effect. In summary, even though researchers have been urged to report ESs to supplement the results of null hypothesis testing in conducting moME analysis, few such measures are available or they do not serve the purpose.

The present investigation

The current article has five goals: (1) to extend the two-level moderated regression model proposed by Yuan et al. (2014) to a two-level moderated mediation (2moME) model within the framework of structural equation modelling (SEM); (2) to develop ES measures for the moME effect by decomposing the total variance of mediation effect; (3) to estimate the parameters of the 2moME model and the ES measures of the indirect effect by the Bayesian method; (4) to evaluate the performance of the 2moME model and the proposed ES measures using a Monte Carlo simulation study; and (5) to illustrate the application of the proposed model and measures with a real dataset. In addition, pros and cons of the new model and the ES measures, as well as issues for further research will also be discussed.

Model formulation and definition of effect size measures

In this section, we first describe the formulation of the 2moME model; then we define several ES measures for evaluating the moME effect. We will consider four scenarios of moME corresponding to the conceptual models in Fig. 3. Because Scenarios A, B, and C become special cases of Scenario D when letting Z_i2 = 0, Z_i1 = 0, and Z_i1 = Z_i2 = Z_i, respectively (Wang & Preacher, 2015), we only present the development for Scenario D.

A two-level moderated mediation model

The 2moME model for Scenario D can be expressed by the following equations.

Level 1:

$$ {M}_i={d}_{Mi}+{a}_i{X}_i+{\varepsilon}_{Mi}, $$

(15)

$$ {Y}_i={d}_{Yi}+{b}_i{M}_i+{c}_i{X}_i+{\varepsilon}_{Yi}; $$

(16)

Level 2:

$$ {d}_{Mi}={\gamma}_{d_{M0}}+{\gamma}_{d_{M1}}{Z}_{i1}+{u}_{d_{Mi}}, $$

(17)

$$ {a}_i={\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}, $$

(18)

$$ {d}_{Yi}={\gamma}_{d_{Y0}}+{\gamma}_{d_{Y1}}{Z}_{i1}+{\gamma}_{d_{Y2}}{Z}_{i2}+{u}_{d_{Yi}}, $$

(19)

$$ {b}_i={\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}, $$

(20)

$$ {c}_i={\gamma}_{c_0}+{\gamma}_{c_1}{Z}_{i1}+{\gamma}_{c_2}{Z}_{i2}+{u}_{c_i}. $$

(21)

Due to the limitation with single level data, we cannot distinguish the level-1 error term ε_Yi from the level-2 error term ${u}_{d_{Yi}}$ nor the level-1 error term ε_Mi from the level-2 error term ${u}_{d_{Mi}}$. They are combined with ${e}_{Mi}={\varepsilon}_{Mi}+{u}_{d_{Mi}}$ and ${e}_{Yi}={\varepsilon}_{Yi}+{u}_{d_{Yi}}$. Note that the error terms e_Mi and e_Yi are respectively the left-over effects of M and Y in the process of moderated mediation, whereas the error terms ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ from the slopes are the residuals due to incomplete moderation effects or the sources for heteroscedastic variances conditional on X and (or) M. In the development, we assume that the error terms e_Mi, e_Yi, ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ are independent and follow normal distributions with ${e}_{Mi}\sim N\left(0,{\sigma}_{eM}^2\right)$, ${e}_{Yi}\sim N\left(0,{\sigma}_{eY}^2\right)$, ${u}_{a_i}\sim N\left(0,{\sigma}_{ua}^2\right)$, ${u}_{b_i}\sim N\left(0,{\sigma}_{ub}^2\right)$, ${u}_{c_i}\sim N\left(0,{\sigma}_{uc}^2\right)$. Note that the different error terms are not necessarily independent for the 2moME model in practice, but we use such an assumption for more accurate variance-parameter estimates with single level data (see Yuan et al., 2014). We will also assume that variables X, Z₁, and Z₂ are mean-centered in the following development.

Plugging Eqs. (17) and (18) into Eq. (15) gives us the combined form of the model for the mediator variable M:

$$ {M}_i={\gamma}_{d_{M0}}+{\gamma}_{d_{M1}}{Z}_{i1}+{u}_{d_{Mi}}+\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right){X}_i+{\varepsilon}_{Mi}. $$

(22)

Equation (22) implies that the effect of X on M varies across individuals in addition to depending on the value of Z₁. Conditional on X, the composite error, ${\zeta}_{Mi}={u}_{d_{Mi}}+{u}_{a_i}{X}_i+{\varepsilon}_{Mi}={u}_{a_i}{X}_i+{e}_{Mi}$, is heteroscedastic, that is,

$$ Var\left({\zeta}_{Mi}|{X}_i={x}_i\right)= Var\left({u}_{a_i}{X}_i+{e}_{Mi}|{X}_i={x}_i\right)={x}_i^2{\sigma}_{ua}^2+{\sigma}_{eM}^2. $$

(23)

Plugging Eqs. (19), (20), and (21) into Eq. (16) gives us the combined form of the model for the outcome variable Y:

$$ {\displaystyle \begin{array}{c}{Y}_i=\left({\gamma}_{d_{Y0}}+{\gamma}_{d_{Y1}}{Z}_{i1}+{\gamma}_{d_{Y2}}{Z}_{i2}+{u}_{d_{Yi}}\right)+\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right){M}_i\\ {}+\left({\gamma}_{c_0}+{\gamma}_{c_1}{Z}_{i1}+{\gamma}_{c_2}{Z}_{i2}+{u}_{c_i}\right){X}_i+{\varepsilon}_{Yi}.\end{array}} $$

(24)

Equation (24) implies that the effect of M on Y varies across individuals in addition to depending on the value of the moderator variable Z₂. Again, the composite error, ${\zeta}_{Yi}={u}_{d_{Yi}}+{u}_{b_i}{M}_i+{u}_{c_i}{X}_i+{\varepsilon}_{Yi}={u}_{b_i}{M}_i+{u}_{c_i}{X}_i+{e}_{Yi}$, has heteroscedastic variances conditional on X and M, that is,

$$ Var\left({\zeta}_{Yi}|{X}_i={x}_i,{M}_i={m}_i\right)={m}_i^2{\sigma}_{ub}^2+{x}_i^2{\sigma}_{uc}^2+{\sigma}_{eY}^2. $$

(25)

Similar to the advantages of the 2MMR model over the MMR model discussed in section 1.2, the models in Eqs. (22) and (24) better describe the empirical phenomena that the variance of the outcome variable typically increases with the value of the predictor than the models in Eqs. (11) and (12). In addition, the 2moME model is also a natural translation of the moME effect in Fig. 3d.

The 2moME model also represents a direct translation of the conceptual model of moME into a statistical model, which can be represented by the diagram in Fig. 4. The level-1 model describes the mediation effect of X on Y through M with random intercepts d_Mi, d_Yi and regression coefficients a_i, b_i, and c_i due to individual differences, and the coefficients a_i and b_i are the focus in moderated mediation analysis (the bolded paths in level 1). The level-2 model describes the effects of the moderator variables Z₁ and Z₂ on the first level random coefficients. The parameter γ_a1 captures the moderation effects of Z₁ on X→M, and the parameter γ_b1 captures the moderation effects of Z₂ on M→Y (the bolded paths in level 2). The 2moME model highlights the interpretation of different variables in moME analysis, that is, how the “varying mediation effect” (i.e., a_ib_i) of X on Y via M (level 1) is influenced by the moderator variables Z₁ and Z₂ (level 2). However, unlike the traditional multilevel model (e.g., Raudenbush & Bryk, 2002), the 2moME model does not require a nested data structure. In the 2moME model, the role of the variable determines its level in the model. In particular, X, M, Z₁, Z₂, and Y come from the same unit in the dataset, but in the 2moME analysis, the predictor, mediator, and outcome variables (i.e., X, M, and Y ) are in level 1, while the moderator variables (i.e., Z₁ and Z₂) are in level 2. In contrast, in the traditional multilevel model the level of a variable is determined by the unit (e.g., individual or cluster) it comes from. Thus, in terms of data structure and the scope of applicability, the 2moME model in Fig. 4 is different from the traditional multilevel model.

Fig. 4

A diagram of the two-level moderated mediation model

The main difference between the moME model and the 2moME model is that the later contains random terms ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ to account for individual differences. They are needed because the strengths of the regression relationships X → M, M → Y, and X → Y for different individuals are most likely different, and part of such differences can be accounted for by Z₁ and (or) Z₂. The model including individual differences automatically accounts for the heteroscedastic errors that are related to X and (or) M. The values of ${u}_{a_i}$ and ${u}_{b_i}$ represent the size of the residuals of the mediation effect after it is accounted for by the moderator variables Z₁ and Z₂ for the ith individual; the size of the level-2 residuals also suggests that there may be other moderator variables that are not included in the model in addition to the variables Z₁ and (or) Z₂. Thus, the 2moME model provides a more refined approach to modeling individual differences. But we should be aware that the variations at individual level are random effects instead of being estimable parameters, due to the limitation with single level data. However, we can estimate the fixed effects (i.e.,${\gamma}_{d_{M0}},{\gamma}_{d_{M1}},{\gamma}_{d_{Y0}},{\gamma}_{d_{Y1}},{\gamma}_{d_{Y2}},{\gamma}_{a_0},{\gamma}_{a_1},{\gamma}_{b_0},$ ${\gamma}_{b_1},{\gamma}_{c_0},{\gamma}_{c_1},{\gamma}_{c_2}$) and the variance of ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ (Yuan et al., 2014).

It follows from Eqs. (22) and (24) that the indirect effect based on the 2moME model is given by

$$ {IND}_i={a}_i{b}_i=\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right). $$

(26)

Equation (26) implies that the mediation effect of X on Y via M also varies across individuals, and the mediation effect is moderated by both the stage one (X→M) moderator variable Z₁ and the stage two (M→Y) moderator variable Z₂. For mean-centered variables Z₁ and Z₂, the expected value or the mean of a_ib_i is (Goodman, 1960, p.712)

$$ E\left({IND}_i\right)=E\left({a}_i{b}_i\right)=E\left({a}_i\right)E\left({b}_i\right)+ Cov\left({a}_i,{b}_i\right)={\gamma}_{a_0}{\gamma}_{b_0}+{\gamma}_{a_1}{\gamma}_{b_1} Cov\left({Z}_{i1},{Z}_{i2}\right). $$

(27)

It is clear that the conventional moME model is a special case of the 2moME model when ${u}_{a_i}=0$, ${u}_{b_i}=0$, and ${u}_{c_i}=0$. In practice, to check ${\sigma}_{ua}^2=0$, ${\sigma}_{ub}^2=0$, or ${\sigma}_{uc}^2=0$, we can use a Wald test (or Z-test) following normal-distribution-based maximum likelihood (see Yuan et al., 2014), or the Bayes Factor (BF; Verhagen & Fox, 2012), and Deviance Information Criteria (DIC; Spiegelhalter et al., 2002; Cain & Zhang, 2019) in the framework of Bayesian estimation that we will discuss further in the empirical example section. If all the estimates of the variances are not statistically significant², the conventional moME model will be preferred for parsimony. Otherwise, Eq. (26) provides a more accurate description of moderated mediation.

Effect size measures of moderated mediation

In this subsection, we define several measures of ESs to quantify the extent to which the moderator variables explain the variance of the indirect effect in Eq. (26).

For the convenience of presentation and explanation, let

Then,

(28)

Appendix A contains a detailed derivation of this equation.

The term ➀ is the moME variance due to the first stage moderator Z₁ on X→M alone; the term ➁ is the moME variance due to the second stage moderator Z₂ on M→Y alone; the term ➂ is the moME variance due to the first stage moderator variable Z₁ on X→M interactively with the second stage moderator variable Z₂ on M→Y; the term ➃ is the moME effect due to the covariances between Z₁ and Z₂, Z₁ and Z₁Z₂, Z₂ and Z₁Z₂; the term ➄ is the unexplained variance of the mediation effect, including the residual variance of the unexplained effect of X→M and the residual variance of the unexplained effect of M→Y.

The percentage of variance collectively accounted by the moderator variables Z₁ and Z₂ is measured by

(29)

which is the total moderated mediation ES by the moderator variables Z₁ and Z₂.

After controlling for Z₂, the ratio³ of the explained variance of a_ib_i by Z₁ alone to the total variance of a_ib_i is given by

(30)

which measures the first stage moME effect by Z₁ on X→M. Similarly, after controlling for Z₁, the ratio of the explained variance of a_ib_i by Z₂ alone to the total variance of a_ib_i is evaluated by

(31)

which measures the second stage moME effect by Z₂ on M→Y.

Note that the stage one coefficient a_i of X→M is moderated by Z₁, and stage two coefficient b_i of M→Y is moderated by Z₂. The ratio of the explained variance by Z₁Z₂ to the total variance of a_ib_i is given by

(32)

If we are interested in the proportions of the model-explained variance of the mediation effect a_ib_i contributed by different parts, then the unexplained variance (the part denoted by ➄) can be removed from the denominators of Eqs. (30)-(32), resulting in their fixed-effect versions

(33)

(34)

(35)

where the superscript (f) is to indicate that these ratios are for fixed effect. Equations (33) to (35) measure the proportions (or ratios) of the model-explained moME variance of a_ib_i attributed to Z₁ alone (the first stage moME), Z₂ alone (the second stage moME), and Z₁ and Z₂ interactively, respectively.

When ${\sigma}_{ua}^2$=${\sigma}_{ub}^2$=${\sigma}_{uc}^2$=0, then the homoscedasticity assumptions on e_Mi and e_Yi hold, and the model specified by Eqs. (15) to (21) become the conventional moME model. The measures defined in Eqs. (30)-(32) automatically become those in Eqs. (33)-(35). Thus, the three measures defined in Eqs. (33) to (35) are applicable to both the conventional moME and the 2moME models. In practice, we should decide which model is preferred by trade-off between goodness of fit with data and model complexity.

In operation, we recommend mean-centering X, M, Z₁, and Z₂ prior to conducting the 2moME analysis. The advantages and disadvantages of centering variables in moME analysis are similar to those in the analysis of the MMR model, which have been discussed in details by Dalal and Zickar (2012). The main reason for mean-centering is that it can remove the nonessential multicollinearity between the interaction terms and their constituent variables, and increase the interpretability of the coefficients by giving a meaningful zero-points of X, M, Z₁, and Z₂. From the perspective of variance decomposition, reducing the correlations among Z₁, Z₂, and Z₁Z₂ enhances the interpretability of the moderated mediation effect.

Moderated mediation measures for special cases

As noted earlier, Scenarios A, B, and C are special cases of Scenario D. Thus, the measures defined in the previous subsection also apply to these scenarios. This subsection describes the simplified forms for these special cases.

For Scenario C, Z_i1 = Z_i2 = Z_i, then

Parallel to those in Scenario D, the φs and ${\varphi}_s^{(f)}$ under Scenario C are defined as in Eqs. (29) to (35).

For Scenario A, Z_i1 = Z_i, Z_i2 = 0, and ${\sigma}_{ub}^2=0$, so only the first stage moME exists in the model. The formulations of ➀ to ➄ are simplified to ➀$={\gamma}_{a_1}^2{\gamma}_{b_0}^2 Var\left({Z}_i\right)$, ➁=0, ➂=0, ➃=0, and ➄$={\gamma}_{b_0}^2{\sigma}_{ua}^2$. Thus,

(36)

which measures the variance of moME attributed to the moderator Z_i (first stage moME).

For Scenario B, Z_i1 = 0, Z_i2 = Z_i, and ${\sigma}_{ua}^2=0$, only the second stage moME exists in the model. The formulations of ➀ to ➄ are simplified to ➀=0, ➁$={\gamma}_{a_0}^2{\gamma}_{b_1}^2 Var\left({Z}_1\right)$, ➂=0, ➃=0, and ➄$={\upgamma}_{a_0}^2{\sigma}_{ub}^2$. Consequently,

(37)

which measures the variance of moME attributed to the moderator Z_i (second stage moME).

It is worth noting that for Scenarios A and B, there is only one non-null term, ${\gamma}_{a_1}^2{\gamma}_{b_0}^2 Var\left({Z}_i\right)$ or ${\gamma}_{a_0}^2{\gamma}_{b_1}^2 Var\left({Z}_i\right)$, to describe the explained moME variance. Also, there is only one non-null residual term, ${\gamma}_{b_0}^2{\sigma}_{ua}^2$ or ${\gamma}_{a_0}^2{\sigma}_{ub}^2$, to describe the unexplained moME variance. In these cases, ${\varphi}_1^{(f)}$ or ${\varphi}_2^{(f)}$ is always 1, which means that the explained variance of the mediation effect is only attributed to the single moderator Z.

It can be seen from the denominators of Eqs. (29) to (35) that the new measures focus on the variance of the mediation effect a_ib_i or the explained variance of the mediation effect a_ib_i. Each measure captures the variance of X→M→Y and closely matches the conceptual model of moderated mediation analysis. Therefore, the new measures allow us to answer the question regarding the extent to which the moderator variable (Z) moderates the indirect effect of X on Y via the mediator variable (M) in the moME models.

Bayesian estimation

We describe how to estimate the 2moME model in this section. Wang and Preacher (2015) studied the conventional moME model for estimating the conditional indirect effects in Eqs. (11) and (12). They showed that the Bayesian method with diffuse (vague) priors yielded unbiased estimates and higher power than both maximum likelihood (ML) with delta-method standard errors and ML with bootstrap percentile confidence intervals, and its power was comparable to the ML method with bootstrap bias-corrected confidence intervals. The Bayesian method is more flexible and feasible in estimating more complex models than ML. It also provides a natural and principled way of including prior information, which will improve estimation efficiency and accuracy, especially for small samples (Zondervan-Zwijnenburg et al., 2017). Thus, we will use the Bayesian method to estimate the 2moME model, and also the conventional moME model for fair comparison.

In the Bayesian framework, model parameters θ are treated as random variables, which have a joint prior distribution with a density function p(θ). With the observed data and the prior distribution, Bayesian inference can be derived from the posterior distribution of parameters p(θ| data) (Song & Lee, 2012). In our study of the 2moME model, the vector

$$ \boldsymbol{\theta} =\left({\gamma}_{d_{M0}},{\gamma}_{d_{M1}},{\gamma}_{d_{Y0}},{\gamma}_{d_{Y1}},{\gamma}_{d_{Y2}},{\gamma}_{a_0},{\gamma}_{a_1},{\gamma}_{b_0},{\gamma}_{b_1},{\gamma}_{c_0},{\gamma}_{c_1},{\gamma}_{c_2},{\sigma}_{eM}^2,{\sigma}_{eY}^2,{\sigma}_{ua}^2,{\sigma}_{ub}^2,{\sigma}_{uc}^2\right)^{\prime }, $$

contains parameters in Eqs. (15) to (21) and the data represent all observed information on X, M, Y, Z₁, and Z₂. Based on the Bayes’ theorem, the posterior distribution of the parameters is proportional to the product of the likelihood function and the density function of the prior distribution,

$$ p\left(\boldsymbol{\theta} | data\right)\propto p\left( data|\boldsymbol{\theta} \right)\times p\left(\boldsymbol{\theta} \right) $$

where p(data| θ) is the likelihood function, which is the probability density of the observed data conditional on the parameter vector θ.

In selecting a prior distribution for θ, it is desirable that the resulting posterior distribution has a convenient form so that it is relatively easy to simulate random values that follow p(θ| data). Based on the recommendations and suggestions in the Bayesian SEM literature (Song & Lee, 2012; Wang & Preacher, 2015), independent normal priors for the regression coefficients $\boldsymbol{\gamma} =\left({\gamma}_{d_{M0}},{\gamma}_{d_{M1}},{\gamma}_{d_{Y0}},{\gamma}_{d_{Y1}},{\gamma}_{d_{Y2}},{\gamma}_{a_0},{\gamma}_{a_1},{\gamma}_{b_0},{\gamma}_{b_1},{\gamma}_{c_0},{\gamma}_{c_1},{\gamma}_{c_2}\right)^{\prime }$ and independent inverse gamma priors for the variance parameters ${\boldsymbol{\sigma}}^{\mathbf{2}}={\left({\sigma}_{eM}^2,{\sigma}_{eY}^2,{\sigma}_{ua}^2,{\sigma}_{ub}^2,{\sigma}_{uc}^2\right)}^{\prime }$ are used. These priors are semi-conjugate (Gelman et al., 2004) and most frequently used in Bayesian regression analysis. But we should notice that the Bayesian method itself does not tell us how to select an appropriate prior. Bayesian inferences require skills to translate subjective prior beliefs into a mathematically formulated prior. Cautions are needed in formulating the priors to avoid misleading results.

After specifying the model and the priors, the sampling-based Markov Chain Monte Carlo (MCMC) techniques can be used to estimate the posterior distributions of the model parameters (Gilks et al., 1996). One popular MCMC method is Gibbs sampling, which iteratively draws samples from the full conditional distributions of all the parameters. For each parameter in the model, we use the Gelman–Rubin potential scale reduction (PSR) statistic for checking the convergence of Gibbs sampling. According to Brooks and Gelman (1998), convergence is achieved if the PSR statistic is less than 1.05. For converged samples, we define the Bayesian estimate of θ as the mean of the posterior distribution of θ (called the posterior mean), and the posterior standard deviation is obtained using the standard deviation of the converged samples. The 95% CI is obtained based on the empirical 2.5% and 97.5% quantiles of the sample values for each parameter in θ.

In this study, the process of Gibbs sampling is as follows.

• (1) Sampling the model parameters from the full conditional distributions. For the 2moME model, draw samples of γ_a1 from $p\left({\gamma}_{a1}|{\gamma}_{d_{M0}},{\gamma}_{d_{M1}},{\gamma}_{a_0},{\sigma}_{eM}^2,{\sigma}_{ua}^2,\mathrm{data}\right)$ and γ_b1 from $p\left({\gamma}_{b_1}|{\gamma}_{d_{Y0}},{\gamma}_{d_{Y1}},{\gamma}_{d_{Y2}},{\gamma}_{b_0},{\gamma}_{c_0},{\gamma}_{c_1},{\gamma}_{c_2},{\sigma}_{eY}^2,{\sigma}_{ub}^2,{\sigma}_{uc}^2,\mathrm{data}\right)$. Note that γ_a1 is in the regression model with the mediator variable as the dependent variable, while γ_b1 is in the regression model with the outcome variable as the dependent variable (see Eqs. 15 to 24). Parallel to γ_a1 and γ_b1, other parameters are drawn subsequently and iteratively until convergence.

• (2) Compute and test the moME effect for the given values of the moderator variable(s). With Z₁ = z₁ and Z₂ = z₂ given, we can compute the conditional indirect effect (γ_moME) according to Eq. (13) using the corresponding estimated parameters from either the 2moME model or the conventional moME model. Then, the difference between mediation effects (dif_me) under different sets of moderator values (e.g., Z₁ = z₁₁, Z₂ = z₂₁ versus Z₁ = z₁₂, Z₂ = z₂₂) is computed by Eq. (14). Using Bayesian methods, we can obtain point estimates and credibility intervals (CIs) for γ_moME and dif_me as well as conduct the tests for H₀ : γ_moME = 0 and H₀ : dif_me = 0. The test for H₀ : dif_me = 0 shows whether the mediation effect varies across two sets of moderator values.

• (3) Compute the effect sizes of moME. For evaluating the ESs of moME, appropriate φs and φ^(f)s should be selected from Eqs. (29) to (35) based on the research questions of interest and the specific model. We can also obtain point estimates and the corresponding CIs of the ESs to measure the proportions (or ratios) of mediation variances attributed to different moderator variables at different stages.

Simulation study

A simulation study was conducted to (i) compare the performance of the 2moME model against that of the conventional moME model, and (ii) examine the performance of Bayesian methods in estimating and testing the moME effects and the corresponding ESs under different conditions.

Design

We also just consider Scenario D in the simulation study. For simplicity and without loss of generality, the intercepts ${\gamma}_{d_{M0}}$ and ${\gamma}_{d_{Y0}}$ for the 2moME model in Eqs. (15) to (21) are set to 0. The coefficients ${\gamma}_{d_{M1}}$, ${\gamma}_{d_{Y1}}$, ${\gamma}_{d_{Y2}}$, ${\gamma}_{a_0}$, ${\gamma}_{b_0}$ are all set at 0.4. In addition, we let ${\gamma}_{c_0}={\gamma}_{c_1}={\gamma}_{c_2}=0$ because the coefficients associated with the direct effect are not the focus of moME. All the predictor and moderator variables X, Z₁, and Z₂, and the error terms, ${e}_{Mi}={\varepsilon}_{Mi}+{u}_{d_{Mi}}$, ${e}_{Yi}={\varepsilon}_{Yi}+{u}_{d_{Yi}}$ are normally distributed with zero means and unit variances. The correlations between X, Z₁, and Z₂ are set to 0.3.

The conditions manipulated in our design include: (1) three levels of the coefficients ${\gamma}_{a_1}$ and ${\gamma}_{b_1}$ (0, 0.2, and 0.4, where ${\gamma}_{a_1}={\gamma}_{b_1}$) that determine the size of the moderation effects, (2) four levels of the moderation-residual variances ${\sigma}_{ua}^2$, ${\sigma}_{ub}^2$, and ${\sigma}_{uc}^2$ (0, 0.1, 0.25, and 0.5, where ${\sigma}_{ua}^2={\sigma}_{ub}^2={\sigma}_{uc}^2$), (3) five levels of sample size (50, 100, 200, 500, and 1000). The values of the population ES under different measures corresponding to these conditions are reported in Tables 2 and 3. Note that homoscedasticity holds under the condition ${\sigma}_{ua}^2={\sigma}_{ub}^2={\sigma}_{uc}^2=0$, which gives the conventional moME model a theoretical advantage over the 2moME model. For all the conditions with ${\sigma}_{ua}^2={\sigma}_{ub}^2={\sigma}_{uc}^2=0$, we have ${\varphi}_1={\varphi}_1^{(f)}$, ${\varphi}_2={\varphi}_2^{(f)},$ and ${\varphi}_{12}={\varphi}_{12}^{(f)}$. The conditions on moderation ES, moderation-residual variance, and sample size are crossed, and 1000 replications are used under each of the 60 conditions. Data are simulated using R (R Core Team, 2016) based on the model shown in Eqs. (15) to (21). For the conditions of ${\sigma}_{ua}^2={\sigma}_{ub}^2={\sigma}_{uc}^2=0$, data are generated based on the conventional moME model, whereas for the conditions of ${\sigma}_{ua}^2={\sigma}_{ub}^2={\sigma}_{uc}^2=0.1,0.25,0.5$, data are generated based on the 2moME model.

Analysis

For the 2moME model, Bayesian estimations are conducted in Mplus 8.3 (Asparouhov & Muthén, 2019; Muthén & Asparouhov, 2012). In order to estimate the 2moME model with single-level data, we “trick” the software by including a cluster variable that has only one individual in each cluster. Thus, the cluster variable is essentially the individual’s ID. The default prior distributions are adopted. Three MCMC chains are applied, and convergence is regarded as being achieved if the PSR value is less than 1.05. After 10,000 burn-in iterations, the parameter estimates are obtained using 10,000 simulated observations. In this article, the parameters of interest include the conditional indirect effect γ_moME and dif_moME. We used Z₁ = 1 and Z₂ = 1 to evaluate the estimated results of γ_moME, and Z₁ = 1 and Z₂ = 1 versus Z₁ =  − 1 and Z₂ =  − 1 to compute and test dif_moME = 0. The population values of all interested parameters under different conditions are included in Tables A1 to A9 of the supplementary material (www3.nd.edu/~kyuan/2moME).

To compare the difference between the conventional moME model and the 2moME model, both are applied to analyzing the data under each condition. Five measures, the bias, the mean square error (MSE), the coverage rate of the 95% nominal CI, the power, and the type I error rate, are used to evaluate the performance of the two models in estimating and testing γ_moME and dif_moME. Similarly, bias, MSE, and coverage rate of the 95% nominal CI are used to evaluate the performances of the two models in estimating ESs.

Let $\overline{\theta}={\sum}_{r=1}^R{\hat{\theta}}_r/R$ be the average of the parameter estimates across R=1000 replications, with ${\hat{\theta}}_r$ being the estimate in the r-th replication. Bias is computed as the difference between the average and its corresponding population value, i.e.,

$$ Bias\left(\hat{\theta}\right)=\overline{\theta}-{\theta}_0, $$

(38)

and MSE is the average of the squared deviation of each parameter estimate from the corresponding population value, i.e.,

$$ MSE\left(\hat{\theta}\right)=\frac{\sum_{r=1}^R{\left({\hat{\theta}}_r-{\theta}_0\right)}^2}{R}. $$

(39)

The coverage rate is the proportion for the CI to contain the population value of the parameter across R=1000 replications. The estimation procedure is more reliable if the coverage rate is closer to 95%. The values of power are calculated as the proportion of the times that the CI does not contain zero across the replications within each condition that the population moME exists. The type I error rate is calculated in the same way as calculating the value of power but for conditions with zero population moME effect, and the nominal rate is set at 5%.

Results

Accuracy in estimating γ_moME and dif_moME

Since the results in estimating γ_moME and dif_moME are about the same, only those for estimating dif_moME are presented to save space. The results of γ_moME can be downloaded at www3.nd.edu/~kyuan/2moME/SupplementaryA.pdf.

For the estimation of dif_moME, the values of the empirical bias, MSE, coverage rate of the 95% confidence interval, and rejection rate (power or type I error) for testing dif_moME = 0 by the conventional moME model and the 2moME model are reported in Table 1. Overall, the size of bias is small for the two models. When the level-2 error variances are zero (i.e., the conventional moME model is literally correct, see Eqs. 16 to 20) and the sample size is small, the values of MSE following the 2moME model are slightly larger than those following the conventional moME model. Even when the conventional moME model is literally correct, the difference between the two models can be ignored with the increase of sample size. However, for all the conditions when the moderation-residual variances are nonzero, the 2moME model yields more accurate estimates for dif_moME than the conventional moME model does. The advantages of the 2moME model over the conventional moME model become more obvious as the moderation-residual variances increase.

Table 1 Empirical bias, mean square error (MSE), coverage rate of the 95% CI, and rejection rate in estimating dif_moME

The results of the coverage rate of the 95% CI for dif_moME indicate that 2moME outperforms the conventional moME model when the moderation-residual variance is nonzero, which is consistent with the results of MSE. Moreover, there is little difference between the two models when homoscedasticity assumption is met.

The results of type I error rate indicate that 2moME controls type I error rather well, as the rates are close to 0.05 or below 0.05 under all the conditions. However, the type I error rates following the conventional moME model tend to be higher than 0.05 when the moderation-residual variance is nonzero.

The results in Table 1 indicate that the power of each model in testing dif_moME = 0 is clearly affected by the population value of the moderation effect and the sample size. The value of the power increases as the magnitude of dif_moME and/or sample size increase. The values of power following the conventional moME and 2moME models are comparable for medium to large sample sizes (n=200, 500, or 1000), or when there is a large difference in mediation effects due to the moderators (e.g., dif_moME = 0.64). While the value of power following the conventional moME model is slightly higher than that following the 2moME model at a small sample size, this result is mostly due to the inflated type I error rate of the conventional moME model.

In summary, the 2moME model yields more accurate estimate of dif_moME and the corresponding coverage rate of the 95% CI is higher in conditions with nonzero moderation-residual variance. Under the conditions of homoscedasticity, there is no difference in the results between the two models. The tests for dif_moME = 0 following 2moME perform well in controlling the type I error rate, whereas the type I error rate following the conventional moME model becomes more inflated as the value of moderation-residual variance increases.

Accuracy in estimating ESs

When moME exists in the population (${\gamma}_{a_1}={\gamma}_{b_1}=$0.2 or 0.4), the measures ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)},$ and ${\varphi}_{12}^{(f)}$ in Eqs. (33)-(35) were estimated under both the conventional moME and the 2moME models. When the moderation-residual variance is not zero, the φ, φ₁, φ₂, and φ₁₂ are estimated only for the 2moME model using Eqs. (29)–(32). Because the results for these measures exhibit essentially the same patterns, only the results for estimating ${\varphi}_1^{(f)}$ and φ₁ are presented. For the results of the other measures please refer to the supplementary material (www3.nd.edu/~kyuan/2moME/SupplementaryA.pdf).

The estimates of ${\varphi}_1^{(f)}$ under the two models are reported in Table 2. The results indicate that larger sample sizes and smaller moderation-residual variances correspond to more accurate estimates of ${\varphi}_1^{(f)}$. Medium to large sample sizes (e.g., more than 200) are required to obtain estimates of ${\varphi}_1^{(f)}$ with little bias. The results also indicate that, when the homoscedasticity assumption of the conventional moME model is satisfied, the ES estimates following the two models are about the same when sample size is large. However, when the moderation-residual variance is not zero, the results following the 2moME model are more accurate than those following the conventional moME model. Moreover, as the moderation-residual variance increases, the advantages of 2moME become more obvious. Specifically, the MSEs of the ES estimates under the 2moME model are smaller than those under the conventional moME model, and the coverage rates for the population ESs by the 95% CI under 2moME are higher than those under the conventional moME model, especially when the moderation-residual variance is large. Similar results are obtained for the other two measures ${\varphi}_2^{(f)}$ and ${\varphi}_{12}^{(f)}$, as presented in the supplementary material.

Table 2 Empirical bias, mean square error (MSE), and coverage rate by the 95% CI in estimating ${\varphi}_1^{(f)}$

The empirical results for estimating φ₁ under 2moME are given in Table 3. Because φ₁ is defined under heteroscedasticity, only the results when moderation-residual variances are not 0 are displayed. It can be seen from Table 3 that the values of bias and MSE are small under all conditions. In addition, the coverage rates of the 95% CI are all close to 95%. As the moderation-residual variance and the sample size increase, the estimate ${\hat{\varphi}}_1$ becomes more accurate. Even when the moderation-residual variances are small, medium to larger sample sizes (e.g., more than 200) can also result in an estimate of φ₁ with little bias. Similar results are obtained for the estimates $\hat{\varphi}$, ${\hat{\varphi}}_2$, and ${\hat{\varphi}}_{12}$, as presented in the supplementary material.

Table 3 Empirical bias, mean square error (MSE), and coverage rate of the 95% CI in estimating φ₁

An empirical example

In this section, we present an empirical example to illustrate the application of the 2moME model and the new measures of ES.

Data and model

The data for our example are from the Program for International Student Assessment (PISA), which is a worldwide study conducted by the Organization for Economic Cooperation and Development (OECD). The program started in the year 2000 and is repeated every three years. The main purpose of the program is to measure the mathematics, science, and reading performance of 15-year-old students. The PISA test includes questionnaires for students, school principals, and parents. The student questionnaire is used to collect information regarding students' background, educational improvement, and their perception of teachers and the school syllabus, as well as their psychological well-being. The dataset can be downloaded at http://www.oecd.org/pisa/. For illustrating the application of the new ESs, we select a subsample of the Hong Kong dataset, with 743 students, from PISA2018.

Five variables with this dataset are: students’ reading performance (READ); self-concept of reading (SCREAD); economic, social, and cultural status (ESCS); parents' emotional support perceived by student (EMOSUP); and teacher's stimulation of reading engagement perceived by student (TSREAD). It was hypothesized that students with a higher ESCS status will have a higher reading performance and the effect of ESCS on READ will be mediated by SCREAD. Furthermore, it was hypothesized that EMOSUP will moderate the effect of ESCS on SCREAD (i.e., the first-stage of the mediation effect); TSREAD will moderate the effect of SCREAD on READ (i.e., the second-stage of the mediation effect); both EMOSUP and TSREAD will moderate the effect of ESCS on READ. Thus, the mediation effect of ESCS on READ via SCREAD will be conditional on EMOSUP and TSREAD. Figure 5 shows the conceptual model of the moME effects, and we will use the 2moME model to estimate the effects. Meanwhile, the conventional moME model will also be used for comparison purposes. Both models are estimated by the Bayesian estimation procedure described in section 3 and by using Mplus8.3 (Muthén & Muthén, 1998–2017). The data, the code, and the output of fitting the model are provided in the online supplementary material (www3.nd.edu/~kyuan/2moME/example/).

Fig. 5

The moderated mediation model with the empirical example. Note. ESCS = economic, social, and cultural status; EMOSUP = parents' emotional support perceived by student; SCREAD = self-concept of reading; TSREAD = teacher's stimulation of reading engagement perceived by student; READ = reading performance

Results

As for the simulation study in the previous section, three chains are used with the MCMC method in the analysis of the empirical dataset. After 10,000 burn-in iterations, the PSR values of parameters in the moME and 2meMO models are all less than 1.05, which supports that the sets of iterations from each of the three chains are close to the target distribution (Brooks & Gelman, 1998). Trace plots for the convergence of the chains for the 17 parameters of the 2moME model are provided as supplementary material (www3.nd.edu/~kyuan/2moME/example/TracePlot.pdf). The plots show that the values of the parameters converge to the same posterior distribution while they vary because of randomness.

To determine a better model between the conventional moME and 2moME for the sample from PISA2018, the significance of the residual variances of ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ (i.e., ${\sigma}_{ua}^2=0$, ${\sigma}_{ub}^2=0$, and ${\sigma}_{uc}^2=0$) are tested via BF (Bayes factor), and the two models are also compared by the Deviance Information Criteria (DIC) (Verhagen & Fox, 2012). Note that testing a variance parameter equal to 0 involves nonstandard procedures because it implies that the parameter lies on the boundary of the permissible space. The classical procedures can break down asymptotically (e.g., likelihood ratio test, Wald test) or require modified asymptotic null distributions (e.g., generalized likelihood ratio tests). These modified distributions are complicated and difficult to apply (e.g., Molenberghs & Verbeke, 2007; Pauler et al., 1999). In the Bayesian framework, the null hypothesis σ² = 0 can be substituted by σ² < 0.01. Then the significance of the residual variances can be tested by an encompassing prior approach (Hoijtink, 2011; Klugkist & Hoijtink, 2007; Klugkist, 2008; Wagenmakers et al., 2010). That is, estimations for the 2moME model were done in two steps: 1) estimate the 2moME model with the default non-informative priors (H₁); 2) in a separate run estimate the model with IG(1, δ) as priors for ${\sigma}_{ua}^2$, ${\sigma}_{ub}^2$, and ${\sigma}_{uc}^2$, where δ is close to zero (H₀). The Bayes factor is computed as the ratio of the marginal likelihood under the hypothesis H₀ to the marginal likelihood under H₁. BF > 3 indicates that the variance of the residual can be regarded as zero (Asparouhov & Muthén, 2012; Verhagen & Fox, 2012). In this example, the Bayes factors for a δ-value of 0.05 are 0.000, 0.000, and 0.876 for testing the hypotheses ${\sigma}_{ua}^2$=0, ${\sigma}_{ub}^2$=0, and ${\sigma}_{uc}^2$=0, respectively; and the corresponding posterior probabilities of P(H₀| data) are 0.000, 0.000, and 0.467. These results show that ${\sigma}_{ua}^2$, ${\sigma}_{ub}^2$, and ${\sigma}_{uc}^2$ cannot be regarded as zero at the level of 0.01 (Asparouhov & Muthén, 2012). In addition, the values of the DIC for the 2moME and the conventional moME models are respectively 3690.69 and 3825.88, indicating that 2moME has a better fit than the conventional moME. Therefore, it can be concluded that the 2moME model is more appropriate than the conventional moME model in fitting the PISA2018 sample.

Table 4 contains the parameter estimates and their posterior standard deviations (SDs) by the conventional moME and 2moME models. The results indicate that both the effects of ESCS on SCREAD (${\hat{\gamma}}_{a0}$=0.112, SD=0.035 under the conventional moME model and ${\hat{\gamma}}_{a0}$=0.081, SD=0.040 under the 2moME model) and SCREAD on READ (${\hat{\gamma}}_{b0}$=0.190, SD=0.036 under the conventional moME model and ${\hat{\gamma}}_{b0}$=0.212, SD=0.041 under the 2moME model) are statistically significant. EMOSUP significantly moderates the effect of ESCS on SCREAD (${\hat{\gamma}}_{a1}$=0.185, SD=0.039 under the conventional moME model and ${\hat{\gamma}}_{a1}$=0.176, SD=0.045 under the 2moME model); TSREAD significantly moderates the effect of SCREAD on READ (${\hat{\gamma}}_{b1}$= -0.100, SD=0.031 under the conventional moME model and ${\hat{\gamma}}_{b1}$= -0.130, SD=0.038 under the 2moME model). Students with a higher ESCS status have a higher reading performance (${\hat{\gamma}}_{c0}$= 0.093, SD=0.034 under the conventional moME model and ${\hat{\gamma}}_{c0}$= 0.080, SD=0.036 under the 2moME model). But EMOSUP and TSREAD do not significantly moderate the direct effect of ESCS on READ. In addition, the residual variances of SCREAD and READ from the conventional moME model (${\hat{\sigma}}_{eM}^2=0.796,$SD=0.042; ${\hat{\sigma}}_{eY}^2=0.735,$SD=0.038) are different than those from the 2moME model (${\hat{\sigma}}_{eM}^2=0.648,$SD=0.048; ${\hat{\sigma}}_{eY}^2=0.510,$SD=0.045), due to different working assumptions. In summary, the estimates following the two models are different, especially for the residual variances, although results of statistical tests on parameter estimates are consistent.

Table 4 Parameter estimates and their standard deviations by different models for a dataset from PISA2018

Table 5 presents the estimates of two conditional indirect effects (i.e., moME₁ and moME₂), their difference (i.e., dif_mo), and the estimates of seven ES measures (i.e., φ, φ₁, φ₂, φ₁₂, ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)}$, and ${\varphi}_{12}^{(f)}$). Fine histograms for the posterior distributions of these estimates are also provided at www3.nd.edu/~kyuan/2moME/example/BayesianPosterior.pdf. The results show that the conditional mediation effect at EMOSUP = mean+SD and TSREAD = mean-SD is statistically significant (moME₁ =0.074, SD=0.022), whereas the conditional mediation effect at EMOSUP= mean-SD and TSREAD= mean+SD is not statistically significant (moME₂ =-0.006, SD=0.007). The two conditional mediation effects are significantly different (dif_me=0.080, SD=0.023). Thus, while these results endorse the existence of the moderated mediation effect, we should note that, as the value of the conditional mediation effect depends on the values of the moderator variables, so does the value of dif_me. This is because dif_me is not a measure of the overall effect of the moderator variables on the mediation effect.

Table 5 Estimations of effect sizes, two conditional indirect effects, and the difference between conditional indirect effects for a dataset from PISA2018

Note that the total variance of READ is 0.782, and the total variance of indirect effect is 0.047. The $\hat{\varphi}$is only 3.9%, which is the percentage of the total variance of the indirect effect (0.047) collectively accounted for by the moderator variables EMOSUP and TSREAD. After controlling the effect of the second stage moderator variable TSREAD, ${\hat{\varphi}}_1=0.030$ is the proportion of the total variance of the indirect effect explained by the first stage moderator variable EMOSUP; after controlling the effect of the first stage moderator variable EMOSUP, ${\hat{\varphi}}_2=0.003$ is the the proportion of the total variance of the indirect effect explained by the second stage moderator variable TSREAD; and the ratio of the explained variance by EMOSUP×TSREAD to the total variance of a_ib_i is ${\hat{\varphi}}_{12}=0.014$. Recall that $Var\Big[\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{1i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{2i}\right)$] is the total explained variance of the indirect effect and its value is 0.002. After controlling the effect of TSREAD (the second stage moderator), ${\hat{\varphi}}_1^{(f)}=0.757$ is the proportion of the total explained variance accounted for by EMOSUP (the first stage moderator); after controlling the effect of EMOSUP (the first stage moderator variable), ${\hat{\varphi}}_2^{(f)}=0.102$ is the proportion of the total explained variance accounted for by TSREAD (the second stage moderator variable); and the ratio of the explained variance by EMOSUP×TSREAD to the total explained variance by EMOSUP and TSREAD is ${\hat{\varphi}}_{12}^{(f)}=0.334$.

Similar to the idea in analyzing the moderated multiple regression model, one might be interested in computing the traditional ΔR² following two sequential moderated mediation models. One is the model that does not include the influence of the product terms ESCS×EMOSUP and SCREAD×TSREAD, and the other model includes these two product terms. These R-squares for the two models are ${R}_1^2=6.3\%$ and ${R}_2^2=7.5\%$, respectively. Thus, 1.2% (ΔR²) of the variance of READ is uniquely explained by the product terms ESCS×EMOSUP and SCREAD×TSREAD, smaller compared to the newly defined moME effect sizes (${\hat{\varphi}}_1^{(f)}=0.757$, ${\hat{\varphi}}_2^{(f)}=0.102$, and ${\hat{\varphi}}_{12}^{(f)}=0.334$). This is because the ΔR² focuses on explaining the variance of the outcome variable (i.e., Read) rather than the variance of the mediation effect by moderators.

To understand how the results from the Bayesian method are affected by the priors, we have also obtained results with informative priors on the residual variances, intercepts, and regression slopes. Specifically, IGamma(0.1, 0.1) is used as the priors for residual variances, N(0, 1) is used as the priors for the intercept and regression slopes. The results indicate that the differences on parameter estimates between the two sets of priors are rather small, suggesting that priors only have minimal effect for the analysis of the PISA2018 sample. Results with the informative priors are provided in the online supplementary material (www3.nd.edu/~kyuan/2moME/example/InformativePrior.pdf).

Discussion and recommendations

In this article, we developed a two-level moderated mediation (2moME) model with single level data and proposed several measures to evaluate the size of the mediation effect (i.e., Var(a_ib_i)) explained by moderator variables at different stages. We further studied the performance of this model and compared it against the conventional moderated mediation (moME) model via Monte Carlo simulations.

According to our results, when the assumption of homoscedasticity holds, the 2moME model yields comparable results with those under the conventional moME model. When the homoscedasticity assumption is violated, estimates for the conditional indirect effects (γ_moME) and the difference between mediation effects (dif_me) under 2moME are more accurate than those under the conventional moME model. These results are consistent with the findings in the literature (Liu et al., 2020; Yang & Yuan, 2016) regarding the comparison between a two-level moderated regression model and the conventional MMR model with manifest and latent variables. More importantly, the measures of moderated mediation ES proposed in this article can be used as a supplement to the test of moME effects and will meet the needs for reporting ES in practice, given the fact that heteroscedasticity is common in moderation analysis (Aguinis & Pierce, 1998; Alexander & DeShon, 1994). Based on our Monte Carlo results, we recommend using the 2moME model for the analysis of moderated mediation and reporting the corresponding ES measures for the interpretation of the effect according to the questions of interest.

The 2moME model and the corresponding ES measures have clear practical advantages in studying the moME effect. First, the 2moME model provides a more general framework in conceptualizing the moME effect and quantifying the size of the effect. Under the framework of 2moME, the roles of the predictors, the moderators, and the mediators are statistically distinguished; that is, the predictors are included in the level-1 model, whereas the moderators are in the level-2 model. The conventional moME model is a special case of the 2moME model even if a variable plays the role as both a predictor and a moderator. For example in the predictor-moderator interaction model, the 2moME model can be specified by setting ${Z}_{i1}={u}_{d_{Mi}}={u}_{a_i}={c}_i=0,$ and Z_i2 = X_i in Eqs. (15)–(21). Second, the ES measures proposed in this article are based on the partition of the variance of the total mediation effect, i.e., Var(a_ib_i). Such a partition yields different types of measures of moME effect and facilitates fine descriptions of different moderation effects collectively or separately. The partition also accurately links a particular ES to the specific research question of interest (e.g., Kelley & Preacher, 2012). Third, because the proposed ES measures are based on the 2moME model, it is unnecessary for the homoscedasticity assumption to hold when interpreting the size of these measures. Researchers do not need to worry about the statistically biased effects due to heteroscedasticity, and consequently the corresponding ESs are also more valid. Fourth, the 2moME model is easy to estimate using either free Bayesian programs or commercially available software⁴. For example, JAGS (Plummer, 2015) is easily accessible and allows flexible specifications of likelihood functions (Wang et al., 2008) as well as prior distributions, and Mplus 8.3 program is user-friendly for empirical researchers. Finally, and most importantly, with the ES measures under the 2moME model, this work fills the lack of interpretable measures of ESs in conducting moME analysis using the conventional moME model and provides the means for researchers who need to quantify ESs.

Lachowicz et al. (2018) discussed desired properties for a good measure of ES (see also Kelley & Preacher, 2012; Preacher & Kelley, 2011; Wen & Fan, 2015). The ES measures defined in this article have multiple such properties in quantifying the effect of moderated mediation. First, the measures closely match the conceptual model of moderated mediation analysis. They have an interpretable scale in the context of variance explanation, and can answer the question as to what extent Z₁ and/or Z₂ explain the total variance of the mediation effect of X on Y through M (i.e., Var(a_ib_i)). Second, the credibility interval (CI) can be constructed for these measures using a Bayesian approach together with the posterior distributions of the involved parameter estimates. Third, the φs and φ^(f)s are independent of sample size, and they do not depend on the metrics of the involved variables. Fourth, the value of φ is between 0 and 1.0. However, for a two-stage moderated model (Scenario C and D in Fig. 3), there is a possibility for the values of φ₁, φ₂, φ₁₂, ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)}$, and ${\varphi}_{12}^{(f)}$ to be greater than 1 when a suppression effect occurs (Deegan, 1978; Lutz, 1983; Maassen & Bakker, 2001; Tzelgov & Henik, 1991). Although the new measures have many advantages, they also have limitations. Similar to the partial η² in ANOVA, Var(a_ib_i) is used as the base variance in the proposed measures, and consequently their explanations are not in absolute⁵ sense. That is, these ES measures are naturally relative to the value of the mediation effect (i.e., Var(a_ib_i)). Similarly, the denominator in the formulations of ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)}$, and ${\varphi}_{12}^{(f)}$ contains only the explained variance attributable to the effect of the moME effect.

In practice, which measures of the ESs to choose depends on the interest and context of the study. If the analysis is about the explained variance of the indirect effect (i.e., Var(a_ib_i)) attributable to the moderator variables (Z₁ or Z₂), the proposed ESs are preferred. We suggest also including the corresponding denominators when such measures are reported. The reason is to avoid over-interpretation of the moME ES, and the value of Var(a_ib_i) also forces one to consider whether the total variance of the indirect effect of X on Y through M has practical significance before further explaining the moME ES for specific moderator variables. We also recommend that researchers select and report ESs according to the substantive interest. Between the measures φs (i.e., φ, φ₁, φ₂, and φ₁₂) and φ^(f)s (i.e., ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)}$, and ${\varphi}_{12}^{(f)}$), researchers can select the most appropriate ones according to the specific research interests. The measure φs are chosen if the emphasis is on the extent to which the total variance of mediation effect (i.e., Var(a_ib_i)) is explained by the moderator(s), and the φ^(f)s are chosen if the emphasis is on the extent to which the explained variance of mediation effect (i.e., $Var\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{1i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{2i}\right)$) is explained by the moderator(s). Among φ, φ₁, φ₂, and φ₁₂, φ is preferred if the interest is in the total moderated mediation effect of Z₁ and Z₂; φ₁ (or φ₂) is preferred if the interest is in the first (or second) stage moderated mediation effect of Z₁ (or Z₂); φ₁₂ is preferred if a researcher is interested in the interactively moderated mediation effect Z₁ and Z₂. Similar considerations are applicable to the selection of ${\varphi}_1^{(f)}$, ${\varphi}_2^{(f)}$, and ${\varphi}_{12}^{(f)}$. However, if the interest is about the effects of Z₁ and Z₂ on the outcome Y, estimates other than the φs (or φ^(f)s) might be used. For example, similar to the idea that the standardized regression coefficient can be used to measure the effect of an independent variable on the dependent variable in multiple regression analysis, we can take the standardized estimates of γ_a1γ_b0, γ_a0γ_b1, and γ_a1γ_b1 to measure the ESs of the first stage moderated mediation effect, the second stage moderated mediation effect, and the interactively moderated mediation effect by the moderators in the first and second stages, respectively. These measures are scale-free and facilitate communication and comparison across studies. But they measure the indirect effect of the interaction term XZ₁ and MZ₂ on Y, rather than the extent Z₁ and Z₂ moderate the indirect effect of X→M→Y.

With Bayesian methods, one has to choose prior distributions, and many researchers have demonstrated the influence of prior distributions on parameter estimates (e.g., Yuan & MacKinnon, 2009). In this article, we set the shape/scale parameter of the inverted Gamma distributions to be vague (diffuse) informative in the simulation studies, and they are most commonly used and recommended in practice (Browne & Draper, 2006). Existing literature indicates that proper informative priors can make SEM parameter estimates more accurate, and Zondervan-Zwijnenburg et al. (2017) provided specific guidelines in collecting prior information and formalizing the information to specify the priors. In practice, we can incorporate the accumulated information about a parameter and to form a prior. When new observations become available, the previous posterior distribution can be used as a prior. In addition, different priors should be examined to investigate the influence of priors on the results. While informative priors are beneficial, how to use the priors can be subjective. For the empirical example, we piloted both informative and non-informative priors to explore the impact of different priors, and results showed that both Mplus and JAGS are little affected by the selected priors. Thus, we only presented the results with non-informative priors. But it should be noted that our findings with the use of priors may not always hold in practice. Sensitivity analysis should still be considered (van de Schoot et al., 2017; Zondervan-Zwijnenburg et al., 2017) to make sure that the results are not strongly influenced by a particular choice of the priors.

In this article the heteroscedasticity of errors ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ are related to X and (or) M in the 2moME model. This form of heteroscedasticity is derived from the fact that the mediation effect X → M → Y for different individuals might be affected differently by Z₁ and (or) Z₂, which naturally stem from the conceptual moderated mediation model. We should notice that there are many different forms of heteroscedasticity in regression analysis, and how to detect the form of heteroscedasticity and how to address it are important practical issues. However, these issues are beyond the scope of our study, and interested readers are referred to Carroll and Ruppert (1988), and Weisberg (2014) for further discussion. In addition, if a researcher only cares about the consistency of parameter estimates and their standard errors rather than the efficiency/accuracy of parameter estimates and/or proper effect sizes, the sandwich-type (also called White, or Huber-White) standard errors will serve the purpose following the LS estimation of the conventional moME model. However, such standard errors are not as good as expected for the analysis of a moderated multiple regression model (see, e.g., Yuan et al., 2014). In addition, we assumed that the error terms ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ are independent for more accurate variance-parameter estimates with single-level data. We can also let the level-2 residuals be correlated; then the expressions for the mean and variance of a_ib_i as well as the decomposition of Var(a_ib_i) will contain more terms. But they can be derived with additional computation, and the definitions of ESs are still applicable.

In the current article, we have focused on a moderated mediation model with one moderator variable at each stage. The two-level moME model can easily include more moderator and mediator variables. Also, when there are multiple moderator variables in the moderated mediation model, the correlations between the moderator variables may lead to reciprocal suppression effects (Tzelgov & Henik, 1991). It is possible that the investigation of suppression effects can provide an opportunity to gain a better understanding of the relationships among the variables (Rucker et al., 2011). Therefore, further studies on the suppression effects in the analysis of moderated mediation are encouraged. It would also be of interest to know the conditions under which the ESs defined in this article are outside the interval [0, 1] and to determine the plausibility of these conditions in practice. In addition, while the Bayesian method is used in estimating the 2moME model in this article, researchers can also explore frequentist approaches to estimate the 2moME model. In particular, Yuan et al. (2014) developed an algorithm for estimating the 2MMR model by normal-distribution-based maximum likelihood (NML), and Yang and Yuan (2016) proposed two robust methods for estimating the same model. These methods can be extended to the 2moME model. With the ML method, models can be compared using AIC or BIC, and sandwich-type SEs might be used to deal with violation of conditions. Other advantages of ML include that the computation is a fixed process and no artistic manipulation is needed, and different researchers will get the same set of results. But the computation/programing of ML estimates may involve coding a large number of equations. In contrast, the Bayesian method is flexible and capable of handling complicated models. But it needs to assume a known form for the distribution of (data| θ) (e.g., normally distributed variables/errors). Also, Bayesian computation involves a lot of manipulations: choice of priors, determination on the number of burn-in iterations, and checking the convergences of the chains. Different researchers may get quite different results. Further studies are needed in this direction and to compare the pros and cons of different methods. Finally, it is worth noting that estimates of the ESs depend on the accuracy of the parameter estimates, and they are not immune to statistical problems inherent in poorly designed studies. Similarly, omitted variables, measurement errors, and other factors that interfere with the estimates of regression coefficients will also affect the new measures of ES. Additional studies are needed to develop proper measures to quantify moME effects under these contexts.

Appendix A

Variance Decomposition of the Moderated Mediation for Scenario D

This appendix provides the derivation of Var(a_ib_i), as needed in computing the ESs described in the article. For easier reference, the two-level moderated mediation model (2moME) for Scenario D, which is given in Eqs. (15)-(21) in the article, is restated here as Appendix Eqs. (40)-(46). The other symbols used here are also defined the same as in the article.

Level-1 model:

$$ {M}_i={d}_{Mi}+{a}_i{X}_i+{\varepsilon}_{Mi}, $$

(40)

$$ {Y}_i={d}_{Yi}+{b}_i{M}_i+{c}_i{X}_i+{\varepsilon}_{Yi}; $$

(41)

Level-2 model:

$$ {d}_{Mi}={\gamma}_{d_{M0}}+{\gamma}_{d_{M1}}{Z}_{i1}+{u}_{d_{Mi}}, $$

(42)

$$ {a}_i={\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}, $$

(43)

$$ {d}_{Yi}={\gamma}_{d_{Y0}}+{\gamma}_{d_{Y1}}{Z}_{i1}+{\gamma}_{d_{Y2}}{Z}_{i2}+{u}_{d_{Yi}}, $$

(44)

$$ {b}_i={\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}, $$

(45)

$$ {c}_i={\gamma}_{c_0}+{\gamma}_{c_1}{Z}_{i1}+{\gamma}_{c_2}{Z}_{i2}+{u}_{c_i}. $$

(46)

Suppose that variables X, Z₁, and Z₂ are mean-centered; the error terms ${e}_{Mi}={\varepsilon}_{Mi}+{u}_{d_{Mi}}$, ${e}_{Yi}={\varepsilon}_{Yi}+{u}_{d_{Yi}}$, ${u}_{a_i}$, ${u}_{b_i}$, and ${u}_{c_i}$ are independent and follow normal distributions with ${e}_{Mi}\sim N\left(0,{\sigma}_{eM}^2\right)$, ${e}_{Yi}\sim N\left(0,{\sigma}_{eY}^2\right)$, ${u}_{a_i}\sim N\left(0,{\sigma}_{ua}^2\right)$, ${u}_{b_i}\sim N\left(0,{\sigma}_{ub}^2\right)$, ${u}_{c_i}\sim N\left(0,{\sigma}_{uc}^2\right)$.

The mean and variance of the effect X→M, as conveyed by a_i, are respectively

$$ \mathrm{E}\left({a}_i\right)=E\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)={\gamma}_{a_0}, $$

(47)

and

$$ Var\left({a}_i\right)= Var\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)={\gamma}_{a_1}^2 Var\left({Z}_{i1}\right)+{\sigma}_{ua}^2. $$

(48)

The mean and variance of the effect M→Y, as conveyed by b_i, are respectively

$$ E\left({b}_i\right)=E\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right)={\gamma}_{b_0}, $$

(49)

and

$$ Var\left({b}_i\right)= Var\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right)={\gamma}_{b_1}^2 Var\left({Z}_{i2}\right)+{\sigma}_{ub}^2. $$

(50)

The indirect effect is

$$ {IND}_i={a}_i{b}_i=\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right). $$

(51)

Equation (51) shows that the mediation effect of X_i on Y_i via M_i varies across individuals, and is moderated by both the stage one moderator variable Z_i1 and the stage two moderator variable Z_i2.

The expected value or the average of a_ib_i is (Goodman, 1960, p. 712)

$$ E\left({IND}_i\right)=E\left({a}_i{b}_i\right)=E\left({a}_i\right)E\left({b}_i\right)+ Cov\left({a}_i,{b}_i\right)={\gamma}_{a_0}{\gamma}_{b_0}+{\gamma}_{a_1}{\gamma}_{b_1} Cov\left({Z}_{i1},{Z}_{i2}\right) $$

(52)

$$ {\displaystyle \begin{array}{c} Var\left({a}_i{b}_i\right)= Var\left[\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right)\right]\\ {}= Var\Big({\gamma}_{a_0}{\gamma}_{b_0}+{\gamma}_{a_0}{\gamma}_{b_1}{Z}_{i2}+{\gamma}_{a_1}{\gamma}_{b_0}{Z}_{i1}+{\gamma}_{a_1}{\gamma}_{b_1}{Z}_{i1}{Z}_{i2}\\ {}+{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\Big).\end{array}} $$

(53)

With centered Z₁ and Z₂, and the assumptions of $Cov\left({u}_{a_i},{u}_{b_i}\right)=0,$ $Cov\left({u}_{a_i},{Z}_{i1}\right)=0,$ $Cov\left({u}_{a_i},{Z}_{i2}\right)=0,$ $Cov\left({u}_{b_i},{Z}_{i1}\right)=0,$ and $Cov\left({u}_{b_i},{Z}_{i2}\right)=0$ and according to the rules of conditional expectation and covariance of two variables U and V given W,

$$ E(UV)=E\left[V\cdotp E\left(U|V\right)\right], $$

(54)

$$ Cov\left(U,V\right)=E\left[ Cov\left(U,V|W\right)\right]+ Cov\left[E\left(U|W\right),E\left(V|W\right)\right], $$

(55)

we have $Cov\left({Z}_{i1},{u}_{a_i}{Z}_{i2}\right)=0$, $Cov\left({Z}_{i1},{u}_{b_i}{Z}_{i1}\right)=0$, $Cov\left({Z}_{i1},{u}_{a_i}{u}_{b_i}\right)=0,$ $Cov\left({u}_{b_i}{Z}_{i1},{u}_{b_i}\right)=0,$ $Cov\left({u}_{b_i}{Z}_{i1},{u}_{a_i}\right)=0,$ $Cov\left({u}_{b_i}{Z}_{i1},{u}_{a_i}{Z}_{i2}\right)=0$, $Cov\left({u}_{b_i}{Z}_{i1},{u}_{a_i}{u}_{b_i}\right)=0,$then

$$ {\displaystyle \begin{array}{c} Cov\left({\gamma}_{a_1}{\gamma}_{b_0}{Z}_{i1},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {} Cov\left({Z}_{i1}{u}_{b_i},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0.\end{array}} $$

In the same way, we have

$$ {\displaystyle \begin{array}{c} Cov\left({\gamma}_{a_0}{\gamma}_{b_1}{Z}_{i2},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {} Cov\left({\gamma}_{a_1}{\gamma}_{b_1}{Z}_{i1}{Z}_{i2},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {}\begin{array}{c} Cov\left({\gamma}_{a_0}{u}_{b_i},{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {} Cov\left({\gamma}_{b_0}{u}_{a_i},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {}\begin{array}{c} Cov\left({\gamma}_{b_1}{Z}_{i2}{u}_{a_i},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\right)=0,\\ {} Cov\left({u}_{a_i}{u}_{b_i},{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}\right)=0.\end{array}\end{array}\end{array}} $$

Therefore,

$$ {\displaystyle \begin{array}{c} Var\left({a}_i{b}_i\right)= Var\left[\left({\gamma}_{a_0}+{\gamma}_{a_1}{Z}_{i1}+{u}_{a_i}\right)\left({\gamma}_{b_0}+{\gamma}_{b_1}{Z}_{i2}+{u}_{b_i}\right)\right]\\ {}= Var\Big({\gamma}_{a_0}{\gamma}_{b_0}+{\gamma}_{a_0}{\gamma}_{b_1}{Z}_{i2}+{\gamma}_{a_1}{\gamma}_{b_0}{Z}_{i1}+{\gamma}_{a_1}{\gamma}_{b_1}{Z}_{i1}{Z}_{i2}\\ {}\begin{array}{c}+{\gamma}_{a_0}{u}_{b_i}+{\gamma}_{a_1}{Z}_{i1}{u}_{b_i}+{\gamma}_{b_0}{u}_{a_i}+{\gamma}_{b_1}{Z}_{i2}{u}_{a_i}+{u}_{a_i}{u}_{b_i}\Big)\\ {}={\gamma}_{a_1}^2{\gamma}_{b_0}^2 Var\left({Z}_{i1}\right)+{\gamma}_{a_0}^2{\gamma}_{b_1}^2 Var\left({Z}_{i2}\right)+{\gamma}_{a_1}^2{\gamma}_{b_1}^2 Var\left({Z}_{i1}{Z}_{i2}\right)\\ {}\begin{array}{c}+{\gamma}_{a_1}^2 Var\left({Z}_{i1}\right){\sigma}_{ub}^2+{\gamma}_{b_1}^2 Var\left({Z}_{i2}\right){\sigma}_{ua}^2+{\gamma}_{a_0}^2{\sigma}_{ub}^2+{\gamma}_{b_0}^2{\sigma}_{ua}^2\\ {}+{\sigma}_{ua}^2{\sigma}_{ub}^2+2{\gamma}_{a_0}{\gamma}_{b_1}{\gamma}_{a_1}{\gamma}_{b_0} Cov\left({Z}_{i1},{Z}_{i2}\right)\\ {}+2{\gamma}_{a_0}{\gamma}_{a_1}{\gamma}_{b_1}^2 Cov\left({Z}_{i2},{Z}_{i1}{Z}_{i2}\right)\\ {}+2{\gamma}_{a_1}^2{\gamma}_{b_0}{\gamma}_{b_1} Cov\left({Z}_{i1},{Z}_{i1}{Z}_{i2}\right).\end{array}\end{array}\end{array}} $$

(56)

This is Eq. (28) used in the denominators of several effect size measures presented in section 2.2.