A key question in the study of collective behavior is that of understanding how multiple, possibly unrelated, individuals can make efficient consensus decisions despite often possessing incomplete or conflicting information. Although important theoretical breakthroughs have occurred during the last 15 years (e.g., Couzin, Krause, Franks, & Levin, 2005; Couzin et al., 2011; Leonard et al., 2012; Ward Sumpter, Couzin, Hart, & Krause, 2008), there is still a lack of standardized experimental methods with which to empirically test these findings.

Occurring across a wide range of species and ecological contexts, fish schooling is a phenomenon of long-lasting interest in ethology and ecology that has also attracted interest from the fields of statistical physics and theoretical biology as an example of self-organized behavior (U. Lopez, Gautrais, Couzin, & Theraulaz, 2012). To study these dynamic collective processes, it is necessary to identify groups and subgroups, as well as to take into account the possible effects of environmental heterogeneity on the outcome of the collective behavior. Though shoals and schools have qualitative (Pitcher, 1983) and quantitative definitions (Delcourt & Poncin, 2012), determining membership in a group, especially using a quantitative method, is still under debate (Miller & Gerlai, 2008, 2011; Quera, Beltran, & Dolado, 2011; Quera, Beltran, Givoni, & Dolado, 2013). For instance, in the study of fission-fusion processes, it is necessary to determine whether an individual belongs to one group or another, or is isolated. We therefore need an approach in which each individual must make a clear choice to join, stay with, or leave a group, so that the delimitation of the group is unambiguous.

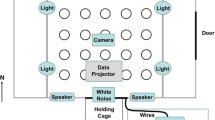
To achieve these objectives, we propose the use of the radial arm maze as a new standardized tool to investigate collective exploration and decision-making. A radial arm maze consists of a number of arms radiating away from a central zone (see Fig. 1). During a typical experimental trial, a single animal is introduced into the central zone (or one of the arms, depending on the experimental protocol), and allowed to move freely into one of the arms, thus making an easy-to-classify categorical choice. After each choice, the tested animal can return to the central zone and select a new arm from the available alternatives (again, depending on the experimental protocol and question). This experimental setup allows the animal to sample—possibly with replacement—from a known set of well-defined alternatives (Olton, Collison, & Werz, 1977; Olton & Samuelson, 1976).

Fig. 1
figure 1

(Left) The six-arm radial maze seen from above, with zones denoted Arms 1–6 and the central zone. (Middle) Example of automatic counting of the number of fish in each zone. (Right) The same image with each arm labeled relative to the arm M containing the majority of the fish (n > 5). L1, L2, R1, R2, and Op are, respectively, the first and second arms to the left (L) or the right (R) of M, and the arm opposite M

Full size image

Our first contribution in this article is to illustrate how the radial arm maze paradigm can be used for the study of collective behaviors for the first time, as it has been previously for single subjects (Hodges, 1996; Olton & Samuelson, 1976; Vorhees & Williams, 2014). Our paradigm permits observing an animal group for extended durations, during which the individuals can make numerous successive individual and collective choices without having to be removed from the maze or interact with the experimenter in any way, potentially generating a large amount of detailed data. The radial arm maze can also be used to explore classic themes, previously studied with solitary animals (spatial learning, discrimination of cues, exploratory strategies, or algorithmic behaviors), but can now also become a convenient tool to study other phenomena that are specific to social and collective behavior (consensus decision-making, fission-fusion dynamics, etc.).

As an alternative to video multitracking, our second purpose is to suggest a simplified way to investigate collective exploration and decision-making in animal groups. We propose to characterize group behavior by observing the dynamical distribution of the individuals across a structured, discrete space. We describe how to simply determine the group’s cohesion by counting the number of fish in each section of the maze. We use majority transitions between arms to characterize collective dynamics and introduce a new index to quantify the degree of group cohesion in the discrete structure of the radial arm maze. Finally, we demonstrate the use of this methodology by performing simple refuge-site selection experiments with groups of fish.

The proposed approach goes beyond simply reusing an existing paradigm used almost exclusively with isolated animals. It introduces quantification and analysis methods specifically crafted for group behavior, and therefore offers a new and standardized way to study collective behavior.

Methodology

Radial arm maze

A radial arm maze is usually composed of three to eight arms radiating away from a central zone, though this number can be much higher (e.g., 48 arms in Cole & Chappell-Stephenson, 2003). It is a well-established paradigm in experimental psychology since the pioneering research of Tolman, Ritchie, and Kalish (1946) and Olton and Samuelson (1976). It is used in cognitive research to understand exploratory behaviors (Olton et al., 1977), algorithmic behaviors (Hughes & Blight, 1999), spatial learning (Brown & Giumetti, 2006), social learning (Brown, Prince, & Doyle, 2009), the ability to discriminate different types of—often visual—cues (Colwill, Raymond, Ferreira, & Escudero, 2005), learning ability and underlying brain structures (Crusio & Schwegler, 2005; J. C. Lopez, Bingman, Rodriguez, Gomez, & Salas, 2000), and neurotoxicology (Creson, Woodruff, Ferslew, Rasch, & Monaco, 2003; Walsh & Chrobak, 1987).

Radial arm mazes are used mostly with isolated animals such as rodents, pigs, rabbits, hedgehogs, dogs (Lipp et al., 2001; Macpherson & Roberts, 2010; Wilkie & Slobin, 1983), a number of bird species (Lipp et al., 2001; Pleskacheva, 2009), and reptilians (Mueller-Paul, Wilkinson, Hall, & Huber, 2012; Wilkinson, Coward, & Hall, 2009). Several fish species have also been tested in these mazes: Siamese fighting fish (Betta splendens; Roitblat, Tham, & Golub, 1982), fifteen-spined sticklebacks (Spinachia spinachia) and corkwing wrasse (Crenilabrus melops; Hughes & Blight, 1999, 2000), goldfish (Carassius auratus; Washizuka & Taniuchi, 2006), and zebrafish (Danio rerio; Al-Imari & Gerlai, 2008; Sison & Gerlai, 2010; Washizuka & Taniuchi, 2007). However radial arm mazes have only rarely been used to test the collective performance of groups of animals (see Brown et al., 2009; Miller, Garnier, Hartnett, & Couzin, 2013). In Brown et al. (2009), a pair of rats were tested to study social influence on individual choice. In Miller et al. (2013), fish schools were tested in repeated trials of short duration, recording only the first choice of the group among three options. Here, for the first time we present a study of multiple successive choices of a group in a radial arm maze, over an extended period of time, without the animals being removed from the maze between choices.

One of the strengths of the radial arm maze paradigm is that it allows the observer to determine without ambiguity that an animal has made a decision by simply recording whether or not the animal has entered one of the arms of the maze. We can take advantage of the simplicity of this measure to determine the location and size of all the groups in the maze at any time during an experiment.

Tracking group dynamics

During a collective decision-making event, it is important to (1) estimate when the individuals in a group have made a decision, and (2) determine the strength of the consensus amongst the individuals composing the group. For Condition 1, we propose to simply track the movements of the majority of the group between the different arms of the maze, as a way to significantly simplify the collective dynamics (note that other thresholds can be chosen, and that individual movements can be tracked as well, depending on the study needs). For Condition 2, we introduce a new cohesion index that measures how dispersed the animals are in a discretely partitioned environment, here the radial arm maze.

Majority transitions

A majority is reached when half of the individuals plus one are located in a single arm of the maze. The central zone is not considered a valid choice for this purpose. When a majority is reached in a given arm, we call this arm the “majority arm.” At any given moment, as long as a majority exists, we can define the position of the other arms relative to the majority arm by counting the number of arm openings to the left or right of the majority arm. For instance, for a six-arm radial maze, we label the majority arm M, the first and second arms to the left (L) or to the right (R) of M, L1, L2, R1, R2, and the arm directly opposite to M, Op (Op only exists in mazes with an even number of arms; see Fig. 1). This classification method can easily be extended to mazes with different numbers of arms.

A transition of majority is defined as a movement of the majority from a given arm to a different one; a transition period is defined as a period of time between the end of a majority (in an arm) and the beginning of the next majority (in the same or another arm; Fig. S1). The study of majority transition is typically an analysis of the temporal sequence of majority states, without taking into account the durations of these states (one majority episode is defined from the beginning to the end of one majority in an arm). During transition periods, no majority state is observed. We can also analyze second- (or higher-) order transitions to evaluate potential stereotypic motion patterns (see Figs. S2 and S3 for some theoretical examples). A transition of the first order is the direct transition of a majority from one arm to another arm; a second-order transition consists of two sequential majority transitions and records the second next majority arm, and so on for higher orders. For instance, second-order transitions allow us to determine whether the majority returns to the original majority arm after exploring another one (Fig. S3). In some analyses, it could be interesting to filter cases in which transition has been aborted—for example, one or several individuals have moved into the central zone, inducing the loss of the majority, and then returned rapidly to their initial arm, restoring the majority in that arm. We therefore define a first-order “majority transition without repetition,” in which we ignore first-order transitions between the same arm. For higher-order transitions, repetitive identical majorities (i.e., consecutive majorities in the same arm) are considered a single element in the state sequence (see Fig. S2). For example, the second-order transition in the sequence A–B–B–C is A–C.

A new cohesion index for the radial maze

We propose a new cohesion index, Ic, that measures the ability of animals to form cohesive groups in a radial maze. We created Ic for radial arm mazes, but it can also be applied to other types of mazes or arenas divided into discrete zones. This index is an alternative to traditional methods for measuring group cohesion based on the relative topological or metric locations of the individuals composing the group (reviewed in Delcourt & Poncin, 2012). These traditional measures are well adapted to homogeneous open-field arenas but make little sense in more structured environments such as radial mazes. For instance, two individuals located in two contiguous arms of a radial maze can be close to each other without being able to directly perceive or interact with each other. Many natural environments contain barriers or other impediments to movement that impose a structure (which the radial maze may simulate), making our method potentially more useful than traditional measures even in the wild.

We define Dc as the Euclidean distance (norm of the resultant vector) in a multidimensional space between the numbers fi of individuals in each zone of the maze (arms + central zone). All variables (dimensions) are considered independently from each other.

$$ {D}_C=\sqrt{\sum \limits_{i=1}^N{\left({f}_i\right)}^2} $$
(1)

Dc varies as a function of the partition of the number of fish. This partition is dependent on the total number of individuals, N, and the number of zones, Z (see Supplementary Table 1 in Appx. S1). Partition, composition, and the number of possible partitions are described in detail in Appendix S1.

Dmin is the value of Dc for the least cohesive configuration possible (i.e., the most homogeneous distribution of the animals across the possible zones). For instance, for ten individuals with ten zones, Dmin = \( \sqrt{10} \). However, if the number of zones is less than N, Dmin is larger. For instance, for ten individuals in seven zones, Dmin = \( \sqrt{16} \) for the partition 2/2/2/1/1/1/1, which corresponds to the most homogeneous distribution of the animals in this case.

The cohesion index Ic is computed as follows:

$$ {I}_c=\frac{D_C-{D}_{min}}{N-{D}_{min}} $$
(2)

Ic varies between 0 and 1, increasing as the number of occupied zones decreases and the groups are larger. For instance, Ic = .46 for the partition 6/3/1, whereas Ic = .44 for the partition 6/2/2. When all individuals are located in one zone, Dc = N, so Ic = 1. In contrast, Ic = 0 when the group is as dispersed as possible. Ic cannot be calculated if there is just one zone.

The R code details and more examples to calculate partitions, Dc, Dmin, and Ic are presented in Appendix S1.

Case study

Study species

We performed a series of simple resting-site selection experiments in order to demonstrate the usefulness of the radial arm maze paradigm for the study of animal groups. For these experiments, we used golden shiners (Notemigonus crysoleucas, Cyprinidae), a highly gregarious fish species (Berdahl, Torney, Ioannou, Faria, & Couzin, 2013; Couzin et al., 2011; Katz, Ioannou, Tunstrøm, Huepe, & Couzin, 2011; Tunstrøm et al., 2013) native to the freshwaters of eastern North America. This fish is regularly used in collective-behavior studies to investigate collective decision-making processes (Berdahl et al., 2013; Couzin et al., 2011; Leblond & Reebs, 2006; Miller et al., 2013; Reebs, 2000, 2001). Juvenile shiners (average length approximately 5 cm) were purchased from I. F. Anderson Farms (www.andersonminnows.com) and housed in an environmentally controlled laboratory for over 2 months before the start of the experiment. The fish lived in 75-L tanks at a density of approximately 150 fish per tank in dechlorinated, conditioned, oxygenated, and continuously filtered and recycled fresh water. Ambient temperature was maintained at 16 °C and the photoperiod was 14∶10 light∶dark. The fish were fed three times a day ad libitum with crushed flake food and experiments were conducted 2 h after feeding. All experimental procedures were approved by the Princeton University Institutional Animal Care and Use Committee.

Experimental setup

We used a six-arm radial maze with a regular hexagonal central zone (see Fig. 1). The side length of this hexagon was 23 cm; the dimensions of each arm were 42 × 20 × 20 cm (length × width × height). The walls were made of 1.5-cm-thick white PVC boards. Note that other designs are possible, with different dimensions and a different number of arms that would depend on the research question. The maze was placed inside a larger tank (2.1 × 1.2 m) partially filled with water (10 cm deep) and weighted down with bags of gravel attached outside the end of each arm. A 1-cm-thick layer of gravel was deposited at the bottom of the maze. When no trial was running, water in the tank was constantly filtered by four aquarium pumps and filters. The pumps were turned off during trials to prevent water movements from influencing the behavior of the fish. Water temperature and pH were adjusted before each trial to match those of the housing tanks. For this simple experiment, aimed at demonstrating the usefulness of radial arm mazes for studying collective behaviors, all the arms were kept open and empty at all times.

Trials were recorded using a Sony XDCAM EX HD camera (image resolution: 1,920 × 1,080 pixels) whose field of view covered the entirety of the maze. At the beginning of each trial, the fish were placed inside an opaque, movable ring in the central zone to prevent them from visually exploring the maze before the start of a trial. They were left in the ring to habituate for a period of 10 min. A trial started when the opaque ring was slowly raised and removed from the tank using a system of transparent fishing lines and pulleys.

First, we performed several 1-h-long trials using groups of 5, 10, and 20 fish, to compare our automated counting system (see below) to human coders. Second, to validate the use of our study parameters (i.e., majority determination and transitions, indices of cohesion), nine trials were run for a duration of 12 h each using groups of ten fish each (a tenth trial was unusable due to a technical problem during video recording). All trials were recorded at a frequency of one image per second. Upon completion of a trial, the fish were returned to their housing tanks.

Automated image processing

For calculating majority transitions and the cohesion index, Ic only requires knowing the number of individuals in each section of the maze. If the number of observations required is small, this can be easily done manually. However, if the number of observations is large, considerable speed gains in data collection can be achieved through automating the counting process. If the individuals are close enough in space between successive observations (typically if an animal cannot move more than half its body length between two observations—Turchin, 1998), it is possible to use one of the many multitracking programs available on the market, such as CTRAX (Branson, Robie, Bender, Perona, & Dickinson, 2009), idTracker (Pérez-Escudero, Vicente-Page, Hinz, Arganda, & de Polavieja, 2014), or SwisTrack (Correll et al., 2006). However, this option is often limited to relatively short observation periods (typically no longer than an hour) as the computing time increases rapidly for the analysis of high frequency, high definition video recordings.

For the present study, we chose to rely instead on high definition, low frequency recordings (one observation per second) that allowed us to run observations over several hours and that could be automatically processed in a matter of minutes. We developed a simple and robust computer vision algorithm in order to estimate automatically the number of individuals in each section of the radial maze (the central region and each of the arms). This algorithm was implemented using Matlab R2015a and its associated Image Processing Toolbox (Version 9.2). The code is available under the open-source GNU General Public License v3.0 at the following address: https://github.com/sjmgarnier/projectRadial. Below are the different steps of the image processing algorithm that result in the automated estimation of the number of individuals in each section of the radial maze.

  • Software setup The user indicates the location of the video file, as well as the total number of fish used during the trial, the number of arms of the maze, and the desired sampling rate if different from the video frame rate.

  • Maze detection The user indicates the location of the four corners of each arm, starting from any arm (which will be then labeled Arm 1) and moving clockwise from there. The area between the arms will be automatically labeled as the central (or starting) area.

  • Background image A background image is generated by averaging 100 images taken at regular intervals along the video. In general, using a median image would have resulted in a better approximation of the background image than by averaging. However, it would have required a considerably larger amount of memory, and it did not prove necessary, at least in our setup.

  • Presence detection The background image is subtracted from each image in the video. The local contrast of the resulting difference image is then adjusted to balance the low contrast parts of the original image (e.g., in shaded areas where dark animals are less visible) with the high contrast parts (e.g., in well-lit areas where dark animals are more visible). This is done by multiplying the difference image by the inverse of the background image raised to a user-determined power. Noise in the contrast-adjusted, difference image is reduced using a three-pixel uniform disk filter. Finally, a user-determined threshold is applied to the resulting image. Pixels whose values are higher than the threshold are set to 1 (an animal is present), the others are set to 0 (no animal).

  • Blob size and location Nonzero pixels are then grouped into “blobs,” that is contiguous non-zero regions of the image resulting from Step 4. The coordinates (x, y) of the blobs in the maze are determined by their respective centers of mass (i.e., average coordinates of all pixels belonging to a blob). To determine the likely number Bi of animals represented in each blob i, the number p of pixels covered by a single fish is estimated as the total number of nonzero pixels divided by the total number N of animals present in the radial maze (information provided by the user at the beginning of the counting process). The number Mi of animals in each blob i is computed as Ti—the number of pixels in each blob divided by p—rounded down to the closest integer. If ∑Mi < N, the differences Di between each Ti and each Mi are computed and ordered from highest to lowest. The number Mi corresponding to the higher Di is then increased by one unit, and this process repeats for all subsequent ordered Di values until ∑Mi = N.

Note that this algorithm (and the provided Matlab implementation) should work well with other maze sizes, numbers of arms, and animal species, provided that (1) the entire maze is visible in the video, and (2) the floor of the maze has a fairly uniform coloring and contrasts well with the color of the animals.

A blob was determined to be in a particular zone (one of the arms or the central zone) of the maze if its center of mass was located within the polygon delimiting that zone, even if a blob extended across the demarcation line between the central zone and one of the arms (e.g., when a fish was transitioning from one zone to the other). Finally, we simply considered that two (or more) individuals belonged to the same group if they were present in the same zone at a given time. Each group size was therefore defined as the number of individuals in each particular zone of the maze.

Note that this method of determining group membership and size is generally reliable, except when large groups are transitioning between two zones in the maze, in which case a group can potentially span several zones simultaneously. However, such events are usually short-lived and their unique signature can actually be used to detect, automatically, when groups are moving between zones. Note as well that the error rate of the algorithm is likely to increase if the individuals in the group have very different sizes. If this is the case, we recommend using more sophisticated computer vision algorithms (e.g., algorithms trained to detect particular shapes regardless of their size; see, e.g., Qian, Cheng, & Chen, 2014; Wang, Cheng, Qian, Liu, & Chen, 2016) or tagging the animals with unique markers that can be detected individually (e.g., Delcourt, Ylieff, Bolliet, Poncin, & Bardonnet, 2011). For the purpose of this study—which is to demonstrate how radial arm mazes can be used to study collective behavior and not demonstrating a new tracking method—we used fish of approximately the same size.

Validation of the automated counting system

To evaluate the precision of our automated counting algorithm, we selected ten test images at random from each of the 18 videos of the exploration experiments we performed (180 images in total). Approximately 15 human counters—since counts were performed using an anonymous web application, it was not possible to accurately track the identity of each human counter—were asked to count the number of fish in each zone of the radial arm maze. The human counters were aware of the total number of fish in the maze in each case (details of the instructions given to the human counters can be found in Appx. S2). Images shown to the human counters were selected pseudo-randomly from the pool of 180 test images: Images that had been scored more often by chance were subsequently less likely to be displayed again, whereas images that had been scored less often were more likely to be displayed again. Each human counter performed different numbers of counts, and a given human counter may potentially have performed counts for the same image several times, but without being informed of this. All images were manually counted a minimum of eight times and a maximum of 20, with a median count number of 13 (see Fig. S4). For each maze zone in each image, we considered that human counters reached a consensus if at least 75% of them agreed on the number of fish present in that zone.

Data analysis

Statistics and graphs were performed in R (Version 3.3.3; www.r-project.org). An accompanying R package (projectRadial; https://github.com/sjmgarnier/projectRadial) was developed to facilitate the calculation of Ic (see Appx. S1 for details on the installation of the package and details on the calculation process). This package depends on the partitions package (Version 1.9-18; Hankin, 2006, 2007). Flux diagrams were realized in R using the qgraph package (Version 1.4.2; Epskamp, Cramer, Waldorp, Schmittmann, & Borsboom, 2012).

Results

Validation of the automated counting system

Figure 2a shows the proportions of times the human counters reached a consensus for each zone, as well as for all the zones, in a given image. Overall, a consensus was observed in more than 95% of the cases. No significant difference was observed between arms (χ² = 0.07, df = 5, p = .99), with a consensus in 97%–99% of cases. However, in the central zone human counters were less likely to reach consensus (90%). This was due to the organization of the maze: Human counters were most likely to disagree with each other if one or more fish were situated on the demarcation line between two zones. Therefore, they were six times more likely to disagree on the number of fish in the central zone, because it is directly connected to six other zones (the six arms of the maze), whereas each arm is connected to only one other zone (the central zone). Overall, the human counters agreed on all zones at the same time in 89% of the cases.

Fig. 2
figure 2

(a) Proportions of times a 75% consensus was reached between the human counters for each zone in the radial arm maze (first seven bars) and for all the locations at once (final bar). (b) Proportions of times the automated counting software was in agreement with the consensus counts reached by human counters for each location in the radial arm maze (first seven bars) and for all the locations at once (final bar). Broken lines indicate the threshold value of .95

Full size image

Taking into account cases with full consensus only, Fig. 2b shows a comparison of the performance of the automated counting algorithm and the consensus counts obtained by human counters. The proportion of times that the computer counts were in agreement with the consensus counts for each zone was always above 95% for the maze arms. The agreement was slightly less strong for the central zone (94.4%) for the reason explained above. The proportion of times they agreed for all zones at once was 89.4%.

Majority tracking and Ic

Figure 3 shows a typical example of a 12-h trial with a group of ten fish. Periods of time in which a majority is achieved in one of the zones are highlighted (using a different color for each arm). The two zoomed-in time sequences detail the relationship between the size of the largest group (in an arm) and the periods with or without a majority.

Fig. 3
figure 3

Complete trial example of majority transitions, with details of two periods within the trial. The group size was ten fish, and the sequence lasts 12 h. (a) Example of a sequence of 12 h, illustrating periods with and without majorities. Each vertical colored bar shows a period during which a majority were in a specific arm (n ≥ 6); the colors indicate which arm, and the absence of color indicates a period without a majority in any arm. (b) Details of two sequences of 2 h each (top, the first 2 h; bottom, Hours 8 to 10 of the experimental trial), with the relationship between the maximal group size observed in the maze arms (the central zone is not included) and periods with and without a majority

Full size image

From this example (see also Fig. S5), it seems that majority transitions are more frequent between adjacent arms. This is clearly illustrated in the flow diagram in Fig. 4a, which shows that first-order transitions are more likely to occur between adjacent arms. Figure 4c shows the same information, normalized to the position of the majority arm before the transition occurs. Figure 4a confirms that the group majority explored all of the available arms during the 12 h of the trial and that all possible first- and second-order majority transitions were observed at least once during that period. Figure 4c confirms that the more frequent direct majority transitions are between an arm and one of the two adjacent arms. Transitions between an arm and itself are also frequent. Finally, Figs. 4b and 4d show that second-order transitions are usually the consequence of two successive first-order transitions toward the adjacent arms: The most frequently observed transitions are either a direct return to the previous majority arm (M to L1/R1 to M) or transition to the next arm in the same direction (M to L1 to L2 or M to R1 to R2).

Fig. 4
figure 4

Upper panels: Examples of majority transition diagrams for a group of ten fish during 12 h: (a) Majority transitions of the first order (n = 186) and (b) majority transitions of the second order (n = 185). Lower panels: Diagrams of majority transitions between relative arms (relative to the current majority arm, M) for the same video sequence: (c) Transitions of the first order (n = 186) and (d) transitions of the second order without repetition (i.e., excluding leaving and returning to the same arm during first-order transitions; n = 147). The thickness of the arrows is proportional to the maximum observed value in each diagram

Full size image

Figure 5a shows Ic as a function of time in a typical trial with a group of ten fish. Cohesion was low at the beginning of the trial, when the fish had just been released from the central zone and had started exploring the maze. It then increased during the first hour and remained high for the rest of the trial, dropping momentarily every time the group changed location in the maze.

Fig. 5
figure 5

(a) Example of our cohesion index, Ic, as a function of time, in a group of ten fish during a 12-h session. The orange dotted line is the minimal value of Ic (= .39) at which a majority can be observed (corresponding to a partition of 6/1/1/1/1), and the green dotted line is the maximal value of Ic (= .51) at which no majority can be observed (a partition of 5/5). Whenever the data are situated between these two values, a transition of majority can be observed; each time the data fall under the orange line, a transition of majority is being observed with certainty. (b, c) Mean values of Ic as a function of time, based on nine groups of ten fish each. (b) During the 12 h of the experiment, note the lower values during the first hour. (c) Detail of the first hour of the experiment; note the two different profiles in the increase in Ic, before (very rapid increase) and after 12 min (moderate increase). The broken vertical line indicates 12 min from the start of the session

Full size image

Figure 5b shows the mean value of Ic, based on nine groups of ten fish each, as a function of time. As is exemplified in Fig. 5a, mean Ic values are very low in the beginning of an experiment and grow and stabilize after the first hour. Figure 5c shows this progression during just the first hour of the experiment, with a rapid increase in cohesion during the first 12 min (fish associating rapidly with one or two partners), followed by a slower increase corresponding to the buildup of a majority.

Figure 6a shows that a group majority in one of the arms is less likely to be reached during the first 30 min of a trial, and when achieved, it changes arm more frequently during the first hour than during the rest of the trial. The number of majority transitions is also much higher during the first hour (Fig. 6b). These observations indicate that the first hour is a more unstable period, with more exploration taking place in small groups. Group cohesion is more stable during the rest of the 12-h period. However, exploration does not stop, but is instead performed as a cohesive group.

Fig. 6
figure 6

(a) Mean (± SE) percentages of time when a majority was observed in any arm, binned into periods of 30 min for an entire 12-h session, for nine groups of ten fish each. (b) Mean (± SE) frequencies of majority transitions as a function of time

Full size image

Discussion

Using radial arm mazes to study collective behavior

Radial arm mazes have been traditionally used for research on individual cognition. In this article, we have proposed using them to study social cognition and collective behaviors. We illustrate our proposal with a proof-of-concept experiment looking at the collective exploration behavior of fish shoals. With the exception of Brown et al. (2009), who placed two rats together in a radial maze, we do not know of any case in which the radial arm maze paradigm was used to study collective behaviors, in particular for large groups.

The central principle of this paradigm is to allow tested animals to sample multiple discrete options, with or without replacement. After each visit to an arm of the maze (i.e., a discrete choice), the animals are not disturbed by experimenters; they can return to the central zone and make a new choice. Because the options are discrete, it is easy to categorize and quantify the choices made by the animals.

All the traditional uses of the radial arm maze paradigm with single animals can be applied to study animal groups (Table 1). For instance, we can use this paradigm to test group preferences and the ways that individual preferences may be modified in a group context. These are likely to be different from the preferences of isolated individuals, because group living is known to modify individual patterns of exploration and exploitation of the environment (Sumpter, 2010). In a group, an individual may be able to react sooner or more strongly to subtle differences in the environment, thanks to the many-eyes effect; an individual might also be more likely to find the best resources (Berdahl et al., 2013). The radial arm maze paradigm is also used to study how isolated individuals resolve conflicts between bits of information they possess about the different parts of the maze. This can be extended to study conflicts during collective decision-making—when different group members possess different information, for example (Couzin et al., 2011; Miller et al., 2013). Spatial exploratory behaviors, notably stereotypic motion schemes (i.e., algorithmic behaviors), can also be studied at the group level using this paradigm.

Table 1 Some applications of radial mazes to study group behaviors; testing a group also allows for the investigation of a series of new questions
Full size table

The radial arm maze can also be used to study questions that are specific to group behaviors (Table 1). The discrete nature of each animal’s choices in this setup makes it easy to assign each animal to a specific group. This makes the radial arm maze paradigm ideal for studying fission–fusion dynamics in animal groups in the context of constrained physical environments, for instance. It can also be used to study most typical social phenomena, such as collective decision-making, sharing or transmission of information, collaboration, competition, social status establishment, and social learning. In addition, the contents of each arm can be modified independently of the other arms, making it possible to study the effects of environmental heterogeneities on the behavior of the group and of its members. Such heterogeneities are known to have a major impact on animal decision-making and to directly affect the dynamics of group formation (Bode & Delcourt, 2013, Delcourt, Bode, & Denoël, 2016).

If the studied species is not highly gregarious and/or if the number of arms (or zones) is large, it is possible that a majority in any zone will be rarer. The quantification of majority states, majority transitions, and cohesion indices are useful information about the degree of gregariousness of the individuals, notably to test how different factors (e.g., physiological states, ratio of bold and shy individuals, species, or time of day) influence cohesion in the maze. Moreover, such studies could be used to explore, in weakly cohesive or nonsocial species, whether each individual moves completely independently of others, or tends to avoid them. The distribution of individuals across different discrete zones can be informative in this respect. Individuals tending to avoid others will be more homogeneously spread than is predicted by chance. Individuals that are simply ignoring others in their individual choices will be dispersed across different zones following a probability distribution of combination laws (which can be modified to take into account individual preferences, if necessary). A social species will be significantly less dispersed than predicted by combination laws. The comparison of these predicted distributions to the observed distribution can be used as a test to demonstrate the degree of social tendency in a species.

The radial arm maze paradigm presents several other advantages for the study of collective behavior: (1) it is easy to set up; (2) it can be applied to most social species, aquatic or not; (3) guillotine doors can be placed at the entrance to each arm to temporarily or permanently restrict the number of options (Miller et al., 2013); and (4) long periods of experimentation can be carried out without having to remove individuals from the arena between choices, thereby minimizing manipulation-induced stress.

Limitations of the method

In a radial arm maze, two fish located in different zones are not necessary completely disconnected from each other or unable to interact. For example, a fish might be able to perceive by olfaction that another individual was present in a particular arm recently (Sorensen & Wisenden, 2014). Such detections, in addition to other cues (e.g., the presence of feces), can influence the probability that an individual will stay or leave that arm. More direct interactions are also possible. Fish can perceive conspecifics by vision and by their lateral line (Partridge & Pitcher, 1980). Vision is most important for long-distance interaction, for maintaining group cohesion by attraction (e.g., for joining a group or avoiding being isolated from a group). The lateral line is most important for repulsion in short-distance interaction, to avoid collisions and to provide information about the speed and direction of near neighbors (Partridge, 1982). In our experimental setup, a fish located in an arm can visually perceive a fish in the opposite arm, but this is less likely for other arms, since the walls of the maze will generally interfere. If the lateral line sense is more adapted for short-distance perception (Mogdans & Bleckmann, 2012; Yang et al., 2006), the perception of vibration or infrasound produced by another individual might be transmitted at some distance as an imprecise cue. Reflection by the walls of the maze and the attenuation of this signal with the cube of the distance (Partridge & Pitcher, 1980) make this mode of interaction probably quite inefficient at larger distances. Nevertheless, some of these sensory modalities can be blocked by the structure of the maze, and others not, offering an opportunity to explore the respective role of different perceptual modalities in the individual decision to join or leave a group or a zone. For example, it is possible to construct a radial maze from transparent plastic, in which case visual cues would not prevent detection of conspecifics in adjacent arms, but mechanosensory cues would still be blocked.

The design of a radial maze must take into account the body size and number of individuals used. Trivially, it is important for fish to have sufficient space to make individual and collective choices. We suggest that the experimental setup must be at least large enough so that the entire group can comfortably fit in one arm.

Measuring collective behavior in the radial arm maze

Measuring the collective dynamics of animal groups is made simpler by the discretization of space offered by the radial arm maze. As we demonstrated in our proof-of-concept experiment, it is not necessary in this setup to extract each animal’s trajectory (Delcourt, Denoël, Ylieff, & Poncin, 2013) or to determine the identity of each individual (Pérez-Escudero et al., 2014) in order to identify dynamic social processes at the scale of the group. Instead, we resorted simply to counting the number of individuals in each section of the maze, a process that can easily be automated, as demonstrated by the image-processing software provided with this article, which we validated against human counters. Therefore, it is possible with this paradigm to run and analyze very long experiments (the experiments in our study lasted 12 h and were recorded at one frame per second) without requiring exceptional computing resources. Obviously, not having access to individual identities of each member of the group will limit this counting method to answering questions about the collective dynamics of the group. However, in cases in which individual identities are necessary, more advanced tracking tools (e.g., Pérez-Escudero et al., 2014) can be combined with the radial arm maze setup to determine where each individual is exactly located in the maze.

The counting data that we collected allowed us to determine the distribution of group sizes as a function of time as well as the presence of majority choices at any point during each experiment. As is illustrated in Fig. 4, it is easy to analyze and visualize the sequence of choices made by the group by calculating the transition matrix and diagram for the group majority between each of the maze’s arms. This is a convenient way to detect the existence of algorithmic behaviors (stereotyped movement patterns, generally dependent only on the immediately previous choice; Hughes & Blight, 1999; Roitblat et al., 1982) and to have a metric against which to compare the predictions of models and computer simulations, for instance.

Group cohesion—one of the most important characteristics of group behavior—is usually evaluated on the basis of the relative locations of the group members (e.g., using nearest-neighbor distance, the Clark–Evans index, dispersion indexes, the G function, or compactness; see Delcourt & Poncin, 2012, for a review). These metrics cannot be used easily in structured spaces, such as the radial arm maze or many natural environments, where individuals can be close to each other but unable to interact directly because of barriers between them. We proposed a new index to measure group cohesion in a structured space. Denoted Ic, this index quantifies the degree of cohesion, taking into account the number of groups, their respective size, and their distribution in the various zones of the space. Our cohesion index varies between 0 and 1 and is based on the number of individuals in each zone only, without taking into account the relative positions of the individuals. This parameter is also corrected so as to normalize the effect of the total number of individuals and zones in the space, and so could be used to compare the cohesion of groups of different sizes in different spaces. We did not conduct experiments here to study the impact of heterogeneity, and we cannot know what effect its variation might have on behavior. We can speculate that, in a heterogeneous environment, cohesion could be affected in two opposite ways. In more heterogeneous environments, individuals may be more likely to lose sight of conspecifics, which might increase group fission, so that Ic could decrease. However, groups may choose to spend longer in zones with more in them (such as plants that offer shelter, for instance), which might also be reinforced by social facilitation. This would serve to increase cohesion and Ic.

Conclusions

We have proposed a new standardized tool to investigate collective exploration and decision-making that makes it possible to study group cohesion (the degree of aggregation) and the motion of the majority, two of the most important characteristics in collective behavior. Because classical parameters dedicated to the measurement of the degree of cohesion are not well-adapted to the radial maze, a new cohesion index was developed that takes into account the number of groups and their respective size. This cohesion index is normalized, allowing for comparisons between groups of different sizes, and allows for the comparison of cohesion between mazes with different numbers of arms or zones. In a proof-of-concept experiment with Golden shiners, we demonstrated the potential of this new method (radial maze + animal group + counting system), without the need for tagging the fish, tracking, or identifying individuals, but simply automatically counting the number of individuals in each defined zone. The performance of our counting system compares well to that of human scorers. The possibility for animal groups to make a large number of successive choices, each time via the central part of the maze, makes possible long-duration experiments without the intervention of the experimenter, eliminating a significant source of stress that could affect the results. In Appendix S1, we present tools to calculate partitions, combinations of partitions, number of partitions, Dmin, and Ic.