The analysis of 3-D hand movements in interceptive tasks, such as ball catching, is methodically difficult due to the complex trajectory of the interceptive movement. The catcher can intercept the object at several positions along its trajectory within a certain time window (Cesqui, d’Avella, Portone, & Lacquaniti, 2012). To do so, the catcher must guide the hand toward the ball’s future trajectory on the basis of temporal and spatial estimations (López-Moliner, Brenner, Louw, & Smeets, 2010). These temporal and spatial estimations are based on optical information about the spatio-temporal properties of the object (Diaz, Cooper, Rothkopf, & Hayhoe, 2013; Hayhoe & Ballard, 2005; Huys & Beek, 2002; Zago & Lacquaniti, 2005). Depending on how the catcher anticipates the ball’s trajectory in space and time, the overall movement of the hand can be curved in a complex manner and can have an irregular velocity profile that is often interpreted as reflecting feedback-based adjustments during the movement (Dessing, Peper, & Beek, 2004).

For the analysis of grasping objects, hand movements are typically divided into different movement phases (Cesqui et al., 2012; Jeannerod, 1988; Lee, Port, & Georgopoulos, 1997; La Scaleia, Zago, & Lacquaniti, 2015; Yeo, Lesmana, Neog, & Pai 2012). Jeannerod suggested two phases. The first phase consists of an initial fast arm movement, whereas the second phase consists of a slower arm movement beginning after maximum finger aperture, during which the fingers close to grasp the object. Other authors have suggested three phases for interceptive actions: a gross spatial orientation, followed by a fine spatial orientation, and eventually the grasping action (Alderson, Sully, & Sully, 1974; Laurent, Montagne, & Savelsbergh, 1994). According to yet another view, the planning and execution of interceptive and grasping movements constitute a continuous process (Cuijpers, Smeets, & Brenner, 2004; Smeets & Brenner, 1999). Although the concepts that are based on movement phases may help identify episodes over the course of executed movements, the concept that is based on continuous processing stresses the dynamical nature of planning, execution and correction. Thus, the planned endpoint of a movement may change dynamically during even rapid interceptive movements (Brenner, Smeets, & de Lussanet, 1998). Moreover, for interceptive movements the final interception point, which can be anywhere on the trajectory of the ball, may evolve over time while the catcher moves their hand.

To simplify the analysis of interceptive behavior, experiments can be designed in 2-D space—for example, by moving a fingertip or a mouse cursor across a flat surface (e.g., Bosco, delle Monache, & Lacquaniti, 2012), a pen over a tablet (e.g., Aivar, Brenner, & Smeets, 2008) or by manual interaction with a mechanic device that allows only two degrees of freedom (e.g., Gomi & Kawato, 1996). Nevertheless, 2-D paradigms cannot always replace 3-D ones. Consequently, the question of how to analyze complex movements without losing essential information remains important. Evidence suggests that aspects of motor control are habitual rather than optimal (de Rugy, Loeb, & Carroll, 2012). This means, that movement variations (such as moving to a different target location) tend to affect just few aspects of a complex 3-D movement. However, even if not all available degrees of freedom are exploited during natural movements, it is not trivial to choose the relevant dimensions. It is known that different aspects of a rapid movement can be controlled independently, and can depend on different sensory information. For example, apparent velocity influences acceleration but not direction (Smeets & Brenner, 1995a). Acceleration, direction, and a movement’s extent are controlled independently (Brenner, de Lussanet, & Smeets, 2002; Favilla & De Cocco, 1996; Favilla, Gordon, Hening, & Ghez, 1990; Messier & Kalaska, 1997). For catching, two task aspects are of central importance for the overall arm movement—namely, bringing the hand on the trajectory of the ball, and arriving in time and with the right relative velocity in relation to the ball.

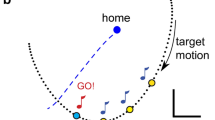
The method presented here provides a means to decompose the 3-D hand movement into functional phases based on these two aspects (cf. Fig. 1). The first aspect, the movement of the hand toward the ball’s trajectory, is defined as the development of the minimum distance between the hand and the parabola of the ball over time (MDHP trajectory: arrows in Fig. 1). Specifically, we will show at which time the catching movement becomes goal-directed—that is, from which time the catcher presumably anticipates the ball’s future trajectory.

Fig. 1
figure 1

Two examples (panels a and b) of the 3-D trajectory of the hand [\( \overrightarrow{P_H}(t) \), red curve] and the ball (blue curve). The red square indicates the movement initiation, and the red star marks the catching position. The gray lines represent the 2-D projections of the hand trajectory. The green curve [\( \overrightarrow{P_B}\left(\uptau \right) \)] shows the projection of the hand’s movement on the ball’s trajectory. Arrows show the shortest distance of the hand to the ball’s trajectory, MDHP(t i )

Full size image

Since the movement is toward a moving target, it is likely that the hand starts to move when the ball becomes visible, rather than when it becomes clear where the ball will be intersected. The exact future trajectory of the ball may become available to the catcher after the movement onset. Thus, we hypothesize that the MDHP trajectory becomes minimally jerked from this point onward. We want to quantify the time point at which the approximation to the ball’s parabola becomes goal-directed. Although the principles that underlie the control of a goal-directed movement are not yet completely clear, many studies have shown that goal-directed movements tend to be smooth—that is, they are minimally jerky (Desmurget, 1998; Kistemaker, Wong, & Gribble, 2014). A minimum jerk trajectory can accurately capture the kinematic features of goal-directed movements (Flash & Hogan, 1985; Hogan, 1984). For instance, it has been used to describe point-to point movements (Thoroughman, Wang, & Tomov, 2007; Wolpert, Ghahramani, & Jordan, 1995) and grasping movements (Smeets & Brenner, 1999), and to describe movement corrections when a sighted target is displaced (Wijdenes, Brenner, & Smeets, 2011). The minimum jerk trajectory has also been used to describe 3-D hand movements in interceptive tasks. In our analysis, a minimum jerk trajectory was fitted for each dimension of the reaching movement, and the integrated error was calculated (Fligge, McIntyre, & van der Smagt, 2012).

We employed the minimum jerk fit as an analysis tool, on the basis of the argument that a nonjerky trajectory is evidence that the movement may be goal-directed. Note that the trajectory of the ball may be reached before the ball arrives there, and that the hand may move for some time along the trajectory of the ball. We predicted that the MDHP trajectory can be segmented into an approximation phase to the ball’s parabola, and an interception phase when the trajectory of the target is reached.

The second aspect that we analyzed was the movement of the displacement of the nearest position to the hand on the parabolic trajectory (the green curve in Fig. 1). The catcher can move the hand toward the ball on its trajectory, to follow the trajectory of the ball downward in order to reduce the relative speed of the ball, or remain at the intersection point and wait for the ball to approach the hand (Fligge et al., 2012).

Method

The following section explains the method in detail, illustrated by two trials of a catching experiment (see the Data Analysis section). We also describe the experimental application, in which two different conditions of a catching experiment were used, providing a demonstration of the practical use of the method.

Experimental application

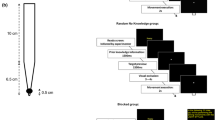
To demonstrate the practical use of the method, we used data from an experiment to present two conditions in which 20 subjects caught a tennis ball with their dominant hand. The ball was thrown by an assistant, over a bar placed at the subject’s height. Vision of the first half of the ball’s flight could be either occluded (OV) or full (FV) (Fig. 2). Each condition was repeated ten times, in separate blocks, the order of which was counterbalanced across subjects. The inclusion criterion for taking part in this study was to have no prior juggling experience. The subjects were informed about the procedure and the aim of the study and then gave their written informed consent to participate. The study was approved by the local ethics committee (Approval No. 2015-16-LSl).

Fig. 2
figure 2

Setup used in the experiment. The assistant on the left threw the ball over the horizontal bar to a right-handed subject (for left-handed subjects, the setup was mirrored). (a) Full-vision (FV) condition. (b) Occluded-vision (OV) condition. Reference system: The ball’s trajectory defined the x–z plane (i.e., the ball plane was at y = 0). Positive x was defined in the direction of the ball’s movement, and positive z was upward

Full size image

Kinematic data for the hand, the ball, and the bar were recorded in 3-D with a motion capture system (Qualisys, Göteborg, Sweden) at 400 frames per second. Three infrared-reflective markers were each placed on the tips of the thumb, the index finger, and the pinkie finger, and two markers were attached to the inner and the outer side of the ventral wrist. The tennis ball was covered with infrared-reflective foil.

The average horizontal distance between the releasing and catching positions was 0.53 ± 0.07 m (mean ± SD). At the beginning of each trial, the catching arm and hand were extended and positioned laterally to the thigh. The initial distance between the hand and the ball’s parabola was on average 0.35 ± 0.08 m. The start of the kinematic recording was accompanied by an acoustic signal, after which the ball was thrown tightly across the horizontal bar. If the catcher dropped the ball, the trial was repeated at the end of the block (1.5% of all trials in the OV condition). The mean flight times of the balls were 709 ± 42 ms in the FV condition and 709 ± 34 ms in the OV condition. On average, the first 159 ± 17 ms of the flight were occluded in the OV condition.

All 3-D trajectories of the reflective markers of the hand, the bar, and the ball were reconstructed (Qualisys Track Manager, version 2.11). If, for a given trial, the number of consecutive missing values for a hand marker exceeded 50 ms, that trial was excluded from the analysis (excluded trials: FV, N = 17; OV, N = 19).

Data analysis

The full analysis was programmed in MATLAB (Version R2017a, The MathWorks, Natick, MA, USA). A MATLAB script (OCAI_Analysis.m), including functions and examples, is provided in the supplementary materials (available at https://uni-muenster.sciebo.de/index.php/s/uzKAdrzKubQDyni).

The 3-D kinematic data of the ball flight and the hand were used for the analysis. Two examples of the kinematics of the hand and ball movements are shown in Fig. 1. The position of the hand (P H ) was defined as the mean of the five markers placed on the hand. The position of the ball (P B ) was defined as a parabola fitted to the measured free-flight part of the ball’s trajectory.

The releasing time (t release) was defined as the maximum upward velocity of the ball (López-Moliner et al., 2010). After release, the ball decelerates due to gravity. The maximum downward velocity was defined as the catching time (t catch).

We first (1) calculated the MDHP trajectory. This trajectory was (2) segmented into an approximation phase, toward the target’s parabola, and an interception phase, beginning when the parabola of the target was reached. In the next step, (3) we segmented the approximation phase into an initial approximation and a smooth approximation. Eventually, (4) we evaluated in which direction the catcher was moving and the velocity in relation to the ball when intercepting the object.

Calculation of the MDHP trajectory

The first step was to determine the minimum distance between the hand and the ball’s parabola over time (black arrows in Fig. 1). The minimum Pythagorean distance from the position of the hand \( \overrightarrow{P_H}\left({t}_i\right) \) at time t i in 3-D space to the trajectory of the ball’s parabola \( \overrightarrow{P_B}\left(\tau \right) \) was defined as

$$ MDHP\left({t}_i\right)=\underset{\tau }{\min}\left(\sqrt{{\left({P}_{Bx}\left(\tau \right)-{P}_{Hx}\left({t}_i\right)\right)}^2+{\left({P}_{By}\left(\tau \right)-{P}_{Hy}\left({t}_i\right)\right)}^2+{\left({P}_{Bz}\left(\tau \right)-{P}_{Hz}\left({t}_i\right)\right)}^2}\right), $$

such that \( \overrightarrow{P_B}\left(\tau \right) \)is the position on the parabola that minimizes the Pythagorean distance for each time t i . \( \overrightarrow{P_B}\left(\tau \right)\ \Big( \)green trajectories in Fig. 1) also shows the projection of the hand’s movement along the parabola. The MATLAB function MinDist2Parabola.m implemented the analytic solution to this equation. Examples of the resulting distance trajectory, MDHP(t), are shown in Fig. 3 (black trajectories). The trajectories were smoothed with a 6th-order, two-way Butterworth low-pass filter with a 15-Hz cutoff frequency. We selected the order and cutoff frequency using an FFT cumulative power analysis (Sinclair, Taylor, & Hobbs, 2013).

Fig. 3
figure 3

Two examples of the analysis of MDHP trajectory (the same two examples are presented as in Fig. 1). Note that the MDHP trajectory at impact time is close to, but not exactly, zero. This is because the impact point can be anywhere on the hand. (a) The smooth approximation starts 217 ms before impact time. (b) The smooth approximation starts 585 ms before impact time (t = 0)

Full size image

Segmentation of the MDHP trajectory into the approximation phase and the interception phase

Next, we segmented the MDHP trajectory into functional phases. The first step was division into an approximation to the parabola and an interception phase along the parabola of the ball. The catcher’s hand could move along the trajectory of the ball if the distance of the hand to the parabola was small enough to grab the ball (e.g., area = MDHP < 0.1 m, or when the parabola intersects with the palm). Within this area, we calculated the first peak deceleration of the MDHP trajectory as the beginning of the intersection phase (t parab) (Fig. 3, red stars).

Segmentation of the approximation phase into an initial approximation and a smooth approximation

The segmentation of the approximation phase into an initial approximation and a smooth approximation was done with a fit of a minimum jerk trajectory. Jerk is defined as the third time derivative of position (\( \overset{\dddot{}}{x}\Big) \). Hence, the minimum jerk trajectory J min between an initial time t i and a final time t f minimizes the sum of the squared jerks along an object’s trajectory to generate the smoothest trajectory using the location, velocity, and acceleration at times t i and t f , as well as the time duration and the measured frequency of the trajectory D(t) (calculated by the MATLAB function minimumJerk.m; Movellan UCSD, 2011):

$$ {J}_{min}=\min \underset{t_i}{\overset{t_f}{\int }}{\overset{\dddot{}}{x}}_1{(t)}^2 dt. $$

To quantify the trajectory toward the ball, we calculated the minimum jerk trajectories for each time step before time t parab (i.e., backward in time) until the integrated root mean square error in position (RMSE) exceeded 1 mm (t goal). We chose an RMSE of 1 mm because it is close to the spatial resolution of the motion capture system (spatial error: 0.74 mm ± 0.12 mm). The smooth approximation phase (beginning at t goal) was preceded by the initial approximation phase. The beginning of the movement was defined by a threshold of 0.1 \( \frac{\mathrm{m}}{\mathrm{s}} \) in the velocity of the MDHP trajectory.

Hand projection along the parabola

The projection of the hand’s movement along the ball’s parabola, P B (τ), shows the direction that the catcher is moving on the parabola. The velocity \( {V}_{\overrightarrow{P_B}\left(\tau \right)} \)shortly before the ball touched the hand (one sample before t catch) indicates whether the catcher moves toward the ball on its trajectory, follows the trajectory of the ball downward, or remains at the intersection place to wait for the ball approaching the hand.

Statistical analysis

The statistical analysis was performed with MATLAB. Both successful and unsuccessful trials were included for the analysis. All calculated parameters (initial approximation phase, smooth approximation phase, and interception phase; see Fig. 4) were averaged for each subject. Since all parameters were normally distributed (according to the Kolmogorov–Smirnov test), we used paired t tests to compare the kinematic parameters of the OV and FV conditions. The level of significance was set to α < .05 and adjusted according to Bonferroni–Holm. For all significant results, Cohen’s d was computed as a measure of the statistical effect size (Lakens, 2013).

Fig. 4
figure 4

Representative MDHP trajectories for each subject for mean initial distances of 0.33 ± 0.08 m (FV) and of 0.36 ± 0.08 m (OV). The symbols are the same as in Fig. 3. The black MDHP trajectories were selected from the FV condition, and the gray ones from the OV condition. Impact is at t = 0

Full size image

Results

The same two examples from Fig. 1 are shown as the analyzed MDHP trajectories in Fig. 3. In contrast to Fig. 1, Fig. 3 reveals that the two movements differed markedly in the ways in which the hand moved to the parabola, which was quantified by the minimum jerk fit (red curves in Fig. 3). In Fig. 3a, the movement was corrected at 217 ms before impact time. From then on, the hand approached the parabola smoothly, to arrive just in time. Although the ball was caught, the center of the hand was still relatively far from the parabola. In Fig. 3b, the movement approached the parabola smoothly almost from movement onset. The hand arrived early at the parabola, and accordingly, more than 200 ms remained for the final interception. Consequently, the final part of the movement was strongly curved (cf. Fig. 1).

Figure 4 shows further examples in the two conditions for all 20 subjects. In almost all examples, the movement started much later for the OV than for the FV condition (in some cases, the subject started to move even before the ball became visible: e.g., the gray curves for Subjects 2, 9, 12, 18, and 20). Since the ball became visible much later in the OV than in the FV condition, the course of the parabola was known later to the subject. Accordingly, the beginning of the smooth phase of the MDHP trajectory in the OV example occurred after that in the FV example for almost all subjects (with the exception of Subject 3). Finally, in most of the examples in Fig. 4, only a part of the MDHP trajectory accords with a minimal jerk trajectory. Some of the trajectories show a very strong correction [e.g., the OV condition for Subjects 9, 10, and 14]. Some trajectories are almost entirely smooth [9 (FV), 10 (FV), 15 (both), and 18 (FV)], and thus are according to a planned movement.

Figure 5 summarizes the results of the analysis for the FV and OV conditions. The smooth approximation phase starts at 332 ± 75 ms before impact time in the FV condition, and at 225 ± 45 ms before impact time in the OV condition. The difference between these time points was statistically significant [t(19) = 6.66, p < .001, Cohen’s d = 1.5]. Nevertheless, the initial approximation phases (indicated as the gray bars in Fig. 5) lasted for comparable durations and did not differ significantly between the conditions [t(19) = – 0.57, p = .57].

Fig. 5
figure 5

Comparison of the three subsequent movement phases in the FV and OV conditions as a function of the ball flight time. In the OV condition the movement initiation is delayed, which is reflected by shorter movement times. Note that the beginning of the hand movement occurs within about 200 ms after ball release. This is due to sensory information the catcher could use to initiate the movement before the ball was released (acoustic signal, throwing movement). Impact is at t = 0

Full size image

All subjects moved the hand up from its initial position, so for most of the movement the velocity along the parabola (\( {V}_{\overrightarrow{P_B}\left(\tau \right)} \)) was negative (i.e., opposite to the direction of the ball). At the end of the movement, \( {V}_{\overrightarrow{P_B}\left(\tau \right)} \) was approximately zero for both conditions (FV, – 0.0006 \( \frac{\mathrm{m}}{\mathrm{s}} \) ± 0.0011 \( \frac{\mathrm{m}}{\mathrm{s}} \); OV, – 0.0013 \( \frac{\mathrm{m}}{\mathrm{s}}\pm \)0.0012 \( \frac{\mathrm{m}}{\mathrm{s}}\Big), \) indicating that the subjects stopped the movement to catch the ball at the end of the interception phase.

Discussion

Most humans find it easy to catch a gently thrown ball (López-Moliner & Brenner, 2016). Nevertheless, the perceptual–motor task is highly complex, which is mirrored in its kinematic profile. This complex and irregular kinematic profile indicates that the catcher updates the prediction of the target’s trajectory (Dessing et al., 2004). Thus, the final interception point might not be predefined at the beginning of the movement, but instead might evolve over time while the catcher moves the hand.

It might sound surprising that corrections to the movement are made at the onset of the movement, given the distance from the brain to the muscles of the arm and the physiological delay of contractions. Although the delay of online corrections to visual perturbations can be remarkably short (~110 ms; Brenner & Smeets, 1997; Brenner et al., 1998; van Donkelaar, Lee, & Gellman, 1992) as compared to the duration of a catching movement, this is still a long time. However, it has been shown that even so-called “ballistic” movements are under continuous visual control (Brenner et al., 1998; Smeets & Brenner, 1995b). It is thought that the brain represents an efference copy of the motor commands (Sperry, 1950; von Holst & Mittelstaedt, 1950) and can, by applying an internal model (Melcher, 2011), continuously predict the accuracy of the commands based on the current sensory information, thus making appropriate corrections. Consequently, as the ball has been visible for a longer time, the estimate of where it can be intercepted becomes more accurate. Our concept underlying the quantification of a planned, goal-directed movement is the large empirical basis suggesting that planned movements tend to be smooth—that is, are minimum-jerk-like (e.g., Kistemaker et al., 2014). Although the goal of the present study was to develop new analysis tools, rather than to present new experimental results, these results are in line with the online correction of motor control.

Using the method, we calculated the anticipation toward the target’s trajectory on which the endpoint was located. In cases in which the catcher anticipated the final endpoint and not the ball’s trajectory, the duration of the interception phase would be reduced (see, e.g., Figs. 1a and 3a).

Overall, two aspects of a catching action were calculated with the method and applied in two conditions of an experiment—that is, the hand’s movement toward the ball’s trajectory (MDHP trajectory) and the hand’s velocity along the parabola. The MDHP trajectory can be used to estimate the dynamics of the subject’s prediction of where the ball will fly. We have hypothesized that the MDHP trajectory becomes minimally jerked once the subject does not correct a movement toward the ball’s trajectory anymore. The aim of the analysis was to identify the transition between the initial approximation at the start of the catching motion (which is corrected while moving) and the smooth approximation, which is goal-directed toward the trajectory of the ball.

In the OV condition, the visual information was delayed by the occlusion of the initial part of the ball’s trajectory. We found, as predicted, that the smooth approximation phase of the movement started significantly later, supporting the plausibility that the method can estimate the instant when the subject has anticipated the trajectory. Moreover, the Initial approximation phase of the movement was of the same duration (on average), indicating that the subjects needed the same time to estimate the ball’s trajectory in each case.

Finally, the minimal jerk fit produced sensible results for the individual trajectories of each subject, since the smooth approximation phases differed considerably between the trials, not only in their start times, but also in their start positions (e.g., Fig. 3a vs. b).

At the beginning of the interception phase, the subject had reached the ball’s trajectory. This final movement phase typically consisted of fine-tuned movements that did not reflect a minimum-jerk approach. Such small movements at the end are typical for movements toward a nonrigid goal. The hand also might undershoot or overshoot the parabola during the intersection phase. In the latter case, the distance to the parabola will increase again. A visible overshoot of the hand was detected in six trials (e.g., a small overshoot can be seen for Subject 10 [FV] in Fig. 4).

The second aspect was the hand’s velocity along the parabola, which dropped to zero for both conditions. A still position can be expected for a strategy to catch a ball securely, in the case of externally thrown balls. One might expect a nonzero velocity in other cases—for example, when the timing of the ball’s arrival is better predictable. This would be the case for cyclic self-thrown balls (e.g., juggling), for which it would be advantageous to move the hand along with the ball at the time of catching. This needs to be addressed in future experiments.

Summary and applications

We introduced a new method for analyzing the catching of free-flying targets in a task-relevant manner. To achieve this, the movement component toward the target’s trajectory (minimum distance of hand to parabola, MDHP) and the movement’s projection on the target’s trajectory were analyzed. The method has the advantage that it reduces the complex 3-D data to a functional 1-D movement (MDHP trajectory), which makes it easier to quantify essential movement components and to make further analysis. Relying on the feature that goal-directed movements are generally smooth, the time from which the catcher recognizes the goal (the target’s future trajectory) is calculated as the time from which the MDHP trajectory can be described by a minimum jerk trajectory.

The results of the catching experiment show that the method can be very helpful to analyze the corrective control process experimentally, in a manner that would not be possible when inspecting just the 3-D movements. Using this method, it is possible to quantify the influence of different conditions on the catching performance by looking not only at successful catches, but also the anticipatory behavior of the catcher to a moving object. The start of the anticipatory movement is relevant in relation to the ball’s flight. With further studies, the method could evaluate which part of the ball flight is relevant to gain useful information for the movement planning.

Our method can be used to analyze various kinematic data of interceptive actions in catching tasks, as it allows a differentiated view on object anticipation and can be used for a discussion about underlying control strategies during catching. For example, it can be used to compare the approach of the moving hand using a ball’s different approaching direction (Dessing et al., 2004; Montagne, Laurent, Durey, & Bootsma, 1999; Peper, Bootsma, Mestre, & Bakker, 1994). Alternatively, experienced and novice catchers can be measured, and the variation in the different stages of learning can be compared. This method can also be used to analyze ball drops and misses. If no final catching point is present, there is still a time of closest approach to the target trajectory. Thus, it can be established whether a miss is due primarily to a temporal or spatial prediction error. If a touch of the ball is existent, as it was in our experiment, it can be used as the interception point and the trial can be included in the analysis.

Our analysis extends previous research by considering the functional aspects of the kinematics of interceptive hand movements toward a moving object. The method takes into consideration the fact that the interception of a moving object has multiple potential endpoints. Thus, in our procedure the endpoint extends along the trajectory of the object, which is included in the analysis.

Author note

We thank Maike Scheffer and Marius Krösche for their support with data acquisition, and Cassandra Kraaijenbrink, Maarten van den Heuvel, and Hugh Riddle for corrections to the manuscript. We also thank the anonymous reviewers for their constructive comments, which greatly improved the manuscript.