Regularization and a general linear model for event-related potential estimation

Abstract

The usual event-related potential (ERP) estimation is the average across epochs time-locked on stimuli of interest. These stimuli are repeated several times to improve the signal-to-noise ratio (SNR) and only one evoked potential is estimated inside the temporal window of interest. Consequently, the average estimation does not take into account other neural responses within the same epoch that are due to short inter stimuli intervals. These adjacent neural responses may overlap and distort the evoked potential of interest. This overlapping process is a significant issue for the eye fixation-related potential (EFRP) technique in which the epochs are time-locked on the ocular fixations. The inter fixation intervals are not experimentally controlled and can be shorter than the neural response’s latency. To begin, the Tikhonov regularization, applied to the classical average estimation, was introduced to improve the SNR for a given number of trials. The generalized cross validation was chosen to obtain the optimal value of the ridge parameter. Then, to deal with the issue of overlapping, the general linear model (GLM), was used to extract all neural responses inside an epoch. Finally, the regularization was also applied to it. The models (the classical average and the GLM with and without regularization) were compared on both simulated data and real datasets from a visual scene exploration in co-registration with an eye-tracker, and from a P300 Speller experiment. The regularization was found to improve the estimation by average for a given number of trials. The GLM was more robust and efficient, its efficiency actually reinforced by the regularization.

Introduction

The event-related potential (ERP) technique is a classical technique (e.g., Luck, 2014) used to study the neural responses to specific events such as the presentation of visual stimuli or auditory stimuli. Using this technique, many cognitive processes have been explained (e.g., Key, Dove, & Maguire, 2005). One popular way to record brain activity is to use electroencephalography (EEG) at the surface of the scalp (see Niedermeyer & Silva, 2005). However, the resulting signal-to-noise ratio (SNR) is very low due to ongoing brain activities. To overcome this drawback, the stimuli are presented repeatedly (typically a few tens of time at least), so that the neural response evoked by these stimuli is obtained by averaging the epochs that are time-locked on each stimulus onset. However, the ERP estimation is only unbiased if two main conditions are verified. (1) The (zero mean) noise due to ongoing brain activities needs to be decorrelated across the epochs. (2) Only a single potential should be elicited at each epoch and it should be elicited within each epoch. In this article, these essential conditions are discussed in practical situations and a methodology based on the general linear model (GLM) is proposed to tackle experiments where the two required conditions are not satisfied. Moreover, a regularization method to estimate the ERP is proposed, especially if the number of epochs is low.

Firstly, if the condition on the zero mean noise decorrelation across the trials is achieved, the SNR increases linearly with the number of epochs. Thus, the more the stimuli are repeated, the better the SNR. However, with a large amount of stimuli, the experiment becomes more time-consuming and very repetitive for the participants. In addition, and more importantly, in practice the linear increasing is not always verified because ongoing activity may be correlated from one trial to another one and the resulting SNR after averaging is lower than expected for a given number of trials. In this article, the Tikhonov regularization (Tikhonov 1963) is used in the ERP estimation to increase the SNR for a given number of trials. The strength of the regularization is given by the value of the regularization parameter. The choice of this ridge parameter is a very common but nonetheless a difficult problem requiring the bias and the variance of the estimator to be balanced as well as possible. In the same context as this EEG study, Lalor and colleagues proposed an approach with a second-order Tikhonov regularization to estimate the event-related potential (ERP). However, they empirically chose the ridge parameter (Lalor, Pearlmutter, Reilly, McDarby, & Foxe, 2006); (Lalor, Power, Reilly, & Foxe, 2009) to give a good compromise between the off-sample errors and the weakness of the potential peaks. To estimate this parameter automatically, the two classical methods are the generalized cross-validation (GCV) procedure (Golub, Heath, & Wahba, 1979) and the “L-curve” method (Engl & Grever, 1994). Also for EEG analysis, Subramaniyam and colleagues (Subramaniyam, Väisänen, Wendel, & Malmivuo, 2010) compared these two methods to estimate the visually evoked cortical potentials. In their study, the Tikhonov regularization was used to solve the inverse problem of the source localization to find the spatial cortical distribution at the presentation of emotional faces. When applied separately on the EEG signals for each subject and each condition, they found that the regularized solutions were more robust with the ridge parameter computed by the GCV procedure rather than by the “L-curve” method. Indeed, the ridge parameter obtained by the “L-curve” method was too large compared to the parameter obtained by the GCV procedure when the SNR was low: as a consequence, the solution was over-smoothed and spatially blurred. Here, in this study, two estimation methods of the regularization parameter are compared but in a context of temporal estimation of the evoked potentials. Moreover, an inter-subject analysis is carried out as is usual for ERP experimental designs instead of an intra-subject study as in (Subramaniyam et al. 2010). The regularization process is thus implemented at the overall level for the whole dataset, but also compared with a regularization for each subject.

Secondly, the last condition for an unbiased estimation by averaging can only be achieved if just a single identical potential is elicited in each epoch time-locked on the event’s onset. This condition does not consider possible distortion of the target neural response due to experimental design and/or latent cognitive processes. For example, Luck in (Luck 2014) described an ERP experiment in which the inter stimuli intervals (ISI) values were between 300 and 500 ms and the studied components were P2, N2, and P3 with latencies between 200 and 400 ms. Luck warned against distortions due to the short ISI values: i.e., latencies of the elicited potentials are shorter than the ISI duration that leads to the overlapping responses evoked by two temporally consecutive stimuli. In this situation, more than one potential is elicited in an epoch so that the estimation by averaging is the summation of the delayed versions of the expected neural components. Consequently, this estimate is not the expected evoked potential itself, but the convolution of this potential with the distribution of ISI values inside one epoch. To reduce overlaps, the experimental design must control the ISI values as far as possible in agreement with the latencies of the expected potentials.

This issue had been addressed in the context of auditory evoked potentials, but it is also a central concern for the estimation of the visual potential elicited by ocular fixations, the eye fixation-related potential (EFRP) (Dimigen, Sommer, Hohlfeld, Jacobs, & Kliegl, 2011; Nikolaev, Meghanathan, & Leeuwen, 2016). Tanaka and colleagues (Tanaka, Komatsuzaki, & Hentona, 1996) had shown that recording auditory brainstem responses at high stimulus rate provided valuable information to detect auditory pathologies. Some methods were proposed to face the overlapping problem due to high stimulus rates. In 1982, Eysholdt and colleagues (Eysholdt and Schreiner 1982) had proposed the maximum length sequence technique, based on a pseudorandom arrangement of stimuli in a maximum sequence length. The evoked potential pattern was obtained by a deconvolution of the averaged responses. Then, another resolution method was developed, in the frequency domain, by adaptive inverse filtering (Hansen 1983). Three other methods, using cyclic stimuli sequences, were elaborated. (1) The continuous loop averaging deconvolution method (Delgado and Ozdamar 2004) consisted of acquiring data from non-isochronic stimuli sequences with a high presentation rate. Then, the deconvolution was performed by matrix computations in the time domain. (2) Jewett and colleagues (Jewett et al. 2004) had applied a similar method in the frequency domain and (3) a Wiener filter was used in (Wang, Özdamar, Bohórquez, Shen, & Cheour, 2006) to deconvolve evoked potential from the noisy observation given cyclic stimuli sequences in the frequency domain. All five of these methods have a common major limitation: they only consider one kind of stimulus, and hence a single elicited potential. Besides, we considered the ADJAR (adjacent response) algorithm developed by Woldorff in 1993 (Woldorff 1993). This algorithm iteratively estimates the average of previous and subsequent responses that are then subtracted from the target response, for the new iteration, and so on. It is a very popular algorithm and has been successfully used in several ERP studies to correct distortions due to overlap (Bekker, Kenemans, Hoeksma, Talsma, & Verbaten, 2005; Brannon, Roussel, Meck, & Woldorff, 2004; Brannon, Libertus, Meck, & Woldorff, 2008; Fiebelkorn, Foxe, McCourt, Dumas, & Molholm, 2013; Hopfinger & Mangun, 1998; Kenemans et al., 2005; Talsma, Doty, & Woldorff, 2007; Schmajuk, Liotti, Busse, & Woldorff, 2006) by an iterative deconvolution. However, in a previous article (Kristensen, Guerin-Dugué, & Rivet, 2015), we had shown that this algorithm presented some limitations as to the temporal distribution of the ISI values, especially for EFRP studies. With this recent technique, the EEG signal can be time-locked on the onset of the ocular fixations of the participants to extract EFRP (or eye saccade-related potentials if the EEG signal is time-locked on the onset of the saccades). Using ocular events, the ISI becomes the inter fixations interval (IFI), i.e., the duration between two consecutive fixations: this interval is thus defined as the duration of one fixation plus that of one saccade. These IFIs cannot be controlled experimentally, because they depend on the participant’s oculomotor pattern. On average, during experiments in reading or visual exploration, the IFIs are about 250–300 ms and thus, precautions are taken to face with overlaps between adjacent EFRPs to allow studies concerning late potentials such as P3 or N400 (latency of between 300 and 600 ms) (Devillez, Guyader, & Guérin-Dugué, 2015; Frey et al., 2013; Kaunitz et al., 2014). More recently, least-square based methods have been proposed to deconvolve multiple overlapping responses (e.g., Lalor et al., 2006; Rivet & Souloumiac, 2007; Burns, Bigdely-Shamlo, Smith, Kreutz-Delgado, & Makeig, 2013; Bardy, Dillon, & Van Dun, 2014; Crosse, Butler, & Lalor, 2015; Congedo, Korczowski, Delorme, et al., 2016; Dandekar, Privitera, Carney, & Klein, 2012). In (Bardy, Dillon, & Van Dun, 2014), a least-square method was proposed for the deconvolution of overlapping multiple responses, and this was applied to auditory potentials (Bardy, Dillon, & Van Dun, 2014; Bardy, Van Dun, Dillon, & McMahon, 2014). This method corresponds exactly to the first step of the xDAWN algorithm (Rivet, Souloumiac, Attina, & Gibert, 2009), which was designed to find optimal spatial filters for best classifying neural responses in the front of brain–computer interfaces. It was used for the first time for the deconvolution of saccadic potentials during free exploration (Dandekar et al. 2012), and for the deconvolution of EFRP during a visual search task on natural scenes in (Devillez, Kristensen, Guyader, Rivet, & Guérin-Dugué, 2015).

In (Lalor et al. 2006; Rivet and Souloumiac 2007; Rivet et al. 2009; Crosse et al. 2015), the least-square method deconvolved overlapping responses assuming that only a unique class of response was present: it only tackled the issue of intra-class overlapping response (i.e., overlapping of responses to the same class of stimulus). If several classes of stimuli are simultaneously present and overlap each other (i.e., inter-class overlapping responses), they must be considered separately by ignoring all the other ones. The least-square method proposed by Rivet and colleagues in the first stage of the xDAWN algorithm (Rivet, Souloumiac, Gibert, & Attina, 2008; Rivet et al., 2009; Rivet & Souloumiac, 2013), or in (Bardy, Dillon, & Van Dun, 2014; Burns et al., 2013; Congedo et al., 2016) extended the previously mentioned methods to the case of intra- and/or inter-class overlapping issues. It belongs to the general linear model (GLM) (Kiebel and Holmes 2003) that provides a very large and flexible framework, routinely used for fMRI studies. In fMRI literature, the GLM is used for the deconvolution of hemodynamic responses (Dale 1999). In the context of EEG studies, the linear analysis of multidimensional EEG signals has been also proposed (Parra, Spence, Gerson, & Sajda, 2005) as a general framework to extract the underlying neural sources or subtract interfering sources like eye movements. Linear discriminant analysis, principal component analysis and independent component analysis were revisited in this context. The linear model between the latent neural sources and the scalp potentials was addressed and solved using only the statistics of observed data with the stimuli and behavioral responses. The deconvolution of temporally overlapping components was mentioned as an application of the proposed methodology but the developments and examples given in (Parra et al. 2005) mainly concerned the estimation of spatial filters for underlying neural source extractions.

As in the work applied to the auditory evoked potentials (Bardy, Dillon, & Van Dun, 2014); (Bardy, Van Dun, et al., 2014), we plan to use the GLM for the deconvolution of the time-locked evoked potentials and thus manage the intra- and/or inter-class overlapping issues. With this GLM, different situations are addressed where the overlapping components may or may not be of the same nature. Besides in our work, which aims to improve the SNR for a given number of trials, the Tikhonov regularization is added to solve the GLM.

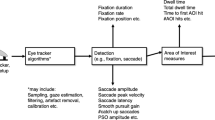
In “Theoretical developments”, the matrix framework for the usual ERP estimation is presented in more detail followed by the introduction of the regularization parameter and the GLM with the Tikhonov regularization. In “Methodology”, the methodology to assess the proposed algorithms is explained, based on artificial data simulations but also on real EEG signals from two experiments (1) free visual exploration to estimate EFRP, and (2) a “P300 Speller” brain computer interface. The results based on simulated and real data are presented and discussed in “Results on simulated signals”, “Results on EFRP estimation during a free visual exploration”, and “Results on P300 Speller data”, respectively. Finally, “Conclusions” summarizes the main results achieved and concludes this article.

Theoretical developments

In this section, we first explain the usual ERP estimation: the “Average” method. Then we introduce a matrix framework to present the regularization procedure and finally, the GLM is described in the context of the temporal deconvolution of overlapped evoked potentials.

Usual event-related potential estimation

To extract the evoked potentials, the temporal window of epochs must be sufficiently long to include the latency and the whole temporal evolution of the potentials of interest. The underlying assumption is as follows: at each presentation of a same stimulus, the same neural potential is evoked. Thus for the i ^th presentation, the observed neural response x _i (t) time-locked on the i ^th stimulus onset can be written as:

$$ x_{i}(t)=a(t)+n_{i}(t) $$

(1)

where a(t) is the evoked potential, and n _i (t) a noise corresponding to the on-going brain activity.

As the signal-to-noise ratio is very low, the stimuli have to be repeated several times. In the simplest configuration, one epoch is extracted at each trial. In this way, a(t) is estimated by averaging across these epochs:

$$ \hat{a}(t)=\frac{1}{E} \sum\limits^{E}_{i=1}x_{i}(t) $$

(2)

where E is the number of epochs.

This estimation is non-biased if the following conditions are fulfilled:

• only one deterministic potential, a(t), is elicited during the epoch synchronized with the stimulus;

• this potential has the same amplitude across the epochs;

• the noise is a zero-mean random variable and decorrelated from one trial to another one. As a consequence, the SNR increases linearly with E.

In “Regularization to reduce the number of trials” and “General linear model used to manage the overlapping issue”, we will explain why these conditions are not always verified in practice, but in this section, we first consider that the two first conditions have been fulfilled. To facilitate and justify the proposed theoretical developments, let us reformulate Eq. 2 in a matrix form.

For this purpose, Eq. 1 can be rewritten using matrix notations as:

$$ \forall i\in\{1,\cdots,N_{e}\},\quad \underline{x}_{i} = \mathbf{D}_{i} \underline{a} + \underline{n_{i}} $$

(3)

where $\underline {x}_{i}=[x_{i}(1),\ldots ,x_{i}(N_{e})]^{\dag }\in \mathbb {R}^{N_{e}}$ and $\underline {n_{i}}=[n_{i}(1),\ldots ,n_{i}(N_{e})]^{\dag }\in \mathbb {R}^{N_{e}}$ with ⋅^‡ the transpose operator. $\underline {a}\in \mathbb {R}^{N_{a}}$ is the vector of the response time-locked on the stimuli onset. N _e is the length of the epoch and N _a is the length of the response a(t). Finally, $\mathbf {D}_{i}\in \mathbb {R}^{N_{e} \times N_{a}}$ is a Toeplitz matrix¹ defined by its first column with entries are all equal to zero except the $\tau _{i}^{th}$ entry equal to one, with $\tau _{i}^{th}$ the onset of the i ^th epoch. Consequently, the epochs can be concatenated to obtain:

$$ \underline{x} = \mathbf{D} \underline{a} + \underline{n}, $$

(4)

with $\underline {x}=[\underline {x}_{1}^{\dag },\ldots ,\underline {x}_{N_{e}}^{\dag }]^{\dag }\in \mathbb {R}^{N}$ and $\mathbf {D}=[\mathbf {D}_{1}^{\dag },\ldots ,\mathbf {D}_{N_{e}}^{\dag }]^{\dag }\in \mathbb {R}^{N \times N_{a}}$ where N = N _e ×E. D is the concatenation of the matrices D _i with i = [1,…,N _e ]. This equation can be understood as the general linear model (GLM) with the matrix D as predictors, as it will be developed in “General linear model used to manage the overlapping issue”. Thus, with these notations, the neural response $\underline {\hat {a}}$ is the least square solution minimizing the noise variance, such as:

$$ \underline{\hat{a}}=\arg\min_{a}\parallel \underline{x}-\mathbf{D}\underline{a} \parallel^{2} $$

(5)

where ∥.∥ indicates the Euclidean norm. This general solution is then expressed as:

$$ \underline{\hat{a}}= (\mathbf{D}^{\dag} \mathbf{D})^{-1}\mathbf{D}^{\dag}\underline{x} $$

(6)

and can be here simplified such as:

$$ \underline{\hat{a}}=\frac{1}{E}\mathbf{D}^{\dag} \underline{x} $$

(7)

since the matrix D ^‡ D is a diagonal one whose diagonal elements are all equal to E. Effectively, each matrix D _i is composed of only one diagonal with values of one because only one potential is elicited at the onset of the stimulus and then D ^‡ D = E.I, with I the identity matrix. Figure 1 illustrates this situation, considering the time interval between two consecutive stimuli (ISI) to be greater than or equal to N _e samples. This configuration of the GLM with a diagonal matrix D ^‡ D is called here the “Average” method corresponding with the usual estimation by averaging on the time-locked onsets.

Fig. 1

Construction of the matrix D considering one unique neural response per trial (4). Here, a same stimulus (red arrow) repeated three times, elicits an unique ERP, $\underline {a}$. The raw data are segmented into three epochs (black boxes) time-locked on the stimulus onset. The vector $\underline {x}$ is the concatenation of these epochs. The Toeplitz matrix D is null except on the diagonals whose entries are synchronized on the onset of each stimulus. The noise $\underline {n}$ is not illustrated

Regularization to reduce the number of trials

By averaging over all epochs, the consistent ERP waveform is extracted above the noise level. Considering a same variance for the noise decorrelated with the neural response for each trial, the variance of the residual noise is inversely proportional to the number E of epochs and thus the SNR linearly increases with the number E of epochs. However, this number is often a compromise between the signal quality and the duration of the experiment. So, an alternative is to introduce a regularization constraint to estimate smooth solutions. Then for a given number of epochs, the SNR can be improved by regularization. For this, a zero-order Tikhonov regularization is implemented using a ridge parameter λ in the ERP estimation, such as $\underline {\hat {a}}_{reg}(\lambda )$ is the least-square solution minimizing this cost function:

$$ \text{CF}(\underline{\hat{a}}_{reg}(\lambda))=\parallel \underline{x}- \mathbf{D} \underline{a}(\lambda) \parallel^{2} + \lambda N \parallel \underline{\hat{a}}_{reg}(\lambda) \parallel^{2} $$

(8)

with N the total number of samples ( N = N _e ×E). Consequently, $\underline {\hat {a}}_{reg}(\lambda )$ can be expressed by:

$$ \underline{\hat{a}}_{reg}(\lambda)=(\mathbf{D}^{\dag} \mathbf{D}+\lambda N \mathbf{I})^{-1}\mathbf{D}^{\dag}\underline{x} $$

(9)

It should be noted that the classical estimation (6) is for λ = 0 (i.e., λ = 0, no regularization).

A correct regularization is a trade-off between the error of the estimation ($\parallel \underline {x}-\mathbf {D} \underline {\hat {a}}_{reg}(\lambda )\parallel$) and its power ($\frac {1}{N_{a}} \parallel \underline {\hat {a}}_{reg}(\lambda ) \parallel ^{2}$). A low value of λ promotes an estimate with a low error but this solution may be dominated by data errors. Conversely, a high value of λ promotes a low power estimate with a low variance relatively to the fluctuation of the observed data but a high average gap with the observed data. These two quantities must be controlled to find the best trade-off. Usually possible values for λ are iteratively set by plotting for increasing values of λ, the “L-curve” which would be, here, $\parallel \underline {x}- \mathbf {D} \underline {\hat {a}}_{reg}(\lambda ) \parallel$ against $\parallel \underline {\hat {a}}_{reg}(\lambda ) \parallel ^{2}$ in a log-log graph (Engl and Grever 1994; Hansen 1992). Then, the optimal value, λ _{o p t} , is chosen at the “corner of the L” corresponding to the maximum of curvature of the “L-curve” but this “corner” can be difficult to discern (Subramaniyam et al. 2010). To overcome this difficulty in objectively finding the “corner of the L”, we opted for a one-step method by using the generalized cross validation (GCV) (Golub et al. 1979) instead of the L-curve method. In short, the GCV considers the linear regression model and is based on a weighted version of cross-validation. In this case, the cross validation uses the “leave one out” strategy by which each observed point is left out in turn and is estimated by the rest of data. The aim of the GCV is to estimate the λ _{G C V} , which minimizes the function V related to the mean square error (MSE). The λ _{G C V} is given by:

$$\begin{array}{@{}rcl@{}} V(\lambda)& = &\frac{\frac{1}{N}\parallel \underline{x}-\mathbf{D}\underline{\hat{a}}_{reg}(\lambda)\parallel^{2}} {\left( \frac{1}{N}\text{tr}\left( \mathbf{I}-\mathbf{D}(\mathbf{D}^{\dag} \mathbf{D}+\lambda N \mathbf{I})^{-1}\mathbf{D}^{\dag}\right)\right)^{2}} \\ \lambda_{GCV} & =& \arg\min_{\lambda}V(\lambda) \end{array} $$

(10)

In the ERP technique, the study is generally an inter-subject study and the final ERP is estimated after a “grand average” (average across all the subjects). Consequently, there needs to be an overall regularization which considers each subject. A single λ _{G C V} is computed for the subjects. So, using the matrix framework, it is possible to consider all the subjects by the concatenation of $\underline {x}_{i}$ signals:

$$ \underline{x}_{all} = \mathbf{D}_{all} \underline{a} + \underline{n}_{all} $$

(11)

with $\underline {x}_{all}=[\underline {x}_{1}^{\dag },\ldots ,\underline {x}_{S}^{\dag }]^{\dag }\in \mathbb {R}^{N_{s}}$, $\underline {n}_{all}=[\underline {n}_{1}^{\dag },\ldots ,\underline {n}_{S}^{\dag }]^{\dag }\in \mathbb {R}^{N_{s}}$ and $\mathbf {D}_{all} =[\mathbf {D}_{1}^{\dag },\ldots ,\mathbf {D}_{S}^{\dag }]^{\dag }\in \mathbb {R}^{N_{s} \times N_{a}}$ where S is the number of subjects and N _s = S × N is the total number of temporal samples. In this way, the “grand average” can be estimated by Eq. 9 with an unique value of λ _{G C V} for all subjects, using D _{a l l} , $\underline {x}_{all}$ and N _S , instead of D, $\underline {x}$ and N.

General linear model used to manage the overlapping issue

The classical ERP method estimates only one evoked potential by epoch. Two situations can occur regarding overlapping. The first is when the experiment has been designed so that a single potential is elicited at each epoch (Fig. 1). In this case, the simplified model (6) where D ^‡ D is really a diagonal matrix, is justified. The second situation is when during an epoch, the evoked response is observed along with a part of the previous and/or the subsequent response (Fig. 2). If the ISI duration is significantly shorter than the latency of the evoked potential and the duration of the response, the amount of distortion due to overlapping can no longer be neglected. Consequently, the right model to take these overlaps into account needs to be built with a non-diagonal matrix D ^‡ D. Its setup will now be explained.

Fig. 2

Construction of the matrix D assuming the same evoked potential $\underline {a}$ for all the neural responses in the each epoch but with shorter ISIs. The subdiagonals (dotted lines) of the matrix D correspond to the other neural responses than the neural response on which the epoch is time-locked (solid lines). The noise $\underline {n}$ is not illustrated

By using the general linear model to take into account overlapping, the Toeplitz matrix D has to be set considering all stimuli inside each epoch. To do so, the neural responses can be deconvolved (Rivet et al. 2009; Bardy et al. 2014; Congedo et al. 2016). We first consider that the overlapping neural responses are of the same type and, second, that they are of different types.

Therefore, inside one epoch, there is more than one elicited response, but let us consider that all of these neural responses have the same waveform. Overlaps occur because the ISI is shorter than both the latency of the expected neural response $\underline {a}$ and the duration N _e of the epochs. Consequently, there is more than one diagonal in each submatrix D _i , as is illustrated in Fig. 2—the solid line diagonals correspond to the neural responses elicited at the onset of the stimuli (i.e., synchronized with them) and the dotted line subdiagonals correspond to another neural response elicited, by another stimulus, in the same epochs. These subdiagonals may or may not be complete depending on the choice of duration of the epoch ( N _e ) in relation to the duration of the response ( N _a ) and the ISI values. We also need to remember that even in this situation, the classical estimation of the neural response only takes into account the diagonals of matrix D at the onset of the stimuli. Also, the contributions of the previous and subsequent responses are mixed with the time-locked observed response $\underline {x}$ and the potential $\underline {\hat {a}}$ estimated using Eq. 7 ( D ^‡ D is a diagonal matrix), is biased by these overlaps. To take overlapping into account, the linear model of the observed data, described by Eq. 6, is used with the Toeplitz matrix D as described in Fig. 2. Thus, the least-square minimization to estimate the neural response $\underline {\hat {a}}$ as the best linear non-biased estimator with the smaller variance is defined by Eq. 5, and the solution $\underline {\hat {a}}$, is computed by Eq. 6.

Now, let us consider that several types of response are evoked during one same epoch. In this situation, the linear model of the observed data is extended to take each evoked potential in the observed data into account. Let us note C the number of different expected types of response. In the following, C will also be called the number of classes. Thus, the model of the observed data can be rewritten as:

$$\begin{array}{@{}rcl@{}} \underline{x}&=&\sum\limits^{C}_{c=1}\mathbf{D}^{(c)}\underline{a}^{(c)} +\underline{n} \\ \underline{x}&=&\mathbf{D}\underline{a} +\underline{n} \end{array} $$

(12)

where D is now the concatenation of the matrices D ^(c) ( D = [D ⁽¹⁾,…,D ^(C)]), and $\underline {a}$ is also the concatenation of the evoked potentials ($\underline {a}=[\underline {a}^{(1)^{\dag }},\ldots ,\underline {a}^{(C)^{\dag }}]^{\dag }$). In this way, all neural potentials inside each epoch are considered instead of a single potential on which the epoch is time-locked.

Some precautions must be taken to avoid an ill-conditioned and noninvertible matrix D ^‡ D: if the variability of the ISI values (referred to as jitter) is too low, it is not possible to accurately separate the contribution of the different stimuli in the observation of the neural response $\underline {x}$: therefore, the matrix D ^‡ D is ill-conditioned. The amount of jitter must be sufficient to enable the deconvolution between the different types of evoked responses (see Bardy, Dillon, & Van Dun, 2014 for a detailed discussion about the amount of jitter as a balance in the case of the deconvolution of cortical auditory potentials). A minimum amount of jitter is necessary, but if it is too large, the variability of the neural response may increase, because the auditory response is affected by the ISI value from the previous stimulus (Näätänen et al. 1988). Consequently, the neural response is no longer time-invariant, and Eq. 6 becomes incorrect. Besides, the length of the responses to be estimated must be smaller than the number of observed samples ( N _a < N).

To assess the estimation of one potential relative to the others, we used the SNR, the signal-to-interference ratio (SIR) and the signal-to-artefact ratio (SAR) as they are commonly used in the “Blind Sources Separation” community (Vincent, Gribonval, & Févotte, 2006). Let Eq. 12 be recast in the case of two potentials, $\underline {a}_{1}$ and $\underline {a}_{2}$ as:

$$ \underline{x} = \mathbf{D}^{(1)} \underline{a}_{1} + \mathbf{D}^{(2)} \underline{a}_{2} + \underline{n} $$

(13)

where D ⁽¹⁾ can be split into two parts: $\mathbf {D}^{(1)}=\mathbf {D}^{(1)}_{erp}+\mathbf {D}^{(1)}_{ov}$, with the matrix $\mathbf {D}^{(1)}_{erp}$ constructed by the synchronized onsets and the matrix $\mathbf {D}^{(1)}_{ov}$ constructed by the other neural responses inside the epoch. In the case of estimating $\underline {a}_{1}$, one can write the estimate as:

$$ \underline{\hat{a}}_{1} =\underline{a}_{1} + \underline{O}_{vl}(a_{1}) + \underline{O}_{vl}(a_{2}) + \underline{n^{\prime}} $$

(14)

where $\underline {O}_{vl}(a_{1})$, $\underline {O}_{vl}(a_{2})$ and $\underline {n^{\prime }}$ are the remaining overlaps due to $\underline {a}_{1}$ and $\underline {a}_{2}$ and the remaining noise, respectively. This expression depends on the algorithm used as detailed below (see Appendix 1 for the theoretical developments of these indicators for the simple “Average” method, and for the general linear model. From Eq. 14, one can define the SNR of the estimate $\underline {\hat {a}}_{1}$ as:

$$ \text{SNR}_{\underline{\hat{a}}_{1}}=10\text{log}_{10}\left(\frac{\parallel \underline{a}_{1} \parallel^{2}}{ \parallel \underline{n^{\prime}} \parallel^{2}}\right) $$

(15)

This index quantifies the remaining noise in $\underline {a}_{1}$. The higher this is, the better.

The signal-to-artifact ratio (SAR), which quantifies the remaining overlap of $\underline {a}_{1}$ in $\underline {\hat {a}}_{1}$, is defined as:

$$ \text{SAR}_{\underline{\hat{a}}_{1}}=10\text{log}_{10}\left(\frac{\parallel \underline{a}_{1} \parallel^{2}}{ \parallel \underline{O}_{vl}(a_{1}) \parallel^{2}}\right) $$

(16)

Again, the higher, the better. Finally, the signal-to-interference ratio (SIR) that quantifies the remaining overlap of $\underline {a}_{2}$ in $\underline {\hat {a}}_{1}$, is defined as:

$$ \text{SIR}_{a_{1}/a_{2}}=10\text{log}_{10}\left(\frac{\parallel \underline{a}_{1} \parallel^{2}}{ \parallel \underline{O}_{vl}(a_{2}) \parallel^{2}}\right) $$

(17)

And yet again, the higher, the better.

Regularization applied to the general linear model

Finally, this formalism serves to set the regularization to reduce the estimation variance overall the classes:

$$ \underline{\hat{a}}_{reg}(\lambda)=(\mathbf{D}^{\dag} \mathbf{D}+\lambda N \mathbf{I})^{-1}\mathbf{D}^{\dag}\underline{x} $$

(18)

This Eq. 18 corresponds to Eq. 9, with the concatenation of the Toeplitz matrices as illustrated in Fig. 3, except that here, the full matrix D ^‡ D is no longer a diagonal matrix.

Fig. 3

Construction of the matrix D assuming two ( C = 2) different evoked potentials inside the epochs. The potential $\underline {a}_{1}$ (resp. $\underline {a}_{2}$) is elicited by the stimulus A (red arrow) (resp. stimulus B (purple arrow)). Here, the epochs are time-locked on the stimulus A’s onset. The diagonals and subdiagonals of the matrix D ₁ (resp. D ₂) are defined according to the onsets of the stimulus A (resp. B) for each epoch. The noise $\underline {n}$ is not illustrated

Finally, as previously, λ _{G C V} is computed according to Eq. 10. In the framework of an inter-subject study, combining GLM and regularization is implemented in the same way as in “Regularization to reduce the number of trials” where a single value of λ _{G C V} is computed for all the subjects.

Methodology

To evaluate the efficiency of the proposed approach combining GLM and regularization, a benchmark with four models was set. We shall denote the four models as follows: on the one hand A v(0) the classical “Average” method, and G l m(0) the GLM, without regularization ( λ = 0), and on the other hand A v(λ) the regularized classical “Average” method and G l m(λ) the regularized GLM. To conduct this benchmark, a two-step methodology was followed. Firstly, realistic EEG signals were generated in order to obtain a ground truth by using controlled parameters. Secondly, real EEG signals from two experiments (visual scene exploration, and a classical P300 Speller paradigm) were used to assess the efficiency of the proposed procedures in real situations. Using these two databases, two different configurations for GLM were illustrated. In the first experiment, the GLM was used to estimate EFRP elicited on adjacent fixations, according to a simple assumption where the evoked potentials were identical at each fixation. In other words, the GLM was configured with only one class to estimate overlapping potentials. In the second experiment, the GLM was configured with two classes to highlight the specifics of a given class. These two experiments used an EEG acquisition device. The simulated and real signals are now presented.

Simulated signals

The EEG signals were generated as described in Eq. 1. The potential a(t) was generated with an early waveform a _{e a r l y} (t) preceding a late one a _{l a t e} (t). This potential was the ground truth. a _{e a r l y} (t) was generated as a white noise filtered by a bandpass filter with a bandwidth between 5 and 10 Hz and multiplied by a Gaussian window whose mean μ was 300 ms and the standard deviation σ, 125 ms. In the same way, a _{l a t e} (t) was a white noise filtered by a low-pass filter with a cutoff of 3 Hz multiplied by a Gaussian window with μ equal to 600 ms and σ to 100 ms. To simulate the on-going brain activity, some noise, n(t) was added to a(t). n(t) was a white noise filtered by a low-pass filter with a cut-off of 50 Hz. For our simulations, the SNR varied between −20 and 0 dB. The sampling frequency was 1000 Hz, and the length of the temporal observation window was 1000 ms.

Three configurations were studied. In the first, without overlapping, each stimulus was presented with the same ISI value equal to 1000 ms and elicited the unique potential a(t). In a second condition—with overlapping—the stimuli were presented with a random ISI value shorter than the latency of the potential. This ISI value was a uniform random variable between 200 and 400 ms. In the third configuration—with overlapping and multiple responses—two different stimuli were presented, eliciting respectively two potentials, a ₁(t) and a ₂(t). The ISI values were generated in a similar way, by a uniform random variable between 200 and 400 ms. For the three situations, data were segmented into epochs of 1000 ms time-locked on each stimulus onset. For the two last configurations with overlaps, there were on average, four stimuli, and the averaged ISI value during the epoch was 300 ms. The number E of epochs varied between 10 and 100. These simulations were used to assess the different methods in both situations with a single evoked potential a(t), and then with two evoked potentials, a ₁(t) and a ₂(t).

Real signals from a visual scene exploration

During a visual scene exploration, a joint EEG and eye movement database was recorded. For the purpose of this study, only one condition of the whole experiment (Devillez, Guyader, & Guérin-Dugué, 2015), called “the free exploration”, which consisted of freely exploring 60 color scenes, was considered. Each trial started with a white central fixation cross displayed for 800–1200 ms. When the participant had stabilized his/her gaze on this central fixation point, a color scene was displayed for 4 s. Each trial ended with a grey screen for 1 s. Thirty-nine healthy volunteers between 20 and 36 years old participated in the experiment. Eye movements were recorded using Eyelink 1000 (SR Research) and sampled at 1000 Hz, for both eyes. The EEG activity was recorded using 32 active electrodes. The right earlobe and FCz electrodes were used respectively as reference and ground. Data were amplified using a g.USBamp gtec system, and sampled at 1200 Hz. An analog bandpass filter ( 0.01−100 Hz) and a 50-Hz notch filter were applied online. Eye movement and EEG signals were synchronized offline, thanks to the triggers sent simultaneously to both the EEG system and the eye-tracker. EEG data were then re-sampled at 1000 Hz (eye-tracker sampling rate). After visual inspection to reject segments contaminated by muscular activity or non-physiological artefacts, ocular artefacts were then corrected by independent component analysis (infomax ICA) (Bell & Sejnowski, 1995).

Since the task was a free exploration, each ocular fixation was assumed to elicit a similar potential, such as the lambda wave at latency of 100 ms (Yagi 1981) and the P2 potential at latencies 200−300 ms, whatever the fixation rank during the exploration. This EFRP was estimated from −200 ms (including the pre-saccadic potential) up to 800 ms, which was a sufficiently long duration to include these early potentials. For the present study, for each trial, three² ranks of fixation (r ₁,r ₂,r ₃)³ were randomly selected for a given subject. An epoch was defined as the temporal window time-locked on the onset of an ocular fixation, the rank of this fixation was r ₁, r ₂ or r ₃. So for a given subject, there were 180 epochs (three per scene) at most. For a given subject, the temporal window was defined as [−200−τ;800 + τ] ms with τ = μ(IFI) + σ(IFI) considering the mean and the standard deviation of the distribution of inter fixation interval values. In this way, the fixation on which the epoch was time-locked was preceded and followed by at least a fixation. By averaging across the participants, the temporal window was equal to [−572;1171] ms and the mean of the inter-fixation interval was equal to 271 ms (std = 91 ms).

In our study, this database was of interest to illustrate the overlapping issue that was one of the main concerns for the eye fixation related potential estimation (Dimigen et al. 2011). Besides, a study was done on real datasets to assess the regularization procedure in two cases. Firstly, the regularization procedure was independently carried out on each subject’s dataset, and secondly, the regularization was simultaneously applied on the whole dataset. Moreover, the estimated regularized component vs. the grand average of the regularized components for each subject was compared.

Real signals from a P300 Speller experiment

An EEG database was recorded during a P300 Speller experiment. The P300 Speller is a brain–computer interface based on the oddball paradigm (Farwell and Donchin 1988) which spells characters. A 6 × 6 matrix was displayed on a screen computer. The participant focused her/his attention on the target symbol that she/he wanted to spell and had to count how many times this symbol was flashed. Each column and row was randomly intensified several times. According to the oddball paradigm, when the target symbol flashes, a P300 wave is elicited whereas the non-target stimuli elicit only a sensory potential. In this experiment, there were 500 intensifications (or stimuli) of target characters and 3000 intensifications of non-target characters. The ISI value was equal to 133 ms.

Ten healthy volunteers, between 22 and 34 years old, participated in this experiment. The EEG signal was recorded via 16 active electrodes with the g.USBamp device from the g.tec company. The reference electrode was on the ear lobe and the ground electrode was on the forehead. The sampling frequency was 1200 Hz. The signal was filtered by a four-order Butterworth band-pass filter with a bandwidth between 1 and 12 Hz.⁴

An epoch was defined as the temporal window time-locked on a target stimulus. This window was from −0.5 s to 1 s and thus, within an epoch, each target stimulus was followed by at least five stimuli. There were six possible configurations of epoch as shown in Fig. 4, and there were 500 epochs.

Fig. 4

The six possible configurations of epochs. The red arrows (resp. black arrows) represent target (resp. non-target) stimuli

This database was interesting for our study firstly because there were two types of stimuli and thus two types of neural responses and, secondly because the ISI value was shorter than the latency of the expected target evoked potential P300 (300-500 ms). So some overlaps occurred. For the purposes of our study, the methods were assessed for different numbers of trials with T = [60,120,180,240,300,360,420]. For each value of T, the epochs were pseudo-randomly chosen in such a way that each configuration gave the same number of epochs (i.e., for T = 60, ten epochs from each configuration).

Results on simulated signals

Effect of the regularization parameter

In this section, the effect of the ridge parameter λ is studied when estimating the evoked potential in the simplest case, without overlapping. Since the ground truth is known, the mean square error (MSE) between a(t) and $\hat {a}_{reg}(\lambda )(t)$:

$$ \text{MSE}(\lambda)=\frac{1}{N_{a}}\parallel \hat{a}_{reg}(\lambda)(t) - a(t)\parallel^{2} $$

(19)

can be evaluated as a function of λ (Fig. 5), with a SNR equal to −20 dB and a number of trials equal to 50 and to 100.

Fig. 5

Evolution of averaged MSE with respect to λ, for SNR = −20 dB, 50 and 100 trials

From these two curves, three areas were clearly noticeable:

• 0≤λ ≤ 10⁻⁴: The regularization was null or very low. The two MSE curves reached a high MSE for λ = 0 (without regularization) but led a non-biased estimation. This value for λ = 0 was larger with 50 trials than with 100 because when averaging, the SNR was higher with more trials.

• 10⁻⁴ < λ ≤ 10⁻²: the MSE decreased to a minimal value corresponding to the optimal λ value ( λ _{M S E} ). As expected, λ _{M S E} with 50 trials ( λ _{M S E} = 2.10⁻³) was greater than with 100 trials ( λ _{M S E} = 1.10⁻³). Indeed, with less trials, the estimated component was less noisy and required more regularization to obtain a smooth estimation.

• λ > 10⁻²: The MSE criterion increased and converged towards the same value, independently of the number of trials. According to Eq. 18, $\hat {a}_{reg}(\lambda )(t)$ converged towards zero when λ increased. Consequently, the MSE converged towards the power of a(t)$\left (\frac {\parallel a(t)\parallel ^{2}}{N_{a}}\right )$.

These three areas are each illustrated by an estimated waveform at Fig. 6 for 50 trials and SNR = −20 dB. On these three graphs, the theoretical expectation $E[\underline {\hat {a}}]$ and the variability ( ±2 standard deviations) are plotted in relation to the ground truth a(t) (see Appendix 2 for the mathematical expressions of the theoretical expectation and variance corresponding to the estimation by Eq. 18). For λ = 0 (Fig. 6a), the estimation was unbiased (the ground truth a(t) and $E[\underline {\hat {a}}]$ are identical) but the variance due to the residual noise was large. When the ridge parameter was at the optimal value λ = λ _{M S E} = 2.10⁻³ (Fig. 6b), the bias was greater but the variance was lower than for the estimation without regularization. In this way, the estimated signal was less noisy, which made this the best compromise between bias and variance. Finally, for a high λ, greater than the optimal value (here λ = 1), the estimated signal became unusable (Fig. 6c), $\hat {a}_{reg}(t)=0$. In other words, with a value which is greater than the optimum, the regularization is too strong.

Fig. 6

Illustration of the estimated potential $\hat {a}_{reg}(\lambda )(t)$ with (a) λ = 0 (no regularization), (b) λ = λ _{M S E} = 2.10⁻³ (optimal regularization), and (c) λ = 1 (over-regularized). These three estimations were computed for the same configuration: SNR = −20 dB and 50 trials

Generalized cross-validation procedure

The aim of this section is to validate the generalized cross validation procedure to estimate the ridge parameter λ when computing the evoked potential a(t) in the simplest case, i.e., a unique potential without overlapping. To begin with, Fig. 7 confirms as in (Subramaniyam et al. 2010) that it is difficult to use the “L-curve” method to choose the optimal λ value. In this figure, the value of λ, λ _{M S E} , which minimizes the MSE, is indicated but does not correspond to a discernible “corner of the L-curve”.

Fig. 7

“L-curve” for 50 trials and SNR = −20d B, $\parallel \underline {x}- \mathbf {D}\underline {\hat {a}}_{reg}(\lambda )\parallel ^{2}$ against $\parallel \underline {\hat {a}}_{reg}(\lambda ) \parallel ^{2}$

The value of λ given by the minimum of the GCV function, λ _{G C V} , was compared to the value which minimized the MSE, λ _{M S E} . The GCV function, V (10), is plotted for 50 trials and SNR = −20 dB in Fig. 8. Both of the values of λ _{M S E} and the values of λ _{G C V} , are indicated on this graph and are close to each other: λ _{M S E} = 2.10⁻³ and λ _{G C V} = 1.10⁻³.

Fig. 8

The GCV function, V(λ), for 50 trials and SNR = −20 dB

In Fig. 9, both the averaged optimal values ($\bar {\lambda }_{MSE}$, $\bar {\lambda }_{GCV}$) computed across ten realizations, are plotted for two SNR values ( −20 dB and −10 dB) against the number of trials.

Fig. 9

Averaged optimal ridge parameter given by minimization of the MSE criterion $\bar {\lambda }_{MSE}$ and by minimization of V, $\bar {\lambda }_{GCV}$, function of the number of trials

In most cases, these two estimates of the ridge parameter were equivalent. With less noise (SNR = −10 dB), these two estimates were similar even for few trials ( ≥10). However, with more noise (here SNR = −20 dB), the estimation of λ by GCV was over-evaluated if there are few trials. In fact, in the GCV process for the regularization of a signal with a very low SNR, the regularization of the noise outweighs the regularization of the target signal. As a result, this signal is too smoothed in these conditions. Figure 9 also shows that λ decreases with the SNR and with an increasing number of trials. The less noisy the signal, the less regularization is necessary.

For the following sections, and for all results with regularization, only the GCV method is used to compute the ridge parameter.

Application to overlapped potentials

In this section, the efficiency of the two methods (“Average” and GLM) with regularization ( A v(λ _{G C V} ), G l m(λ _{G C V} )) or without regularization ( A v(0), G l m(0)) is assessed in the case of overlapping potentials, providing four estimation algorithms to benchmark.

First, the situation with only one overlapping potential $\underline {a}$, was studied. The four estimated waveforms are illustrated in Fig. 10a ( A v(0)), 10b ( G l m(0)), 10c ( A v(λ _{G C V} )) and 10d ( G l m(λ _{G C V} )). As expected, the GLM estimation without regularization ( G l m(0)) was an unbiased estimation (Fig. 10b), because the overlap was taken into account in the model (6). The classical estimation by averaging ( A v(0)) was biased (Fig. 10a): the matrix D ^‡ D in the model was only a diagonal matrix (6). Furthermore, the contributions, due to overlap, were not taken into account. Without regularization, the classical estimation by averaging ( A v(0)) gave a larger variance than the GLM estimation ( G l m(0)) as shown in Fig. 10a and c. Regularization was found to decrease the variance while increasing the bias. This is what we observed for the two estimates given by A v(λ _{G C V} ) method and by G l m(λ _{G C V} )), but the bias on the estimate potential by averaging ( A v(λ _{G C V} )) (Fig. 10c) remained larger than the bias on the estimate by GLM ( G l m(λ _{G C V} )) (Fig. 10d).

Fig. 10

Illustration of the mathematical expectation $E[\underline {\hat {a}}]$ in the case of overlapping between epochs. The four models are illustrated: average method and GLM without regularization ( A v(0), G l m(0)) and with optimal regularization ( A v(λ _{G C V} ), G l m(λ _{G C V} )). These four estimations are with the same configuration: SNR = −20 dB and 50 trials

Secondly, the simulations when two overlapping potentials a ₁(t) and a ₂(t) can be elicited in one epoch were found to produce the same results and interpretations. To avoid repetitions, the corresponding wave forms were not shown. The evolution of λ _{G C V} and of the estimated SNR (see Eq. 15 and Appendix 1), function of the number of trials, were studied. The evolution of λ _{G C V} , for SNR = −20 dB is plotted in Fig. 11. For more trials, the values for the two models were equivalent and decreased with the number of trials. This was in line with the evolution of the estimated SNR, plotted against the number of trials in Fig. 12, for the two methods without regularization ( A v(0), G l m(0)). Both of these SNRs increased with the number of trials, and, consequently, this explains the decreasing of the λ _{G C V} , for the two methods with regularization ( A v(λ _{G C V} ), G l m(λ _{G C V} )) in Fig. 11. The higher the SNR, the less regularization is necessary. Consequently, with regularization, the SNR was improved for the two methods for a given number of trials and it was almost constant across the number of trials. Additionally, the SNR for less trials (i.e., 20), with regularization is better than the SNR for more trials (i.e., 100) without regularization. This is explained by decreased variance using regularization.

Fig. 11

λ _{G C V} for the “Average” method and GLM, function of the number of trials, SNR = −20 dB

Fig. 12

Estimated SNR function of the number of trials, for the four models

Even if the SNR was the same between A v(0) and G l m(0) and, between A v(λ _{G C V} ) and G l m(λ _{G C V} ), the efficiencies of the A v(0) and A v(λ _{G C V} ) models were impacted by distortions due to overlapping. These distortions were evaluated by the signal-to-artifact ratio (SAR) (16) and signal-to-interference ratio (SIR) (17), for the A v(0) and G l m(0) methods (see Appendix 1 for the theoretical developments of these ratios). When only one unique potential is elicited, the SAR assesses the distortions due to the overlaps of the potentials a ₁(t) in the estimation of the a ₁(t) itself. In the case of these simulated data, the SAR for A v(0) was 8 dB. The SAR computation for the estimate given by G l m(0) was not relevant as the overlaps were explicitly taken into account. When two overlapping potentials are elicited ( a ₁(t) and a ₂(t)), for the A v(0) model, the SAR assesses the distortion due to the overlap of a single potential, and the SIR assesses the distortions due to overlap with the other potential. Applied to the estimation of the potential a ₁(t), the SAR for A v(0) was 20 dB and the SIR was 17 dB. For the G l m(0) model, the SAR and SIR were infinite since overlaps between the two potentials were taken into account. Finally, to synthesize results, the MSE illustrated the efficiency of the four models (Fig. 13a), for SNR = −20 dB, for one single evoked potential a(t), and for 30, 50, and 100 trials. The MSE decreased with the number of trials and with regularization. Moreover, the estimation by G l m(0) (resp. G l m(λ _{G C V} )) was more efficient than the classical method A v(0) (resp. A v(λ _{G C V} )). This is explained by the smaller bias and variance, as shown in Fig. 10, as well as the reduction of the distortion due to overlaps. The same observations were made for the situation with two different overlapping potentials, a ₁(t) and a ₂(t). In this case, the MSE criterion was assessed for the estimation of the potential a ₁(t). This MSE (Fig. 13b) had the same behavior function of the number of trials and also function of the four methods, as the MSE evaluated for the estimation of one elicited potential a(t) (Fig. 13a). Even if the SNRs were equivalent, the efficiencies of A v(0) and A v(λ _{G C V} ) models were impacted by the distortions due to overlapping. This is the reason why the G l m(0) (resp. G l m(λ _{G C V} )) was more efficient than the A v(0) (resp. A v(λ _{G C V} )) model.

Fig. 13

MSE for SNR = −20 dB and for 30, 50, 100 trials in two situations. a A single potential. b Two potentials. In the second case, MSE assesses the estimation of a ₁(t)

Results on EFRP estimation during a free visual exploration

In this section, the proposed methods are assessed on the dataset from the free visual exploration. The aim of this study was to extract the neural response to an ocular fixation, a(t), taking into account the contributions of the potential evoked by the immediately precedent and subsequent fixations. The potential was estimated on the temporal window [−200;800] ms with N _a = 1000 samples. The regularization procedures using each subject independently, or using the whole dataset globally, were compared, firstly at the level of the ridge parameter values obtained by the GCV procedure, and secondly at the level of the estimated waveforms by the “Average” method. To avoid repetition, this part was not illustrated here with GLM, because the same conclusions were obtained. In a last subsection, the “Average” method and the GLM are compared with the same regularization procedure (on the whole dataset) to provide results on the quality of the estimations when overlaps occurred.

Comparison between the regularization values on each subject versus on the whole dataset

In this section, the values of the optimal ridge parameter $\lambda _{GCV}^{subject}$ given by the GCV procedure for each subject dataset are compared to the optimal value λ _{G C V} estimated for the whole dataset. The boxplot in Fig. 14 shows the statistical summary of the distribution of the 39 values of $\lambda _{GCV}^{subject}$ compared to the unique value of λ _{G C V} for both the “Average” method and GLM, for the Pz electrode. The values of $\lambda _{GCV}^{subject}$ are higher than the unique value of λ _{G C V} for each of these two models. This was expected because the number of trials was increased (roughly a multiplication by the number of subjects) providing a decreasing value of λ _{G C V} for the whole dataset. Indeed, for the GLM, the value of λ _{G C V} on the whole dataset was λ _{G C V} = 3.10⁻⁵, and $\frac {\overline {\lambda _{GCV}^{subject}}}{39}=\frac {9.4.10^{-4}}{39}=2.4.10^{-5}$. Moreover, the regularization values were lower for the GLM than for the “Average” method. This was in line with the number of synchronization timestamps, which was three times higher for the GLM than for the “Average” method (the GLM took into account three fixations in a given epoch: precedent, current, and subsequent fixations). Lastly, more outlier values were observed for the “Average” method than for the GLM. For six subjects, the search for the optimal value of V(λ) (10) did not converge inside the search interval (from 10⁻⁶ to 100 ),⁵ and for these subjects, the regularization parameter was set to the maximal value (100). When the SNR was low, searching for the optimal value was more difficult than when the SNR was high, because the valley of the V(λ) curve was larger, and less steep with more noise. As a consequence, the regularization was too strong.

Fig. 14

Comparison between the values of $\lambda _{GCV}^{subject}$ estimated by the GCV procedure for each subject and the value of λ _{G C V} obtained by the GCV on the overall dataset for the “Average” method and Glm, on Pz electrode

Estimation with regularization on each subject vs. on the whole dataset with the “Average” method

Estimation with regularization on each subject

With a regularization per subject, the value of the ridge parameter was adjusted depending on the intrinsic level of noise in the acquired signals and on the number of trials for a given subject. The grand average over all subjects was then estimated by averaging all the regularized estimates. Figure 15 illustrates this procedure for the “Average” method on the Pz electrode. In Fig. 15a, the grand averages given by A v(0) and $Av(\lambda _{GCV}^{subject})$ models, for the complete dataset (39 subjects), are plotted. When the grand average without regularization, obtained directly by the A v(0) model (the unbiased estimator), was compared with the grand average computed using each estimate obtained by the $Av(\lambda _{GCV}^{subject})$ models, we observed an increased bias for the latter (see Fig. 15a for the differences between two different estimates).

Fig. 15

a The estimate on Pz electrode, given by the A v(0) model and by the grand average with the $Av(\lambda _{GCV}^{subject})$ models, for the complete dataset with 39 subjects. b The two estimates on Pz electrode, given by the grand average with the $Av(\lambda _{GCV}^{subject})$ models, for the complete dataset with 39 subjects and for the reduced dataset with 33 subjects

To explain this bias, Fig. 15b shows the grand averages given by $Av(\lambda _{GCV}^{subject})$ model for the whole dataset (39 subjects) and for a reduced dataset (33 subjects) without the six subjects’datasets for which the values of the ridge parameter $\lambda _{GCV}^{subject}$ were too high (see the previous section). A multiplication factor was noticeable between these two estimates for 39 and 33 subjects. This gain factor on the whole temporal window can be estimated by maximum likelihood: G = 1.181. This value was equal to $\frac {39}{33}$. In fact, for the complete dataset, the grand average was obtained, as the sum of each estimate by subject divided by 39 (the total number of subjects). However, for six subjects, the predictors in the matrix D were masked by the high value of $\lambda _{GCV}^{subject}$ ($\lambda _{GCV}^{subject}=100$), and consequently the matrix (D ^‡ D + λ N I) in Eq. 9 was close to the diagonal matrix λ N I, and then the resulting estimate was over-regularized near to zero. In addition, to explain completely the bias noticed in Fig. 15a, the impact of the regularization for the 33 other subjects must be considered. Even if the estimates for these subjects were not over-regularized, with an optimal regularization controlled by a suitable ridge parameter, a bias was automatically introduced. This is the reason why the gain factor between the two estimates, in the Fig. 15a, was higher than $\frac {39}{33}$ ( G = 1.58). To conclude, when the distribution of the ridge parameter’s values, $\lambda _{GCV}^{subject}$, has a large variability with high values close to and above 1, the bias of the estimated grand average given by the $Av(\lambda _{GCV}^{subject})$ model increased: the average is computed by dividing with the total number of subjects, but in the sum, some of these subjects’ datasets provide over-regularized estimates near to zero. Nevertheless, for the $Av(\lambda _{GCV}^{subject})$ model, the variance of the grand average estimation decreases, the contribution of signals with high noise being reduced by over-regularization.

Estimation with regularization on the whole dataset

With a unique regularization on the whole dataset, the grand average of the potential of interest a(t) was obtained directly by the A v(λ _{G C V} ) method. The value of the ridge parameter λ _{G C V} was obtained by the GCV procedure applied to the whole dataset. In this way, the same level of regularization has been applied on all subjects. Figure 16 illustrates this regularization procedure for the “Average” method on the Pz electrode, with the complete dataset (39 subjects), compared with the procedure without regularization ( A v(0)), and the previous result described in “Estimation with regularization on each subject” with the regularization applied to each subject ($Av(\lambda _{GCV}^{subject})$). Due to the increased number of trials, the value of the ridge parameter λ _{G C V} was smaller ( λ _{G C V} = 5.10⁻⁵) than the average of the values of $\lambda _{GCV}^{subject}$ (cf. Fig. 14), and tended towards zero. The two waveforms were very similar, and the bias of the regularized estimate $\hat {a}(t)$ is lower. However, its variance was greater because all the trials supplied the same contribution to the estimate $\hat {a}(t)$ of the final potential with the A v(λ _{G C V} ) model, independently of the noise power on the trials for the different subjects.

Fig. 16

Estimations of the potential a(t) on Pz electrode, given by A v(0), and A v(λ _{G C V} ) models, and the grand average of $Av(\lambda _{GCV}^{subject})$ for the complete dataset of 39 subjects

Comparison between the “Average” method and the GLM with regularization on the whole dataset

In this section, the estimates $\hat {a}(t)$ obtained by the A v(λ _{G C V} ) and G l m(λ _{G C V} ) methods are compared for the whole dataset (39 subjects). In other words, here the lower bias and higher variance provided by regularization on the whole dataset were preferred to the higher bias and lower variance provided by the regularization on each subject. In Fig. 17, the estimate given by the A v(λ _{G C V} ) method is plotted in blue, the estimate given by G l m(λ _{G C V} ) is plotted in red and histograms represent the onsets of precedent and subsequent fixations. In this figure, for both estimates, the lambda wave and the P2 potential were clearly noticeable. The pre-stimulus baseline for the A v(λ _{G C V} ) method was not stabilized due to overlapping of the neural responses to adjacent fixations. Because the baseline is not stabilized, it was difficult to compare the amplitude of different components. Furthermore, the return to zero was faster with G l m(λ _{G C V} ) than with the A v(λ _{G C V} ) method, which was still influenced by the neural response to the subsequent fixations. These results showed the influence of the precedent and subsequent responses on the potentials estimated by the A v(λ _{G C V} ) method and the efficiency of G l m(λ _{G C V} ) to deconvolve the neural responses to successive fixations. Concerning the effect of the regularization, the lambda wave and the P2 potential estimated by the A v(λ _{G C V} ) method were attenuated when compared to the potentials estimated by G l m(λ _{G C V} ). This is explained by a higher ridge parameter with the A v(λ _{G C V} ) method ( λ _{G C V} = 5.10⁻⁵) than with G l m(λ _{G C V} ) ( λ _{G C V} = 3.10⁻⁵).

Fig. 17

Estimates on Pz electrode, given by A v(λ _{G C V} ) and G l m(λ _{G C V} ) for the complete dataset of 39 subjects. Histograms represent the onsets of precedent and subsequent fixations

Results on P300 Speller data

In this section, the four methods are compared on the dataset from the P300 Speller experiment. For this illustration, the GLM configuration was done to highlight the distinction between two kinds of potential. For instance, this situation is well adapted for classification purposes. In the present case, the aim was to extract the neural response to a target stimuli. For this, two classes were defined (12): with the first class, the potential a ₁(t) was estimated on the temporal window [−500;800] ms, N _a1 = 1560 samples time-locked on the target stimuli. With the second class the potential a ₂(t) was estimated with the same duration, N _a2 = 1560 samples, time-locked on each stimulus. This potential a ₂(t) must take into account what is common to all the stimuli, both target as well as non-target. The regularization was estimated on the overall dataset providing a single ridge parameter thanks to the concatenation across the subjects as described by Eq. 11. Thus, the regularization was identical for each participant.

Effect of the number of trials on the regularization parameter

We studied the evolution of the optimal value of λ _{G C V} , given by the GCV procedure according to the number of trials. In Fig. 18, the values of λ _{G C V} are plotted against the number of trials for A v(λ _{G C V} ) and for ( G l m(λ _{G C V} )) for the Pz electrode. As for the simulated data, and as expected, the ridge parameter λ _{G C V} decreased when the number of trials increased, and as for EFRP data, the value of the ridge parameter was lower for G l m(λ _{G C V} ) than for A v(λ _{G C V} ). The estimation by G l m(λ _{G C V} ) took into account the overlapping from the other stimuli in contrast to the estimation by A v(λ _{G C V} ). In other words, these neural responses were considered as a signal for GLM, and as noise for the “Average” method. In this last case, it was the equivalent to an increase of the noise level providing a higher regularization.

Fig. 18

λ _{G C V} against the number of trials for the A v(λ _{G C V} ) and G l m(λ _{G C V} ) estimations on Pz electrode

Application of the four models

In this section, the efficiencies of the four models are compared. The potential of interest was the target a ₁(t). The target estimate $\hat {a}_{1}(t)$ given by the four models, and for 60 trials (dashed line) or 420 trials (solid lines) are plotted in Fig. 19. Firstly, for the four estimations, oscillations were observed with a periodicity around 130 ms, which corresponds to ISI value between stimuli. These oscillations were due to the steady-state visual evoked potential (Middendorf, McMillan, Calhoun, Jones, et al., 2000) elicited by each stimulus. Concerning the four estimations of the target potential, the P300 wave was observed on the estimated target potential, at a latency of around 300 ms, as expected with this oddball paradigm. For the estimates given by A v(0) and A v(λ _{G C V} ) (Fig. 19a), the regularization had no significant effect for 420 trials: small value of the ridge parameter ( λ _{G C V} = 2.10⁻⁵), since there was a large number of trials. However, for 60 trials, the P300 wave was more attenuated by the regularization: the ridge parameter was greater with 60 trials ( λ _{G C V} = 1.10⁻⁴) than with 420 trials. The estimates given by G l m(0) and G l m(λ _{G C V} ) are shown in (Fig. 19b). The GLM included the potential a ₂(t)⁶ to estimate the potential of interest a ₁(t), this was not the case for the average estimation. Consequently, the remaining oscillations were attenuated compared to these ones providing by averaging (in both A v(0), and A v(λ _{G C V} ) cases): this was clearly noticeable during the pre-stimuli period. This behavior was observed with both a few number of trials (60), and a large number of trials (420).

Fig. 19

Estimates on Pz electrode, for 60 and 420 trials. a The estimates by A v(0) and A v(λ _{G C V} ) model. b The estimates by G l m(0) and G l m(λ _{G C V} )

Conclusions

The present study develops, applies, and compares four methods (the classical average and the general linear model with and without regularization for both of them) to estimate the evoked potentials in order to improve the SNR and to limit the distortions due to overlapping between adjacent temporally neural responses. To this end, (i) the GLM was proposed to manage the overlapping issue (Kiebel & Holmes, 2003; Dale, 1999; Bardy, Dillon, & Van Dun, 2014) and (ii) the zero-order Tikhonov regularization procedure (Tikhonov 1963) was used to increase the SNR for a given number of trials. The regularization parameter was estimated by the generalized cross validation procedure (Golub et al. 1979). The interest of this study was to validate and compare these methods on simulated but realistic data, and also on real EEG signals registered during two experiments: a co-registration of eye movements and EEG experiment and a brain–computer interface experiment. To our knowledge, with this article the regularization and the GLM are applied, for the first time, in the context of the EFRP technique. The results demonstrate the interest of the regularization associated to the GLM to estimate evoked potentials in practical contexts (noisy EEG signals, few trials, overlapped potentials). The main assumption of GLM is the linearity of the additive model to take account the different neural responses elicited by a specific event. The non-linearity of the neural responses is a sensitive question, for the relationship between the ERP components through their amplitude/latency and the variables tested by the experimental conditions (Tremblay and Newman 2015), but also for the interferences between adjacent responses where the neural responses are no longer time-invariant (Näätänen et al. 1988). Integrate suitable non-linearity remains a great challenge for future work, however this linear model can still be very useful in a wide variety of applications.

Appendices

Appendix 1: Theoretical developments to estimate the signal-to-noise ratio (SNR), signal-to-artifact ratio (SAR), signal-to-interference ratio (SIR)

The signal noise ratio, signal-to-artifact ratio, and signal-to-interference ratio are defined by Eqs. 15, 16 and 17, respectively.

The remaining overlaps, $\underline {O}_{vl}(a_{1})$ and $\underline {O}_{vl}(a_{2})$, and the remaining noise, $\underline {n'}$, due to $\underline {a}_{1}$ and $\underline {a}_{2}$, for “Average” method and GLM are estimated as followed:

• 1. “Average” method

  In the case of the “Average” method, $\underline {\hat {a}}_{1}$ is expressed as:

  $$\begin{array}{@{}rcl@{}} \underline{\hat{a}}_{1} &=& \frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\underline{x} \\ &=& \underline{a}_{1}+\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\mathbf{D}_{1_{ov}}\underline{a}_{1}+\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\mathbf{D}_{2}\underline{a}_{2}+\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\underline{n}\\ \end{array} $$

  (20)

  Consequently

  $$\begin{array}{@{}rcl@{}} \underline{O}_{vl}(a1) & = &\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\mathbf{D}_{1_{ov}}\underline{a}_{1} \\ \underline{O}_{vl}(a2) & = &\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\mathbf{D}_{2}\underline{a}_{2} \\ \underline{n^{\prime}} & = &\frac{1}{E}\mathbf{D}_{1_{erp}}^{\dag}\underline{n} \end{array} $$

• 2. General linear model

  In the case of the GLM method, $\underline {\hat {a}}_{1}$ is expressed as

  $$ \underline{\hat{a}}_{1} = \mathbf{B}_{1} \mathbf{D}^{\dag}\underline{x} $$

  (21)

  where $\mathbf {B}_{1} \quad \in \mathbb {R}^{N_{a_{1}} \times N_{a}}$ are the first rows of the matrix (D ^‡ D)⁻¹, with D = [D ₁ D ₂]. Consequently, $\underline {\hat {a}}_{1} = \underline {a}_{1} + \underline {n^{\prime }}$ with $\underline {n^{\prime }} =\mathbf {B}_{1} \mathbf {D}^{\dag } \underline {n}$. This means that $\underline {O}_{vl}(a1)$ and $\underline {O}_{vl}(a2)$ vanish, leading thus to infinite SIR and SAR.

Appendix 2: Theoretical mathematical expectation and variance

The Eq. 18 can be developed:

$$\begin{array}{@{}rcl@{}} \underline{\hat{a}}_{reg}(\lambda)&=&(\mathbf{D}^{\dag} \mathbf{D}+\lambda N \mathbf{I})^{-1}\mathbf{D}^{\dag}(\mathbf{D}\underline{a}+\underline{n}) \\ \underline{\hat{a}}_{reg}(\lambda)&=& \mathbf{\Delta} \underline{a}+ \mathbf{\Omega} \underline{n} \\ \end{array} $$

(22)

with Δ = (D ^‡ D + λ N I)⁻¹ D ^‡ D and Ω = (D ^‡ D + λ N I)⁻¹ D ^‡.

In the simulated situations, $\underline {a}$ and $\underline {n}$ are known. So, the mathematical expectation $E[\underline {\hat {a}}]$, plotted in Figs. 6 and 10, is calculated as:

$$\begin{array}{@{}rcl@{}} E[\underline{\hat{a}}] & = &\mathbf{\Delta} \underline{a}+ \mathbf{\Omega} E[\underline{n}] \\ E[\underline{\hat{a}}] & = &\mathbf{\Delta} \underline{a} \end{array} $$

(23)

$\underline {n}$ is not zero-centered so $E[\underline {n}]=0$.

In the same way, the variance $\text {Var}[\underline {\hat {a}}]$ is equal to:

$$\begin{array}{@{}rcl@{}} \text{Var}[\underline{\hat{a}}] & =& E[(\underline{\hat{a}}-E[\underline{\hat{a}}])(\underline{\hat{a}}-E[\underline{\hat{a}}])^{\dag}] \\ \text{Var}[\underline{\hat{a}}] & =& \mathbf{\Omega} E[\underline{n} \underline{n}^{\dag}] \mathbf{\Omega}^{\dag} \end{array} $$

(24)

Appendix: 3: Results concerning the P300Speller dataset: Estimation of potential a ₂(t)

The potential a ₂(t) can be explained by the P300 Speller paradigm. In this latter experiment, target and non-target stimuli were presented at a regular rate (here equal to 133 ms). Consequently, these regular intensifications elicited steady-state visual evoked potentials (SSVEP) over parietal and occipital areas. These SSVEP corresponded in the GLM to the term D ⁽²⁾ a ₂(t). From a numerical point of view, the estimation of the potential a ₂(t) is inaccurate because of the regularity of the ISI. Indeed, the matrix $\mathbf {D}^{(2)^{\dag }} \mathbf {D}^{(2)}$ is closed to be singular. The contribution D ⁽²⁾ a ₂(t) in the GLM (12) is well estimated. See Fig. 20 for this estimate on one epoch. This figure shows the SSVEP signal for an epoch. As expected, oscillations were observed with a periodicity of around 133 ms.

Fig. 20

SSVEP estimate on one epoch