Researchers’ choice of the number and range of levels in experiments affects the resultant variance-accounted-for effect size

Abstract

In psychology, the reporting of variance-accounted-for effect size indices has been recommended and widely accepted through the movement away from null hypothesis significance testing. However, most researchers have paid insufficient attention to the fact that effect sizes depend on the choice of the number of levels and their ranges in experiments. Moreover, the functional form of how and how much this choice affects the resultant effect size has not thus far been studied. We show that the relationship between the population effect size and number and range of levels is given as an explicit function under reasonable assumptions. Counterintuitively, it is found that researchers may affect the resultant effect size to be either double or half simply by suitably choosing the number of levels and their ranges. Through a simulation study, we confirm that this relation also applies to sample effect size indices in much the same way. Therefore, the variance-accounted-for effect size would be substantially affected by the basic research design such as the number of levels. Simple cross-study comparisons and a meta-analysis of variance-accounted-for effect sizes would generally be irrational unless differences in research designs are explicitly considered.

Let us begin with a hypothetical cover story. Psychology students are preparing for a mental rotation experiment for their laboratory course. The study objective is to evaluate the effect of the rotation angle on the reaction time. Because a considerable number of publications have criticized the paradigm of null hypothesis significance testing, the instructor tells the students that they should primarily resort to variance-accounted-for effect sizes to evaluate the effect. In the computer program used in this lab experiment, two rotation angles, 0° and 60°, are preset as the default experimental conditions. The students would like to obtain the largest variance-accounted-for effect size as possible in order to appeal to their audience. For simplicity, assume that the relationship between the rotation angle and reaction time is linear and that all the levels are equispaced. Now, let us consider the following questions.

• Question 1: Consider the case when the students can add additional levels, if they want to, only between 0° and 60°. Should they add additional levels and how much would this affect the resultant effect size?

• Question 2: Consider the case where they are allowed to expand (or shrink) the default range of levels as well as add additional levels. In this case, should they expand (or shrink) the range of levels? Furthermore, should they add additional levels? How much would these actions affect the resultant effect size?

Calculating, reporting, and interpreting effect size indices have become more important than ever in the current movement away from the routine use of null hypothesis significance testing in psychology (Francis, 2012; Guan & Vandekerckhove, 2016; Kline, 2013; Lakens, 2013; Peng, Chen, Chiang, & Chiang, 2013; Vacha-Haase & Thompson, 2004; Wetzels et al., 2011) as well as other fields (Nakagawa & Cuthill, 2007; Park et al., 2010; Richardson, 2011). In this paper, our interest is on the variance-accounted-for effect size. This class of effect size represents the proportion of variance explained by a factor of interest. This idea has a high affinity with the analysis of variance (ANOVA), which has been one of the most popular statistical analyses in psychological science. Empirical evidence also reveals that when ANOVA results are presented, the variance-accounted-for effect sizes are most often reported together in contrast to other indices (Alhija & Levy, 2009; Fritz, Morris, & Richler, 2012).

However, despite their popularity, the statistical properties of variance-accounted-for effect sizes may not be well understood by psychological researchers. The fact that many readers might not instantly come up with the answers to the questions that arose from our cover story would be collateral evidence.

In a typical psychological experiment, researchers have a choice of two main research design components: the number and range of levels. For example, in our mental rotation experiment, they can choose the range of angles (e.g., between 0° and 60°) and the number of levels (e.g., four equispaced levels of 0°, 20°, 40°, and 60°). Textbooks and methodological papers on this topic state that the effect size depends on the research design (Grissom & Kim, 2012; Kelley & Preacher, 2012; Kline, 2013; Olejnik & Algina, 2000). Still, in reality, it is our view that experimental design is rarely taken into consideration when reporting and interpreting variance-accounted-for effect sizes. There may be at least two reasons for this. First, some researchers might report effect size measures just because they are required by the APA Publication Manual (American Psychological Association, 2009) or because it is customary to report such measures in the field (i.e., they have not carefully considered the meaning of effect sizes in the quantitative sense). Second, although they know that the research design can affect the resultant effect size, they may not have noticed how much it is affected by simply changing the research design.

Thus, the objective of this study was to show quantitatively how and how much the variance-accounted-for effect size depends on the researcher’s choice of these experimental designs. To this end, for the population effect size, we derived an equation that describes the relationship. For the sample effect size, we used Monte Carlo simulation to find their expected values. By using these results, we argue that researchers can substantially affect the effect size simply by manipulating the number of levels and their range. Next, we revisited the assumptions and a further generalization is made. Finally, the importance and implications of our results as well as important related studies is discussed. To ensure the replicability and generalizability of our results, the R programs used to generate all figures and conduct the simulation study in this article are shown in Supplemental Material B.

A rich, related literature shows how design affects the variance components. In particular, an important area of previous studies is the field of the optimal research design. There, the optimality of the research design is typically measured by certain design criteria such as A-, D-, and E-optimality. These criteria are functions of the variance of the parameters (Atkinson, Donev, & Tobias, 2007; Melas, 2006), and therefore one may directly relate them to the variance-accounted-for effect size. Meanwhile, the focus of the current paper is not primarily to find or discuss the optimal design given some prior assumptions. Rather, our goal is to demonstrate how and how much researchers can affect the resultant effect size by simply selecting the number (and range) of levels and how we can quantitatively study them. An accessible cover story, straightforward mathematical derivations, and a simulation study are provided for this purpose. Related studies are discussed in more detail in the Summary and Discussion section.

Population and sample effect sizes

We start by introducing the effect size measures in which we are interested. The population variance-accounted-for effect size, η ² _pop , is defined as the ratio of the total population variance (of the dependent variable Y), which is explained by the factor of interest (represented by the design variable X). Because the population value is generally not known, researchers typically use one of three major sample effect size indices (Grissom & Kim, 2012; Olejnik & Algina, 2000). Eta squared (η ²; Fisher, 1925), which is obtained by replacing the population variances with the respective sample sum of squares, is a traditional index. Although η ² is easy to understand and can be useful as a descriptive measure, it is known to have a positive bias. Less biased alternative estimators are epsilon squared (ε ²; Kelley, 1935) and omega squared (ω ²; Hays, 1963). Table 1 summarizes the population and three sample effect size indices in a single between-subjects factor design, which we consider in this study for simplicity.

Table 1 Formulas for the population variance-accounted-for effect size and corresponding sample effect size indices in a single between-subjects factor design

Population effect size as a function of the number and range of levels

Method

For the population effect size, we derive the closed-form function that describes the relation between the effect size and number and range of levels. In our cover story, we made two assumptions. First, the relationship between the rotation angle and reaction time is considered to be linear. Shepard and Metzler (1971) showed evidence of the linearity between these two variables (see Fig. 2 in their paper). Second, levels are chosen to be equispaced. When the range of levels is [0°, 60°] and the number of levels, which we denote by k, is k = 3, this means that the levels are chosen as 0°, 30°, and 60°; when k = 4, they are 0°, 20°, 40°, and 60°; and so on. We feel that our choice of assumptions is one of the most natural compared with other choices when no particular reason exists to the contrary. However, as shown in Summary and Discussion, these two assumptions can be further relaxed and substituted by the condition of equispacedness in the dependent variable.

To investigate the effect of the range of levels, let us denote the standardized mean difference effect size between the maximum and minimum treatments by d. That is, d is given by

$$ d=\frac{\mu_{max}-{\mu}_{min}}{\sigma_E}, $$

(1)

where μ _max and μ _min represent the population dependent variable values that correspond to the maximum and minimum treatment and σ _E represents the error standard deviation. Thus, d can be understood as the popular population Cohen’s d (Cohen, 1988) between the minimum and maximum treatment. Although d is a measure of the dependent variable, in our cover story we can also see d as a measure of the range of levels because when the relationship between the rotation angle and reaction time is linear, μ _max  − μ _min is a linear deterministic function of the range of levels.

Results

In the above setting, we find that the population effect size is represented in closed form as

$$ {\eta}_{pop}^2=\frac{d^2\left(k+1\right)}{12\left(k-1\right)+{d}^2\left(k+1\right)}. $$

(2)

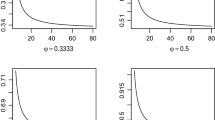
To our knowledge, Equation (2) is novel. The derivation is straightforward, and is given in the Appendix. Importantly, as shown in the Appendix, this is found to be a monotonically decreasing function of the number of levels k and a monotonically increasing function of standardized range d. To clarify the implications, Fig. 1 plots Equation (2) for different k s and d s.

Fig. 1

Population variance-accounted-for effect size (η ² _pop ) as a function of (a) the number of levels k and (b) the standardized range of levels d

Thus, given that the range of levels is fixed, such as between [0°, 60°], then the maximum variance-accounted-for effect size is achieved when we choose the number of factors to be the least possible value, that is, k = 2. From their slopes, it can also be seen that the effect of the number of levels is rather substantial. For example, suppose that the standardized range is d = 0.3. Then, η ² _pop is 0.022 when k = 2. However, η ² _pop decreases to two-thirds of the previous level just by adding one more level (k = 3). The rate of decrease reaches very close to 50 % when k = 5. The fact that the population effect size is a decreasing function of the number of levels with such a large dependence may be ironic for psychological science researchers because more levels in an experiment would generally lead to more elaborate measurement and a better understanding of the phenomenon of interest. However, despite researchers’ efforts to add more levels to better understand the phenomenon, the resultant effect size monotonically decreases. If researchers want to maximize η ² _pop , they should use just two levels.

The other finding that η ² _pop is a monotonically increasing function of the range of levels d may not be as surprising as the case for k, but it is still important because it implies that researchers can intentionally “manipulate” the effect size. For example, assume in our cover story that the original range of [0°, 60°] amounts to d = 0.3, which yields η ² _pop  = 0.022 when k = 2. Without changing the number of levels, if researchers double the range to [0°, 120°], the effect size becomes η ² _pop  = 0.083, which is 3.75 times larger than the original effect. Furthermore, if they triple the range to [0°, 180°], it yields η ² _pop  = 0.168, which is 7.65 times larger.

Sample effect size as a function of the number and range of levels

Method

The next question is whether this population relationship also holds in the sample. Because the finite sample expected values of the sample effect size indices are not available in closed form, we used Monte Carlo simulation to understand their behavior. For a meaningful comparison between the number of levels, we need to consider an appropriate sample size. Two possible scenarios are considered. One is when the total sample size is fixed (fixed total-N scenario) and the other is when the sample size per condition is fixed (fixed N-in-each-level scenario). In the former scenario, the total sample size is set to N = 120, and thus the sample size for the j -th level is given by n _j  = 120/k. In the latter scenario, the sample size for the j -th level is set to be n _j  = 20, and thus the total sample size is given by N = 20k. In both scenarios, we considered the number of levels in k = 2, 3, 4, 5, 6, 8, 10, and 12. Table 2 summarizes the sample size settings.

Table 2 Simulation settings of total and per-level sample size in the two scenarios

The true range d is set to be one of 0.2, 0.5, and 0.8, corresponding to Cohen’s small, medium, and large criteria for the standardized mean difference (Cohen, 1988). The artificial dataset for the j -th level is generated from a normal distribution with a corresponding mean and variance one. For the generated dataset, the sample effect sizes η ², ε ², and ω ² are calculated. This process is repeated 1,000,000 times per condition.

Results

The resultant Monte Carlo expected values of the three sample effect size indices are illustrated in Figs. 2 and 3 for the fixed total-N scenario and fixed N-in-each-level scenario, respectively. It is clearly seen that the expected behavior of samples ε ² and ω ² is similar to that of the population effect size (compare c–f in Figs. 2 and 3 with Fig. 1) in both scenarios. Therefore, the interpretation for them is also the same. That is, researchers can intentionally inflate the resultant expected values of the sample effect sizes, ε ² and ω ², by using the minimum number of levels and a large range of levels, while the effect of this manipulation is substantial; intentional choice can easily double or half the resultant effect size. Thus, one can expect that our findings for the population (Equation (2), Fig. 1) similarly hold in the sample as long as bias-corrected sample effect size indices are used.

Fig. 2

Monte Carlo expected values of the sample effect size indices in the fixed total-N scenario. Top panels: η ² as a function of (a) the number of levels k and (b) the standardized range of levels d. Middle panels: ε ² as a function of (c) the number of levels k and (d) the standardized range of levels d. Lower panels: ω ² as a function of (e) the number of levels k and (f) the standardized range of levels d

Fig. 3

Monte Carlo expected values of the sample effect size indices under the fixed N-in-each-level scenario. Top panels: η ² as a function of (a) the number of levels k and (b) the standardized range of levels d. Middle panels: ε ² as a function of (c) the number of levels k and (d) the standardized range of levels d. Lower panels: ω ² as a function of (e) the number of levels k and (f) the standardized range of levels d

However, the relationship between the number of levels k and sample η ² differs from others. In the fixed total-N scenario, η ² is shown to be an increasing function of the number of levels k, although it decreases once when d is not small (d = 0.5 and 0.8; Fig. 2a). In the fixed N-in-each-level scenario, η ² is an increasing function of the number of levels when d is small and a decreasing function when d is large (Fig. 3a). In the literature, it has been argued that generally η ² may not be a recommended sample effect size because it tends to largely overestimate the population value (Fisher, 1925; Okada, 2013; Olejnik & Algina, 2003). Still, in practice, it is one of the most often used effect size indices (Peng et al., 2013). Our result reveals an additional reason for not recommending η ²: although the population effect size is a decreasing function of the number of levels k, sample η ² can sometimes be its increasing function. Thus, it may be possible for researchers to obtain a seemingly large value of sample η ² by setting a large number of levels. However, in fact, the population effect size becomes smaller by this manipulation. Therefore, this seeming increase is deceptive, and such research practice is far from recommended.

Note that because our objective is to analyze the behavior or expected values and that reporting intervals would complicate the figure, we only reported the Monte Carlo expected values in Figs. 2 and 3. However, for the complete results and details on the 2.5 %, 25 %, 75 %, and 97.5 % quantiles, see Supplemental Material A.

Summary and discussion

“Answers” to the question

Let us return to our cover story of mental rotation. From the findings of this study, the “answer” to Question 1 is that students should choose the number of levels to be as small as possible, that is, just two levels (k = 2). For Question 2, they should choose the range of levels to be as large as possible, that is, between [0°, 180°], and again just two levels. If the initial range [0°, 60°] corresponds to d = 0.3, then choosing two levels rather than five would double the resultant expected effect size. Further, widening the range to [0°, 180°] would make it more than seven times larger. It now becomes clear that researchers’ choice of the number and range of levels substantially affects the resultant effect size.

Revisiting the assumptions

Although we made a linearity assumption in our cover story for simplicity, this can be relaxed a little further. As clarified in the derivation in the Appendix, the critical premise of our derivation is the equispacedness of the population means of the dependent variable (Y). If this holds, our results do not depend on the functional form between X and Y. Of course, the equispacedness of Y holds when the following three hold: X is continuous, the levels are equispaced in X, and the relationship between X and Y is linear. Still, equispacedness can also hold in many other scenarios. When the relationship is nonlinear, one can still find non-equispaced levels in X that result in equispaced Y. Moreover, although some readers might have thought that our results are based on continuous or ordinal X, as implied by our cover story, that is not actually the case. In fact, X can also be a purely categorical variable. In such a case, dummy indicator variables that correspond to each level are introduced. Then, their coefficients are quantitative variables even when X is categorical. Thus, we can choose the level (category) that results in the minimum and maximum treatments. Our critical assumption is just that the dependent means are equispaced within this range.

Some readers may find that this equispacedness is still a strong assumption. Our view is that equispacedness is one of the most natural assumptions when no further information is given. Even so, we can also likewise study other cases. The approach we took in this paper can be similarly used to evaluate both the population and the sample behaviors of the effect size in different scenarios. The “answers” to the research questions posed may differ when the assumptions of an equispaced dependent variable change. Investigating the consequences in other scenarios would thus be a fruitful avenue of future research, and the literature on the optimal research design would serve as a valuable reference.

Why is this the case?

Some readers may find difficulty in intuitively accepting the above “answers.” The formal mathematical derivation is given in the Appendix. Instead, here, we show an intuitive explanation of why this is the case.¹ For the decomposition of variance, the following law of total variance is well known:

$$ Var(Y) = E\left(Var\left(Y\Big|X\right)\right) + Var\left(E\left(Y\Big|X\right)\right). $$

(3)

On the right-hand side, the first term is the expected value of the error variance, which is σ ² _E in our scenario and therefore not affected by the researcher’s choice of the number of levels. The second term involves the average sum of the squares over the group means, which thus corresponds to σ ² _M . In our scenario of equispaced Y within a fixed range, it would be intuitive that this term is a decreasing function of the number of levels. Because the variance-accounted-for effect size is given as the ratio of the second term to the total, it is also a decreasing function of the number of levels.

The above leads us to understand this issue in a broader sense. The seemingly paradoxical fact discussed in this paper occurs in part because the variance-accounted-for effect size is standardized by using the total variance. As discussed in Baguley (2009), standardized effect sizes are affected, or “distorted,” by the research design (or anything) that affects the variance even though it does not affect the essential relationship between X and Y. In this sense, the standardized effect size may be better understood as a measure of the detectability of the effect rather than the magnitude of the effect itself. Then, the use of simple (i.e., unstandardized) effect sizes may be recommended in more applications than currently. Refer to Baguley (2009) for discussions on when standardized and simple effect sizes are appropriate and to Baguley (2004) for related discussions on the effect of the research design.

That being said, the current popularity of standardized effect sizes in psychology is also understandable. A standardized effect size may be more natural in psychology compared with physical science because the metrics of variables studied in psychology rarely have an intrinsic meaning. Furthermore, in meta-analytic studies, standardized effect size measures are often used to combine the results of various studies that have different metrics for the dependent variable (as well as other research designs). In fact, as pointed out by Kelly and Preacher (2012), some authors such as Olejnik and Algina (2003) and the National Center for Education Statistics (2002) define the effect size as a “standardized” measure of effect. However, as demonstrated in this paper, standardized effect sizes have some undesirable side effects (i.e., they are more vulnerable to differences in the research design).

Related studies

As mentioned at the beginning of the paper, the fact that variance components depend on the experimental design has been investigated and pointed out by a variety of studies². A rich literature exists in the field of the optimal research design. Some are quite mathematically oriented, whereas other works are readily accessible to psychological researchers. For example, Mead (1988, Chapter 17) discussed how the variance of the parameter estimates is affected by the experimental design. Moreover, McClelland (1997) demonstrated that one can determine the allocation of observations across the five levels of the explanatory variable that maximizes the variance. The Appendix of McClelland (1997) mathematically shows (in the case of five levels) that the maximum variance of X is obtained when half of the observations are allocated to each extreme condition. Thus, the results we have shown in this paper are in line with those of the literature, although our focus is not on finding the optimal design but rather quantitatively investigating how and how much the effect size is affected by the research design. We made the equispacedness assumption and derived the functional form of the relationship, which can be used to evaluate how the resultant effect size would change when we manipulate the design.

Another important field of the literature is that of extreme group analysis (EGA). In our settings, we have shown that one can obtain the maximum effect size by choosing the minimum number of levels and maximum range. This is similar to the case of EGA, which refers to the practice sometimes used in empirical studies of examining the effect of X on Y, typically when X is continuous, by selecting only those individuals who are on the extreme ends of the distribution on X. Typically, the objective of conducting EGA is to increase power; however, it also affects the resultant effect size. For example, Humphreys (1985) pointed out that standardized effect sizes are “inflated” when extreme groups are analyzed. The same was discussed in detail by Preacher, Rucker, MacCallum, and Nicewander (2005). Our setting in this paper is different from the typical context of EGA in that we consider the choice of levels, which is a categorical explanatory variable, while EGA typically considers the choice of groups based on continuous explanatory variables. Still, the intuition obtained from the literature can help researchers better understand the phenomenon.

Take-home messages and future studies

Effect sizes have been considered to be important because they allow comparisons across studies, even when different scales are used, and consequently constitute the basic elements of research synthesis (Fritz, Scherndl, & Kühberger, 2012). The effect size obtained in a study has often been considered to be beyond the control of the researchers. However, in this paper, we demonstrated that effect size is vulnerable to the research design. The variance-accounted-for effect size can be better understood as “the ratio of the variance explained by X in the given research design.” This does not represent the pure measure of the relationship between X and Y, but rather measures the discriminability of the effect of X in the given research design. This point is in line with previous studies (Baguley, 2009; Kelley & Preacher, 2012).

The important take-home message of this paper is that the variance-accounted-for effect size substantially depends on the researcher’s choice of experimental design such as the number and range of levels, and that this dependency between the effect size and research design can be studied mathematically. Thus, a simple meta-analysis of the variance-accounted-for effect size would be irrational unless the effect of the research design, such as the number and range of levels, is explicitly considered and handled.

In our view, despite the extensive literature, relatively little attention has been paid to how much the variance-accounted-for effect size depends on the research design, even though many authors now report it in their papers. Of course, it is not our intention to argue that the variance-accounted-for effect size is useless. Rather, the current paper calls for more attention: the research design needs to be explicitly considered and handled when we interpret, compare, and synthesize the variance-accounted-for effect size.

The idea of a generalized effect size (Olejnik & Algina, 2003) is an appealing approach to retain comparability among different designs in terms of the use of blocking factors or covariates, or the inclusion of additional factors. Still, it is not intended to retain the comparability between studies that have different designs in terms of the number and range of levels. Future studies could investigate better ways of combining the effect sizes from multiple studies that differ in aspects of the research design.

Recently, the undesirable research practice called “p-hacking” has become a concern. This refers to the fallacy of exploiting a researcher’s degree-of-freedom until p < 0.05 is reached by, for example, keep adding participants in an experiment (Murayama, Pekrun, & Fiedler, 2013; Rouder, 2014; Simmons, Nelson, & Simonsohn, 2011). Thus, the practice of reporting effect sizes has been recommended through the movement away from an overdependence on p values. However, if the scientific community resorts too much to the variance-accounted-for effect size as a primary measure of research instead of p values without paying attention to the given research design, then another undesirable research practice of “eta squared hacking” might occur in turn, in which researchers intentionally choose to use the design that inflates the effect size. Standardized effect sizes are dependent on the research design, and therefore researchers can affect them simply by choosing an appropriate research design.

We considered the case of a single between-subjects factor design for simplicity. However, our argument should essentially apply to within-subjects factor and more complex designs as this concerns the decomposition of the error term. Our argument should also apply to the partial effect size measures often reported in practice, because these are defined by subtracting a constant from the denominator of the ordinary (non-partial) effect size. Our results also are strongly expected to be applicable to the sample ε ² and ω ² as well as their partial versions in more complex designs because their biases are known to be small. Additional future simulation research may prove this point.

Appendix: Derivation and derivatives of equation (2)

Let μ _j be the population mean in the j -th (j = 1, …, k) level³. Without loss of generality, let μ ₁ = 0 and μ _k  = d*. This means that μ ₁ corresponds to the population mean in the condition that results in the minimum effect μ _min , and μ _k corresponds to the population mean in the condition that results in the maximum effect μ _max . Because the scale is arbitrary, we choose μ ₁ to be 0 and μ _k to be d*. Then, Equation (1) can be rewritten as

$$ d=\frac{\mu_{max}-{\mu}_{min}}{\sigma_E}=\frac{d^{*}}{\sigma_E}. $$

(4)

We also assume that when the number of levels increase, the population mean takes the equispaced values between μ ₁ and μ _k . Then, each μ _j can be represented as

$$ {\mu}_j=\frac{d^{*}}{k-1}\left(j-1\right). $$

(5)

Note that this is a slightly relaxed assumption compared with the original assumptions of equispaced independent variables and linearity. From Equation (5), the mean of μ _j is given as

$$ \overline{\mu}=\frac{1}{k}{\displaystyle \sum_{j=1}^k}{\mu}_j=\frac{d^{*}}{2}. $$

(6)

By substituting Equations (5) and (6) into the definition of variance of the population means σ ² _M ,

$$ {\sigma}_M^2=\frac{{\displaystyle {\sum}_{j=1}^k}{\left({\mu}_j-\overline{\mu}\right)}^2}{k}=\frac{{\displaystyle {\sum}_{j=1}^k}{\left(\frac{d^{*}}{k-1}\left(j-1\right)-\frac{d^{*}}{2}\right)}^2}{k}=\frac{d^{*2}\left(k+1\right)}{12\left(k-1\right)}. $$

(7)

Further, from Equation (4), σ ² _E is given as

$$ {\sigma}_E^2=\frac{d^{*2}}{d^2}. $$

(8)

By substituting Equations (7) and (8) into the definition of η ² _pop ,

$$ {\eta}_{pop}^2=\frac{\sigma_M^2}{\sigma_T^2}=\frac{\sigma_M^2}{\sigma_M^2+{\sigma}_E^2}=\frac{\frac{d^{*2}\left(k+1\right)}{12\left(k-1\right)}}{\frac{d^{*2}\left(k+1\right)}{12\left(k-1\right)}+\frac{d^{*2}}{d^2}} = \frac{d^2\left(k+1\right)}{12\left(k-1\right)+{d}^2\left(k+1\right)}, $$

(9)

which proves Equation (2).

The partial derivative with respect to k is

$$ \frac{\partial }{\partial k}\frac{d^2\left(k+1\right)}{12\left(k-1\right)+{d}^2\left(k+1\right)}=-\frac{24{d}^2}{{\left(12\left(k-1\right)+{d}^2\left(k+1\right)\right)}^2}\le 0. $$

(10)

Therefore, η ² _pop is a monotonically decreasing function of k. Similarly, the partial derivative with respect to d is

$$ \frac{\partial }{\partial d}\frac{d^2\left(k+1\right)}{12\left(k-1\right)+{d}^2\left(k+1\right)}=\frac{24d\left({k}^2-1\right)}{{\left(12\left(k-1\right)+{d}^2\left(k+1\right)\right)}^2}\ge 0. $$

(11)

Note that the last inequality holds because by definition d ≥ 0 and k ≥ 2. Therefore, η ² _pop is a monotonically increasing function of d.