Introduction

Many animal species were previously shown to keep track of discrete quantities though a nonverbal counting-like process (Davis, 1984; Mechner, 1958; Platt & Johnson, 1971; Brannon & Roitman, 2003, Gallistel, 1990; Gallistel & Gelman, 2000). Number (set cardinality) is not only an important quantity in and of itself in some behaviorally important decisions, but it also enters into the determination of other quantities that have demonstrated importance (e.g., rate in the matching phenomenon [Gallistel et al., 2007], and discrete probability in temporal discrimination [Balci, Freestone, Gallistel, 2009]).

The counting ability has been claimed to rely on mechanisms that are similar to those that underlay interval timing (Gallistel & Gelman, 1978, 2000; Meck & Church, 1983). Supporting a possible link between these two quantitative domains, the scalar property (e.g., proportionality of standard deviation to the mean)—more commonly known as Weber’s Law in psychophysics—has been demonstrated for both interval timing and nonverbal counting (Cordes et al., 2001; Mechner, 1958; Platt & Johnson, 1971; Whalen et al., 1999). For instance, the spread in number of responses or in delay increases in proportion to the target number or target delay, respectively (Platt & Johnson, 1971; Whalen et al., 1999 for counting and Buhusi et al., 2009; Gibbon, Fairhurst, & Goldberg, 1997 for timing). In more formal terms, the coefficient of variation (standard deviation/mean) of the relevant response dimension (number and time) was found to be constant (Brannon & Roitman, 2003, Gallistel & Gelman, 2000; Malapani & Fairhurst, 2002). When the coefficient of variation is constant, the discriminability becomes a function of the ratio between the to-be-discriminated quantities (Weber’s Law).

There are now a number of studies showing that the decision process takes into account the uncertainty and its statistical properties when it sets the target (or decision threshold, for review see Balcı et al, 2011). Importantly, as summarized above these statistical properties of timing uncertainty are shared by numerical cognition pointing at a relationship between endogenous numerical uncertainty and reward maximizing numerical decisions. The current study aims to fill this empirical and theoretical gap between numerical cognition and optimal decision-making. Specifically, the aims of the current study are to test: 1) if evidence for counting ability and its scalar property generalize to mice, and 2) if and how mice can incorporate their endogenous uncertainty about counts into their numerosity-based decisions to maximize reward rate.

The fixed consecutive number (FCN) schedule (Mechner, 1958) constitutes an ideal test for addressing these research questions. In this procedure, animals are required to press one of the levers (run lever) for a minimum number of times before collecting the armed-reward by pressing a second lever (reinforcement lever). If the number of lever presses emitted before pressing the second lever was less than the minimum requirement, the accrued number of run lever presses would reset without reinforcement. If the number of run-lever presses before pressing the second lever was equal to or more than the minimum requirement, the run-lever presses would reset with reinforcement.

The mean and the spread of the number of run-lever responses in this task are proportional to the minimum requirement (Mechner, 1958); however, animals typically emit more responses than needed (Mechner, 1958; Rivalan et al., 2007; Smith et al., 1976; Szostak & Tombaugh, 1981). Although this behavioral tendency can be interpreted in terms of biased estimates of numerosities, given the imprecision in numerical representations, responding more than the minimum requirement qualitatively points at the optimal numerical decision strategy in this task. On the other hand, how much more than the minimum requirement the subject should aim at responding before “claiming” the reward depends on the endogenous numerical uncertainty.

The reward rate in the FCN task can be defined in terms of the reward earned per unit effort exerted: p(reward)/number of responses. Thus, the optimality problem can be conceptualized as maximizing the unit of reinforcements per lever press. Assuming that the number of run-lever responses is an inverse-Gaussian distributed random variable, the expected reward rate in the FCN task can be calculated as \( \left(1- waldcdf\left(FCN,\widehat{n},\widehat{\lambda}\right)\right)/\widehat{n} \), where \( \widehat{n} \) is mean number of run-lever responses and \( \widehat{\lambda} \) is the shape parameter. The CV is \( \sqrt{\widehat{n}/\widehat{\lambda}} \). When this calculation is conducted for different target number of responses (\( \widehat{n} \)) for a given level of CV (\( \sqrt{\widehat{n}/\widehat{\lambda}} \)), the reward-rate maximizing target number of responses can be determined for that level of CV by finding the \( \widehat{n} \) that maximizes this function. The resultant optimal performance curve dictates a non-linear increase in target number of responses with increasing levels of numerical uncertainty. This in turn provides an objective reward function for the evaluation of decision-making performance in the FCN task.

In the current study, we tested mice with three different FCN schedules (FCN-10, FCN-20, FCN-40) in different phases and evaluated their performance within the framework of optimality outlined above. Our findings showed that mice can count the lever presses they have emitted with scalar variability and integrate their representational uncertainty about numerosities into their decisions in a nearly optimal fashion.

Method

Subjects

Fifteen, 8-week-old, naïve, C57BL/6j male mice acquired from LifeSci, Boğaziçi University (Istanbul, TR) served as subjects in this experiment. Mice were housed in groups of four per individually ventilated cages (IVC) made of polysulfone. They were kept with 12:12 h light-dark cycle with lights on at 6 a.m. Experiments were run only during the light phase. The mice were maintained at 85 % of their free-feeding weight and had ad libitum access to water. All animal procedures were approved by the Koç University Animal Research Local Ethics Committee.

Apparatus

The experiment was conducted in 12 operant chambers (Med Associates, ENV-307 W: 21.6 cm × 17.8 cm × 12.7 cm), which were placed inside sound-attenuating boxes. Two retractable levers (ENV-213 2 W) were placed 2.2-cm above the grid floor and 11-cm apart from each other on one of the two metal walls. The other metal wall contained three illuminable feeding hoppers (ENV-203-20). Only the middle hopper was active during the experiment. A cooling fan was turned on during testing. The experimental protocol was coded in MED-PC IV software. The temporal resolution for data recording was 10 ms.

Procedure

Lever Press Training

Each mouse was magazine and lever press trained for at least 5 sessions. The insertion of both levers into the chamber initiated the trials. The levers remained available until the mouse pressed one of them or 60 s has elapsed without a response (FR1–FT60s), whichever occurred first. The middle food dispenser delivered 0.01 cc of liquid feed (Nestlé Nutrition Isosource, vanilla flavor) for 6 seconds and the mid magazine was illuminated with the retraction of the lever. To finish this phase, the mice had to press each lever for at least 20 times per session for three consecutive sessions. If this criterion was not met within 10 sessions, an FR-1 schedule of reinforcement was then commenced. In the FR-1 training, one of the two levers (randomly picked) was inserted in a trial and reinforcement was delivered only contingent upon a lever press. The criterion was kept the same with the FR-1/FT-60 phase.

Fixed Ratio Training

In this phase, each animal was assigned to FR10, FR20, or FR40 schedule in a pseudo-random fashion to equate the sample sizes. Half of the animals had only the left lever, whereas the other half had only the right lever inserted during training. Emitting the scheduled number of responses on the available lever was reinforced. This phase was completed if and when 20 reinforcements were obtained per session for three consecutive sessions. The success criterion was in effect after the first two sessions. Animals who obtained less than five rewards for two consecutive sessions were moved to a lower FR schedule (i.e., FR40 → FR20 and FR20 → FR10) and had to reach the success criterion to move back to their original schedule.

Fixed Consecutive Number Schedule Testing

In this phase of testing, the FCN and FR trials were presented with equal probability in a session. The first three trials of each session were always FR trials. The FR trials were identical to the previous training phase but in FCN trials animals were required to press a second lever (inserted at the same time with the first lever) after pressing the first lever at least for a fixed minimum number of times to obtain the reward. Pressing the second lever before emitting the necessary number of run-lever responses terminated the trial without the delivery of a reward. Failure to obtain a reward in an FCN trial forced the next trial to be another FCN trial until the subject obtained a reward or failed to obtain a reward for five consecutive trials.

After finishing 35 sessions of testing in the initially assigned schedule, animals were moved to another schedule (random assignment) and tested with the new schedule for 15 sessions (e.g., FCN10 → FCN40). After finishing the 15 sessions of testing with the second schedule, animals were trained in the remaining schedule for another 15 sessions (e.g., FCN40 → FCN20).

Data Analysis

The steady-state (last five sessions of each phase) response frequencies were fit with an exponential inverse-Gaussian mixture distribution (MLE) that has been previously shown to fit inter-response time data in a time-based paradigm with similar rules (i.e., DRL; Freestone, Balcı, Simen & Church, 2015). Information regarding the comparison of these fits to other distributions is presented in the SOM. The best fit mean and shape parameters of each mouse for each FCN schedule were used to calculate the optimal strategy for that mouse for the corresponding phase. To test whether animals relied on the time instead of number of responses, the time interval between the first and the last run-lever press (steady state) were fit with an exponential inverse-Gaussian distribution. The best-fit inverse-Gaussian parameters were used to estimate the CV of response times. FCN-10 condition of one subject was excluded from the analyses due to loss of data caused by a programming error. The data collected from different FCN schedules were compared with repeated-measures ANOVA tests.

Since the null-hypothesis significance testing cannot deliver evidence in favor of the null-hypothesis (Gallistel, 2009) and some of the invariances are theoretically important in our case (i.e., indifference between empirical vs. optimal number of run-lever responses), we complemented several of our conventional t-test comparisons with the corresponding Bayesian t-test (Rouder et al., 2009). This test allowed us to state preference for null vs. alternative hypothesis based on the relative evidence gathered for one hypothesis over the other given the data (i.e., Bayes Factor). Finally, we have conducted three analyses (i.e., CV, regression, and response pattern analyses) to determine if mice relied on the number or duration of their responses. Information regarding the regression and response pattern analyses and their outputs are presented in the SOM.

Results

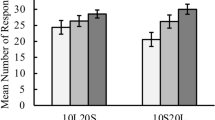
Figure 1 shows the average response curves separately for three different FCN schedules after normalizing each subject’s frequencies by the total number of FCN trials of that subject in the corresponding schedule (see SOM Figures 1 and 2 for representative individual subject’s data and the response curve defined as a function of response duration). The average number of responses emitted on the first lever before claiming the reward (run responses) was 14.43 (standard error of mean [SEM] = 0.41, median = 14.55, interquartile range [IQR] = 2.13) in the FCN-10 condition, 27.35 (SEM = 0.56, median = 27.42, IQR = 2.65) in the FCN-20 condition, and 52.00 (SEM = 1.00, median = 50.78, IQR = 6.32) in the FCN-40 condition. In each of these conditions, the average number of responses was significantly higher than the minimum requirement, t(13) = 10.72, p < 0.001, t(14) = 13.20, p < 0.001, and t(14) = 12.06, p < 0.001, respectively. As expected, the average response numbers differed significantly between the three FCN schedules, F(2,26) = 916.33, p < 0.001, η 2 p = 0.99. Post-hoc analysis showed that the average number of responses were different between each pair of FCN-schedule (all p < 0.001). The FCN-schedule also had a significant effect on the normalized number of responses, F(2,26) = 6.10, p < 0.01 η 2 p = 0.32. Post-hoc analysis showed that normalized response numbers were higher for the FCN-10 schedule compared to the FCN-40 schedule, p < 0.05 (Bonferroni corrected).

Fig. 1
figure 1

Average normalized response curves separately for FCN-10, FCN-20, and FCN-40 schedules. Errors bars show the SEM

Full size image
Fig. 2
figure 2

Expected gain curves calculated separately for three different FCN schedules each calculated for the average CVs of the number of run-lever responses estimated for the corresponding FCN condition. The vertical thick lines show the average empirical response numbers for the corresponding FCN schedule whereas the vertical thin lines mark the FCN schedule. Filled circles indicate the optimal strategy for the corresponding FCN schedule

Full size image

There was no significant difference between optimal and empirical number of run responses in FCN-10 (t(13) = 1.24, p = 0.23), FCN-20 (t(14) = 0.59, p = 0.57) or FCN-40 schedules (t(14) = −1.93, p = 0.07). We complemented these statistics with one-sample Bayesian t-test since the corresponding null hypothesis is theoretically important in our case (Rouder et al., 2009). With the scale r on effect size = 0.707, the scaled JZS Bayes Factors were 1.95 (anecdotal evidence) and 3.27 (substantial evidence) in favor of the null, and 1.14 (anecdotal evidence) in favor of the alternative hypothesis for the FCN-10, 20, and 40 schedules, respectively. With the scale r on effect size = 1, these values were 2.49 (anecdotal evidence), 4.36 (substantial evidence), and 1.06 (anecdotal evidence) in favor of the null hypothesis. Overall, these results revealed more support for the null hypothesis that the empirical number of run-lever responses was not different from the corresponding optimal number responses.

Figure 2 shows the expected reward rate curves separately for three different FCN schedules each calculated for the average CV estimates in the corresponding FCN condition along with the corresponding average empirical response numbers. The visual inspection of this figure also pointed at the nearly optimal decision strategies in this task. The proportion of maximum expected reward rates corroborated these observations. Subjects achieved 97.9 % (SEM = 0.5 %, median = 98.4 %, IQR = 2.3 %), 98.8 % (SEM = 0.3 %, median = 99.2 %, IQR = 0.8 %), and 98.3 % (SEM = 0.5 %, median = 98.7 %, IQR = 1.9 %) of the maximum possible expected reward rate defined for their level of numerical uncertainty (i.e., CV of run-lever response numbers) in the FCN-10, FCN-20, and FCN-40 schedules, respectively. There was no significant effect of the FCN-schedule on this measure, F(2,26) = 1.04, p = 0.37 η 2 p = 0.07.

The average CVs for the number of run-lever responses were 0.30 (SEM = 0.02) for the FCN-10 schedule, 0.25 (SEM = 0.02) for the FCN-20 schedule, and 0.25 (SEM = 0.02) for the FCN-40 schedule. The FCN-schedule had a significant effect on CV, F(2,26) = 3.81, p < 0.05 η 2 p = 0.23. However, further analysis showed that CVs were not significantly different from each other after Bonferroni correction (there was a significant difference between FCN10 and FCN40 before the correction).

It is possible that subjects relied on timing rather than number of responses they emitted in this task. To address this issue, we conducted three independent analyses (only the comparison of CVs are presented in the main text). We compared the CVs of the number of run-lever responses with the CVs of the response durations under the assumption that the dimension that had stronger control over the response pattern would exhibit lower CV (see also Fetterman et al., 1985). The average CVs for the duration of the run-lever responses were 0.42 (SEM = 0.05), 0.38 (SEM = 0.05), and 0.47 (SEM = 0.08) for the FCN-10, 20, and 40 schedules, respectively. When we compared the CVs of the number and duration (since first response) of run-lever responses CVs across all schedules, we found that response number based CVs were significantly lower, F(1,13) = 24.94, p < 0.001, η 2 p = 0.66. There was no main effect of schedule, F(2,13) = 0.50, p = 0.61, η 2 p = 0.04 or an interaction effect, F(2,13) = 1.33, p = 0.28, η 2 p = 0.09. The same results held when the response duration was calculated as the interval between trial onset and the last run-lever response (see SOM). Consistent with these findings, the results of our regression and response-pattern analyses also showed that mice relied on the number rather than the duration of their responses (for details see SOM).

Discussion

In the current study, mice were required to emit a minimum number of responses on one lever before pressing the second lever to collect the armed reward. The optimal strategy in this task required the animals to aim at responding more than the minimum response requirement (i.e., FCN schedule). Importantly, how much more than the minimum requirement should the animals respond depended on the level of an individual animal’s endogenous uncertainty about counts. Our findings showed that animals can optimize the number of responses by integrating their numerosity-related uncertainty into their decisions and maximize the reward-rate attained in this task. These findings are consistent with the conclusions of previous studies that utilized temporal decision-making tasks; these studies showed that humans and other animals can adopt reward maximizing temporal decision strategies by taking account of their scalar endogenous timing uncertainty (Balcı et al., 2011; Çavdaroğlu et al., 2014). Thus, this study extended the scope of optimal temporal risk assessment to the domain of numerosity-based decision-making.

The DRL task in the interval timing domain highly resembles the FCN procedure and the related reward-rate maximizing decision strategies. In the DRL task, animals are trained to wait for a minimum delay since their previous response to attain reward. Responses emitted earlier than this minimum delay resets the corresponding wait time without the delivery of the reward. If animals respond after this delay, their wait time resets with reward delivery. Reward-rate maximization in this task requires animals to aim at waiting longer than the minimum delay and how much more than the minimum delay animals should on average wait depends on their level of scalar endogenous timing uncertainty. Our previous findings showed that humans and non-human animals can optimize their wait time and maximize the reward-rate (Balcı et al., 2011; Çavdaroğlu et al., 2014; but see Freestone et al., 2015). The results of the current study showed that similar optimal decision-strategies can be attained when the reinforcement schedule is based on the number of responses rather than their timing. These findings overall emphasize the generality of optimal risk-assessment in experiential tasks that entail the representation of both continuous and discrete quantities and the associated scalar uncertainty.

Previous studies on nonverbal counting ability were primarily conducted with rats and pigeons. We tested each mouse in three different FCN schedules (FCN-10, FCN-20, and FCN-40). The mean number of responses emitted by mice was proportional to the FCN schedule. Moreover, the CV of the number of responses emitted per FCN-schedule was nearly constant within individual animals, at least for the larger schedules (i.e., FCN-20 and FCN-40). These findings showed that counting ability also applies to mice and that the scalar property also is apparent in their numerosity-based judgments. Overall, these findings support the notion that non-human animals can count and the psychophysical properties of this ability is similar to interval timing. We believe that these recent findings along with the earlier results point at the need for the development and refinement of models of non-verbal counting in a way that is consistent with the processing dynamics that are assumed to underlie interval timing.

Although animals were assumed to perform in the FCN task primarily by counting the number of run-lever presses, it is possible that they instead relied on time (a correlate of lever press). This possibility has been ruled out by a number of early studies (see SOM for summary). For instance, Fetterman et al. (1985) found that the CV of number of responses was lower and less variable (between different experimental conditions) than the CV of the timing of responses in a numerical discrimination task. Dehaene (1997) argued that earlier findings point at numerical rather than temporal control over responding in animals.

In our study, we tested the possible reliance on timing by running a series of independent analyses. We first looked at if mice were more precise in terms their run response numbers or response times before claiming reward under the assumption that more precision in one domain would suggest its stronger control over behavior. The variability of the number of responses was lower than the variability of the timing of responses. Furthermore, we did not observe the break-run pattern of responding (transitioning from low rates of responding to high rates of responding as a function of trial time), which is the typical response pattern observed in fixed-interval schedules (Schneider, 1969). Finally, our regression analyses showed that the number of run-lever responses had more predictive power regarding decisions than the response duration (see SOM). Thus, consistent with the conclusion of earlier studies, our findings from a number of independent analyses point at numerical rather than temporal control over responding in the FCN task.

Future studies that use different procedures are required to test the generality of optimal numerical risk assessment performance. The ability to utilize a count-based task, such as FCN in mice, also enables the study of genetic basis of numerical cognition.