Three regularities of recognition memory: the role of bias

Abstract

A basic assumption of Signal Detection Theory is that decisions are made on the basis of likelihood ratios. In a preceding paper, Glanzer, Hilford, and Maloney (Psychonomic Bulletin & Review, 16, 431–455, 2009) showed that the likelihood ratio assumption implies that three regularities will occur in recognition memory: (1) the Mirror Effect, (2) the Variance Effect, (3) the normalized Receiver Operating Characteristic (z-ROC) Length Effect. The paper offered formal proofs and computational demonstrations that decisions based on likelihood ratios produce the three regularities. A survey of data based on group ROCs from 36 studies validated the likelihood ratio assumption by showing that its three implied regularities are ubiquitous. The study noted, however, that bias, another basic factor in Signal Detection Theory, can obscure the Mirror Effect. In this paper we examine how bias affects the regularities at the theoretical level. The theoretical analysis shows: (1) how bias obscures the Mirror Effect, not the other two regularities, and (2) four ways to counter that obscuring. We then report the results of five experiments that support the theoretical analysis. The analyses and the experimental results also demonstrate: (1) that the three regularities govern individual, as well as group, performance, (2) alternative explanations of the regularities are ruled out, and (3) that Signal Detection Theory, correctly applied, gives a simple and unified explanation of recognition memory data.

Introduction

In a preceding paper, Glanzer et al. (2009) demonstrated that recognition memory performance is consistent with normative Signal Detection Theory (Green & Swets, 1966/1974)¹ based on likelihood ratios (LR). The demonstration consisted of three steps:

(1) formal proofs that the LR assumption implies three regularities. These regularities, defined shortly, are the Mirror Effect, the Variance Effect, and the normalized Receiver Operating Characteristic (z-ROC) Length Effect, (2) computed examples showing how LR decisions generate the regularities, and (3) a survey of recognition memory data establishing the ubiquity of the three regularities.

The 2009 paper also briefly discussed two other topics: how bias can obscure the Mirror Effect and also how that obscuring can be countered. Those two topics are developed in detail here. We show that the Mirror Effect – measured in the usual way – is obscured by bias. We then counter the bias effect in four different ways. (1) by using a more informative index of the Mirror Effect, (2) by canceling the bias with a pay-off arrangement, (3) by using a between-list design, and (4) by increasing the difference in accuracy between the two experimental conditions (familiar vs. unfamiliar names).

With respect to the survey in Glanzer et al. (2009), the following objection can be made. The surveyed data consisted of pooled group data. It is possible that group data give a different picture of the underlying processes than do individual data. The possible disagreement of group and individual data is discussed at length by Estes (1956) and Estes and Maddox (2005). The results reported here answer that objection by demonstrating that the three regularities govern individuals’ performance.

In a recognition memory experiment, participants are shown a study list of items and are later shown a test list consisting of items from the first list (“old”) and items which were not (“new”). They are then asked to judge whether each item is “old” (O) or “new” (N), a YES-NO task. Or they are asked to rate their confidence that each item is “old” or “new”.

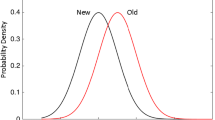
Signal detection theory (SDT) represents such memory tests as generating two distributions of a univariate random variable X, the information available on a single trial (see Fig. 1A). The two distributions are typically assumed to be normal, differing in mean and possibly standard deviation. The distribution of X when the item is “old” (O) is f _O (x) and when the item is new (N), f _N (x). A distribution of new items, f _N (x), on the left and a distribution of old (studied) items, f _O (x), on the right

$$ {f}_N(x)=\frac{1}{\sqrt{2\pi }{\sigma}_N}{e}^{- \frac{{\left(x-{\mu}_{\mathit{\mathsf{N}}}\right)}^{\mathsf{2}}}{\mathsf{2}{\sigma}_{\mathit{\mathsf{N}}}^{\mathsf{2}}}} $$

and

$$ {f}_O(x)=\frac{1}{\sqrt{2\pi }{\sigma}_{\mathsf{O}}}{e}^{-\frac{{\left(x-{\mu}_{\mathsf{O}}\right)}^{\mathsf{2}}}{\mathsf{2}{\sigma}_{\mathsf{O}}^{\mathsf{2}}}} $$

on the left. When ${\sigma}_{\mathit{\mathsf{O}}}={\sigma}_{\mathit{\mathsf{N}}}=\sigma$ we refer to the model as “normal equal variance.” We can set μ _N  = 0 and σ = 1 with no loss in generality. The sole remaining parameter ${\mu}_{\mathit{\mathsf{O}}}$ is typically denoted d ′.

Fig. 1

Signal detection theory (SDT) representation of decision for simple one-condition case. (A) initial new (left) and old (right) distributions. Vertical lines indicate five criteria. (B) Receiver Operating Characteristic (ROC) based on the distributions. (C) normalized ROC, z-ROC

The individual compares x to a fixed criterion c ₀ responding “old” if x > c ₀, otherwise “new.” We label the outcome of a trial as a “hit” (H) p[Hit|Old] = p[X > c ₀|Old] when the item is old (is from f _O (x)) and the response is “old.”

The conditional probability of a “hit”, P[Hit|Old] = P[X > c ₀|Old] is the area under ${f}_{\mathit{\mathsf{O}}}(x)$ to the right of the criterion ${c}_{\mathsf{0}}$. The area under f _N (x) to the right of the criterion ${c}_{\mathsf{0}}$ corresponds to “false alarms” (FA) (Green & Swets, 1966/1974). If the criterion is set at a point where the old and new distributions intersect, then the choice is called unbiased. It is represented by the middle vertical line in Fig. 1A.

More information about the individuals’ memory is obtained by asking them how confident they are about their classification of an item as new or old. They now respond by selecting a rating response from an ordered set of ratings {R ₁ < R ₂ < ⋯ < R _n }. A typical choice of ratings would go from 1 to 6 with 1 representing “most sure the item is old” to 6 “most sure the item is new.” We assume that the rating responses are obtained by setting up n − 1 criteria ${c}_1<{c}_2<\cdots <{c}_{n-\mathsf{1}}$ represented by the dotted vertical lines in Fig. 1A. The criteria divide the horizontal axis into bins and the ratings are assumed to correspond to the bin containing the variable X.

A plot of the probability of each response for an old item versus the probability of the same response to a new item is called a receiver operating characteristic (ROC):

$$ \begin{array}{lll}P\left[R\le {R}_i\Big|O\right]=f\left(P\left[R\le {R}_i\Big|N\right]\right)\hfill &, \hfill & i=1,\cdots, n-1\hfill \end{array}. $$

where

$$ \begin{array}{l}\begin{array}{ll}P\left[R\le {R}_i\Big|O\right]={\displaystyle \underset{-\infty }{\overset{c_i}{\int }}{f}_O(x)dx,}\hfill & i=1,\cdots, n-1\hfill \end{array}\hfill \\ {}P\left[R\le {R}_n\Big|O\right]=1\hfill \end{array} $$

is the conditional probability that the rating is R _i or less when the stimulus is old and

$$ \begin{array}{l}\begin{array}{ll}P\left[R\le {R}_i\Big|N\right]={\displaystyle \underset{-\infty }{\overset{{\mathit{\mathsf{c}}}_{\mathit{\mathsf{i}}}}{\int }}{f}_N(x)}dx,\hfill & i=1,\cdots, n-1\hfill \end{array}\hfill \\ {}P\left[R\le {R}_n\Big|N\right]=1\hfill \end{array} $$

is the conditional probability that the rating R is R _i or less when the stimulus is new. The confidence rating ROC for item recognition is a function relating the ratings of old items to the ratings of new items. The ROC for the distributions in Fig. 1A is shown in Fig. 1B.

The ROC is often re-plotted on normalized (double probability) axes with proportions transformed into z-scores. Each proportion is transformed to z = Φ ^− 1(p), where Φ(z) is the cumulative distribution function of a normal random variable with mean 0 and variance 1. When data are plotted on transformed axes, as shown in Fig. 1C, the resulting plot is called a “z-ROC.” It yields additional information about the two underlying distributions: If the underlying distributions are normal or near normal the z-ROC will be a straight line with a slope = σ _N /σ _O . The two distributions in Fig. 1A are normal with the same standard deviation and, therefore, the z-ROC is a straight line with slope 1.0.

If the underlying distributions are normal or near normal and have unequal standard deviations, the z-ROC is still a straight line but slope will not be equal to 1.0. It will instead be equal to the ratio of the standard deviation of the new distribution to that of the old, σ _N /σ _O .

In the preceding description, for the sake of simplicity, decisions were described as being made on the basis of X, some form of mnemonic evidence. A full description of SDT requires an expanded description of the basis for decisions. In that description decisions are made on the basis of likelihood ratios (LR) (see Green & Swets, 1966/1974).

The LR in favor of “old” over “new,”

$$ L(X)=\frac{f_O(X)}{f_N(X)}. $$

is a measure of the evidence favoring “old” over “new.” On each test trial, given X, the individual compares its LR in favor of old to a fixed LR criterion,

$$ L(X)>\beta $$

responding “old” if the LR exceeds β and otherwise responds “new.” β is the LR equivalent of c ₀ discussed earlier.

The prior probability that an item is “old” is π. If the criterion β is set to (1 − π)/π (the prior odds in favor of “new”), then the resulting decision rule has the highest expected proportion of correct responses (Green & Swets, 1966/1974).

If there are more than two response categories then the LR rule is easily generalized by assuming that there are multiple criteria (Green & Swets, 1966/1974). For example, if the categories are “Very Strong No,” “Strong No,” “Weak No,” “Weak Yes,” “Strong Yes,” and “Very Strong Yes,” then the individual sets are five criteria β ₁ < β ₂ < β ₃ < β ₄ < β ₅ that guide this selection among six categories.

The decision rule assumed in much work on recognition memory is not LR but simple strength or familiarity. For the case presented in Fig. 1 it is not obvious how to determine whether memory decisions are based on LR or on strength. It is, however, possible to make the determination in the case of two-condition recognition.

Two-condition recognition

There are many experiments in which individuals are presented with two different kinds of items (e.g., high vs. low frequency words) or two different study conditions (e.g., single vs. repeated presentation) that produce a difference in accuracy. These two-condition experiments are important because they show three regularities that are produced by LR decisions: (1) the Mirror Effect, (2) the Variance Effect, and (3) the z-ROC Length Effect.

We describe each regularity in turn.

The mirror effect

When there are two sets of items or conditions in a recognition test that produce a difference in accuracy and the decisions are based on LR, then the superior condition (S) will give better recognition of old items as old and also better recognition of new items as new. In a yes/no recognition test the effect is seen in the mirror symmetric pattern of hits (H) and false alarms (FA):

$$ \mathrm{F}{\mathrm{A}}_{S,N}<\mathrm{F}{\mathrm{A}}_{W,N}<{\mathrm{H}}_{W,O}<{\mathrm{H}}_{S,O} $$

where the subscript S denotes superior, W, weaker, and N and O refer to new and old, respectively. We will use a transparent notation for such inequalities in which each term refers to the proportion of yes responses:

$$ SN<WN<WO< SO $$

(1)

There is extensive evidence for the mirror effect in the literature (Glanzer & Adams, 1985; Glanzer et al., 2009).

The variance effect

When there are two sets of items or conditions in a recognition test that produce a difference in accuracy, decisions based on LR will affect the relative variances of new distributions. SN, the new distribution of the superior condition, will have a larger variance than WN, the new distribution of the weaker, lower accuracy condition. This is a novel general effect, not previously noted in the literature. It is measured using the slope of the z-ROC that plots superior (S) new items ratings against weaker (W) new items ratings, the new/new z-ROC. If decisions are based on LR, the slope will be less than 1.0. Decisions based on LR also produce a parallel effect on the relative variances of the old distributions. SO, old distribution of the S condition, will have a larger variance than WO, the old distribution of the W condition. The effect is measured using the slope of the old/old z-ROC that plots the S old items ratings against the W old items ratings. Again, if decisions are based on LR , the slope will be less than 1.0.

The z-ROC length effect

When decisions are made on the basis of LR, the length of the z-ROC contracts as a function of accuracy. The more accurate the condition, the shorter the z-ROC.

From this point on we will use the log likelihood ratio, Λ, for convenience. Its use allows us to present simpler equations. The log likelihood ratio Λ = λ(X) is a function of a random variable X and is therefore a random variable itself with its own distribution, mean, and variance. The distribution of Λ is determined by the form of the distribution of X and the function λ().

We note that we used ordinary linear regression to estimate linear fits and obtain slopes for the computed examples of the following models. There is no issue with using linear regression in this way. The ROCs are plots of one theoretical distribution against another theoretical distribution. Neither axis is affected by random error.

The normal equal variance model and generation of the three regularities

We now present a simple example, a Normal Equal Variance Model that shows the regularities and how they are generated. In the example we assume a model of recognition memory based on normal equal variance distributions because the equations that govern the regularities are simple and the displays that show the regularities are also simple. We demonstrated in Glanzer et al. (2009) that the unequal variance normal model (which is a better fit to most recognition memory data) produces the same regularities as the equal variance case. The regularities seen in the example hold as well for models of recognition memory based on binomial and exponential distributions (see Glanzer et al., 2009). In this example we also convert LR to log LR, Λ. The conversion does not change any of the effects discussed but allows us to present simpler equations and simpler plots.

For the current example, SN and WN are both Normal (0,1), WO is Normal (1,1) and SO is Normal (1.75,1) (the first number in the parentheses is the mean, the second number is the standard deviation). The model also assumes decisions being made on the basis of LR.

Figures 2A and B describe the model at the theoretical level. Figures 2C and D represent observable data based on the model. Figure 2A represents the initial distributions of raw information for SN, WN, WO, and SO usually referred to as “strength,” “familiarity,” or “amount of marking.” SO is placed to the right of WO, representing greater accuracy. SN and WN are not separated. It can be argued that new, unstudied items, because they have not been studied, cannot differ in strength.² We do not separate the new distributions here; moreover, in order to show the effects of the LR transformation clearly – namely, that when SO moves above WO, SN will move in the opposite direction, below WN, on the LR decision axis.

Fig. 2

Signal detection theory (SDT) normal equal variance model for two-condition case. (A) Four initial distributions − SN, WN, WO, and SO on X, an initial information or strength axis. SN and WN are not separated. (B) The distributions in A re-plotted on a log likelihood decision axis. (C) Standard normalized Receiver Operating Characteristics (z-ROCs) for S(+) and W(x) showing the Length Effect. (D) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

When the individual decides on the basis of LR, the densities in Fig. 2A are effectively redistributed on a log likelihood axis, as in Fig. 2B. The log likelihoods, are random variables whose distributions are also normal (see Glanzer et al, 2009). Figures 2B, C, and D illustrate the three regularities.

The mirror effect

Figure 2B shows that when the densities of Fig. 2A are re-plotted on a log likelihood decision axis, the new distributions SN and WN which were at the same position in Fig. 2A are now separated. The Mirror Effect appears with the distributions ordered

$$ SN<WN<WO< SO. $$

The effect is obvious in Fig. 2B in the order of the distributions’ modes.

The H/FA mirror index

This mirror pattern of the distributions is usually indicated by inequalities from the hits and false alarms (H/FA) of a yes/no test

$$ F{A}_{SN}<F{A}_{WN}<{H}_{WO}<{H}_{SO} $$

Glanzer et al. (2009), however, demonstrated that H/FA Mirror Index functions poorly when there are bias effects. In such cases the index may indicate the absence of a Mirror Effect even when the underlying distributions are actually in mirror order. We consider this H/FA Mirror Index at length in this paper, however, because it is widely used.

The distance mirror index

A better index of the Mirror Effect is obtained with more complete measures of the distance between the means of SN and WN and the distance between the means of WO and SO. When confidence ratings have been obtained, we can plot two novel z-ROCs that give more complete information on those distances. One z-ROC is the plot of the normalized SN ratings against the normalized WN ratings – called the new/new z-ROC. The other z-ROC is the plot of the normalized SO ratings against the normalized WO ratings – the old/old z-ROC. These two z-ROCs are presented in Fig. 2D. The new/new z-ROC falls below the positive diagonal, indicating that SN is lower (further to the left) on the decision axis than WN. The distance below the positive diagonal can be measured by fitting the new/new z-ROC with a linear equation. The equation’s intercept indicates the distance from SN to WN. Because the intercept is affected by the slopes of the z-ROC it is recommended that its value be corrected to take account of that effect, converting the intercept, i, to d _e = 2 i/(1+s) where s is the slope (Wickens, 2002, p. 65). We use this measure, d_e, for all the z-ROC distances in this paper. The distance between SN and WN in the new/new z-ROC, referred to as d _nn , is -0.76, the negative value indicating that SN<WN.

The old/old z-ROC is predominantly above the positive diagonal in Fig. 2D, indicating that SO is higher (further to the right) on the decision axis than WO. Fitting the old/old z-ROC with a linear equation finds the intercept, i. This is used to derive the measure of the distance from WO to SO, d _∞ = +0.74, the positive value indicating that WO<SO. Those two inequalities and the inequalities from the standard z-ROCs of Fig. 2C, namely WN<WO and SN<SO, give the full order of the underlying distributions as

$$ \mathrm{S}\mathrm{N}<\mathrm{W}\mathrm{N}<\mathrm{W}\mathrm{O}<\mathrm{SO}, $$

i.e., the mirror order.

We use the distance mirror Indices, d _nn and d _∞ – the measures derived from the new/new and old/old z-ROCs – as the preferred index in analyzing the data of the experiments reported later. The distance index is superior to the H/FA index because it is based on more information, all criterion positions on the ROC. The H/FA index, on the other hand, reduces the positions to two. Cohen (1983) has demonstrated the loss of power that occurs when multiple-valued scales are reduced to dichotomies.

The distance index is closely related to two other measures that have been used to analyze the Mirror Effect. One is the mean confidence rating. That measure will also reveal an underlying mirror order when the H/FA index does not. Another related measure is obtained from “null choices” in forced choice recognition experiments (Glanzer, Adams, & Iverson, 1991; Glanzer, Adams, Iverson, & Kim, 1993; Hilford, Glanzer, & Kim 1997; Kim & Glanzer, 1995) Null choices are those between the two new conditions SN versus WN and between the two old conditions SO versus WO The SN versus WN choice indicates the distance between the two new distributions. It corresponds to d _nn . The SO versus WO choice, indicates the distance between the two old distributions. It is equivalent to d _∞.

The variance effect

Figure 2B also shows the Variance Effect, a larger variance for the strong condition than the corresponding weak condition. When the distributions in Fig. 2A are re-plotted on the log likelihood axis in Fig. 2B the variance of SN which was equal to the variance of WN in Fig. 2A becomes greater than the variance of WN. This can be seen in the relative spread of the SN and WN distributions in Fig. 2B. Similarly, the variance of SO which was equal to that of WO in Fig. 2A is greater than the variance of WO in Fig. 2B. This change can be seen in the relative spread of SO compared with WO in Fig. 2B. To measure these relative variances we again use the two z-ROCs of Fig. 2D. The new/new z-ROC plots SN ratings against WN. If decisions are being made on the basis of LR, sl_nn, the slope of the new/new z-ROC, which equals σ _WN /σ _SN , denoted sl _nn , will be less than 1.0. Linear fitting of the new/new z-ROC gives a slope for the new/new z-ROC of 0.57 < 1.0.

The parallel effect on the relative variances of the old distributions, SO and WO effect is measured by the slope of the old/old z-ROC that plots the SO items’ ratings against the WO items’ ratings. Again, if the Variance Effect holds, the slope σ _WN /σ _SN -- denoted sl _∞ -- will be less than 1.0. In the example, the old/old z-ROC has a slope of 0.57 < 1.0. In recognition memory data, however, the slope of the old/old z-ROC is affected by another factor that complicates its interpretation.³ We therefore concentrate on the new/new z-ROC but will document the results for the old/old z-ROC as well.

The z-ROC length effect

Figure 2C shows the two standard z-ROCs for SO/SN and WO/WN with the more accurate the condition, S, producing the shorter z-ROC. The z-ROC Length Effect is obtained by computing the Euclidean distance between the end points of each z-ROC. In the example, length of S, len_S = 3.24; the length of W, len_W = 5.66. In other words, when decisions are made on the basis of LR, the length of the z-ROC contracts as a function of accuracy. This was first proved for the equal variance normal model by Stretch and Wixted (1998). It has also been proved to hold as well for the unequal variance normal, the binomial, and the exponential models (Glanzer et al. 2009).

Key equations

The reasons why the three regularities hold for the normal equal variance model presented may be summarized briefly. See Glanzer et al. (2009) for complete derivations and proofs.

The mirror effect

For this model it is assumed that f _N (x) is normal with mean 0, variance 1 and f _O (x) is normal with mean d ′, variance 1. Then Λ is also normally distributed. The conditional means of the Λ distributions are then

$$ \begin{array}{l}E\left[\varLambda \Big| Old\right]=\frac{d{\prime}^2}{2}\hfill \\ {}E\left[\varLambda \Big| New\right]=\frac{-d{\prime}^2}{2}\hfill \end{array} $$

Since d ^′ _s  > d ^′ _w these equations produce the Mirror Effect:

$$ E\left[\varLambda \Big| New,S\right]<E\left[\varLambda \Big| New,W\right]<E\left[\varLambda \Big| Old,W\right]<E\left[\varLambda \Big| Old,S\right] $$

The variance effect

The variances in this model were shown to be

$$ Var\left[\varLambda \Big| New\right]=Var\left[\varLambda \Big| Old\right]=d{\prime}^2 $$

This equation, making the size of the variances a simple function of the size of d’, leads to the variance effect. For example, since d ^′ _s  > d ^′ _w , the slopes of both the new/new z-ROC and the old/old z-ROC, equal to d ^′ _s  > d ^′ _w , are less than 1.0.

The z-ROC length effect

In recognition memory experiments there are multiple criteria c _i , i = 1, n _c on the decision axis that correspond to log likelihood ratios λ _i , i = 1, n _c . It was proved in Glanzer et al. (2009) that the length c _n  − c ₁ of the z-ROC decreases as a function of d’.

Finally, we note that all three regularities depend on the difference between the values of d’.

Bias effects

The preceding section did not include consideration of bias effects. In normative signal detection theory for a yes/no task the setting of the single log likelihood criterion c is the sum of two terms. The first term is the negative of the log prior odds that a signal will occur. If π denotes the probability of occurrence of the signal on any trial, then the log prior odds that a signal will occur is log[π/(1 − π)] and the term we use is its negative, $\log \left[\left(\mathsf{1}-\pi \right)/\pi \right]$. Intuitively, if the signal is more likely to occur in one condition than another then the individual should have a lower criterion and be more likely to respond “Yes” in that condition.

The second term reflects the losses and gains associated with different correct and incorrect responses. If the penalty for a FA is increased, for example, the individual should increase his log likelihood criterion and be more hesitant to respond “Yes.”

In recognition memory experiments, bias can result if the observer misperceives the prior probability that the item presented on a given trial is old or, for some reason, believes that different outcomes are not equally rewarded or punished. The possibility of changes in bias by likelihood ratio observers in responding to different test conditions has been discussed by Wickens (2002): “As a psychological model, the likelihood-ratio procedure gives a simple description of how decisions are made. From past experience the observer has a feeling for the distribution of effects produced by stimuli from the two conditions…Bias can arise in this scheme in several ways.... Alternatives whose likelihoods are overestimated, perhaps because they are particularly salient, are more often chosen than those that are not.”

With multiple log likelihood ratio criteria ${\lambda}_{\mathit{\mathsf{i}}},i=1,{n}_{\mathit{\mathsf{c}}}$, the effect of bias, β, is to rigidly shift all the criteria that partition the LR distributions by an amount log β. Liberal bias, β< 1.0 or, equivalently, log β < 0, moves the criteria to the left on the decision axis, increasing both hits and false alarms. Conservative bias, β > 1.0 or, equivalently log β > 0 moves the criteria to the right on the decision axis, decreasing both hits and false alarms. The bias evidently cannot affect d’ or the regularities that are solely functions of d’, e.g., the Variance Effect and the Length Effect. However, when there is a marked difference in bias between the S and W conditions the Mirror Effect can be disrupted. If the conservative bias is relatively large for the W condition and moves the criteria sufficiently far to the right in relation to the two distributions for W, the inequality SN < WN of Eq. 1 will disappear, as will be shown shortly. If the conservative bias is large for the S condition with the criteria for the S distributions sufficiently far to the right the inequality WO < SO of Eq. 1 will disappear.

To show the working of bias we take the model examined earlier with SN and WN Normal (0,1), WO Normal (1,1) and SO Normal (1.75,1). We now impose a liberal bias, β _s = .50 (log β_s = -0.69), on the S distribution. The z-ROCs obtained are shown in Fig. 3A. They show the same Length Effect as the unbiased case in Fig. 2C, len_W = 5.66, len_S = 3.22. The slopes of d _nn and d _∞ are both 0.5, less than 1.0. Both therefore indicate the Variance Effect.

Fig. 3

Signal detection theory (SDT) normal equal variance model with differential bias on a log likelihood decision axis. (A) Standard normalized Receiver Operating Characteristics (z-ROCs) for S(+) and W(x) showing the Length Effect. (B) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

The bias has, however, shifted the S z-ROC in Fig. 3A and both z-ROCs in Fig. 3B. The intercepts of Fig. 3B give d _nn = -.20 and d _∞ = .98, values that reflect the Mirror Effect, but also values that indicate a shift of the S distributions to the right relative to the W distributions. Compare them to the corresponding d _nn = -.76 and d _∞ = .74 in Fig. 2D. The less informative H/FA measure indicates a complete loss of the Mirror Effect with

$$ {\mathrm{FA}}_{\mathrm{SN}}=.32>{\mathrm{FA}}_{\mathrm{WN}}=.31<{\mathrm{H}}_{\mathrm{WO}}=.69<{\mathrm{H}}_{\mathrm{SO}}=.90 $$

The effect of changing the bias on the LR regularities for the normal equal variance model is shown in Table 1. In it the bias, β _s for S is varied from = 0.25 to 3.00 in steps of .25 (log β _s = -1.39 to +1.10), with W left unbiased, log β _w = 0 . With the H/FA Mirror Index, the Mirror Effect fails at β _s of .50 or less and 2.00 or greater. The Distance Mirror Indices, d _nn and d _∞, however, fail only for much more extreme bias values, less than .50 or greater than 2.75. The Length Effect and the Variance Effect remain.

Table 1 Effect of bias on the H/FA Index and the three regularities, equal variance normal model with bias, β_{s ,} varied in the strong condition (SO), weak condition (WO) held constant, unbiased

We also explored the effect of bias on the normal unequal variance model. This model is important because most recognition data evidence unequal variance (Egan, 1958, 1975; Glanzer, Kim, Hilford, & Adams, 1999; Ratcliff, Sheu, & Gronlund, 1992). It therefore offers a better fit to recognition memory data than the normal equal variance model (Mickes, Wixted, & Wais, 2007 )

The parameters selected were SN and WN Normal (0,1), WO Normal (1,1.18), and SO Normal (1.75,1.25). The results are shown in Table 2.

Table 2 Effect of bias on the H/FA index and the three regularities, normal unequal variance model with bias, β_{s ,} varied in the strong condition (SO), weak condition (WO) held constant, unbiased

In this case the H/FA Index of the Mirror Effect fails again at β _s of .50 or less and 2.00 or greater. The Distance Mirror Index is unaffected. The measures for the Variance Effect vary but all are less than 1.0 as evidenced of that effect. Both measures for the Length Effect also vary but at every bias level len_s < len_w

In summary, bias has little or no effect on the LR Variance and the Length Effects. It can eliminate the Mirror Effect, particularly when the H/F index is used.

Empirical work

We now report the results of five experiments that show the three LR regularities and the effects of bias. In the first experiment, normative word frequency is the strength variable. In the four that follow familiarity of names is the strength variable

All five experiments’ results show the three regularities. The second experiment, however, shows that bias can obscure the Mirror Effect when measured by the H/FA Index. The Distance Mirror Index, however, reveals the effect. The third, fourth, and fifth experiments demonstrate three other methods for countering those bias effects on the H/FA Index.

We report experiment results in four stages. First, we report group, pooled results. All the individuals' confidence ratings are pooled to give a single ROC. These give a compact, general picture of the regularity results but do not permit standard statistical analyses. It will be seen, however, that the measures derived from the group results correspond closely to the measures obtained from the standard analyses that follow. Second, we give the H/FA Index of the Mirror Effect, the conventional analysis of the effect. Third, we report the three LR regularities based on ROCs computed for each individual. These give distributions of measures that can be subjected to statistical analysis. Fourth, we report a more detailed analysis of each individual's performance.

Experiment 1. The three LR regularities and no bias effect

To show the three LR regularities in a simple case without the complications of bias we review and reanalyze the data from a recognition experiment with normative word frequency as the variable: high frequency (H) versus low frequency (L) (Glanzer & Adams, 1990). Here L is the more accurate or strong (S) condition and H is the less accurate or weak (W) condition.

The 16 undergraduate participants were first given a lexical decision task with 248 words, half H, half L, and 248 non-words. They were then given an eight-level confidence rating recognition test with the 248 old words and 248 new (half H and half L). Further details on the procedure and method are given in the original publication.

Results

Group

The four group z-ROCs, based on the pooled confidence ratings of all 16 participants, are shown in Fig. 4A and B. The regularities can be seen in the four z-ROCs as in the z-ROCs for the theoretical model discussed earlier (e.g., Fig. 2C and D). The examination is supplemented by sets of measures based on those z-ROCs. For the Mirror Effect, we measure the distances between the four underlying distributions. Those are obtained from the intercepts of the two z-ROCs in Fig. 4A and the two z-ROCs in Fig. 4B. For the Variance Effect, we measure the slopes of the old/old and new/new z-ROCs (see Fig. 4B). Here and in all subsequent analyses of group and individuals’ z-ROCs those measures are obtained by fitting each z-ROC with a linear function using the Wickens maximum likelihood program (Wickens, 2002) which furnishes intercepts and slopes. For the z-ROC Length Effect we compute the Euclidean distance between the end points of the standard z-ROCs in Fig. 4A.

Fig. 4

Normalized Receiver Operating Characteristics (z-ROCs) for Experiment 1, low (L) versus high (H) frequency words. (A) Standard z-ROCs for L(+) and H(x) showing the Length Effect. (B) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

Figure 4A shows the standard z-ROCs for L and H. The greater accuracy of L over H is seen in the superior position of the L z-ROC and its greater (positive) distance from the main diagonal. Fitting the two z-ROCs with linear functions and obtaining the intercepts gives us accuracy measures, the numerical distances between LN and LO (d _L ) and between HN and HO (d _H ). With d _L = .91> d _H = .56. The z-ROC Length Effect is evident. Computation gives us len_L = 2.48 < len_H = 2.99.

Figure 4B shows the new/new and old/old z-ROCs. The new/new z-ROC is below the main diagonal, indicating that LN is below HN on the decision axis as required for the Mirror Effect, with a distance measure d _nn = -0.22: that is, LN < HN. The old/old z-ROC is above the main diagonal, indicating that LO is above HO on the decision axis as required for the Mirror Effect, with a distance measure of d _∞ = 0.28: that is, HO<LO. The slope of the new/new z-ROC = 0.89, less than 1.0, as required for the Variance Effect: variance LN > variance HN. The slope of the old/old z-ROC = 0 .74, less than 1.0, as again required for the Variance Effect: the variance of LO is greater than the variance of HO.

Statistical analyses

We now report the results of the statistical analyses of the participants’ responses in three stages. First, the conventional analysis of the H/FA Index of the Mirror Effect. Second, the analysis of the three LR regularities. Finally, a third analysis of individual responses with respect to the three LR regularities.

Conventional analysis

The standard analysis of the Mirror Effect consists of a comparison of the accuracy of the two conditions (a difference is necessary for the effect to occur), and comparison of the hit and FA rate for each condition. The measures of interest are presented in Table 3. The table also includes measures of bias.

Table 3 Experimental results: accuracy, bias and H/FA mirror

In the first row of Table 3 entries one and two are the d’s for the Strong condition (d _S ) and for the Weak condition (d _W ): d _S = 0.96 and d _W = 0.60. They show that L words (S) are recognized significantly better than H words (W): F(1,15) = 45.31, MSE = 0.02 . This is a pre-condition for the Mirror Effect. The next two entries present the mean bias indices, c = .5x[ z(H) + z(FA) ] (Wickens, 2002, p. 28), for the L and the H condition.⁴ The means are +0.06 for L and +0.07 for H, indicating minimal bias and minimal bias difference. The two do not differ significantly, F(1, 15) = 0.18, MSE = 0.01. Since there are accuracy differences but no differential bias effects we expect the H/FA Mirror Index to indicate the mirror pattern, and it does. The next four columns give the H/FA Index: FA _SN =.30 < FA _WN =.36 < H _WO = .59 < H _SO = .66. Statistical evaluation is done by testing the differences, FA _SN vs FA _WN and H _WO vs H _SO. Those tests find each difference significant, t(15) = 3.72, SE = 0.02, and t(15) = 4.52, SE = 0.02. Therefore, with this index the mirror regularity holds. (Here and for the tests that follow we will use the words “significant” or “significantly” without the preceding “statistically”).

LR regularity analysis

For this analysis we fitted each individual’s confidence ratings with linear functions using the Wickens (2002) maximum likelihood program as was done for the pooled group data. For each individual we obtained two standard z-ROCs (Weak and Strong), an old/old z-ROC, and a new/new z-ROC. For each z-ROC we then obtained a d _e and slope.⁵ The lengths of each individual’s standard z-ROCs were computed using the Euclidean distance formula

Table 4 presents the mean measures of the three regularities based on the individuals' z-ROCs. The first two columns give the Distance Mirror Index: the mean distance between the two new distributions, d _nn , and the mean distance between two old distributions, d _∞. These means are obtained from the intercepts of the individual new/new z-ROCs and the individual old/old z-ROCs. The mean d _nn = -0.26 is negative and with t(15) = 5.20, SE = 0.05 is significantly below zero: SN < WN. The mean d _∞ = 0.29 is positive and with t(15) = 6.03, SE = 0.05 is significantly above zero: SO > WO. Again, the Mirror Effect holds.

Table 4 LR regularities

The next two columns, giving the mean slopes of the new/new and old/old z-ROCs (sl_nn and sl_oo), indicate the Variance Effect. They should be less than 1.0 for the effect to hold. The mean sl_nn = 0.88 with t(15) = 5.18 , SE = 0.02 is significantly below 1.0. The mean sl_oo = 0.73 with t(15) = 7.54, SE = 0.04 is also significantly below 1.0. The Variance Effect holds.

The next two columns, len_S and len_W, list the mean lengths of the standard z-ROCs for L =2.74 and H = 3.32. len_S is less than len_W with the difference significant, F(1, 15 ) = 35.37, MSE = 0.08. The z-ROC Length Effect holds.

In summary, all analyses find significant effects of all three LR regularities.

Further analysis of individual responses

We raised earlier the question of whether the regularities hold for individuals as well as for the pooled, group data. To answer that question we tabulated the presence of the regularities in each individual's data. The proportions of the 16 participants that show each of the three regularities are shown as ratios in the first row of Table 5. For example, all 16 participants showed SN < WN (d_nn negative). All the regularities are evident and differ significantly from chance (.50) by a binomial test. These results fully support the analyses of the corresponding statistics in Table 4.

Table 5 Proportion of participants showing each Λ regularity

We next report four studies in which, instead of word frequency, familiarity of names is the variable. We switch to this variable primarily to document further the three regularities. The use of familiarity will, furthermore, permit us to evaluate an alternative explanation of the Mirror Effect, the two-process explanation, considered later. All four experiments evidence the three LR regularities. They show, moreover, how the bias effects that conceal the mirror effect as measured by the H/FA Index can be countered.

Experiment 2. The three LR regularities and a bias effect

In the preceding experiment we observed the three regularities, no differential bias effects, and the Mirror Effect as measured by both the Distance Index and the H/FA Index. In this experiment, we see the effect of differential bias.

Method

The participants viewed a study list of 60 familiar (F) and 60 unfamiliar names (U) on a computer monitor. F is the strong condition, U the weak condition. Following the study list, they completed a confidence rating recognition test. The recognition test consisted of the names on the study list, and an equal number of 60 F and 60 U new names. The selection of study list names and test list names, and their order of presentation were randomized individually for each participant.

Materials

Two main lists, one of F and one of U names, were used to construct the study and test list for each participant. The F list consisted of 120 names of well-known actors, actresses, athletes, and politicians. The U list consisted of names from a local telephone book. Examples of the F names were Drew Barrymore, Edward Koch, and Tom Hanks. Examples of the U names were Aaron Hutchings, Basil Madsen, and Dawn Wise. Preliminary testing was carried out with a group of 15 undergraduates who rated each of the names on a 6-point scale with 1 being “very familiar” and 6 being “very unfamiliar.” The F names had a mean rating of 1.14, σ = 0.15, with 98 % judged familiar. The U names had a mean rating of 4.83, σ = 1.01, with 21 % deemed familiar. An additional 18 U names were selected and used as practice and filler items. Twelve were used for a practice study and test list. Six were used as unscored filler items: two, at the beginning and two at the end of each study list, and two at the beginning of each test list. The filler names served to eliminate primacy and recency effects. List names were randomly selected and individually randomized for each participant.

Procedure

During study and test each name appeared in the center of the screen, in capital letters. During study each name appeared for 1250 ms, with a blank screen for 750 ms, separating successive items. The test list was presented immediately after the completion of the study list. The test list consisted of 120 F names and 120 U names, half of each studied and half new. The test was self-paced, each name remaining on the screen until the participant responded.

Participants were instructed to decide, for each name, whether the item was “old” (had appeared in the study list) or “new” (had not) using a 6-point confidence rating scale. The confidence ratings were: (1) very sure old; (2) moderately sure old; (3) slightly sure old; (4) slightly sure new; (5) moderately sure new; and (6) very sure new. The numbers and their descriptions stayed on the monitor so that participants did not have to commit the scale to memory. The experiment began with a short practice session which consisted of a 6-item study list followed by a 12-item test list, six studied and six new items.

Participants

The data for 38 undergraduates are reported (one individual’s data whose responses were below chance are not). The participants had all been speaking English since the age of 10 years or earlier. They participated to fulfill a class requirement. This description also holds for the participants in Experiments 3, 4, and 5.

Results

Group

The group z-ROCs are presented in Fig. 5. All three LR regularities can be seen. Analysis of d’ (in Fig. 5A the strong condition is F) shows d_F = 1.93 > d_U = 0.93. The z-ROC length of F = 2.27 is less than the length of U = 3.83: the Length Effect. In Fig. 5B the old/old z-ROC lies above the main diagonal, with d_oo = 1.12: FO is above UO on the decision axis. The new/new z-ROC lies below the main diagonal, with d_nn = -0.50: FN is below UN on the decision axis. The Distance Index evidences the Mirror Effect. This is a striking effect of LR decisions since FN is greater than UN in the initial familiarity ratings cited earlier in the section on Materials. The Distance Index does, however, show the effect of bias in that d_nn is a much smaller distance than d_oo. Finally, the slopes of both those z-ROCs are less than 1.0, sl_oo =.0.57 and sl_nn = 0.61: the Variance Effect. This is another striking effect of LR decisions. The Variance Effect means that variance of the familiar names is greater than that of the unfamiliar names. But the initial ratings of those names, cited earlier in Materials, show the unfamiliar names starting with the greater variance.

Fig. 5

Normalized Receiver Operating Characteristics (z-ROCs) for Experiment 2, familiar (F) versus unfamiliar (U) names. (A) Standard z-ROCs for F(+) and U(x) showing the Length Effect. (B) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

Statistical analyses

Conventional analysis

The second row of Table 3 displays some of the results for the experiment. The first two entries show d_F = 2.11 > d_U = 1.04, t(37) = 77.69, MSE = 0.28. The significant difference in accuracy indicates that the Mirror Effect should be present. The next two entries are the bias indices. The mean bias index c_U = +0.38 (a strong conservative bias) for the unfamiliar items and c_F -0.03 (a slight liberal bias) for the familiar names. They differ significantly, F( 1, 37)= 20.93, MSE= 0.15 .The difference reflects the fact that participants tended to say “yes” less often to the unfamiliar names, both new and old, than to the familiar names. This differential bias moves the two false alarm rates together. The pattern of hits and false alarms shows the effect of the differential bias, with FA_FN and FA_UN barely separate. The effect of the bias is severe on the H/FA Mirror Index. The statistical analysis of that index is the test of FA_FN versus FA_UN and H_UO versus H_FO. That statistical evaluation finds only H_WO versus H_SO significantly different, t(37) = 9.30, SE=0.03. The difference between FA_FN versus FA_UN, however, is not, t(37) = 0.45, SE = 0.03. If the H/FA Index was the only measure available, the conclusion would be that there was a failure of the Mirror Effect.

LR regularity analysis

The second row of Table 4, shows, however, that the Mirror Effect is present as shown by the significant d_nn and d_oo Distance Index (entries 1 and 2). The mean distance between to two new distributions is negative, d_nn = −0.57, and with t(37) = −4.41, SE = 0.13 is significantly below zero: FN < UN. The mean distance between two old distributions, d_oo = 1.28, is positive and with t(37) = 16.73, SE= 0.08 is significantly above zero: FO > UO. In sum, the Distance Index finds that the Mirror Effect holds. The distributions are in the order FN < UN < UO < FO. When there is differential bias, the H/FA Index, based on minimal distance information, fails to show the mirror pattern while the Distance Index reveals the pattern’s presence.

The next two entries, the mean slopes of the new/new and old/old z-ROCs, indicate the Variance Effect. Both are less than 1.0. The mean of the new/new slope = 0.64, with t(37) = 7.55, SE = 0.05 is significantly below 1.0. The mean of the old/old slope = 0.59, with t(37) = 10.28 is also significantly below 1. The Variance Effect holds. The presence of the Variance Effect, that the L conversion makes the σ for the F names greater than that for the U names, is particularly striking since the initial measures of familiarity indicated the reverse. As noted in the section on Materials above the initial variance of the familiarity ratings of F names were less than that of the ratings of the U names.

The last two entries, the mean lengths of the standard z-ROCs for F = 2.39 and U = 3.68, are significantly different, F(1, 37) = 90.08, MSE= 0.35. The Length Effect holds.

In summary, all three LR regularities hold, including the Mirror Effect. The H/FA Mirror Index, however, is strongly affected by the bias difference and indicates, incorrectly, the absence of a Mirror Effect.

Further analysis of individual responses

The proportions of individual participants that show each of the three regularities are presented in the second row of Table 5. All the regularities are again evident and statistically significant by a binomial test. These data fully support the analyses of the corresponding statistics in Table 4. The denominators of the ratios vary because the data of two participants did not permit the computation of all four z-ROCs (they did not use a sufficient number of confidence categories). For the following experiments this variation in the Table 5 denominators occurs for the same reason: participants' responses that do not permit computation of particular z-ROCs.

In summary, we have again demonstrated the presence of the three regularities in the performance of individuals, this time for familiarity of names as the variable. We have furthermore demonstrated that the conventional H/FA Index for the Mirror Effect is inadequate when there is differential bias. In that case, the more informative Distance Index based on d_nn and d_oo should be used. We develop this point further by showing how to cope with differential bias when the H/FA Index is used.

Experiment 3. Bias removed with payoff schedule

In the preceding experiment the participants showed a differential bias. They tended to say “yes” less often to unfamiliar names than to familiar names. This bias concealed the Mirror Effect when measured by the H/FA Index. We now remove the differential bias directly by arranging differential payoffs for responses to the two classes of names. If our reasoning is correct then all three regularities should appear including a mirror pattern for the H/FA Index. We use the payoffs to induce a counter-bias canceling the observed bias. This experiment is particularly important because any apparent failure of the Mirror Effect is necessarily accompanied by differential bias. This accompaniment is seen in the data of Experiment 2 when the H/FA Index is used. Our interpretation of the relation between bias and Mirror Effect is that the bias conceals the effect, particularly with the H/FA Index. An alternative interpretation is that the differential bias is a by-product of the intrinsic failure of the Mirror Effect with the materials of Experiment 2. To test which interpretation is correct, we now repeat Experiment 2 but with a feedback operation, pay-offs, to remove the differential bias of Experiment 2. If our interpretation is correct, then the Mirror Effect should be evident, full-blown, even for the H/FA Index.

Method

The materials, procedure, and characteristics of participants were the same as in Experiment 2, except that, before the test, the participants were told that their responses would be scored with the following schedule: For each old, unfamiliar name correctly identified as “old”, +50 points would be assigned. For each old, unfamiliar name incorrectly identified as “new”, −50 would be assigned. For all other correct responses, +10 and all other incorrect responses, −10 would be assigned. Total scores were reported to the participants at the end of the test.

Participants

Forty-two undergraduates.

Results

Group

The group z-ROCs are presented in Fig. 6. All three LR regularities can be seen. In Fig. 6A the z-ROC for F is above that for U with d_F = 1.45 and d_U = 0.77. The length of the F z-ROC, 1.60, is less than the length of U, 2.13: the z-ROC Length Effect. In Fig. 6B the old/old z-ROC lies above the main diagonal, with d_oo = 0.61: FO is above UO on the decision axis. The new/new z-ROC lies below the main diagonal, with d_nn = -0.40: FN is below UN on the decision axis. Those two z-ROCs indicate the Mirror Effect. Also the slopes of both those z-ROCs are less than 1.0, sl_nn= 0.67 and sl_oo= 0.83: the Variance Effect.

Fig. 6

Normalized Receiver Operating Characteristics (z-ROCs) for Experiment 3, familiar (F) versus unfamiliar (U) names. (A) Standard z-ROCs for F(+) and U(x) showing the Length Effect. (B) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

Statistical analyses

Conventional analysis

The third row of Table 3 presents the mean accuracy, bias, and H/FA index. The accuracy d’s are based on 34 of the 42 participants tested. With the introduction of payoff instructions, eight of the participants used too few categories to permit construction of some z-ROCs, e.g., using only two confidence ratings: very sure old and very sure new.

The first two entries are d_F = 1.80 and d_U = 0.91. These measures of sensitivity differ significantly, with F(1,33) = 109.06, MSE = 0.12. With a difference in accuracies across the two conditions, the regularities appear. The next two entries present the mean bias indices, cF = +0.04 and cU = +0.08. These indices do not differ, F(1, 41) = 0.58, MSE = 0.07. No disruption of the mirror regularity should be expected. The next four entries show the mirror pattern in the H/FA data: FA_FN= 0.20 < FA_UN= 0.30 < H_UO = 0.64 < H_FO = 0.78. Statistical evaluation of FA_FN versus FA_UN and H_UO versus H_FO find the values in each pair significantly different, t( 41) = 7.65, SE = 0.01, and t(41 ) = 9.29, SE = 0.01. The argument presented in the introduction to this experiment is supported. Differential bias in Experiment 2 caused the obscuring of the Mirror Effect as measured by the H/FA Index. Removal of that differential bias with a payoff schedule revealed the effect even when measured by the weaker H/FA index.

LR regularity analysis

Table 4 contains the z-ROC-based regularity measures. The first two means for the Distance Mirror Index, are d_nn = −0.46 and d_oo = 0.71. Both differ significantly from zero. The mean d_nn is negative with t(33) = −5.15, SE = 0.09: SN < WN. The mean d_oo is positive with t(33)= 7.14 , SE = 0.10 : WO < SO. The next two entries, the mean slopes of the new/new and old/old z-ROCs, indicate the Variance Effect regularity. Both are significantly less than 1.0. The mean of d_nn = 0.75 with t(33) = 3.93, SE = 0.06. The mean of d_oo = 0.76 with t(33) = 3.00, SE = 0.08. The Variance Effect holds.

The next two entries, the mean lengths of the standard z-ROCs for F = 2.75 and U = 3.60 are significantly different, F(1, 33 ) = 12.32, MSE = 0.60. The z-ROC Length Effect holds.

Further analysis of individual responses

The proportions of individual participants that show each of the three regularities are presented as ratios in the third row of Table 5. All the regularities are evident and statistically significant by a binomial test. These data fully support the analyses of the corresponding statistics in Table 4.

Experiment 4. Bias removed with between-list paradigm

All three preceding experiments displayed the three regularities. In Experiment 2, however, sizable bias difference effects removed the Mirror Effect according to the H/FA Index. In Experiment 3 we removed that bias with a payoff schedule and recovered the H/FA Mirror Effect. Another way to accomplish that removal and thereby recover the H/FA Mirror Effect is by moving to a between-list rather than a within-list paradigm. In a within-list paradigm, the two conditions, e.g., F and U, are both present in a single study and a single test list as in the preceding experiments. In a between-list paradigm, the two conditions appear in separate study-test sequences.

The effect of separate test lists on bias was discovered by Hoshino (1991). In a series of experiments, he tried to replicate the word frequency Mirror Effect using Japanese kanji (ideograms) with a yes/no procedure and the H/FA Mirror Index. His first two experiments failed to show the effect, with P(HO) > P(LO). He ascribed the failure to a differential bias, a difference in the tendency to say “old” more frequently to H versus L words. The c bias indices are significantly different. In a third experiment he tested two groups in different conditions. One was tested as in his Experiments 1 and 2, with a test list consisting of a mixture of L and H words. That group showed the same pattern of results as his preceding two experiments, differential bias and violation of the Mirror Effect with the H/FA Index.

$$ {\mathrm{FA}}_{\mathrm{LN}}=0.10<{\mathrm{FA}}_{\mathrm{H}\mathrm{N}}=0.27<{\mathrm{H}}_{\mathrm{H}\mathrm{O}}=0.76>{\mathrm{H}}_{\mathrm{LO}}=0.75. $$

The other group, with separate H and L test lists, obtained the Mirror Effect with the H/FA Index.

$$ {\mathrm{FA}}_{\mathrm{LN}}=0.14<{\mathrm{FA}}_{\mathrm{H}\mathrm{N}}=0.24<{\mathrm{H}}_{\mathrm{H}\mathrm{O}}=0.68<{\mathrm{H}}_{\mathrm{LO}}=0\ .71 $$

(Hoshino presented and analyzed his data in a more complex form, separating results from the first half and second half of the test list. We have presented the combined results.)

We aimed, therefore, in this experiment, to accomplish two things: (1) replicate evidence of the three regularities, and (2) remove the difference in bias by using a between-list design and thereby allow the H/FA Index to show the Mirror Effect.

Method

Experiment 4 was similar to Experiment 2 except that each participant studied and was then tested on two separate lists, one of F names, the other of U names. Order was counterbalanced across participants. Half the participants studied and were tested on the F lists (120 names) first; the other half of the participants had the U lists (120 names) first.

Participants

Thirty undergraduates were tested.

Results

Group

The group z-ROCs are presented in Fig. 7. All three LR regularities can be seen again. The standard z-ROCs in Fig. 7A have d_F = 2.26 and d_U = 1.02. They show the z-ROC Length Effect, with length F = 2.12, and length U = 3.26. In Fig. 7B the old/old z-ROC lies above the main diagonal with d_oo = 1.16 and the new/new z-ROC, lies below the main diagonal, d_nn = - 0.80: the Mirror Effect. Also the slopes of both those z-ROCs are less than 1.0, 0.54 and 0.75, respectively: the Variance Effect.

Fig. 7

Normalized Receiver Operating Characteristics (z-ROCs) for Experiment 4, familiar (F) versus unfamiliar (U) names. (A) Standard z-ROCs for F(+)and U(x) showing the Length Effect. (B) old/old (o) and new/new (*) z-ROCs showing the Mirror and the Variance Effect

Statistical analyses

Conventional analysis

The first two entries in row 4 of Table 3, the accuracy means, are d_F = 2.49 and d_U = 1.21. They differ significantly, F(1,29) = 112.96, MSE = 0.21. The next two entries the mean bias indices, c_F = +0.11, c_U = +0.15 do not differ, F(1,29) = 0.21, MSE = 0.10. The bias difference seen in mixed-list Experiment 2 has disappeared. Moving to a between-list paradigm removes the bias difference. With the elimination of differential bias the H/FA Index again shows a clear Mirror Effect.

$$ {\mathrm{FA}}_{\mathrm{FN}}=.11<{\mathrm{FA}}_{\mathrm{UN}}=.26<{\mathrm{H}}_{\mathrm{UO}}=.65<{\mathrm{H}}_{\mathrm{FO}}=.87 $$

The difference in the false alarms for F and U is significant, t( 29) = 6.61, SE = 0.02. The difference in the hit rates is also significant, t(29) = 9.62, SE = 0.02.

LR regularity analysis

The fourth row of Table 4 lists the regularity measures. The first two entries for the Distance Mirror Index, d_nn = −0.80 and d_oo = 1.31, show a significant Mirror Effect with mean d_nn < zero, t( 29 ) = −6.24, SE = 0.13 and mean d_oo > zero, t( 29 ) = 9.75, SE = 0.13. The next two entries, the slopes of the new/new and old/old z-ROCs show a significant Variance Effect. Both are less than 1.0: sl_nn= 0.77, t(29 ) = 3.18, SE = 0.07 and sl_oo= 0.54, t( 29 ) = 9.25, SE = 0.05. The next two entries, mean length F = 2.55 < mean length U = 4.07 show a significant length difference, F(1, 29) = 40.51, MSE = 0.85. The z-ROC Length Effect holds.

Further analysis of individual responses

The proportions of individual participants that show each of the three regularities are presented in the fourth row of Table 5. All the regularities are evident and significant by a binomial test. These data fully support the analysis of the corresponding statistics in Table 4.

Experiment 5. Bias removed by increased accuracy difference

In Glanzer et al. (2009), we showed, by computation, that bias effects that conceal the Mirror Effect with the H/FA Index are countered by increasing the accuracy difference between the S and W conditions. To show this countering of bias we take the model examined earlier with SN and WN Normal(0,1), WO Normal(1,1), and SO Normal(1.75,1) and impose a liberal bias, β_s = .50 on the S distribution. The H/FA measure, based on those parameters, shows a complete loss of the Mirror Effect with

$$ {\mathrm{FA}}_{\mathrm{SN}}=.32>{\mathrm{FA}}_{\mathrm{WN}}=.31<{\mathrm{H}}_{\mathrm{WO}}=.69<{\mathrm{H}}_{\mathrm{SO}}=.89 $$

If we increase the difference between WO and SO to WO Normal(1,1) and SO Normal(1.85,1) in this model, the Mirror Effect as measured by the H/FA Mirror Index reappears.

$$ {\mathrm{FA}}_{\mathrm{SN}}=.29>{\mathrm{FA}}_{\mathrm{WN}}=.31<{\mathrm{H}}_{\mathrm{WO}}=.69<{\mathrm{H}}_{\mathrm{SO}}=.90 $$

We will now counter the bias effect of Experiment 2 by increasing the accuracy for the familiar names vis-à-vis the unfamiliar names. We do that by decreasing the number of familiar names in the study and test lists. Experiments on list composition in which study lists are composed of items from different sub-lists (Dorfman & Glanzer, 1988; Malmberg & Murnane, 2002; Shiffrin, Huber, & Marinelli, 1995) have shown that decreasing the number of items drawn from one of the sub-lists increases recognition accuracy for those items.

Method

Experiment 5 was identical with Experiment 2 except that the number of familiar names was reduced by half in the study and test lists. The study lists consisted of 30 familiar and 60 unfamiliar names. The test lists consisted of 30 familiar old, 30 familiar new, 60 unfamiliar old, and 60 unfamiliar new. Except for the change in number of items the procedure in this experiment was the same as Experiment 2: construction of lists, presentation, and characteristics of participants.

Participants

Forty-five undergraduates were tested.

Results

Group

The group z-ROCs are presented in Fig. 8. All three LR regularities can be seen again. The standard z-ROCs in Fig. 8A have d_F = 2.18 and d_U = 0.83. They show the z-ROC Length Effect, with length F = 1.78, and length U = .3.55. In Fig. 8B, the old/old z-ROC lies above the Main Diagonal with d_oo = 1.61, and the new/new z-ROC, lies below the main diagonal, d_nn = -1.12: the Mirror Effect holds. Also the slopes of both those z-ROCs are less than 1.0, 0.41 and 0.55, respectively: the Variance Effect holds.

Fig. 8

Normalized Receiver Operating Characteristics (z-ROCs) for Experiment 5, familiar (F) versus unfamiliar (U) names. (A) Standard z-ROCs for F(+) and U(x) showing the Length Effect. (B) old/old (o) and new/new (u) z-ROCs showing the Mirror and the Variance Effect

Statistical analyses

Conventional analysis

The means in row 5 of Table 3 show a significant accuracy difference. The first two entries for d_F = 2.76 and d_U = 1.10 differ significantly, F(1,44) = 282.37, MSE = 0.22. The next two entries the mean bias indices, c_F = -0.14, c_U = +0.42, do differ significantly, F(1,44) = 44.83 , MSE = 0.15. Despite the increased difference in bias (compared to that in Experiment 2) the H/FA Index shows a clear H/FA Mirror Effect.

$$ {\mathrm{FA}}_{\mathrm{FN}}=.16<{\mathrm{FA}}_{\mathrm{UN}}=.20<{\mathrm{H}}_{\mathrm{UO}}=.56<{\mathrm{H}}_{\mathrm{FO}}=.89 $$

The difference in the false alarms for F and U is significant, F(1, 44) = 5.59, MSE = .0.01 The difference in the hit rates is also significant, F(1,44) = 343.83, MSE = .01.

LR regularity analysis

Row 5 of Table 4 gives the regularity means. The first two entries for the Distance Mirror Index, d_nn = -0.22 and d_oo = +1.14, show a significant Mirror Effect with mean d_nn < zero, t(40) = 14.93, SE = 0.09, and mean d_oo > zero, t(34) = 18.37, SE = 0.06. The next two entries, the slopes of the new/new, and old/old, z-ROCs show a significant Variance Effect with both slopes less than 1.0. For sl_nn = 0.55 t(40) = 3.18, SE = 0.07. For sl_oo = 0.44, t(34) = 13.75, SE = 0.04 are less than 1.0. The next two entries, mean length F = 1.97< mean length U = 3.81, show a significant length difference, F(1, 42) = 76.47, MSE = 0.76. The z-ROC Length Effect holds.

Reducing the number of familiar names increased the accuracy of recognition for those items from d' = 2.11 in Experiment 2 to d' = 2.76 here. It thereby increased the difference in accuracy between the familiar and unfamiliar items. This had the expected effect of recovering the Mirror Effect according to the H/FA Index (see line 2 of Table 3.) It had the unexpected effect, however, of also increasing the bias difference by making the responses to the familiar names more liberal. This effect is of considerable interest. It indicated that an experimental operation may have a double effect: a change in accuracy and a change in bias. The reason for the bias change may be that familiar names generate relatively liberal responses initially (as in Experiment 2) because they are more salient for participants. When we reduced the number of familiar names in the present experiment, we increased their salience further and thus increased further the tendency for liberal responses (see Wickens, 2002, on the relation of salience to bias).

Further analysis of individual responses

The proportions of individuals that show each of the three regularities are presented in the fifth row of Table 4. All the regularities are evident and significant by a binomial test.

Discussion

One goal of the preceding experiments was to demonstrate the three LR regularities for individual as well as group data. This has been done. We also developed further information concerning the Mirror Effect, the regularity that has been most extensively studied, and how it may be concealed by bias. We have shown that the concealing can be countered in four ways:

• 1) Use of a more informative index of the effect, the Distance Index instead of the H/FA Index (Experiment 2).

• 2) Use of a payoff schedule to eliminate bias differences (Experiment 3).

• 3) Use of a between-list paradigm that separates the two conditions (Experiment 4).

• 4) Increase of the accuracy difference between the weak and strong conditions (Experiment 5).

Our contention is that SDT with its three basic concepts – sensitivity, bias, and LR decision axis explains the three regularities. It also explains when the mirror regularity does not appear. There are process models of recognition memory that incorporate SDT and its LR component (McClelland & Chappell, 1998; Shiffrin & Steyvers, 1997). There is no conflict between such models and the more general SDT model considered here. What is involved are two different levels of theory (Marr, 1982).

Alternative explanations and criticisms

Strength versus LR decisions

LR decisions need not be invoked to explain the data of a simple one-condition memory experiment such as the one represented in Fig. 1. The assumption that decisions are made on the basis of unprocessed “strength” will do. When we move to two-condition experiments such as the one represented in Fig. 2 simple strength-based decisions fail. This can be seen by taking the same parameters used there: SN and WN are Normal(μ = 0, σ = 1), WO is Normal(μ = 1, σ = 1) and SO is Normal(μ = 1.75, σ = 1). If we omit the LR conversion from the computations then none of the regularities appear. The initial new distributions do not move: d_oo = .75 but d_nn = 0, no Mirror Effect. The slope_oo = slope_nn = 1.0: no Variance Effect. And len_W = len_S = 5.66: no Length Effect.

It is, of course, possible to hold on to strength decisions by adopting additional, ad hoc assumptions, to explain a regularity. To date, two such proposals have been made to explain the Mirror Effect: Criterion Shift and Two-Process. Their ad hoc assumptions are indicated below.

Criterion shift

The criterion shift explanation, e.g., Cary & Reder (2003), assumes the following.

• 1) The decision axis is an unconverted strength axis.

• 2) WN and SN stay fixed, as in Fig. 2A, while WO and SO separate, producing H_WO < H_SO.

• 3) The criterion for the S distributions moves to follow SO. (ad hoc assumption) This criterion movement reduces the FA_SN so that FA_SN < FA_WN.

The last two steps produce the full Mirror Effect FA_SN < FA_WN < H_WO < H_SO.

There is ample evidence, however, that WN and SN do not stay fixed. Experiments on forced choice in which participants were required to choose WN versus SN items, called null choices, showed that the two new distributions are separated, SN < WN ( Glanzer et al., 1991, 1993; Hilford et al., 1997; Kim & Glanzer, 1995). In all five experiments reported here d_nn is negative (see Table 3), indicating again that the two new distributions are separated, SN < WN with distance -d_nn .

Two-process

A popular explanation of the Mirror Effect, is the two-process explanation, e.g., Balota, Burgess, Cortese, and Adams (2002). This explanation is limited to the word frequency Mirror Effect (seen in Experiment 1). It makes the following assumptions:     (1) Individuals use a familiarity/strength decision axis, unconverted;     (2) process one: Low frequency new (LN) words start out situated lower on the familiarity/strength decision axis than high frequency new (HN) words because they are less familiar (ad hoc assumption). This gives one of the inequalities that define the Mirror Effect, LN < HN;     (3) process two: Low frequency words are learned and recollected much more effectively than high frequency words, overcoming the initial position difference (ad hoc assumption). This gives the second inequality, HO < LO, of the Mirror Effect. The three assumptions in combination produce the Mirror Effect, LN < HN < HO < LO.

  To support the explanation, the Mirror Effect is first shown in a baseline condition. Then an operation is carried out, e.g., speeded presentation, that disrupts the Mirror Effect (using the H/FA Index). This is interpreted as a result of disruption of recollection. The two-process explanation is limited in two ways:     (1) It explains only the word-frequency mirror effect, not, as will be shown, the name familiarity mirror effect (Experiments 2, 3, 4 and 5), and     (2) it does not cover the other two regularities, the Variance Effect and the Length Effect.

  The LR SDT interpretation of the mirror disruption as a result of speeding differs. L words require more processing time than H words (Glanzer & Adams, 1990; Wright, 1979). Speeding therefore has a differential effect on L versus H words. It decreases the accuracy for both L and H words but more so for L words. It therefore decreases the difference in accuracy, d’, between the two conditions. In Glanzer et al. (2009) and in Experiment 5 we showed that the size of the accuracy difference between conditions was critical for the H/FA Index of the mirror effect. If there is any differential bias, the smaller the d’ difference, the less likely the H/FA Index (used in the two-factor mirror disruption studies) will show the mirror effect.

  SDT with its LR decision axis handles the data summoned to support the two-process explanation without postulating any additional processes such as familiarity and recollection. It is not, moreover restricted to the explanation of word frequency effects as is the two-process explanation.

  Finally and more generally, Experiments 2, 3, 4, and 5 rule out a two-process explanation and, more generally, any explanation that assumes a strength/familiarity decision axis. Such explanations require that the unfamiliar new names (UN) should be lower than familiar new names (FN) on the decision axis, UN < FN. Therefore no mirror effect should occur. SDT with its LR decision axis predicts the reverse order, FN < UN, and a full Mirror Effect. All three preceding experiments on familiarity produce the LR SDT mirror inequalities

$$ \mathrm{F}\mathrm{N}<\mathrm{U}\mathrm{N}<\mathrm{U}\mathrm{O}<\mathrm{F}\mathrm{O}, $$

not the strength/familiarity inequalities:

$$ \mathrm{U}\mathrm{N}<\mathrm{F}\mathrm{N}<\mathrm{U}\mathrm{O}<\mathrm{F}\mathrm{O}. $$

Our finding that familiarity produces a Mirror Effect is supported by evidence from five other studies on recognition that have varied familiarity of words, names, faces, and tunes (Bäckman 1991; Bäckman & Herlitz, 1990; Bartlett, Halpern, & Dowling, 1995; Brown, Lewis, & Monk, 1977; Schulman, 1976). Those investigators use different names for the familiarity variable, e.g., prior knowledge, but it is clear that the two sets of items used in each study differ in initial familiarity.

Other criticisms

Rouder and his co-authors have raised questions about the legitimacy of statements about the relation of asymmetry of ROCs (slopes other than 1.0 of z-ROCs) to the variance of the underlying distributions. Rouder, Pratte, and Morey (2010) challenged results presented by Mickes, Wixted, and Wais (2007) in support of the relation between slopes and variance in the normal unequal variance SDT model. Rouder et al. presented z-ROCs from other models (e.g., log normal, inverse probit transforms of normal) with other variances that mimic the Mickes et al. findings. They concluded that “there is no principled method for assessing the relative variability of latent mnemonic strength distributions” (p. 427). The argument has, however, been rebutted in detail by Wixted and Mickes (2010). The controversy cannot be resolved here. It requires, at a minimum, a demonstration by Rouder et al. that the alternative models proposed do as good a job as the standard SDT normal models with a range of data. Wixted and Mickes (2010) present analyses that they do not.

Pratte, Rouder, and Morey (2010) are concerned with a different presumed problem in interpreting ROC asymmetries (z-ROC slopes less than 1.0). Their concern is whether they are an artifact of “distortions due to averaging data over items” (p. 224). They conclude, however, that “Application of a hierarchical unequal-variance signal detection model reveals that asymmetries are in fact a real phenomenon and do not reflect distortions from averaging data” (p. 224).

Neither paper requires change in our theoretical or data analyses.

Final summary

• 1) All five experiments show the three LR regularities for both group and individuals’ data.

• 2) Only the Mirror Effect regularity is affected by bias. Even in that case, the bias effect is mitigated when the better Mirror Distance Index is used.

• 3) Experiments 2, 3, 4, and 5 show Mirror Effects obtained by varying familiarity. Those Mirror Effects cannot be predicted by the two-process explanation or any explanation based on a strength/familiarity decision axis.

• 4) The five experiments, in combination, show systematic changes in bias as a function of experimental paradigm.

• 5) SDT with its LR decision axis and factor of bias offers simple explanations of the regularities. It does not require assumption of additional processes, e.g., familiarity and recollection, to explain the Mirror Effect regularity. It does not require postulation of different kinds of Mirror Effects to explain the fact that H/FA Index does not find a Mirror Effect when differential bias has been induced.

• 6) Green and Swets (1966/1974) have demonstrated that LR decisions are optimal. In these days when many investigations find cognitive functions inefficient, it is good to find that individuals – at least in the experiments reported here – carry out a key function, recognition memory, close to optimally.