Numerous carefully performed experiments have shown that many animals—such as bees (Gross et al., 2009), fish (Gomez-Laplaza & Gerlai, 2013; Krusche, Uller, & Dicke, 2010; Petrazzini, Agrillo, Piffer, & Bisazza, 2014; Piffer, Agrillo, & Hyde, 2012), salamanders (Krusche et al., 2010), pigeons (Emmerton & Renner, 2006), dogs (Ward & Smuts, 2007), chimpanzees (Beran, Evans, & Harris, 2008), to say nothing about human infants (Brannon & Van de Walle, 2001) or people whose language lacks words for numbers beyond five (Pica, Lemer, Izard, & Dehaene, 2004)—are capable of discriminating relatively large quantities with remarkable precision, even when other cues are not available and there is no opportunity or ability for one-by-one counting. Considerable progress has been made in understanding where and how the brain represents quantities, including numerical proportions (Jacob, Vallentin, & Nieder, 2012). It was noted, for example, that the same cortical regions participate in the encoding of both absolute quantities and quantity ratios (proportions), and that single neurons in the prefrontal and parietal cortices of various species are tuned to preferred proportions (Nieder & Miller, 2004; Vallentin & Nieder, 2010). Based on these and other observations, it was proposed that the brain uses an analog, labeled-line code to represent the true numerical values of quantity ratios (Jacob et al., 2012; Moskaleva & Nieder, 2014; Vallentin, Jacob, & Nieder, 2012; Viswanathan & Nieder, 2013). Although discrimination of nonsymbolic proportions does not require verbal coding or propositional thinking, an intuitive approximate number sense, which is believed to form the basis of the perception of proportions, may serve as an antecedent of higher numerical abilities (Halberda, Mazzocco, & Feigenson, 2008). However, the last proposition is vigorously debated in the recent literature (Agrillo, Piffer, & Adriano, 2013; Göbel, Watson, Lervåg, & Hulme, 2014).

If the observer’s task is to discriminate the relative proportion of two distinct sets of randomly distributed elements, these two sets can be separated in two principal ways. First, the sets occupying two distinct areas can differ by their spatial or temporal position (Allik & Tuulmets, 1991, 1993); second, they can be spatially intermixed but distinguished by a certain visual attribute, such as color, orientation (Honig & Matheson, 1995; Honig & Stewart, 1993; Tokita & Ishiguchi, 2009, 2010), or motion in two different directions (Raidvee, Averin, Kreegipuu, & Allik, 2011). As it turned out, the ability to discriminate numerical proportion depends heavily on the visual attributes by which the two sets can be distinguished. Rather surprisingly, human observers are extremely inaccurate in discriminating proportion between two spatially overlapping sets of randomly distributed elements moving in opposite directions (Raidvee et al., 2011). In a wide range of set sizes, decisions about motion direction are made as if only a very limited number of elements (in some cases, less than 0.5 %) are taken into account, even if the motion direction of each element in isolation can be determined with near absolute certainty (Raidvee, Averin, & Allik, 2012). In a similar task, where instead of motion direction the elements differed by color, observers were able to discriminate the relative number of red and green dots as if they had taken into account 69 elements from a total of 100 (Tokita & Ishiguchi, 2009) provided that psychometric response curves are interpreted in terms of dot counts used in the decision (Raidvee, Averin, et al., 2012; Raidvee et al., 2011). However, the same observers’ ability to discriminate between the relative number of parallel and converging lines was much poorer, with a precision equal to discrimination decisions made on the basis of no more than two elements out of the 100 available (Tokita & Ishiguchi, 2009). This may mean that there is no single fixed brain circuitry for the discrimination of numerical proportions. It is more likely that differences in the discrimination of proportion based on varying stimulus attributes share the same late stages in the processing stream from the sensory code to the motor response. Nevertheless, the brain’s representation of proportions must also include sensory codes which are specific to different visual attributes and which are probably located in different brain regions (cf. Gebuis & Reynvoet, 2012, 2013; Tokita & Ishiguchi, 2012).

When the observer’s task is to discriminate between numerical proportions, empirical psychometric functions are typically approximated by a cumulative normal distribution, with a mean (μ) roughly corresponding to the perceived level of balance between the two judged quantities, and with a standard deviation (σ) characterizing the precision of numerosity discrimination. The slope of the psychometric function can be characterized by the inverse value of the standard deviation, 1/σ. According to a customary approach, this imprecision σ is caused by a spontaneous, irreducible noise in the nervous system that stochastically transforms a fixed stimulus value into one of many possible internal states. All these explanations, relating response errors to internal noise, are variants of the Thurstonian psychophysical analysis (Thurstone, 1927a, b), according to which, stimuli are projected onto a set of psychological states, thus forming subjective images with positions varying randomly among these states. The magnitude of this internal noise, the discriminal dispersion, in Thurstonian terminology, is believed to be quite straightforwardly related to the slope of the observed psychometric function.

Because the normal or Gaussian distribution usually fits empirical data rather well, it has been convenient to assume that the internal noise can indeed be modeled by a continuum of internal states with approximately normally distributed occurrence probabilities. Because numerous stochastic distributions, including discrete ones, closely approach the normal distribution, the assumption about the distribution of internal noise remains hypothetical in the least (cf. Neri, 2013). Furthermore, the assumption of normally distributed internal noise is not very convincing when the observer’s task is to estimate other than the magnitude of continuous physical attributes such as weight, size, or luminance. For example, it is rather problematic to assume that, in the numerosity discrimination task, discrete visual elements would give rise to continuous subjective images. According to this conception, even small quantities are projected onto a continuum of internal states resembling the axis of real numbers. For instance, sometimes a set consisting of six visual elements may be perceived as more numerous than another set consisting of seven elements because the internal image of the first set has a higher value (e.g., 6.6 perceptual units) than the internal image of the second set (e.g., 6.5 perceptual units). This is not an unlikely outcome, provided that the standard deviation of the internal noise is equal to, for example, three or four elements. This assumption, however, runs into problems when trying to explain why there is no confusion when the number of elements is less than four (Jevons, 1871), to say nothing about finding a good explanation for what it really means to perceive one half or two thirds of a dot or of any other geometrical element. In addition, all Thurstonian–Gaussian models make an unrealistic assumption that the observer’s decisions are based on all information. It is much more realistic to assume that the capacity of the visual system is strongly limited in the result of which only a fraction of all information is used.

At least hypothetically, we can entertain a version of the Thurstonian model in which internal states are represented not by a continuum, but by a finite set of discrete states. Let us suppose that a psychophysical function transforms each element presented on the screen into a corresponding mental state, which can take only two values: zero (“off”) when the presence of the element was not recorded, or one (“on”) when the element was noticed and recorded. Each element of a certain type is transformed into its “on” state with a probability β. This general definition leaves the probability β open to various psychological interpretations. For instance, the probability β can be interpreted as perceptual salience of a certain type of elements, but it could also be considered as the level of attentiveness with which elements can be noticed and registered by the perceptual system. We can call this the Thurstonian-binomial approach to discrimination of numerical proportions.

If we accept these simple premises, then the derivation of computational formulae for the perception of numerical proportions is a matter of simple calculations. Let N A and N B be the numbers of elements in two distinct sets of elements of Type A and B (e.g., red vs. green), respectively. It is easy to predict how many K A and K B elements from the total number of presented elements N A and N B are on average taken into account if there is the constant probability β i with which each element of a certain type is counted (where i = 1, . . . , n, and n is the number of different types of elements in the display; in this case, n = 2). These two numbers, K A and K B, are obviously not constants but two random variables, with the binomial distributions B(N A, β1) and B(N B, β2), respectively, whereas the two binomial distributions are assumed mutually independent. The expected values of these two binomially distributed variables are E(K A) = N Aβ1 and E(K B) = N Bβ2. Observers’ decisions about relative numerosity are assumed to be based on a comparison of these two binomial values in a given trial: if K A > K B, the observer answers that “Type A is more numerous than Type B.” Otherwise, Type B is judged as more numerous than Type A. In case of equality of K A = K B, an unbiased observer answers randomly, with each answer being equally probable. To know how often K A is expected to be larger than K B, the distribution of the difference between these two binomially distributed variables is required.

The exact probability of responding “Type A is more numerous than Type B” (denoted as “Answer = A”) is equal to the sum of the probability of K A being larger than K B plus 0.5 times the probability of K A being equal to K B, given certain probabilities β1 and β2 of detecting Type A and Type B elements, as described by the following formulae for the situations where Type A is either less numerous than Type B (Eq. 1), or more numerous than Type B (Eq. 2; for derivation, consult Appendix 1):

$$ \begin{array}{l}P\left(\mathrm{Answer}=\left.A\right|{N}_A<{N}_B\right)=P\left({K}_A>{K}_B\left|{N}_A<{N}_B\right.\right)+0.5P\left({K}_A={K}_B\left|{N}_A<{N}_B\right.\right)\hfill \\ {}\kern10.5em ={\displaystyle \sum_{k_1=0}^{N_A}{\displaystyle \sum_{k_2=0}^{k_1-1}\left({}_{k_1}^{N_A}\right)\left({}_{k_2}^{N_B}\right){\beta_1}^{k_1}{\left(1-{\beta}_1\right)}^{N_A-{k}_1}\times {\beta_2}^{k_2}{\left(1-{\beta}_2\right)}^{N_B-{k}_2}}}\hfill \\ {}\kern10.5em +0.5{\displaystyle \sum_{k=0}^{N_A}\left({}_k^{N_A}\right)\left({}_k^{N_B}\right){\beta_1}^k{\left(1-{\beta}_1\right)}^{N_A-k}\times {\beta_2}^k{\left(1-{\beta}_2\right)}^{N_B-k}}\hfill \end{array} $$
(1)
$$ \begin{array}{l}P\left(\mathrm{Answer}=\left.A\right|{N}_A>{N}_B\right)=P\left({K}_A>{K}_B\left|{N}_A>{N}_B\right.\right)+0.5P\left({K}_A={K}_B\left|{N}_A>{N}_B\right.\right)\hfill \\ {}\kern10.5em =1-{\displaystyle \sum_{k_1=0}^{N_B}{\displaystyle \sum_{k_2=0}^{k_1-1}\left({}_{k_1}^{N_B}\right)\left({}_{k_2}^{N_A}\right){\beta_2}^{k_1}{\left(1-{\beta}_2\right)}^{N_B-{k}_1}\times {\beta_1}^{k_2}{\left(1-{\beta}_1\right)}^{N_A-{k}_2}}}\hfill \\ {}\kern10.5em -0.5{\displaystyle \sum_{k=0}^{N_B}\left({}_k^{N_A}\right)\left({}_k^{N_B}\right){\beta_1}^k{\left(1-{\beta}_1\right)}^{N_A-k}\times {\beta_2}^k{\left(1-{\beta}_2\right)}^{N_B-k}}\hfill \end{array} $$
(2)

where N A and N B are the total numbers of elements in the Categories A and B, respectively (e.g., red vs. green); K A and K B are the numbers of elements taken into account from the total number of presented elements N A and N B, given constant binomial probabilities β1 and β2 with which each element of a certain type is counted.

If the expectations of K A and K B are sufficiently large, they are approximately normally distributed (given that with large N, binomial distribution approximates the Gaussian distribution) and we can use normal approximation. For this we need to express the difference between N Aβ1 − N Bβ2 in z scores (units of the standardized normal distribution):

$$ z=\frac{N_A{\beta}_1-{N}_B{\beta}_2}{\sqrt{N_A{\beta}_1\left(1-{\beta}_1\right)+{N}_B{\beta}_2\left(1-{\beta}_2\right)}}. $$
(3)

If these two detecting probabilities are identical, β1 = β2, then the psychometric function becomes symmetrical, and its shape can be approximated by a normal cumulative distribution. In fact, there is a simple equation relating the standard deviation σ of a cumulative normal distribution to the counting probability β (see Appendix 2 for derivation):

$$ \sigma =\sqrt{\frac{1-\beta }{4N\beta }.} $$
(4)

By a direct analogy, we can also construct the classical Thurstonian model assuming that there is a continuum of internal states and the distribution of the internal noise is sufficiently close to normal. However, it is important to notice that mechanical approximation of empirical data with a single Gaussian function is not necessarily an implementation of the Thurstonian model. As with the previously described binomial model, we need to start from a proposition that each stimulus element has a stochastic internal representation, and all these elementary representations are pooled to make a decision about relative numerosity of elements. A formula describing the Thurstonian normal or Gaussian model is as follows:

$$ P\left({N}_A\ge {N}_B\right)=\varPhi \left(\frac{\mu_1{N}_A-{\mu}_2{N}_B}{\sqrt{N_A{\sigma}_1+{N}_B{\sigma}_2}}\right), $$
(5)

where P(N A ≥ N B) is the probability with which elements from Category A are judged to be more numerous than elements from the Category B (e.g., red vs. green); N A and N B are the total numbers of elements in the Categories A and B, respectively; μ 1 and μ 2 are the mean values, and σ 1 and σ 2 standard deviations of stochastic internal representation of individual visual elements of Type A and B, respectively; and Φ stands for the standard normal integral. Please notice that this formula does not coincide with a simple cumulative normal approximation that is widely used for the description of empirical psychometric functions. For its derivation, it is useful to remember that the sum of two independent, normally distributed random variables is normal, with its mean being the sum of the two means, and its variance being the sum of the two variances. Only when μ1 = μ2 and σ1 = σ2, Eq. 5 reduces to the most simple case, Case V, in Thurstone’s (1927a) own terminology.

The aim of this article is to compare the classical Thurstonian–Gaussian model (Eq. 5) with the Thurstonian-binomial model (Eqs. 1 and 2). We expect that, in terms of model residuals, both models perform sufficiently well, especially because with large N, binomial distribution approximates the Gaussian distribution. When the greater parsimony of Thurstonian-binomial model is taken into account (using, for example, an AIC-based approach), it clearly surpasses the Thurstonian–Gaussian model.

We expected the differences in the predictions from the two models to be most pronounced in cases where the number of trials, or in this case, number of sampled elements, is small. This could happen, for example, when discriminating between relatively small numbers of visual elements, or when a visual attribute by which the two sets of elements can be distinguished is not salient enough, and thus the expected values of K A and K B are small. This expectation derives directly from the fact that binomial distribution approaches the normal distribution when the number of trials—in this case, the number of elements that are taken into account in the discrimination process—increases.

For this reason we selected two visual attributes—color and orientation—which are known to have considerably different capacities to distinguish between two sets of visual elements (Tokita & Ishiguchi, 2009). We are also going to discuss which of these two models is intuitively more plausible and provides a psychologically more reasonable interpretation.

Method

Participants

Four 20-year-old female observers (Agne, Dea, Kristin, and Moonika), with normal or corrected-to-normal vision, were asked to decide which of the two distinctive sets of objects was more numerous.

Stimuli

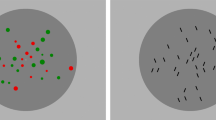
In two separate series, these two sets of objects were distinguished either by color or by orientation. A schematic view of the two types of stimulus configurations is depicted in Figure 1. In the first series, a randomly distributed collection of red and green circles was presented. The red and green circles had equal luminance of about 23.5 cd/m2. To diminish the impact of total red versus green area on responses, the size of the circles was randomly varied in the range of 11 to 22 minutes of arc (the summed area being proportional to the number of elements). In the second series of experiments, a collection of short, black line segments of luminance 0.3 cd/m2 and a tilt of 20°, either to the left or to the right of the vertical direction, was presented. The width and length of a line subtended 2' and 19', respectively (and the height of its vertical projection was 16'). Both types of stimuli were presented within an elliptical gray background, with a luminance of 54 cd/m2 and with lengths of horizontal and vertical axes of 8.86° and 8.70°, respectively. This elliptical background was in the center of a rectangular area of luminance 64 cd/m2, filling the rest of the screen. To avoid overlap between elements, each element was positioned within an invisible inhibitory area that prevented other elements from being closer than 22'. Each stimulus element had contrast sufficient to guarantee its 100 % identification had it been presented in isolation. The total number of objects, N, presented on the display was kept constant through each experimental session and was equal to N = 9, 13, 33, or 65 elements. During experimental sessions, the relative proportion of Type A and Type B elements was varied in random order. The total number of elements was constant throughout each session. For the total number of elements N = 9 and N = 13, the relative proportions of Type A (red or tilted to the left) and Type B (green or tilted to the right) elements were varied with a change of one element to the numerosity of both sets: from 1:8 to 8:1 and from 1:12 to 12:1, respectively. For the total number of elements N = 33, the proportions 13:20, 14:19, 15:18, 16:17, and the reverse, were used; for N = 65, the proportions 23:42, 26:39, 32:33, and the reverse, were used. The given proportions were chosen in an attempt to yield psychometric functions covering most of the range of response probabilities. The stimuli were presented for 200 milliseconds, with 3 seconds for responding. In the case of nonresponse, the trial was repeated at a later, randomly selected position in the same series of trials.

Fig. 1
figure 1

Schematic view of two types of stimuli used for the study of discrimination of numeric proportions

Full size image

Every stimulus condition was replicated 100 times. The choice probability of red circles was plotted as a function of the proportion of red elements N A of the total number of elements on the display N = N A + N B, where N B refers to the number of green elements. Similarly, in the orientation experiment, the probability of the choice of leftward-tilted elements was measured as a function of the proportion of leftward-tilted elements N A in the total number of elements on the display N.

Part of the data presented here has been published previously (Raidvee, Põlder, & Allik, 2012) in a different modeling approach.

Apparatus

All stimuli were presented at a viewing distance of 170 cm on the screen of a Mitsubishi Diamond Pro 2070SB 22-in. color monitor (the frame rate was 140 Hz, with a resolution of 1024 × 768 pixels, subtending 12.9° horizontally and 9.8° vertically) with the help of a ViSaGe (Cambridge Research Systems Ltd.) stimulus generator.

Statistical analysis

The models described by Eqs. 1 and 2, and 5, were fitted to the data by custom software written in MATLAB. Nonlinear least squares optimization was used to find the best fit parameter estimates. The 95 % parameter confidence intervals were obtained by bootstrap resampling of the model residuals (1,000 repetitions). The explained variance was estimated by the degrees of freedom adjusted R 2 of the nonlinear regression fit. Corrected Akaike information criterion (AICc; Hurwitsch & Tsai, 1989) was computed as AIC = n ∙ ln(SSE/n) + 2 K, and AICc = AIC + 2 K∙(K + 1)/(n-K-1), where n is the number of data points (in this experiment, varies from six to 12); K is the number of model parameters + 1; and SSE is sum of squared errors of the model.

Results

Figure 2 demonstrates empirical data (red circles) fitted by theoretical psychometric functions: Thurstonian–Gaussian model (black dotted curves) described by Eq. 5, and Thurstonian-binomial model (black plus signs), described jointly by Eqs. 1 and 2. The probability of saying that the number of elements from Type A (red or tilted to the right) is larger than Type B (green or tilted to the left) is plotted against the proportion of N A elements: N A / (N A + N B). Each panel corresponds to the total number of elements (N = 9, 13, 33, and 65) separately for color and orientation as two distinguishing attributes, pooled across the four participants.

Fig. 2
figure 2figure 2figure 2

Empirical choice probabilities (red circles) and predictions of the Thurstonian–Gaussian (continuous curves) and Thurstonian-binomial (black hollow squares) models separately for each subject: a. N = 9, b. N = 13, c. N = 33, d. N = 65, and e. pooled across the four subjects. Vertical lines denote the 95 % bootstrap confidence intervals for the Thurstonian-binomial estimates of the response probabilities. (Color figure online). %EV denotes the percentage of explained variance in terms of (adjusted) R 2

Full size image

Because the majority of binomial predictions lay on the continuous Gaussian psychometric functions it is expected that both models, Gaussian and binomial, provide similarly close fit to empirical data. Under the information theoretic approach, the more parsimonious binomial model has an advantage.

Table 1 provides an overview of the best-fitting values for both Thurstonian–Gaussian and Thurstonian-binomial models. The most optimal parameter values were determined by fitting the functions to empirical data by nonlinear least squares. There are several points of principal interest in the presented data, as follows.

Table 1 The best-fitting parameter values and goodness of fit indices (percentages of explained variance as reflected by adjusted R 2-s, and AIC-s) for the Thurstonian-binomial and Thurstonian-Gaussian models
Full size table

Which of the two models provides a better fit?

The differences between the two models in terms of R 2 and AIC values are outlined in Table 2. Judging by the values of adjusted R 2s, both models, the binomial and Gaussian, provided approximately equally good fits to the collected response data. Averaging across all conditions and observes the binomial function explained on average 98.87 % of the observed variance. The Gaussian model explained 98.62 % of the variance in exactly the same set of response data. Thus, both models left on average only about 1.26 % of variance unexplained. Both models explained color data about 1.3 % . . . 1.6 % better than orientation data. The average AIC values were -46.65 and -48.22 for Thurstonian-binomial and Thurstonian–Gaussian models, respectively. On average, the AICs were smaller by 3.4 (for the binomial model) and by 2.86 (for the Gaussian model) for color data compared to the orientation data. The differences in terms of the adjusted R 2 (values differ by 0.24 % in favor of the binomial model), and the AIC statistics (difference of 1.95 in favor of the Gaussian model) are small and imply that both models should receive full consideration in the explanation of proportion discrimination data.

Table 2 Difference between the two models: the values of adjusted R 2 and AIC of the Thurstonian–Gaussian model are subtracted from the respective values for Thurstonian-binomial model.
Full size table

Because the number of fitted data points in this study was small, we applied the corrected AIC, denoted as AICc (Hurvich & Tsai, 1989) as it provides an unbiased estimate of relative loss of information. It is shown that in practice, AICc should always be preferred over AIC, for AICc will asymptotically reach AIC as n gets large (Burnham & Anderson, 2004). The average AICc values were -44.35 and -35.22 for Thurstonian-binomial and Thurstonian–Gaussian models, respectively. Thus, on average, the AICc statistics favored the binomial model by -35.22 - (-44.35) = 9.13, which means that the relative likelihood of the binomial model, compared to the Gaussian model, is exp(9.13/2) = 96.1 (Burnham & Anderson, 2002).

Because there is a simple formula (Eq. 4) on how to convert binomial β into standard deviation of the normal distribution, it was expected that in terms of the percentage of explained variance, both models provided almost equally good fits to the observed data. One obvious difference between these two models is the number of the model’s free parameters. The binomial model has only two free parameters, contrary to the Gaussian model, which has four. For the sake of clarity we have to notice that Eq. 5 cannot be reduced, unlike customary practice, to two parameters, because the difference between two means μ1 – μ2 and the sum of two standard deviations σ1 + σ2 cannot be partialled out. Thus, the greater parsimony of the binomial model compared to the Gaussian model is irreducible.

What is the impact of the total number of elements N?

The Thurstonian-binomial model is particularly transparent with regard to the total number of elements. With the increase of N from nine to 65, the best fitting value of βi drops approximately two times, irrespective of the distinguishing attribute, be it color or orientation. Because the number of elements increased more than 7 times and probability of counting βi only 2 times, this means that the relative number of elements taken into account does not remain constant. In the Gaussian model, the relationship between the model’s free parameters μi and σi and the total number of elements is not so evident. It seems that for color, the mean values μi slightly decrease whereas the standard deviations σi increase. For the orientation, there seems to be no simple pattern of changes.

However, it is obvious that the decrease of βi with the increase on N is not a linear function. If we approximate the observer’s responses simply with a simple cumulative normal function, not with the function given in Eq. 5, then the standard deviation of this function characterizes the minimal number of elements (just noticeable difference, or JND) that was required to tell the difference between numerical proportions in 84.1 % of all trials. When we tested how JND is related to the total number of elements N, it turned out that the relationship is fairly linear. Many previous studies have shown that the precision of discrimination of numerical proportions decreases in about proportion to the total number of elements (Allik & Tuulmets, 1991; Burgess & Barlow, 1983; Emmerton & Renner, 2006; Halberda & Feigenson, 2008). This means that Weber’s law JND/N ≈ Constant held, approximately at least, for this and many previous studies. Usually, confirmation of Weber’s law is interpreted as evidence for a universal measurement unit (Dehaene, Dehaene-Lambertz, & Cohen, 1998; Merten & Nieder, 2009). Besides single cell recordings (Nieder & Miller, 2004; Vallentin & Nieder, 2010), Weber’s law is also perceived as evidence for the existence of neurons tuned for numbers (Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004; Ross, 2003). Because N was not related, transparently at least, to the either model’s free parameters, βi in the binomial model and σi in the Gaussian model, we are slightly cautious of attributing any critical significance to the fact that the slope of the empirical psychometric function is very often a linear function of the total number of elements N.

Which attribute—color or orientation—is perceptually more salient?

Irrespective of the total number of elements N, color is always more salient attribute than orientation. For all N elements distinguished by their color had higher probability to be counted β1 or larger weight μi in an internal representation. This is not surprising because it was repeatedly shown that color is a more salient attribute than form or orientation for the discrimination of numerical proportions at least (Tokita & Ishiguchi, 2009, 2010). Of course, not only numerosity discrimination has shown that color is perceptually a stronger or more salient feature than orientation for segmenting visual scenes and searching for elements in it (Anderson, Heinke, & Humphreys, 2010, 2011; Nothdurft, 1993; Zhuang & Papathomas, 2011). Thus, it was not news that the observers were more accurate in the discrimination of proportions when elements were discriminated by color rather than by orientation. However, this indicates that exactly the same proportion between the two sets of elements may have quite different psychological significance (discriminability), dependent on the distinctive visual attribute. Therefore, the recent discovery of neurons tuned to a fixed proportion (Jacob et al., 2012; Nieder & Miller, 2004; Vallentin & Nieder, 2010) remains at least psychologically ambiguous because there is no information whether this corresponds to all available elements N, or to a smaller sample of elements, actually represented in the perceptual system. Thus, results of this study seem to support those who do not believe in one universal code for the discrimination of proportions irrespective of visual attributes which determines segregation visual elements into two categories (Gebuis & Reynvoet, 2012; Tokita & Ishiguchi, 2012).

How symmetric are empirical response functions?

If empirical response functions are symmetrical, then there will be no need for two sets of parameters characterizing perception, each value of the distinguishing attributes, green versus red and left tilt versus right tilt (β1 = β2, μ1 = μ2, and σ1 = σ2). In reality, most of the empirical responses were nearly symmetric, and the optimal pairs of values are not very far from each other. Only in a minority of experimental series, and only for some of the participants, the parameter values for the Type A elements needed to be substantially different from the values for the Type B elements. The average difference between β1 and β2 was about 7 % for color and 4 % for orientation. Beside these probably erratic results, both models, the binomial and Gaussian, also described a systematic asymmetry in a similar way. Table 1 shows that in 30 out of 32 cases, β1 ≥ β2. This means, in terms of the binomial model, that red dots and bars tilted to the right were noticed and counted with a slightly higher probability than were green dots and bars tilted to the left. In the same proportions, μ1 ≥ μ2, in the Gaussian model, red color and rightward orientation had slightly more weight than green color and leftward orientation. Thus, a minor asymmetry in empirical response functions originates from the fact that Type A elements were perceived slightly differently from the Type B elements.

Discussion

It has been noted that the idea behind Thurstonian models is so irresistible that nobody has ever really tried to escape it (Luce, 1977). Indeed, the Thurstonian–Gaussian model has been the main tool for the description of empirically collected psychometric functions. However, its frequent use has led to numerous abuses. It has become perhaps too easy to approximate the observer’s choice probabilities with a cumulative normal distribution identifying its mean and standard deviation that provide the best fit to data. Very often, the obtained standard deviation is automatically identified with a hypothetical sensory noise, forgetting that to get an estimate of internal noise it is, in even the simplest, Thurstonian Case V, necessary to divide the standard deviation by a factor of √2 (Thurstone, 1927a). Perhaps the most typical mistake is to equate the determined standard deviation with an unidentified general noise. There is no abstract general noise in perception. The noise is always associated with particular operations and originates from specific processes of how these elements are transformed and represented in a corresponding set of perceptual states. For this very reason, both proposed models, the binomial and Gaussian, start from the description of what every single and identifiable visual element could contribute. General noise can be nothing but an aggregate of individually identifiable noises that are pooled together by certain rules.

An almost default assumption that each visual event can be represented by a continuum of ordered sensory states, occurrences of which are sufficiently well approximated by a Gaussian function, is a result of deeply rooted habits and computational convenience. The success of Gaussian approximation is primarily due to lack of viable alternatives. This study presented, we hope, a feasible alternative, which describes internal representation, not by a continuous and infinite Gaussian function, but with a discrete binomial function. This replacement also means that, instead of an infinite number of sensory states, it is sufficient to have a single perceptual mechanism that has two possible outcomes. Although single neurons can represent highly sophisticated information (Barlow, 1972, 2009), there is no pressure to identify these hypothetical processing elements with any known neurophysiological mechanisms. Indeed, if there are neurons sensitive to human faces and other complex attributes, it is also realistic to suppose the existence of neurons, single or joined into an assembly of neurons, which are able to record relatively simple perceptual elements such as colored dots. For the construction of the model, it was enough to assume that these hypothetical perceptual mechanisms or automatons are endowed with a single ability to register the presence of displayed elements and remember to which of the two types, A or B, they belonged. Because nothing is perfect, these perceptual automatons make mistakes. Each displayed element can be recorded and used in subsequent processing with a more or less fixed probability β. Although the internal representation of each displayed element has only two values, on and off, the resulting psychometric curve of discrimination has the shape that is practically indiscriminable from that of cumulative normal distribution.

Like Gaussian models, the binomial models also have a long and respectable history. This tradition is first associated with attempts to determine efficiency of visual perception or, in other words, the proportion out of all available information that an observer is able to take into account in decision making. In many situations, it is obvious that that the observer’s decisions are not based on all available information. Only a fraction of all available information appears to be exploited in many perceptual judgments. For example, from all light quanta that fall on the cornea, only every 10th or even every 100th is actually used for visual processing (Jones, 1959). At a higher level of processing, it is also typical that only a small fraction of all available information is effectively used for making perceptual decisions. Although, in some exceptional cases, the estimated efficiency of the perceptual system reaches the 50 % level (Barlow & Lal, 1980; Burgess, Wagner, Jennings, & Barlow, 1981; Morgan, Raphael, Tibber, & Dakin, 2015), it is not uncommon that only a few percent from all available information are effectively used (Raidvee et al., 2011; Simpson, Falkenberg, & Manahilov, 2003; Swensson & Judy, 1996). This study provided further evidence that, under the most favorable conditions, efficiency hardly surpasses the 70 % level for color and 40 % level for orientation, and, in many cases, the observer is behaving as if she can take into account no more than one fifth or even one tenth of all elements. One relevant conclusion of this study is that efficiency with which visual elements are counted is not a fixed value. Different visual attributes, even in their most distinctive forms, lead to quite different counting probabilities. It is also obvious that processing efficiency drops with the number of processed elements N, irrespective of the visual attributes that are used to discriminate between the two sets. Overall, the proposed binomial model can be conceptualized as a counting model that gives the following simple meaning to the parameter β—a probability with which any displayed element is recorded and processed to make perceptual judgments about numerical proportions.

Based on the strict formal criteria alone, the Thurstonian-binomial model wins by greater parsimony over the Thurstonian–Gaussian model. As we have already stressed, the formal equality of the goodness of fits is not surprising, given a relatively simple link (see Eq. 4) between the parameters of these two models. It is well known that binomial function becomes practically inseparable from the normal distribution with the increase of the number of binomial trials N. If only the total number of elements is sufficiently small, it becomes possible to distinguish between different distributions, even as close as binomial and hypergeometric (Raidvee, Põlder, et al., 2012). Thus, we expected to see some meaningful differences between binomial and Gaussian models, mainly with the smallest number of used elements, N = 9. This means that it was necessary to discriminate, for example, five red dots from four green dots. Nevertheless, even in the range close to absolute accuracy, which by the way was established by one of the fathers of neoclassical economics (Jevons, 1871), we did not observe that the predictions of the binomial model were much more accurate than those of the Gaussian model.

If all preconceptions are left behind, a binomial model, which among other things does not presume an infinite continuum of perceptual states, looks as a rather promising explanation for how numerical proportions are judged. It does not make unrealistic pledges and is intuitively transparent. One obvious advantage of the binomial model before the Gaussian is to question whether the already-processed elements are separated from the to-be-processed elements, or is it possible that some of the elements are processed more than once (Raidvee, Põlder, et al., 2012). Perhaps the most salient benefit of the binomial model over the Gaussian is that it is not committed to an unrealistic, and only occasionally tested, assumption that all available information is used for making perceptual decisions.

Finally, there may be a good reason why it was so difficult to distinguish predictions of the Gaussian model from the predictions of the binomial model. Although their mathematical predictions are similar, and in limiting conditions even identical, they are still expressing two fundamentally different principles. The Gaussian model is based on the idea that every measurement executed by the perceptual system is susceptible to an unavoidable internal noise. In contrast, the binomial model is implementing an equally basic idea that, unlike an ideal observer, the real perceptual devices have capacity limitations as a result of which perceptual decisions are always made on the basis of a fraction of available information. These two fundamental principles—internal noise and using only a fraction of all information—are complementary, and possibly both necessary, for the description of how perception operates (Allik, Toom, Raidvee, Averin, & Kreegipuu, 2013). In this perspective, the most demanding task is not to decide which of the two models describes data best, but to devise new experimental protocols that will be able to separate consequences of both principles operating concurrently.