Changes in Residual Stresses in the Vicinity of a Continuity Defect in an Elastoviscoplastic Material under Repeated Loading

Abstract

The results of calculations of the stress-strain states of an elastoplastic material containing a single cylindrical continuity defect and loaded with external pressure are presented. The hydrostatic pressure on the surface distant from the defect initially increases, remains constant for some time and then gradually decreases to zero. The process of comprehensive compression leaves, after unloading, a formed level and distribution of residual stresses in the vicinity of the continuity defect. The change in such stresses is calculated upon repeated loading and unloading. Intensity and nature of repeated loads are considered identical to the original ones. Calculations are carried out within the framework of the stated one-dimensional problem of the theory of large deformations. The material is assumed to be incompressible. The development of areas of viscoplastic flow in the active part of the process and their attenuation during unloading are taken into account. Changes in the geometric dimensions of the evolving defect are assessed.

1 INTRODUCTION

Continuity defects in the form of micropores or microcracks are inevitably present in metal product materials. Under operating conditions of products, defects may increase in size and new ones may appear. This circumstance leads to the development of a defective structure of the material. Taking into account such facts in mechanics is associated with a special state parameter called damageability, and in this way an approach to the study of long-term strength of materials is established. The destruction associated with the evolution of the defect structure was described in the Rabotnov [1] and Kachanov [2] studies. This scientific direction remains relevant and developing at the present time [3–5]. A fairly complete review of the results obtained in this area of research is given in [6].

On the other hand, strengthening of materials was also noted when they were treated with an increased level of hydrostatic compression [7–11]. This effect was explained by the phenomenon of “healing” of microdefects of continuity due to the intense impact on the material of all-round pressure. Attempts to calculate this phenomenon [10–13] led to problems in the theory of large elastoplastic deformations, since in the vicinity of a defect the displacements are comparable to its geometric dimensions and therefore the deformations cannot be assumed to be small. The results of calculations for the one-dimensional problem of all-round compression of an elastoplastic material with a single continuity defect have great impact for further considerations [14, 15]. The effect of “adaptability” of the defect to cyclic loading of the “load-unload” type was observed, when after each unloading the size of the defect, the level and distribution of residual stresses in its vicinity were repeated. This paradoxical circumstance was explained by the fact that the calculations used a mathematical model of an ideal elastoplastic medium. It was believed that rejection of the ideality of plastic flow would lead either to the development of a defect or to its “healing”. Here we abandon the ideality of elastoplastic deformation, adding viscous resistance to plastic flow to the dissipative properties of the material. The mathematical model used, as in [14, 15], is based on the determination of reversible and irreversible deformations using differential equations for their change [15–17]. Due to the increase in the amount of calculations, we limit ourselves to only two steps. First one is creation of a field of residual stresses in the vicinity of the defect during the initial loading and unloading; and the second one is its changing during repeated loading and unloading. This makes it possible to trace the direction of such changes, including the beginning of the evolution of the defect size.

2 BASIC RELATIONS OF THE MODEL

In the large deformation model, the tensors of reversible e and irreversible p deformations are determined by the differential equations of their change (transfer) [15]

$$\begin{gathered} \frac{{D{\mathbf{e}}}}{{Dt}} = \boldsymbol\varepsilon - {{\boldsymbol\varepsilon }^{p}} - \frac{1}{2}((\boldsymbol\varepsilon - {{\boldsymbol\varepsilon }^{p}} + {\mathbf{z}}) \cdot {\mathbf{e}} + {\mathbf{e}} \cdot (\boldsymbol\varepsilon - {{\boldsymbol\varepsilon }^{p}} - {\mathbf{z}})), \\ \frac{{D{\mathbf{p}}}}{{Dt}} = \frac{{d{\mathbf{p}}}}{{dt}} - {\mathbf{r}} \cdot {\mathbf{p}} + {\mathbf{p}} \cdot {\mathbf{r}} = {{\boldsymbol\varepsilon }^{p}} - {\mathbf{p}} \cdot {{\boldsymbol\varepsilon }^{p}} - {{\boldsymbol\varepsilon }^{p}} \cdot {\mathbf{p}}, \\ \end{gathered} $$

$$\begin{gathered} \boldsymbol\varepsilon = \frac{1}{2}(\nabla {\mathbf{v}} + {{\nabla }^{T}}{\mathbf{v}}),\quad {\mathbf{r}} = \boldsymbol\omega + {\mathbf{z}}\left( {\boldsymbol\varepsilon ,{\mathbf{e}}} \right),\quad \boldsymbol\omega = \frac{1}{2}(\nabla {\mathbf{v}} - {{\nabla }^{T}}{\mathbf{v}}), \\ {\mathbf{z}} = A_{1}^{{ - 1}}[A_{2}^{2}\left( {\boldsymbol\varepsilon \cdot {\mathbf{e}} - {\mathbf{e}} \cdot {\mathbf{\boldsymbol\varepsilon }}} \right) + {{A}_{2}}(\boldsymbol\varepsilon \cdot {{{\mathbf{e}}}^{2}} - {{{\mathbf{e}}}^{2}} \cdot \boldsymbol\varepsilon ) + {\mathbf{e}} \cdot \boldsymbol\varepsilon \cdot {{{\mathbf{e}}}^{2}} - {{{\mathbf{e}}}^{2}} \cdot \boldsymbol\varepsilon \cdot {\mathbf{e}}], \\ \end{gathered} $$

(2.1)

$$\begin{gathered} {{A}_{1}} = 8 - 8{{L}_{1}} + 3L_{1}^{2} - {{L}_{2}} - \frac{1}{3}L_{1}^{3} + \frac{1}{3}{{L}_{3}},\quad {{A}_{2}} = 2 - {{L}_{1}},. \\ {{L}_{1}} = tr{\mathbf{e}},\quad {{L}_{2}} = tr{{{\mathbf{e}}}^{2}},\quad {{L}_{3}} = tr{{{\mathbf{e}}}^{3}} \\ \end{gathered} $$

In these dependencies ${\mathbf{v}}$ is the velocity vector, ${{\boldsymbol\varepsilon }^{p}}$ is the tensor of rates of change of irreversible deformations. The second equation (2.1) determines the objective time derivative, which ensures the geometric correctness of the kinematics of the deformable medium. If ${{\boldsymbol\varepsilon }^{p}} = {\mathbf{0}}$, the irreversible deformation tensor p remains unchanged, and its components change in accordance with the second equation (2.1), which is typical for the unloading process.

Almansi total deformation tensor d according to (2.1) has the form

$${\mathbf{d}} = {\mathbf{e}} + {\mathbf{p}} - \frac{1}{2}{{{\mathbf{e}}}^{2}} - {\mathbf{e}} \cdot {\mathbf{p}} - {\mathbf{p}} \cdot {\mathbf{e}} + {\mathbf{e}} \cdot {\mathbf{p}} \cdot {\mathbf{e}}.$$

(2.2)

From (2.2) it follows that the tensor e is the linear part of the reversible deformation tensor ${\mathbf{c}} = {\mathbf{e}} - 0.5{{{\mathbf{e}}}^{2}}$. However, as a measure of reversible deformations we use the tensor e, for which the first equation of change (2.1) is written.

We assume that the material is incompressible. Then it follows from the law of conservation of energy that the stresses in the material are completely determined by reversible deformations

$$\boldsymbol\sigma = \left\{ \begin{gathered} - {{P}_{1}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{d}}}} \cdot ({\mathbf{I}} - 2{\mathbf{d}}){\text{,}}\quad {\mathbf{p}} \equiv {\mathbf{0}}, \hfill \\ - {{P}_{2}}{\mathbf{I}} + \frac{{\partial W}}{{\partial {\mathbf{e}}}} \cdot \left( {{\mathbf{I}} - {\mathbf{e}}} \right),\quad {\mathbf{p}} \ne {\mathbf{0}}. \hfill \\ \end{gathered} \right.$$

(2.3)

Here, ${{P}_{1}}$ and ${{P}_{2}}$ are the unknown functions of additional hydrostatic pressure; I is the unit tensor; $W = {{\rho }_{0}}\Psi$ is the elastic potential; ${{\rho }_{0}}$ is the density of the material in its free state; $\Psi$ is the thermodynamic potential (free energy distribution density), for which the hypothesis of its independence from the irreversible deformation tensor p is accepted. For an isotropic deformable material, we expand the elastic potential into the Maclaurin series

$$\begin{gathered} W = \left( {a - \mu } \right){{J}_{1}} + a{{J}_{2}} + bJ_{1}^{2} - \kappa {{J}_{1}}{{J}_{2}} - \zeta J_{1}^{3} + ..., \\ {{J}_{k}} = \left\{ \begin{gathered} {{L}_{k}}{\text{,}}\quad {\mathbf{p}} = {\mathbf{0}}, \hfill \\ {{I}_{k}},\quad {\mathbf{p}} \ne {\mathbf{0}}, \hfill \\ \end{gathered} \right. \\ {{L}_{1}} = tr{\mathbf{d}},\quad {{L}_{2}} = tr{{{\mathbf{d}}}^{2}},\quad {{I}_{1}} = tr{\mathbf{c}},\quad {{I}_{2}} = tr{{{\mathbf{c}}}^{2}}. \\ \end{gathered} $$

(2.4)

In dependencies (2.4), μ is the shear modulus, a, b, $\kappa$, $\zeta$ are the other mechanical constants.

As the loading surface, we take the generalized Tresca–Saint-Venant yield criterion [18]

$$F(\boldsymbol\sigma ,{{\boldsymbol\varepsilon }^{p}}) = k,\quad F(\boldsymbol\sigma ,{{\boldsymbol\varepsilon }^{p}}) = \frac{1}{2}\max \left| {{{\sigma }_{i}} - {{\sigma }_{j}}} \right| - \eta \max \left| {\boldsymbol\varepsilon _{k}^{p}} \right|$$

(2.5)

the consequence of which is the associated law of plastic flow [18, 19]

$${{\boldsymbol\varepsilon }^{p}} = \xi \frac{{\partial F}}{{\partial \boldsymbol\sigma }},\quad \xi > 0.$$

(2.6)

In relations (2.5) and (2.6), ${{\sigma }_{i}}$, $\boldsymbol\varepsilon _{k}^{p}$ are the main values of the stress tensors and plastic strain rates; k is the yield strength; η is the coefficient of viscous resistance to plastic flow.

3 STATEMENT OF THE PROBLEM. ELASTIC EQUILIBRIUM

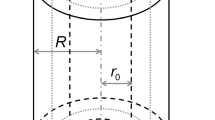
We consider a boundary value problem about the behavior of a continuity defect in a deformable material under conditions of repeated loads being applied to it. Since the loaded surface of the material significantly exceeds the dimensions of the continuity defect, the deformation can be considered as one-dimensional, and the boundary of this defect can be taken as a circular cylindrical surface of the original radius ${{r}_{0}}$. We also assume that the boundary action is carried out on a cylindrical surface of the original radius ${{R}_{0}}$(${{R}_{0}} \gg {{r}_{0}}$). Let the material be deformed under the following boundary conditions

$${{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = R{\kern 1pt} \text{*}}}} = - p{\kern 1pt} \text{*},\quad {{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = r{\kern 1pt} \text{*}}}} = 0.$$

(3.1)

Here, ${{\sigma }_{{rr}}}$ is the radial component of the stress tensor in the cylindrical coordinate system $r$, $\varphi$, z, R* and s* are the radii of the outer and inner cylindrical surfaces under equilibrium conditions. For the conditions under consideration, we find that the displacement vector has only one nonzero component ${{u}_{r}} = u$. On the boundary surfaces we obtain

$$\begin{array}{*{20}{c}} {u\left( {R{\kern 1pt} \text{*}} \right) = R{\kern 1pt} \text{*}\; - {{R}_{0}},}&{u\left( {r{\kern 1pt} \text{*}} \right) = r{\kern 1pt} \text{*}\; - {{r}_{0}}} \end{array}.$$

(3.2)

From relation (2.2), we write out the nonzero components of the Almansi strain tensor

$${{d}_{{rr}}} = u{\kern 1pt} '\; - \frac{{{{{\left( {u{\kern 1pt} '} \right)}}^{2}}}}{2},\quad {{d}_{{\varphi \varphi }}} = \frac{u}{r} - \frac{{{{u}^{2}}}}{{2{{r}^{2}}}},\quad u{\kern 1pt} ' = \frac{{\partial u}}{{\partial r}}.$$

(3.3)

From the condition of incompressibility of the medium and dependencies (3.3), we get the differential equation for the displacement component

$$\left( {1 - u{\kern 1pt} '} \right)\left( {1 - \frac{u}{r}} \right) = 1.$$

(3.4)

Solving equation (3.4) with the assumption that the points of the boundary surfaces with the initial coordinates $r = {{R}_{0}}$ and $r = {{r}_{0}}$ at the current moment of time have coordinates $r = R\left( t \right)$ and $r = s\left( t \right)$, accordingly, we have

$$u = r - \sqrt {{{r}^{2}} + \varphi \left( t \right)} ,\quad \varphi \left( t \right) = R_{0}^{2} - {{R}^{2}}\left( t \right) = r_{0}^{2} - {{s}^{2}}\left( t \right).$$

(3.5)

From (3.3) and (3.5) for the components of the Almansi strain tensor, we get

$${{d}_{{rr}}} = \frac{1}{2}(1 - {{H}^{{ - 1}}}),\quad {{d}_{{\varphi \varphi }}} = \frac{1}{2}\left( {1 - H} \right),\quad H = 1 + \frac{\varphi }{{{{r}^{2}}}}.$$

(3.6)

For non-zero components of the stress tensor, we obtain the following dependencies from (2.3) and (2.4)

$$\begin{gathered} {{\sigma }_{{rr}}} = - P + G\left( {{{d}_{{rr}}},{{d}_{{\varphi \varphi }}}} \right),\quad {{\sigma }_{{\varphi \varphi }}} = - P + G\left( {{{d}_{{\varphi \varphi }}},{{d}_{{rr}}}} \right),\quad {{\sigma }_{{zz}}} = - P, \\ P = {{P}_{1}} - a + \mu - 2b\left( {{{d}_{{rr}}} + {{d}_{{\varphi \varphi }}}} \right) + \left( {\kappa + 3\zeta } \right)(d_{{rr}}^{2} + d_{{\varphi \varphi }}^{2}) + 6\zeta {{d}_{{rr}}}{{d}_{{\varphi \varphi }}}, \\ \end{gathered} $$

$$G\left( {x,y} \right) = {{k}_{1}}x - {{k}_{2}}{{x}^{2}} - {{k}_{3}}xy + {{k}_{4}}{{x}^{3}} + {{k}_{5}}(x{{y}^{2}} + 2{{x}^{2}}y),$$

(3.7)

$$\begin{gathered} {{k}_{1}} = 2\mu ,\quad {{k}_{2}} = 2\left( {2a + 2b + \kappa } \right),\quad {{k}_{3}} = 2\left( {2b + \kappa } \right), \\ {{k}_{4}} = 6\left( {\kappa + \zeta } \right),\quad {{k}_{5}} = 2\left( {\kappa + 3\zeta } \right). \\ \end{gathered} $$

Taking into account dependencies (3.6) for the strain components from (3.7), we determine the stresses

$$\begin{gathered} {{\sigma }_{{rr}}} = - P + L\left( H \right),\quad {{\sigma }_{{\varphi \varphi }}} = - P + L({{H}^{{ - 1}}}),\quad {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = N\left( H \right), \\ L\left( H \right) = \frac{{{{k}_{4}}}}{8}(1 - {{H}^{{ - 3}}}) + {{a}_{1}}(1 - {{H}^{{ - 2}}}) + {{a}_{2}}(1 - {{H}^{{ - 1}}}) + {{a}_{3}}\left( {H - 1} \right) + \frac{{{{k}_{5}}}}{8}({{H}^{2}} - 1), \\ \end{gathered} $$

$$N\left( H \right) = {{a}_{4}}(H - {{H}^{{ - 1}}}) + {{a}_{5}}({{H}^{2}} - {{H}^{{ - 2}}}) + \frac{{{{k}_{4}}}}{8}({{H}^{3}} - {{H}^{{ - 3}}}),$$

(3.8)

$$\begin{gathered} {{a}_{1}} = a + b - \frac{3}{4}\left( {3\kappa + 5\zeta } \right),\quad {{a}_{2}} = \mu - 2a - 3b + \frac{5}{2}\left( {\kappa + 3\zeta } \right),\quad {{a}_{3}} = b - \frac{3}{4}\left( {\kappa + 5\zeta } \right), \\ {{a}_{4}} = \mu - 2a - 2b + \frac{1}{4}\left( {7\kappa + 15\zeta } \right),\quad {{a}_{5}} = a + b - 2\kappa - 3\zeta . \\ \end{gathered} $$

To calculate the unknown function, $P = P\left( r \right)$ we use the equilibrium equation

$$\sigma _{{rr}}^{'} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = 0.$$

(3.9)

Integrating Eq. (3.9) taking into account (3.8), for the stress components and function P we obtain the final dependences

$$\begin{gathered} {{\sigma }_{{rr}}} = M\left( {H,x} \right),\quad {{\sigma }_{{\varphi \varphi }}} = M\left( {H,x} \right) - N\left( H \right),\quad P = L\left( H \right) - M\left( {H,x} \right), \\ M\left( {H,x} \right) = {{a}_{6}}\ln \frac{H}{x} + \frac{{{{k}_{1}}}}{4}\left( {H - x} \right) + {{a}_{7}}({{\left( {H - 1} \right)}^{2}} - {{\left( {x - 1} \right)}^{2}}) \\ \end{gathered} $$

$$\, + \frac{{{{k}_{4}}}}{{48}}({{(H - 1)}^{3}} - {{(x - 1)}^{3}}) + {{a}_{8}}({{x}^{{ - 1}}} - {{H}^{{ - 1}}}) + \frac{{{{k}_{4}}}}{{32}}({{(1 - {{x}^{{ - 1}}})}^{2}} - {{(1 - {{H}^{{ - 1}}})}^{2}}),$$

(3.10)

$$\begin{gathered} x = \frac{{r_{0}^{2}}}{{s_{0}^{2}}},\quad {{a}_{6}} = \frac{1}{2}\left( {\mu - a - b + \frac{1}{2}\left( {\kappa + 3\zeta } \right)} \right) \\ {{a}_{7}} = \frac{1}{4}\left( {a + b + \frac{1}{4}\left( {\kappa - 3\zeta } \right)} \right),\quad {{a}_{8}} = \frac{1}{2}\left( {a + b - \frac{1}{2}\left( {\kappa + 3\zeta } \right)} \right). \\ \end{gathered} $$

When writing (3.10), the second boundary condition (3.1), in which r* is replaced by s₀, has been used. The notation s₀ is introduced for the extreme value of the radius of the inner surface corresponding to the pressure p₀ on the outer surface, at which the yield criterion (2.5) is first satisfied on the inner boundary surface in the form

$${{\left. {\left( {{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}} \right)} \right|}_{{r = {{s}_{0}}}}} = 2k,\quad N\left( x \right) = 2k.$$

(3.11)

The second Eq. (3.11) is used to find the value of s₀. The value of loading pressure p₀ at which the yield criterion is first satisfied on the inner surface follows from the first relation (3.10) and the first boundary condition (3.1) in the following form ${{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = R}}} = - {{p}_{0}}$:

$${{p}_{0}} = M\left( {x,h} \right),\quad h = H\left( R \right) = \frac{{R_{0}^{2}}}{{{{R}^{2}}}} = 1 + \frac{\varphi }{{R_{0}^{2} - \varphi }}.$$

(3.12)

4 VISCOPLASTIC FLOW UNDER INCREASING AND CONSTANT LOADING PRESSURE

In a state of elastic equilibrium, the deformable material is under the influence of pressure $p = {{p}_{0}}$ until time t = 0. Then, from time t = 0, we begin to increase the external pressure. Thus, the boundary conditions of the problem take the form

$${{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = R\left( t \right)}}} = - p\left( t \right),\quad {{\left. {{{\sigma }_{{rr}}}} \right|}_{{r = s\left( t \right)}}} = 0,\quad p\left( t \right) = {{p}_{0}}\left( {1 + \gamma t} \right),\quad \gamma > 0.$$

(4.1)

As the pressure p(t) increases from the inner boundary surface, $r = s\left( t \right)$ the region $s\left( t \right) \leqslant r \leqslant m\left( t \right)$ in which viscoplastic flow occurs increases. The elastoplastic boundary $r = m\left( t \right)$ separates the expanding flow region from the region $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ in which the material is deformed reversibly. In the entire region of viscoplastic flow, the yield criterion (2.5) is satisfied in the form

$${{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = 2k + 2\eta \varepsilon _{{rr}}^{p}.$$

(4.2)

Equilibrium equation (3.9) at $t \geqslant 0$ replace with the equation of motion of the medium

$$\sigma _{{rr}}^{'} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = {{\rho }_{0}}{\dot {v}},\quad {\dot {v}} = \frac{{d{v}}}{{dt}}.$$

(4.3)

Here, ${v} = {{{v}}_{r}}$ is the nonzero component of the velocity vector. For this component and its time derivative, from relations (2.1) and (3.5), we have

$${v} = \frac{{\partial u}}{{\partial t}}{{\left( {1 - u{\kern 1pt} '} \right)}^{{ - 1}}} = - \frac{{\dot {\varphi }}}{{2r}},\quad {\dot {v}} = \frac{{\partial {v}}}{{\partial t}} + {vv}{\kern 1pt} ' = - \frac{{\ddot {\varphi }}}{{2r}} - \frac{{{{{\dot {\varphi }}}^{2}}}}{{4{{r}^{3}}}}.$$

(4.4)

Then equation (4.3), taking into account (4.4), takes the form

$$\sigma _{{rr}}^{'} + \frac{{{{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}}}}{r} = - \frac{{{{\rho }_{0}}}}{2}\left( {\frac{{\ddot {\varphi }}}{r} + \frac{{{{{\dot {\varphi }}}^{2}}}}{{2{{r}^{3}}}}} \right).$$

(4.5)

Integrating the equation of motion (4.5) in the region of reversible deformation $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ and taking into account the first boundary condition (4.1), we find the stress components

$$\begin{gathered} {{\sigma }_{{rr}}} = - p\left( t \right) + M\left( {H,h} \right) + S\left( {\varphi ,R,r} \right),\quad {{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{rr}}} - N\left( H \right), \\ S\left( {\varphi ,R,r} \right) = \frac{{{{\rho }_{0}}}}{2}\left( {\ddot {\varphi }\ln \frac{R}{r} + \frac{{{{{\dot {\varphi }}}^{2}}}}{4}\left( {\frac{1}{{{{r}^{2}}}} - \frac{1}{{{{R}^{2}}}}} \right)} \right). \\ \end{gathered} $$

(4.6)

In the flow region $s\left( t \right) \leqslant r \leqslant m\left( t \right)$, from (2.4) the stress components, we get

$$\begin{gathered} {{\sigma }_{{rr}}} = - P + G\left( {{{c}_{{rr}}},{{c}_{{\varphi \varphi }}}} \right),\quad {{\sigma }_{{\varphi \varphi }}} = - P + G\left( {{{c}_{{\varphi \varphi }}},{{c}_{{rr}}}} \right),\quad {{\sigma }_{{zz}}} = - P,\quad {{c}_{{rr}}} = {{e}_{{rr}}} - \frac{{e_{{rr}}^{2}}}{2}, \\ {{c}_{{\varphi \varphi }}} = {{e}_{{\varphi \varphi }}} - \frac{{e_{{\varphi \varphi }}^{2}}}{2},\quad P = {{P}_{2}} - a + \mu - 2b\left( {{{c}_{{rr}}} + {{c}_{{\varphi \varphi }}}} \right) + \left( {\kappa + 3\zeta } \right)\left( {c_{{rr}}^{2} + c_{{\varphi \varphi }}^{2}} \right) + 6\zeta {{c}_{{rr}}}{{c}_{{\varphi \varphi }}}. \\ \end{gathered} $$

(4.7)

From dependencies (2.2), (3.6) and (4.7) we obtain

$$\begin{gathered} {{\sigma }_{{rr}}} = - P + L\left( {{{H}_{1}}} \right),\quad {{\sigma }_{{\varphi \varphi }}} = - P + L(H_{1}^{{ - 1}}), \\ {{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}} = N\left( {{{H}_{1}}} \right),\quad {{H}_{1}} = H\left( {1 - 2{{p}_{{rr}}}} \right). \\ \end{gathered} $$

(4.8)

We integrate the equation of motion (4.5) in the region of viscoplastic flow $s\left( t \right) \leqslant r \leqslant m\left( t \right)$ taking into account the third dependence (4.8) and the second boundary condition (4.1) and find the stress component ${{\sigma }_{{rr}}}$, eliminating the unknown function $P = P\left( r \right)$

$${{\sigma }_{{rr}}} = - \int\limits_s^r {\frac{{N\left( {{{H}_{1}}} \right)}}{r}} dr + S\left( {\varphi ,s,r} \right).$$

(4.9)

From dependencies (2.1) follow the relations

$$\varepsilon _{{rr}}^{p} = - \varepsilon _{{\varphi \varphi }}^{p} = \frac{{{{{\dot {p}}}_{{rr}}}}}{{1 - 2{{p}_{{rr}}}}},\quad {{p}_{{\varphi \varphi }}} = - \frac{{{{p}_{{rr}}}}}{{1 - 2{{p}_{{rr}}}}},\quad {{\dot {p}}_{{rr}}} = \frac{{\partial {{p}_{{rr}}}}}{{\partial t}} + {v}p_{{rr}}^{'}.$$

(4.10)

Dependencies (4.2), (4.8) and (4.10) lead to a differential equation for the component of irreversible deformations p_rr

$$\frac{{\partial {{p}_{{rr}}}}}{{\partial t}} - \frac{{\dot {\varphi }}}{{2r}}p_{{rr}}^{'} = \frac{{1 - 2{{p}_{{rr}}}}}{{2\eta }}\left( {N\left( {{{H}_{1}}} \right) - 2k} \right).$$

(4.11)

At the elastoplastic boundary, $r = m\left( t \right)$ the relation following from the stress continuity condition $N\left( H \right) = 2k$ is satisfied. Comparing this condition with the second equation (3.11), we obtain the relation for $r = m\left( t \right)$

$$m = \sqrt {\frac{\varphi }{{x - 1}}} .$$

(4.12)

From the condition of continuity of the stress tensor component ${{\sigma }_{{rr}}}$ on the elastoplastic boundary $r = m\left( t \right)$ and dependencies (4.6) and (4.9), we have the integro-differential equation for the function $\varphi \left( t \right)$

$$S\left( {\varphi ,s,R} \right) - \int\limits_s^m {\frac{{N\left( {{{H}_{1}}} \right)}}{r}dr} - M\left( {1 + \frac{\varphi }{{{{m}^{2}}}},h} \right) = - p.$$

(4.13)

The initial conditions for Eq. (4.13) are the following conditions

$$\varphi \left( 0 \right) = r_{0}^{2} - s_{0}^{2},\quad \dot {\varphi }\left( 0 \right) = 0.$$

(4.14)

The system of equations (4.11)–(4.14) for unknown functions p_rr, m(t) $\varphi \left( t \right)$ has been solved numerically using the finite-difference method.

In the region of reversible deformation, from (2.2) and (3.6) we find the components of the reversible deformation tensor

$${{e}_{{rr}}} = 1 - \sqrt {1 - 2{{d}_{{rr}}}} = 1 - \sqrt {{{H}^{{ - 1}}}} ,\quad {{e}_{{\varphi \varphi }}} = 1 - \sqrt {1 - 2{{d}_{{\varphi \varphi }}}} = 1 - \sqrt H .$$

(4.15)

Relations (2.2), (3.6) and (4.10) make it possible to obtain dependencies for the components of the reversible strain tensor in the region of viscoplastic flow

$${{e}_{{rr}}} = 1 - \sqrt {\frac{{1 - 2{{d}_{{rr}}}}}{{1 - 2{{p}_{{rr}}}}}} = 1 - \sqrt {H_{1}^{{ - 1}}} ,\quad {{e}_{{\varphi \varphi }}} = 1 - \sqrt {\frac{{1 - 2{{d}_{{\varphi \varphi }}}}}{{1 - 2{{p}_{{\varphi \varphi }}}}}} = 1 - \sqrt {{{H}_{1}}} .$$

(4.16)

At some point in time t₁ we fix the external loading pressure at a value ${{p}_{1}} = p\left( {{{t}_{1}}} \right)$ and assume that it remains constant. Such a change in the loading mode does not lead to significant changes in the deformation pattern. All relations in this section are satisfied in this case.

5 SLOWING DOWN OF THE FLOW WITH DECREASING PRESSURE

At the moment of time ${{t}_{2}} > {{t}_{1}}$ we begin to reduce the pressure at the outer boundary $r = R\left( t \right)$ according to the law

$$p\left( t \right) = {{p}_{1}}\left( {1 - {{\gamma }_{1}}\left( {t - {{t}_{2}}} \right)} \right),\quad {{\gamma }_{1}} > 0.$$

(5.1)

A decrease in pressure (5.1) leads to the appearance of an unloading region in the deformed material ${{m}_{1}}\left( t \right) \leqslant r \leqslant m\left( t \right)$, in which $\varepsilon _{{rr}}^{p} = 0$. In this case, the components of the irreversible deformation tensor ${\mathbf{p}}$ continue to change according to the second Eq. (2.1). The new elastoplastic boundary $r = {{m}_{1}}\left( t \right)$ separates the unloading region ${{m}_{1}}\left( t \right) \leqslant r \leqslant m\left( t \right)$ from the contracting region $s\left( t \right) \leqslant r \leqslant {{m}_{1}}\left( t \right)$ in which viscoplastic flow is present. And in the region $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ the material is still deformed reversibly.

The components of the stress tensor in the region of reversible deformation $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ satisfy relations (4.6), and in the region of viscoplastic flow we have $s\left( t \right) \leqslant r \leqslant {{m}_{1}}\left( t \right)$ (4.8) and (4.9). Integrating the equation of motion (4.5) in the unloading region ${{m}_{1}}\left( t \right) \leqslant r \leqslant m\left( t \right)$, we establish that the stress tensor component ${{\sigma }_{{rr}}}$ satisfies dependence (4.9). Also from (2.2), (2.4) and (3.6) for the stress components in this region, we get relations (4.7) and (4.8).

In the flow region, the irreversible deformation component ${{p}_{{rr}}}$ satisfies the differential equation (4.11). In the unloading region, ${{m}_{1}}\left( t \right) \leqslant r \leqslant m\left( t \right)$ according to the last dependence (4.10) and the second equation (2.1), ${{p}_{{rr}}}$the differential equation follows for the component of the irreversible deformation tensor

$$\frac{{\partial {{p}_{{rr}}}}}{{\partial t}} - \frac{{\dot {\varphi }}}{{2r}}p_{{rr}}^{'} = 0.$$

(5.2)

The condition of stress continuity at the elastoplastic boundary $r = {{m}_{1}}\left( t \right)$ leads to the equality ${{\left. {N({{H}_{1}})} \right|}_{{r = {{m}_{1}}}}}$ = 2k. Comparing it with the second equation (3.12), we obtain

$$q = \sqrt {\varphi \frac{{1 - 2{{p}_{{rr}}}\left( q \right)}}{{x + 2{{p}_{{rr}}}\left( q \right) - 1}}} ,\quad q = {{m}_{1}}.$$

(5.3)

The continuity of the stress tensor component ${{\sigma }_{{rr}}}$ at the boundary $r = m\left( t \right)$ leads to the integro-differential equation (4.13) for the function $\varphi \left( t \right)$, the initial conditions for which are the conditions of continuity of the functions $\varphi \left( t \right)$ and $\dot {\varphi }\left( t \right)$ at the time t₂.

From dependencies (3.2) and (3.5) follows the equation for the boundary $r = m\left( t \right)$

$$m\left( t \right) = \sqrt {{{m}^{2}}\left( c \right) + \varphi \left( c \right) - \varphi \left( t \right)} ,\quad c = {{t}_{2}}.$$

(5.4)

Equations (4.11), (4.13), (5.2)–(5.4) with respect to unknown functions ${{p}_{{rr}}}$ (in the flow and unloading regions), $\varphi \left( t \right)$, $m\left( t \right)$ and ${{m}_{1}}\left( t \right)$ have been solved simultaneously using the finite-difference method.

The components of the reversible deformation tensor have the form (4.15) in the region of reversible deformation and (4.16) in the regions of viscoplastic flow and unloading.

At the calculated moment of time ${{t}_{3}} > {{t}_{2}}$, the elastoplastic boundary $r = {{m}_{1}}\left( t \right)$ reaches the internal boundary surface $r = s\left( t \right)$. From this point in time, the deformable material is divided into two regions: the region of reversible deformation $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ and the region with accumulated irreversible deformations $s\left( t \right) \leqslant r \leqslant m\left( t \right)$.

Stresses are determined by relations (4.6) in the region of reversible deformation and (4.8), (4.9) in the region with residual irreversible deformations. The component of residual irreversible deformations p_rr in the region $s\left( t \right) \leqslant r \leqslant m\left( t \right)$ satisfies Eq. (5.2). For the function, $\phi \left( t \right)$ the integro-differential equation (4.13) remains valid with the conditions of continuity of functions $\varphi \left( t \right)$ and $\dot {\varphi }\left( t \right)$ at time ${{t}_{3}}$. Equation (5.4) continues to hold for the boundary $r = m\left( t \right)$. The system of Eqs. (4.13), (5.2) and (5.4) for unknown functions $\varphi \left( t \right)$, ${{p}_{{rr}}}$ and $m\left( t \right)$ is also solved by the finite-difference method.

At the moment of time ${{t}_{4}} = {{t}_{2}} + \gamma _{1}^{{ - 1}}$ corresponding to complete unloading, the pressure at the outer boundary $r = R\left( t \right)$ becomes equal to zero. At this moment in time, the stress tensor component ${{\sigma }_{{rr}}}$ on the inner and outer boundary surfaces is also equal to zero. However, at the same time, residual stresses, as well as elastic and plastic deformations, are present in the deformed material.

6 REPEATED LOADING

From the moment of complete unloading ${{t}_{4}}$, we again increase the external load according to the law $p\left( t \right) = {{p}_{1}}\gamma \left( {t - {{t}_{4}}} \right)$. With increasing pressure, reversible deformation of the material first occurs. In this case, the functions $\varphi \left( t \right)$, ${{p}_{{rr}}}$ and $m\left( t \right)$ are calculated from the system of equations (4.13), (5.2) and (5.4). To find stresses and reversible deformations, relations (4.6) and (4.15) are used in the region of reversible deformation and (4.8), (4.9) and (4.16) in the region with residual irreversible deformations.

At some point in time ${{t}_{5}} > {{t}_{4}}$, under external pressure, ${{p}_{2}} = p\left( {{{t}_{5}}} \right) > {{p}_{0}}$ the yield criterion ${{\left. {({{\sigma }_{{rr}}} - {{\sigma }_{{\varphi \varphi }}})} \right|}_{{r = {{s}_{2}}}}}$ = 2k where ${{s}_{2}} = s\left( {{{t}_{5}}} \right) < {{s}_{0}}$ is satisfied on the internal boundary surface $r = s\left( t \right)$. From the moment of time ${{t}_{5}}$ with a further increase in the external load from the internal boundary surface $r = s\left( t \right)$, a region of viscoplastic flow $s\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$ develops. The boundary $r = {{m}_{2}}\left( t \right)$ separates it from the area with residual irreversible deformations ${{m}_{2}}\left( t \right) \leqslant r \leqslant m\left( t \right)$. And in the region $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ the material continues to deform reversibly. Integrating the equation of motion (4.5) taking into account the boundary conditions and the condition of stress continuity, we obtain dependencies for calculating the components of the stress tensor: in the areas $s\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$ and ${{m}_{2}}\left( t \right) \leqslant r \leqslant m\left( t \right)$ – (4.8), (4.9), in the area $m\left( t \right) \leqslant r \leqslant R\left( t \right)$ – (4.6). To determine the component of the irreversible deformation tensor p_rr in the flow region, one can use equation (4.11), and in the region with accumulated irreversible deformations, one can use equation (5.2). From the condition of continuity of stresses on the elastoplastic boundary $r = {{m}_{2}}\left( t \right)$, it follows that Eq. (5.3) where $q = {{m}_{2}}\left( t \right)$ is satisfied. The elastoplastic boundary $r = m\left( t \right)$ satisfies equation (5.4) where $c = {{t}_{4}}$.

At the calculated moment of time ${{t}_{6}} > {{t}_{5}}$, the elastoplastic boundary $r = {{m}_{2}}\left( t \right)$ reaches the boundary $r = m\left( t \right)$. Thus, with a subsequent increase in pressure from time t₆, two regions remain in the material: the region of viscoplastic flow $s\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$ and the region of reversible deformation ${{m}_{2}}\left( t \right) \leqslant r \leqslant R\left( t \right)$. Next, at the moment of time ${{t}_{7}} = {{t}_{4}} + {{\gamma }^{{ - 1}}} > {{t}_{6}}$, we stop the increase in external pressure at the value $p\left( {{{t}_{7}}} \right) = {{p}_{1}}$ and continue loading at constant pressure. Such a change in loading conditions does not cause qualitative changes in the deformation process.

Starting from a certain point in time ${{t}_{8}} > {{t}_{7}}$, we reduce the pressure according to the law $p\left( t \right) = {{p}_{1}}\left( {1 - {{\gamma }_{2}}\left( {t - {{t}_{8}}} \right)} \right)$ where ${{\gamma }_{2}} > 0$. This change in the loading mode leads to the emergence of a new unloading area ${{m}_{3}}\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$. In the decreasing region $s\left( t \right) \leqslant r \leqslant {{m}_{3}}\left( t \right)$ the viscoplastic flow is present and in the region ${{m}_{2}}\left( t \right) \leqslant r \leqslant R\left( t \right)$ the material deforms reversibly. At the calculated moment of time ${{t}_{9}} > {{t}_{8}}$, the elastoplastic boundary $r = {{m}_{3}}\left( t \right)$ reaches the internal boundary $r = s\left( t \right)$, after which the viscoplastic flow in the material stops. Two regions remain in the material: the reversible deformation region ${{m}_{2}}\left( t \right) \leqslant r \leqslant R\left( t \right)$ and the unloading region $s\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$. At the moment of time, ${{t}_{{10}}} = {{t}_{8}} + \gamma _{2}^{{ - 1}}$ the external pressure becomes equal to zero, as well as the values of the stress tensor components ${{\sigma }_{{rr}}}$ at the internal and external boundaries. However, as with the first unloading, there are residual stresses and deformations in the material. In this case, the level of residual stresses during repeated complete unloading becomes higher, and the radius of the internal boundary surface is smaller than during the first complete unloading. Thus, if we now again load the material with external pressure, then viscoplastic flow begins to develop at a pressure value greater than p₂. That is, the viscosity of the material with each repeated loading contributes to an increase in the threshold that the pressure must reach to begin the flow process in the material. If the external pressure is assumed to be sufficiently high, then a repeated (reverse) viscoplastic flow may occur during unloading [15, 20]. The possibility of this effect occurring at some subsequent load cycle cannot be ruled out. In this case, the calculations become significantly more complicated, but when formulating conclusions, this circumstance should be taken into account.

Calculations have been carried out in dimensionless variables $x = {r \mathord{\left/ {\vphantom {r {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ and $\tau = \gamma t$ with constant values: ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}} = 0.03$, ${a \mathord{\left/ {\vphantom {a \mu }} \right. \kern-0em} \mu } = 0.9$, ${b \mathord{\left/ {\vphantom {b \mu }} \right. \kern-0em} \mu } = 4$, ${\kappa \mathord{\left/ {\vphantom {\kappa \mu }} \right. \kern-0em} \mu } = 20$, ${\zeta \mathord{\left/ {\vphantom {\zeta \mu }} \right. \kern-0em} \mu } = 80$, ${k \mathord{\left/ {\vphantom {k \mu }} \right. \kern-0em} \mu } = 0.003$, ${{\gamma \eta } \mathord{\left/ {\vphantom {{\gamma \eta } \mu }} \right. \kern-0em} \mu } = 2.395$, ${{{{\rho }_{0}}{{\gamma }^{2}}R_{0}^{2}} \mathord{\left/ {\vphantom {{{{\rho }_{0}}{{\gamma }^{2}}R_{0}^{2}} \mu }} \right. \kern-0em} \mu } = 2.585 \times {{10}^{{ - 12}}}$, ${{{{\gamma }_{1}}} \mathord{\left/ {\vphantom {{{{\gamma }_{1}}} \gamma }} \right. \kern-0em} \gamma } = 1$, ${{{{\gamma }_{2}}} \mathord{\left/ {\vphantom {{{{\gamma }_{2}}} \gamma }} \right. \kern-0em} \gamma } = 1$. Figure 2a shows a graph of the radius of the inner boundary surface ${{s\left( t \right)} \mathord{\left/ {\vphantom {{s\left( t \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ versus time. Here ${{\tau }_{1}} = 1$, ${{\tau }_{2}} = 2$, ${{\tau }_{3}} = 2.21$, ${{\tau }_{4}} = 3$, ${{\tau }_{5}} = 3.79$, ${{\tau }_{6}} = 3.99$, ${{\tau }_{7}} = 4$, ${{\tau }_{8}} = 5$, ${{\tau }_{9}} = 5.12$. Figure 1b illustrates the change in elastoplastic boundaries ${{\tilde {m} = m\left( t \right)} \mathord{\left/ {\vphantom {{\tilde {m} = m\left( t \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ in the time interval from 0 to ${{\tau }_{6}}$, ${{{{{\tilde {m}}}_{1}} = {{m}_{1}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\tilde {m}}}_{1}} = {{m}_{1}}\left( t \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ in the interval from ${{\tau }_{2}}$ to ${{\tau }_{3}}$, ${{{{{\tilde {m}}}_{2}} = {{m}_{2}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\tilde {m}}}_{2}} = {{m}_{2}}\left( t \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ in the interval from ${{\tau }_{5}}$ to ${{\tau }_{{10}}}$ and ${{{{{\tilde {m}}}_{3}} = {{m}_{3}}\left( t \right)} \mathord{\left/ {\vphantom {{{{{\tilde {m}}}_{3}} = {{m}_{3}}\left( t \right)} {{{R}_{0}}}}} \right. \kern-0em} {{{R}_{0}}}}$ in the interval from ${{\tau }_{8}}$ to ${{\tau }_{9}}$.

Fig. 1.

Graphs of (a) radius of the internal boundary surface and (b) elastoplastic boundaries as a function of time.

Fig. 2.

Residual stresses (a) ${{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \mu }} \right. \kern-0em} \mu }$ and (b) ${{{{\sigma }_{{\varphi \varphi }}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{\varphi \varphi }}}} \mu }} \right. \kern-0em} \mu }$.

Figure 2 shows graphs of residual stresses. The solid line shows the components of residual stresses ${{{{\sigma }_{{rr}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{rr}}}} \mu }} \right. \kern-0em} \mu }$ (Fig. 2a) and ${{{{\sigma }_{{\varphi \varphi }}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{\varphi \varphi }}}} \mu }} \right. \kern-0em} \mu }$ (Fig. 2b) at the moment of complete unloading ${{\tau }_{4}}$ during the first loading, and the dotted line shows the same components at the moment of complete unloading τ₁₀ upon repeated loading.

Residual irreversible and reversible deformations at time τ₁₀ are presented in Figs. 3a and 3b respectively.

Fig. 3.

Residual (a) irreversible and (b) reversible deformations.

7 CONCLUSIONS

This article analyzes the processes of development and stopping-down of viscoplastic flow in a material with a single continuity defect under two successive loadings. Loading has been carried out by applying external pressure, first increasing with time, then constant and then decreasing to zero. Next, the second cycle of loading with external pressure has been carried out in the same order. Taking into account the additional dissipative factor introduced by viscous resistance to plastic flow leads to the disappearance of the effect of defect adaptability to cyclic loads of the “load-unload” type, which occurs under conditions of ideal elastoplasticity. The level of residual stresses increases, the radius of the defect decreases, despite the non-increasing value of the loading pressure. The pressure is chosen so that recurrent flow does not occur during unloading. However, with each loading cycle the probability of its occurrence increases, which leads to more complicated calculations.