1 Introduction

As an important part of the turbomachinery, such as turbines, pumps, and compressors, the rotor-bearing system has been upgraded to provide a high rotating speed in order to meet the demand of high power production. In such a rotor-bearing system, multi-support, multi-stage shafts connected by gear coupling might undergo nonlinear supported forces and fault excitations. Under such circumstances, the dynamic response analysis of the rotor-bearing system therefore becomes increasingly important and challenging in the product design, vibration control, and fault diagnosis.

Usually, the supporting force and the elastic deformation of the ball bearing mounted on the rotor system are calculated based on the Hertzian contact condition (Hertz, 1881). Hagiu and Gafitanu (1997), Houpert (1997), Alfares and Elsharkawy (2003), and Harsha et al. (2003) analyzed the vibration response of a rotor-bearing system by considering the Hertzian contact forces between the rolling elements and races as the sources of nonlinearity. Harsha (2006) and Sinou (2009) ignored the effect of the lubricating oil, and could well simulate the load of the ball bearing using the Hertzian contact theory. While taking into account the oil film, the Hertzian contact alone is not able to describe the nonlinear supporting force comprehensively. Nowadays, the dynamics of bearing is considered to be governed by its structural elements, such as the inner ring, the outer ring, and the rolling elements, as well as the elastohydrodynamic lubricated (EHL) contacts connecting these structural elements, from the study of Wijnant et al. (1999). Liu et al. (2010) studied the lubrication of a rotor-bearing system using computational fluid dynamics and the fluid-structure interaction method. Zhang et al. (2014) investigated the nonlinear dynamic behaviors of a high-speed rotor-ball bearing system under elastohydrodynamic lubrication. Nonato and Cavalca (2014) investigated the elastohydrodynamic film effects on a lateral vibration model of a deep-groove ball bearing using a novel approximation for the elastohydrodynamic contacts by a set of equivalent nonlinear spring and viscous damper. Ma et al. (2014) established a lumped mass model (LMM) of the rotor system considering the gyroscopic effect and studied the effects of two loading conditions (the first- and second-mode imbalance excitations) on the onset of instability and nonlinear responses of the rotor-bearing system. Tian et al. (2012) discussed the effect of the bearing outer clearance on the rotor dynamic characteristics of a realistic turbocharger rotor using the run-up and run-down simulation method. Ma et al. (2013) established an LMM of a rotor-bearing seal system under two loading conditions and found that the nonlinear seal force can mainly restrain the first mode instability, which contributes a lot in the understanding of the rotor system with oil-film bearings. All the above studies show that the investigation of the transient response of the bearing, including the EHL effect, can improve the representation of a real rotor-bearing system.

Besides the supporting force of the ball bearing, excitation due to fault is considered as another important nonlinear source. So far, a number of investigations on the nonlinear dynamic behaviors of rotor-bearing systems have been carried out under the misalignment faults (Prabhakar et al., 2002; Rybczynski, 2006; 2011). Xu and Marangoni (1994) developed a theoretical model of a motor-flexible coupling−rotor system to describe the vibration resulting from misalignment and unbalance. Lee and Lee (1999) derived a dynamic model for a misaligned rotor-bearing system driven through a flexible coupling by treating the reaction loads and deformations at the bearing and coupling elements as misalignment effect. Based on the engagement conditions of gear couplings, Li and Yu (2001) studied the nonlinear coupled lateral torsional vibration of a rotor-bearing-gear coupling system and found that the forces and moments acting on gear couplings due to the initial misalignment are from the inertia forces of the sleeve and the internal damping between the meshing teeth. Al-Hussain and Redmond (2002) investigated the effect of parallel misalignment on the lateral and torsional responses of two rotating shafts. Wan et al. (2012) derived a dynamic model of a multi-disk rotor system with coupling misalignment considering the nonlinear oil film force, which indicated that coupling misalignment can cause 2×, 3×, 4×, and other multiple frequency responses. Ma et al. (2015) established a finite element (FE) model of the overhung rotor system considering the gyroscopic effect and investigated the oil-film instability laws of an overhung rotor system with parallel and angular misalignments in the run-up and run-down processes. As a typical fault of a rotor system, misalignment can cause a great change in the rotor dynamic responses, so finding out the mechanism and the evolution of misalignment is of huge value for vibration control as well as fault diagnosis of high-speed rotational machinery.

With increasing demand for stability, the squeeze film damper (SFD) has been widely used in industrial machinery because it can reduce the vibration amplitude of the rotor and suppress the external force at the same time (Zhu et al., 2002; Chang-Jian and Kuo, 2009; Chang-Jian, 2010). An SFD can be designed through filling the clearance with lubricating oil and introducing a centralizing spring. In an SFD-mounted rotor-bearing system, the journal can be held in its position statically by the fluid supporting pressure. Meanwhile, the critical speed of the rotor system, as well as its stability, can be controlled by adjusting the SFD parameters. Chang-Jian et al. (2010) analyzed the dynamic behavior of a hybrid SFD-mounted gear-bearing system based on the typical unbalance approximation and discussed the rotating speed and damping effects. Inayat-Hussain (2005; 2009) presented the dynamic analysis of a flexible rotor mounted in SFD with and without retaining springs independently, and the results showed that the onset of bifurcation increased with the stiffness of the retainer spring, which provided insights into the effect of the design parameters of SFD on the rotor response. Zhao et al. (1994) investigated the stability as well as the unbalance response of a rotor supported in an eccentric SFD and found that the eccentricity enhanced undesirable nonsynchronous vibrations and decreased the stable working range of the rotor system. Zhou et al. (2013) developed a nonlinear dynamic model of a rotor-ball bearing system with a floating-ring SFD and discussed the effects of supporting stiffness, floating-ring mass, and bearing stiffness in preventing nonsynchronous system response. Consequently, there is no doubt that the application of SFD in rotor system can enhance the operational stability to a large extent. However, the improvement not only depends on the advanced structure design but also relates to the correlation of SFD parameters and the real condition of the rotor system. In other words, it is important to find out a suitable parameter set of SFD to prevent system instability due to fault occurrence as well as to facilitate product design and vibration control.

The aim of this paper is to investigate the influences of the nonlinear oil film force of ball bearing under different lubrication conditions, the centralizing spring stiffness, and the radial clearance of SFD on the stability of a misaligned rotor-ball bearing-gear coupling SFD system. This novel dynamic model takes into account the nonlinear oil film force of the ball bearing, the supporting force of SFD, and the meshing force, as well as the misalignment of gear coupling. Rohde and Li (1980) built a nonlinear oil film force model under short bearing assumption, which is based on the Hertzian contact and the EHL theory. Numerical integrations are used to obtain the solutions, and the analytical results are verified experimentally. Power spectra, bifurcation diagrams, and Pointcaré maps are applied to analyze nonlinear behaviors and unstable processes of the rotor system.

In this paper, the mathematical model of a rotor-ball bearing-gear coupling-SFD system considering the nonlinearity of oil film and misalignment is built first. Then the dynamic responses under various misalignment degrees are measured in the test rig, and the validity of numerical results is confirmed by experimental power spectra. Finally, the main results obtained in this study are discussed, and the effects of the lubricating condition, the stiffness of the centralizing spring, and the radial clearance of SFD on the dynamic responses and the stability of the rotor system under misalignment faults are analyzed.

2 Mathematical model

2.1 Rotor system

In this study, the rotor system is modeled as a two-shaft rotor connected by a gear coupling, with each shaft having a disk. The rotor is supported in the “0-2-1” form, where “0” means there is no support in front of the first disk, “2” means there are two supports between the two disks, and “1” means there is one support in the rear of the second disk. The gear coupling is in the middle of the first and second supports, and SFDs are mounted on the supports at both ends.

To study the nonlinear dynamic behavior under a misalignment fault, a mathematical model of a rotor-bearing system with squeeze film damper and gear coupling, which is depicted in Fig. 1, is established according to the following assumptions:

  1. 1.

    The movements of the rotor in axial and torsional directions are negligible;

  2. 2.

    The journals, the disks, the gear coupling, and the ball bearings are simulated by 11 lumped mass points, and the corresponding points are connected by massless shaft sections of axial stiffness;

  3. 3.

    Each lumped mass point has four degrees of freedom including two translations and two rotations.

  4. 4.

    For the experimental rotor system, power is drawn from the motor by the drive belt, but in this model the motor and drive belt are neglected.

Fig. 1
figure 1

Schematic diagram of the rotor system

Full size image

2.2 Squeeze film damper

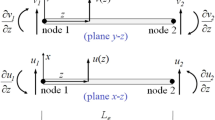
The schematic diagram of the SFD is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of the SFD

Full size image

The instantaneous pressure distribution can be computed from the incompressible Reynolds equation (Cameron and Mc Ettles, 1976):

$${1 \over {R_{\rm{s}}^2}}{\partial \over {\partial \theta }}\left({h_{\rm{s}}^{{3}}{{\partial {p_{\rm{s}}}} \over {\partial \theta }}} \right) + h_{\rm{s}}^{{3}}{{{\partial ^2}{p_{\rm{s}}}} \over {\partial {x^2}}} = - 12{\mu _{\rm{s}}}\Omega {{\partial {h_{\rm{s}}}} \over {\partial \theta }} + 12{\mu _{\rm{s}}}{{\partial {h_{\rm{s}}}} \over {\partial t}},$$
(1)

where Rs is the radius of SFD, ps is the pressure distribution of oil film, μs is the oil viscosity, hs is the oil thickness, x is the journal displacement in the x-direction, Ω is the precession angular velocity of the journal, t is the time, and θ is the angular displacement from the maximum oil thickness position.

According to the SFD structure in this study, the short bearing assumption is used in the axial pressure condition, and there are no seals at the two ends. In this case, the variation of oil film pressure along the circumferential direction is so small compared with that in the axial direction that it can be neglected. Eq. (1) is then transformed into

$${\partial \over {\partial x}}\left({h_{\rm{s}}^{{3}}{{\partial {p_{\rm{s}}}} \over {\partial x}}} \right) = - 12{\mu _{\rm{s}}}\Omega {{\partial {h_{\rm{s}}}} \over {\partial \theta }} + 12{\mu _{\rm{s}}}{{\partial {h_{\rm{s}}}} \over {\partial t}},$$
(2)

where \({h_{\rm{s}}} = {c_{\rm{s}}}(1 + {\varepsilon _{\rm{s}}}\cos \theta)\), \({{\partial {h_{\rm{s}}}} \over {\partial \theta }} = - {c_{\rm{s}}}{\varepsilon _{\rm{s}}}\sin \theta\) and \({{\partial {h_{\rm{s}}}} \over {\partial t}} = {c_{\rm{s}}}{\dot \varepsilon _{\rm{s}}}\cos \theta\). cs is the radial clearance of SFD, and εs is the eccentric ratio of the journal and is given by

$${\varepsilon _{\rm{s}}} = {{\sqrt {{y^2} + {z^2}} } \over {{c_{\rm{s}}}}},$$
(3)

where y and z are the displacements of journal in the y and z directions, respectively.

According to Maday (2002), by using the Sommerfeld transformation, the pressure distribution of oil film can be obtained by

$$\begin{array}{*{20}c} {{p_{\rm{s}}} = {{6{\mu _{\rm{s}}}({\varepsilon _{\rm{s}}}\Omega \sin \theta + {{\dot \varepsilon }_{\rm{s}}}\cos \theta)({x^2} - l_{\rm{s}}^{{2}}{{/}}4)} \over {c_{\rm{s}}^2{{(1 + {\varepsilon _{\rm{s}}}\cos \theta)}^3}}}}\\ { + ({p_{{\rm{s}},2}} - {p_{{\rm{s}},1}}){x \over {{l_{\rm{s}}}}} + {1 \over 2}({p_{{\rm{s}},2}} + {p_{{\rm{s}},1}}),} \end{array}$$
(4)

where ps,1 and ps,2 are the SFD boundary pressures, and ls is the land length of SFD.

According to the Reynolds boundary condition, the squeeze film force can be calculated by integrating the pressure distribution along the circumferential and axial directions, expressed as

$$\left\{ {\begin{array}{*{20}c} {{F_{{\rm{s}},y}} = - {{{\mu _{\rm{s}}}{R_{\rm{s}}}l_{\rm{s}}^{{3}}} \over {c_{\rm{s}}^{{2}}\sqrt {{y^2} + {z^2}} }}[y({{\dot \varepsilon }_{\rm{s}}}{I_1} + \varepsilon \Omega {I_2}) - z({{\dot \varepsilon }_{\rm{s}}}{I_2} + {\varepsilon _{\rm{s}}}\Omega {I_3})],}\\ {{F_{{\rm{s}},z}} = - {{{\mu _{\rm{s}}}{R_{\rm{s}}}l_{\rm{s}}^{{3}}} \over {c_{\rm{s}}^{{2}}\sqrt {{y^2} + {z^2}} }}[z({{\dot \varepsilon }_{\rm{s}}}{I_1} + \varepsilon \Omega {I_2}) + y({{\dot \varepsilon }_{\rm{s}}}{I_2} + {\varepsilon _{\rm{s}}}\Omega {I_3})],} \end{array}} \right.$$
(5)

where Fs,y and Fs,z are the supporting forces of the SFD in the y and z directions, respectively, \({I_1} = \int\nolimits_{{\theta _1}}^{{\theta _2}} {{{{{\cos }^2}\theta } \over {{{(1 + {\varepsilon _{\rm{s}}}\cos \theta)}^3}}}{\rm{d}}\theta }\), \({I_2} = \int\nolimits_{{\theta _1}}^{{\theta _2}} {{{\sin \theta \cos \theta } \over {{{(1 + {\varepsilon _{\rm{s}}}\cos \theta)}^3}}}{\rm{d}}\theta}\) and \({I_3} = \int\nolimits_{{\theta _1}}^{{\theta _2}} {{{{{\sin }^2}\theta } \over {{{(1 + {\varepsilon _{\rm{s}}}\cos \theta)}^3}}}{\rm{d}}\theta }\).

2.3 Gear coupling

In the gear coupling, the meshing in the male and female couplings is asymmetric (Fig. 3): the gear teeth of the two half-couplings mesh tightly in the right parts and loosely in the left parts. Consequently, the meshing distance of every tooth is changing. The meshing force in the gear coupling includes two parts: (a) the meshing force caused by torque and (b) the meshing force caused by vibration.

Fig. 3
figure 3

Schematic diagram of the gear coupling

Full size image

2.3.1 Meshing force caused by torque

When the gear teeth are meshing tightly to transmit a large torque, deformation of gear teeth is inevitable and the following meshing force is related to the deformation amount, meshing distance, and meshing rigidity. From Zhao et al. (2008), the torque-induced meshing force is given by

$$F_{\rm{g}}^{\rm{T}} = {\phi _{\rm{g}}}{l_{\rm{g}}}{k_{\rm{g}}},$$
(6)

where \({F_{\rm{g}}}^{\rm{T}}\) is the meshing force due to torque, ϕg is the deformation angle of the gear tooth, lg is the equivalent meshing distance of the gear tooth, and kg is the meshing rigidity of the gear tooth. The values of ϕg of all gear teeth are the same when the coupling is driven by a static torque.

2.3.2 Meshing force caused by vibration

When the torque is getting transmitted by gear teeth, a relative movement between the two meshing teeth takes place, which is induced by the system vibration at the same time. As a result, the displacement of meshing nodes causes a deformation of each tooth so that another meshing force is produced, which is expressed as

$$F_{\rm{g}}^{\rm{D}} = {e_{\rm{g}}}{k_{\rm{g}}}\sin {\varphi _{\rm{g}}},$$
(7)

where \({F_{\rm{g}}}^{\rm{D}}\) is the meshing force caused by vibration, φg is the position angle of the gear tooth, and eg is the misalignment of gear coupling.

If there is no torque to transmit, the meshing force will be zero regardless of the vibration displacement, and the meshing force will not be negative. Accordingly, the total meshing force of the ith tooth can be obtained as

$${F_{{\rm{g}},i}} = \left\{ {\begin{array}{*{20}c} {({\phi _{{\rm{g}},i}}{l_{{\rm{g}},i}} + {e_{\rm{g}}}\sin {\varphi _{{\rm{g}},i}}){k_{{\rm{g}},i}},} & {{\phi _{{\rm{g}},i}}{l_{{\rm{g}},i}} + {e_{\rm{g}}}\sin {\varphi _{{\rm{g}},i}} > 0,}\\ {0,\quad \quad \quad \quad \quad \quad \quad \quad } & {{\phi _{{\rm{g}},i}}{l_{{\rm{g}},i}} + {e_{\rm{g}}}\sin {\varphi _{{\rm{g}},i}} \leq 0{.}} \end{array}} \right.$$
(8)

Then, the reactions of meshing force in the y and z directions of the rotor system are as follows (n is the number of gears):

$$\left\{ {\begin{array}{*{20}c} {{F_{{\rm{g}},y}} = \sum\limits_{i = 1}^n {({\phi _{{\rm{g}},i}}{l_{{\rm{g}},i}} + {e_{\rm{g}}}\sin {\varphi _{{\rm{g}},i}}){k_{{\rm{g}},i}}\sin \theta,} }\\ {{F_{{\rm{g}},z}} = \sum\limits_{i = 1}^n {({\phi _{{\rm{g}},i}}{l_{{\rm{g}},i}} + {e_{\rm{g}}}\sin {\varphi _{{\rm{g}},i}}){k_{{\rm{g}},i}}\cos \theta {.}} } \end{array}} \right.$$
(9)

2.4 Ball bearing

In the ball bearing model, as shown in Fig. 4, the inner race is connected with the journal, and the outer race is connected with the SFD.

Fig. 4
figure 4

Schematic diagram of the ball bearing

Full size image

Generally, the Hertzian contact theory is widely used in the analysis of contact stress and deformation between balls and races of the ball bearing. Considering the centrifugal force of ball due to the high rotating speed, the deformation of ball in the radial direction is given as (Harris, 1991)

$$\begin{array}{*{20}c} {{\delta _{{\rm{b,}}j}} = {\delta _{\rm{b}}} \cdot \cos (j{\varphi _{\rm{b}}}) - {\mu _{\rm{b}}}\quad \quad \quad \quad \quad \quad \quad \quad}\\ { = \left[ {{k_{{\rm{c}},j}^{\rm{i}}}^{-{2 \over 3}} + {k_{{\rm{c}},j}^{\rm{o}}}^{-{2 \over 3}}{{\left({1 + {{{F_{{\rm{b,c}}}}} \over {Q_{{\rm{b}},j}^{\rm{i}}}}} \right)}^{{2 \over 3}}}} \right]{Q_{{\rm{b}},j}^{\rm{i}}}^{2 \over 3},} \end{array}$$
(10)

where δb is the deformation of the ball bearing, φb is the position angle from the y-axis, μb is the radial clearance of the ball bearing, Qb is the load of ball, kc is the contact deformation coefficient of the ball, and Fb,c is the centrifugal force of the ball. “j” refers to the ball number, and the superscripts “i” and “o” refer to the inner and outer races, respectively.

Then, according to the Hertzian contact theory, the contact stiffness of the ball bearing is expressed as (Harris, 1991)

$$\begin{array}{*{20}c} {k_{{\rm{b}},j}^{\rm{H}} = {{\partial Q_{{\rm{b}},j}^{\rm{i}}} \over {\partial {\delta _{{\rm{b}},j}}}} = {3 \over 2}{Q_{{\rm{b}},j}^{\rm{i}}}^{1 \over 3}\left[ {{k_{{\rm{c}},j}^{\rm{i}}}^{-{2 \over 3}} + k_{{\rm{c}}, j}^{\rm{o}}{{\left({1 + {{{F_{{\rm{b}},{\rm{c}}}}} \over {Q_{{\rm{b}},j}^{\rm{i}}}}} \right)}^{{2 \over 3}}}} \right.}\\ {{{\left. { - {k_{{\rm{c}},j}^{\rm{o}}}^{-{2 \over 3}}{{\left({1 + {{{F_{{\rm{b}},{\rm{c}}}}} \over {Q_{{\rm{b}},j}^{\rm{i}}}}} \right)}^{ - {1 \over 3}}}{Q_{{\rm{b}},j}^{\rm{i}}}}^{-1} \right]}^{ - 1}},} \end{array}$$
(11)

where kb is the contact stiffness of ball bearing, and the superscript “H” refers to the Hertzian contact theory.

Although the Hertzian contact theory has been used as one of the main methods in ball bearing analysis, the assumptions of simplification ignore the lubrication effects of the oil film between the balls and races on the dynamic characteristics of ball bearing (Harsha, 2006). Furthermore, considering the Reynolds lubrication theory and Hertzian contact theory comprehensively, the EHL becomes a normal condition in the ball-race contact pair (Rahnejat and Gohar, 1985). In the EHL condition, the oil film pressure is close to Hertzian contact stress in most of the contact zone, but is quite different at the entering and departing ends.

In the case of the point-contact problem, the oil film thickness equation proposed by Hamrock and Dowson (1977) is considered to be suitable for the ball bearing:

$${H_{\rm{b}}} = 2{.}69{U^{0{.}67}}{G^{0{.}53}}{W^{ - 0{.}067}}[1 - 0{.}61\exp (- 0{.}73{e_{\rm{b}}})],$$
(12)

where \(U = {\mu _{\rm{b}}}u/(2E\prime {R_{\rm{b}}})\) is a non-dimensional velocity parameter, G=αE′ is a non-dimensional material parameter, \(W = {Q_{\rm{b}}}/(E\prime R_{\rm{b}}^2)\) is a non-dimensional load parameter, eb is the ellipticity of ball, μb is the dynamic viscosity, u is the linear velocity, E‵= E/(1−ν2) is the equivalent Young’s modulus, ν is Poisson’s ratio, and α is the pressure-viscosity coefficient. Rb is the radius of curvature and can be calculated separately for the inner race and the outer race:

$$\left\{ {\begin{array}{*{20}c} {R_{\rm{b}}^{\rm{i}} = {{{D_{\rm{b}}}} \over 2}\left({1 - {{{D_{\rm{b}}}\cos \beta } \over {{d_{\rm{m}}}}}} \right),}\\ {R_{\rm{b}}^{\rm{o}} = {{{D_{\rm{b}}}} \over 2}\left({1 + {{{D_{\rm{b}}}\cos \beta } \over {{d_{\rm{m}}}}}} \right),} \end{array}} \right.$$
(13)

where Db is the diameter of ball, dm is the diameter of bearing, and β is the contact angle.

Then the oil film thickness, the oil film stiffness, and the radial load of ball under EHL condition can be calculated successively as follows:

$${h_{\rm{b}}} = {H_{\rm{b}}}{R_{\rm{b}}},$$
(14)
$$k_{\rm{b}}^{\rm{E}} = {{\partial {Q_{\rm{b}}}} \over {\partial {h_{\rm{b}}}}},$$
(15)
$${Q_{\rm{b}}} = k_{\rm{b}}^{\rm{E}}{\delta _{\rm{b}}},$$
(16)

where the oil film stiffness of the ball bearing is thought as a series of connections of the inner race and the outer race.

Based on the deformation compatibility condition, the radial load of the ball bearing can be obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {{Q_{\rm{b}}} = Q_{{0}}^{\rm{i}} + 2\sum\limits_{j = 1}^m {Q_{{\rm{b}},j}^{\rm{i}}\cos (j{\varphi _{\rm{b}}}),\quad \quad \quad m{\varphi _{\rm{b}}} < 180^\circ,} }\\ {{Q_{\rm{b}}} = Q_{{0}}^{\rm{i}} + 2\sum\limits_{j = 1}^m {Q_{{\rm{b}},j}^{\rm{i}}\cos (j{\varphi _{\rm{b}}})} + Q_n^{\rm{i}},\;\;\;\;m{\varphi _{\rm{b}}} = 180^\circ,} \end{array}} \right.$$
(17)

where m is the number of balls. Then the supporting forces of ball bearing in the y and z directions are given as

$$\left\{ {\begin{array}{*{20}c} {{F_{{\rm{b}},y}} = - {Q_{\rm{b}}}{y \over {{\delta _{\rm{b}}}}},}\\ {{F_{{\rm{b}},z}} = - {Q_{\rm{b}}}{z \over {{\delta _{\rm{b}}}}},} \end{array}} \right.$$
(18)

where Fb,y and Fb,z are supported forces of ball bearing in the y and z directions, respectively.

2.5 Misalignment fault

In this study, the misalignment takes place at the gear coupling and influences the rotor system by producing two types of force: the meshing force and the misalignment force. The meshing force of gear coupling has been discussed, and the misalignment forces in the y and z directions of the rotor system are expressed by Prabhakar et al. (2001):

$$\left\{ {\begin{array}{*{20}c} {{F_{{\rm{m}},y}} = {M_{\rm{g}}}{{{{\ddot Y}_{{\rm{r}}3}}} \over 2} = - 2{M_{\rm{g}}}{e_{\rm{g}}}{\omega ^2}\cos (2\omega t - \psi),}\\ {{F_{{\rm{m}},z}} = {M_{\rm{g}}}{{{{\ddot Z}_{{\rm{r}}3}}} \over 2} = - 2{M_{\rm{g}}}{e_{\rm{g}}}{\omega ^2}\sin (2\omega t - \psi),} \end{array}} \right.$$
(19)

where Mg is the mass of gear set, Fm,y and Fm,z are the misalignment forces in the y and z directions, respectively, ω is the rotating speed, and ψ is the initial phase angle.

2.6 Equations of motion

The system non-dimensional differential equations of motion rotor system are obtained as follows:

$$\begin{array}{*{20}c} {{{\ddot Y}_{{\rm{d}}1}} = - {{{C_{\rm{d}}}} \over {\omega {M_{{\rm{d}}1}}}}{{\dot Y}_{{\rm{d}}1}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{d}}1}}}}({Y_{{\rm{d}}1}} - {Y_{{\rm{r}}1}}) + {{{e_{{\rm{d}}1}}} \over {{\mu _{\rm{b}}}}}\sin \tau - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},}\\ {{{\ddot Z}_{{\rm{d}}1}} = - {{{C_{\rm{d}}}} \over {\omega {M_{{\rm{d}}1}}}}{{\dot Z}_{{\rm{d}}1}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{d}}1}}}}({Z_{{\rm{d}}1}} - {Z_{{\rm{r}}1}}) + {{{e_{{\rm{d}}1}}} \over {{\mu _{\rm{b}}}}}\cos \tau, \quad \quad \;}\\ {{{\ddot Y}_{{\rm{d}}2}} = - {{{C_{\rm{d}}}} \over {\omega {M_{{\rm{d}}2}}}}{{\dot Y}_{{\rm{d}}2}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{d}}2}}}}(2{Y_{{\rm{d}}2}} - {Y_{{\rm{r}}6}} - {Y_{{\rm{r}}7}})\quad \quad \quad \quad \;\;}\\ { + {{{e_{{\rm{d}}2}}} \over {{\mu _{\rm{b}}}}}\sin \tau - {{{e_{{\rm{d}}2}}} \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad }\\ {{{\ddot Z}_{{\rm{d}}2}} = - {{{C_{\rm{d}}}} \over {\omega {M_{{\rm{d}}2}}}}{{\dot Z}_{{\rm{d}}2}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{d}}2}}}}(2{Z_{{\rm{d}}2}} - {Z_{{\rm{r}}6}} - {Z_{{\rm{r}}7}})\quad \quad \quad \;\;}\\ { + {{{e_{{\rm{d}}2}}} \over {{\mu _{\rm{b}}}}}\cos \tau, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;}\\ {{{\ddot Y}_{{\rm{s}}1}} = - {{{K_{\rm{a}}}} \over {{\omega ^2}{M_{{\rm{s}}1}}}}{Y_{{\rm{s}}1}} + {{{F_{{\rm{s}},y{{1}}}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}1}}}} - {{{F_{{\rm{b}},y{{1}}}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}1}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad } \\ {{{\ddot Z}_{{\rm{s}}1}} = - {{{K_{\rm{a}}}} \over {{\omega ^2}{M_{{\rm{s}}1}}}}{Z_{{\rm{b}}1}} + {{{F_{{\rm{s}},z1}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}1}}}} - {{{F_{{\rm{b}},z1}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}1}}}},\quad \quad \quad \quad \;\;}\\ {{{\ddot Y}_{{\rm{s}}2}} = - {{{K_{\rm{a}}}} \over {{\omega ^2}{M_{{\rm{s}}2}}}}{Y_{{\rm{s}}2}} + {{{F_{{\rm{s}},y2}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}2}}}} - {{{F_{{\rm{b}},y3}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}2}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \;}\\ {{{\ddot Z}_{{\rm{s}}2}} = - {{{K_{\rm{a}}}} \over {{\omega ^2}{M_{{\rm{s}}2}}}}{Z_{{\rm{s}}2}} + {{{F_{{\rm{s}},z2}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}2}}}} - {{{F_{{\rm{b}},z3}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{s}}2}}}},\quad \quad \quad \quad \;\;}\\ {{{\ddot Y}_{{\rm{r}}1}} = - {{{C_{\rm{b}}}} \over {\omega {M_{{\rm{r}}1}}}}{{\dot Y}_{{\rm{r}}1}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}1}}}}(2{Y_{{\rm{r}}1}} - {Y_{{\rm{r}}2}} - {Y_{{\rm{d}}1}})\quad \quad \quad \quad }\\ { + {{{F_{{\rm{b}},y1}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}1}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \quad \quad \quad }\\ {{{\ddot Z}_{{\rm{r}}1}} = - {{{C_{\rm{b}}}} \over {\omega {M_{{\rm{r}}1}}}}{{\dot Z}_{{\rm{r}}1}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}1}}}}(2{Z_{{\rm{r}}1}} - {Z_{{\rm{r}}2}} - {Z_{{\rm{d}}1}}) + {{{F_{{\rm{b}},z1}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}1}}}},}\\ {{{\ddot Y}_{{\rm{r}}2}} = - {{{C_{\rm{b}}}} \over {\omega {M_{{\rm{r}}2}}}}{{\dot Y}_{{\rm{r}}2}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}2}}}}(2{Y_{{\rm{r}}2}} - {Y_{{\rm{r}}1}} - {Y_{{\rm{r}}3}}) + {{{F_{{\rm{b}},y2}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}}\;\;}\\ { + {{{F_{{\rm{m}},y}}} \over {{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}} + {{{F_{{\rm{g}},y}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \;}\\ {{{\ddot Z}_{{\rm{r}}2}} = - {{{C_{\rm{b}}}} \over {\omega {M_{{\rm{r}}2}}}}{{\dot Z}_{{\rm{r}}2}} - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}2}}}}(2{Z_{{\rm{r}}2}} - {Z_{{\rm{r}}1}} - {Z_{{\rm{r}}3}}) + {{{F_{{\rm{b}},z2}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}}}\\ { + {{{F_{m,z}}} \over {{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}} + {{{F_{{\rm{g}},z}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}2}}}},\quad \quad \quad \quad \;\quad \quad \;\;}\\ {{{\ddot Y}_{{\rm{r}}3}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}3}}}}(2{Y_{{\rm{r}}3}} - {Y_{{\rm{r}}2}} - {Y_{{\rm{r}}4}}) - {{{F_{{\rm{g}},y}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}3}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad }\\ {{{\ddot Z}_{{\rm{r}}3}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}3}}}}(2{Z_{{\rm{r}}3}} - {Z_{{\rm{r}}2}} - {Z_{{\rm{r}}4}}) - {{{F_{{\rm{g}},z}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}3}}}},\quad \quad \quad \;}\\ {{{\ddot Y}_{{\rm{r}}4}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}4}}}}(2{Y_{{\rm{r}}4}} - {Y_{{\rm{r}}3}} - {Y_{{\rm{r}}5}}) - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \;\;}\\ {{{\ddot Z}_{{\rm{r}}4}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}4}}}}(2{Z_{{\rm{r}}4}} - {Z_{{\rm{r}}3}} - {Z_{{\rm{r}}5}}),\quad \quad \quad \quad \quad \quad \;\;\;}\\ {{{\ddot Y}_{{\rm{r}}5}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}5}}}}(2{Y_{{\rm{r}}5}} - {Y_{{\rm{r}}4}} - {Y_{{\rm{r}}6}}) - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \;\;\;}\\ {{{\ddot Z}_{{\rm{r}}5}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}5}}}}(2{Z_{{\rm{r}}5}} - {Z_{{\rm{r}}4}} - {Z_{{\rm{r}}6}}),\quad \quad \quad \quad \quad \quad \quad }\\ {{{\ddot Y}_{{\rm{r}}6}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}6}}}}(2{Y_{{\rm{r}}6}} - {Y_{{\rm{r}}5}} - {Y_{{\rm{d}}2}}) - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \quad \;\;\;}\\ {{{\ddot Z}_{{\rm{r}}6}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}6}}}}(2{Z_{{\rm{r}}6}} - {Z_{{\rm{r}}5}} - {Z_{{\rm{d}}2}}),\quad \quad \quad \quad \quad \quad \quad }\\ {{{\ddot Y}_{{\rm{r}}7}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}7}}}}({Y_{{\rm{r}}7}} - {Y_{{\rm{d}}2}}) + {{{F_{{\rm{b}},y3}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}7}}}} - {g \over {{\omega ^2}{\mu _{\rm{b}}}}},\quad \quad \quad \;}\\ {{{\ddot Z}_{{\rm{r}}7}} = - {{{K_{\rm{r}}}} \over {{\omega ^2}{M_{{\rm{r}}7}}}}({Z_{{\rm{r}}7}} - {Z_{{\rm{d}}2}}) + {{{F_{{\rm{b}},z3}}} \over {{\omega ^2}{\mu _{\rm{b}}}{M_{{\rm{r}}7}}}},\quad \quad \quad \quad \quad \;} \end{array}$$
(20)

where g represents the gravitational acceleration. The non-dimensional time τ=ωt, non-dimensional displacements Y=y/μb and Z=z/μb, non-dimensional velocities and and non-dimensional accelerations and are defined.

2.7 Numerical method

In this paper, the differential equations of motion are solved using the fourth-order Runge-Kutta method, and the time step in the iterative procedure is set as ∆t1×10−5 s. The time-varying data corresponding to the first 500 periods generated by numerical integration are deliberately excluded to discard the transient solutions. The bifurcation diagram, Pointcaré map, and power spectrum are obtained to analyze the system dynamic behavior. In order to identify the onset of bifurcation, the Floquet multiplier is calculated and its position on the complex plane is used as the stability criterion of the rotor system.

3 Model verification

3.1 Experimental rotor system

In this study, we built a test facility to simulate a compressor rotor system. Fig. 5 shows the overall test setup and the details of the gear coupling. As discussed in Fig. 1, system components in the test rig are the same. The AC motor is used to drive the rotor and the rotating speed is controlled by a programmable logic controller. The misalignment is produced and controlled by adjusting the relative height of the two shafts. Four levels of misalignment fault are simulated and each single measurement is repeated twice at least to confirm the validity.

Fig. 5
figure 5

Experimental rotor system

Full size image

3.2 Verification of analytical results

Experimental power spectra of the rotor system under four misalignment levels (0.7×10−4, 1.4×10−4, 2.1×10−4, and 2.8×10−4 m) are obtained to verify the correctness of the numerical simulation results in Fig. 6. The amplitude of frequency in the figure can be transformed into Table 1. The numerical simulations are carried out under two lubrication conditions: the Hertzian contact condition and the EHL condition. It can be seen that the experimental response at 2×, 3×, 4×, and 5× the fundamental frequency is generated by the misalignment fault of gear coupling (Wan et al., 2012), and this fault feature can be found in both numerical simulations under different lubrication conditions. In addition, both the experimental and numerical spectra show the same trend, indicating that the response amplitude increases with the increase of the misalignment level. Roughly, it can be concluded that the numerical results agree with the experimental data in most of the frequency region for different values of misalignment, especially at even multiples of the fundamental frequency. However, the comparison illustrates that the computed response amplitudes considering the lubrication effect of the oil film are lower than those numerical results under Hertzian condition, and much closer to the test data. Accordingly, it means that the effect of oil film on the supported force of the ball bearing cannot be overlooked, and the numerical results considering EHL condition are more accurate. Consequently, all kinds of dynamic behavior of rotor system may change under different lubrication conditions.

Fig. 6
figure 6

Comparison between experimental and numerical results

a) e g =0.7×10−4 m; (b) e g =1.4×10−4 m; (c) e g =2.1×10−4 m; (d) e g =2.8×10−4 m

Full size image
Table 1 Rotor system vibration amplitudes with different misalignment levels on experimental and numerical
Full size table

4 Results and discussion

4.1 Effects of lubrication condition

Fig. 7 (p.623) shows the bifurcation diagrams with rotating speed 1200–2400 rad/s as the bifurcation parameter under three conditions: (a) the rotor without misalignment under Hertzian condition, (b) the misaligned rotor under Hertzian condition, and (c) the misaligned rotor under EHL condition. Fig. 8 (p.623) shows the corresponding Pointcaré maps. The following dynamic phenomena can be observed:

  1. 1.

    For the normal rotor system under Hertzian condition, the dynamic orbit shows period-one motion when ω≤1800 rad/s and loses its regularity in a small range of ω∈[1801, 1817] rad/s, then returns to period-one motion in the range of ω∈[1818, 1854] rad/s. After that, the orbit becomes quasi-periodic or chaotic for another short period of ω∈[1855, 1870] rad/s, and then returns to period-one motion again in the range of ω∈[1871, 1983] rad/s. However, the orbit performs period-doubling motion in a short duration of ω∈[1984, 2003] rad/s. Finally, the orbit returns to and persists in period-one motion when ω≤2004 rad/s.

  2. 2.

    For the misaligned rotor system under Hertzian condition, the dynamic orbit exhibits period-one motion when ω≤1848 rad/s. The orbit becomes period-two motion in the range of ω∈[1849, 1892] rad/s, then performs quasi-periodic or chaotic motion in the range of ω∈[1893, 2200] rad/s. Finally, the orbit returns to and persists in period-one motion when ω>2200 rad/s.

  3. 3.

    For the misaligned rotor system under EHL condition, the dynamic orbit exhibits period-one motion when ω≤1900 rad/s. The orbit becomes period-two motion in the range of ω∈[1901, 1968] rad/s, and then performs quasi-periodic or chaotic motion in the range of ω∈[1969, 2224] rad/s. Finally, the orbit returns to and persists in period-one motion when ω≥2225 rad/s.

Fig. 7
figure 7

Bifurcation diagrams of the rotor system

(a) Normal rotor under Hertzian condition; (b) Misaligned rotor under Hertzian condition; (c) Misaligned rotor under EHL condition

Full size image
Fig. 8
figure 8

Pointcaré maps of the rotor system

(a) Normal rotor under Hertzian condition; (b) Misaligned rotor under Hertzian condition; (c) Misaligned rotor under EHL condition

Full size image

From the comparisons in Figs. 7 and 8, it can be observed that the stability of the rotor system is decreased because of the misalignment fault; in addition, the lubricating condition also affects the dynamic behavior of the rotor system. Under the EHL condition, the onset of bifurcation is delayed by 52 rad/s (from 1848 rad/s to 1900 rad/s) compared with that under Hertzian condition, and the unstable region of rotating speed is shortened.

4.2 Effects of centralizing spring stiffness

Centralizing spring stiffness is one of the key parameters affecting the dynamic characteristics of the rotor system. Fig. 9 shows the effect of the centralizing spring stiffness on the natural frequency of the rotor system. The first-order critical rotating speeds are 860 rad/s (15.14 in non-dimensional amplitude) for kc8×106 N/m, 930 rad/s (18.58 in non-dimensional amplitude) for kc2×107 N/m, and 1160 rad/s (29.03 in non-dimensional amplitude) for kc9×109 N/m. The results illustrate that increasing the centralizing spring stiffness raises the first-order critical speed of the rotor system as well as the vibration amplitude. However, this improvement is limited and the first-order modal frequency can be increased up to around 1200 rad/s. Accordingly, it gives an option to avoid resonance under common operating conditions by adjusting the centralizing spring stiffness in the rotor system design.

Fig. 9
figure 9

Natural frequencies of the rotor system with different centralizing spring stiffness values

Full size image

Under the EHL condition, bifurcation diagram and Pointcaré maps are shown in Fig. 10, which shows the following dynamic phenomena:

  1. 1.

    When the centralizing spring stiffness is lower than 3.1×107 N/m, the dynamic orbit performs period-one motion, and a jump phenomenon appears at kc2.6×107 N/m. In the range of kc∈[3.1, 6.3] ×107 N/m, the orbit loses its regularity and becomes quasi-periodic or chaotic. Then, the orbit returns to period-one motion in a long range of kc∈[0.64, 2.35]×108 N/m. With continuously increasing centralizing spring stiffness, the orbit becomes irregular (quasi-periodic or chaotic).

  2. 2.

    Pointcaré maps give more details of the dynamic behavior of the rotor system. It can be seen that the dynamic orbit shows strong nonlinear characteristics in the range of kc∈[3.1, 6.3]×107 N/m, in particular, period-five motion when kc3.5×107 N/m, then chaotic motion when kc is increased to 4.5 ×107 N/m, after that period-three motion when kc is further increased to 5.5×107 N/m. After a long range of period-one motion when kc∈[0.64, 2.35]×108 N/m, the dynamic orbit changes into quasi-periodic or chaotic.

Fig. 10
figure 10

Dynamic behavior of the rotor system under EHL condition using centralizing spring as bifurcation parameter: (a) bifurcation diagram; (b) Pointcaré maps

Full size image

It can be observed that the centralizing spring stiffness strongly affects the stability of the rotor system and the effect is complicated. In the case of 0.7×10−4 m misalignment, the dynamic orbit loses its regularity in two ranges of kc∈[3.1, 6.3]×107 N/m and kc2.35×108 N/m, which means that a too low or too high centralizing spring stiffness cannot help the rotor system maintain its stability. In this case, the parameter range of kc∈[0.7, 2.0]×108 N/m is suggested to keep the rotor system operating under a comparatively steady state.

4.3 Effects of SFD radial clearance

By introducing the SFD into the rotor system, the trajectory of the rotor system is significantly changed (Fig. 11). Compared with the rotor system without SFD (Fig. 7c), the bifurcation onset of the rotor system with SFD mounted is delayed from 1900 rad/s to 1938 rad/s. Furthermore, the end of the unsteady motion is shifted to a lower rotating speed from 2224 rad/s to 2070 rad/s. According to the Pointcaré maps shown in Fig. 11b, the dynamic orbit shows period-two motion in the range of ω∈[1938, 1996] rad/s and quasi-periodic motion during the range of ω∈[1997, 2070] rad/s. The variations of the dynamic behavior of the rotor system with and without SFD are similar, but it is noteworthy that the steady motion period is extended by introducing the squeeze film force.

Fig. 11
figure 11

Dynamic behavior of the misaligned rotor system with SFD mounted under EHL condition when e g =0.7×10−4 m, k c =8×106 N/m, and c s =5×10−5 m: (a) bifurcation diagram; (b) Pointcaré maps

Full size image

The radial clearance of SFD is an important parameter influencing the dynamic behavior of the rotor system. Fig. 12 shows the spectrum cascade of the rotor system using radial clearance as variable under given rotating speed (ω=2000 rad/s) and misalignment (eg=2.1×10−4 m). The corresponding vibration amplitudes under different frequency ratios are shown in Table 2. It can be seen that the response amplitude of the rotor system at the fundamental frequency slowly reduces with the increase in the radial clearance of SFD. However, at 2× the fundamental frequency, which is the fault characteristic of misalignment, the vibration amplitude increases when the radial clearance of SFD increases from 4×10−5 m up to 5×10−5 m, and then slowly decreases when the radial clearance of SFD continues to increase. Meanwhile, the vibration amplitude at the 3× fundamental frequency shows up and becomes increasingly notable with increase in the radial clearance of SFD. In addition, some dividing frequency components arise when the radial clearance of SFD is 4×10−5 m, and they disappear when the radial clearance of SFD is increased.

Fig. 12
figure 12

Spectrum cascade of the rotor system under ω =2000 rad/s and e g =2.1×10 −4 m

Full size image
Table 2 Rotor system vibration amplitudes with different radial clearances of SFD
Full size table

Moreover, the bifurcation diagram of the rotor system by using the radial clearance of SFD as the bifurcation parameter is given in Fig. 13a, and the corresponding Pointcaré maps are shown in Fig. 13b. It can be seen that the dynamic orbit shows period-one motion when cs<1.05×10−4 m. With increasing radial clearance of SFD, the dynamic orbit changes into chaotic motion in the range of cs∈[1.05, 1.40] ×10−4 m. When the radial clearance of SFD is further increased, the orbit returns to period-one motion in the range of cs∈[1.41, 1.77]×10−4 m, and then becomes period-two motion in the range of cs∈[1.78, 2.13]×10−4 m. After that, the dynamic orbit loses its regularity again when cs>2.14×10−4 m. Consequently, two ranges of the radial clearance of SFD are preferred to reduce the vibration of the rotor system, namely cs<1.05×10−4 m and 1.40×10−4 m<cs≤1.77×10−4 m.

Fig. 13
figure 13

Dynamic behavior of the rotor system under EHL condition using SFD radial clearance as bifurcation parameter: (a) bifurcation diagram; (b) Pointcaré maps

Full size image

Furthermore, the bifurcation diagrams and Pointcaré maps of the rotor system under different radial clearance of SFD are depicted in Figs. 14 and 15, respectively, using misalignment as bifurcation parameter. As shown in Figs. 14 and 15, four cases (cs3×10−5, 5×10−5, 7×10−5, and 1.5×10−4 m) are taken as examples to illustrate the effect of radial clearance of SFD on the stability of the misaligned rotor system. The four values of the radial clearance of SFD are picked from the ranges of cs1.05×10−4 m and 1.40×10−4 m<cs≤1.77×10−4 m, which are proven to be two stable periods. The aim of the comparison is to find out the influence of radial clearance of SFD on the stability of rotor system.

Fig. 14
figure 14

Bifurcation diagrams of the rotor system varying with misalignment degree under different SFD radial clearance: (a) cs=3×10−5 m; (b) c s =5×10−5 m; (c) c s =7×10−5 m; (d) c s =1.5×10−4 m

Full size image

From the bifurcation diagrams shown in Fig. 14, it can be seen that the variation of the radial clearance of SFD strongly affects the dynamic behavior of the rotor system. The results are given as follows:

  1. 1.

    In the case of cs3×10−5 m, the orbit shows period-one motion when eg<0.49×10−4 m, and then becomes period-two motion in the range of eg∈[0.49, 0.93]×10−4 m (Fig. 15a). After that, as shown in Fig. 15b, the orbit returns to period-one motion again in the range of eg∈[0.93, 1.67]×10−4 m. Finally, the orbit loses its regularity when eg>1.67×10−4 m (Figs. 15c–15f).

  2. 2.

    In the case of cs5×10−5 m, the period-one motion is the main movement form of the rotor system. The orbit becomes period-three motion in the short range of eg∈[2.5, 2.76]×10−4 m (Fig. 15d) and quasi-periodic or chaotic motion in another short range of eg∈[2.77, 2.96]×10−4 m (Fig. 15e). Besides, as shown in Figs. 15a–15c and 15f, the dynamic behavior of the rotor system is regular and stable.

  3. 3.

    In the case of cs7×10−5 m, the rotor orbit shows period-one motion when eg<2.14×10−4 m, which is shown in Fig. 15a. Then the orbit becomes period-two motion (Figs. 15b and 15c) and period-four motion (Fig. 15d) in two small ranges of eg∈[2.14, 2.50]×10−4 m and eg∈[2.51, 2.76]×10−4 m, respectively. Afterward, the orbit changes into quasi-periodic or chaotic motion when 2.76×10−4<meg<3.48×10−4 m, as shown in Fig. 15e. However, the orbit shows period-one (Fig. 15f) and period-two motions in two short periods, and finally loses its regularity when eg>3.70×10−4 m.

  4. 4.

    In the case of cs1.5×10−4 m, the orbit shows period-one motion when eg<1.12×10−4 m (Fig. 15a), then changes into period-two motion in a short range of eg∈[1.12, 1.34]×10−4 m (Fig. 15b), and returns to period-one motion when 1.34×10−4 m<eg<1.66 ×10−4 m. After that, the orbit becomes quasi-periodic when 1.66×10−4 m<eg<2.86×10−4 m (Figs. 15c–15e) and turns into chaotic motion when eg>2.86×10−4 m (Fig. 15f).

Fig. 15
figure 15

Pointcaré maps of the rotor system under different misalignment fault degrees(a) eg=0.8×10−4 m; (b) eg=1.3×10−4 m; (c) eg=2.3×10−4 m; (d) eg=2.7×10−4 m; (e) eg=2.8×10−4 m; (f) eg=3.5×10−4 m

Full size image

5 Conclusions

In this paper, the effects of lubrication condition, centralizing spring stiffness, and SFD radial clearance on the stability of a rotor-bearing-gear coupling-SFD system under misalignment fault were investigated. A squeeze film force model of SFD, a meshing force model of gear coupling, and a supported force model of ball bearing were adopted. The stabilities of the rotor system under misalignment fault were discussed under Hertzian condition and considering the lubrication of oil film. The advantage of the model including EHL effect was verified experimentally. Besides, the stabilities including and excluding the SFD effect in the rotor system were studied. Some conclusions drawn from the study can be summarized as follows:

  1. 1.

    For the rotor system with gear coupling misalignment under Hertzian condition, the instability rotating speed range increases from 64 rad/s (excluding the misalignment effect) to 352 rad/s (including the misalignment effect) in total. When misalignment happens, the bifurcation onset delays a little from 1796 rad/s to 1848 rad/s; however, the stable operation range shortens considerably due to the misalignment fault of the gear coupling.

  2. 2.

    For the rotor system under EHL condition with gear coupling misalignment, the fault characteristic in vibration response is completely preserved as compared with the system under Hertzian condition. Moreover, the energy distribution of spectra cascade is described more precisely due to the consideration of the nonlinear oil film force, and more characteristics of fault variation are shown. Besides, the bifurcation onset delays from 1848 rad/s (under Hertzian condition) to 1900 rad/s (under EHL condition) with the misaligned gear coupling, and the instability range of the rotating speed is shortened.

  3. 3.

    For the rotor system with centralizing spring, the first-order critical rotating speed of the rotor system as well as the vibration amplitude of the first mode increases with the increasing stiffness of the centralizing spring. Neither an excessively high nor a low stiffness of the centralizing spring is helpful for the vibration control of the rotor system. In the case of 0.7×10−4 m misalignment, the stiffness range is suggested to be [0.7, 2.0]×108 N/m, which can keep the rotor system operating under a relatively long stable state.

  4. 4.

    For the rotor system with SFD under misalignment fault, the dynamic behavior is strongly influenced by the radial clearance and the misalignment comprehensively. Overall, the introduction of the squeeze film increases the system stability but the effect of stability improving depends on the correlation between the radial clearance of SFD and the misalignment of gear coupling. According to the comparison of various radial clearance values, the case with clearance of 5×10−5 m is able to enhance the stable operating range when the misalignment varies within [0.2, 4.0]×10−4 m.