Introduction

The commercialization of lithium (Li)-ion batteries, in which Li ions are inserted into the anode during charging of the cell and are then released to the cathode upon discharge, was a technological breakthrough that enabled wider availability of portable/wireless electronics such as mobile phones due to its high energy density. The far-reaching impacts of the technology have been recognized by, among others, the 2019 Nobel Prize in Chemistry, which was awarded to John B. Goodenough, M. Stanley Whittingham, and Akira Yoshino.1

Li-ion rechargeable batteries are complex systems involving multiple components and materials. The cathode alone is a composite that includes an electrochemically active material (hereafter, active material), an electronically conducting material, an ionic conductor (also referred to as the electrolyte), and inactive components such as a binder that provides structural integrity. The processes of charging and discharging (“cycling”) involve transport of Li+ in electrolytes and Li in the active materials, as well as electrochemical reactions at interfaces. Transport mechanisms include diffusion, driven by the concentration/chemical potential gradient, and migration, driven by the electric potential gradient. The presence of multiple physical phenomena, compounded by the complex microstructures of electrodes (i.e., cathode and anode—see Figure 1 for representative examples), has led to simulation techniques that rely on significant simplifications that only roughly capture microstructure effects through tortuosity and porosity, largely ignoring the interplay between morphology, kinetics, and material thermodynamics at the particle scale. These models include the porous electrode theory,2,3,4,5,6,7 which considers mass and charge conservation averaged over volumes containing both active material particles and electrolyte. Despite these approximations, they were shown to be effective in predicting the cell behavior when the model is parameterized for specific materials/cells (see References 8,9,10,11,12,13,14). These models remain a key tool in understanding and designing electrochemical devices such as batteries because of their computational efficiency.

Figure 1
figure 1

Examples of complex microstructures in battery electrodes obtained by x-ray tomography: (a, b) A cathode microstructure showing (a) the active material (LiCoO2) and (b) the rest of the volume. Axes shown in (a) and (b) are in units of μm. Adapted with permission from Reference 15. (c) An anode microstructure, showing the graphite component. Reprinted with permission from Reference 13. © 2020.

Full size image

In the 2000s, the growth in computational power began to allow researchers to consider microstructures explicitly in many areas of materials research using interfacial-capturing approaches such as the level set methods16,17 and diffuse interface methods.18,19 The phase-field approach falls within the category of diffuse interface methods, with a wide variety of applications,18,20 including solidification,21,22,23 solid-state phase separation and coarsening,24,25,26,27 grain growth,28,29,30,31 martensitic transformation,32,33,34,35 and fracture.36,37,38 In investigations of phase transformations, the effects of detailed thermodynamics and kinetics of materials are accounted for by applying a phase-field modeling approach. Problems in electrochemistry were no exception. Microstructural effects on electrochemical dynamics during battery cycling began to be examined with explicit consideration of microstructures.39,40,41,42 This article will focus on the work performed by the authors’ group based on the combination of phase-field modeling with the extended smoothed boundary method (SBM).43 This approach has also been extended beyond battery simulations, including to solid-oxide fuel-cell microstructure evolution,44,45 corrosion,46,47,48 and solidification in confined environments.49,50 Readers interested in other types of modeling approach are referred to review articles focusing on atomistic modeling,51 multiscale modeling,52 and references therein.

In the remaining portion of the article, we primarily highlight two of the works by the authors’ group. First, we describe the methodology. We then describe the work that investigated the interactions between active particles when the active material has a two-phase behavior (i.e., its free energy has a double-well form and thus two phases can co-exist in equilibrium), which alter the charge/discharge behavior. This work focused on intercalation of LiFePO4 (LFP). Next, we will summarize the study of the Li–Cu–TiS2 displacement reaction. Similar approaches have been applied to conversion chemistry (FeF253), as well as metal deposition for metal anodes (e.g., Li54,55,56 and Mg57); we refer the readers to these articles for additional information.

Simulation method and approach

In this section, we briefly describe the concept behind phase-field modeling applied to rechargeable Li-ion battery materials. In this case, phase-field models follow Li concentration, which is a conserved quantity. We focus here on models employing the Cahn–Hilliard equation,58,59 which accounts for the thermodynamics of the material through an expression for the total free energy of the system. The evolution equation for a concentration of chemical species can be derived under the assumption that the system evolves toward a state that reduces this total free energy using calculus of variations. For example, a simple free energy, when the free energy depends solely on the Li concentration, could be written as

$${F}^{CH}\left({c}_{Li}\right)={\int }_{\Omega }{[f}_{chem}({c}_{Li})+{f}_{{\text{g}}rad}(\nabla {c}_{Li})]d\Omega ,$$
(1)

where \({F}^{CH}\) is the total free energy of the system, \({c}_{Li}\) is the Li concentration, \({f}_{chem}\) is the chemical free-energy density (which is related to the integral of the concentration-dependent open-circuit voltage of the active material), \({f}_{{\text{g}}rad}\) is the gradient energy density, which penalizes sharp interfaces and introduces interfacial energy of the phase boundaries, \(\Omega\) denotes the system’s domain, and \(d\Omega\) is the volume element of the domain. When there are other sources of driving force, additional terms, such as an elastic strain energy term, can be included in Equation 1. Intercalation of Li is modeled as a pseudo-binary system of Li and vacancies (i.e., unoccupied interstitial sites). (For more information on the thermodynamics of interstitial solid solutions, see References 60, 61.) In this case, the chemical potential of Li is related to the free energy via

$${\upmu }_{Li}^{CH}=\frac{\updelta {F}^{CH}}{\updelta {c}_{Li}}=\frac{\partial {f}_{chem}({c}_{Li})}{\partial {c}_{Li}}-\nabla \cdot \frac{\partial {f}_{{\text{g}}rad}(\nabla {c}_{Li})}{\partial \nabla {c}_{Li}}.$$
(2)

Note that the first term in the right-hand side is the chemical potential of Li in a homogeneous phase, \({\upmu }_{Li}({c}_{Li})\). Extending the concept of Fick’s Law of Diffusion to incorporate the chemical potential gradient as the driving force for diffusion, the governing equation can be obtained via the mass conservation law

$$\frac{\partial {c}_{Li}}{\partial t}=\nabla \cdot \left(M\nabla {\upmu }_{Li}^{CH}\right),$$
(3)

where \(M\) is a mobility, which is related to the diffusivity by a thermodynamic factor that depends on \({f}_{chem}\). Equation 3 is known as the Cahn–Hilliard equation.58,59

To apply these equations to battery simulations at the microstructure scale, one needs to solve them along with equations describing Li-ion transport through the electrolyte and the reaction boundary conditions at the interfaces between the electrolyte and the electrode material. Such coupling could be accomplished with the extended SBM.43 The SBM uses phase-field-like functions called domain parameters that define various bulk regions such as the electrolyte region and the active material regions. The gradients of the domain parameters indicate the boundaries of these regions. The partial differential equations that are applicable in individual regions are multiplied by the corresponding domain parameter (or its square, depending on the type of boundary condition), and the equations are transformed using the product rule of differentiation. The resulting equation can then be solved over the entire regularly shaped computational domain, while imposing the boundary conditions based on the magnitude of the gradient of the domain parameters. More details on the SBM and their various applications can be found in References 43, 46, 62, 63, and numerical error quantification43,62,64 and formal mathematical analyses and error estimates63,64,65 for some of its applications are available in the literature. Examples of equations resulting from this approach can be found in each of the next two sections.

A significant advantage of the phase-field method is that the free energy functional can be parameterized to reflect the realistic thermodynamics of materials. In the case of battery materials, the chemical potential can be obtained from the measurements or calculations of open-circuit voltage. Due to the technological importance of battery materials, there are also studies aiming to quantify kinetic parameters such as diffusivities and reaction rate parameters (see References 66,67,68). The two examples described here will highlight the capability of the phase-field modeling to incorporate such data.

Modeling of charging/discharging behavior in intercalation compounds with intrinsically two-phase behavior

Phase separation occurs in a wide variety of materials, including metals, ceramics, and semiconductors. Phase separation can occur spontaneously or through a process of nucleation and growth. While phase separation can occur even in commercial Li intercalation materials such as graphite and LiCoO2, it is typically considered undesirable because the lithiation/delithiation process could require formation of interfaces (during nucleation and growth or spinodal decomposition), which can lead to hysteresis and loss of Coulombic efficiency.69,70 LFP, which is known to phase separate with a particularly large miscibility gap and also to possess low electric conductivity, was not originally considered to be a practical cathode material.71 However, after nanosizing the LFP and coating it with carbon to mitigate low intrinsic electrical conductivity,72,73 it was demonstrated to be a commercially viable choice for battery cathodes that provide improved safety,74 cycle life,75 and material cost.76 Consequently, the question of why this material was so successful despite its large miscibility gap attracted considerable interest in the scientific community.

Armed with the phase-field model, combined with the SBM, we began our investigation into the origin of LFP’s performance in the early 2010s. The reaction at the interface between the active particle and the electrolyte can be written as Li+ + e− + FePO4 \(\leftrightarrows\) LiFePO4. The forward and reverse directions of this reaction are referred to as lithiation and delithiation, respectively, and they correspond to discharging and charging of the LFP battery. The rate \({r}_{Li}\) of this reaction is modeled via the Butler–Volmer equation,77

$${r}_{Li}={i}_{0}\left({\text{exp}}\left(-\frac{\upalpha F}{RT}\upeta \right)-{\text{exp}}\left(\frac{(1-\upalpha )F}{RT}\upeta \right)\right),$$
(4)

where \({i}_{0}\) is the exchange current density, \(\upalpha\) is the charge-transfer coefficient, \(R\) and \(T\) are the molar gas constant and temperature, respectively, and \(F\) is Faraday’s constant. The reaction rate \({r}_{Li}\) is coupled to the electric potential in the electrolyte via the overpotential \(\upeta =\left({\upphi }_{p}-{\upphi }_{e}\right)-{\upphi }_{eq}\), where \(\left({\upphi }_{p}-{\upphi }_{e}\right)\) is the potential difference across the particle/electrolyte interface and \({\upphi }_{eq}\) is the equilibrium potential of LFP measured with respect to metallic Li. The equilibrium potential is related to the chemical potential \({\upmu }_{Li}\) of Li at the surface of the particle by \({\upphi }_{eq}={V}_{plateau}-{\upmu }_{Li}({c}_{Li})/F\), where \( {V}_{plateau}=3.42 \,\text{V}\) is a value of LFP’s open-circuit voltage relative to metallic Li corresponding to two-phase equilibrium (and thus a plateau in experimental voltage-composition measurements in which phase separation is observed).71,78,79 Thus, Equation 4 links the reaction rate to the applied voltage as well as the surface concentration of Li in the LFP particle.

We employed SBM to couple the Butler–Volmer equation (Equation 4) to the Cahn–Hilliard equation (Equation 3), resulting in the following expression for concentration evolution in the LFP particles,80

$$\frac{\partial {C}_{p}}{\partial t}= \frac{1}{\uppsi } \nabla \cdot \left(\uppsi {M}_{p}\nabla \left({\upmu }_{Li}-\nabla \cdot \frac{\upkappa }{{\uprho }^{2}}\nabla {C}_{p}\right)\right)-\frac{\left|\nabla \uppsi \right|}{\uppsi } {r}_{Li},$$
(5)

where \({C}_{p}\) is the local volumetric concentration of Li in the particles, \(\uprho\) is the density of Li sites, \(\uppsi\) is the particle domain parameter, and \(\upkappa\) is the gradient energy coefficient. In studies where intraparticle phase separation was not expected, we simplified the dynamics in Equation 5 to the diffusion equation, which can still incorporate the thermodynamics of the LFP phase via the equilibrium potential used to calculate \({r}_{Li}\) (see References 79, 81, 82). However, here we will focus on our work using Equation 5 to study phase separation within the particle (“intraparticle” phase separation) and that between separate particles (“interparticle” phase separation).83 In this study, electric potential was assumed to be uniform in the electrolyte, which is a good approximation when examining a small domain within a cell, and thus we will not present equations for the electrolyte.

Parametrizing our combined phase-field and SBM model for LFP was a true multiscale modeling endeavor, incorporating the results of atomistic simulations as well as findings from smaller-scale phase-field simulations and experiments. The Li chemical potential \({\upmu }_{Li}\) as a function of Li site fraction, \({X}_{Li}={C}_{p}/\uprho\), was provided from the calculations by Malik et al.84 In their work, reproduced in Figure 2a–b, the formation energies of different Li and Fe2+ orderings on the parent FePO4 lattice were calculated using density functional theory (DFT) and were used to parametrize cluster expansions for the energies of cation configurations. These cluster expansions were used in Monte Carlo simulations to obtain the free energy as a function of \({X}_{Li}\). (An overview of these methods applied to Li-ion battery materials can be found in Reference 51). Figure 2a depicts this free energy alongside DFT formation energies for specific configurations from Reference 84. Figure 2b shows orderings of Li atoms and Fe2+ ions, as well as the (010) planes that are preferentially occupied by Li, also from Reference 84.

Figure 2
figure 2

(a) The room-temperature nonequilibrium free energy calculated from Monte Carlo simulations (solid red curve) and its spline fit (dashed blue curve) as a function of Li site fraction, \({X}_{Li}\). Zero-temperature mixing energies from density functional theory calculations for various configurations are shown with solid black circles. Reprinted with permission from Reference 84. (b) Selected configurations of Li (green spheres) and Fe2+ (brown spheres) from Monte Carlo simulations, also from Reference 84. © 2011 Springer Nature. (c) A schematic showing the mechanism of phase separation in materials that have two low-energy configurations. Reprinted with permission from Reference 83. © 2015 IOP Publishing.

Full size image

Figure 2c schematically depicts the equilibrium potential, \({\upphi }_{eq}={V}_{plateau}-{\upmu }_{Li}/F\), resulting from the fitted free energy in Figure 2a and illustrates how this chemical potential can result in interparticle phase separation. If there are two particles with similar surface concentrations of Li between the spinodal concentrations (\({x}_{Li}=0.05\) and \(0.93\)), and the cell voltage is between their equilibrium potentials, then the particle with a higher surface concentration of Li will be driven to lithiate faster, while the particle with a lower surface concentration will be driven to delithiate. Lowering the cell voltage outside of the inverted potential range will suppress this delithiation. This state corresponds to larger overpotential and thus higher current.

Intraparticle phase separation has the same origin in bulk thermodynamics as interparticle phase separation with the additional effects of the solid–solid interface. With \({\upmu }_{Li}\) given by Reference 84, the width and energy of the interface between Li-rich and Li-poor phases are determined by \(\upkappa\), the gradient energy coefficient. Based on atomistic simulation results85 and the orthorhombic structure of the parent FePO4 crystal, we made \(\upkappa\) an anisotropic second rank tensor with one low-energy orientation that would be most likely to appear. As this work focused on the interparticle interactions, mechanical effects were not included in the study, even though coherency strain can contribute to the suppression of phase separation.59,86 Instead, the value of \(\upkappa\) was set to suppress phase separation in a nanoparticle (leading to an interfacial width of 11 nm), in a similar manner to Singh et al.,87 who examined the “traveling-wave”-type phase evolution in a LFP single particle. This approach was selected due to its computational efficiency, allowing for three-dimensional simulations containing multiple particles. The phase-field mobility \({M}_{p}\) was calculated from a literature value for the diffusivity,67 \({D}_{p}=5\cdot {10}^{-13}{{\text{cm}}}^{2}/{\text{s}},\) using \({M}_{p}={D}_{p}\uprho /(RT)\), and the exchange current density \({i}_{0}\) was estimated based on experimental measurements.79

Figure 3 shows three characteristic examples of our phase-field simulations of lithiation in the two-particle system with various combinations of particle sizes, all of which are simulated under galvanostatic conditions. The figures are snapshots of the surface Li site fraction taken at various depth of discharge (DOD), which is equal to the Li site fraction averaged over the LFP volume, expressed as a percentage. The current was set such that the average current density (the net current divided by the sum of the surface areas of the two particles) was the same for all cases. As intended, phase separation is not observed in particles with diameter less than \(\sim\)20 nm. This is illustrated in Figure 3a–c, where the particles were 10 and 17.5 nm in diameter, and Figure 3d–f, where phase separation was observed in the larger particle, with diameter 35 nm, but not in the smaller particle with diameter 20 nm. In Figure 3g–i, phase separation was observed in both particles, with particle diameters 40 and 70 nm. Interestingly, the smaller particle lithiates completely before the larger particle when both particles have the same phase separation behavior (Figure 3b, h), but the larger particle lithiates first when it is the only particle to phase separate (Figure 3e). Such results show the complexity of the behavior of electrochemical systems originating from the thermodynamics of materials and microstructure.

Figure 3
figure 3

Snapshots of lithiation simulated using Equations 4 and 5 in cells containing two spherical LixFePO4 particles with diameters 10 and 17.5 nm (a–c), 20 and 35 nm (d–f), and 40 and 70 nm (g–i). The color represents the Li site fraction XLi, and the cell depth of discharge (DOD) is noted below each snapshot. Adapted with permission from Reference 83.

Full size image

The behavior observed in Figure 3 is quantified in Figure 4. As a function of the cell DOD, Figure 4a plots DOD of the smaller particle, Figure 4b plots DOD of the larger particle, and Figure 4c plots cell voltage, all for the cases where particles have the same phase separation behavior. The same plots are made, respectively, in Figure 4d–f for the case where phase separation is only observed in the larger particle. Figure 4 also shows results for different current densities, where all cases in Figure 3 represent an average current density of \(6\% \,{i}_{0}\), where \({i}_{0}\) is the Butler–Volmer exchange current density in Equation 4. The plots of particle DOD demonstrate the trends seen in Figure 3, but we can now quantitatively observe that, at low current (\(6\% \,{i}_{0}\) or \(18\% \,{i}_{0}\)), the particles that lithiate later in Figure 3 delithiate after having lithiated to a relatively low DOD. At a higher current (\(54\% \,{i}_{0}\)), this partial extra cycle is kinetically suppressed as both particles lithiate simultaneously until the faster one is fully lithiated. Interestingly, a current density of \(54\% \,{i}_{0}\) also results in the smaller particle lithiating more quickly in Figure 4e, switching the order of lithiation from what it was at low current.

Figure 4
figure 4

Depth of discharge (DOD) of the individual particles (larger: a, d, smaller b, e) and the cell voltage (c, f) plotted against cell DOD. Plots (a–c) make a four-way comparison between two average currents,  \(6\% \,{i}_{0}\) (red lines) and \(54\% \,{i}_{0}\) (blue lines) and two sets of particle sizes, 40 and 70 nm (dashed lines) and 10 and 17.5 nm (solid lines). Plots (d–f) compare three average currents, \(6\% \,{i}_{0}\) (dotted red line), \(18\% \,{i}_{0}\) (dashed green line), and \(54\% \,{i}_{0}\) (solid blue line) for the system with particle diameters 20 and 35 nm. In plots (a, b, d, e), the spinodal compositions are indicated with black dashed-dotted lines and the cell DOD with a solid black line. In plots (c) and (f), the single-particle equilibrium potential is indicated with a solid black line. Reprinted with permission from Reference 83. © 2015 IOP Publishing.

Full size image

The voltage versus DOD curves in Figure 4c, f are determined by the equilibrium voltage of the particle or particles that are currently lithiating as well as the applied average current. At low current and no intraparticle phase separation, the voltage versus DOD curve (red curves in Figure 4c) shows two peaks approximating the equilibrium potentials of the two particles as they lithiate sequentially. This is because the particle that is actively supplying the current is in the solid-solution state. At low current with phase separation, voltage reaches a plateau at an intermediate value before reaching a peak (red curves in Figure 4d). This plateau is characteristic of two phases coexisting in the system in which the DOD changes through phase boundary motion.71,78 In the high current cases, the overpotential is increased by lowering the cell voltage (see the blue curves in Figure 4c, f), which reduces the difference in the reaction rate between the two particles and thus in the particle DODs, leading to smaller fluctuations in voltage during discharge.

By showing that a larger particle that allows intraparticle phase separation can lithiate faster than a smaller particle, this work uncovered a new mechanism that affects the lithiation dynamics of LFP particles and phase-separating active material particles in general. Lithiation dynamics can affect degradation pathways by influencing current localization (hot spots) within the composite cathode and concentration fluctuations during a single cycle (subcycling) in active material particles.8 This work also demonstrated the power of phase-field modeling to bridge length scales. We used results of atomistic simulations and phase-field simulations at smaller length scales to build a model that could simulate phase separation in multiple particles simultaneously. This model was in turn used to validate use of the diffusion equation (instead of the Cahn–Hilliard equation) for cases where phase separation was not expected.83 In another study, our model with the diffusion equation was compared to porous electrode theory, linking modeling techniques that span from the atomistic to the cell scale.81 Recently, efforts have been made to directly link phase-field models to a porous electrode theory model via an assumption of spherical or planar particles to further advance the utility of phase-field modeling by improving the accuracy of electrode/cell-level simulation predictions.88,89

Modeling of displacement reaction materials

Another example in which we have incorporated realistic thermodynamics and kinetics of materials into phase-field modeling is our study of the displacement reaction in the Li–Cu–TiS2 system. Chemistries involving sulfides of titanium have a historical importance, as it was the compound used in the first demonstration of rechargeable batteries based on layered LixTiS2.80 The Li–Cu–TiS2 system has a spinel structure, and it was considered as a model system to develop scientific understanding of displacement reactions, which could share common behaviors as systems that undergo structural changes during Li insertion/extraction (the so-called conversion reaction materials), rather than for its promise as a potential candidate as a material for rechargeable batteries. Readers who are interested in the application of phase-field modeling to conversion materials are referred to Reference 90.

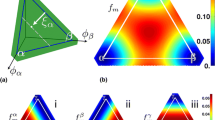
In this work,80 the free energy landscape and kinetic parameters of the Li–Cu–TiS2 system were computed using a combination of DFT, the lattice Hamiltonian (cluster expansion) approach, and the Monte Carlo method, similar to the work by Malik et al. on LFP,84 which provided the input to phase-field simulations. The compositional state of the Li–Cu–TiS2 system can be mapped effectively onto a ternary diagram, shown in Figure 5a, where TiS2 is treated as a unit. This is a reasonable approach because TiS2 forms a host structure that is highly stable and allows Li and Cu to enter into its open interstitial sites. The ternary diagram is formed by its vertices at pure Li, pure Cu, and TiS2 with no Li or Cu. Since we consider intercalation of Li or Cu into TiS2, the relevant portion of the ternary diagram is a triangle formed by vertices at Cu0.5TiS2, LiTiS2, and TiS2. The phase diagram computed by the first-principles approach is shown within that triangle, along with the crystal structure of the spinel TiS2 with three different compositions, ranging from Cu0.5TiS2 to LiTiS2. The Li insertion reaction into Cu0.5TiS2 can be written as Li+ + e− + Cu0.5TiS2 \(\to\) LiTiS2 + 0.5Cu, which is an electrochemical reaction involving charge transfer. Cu does not undergo charge transfer in this reaction but is simply displaced from the host structure because of the electrochemical driving force for Li to be inserted. The displaced Cu is extruded on the surface of the host particle. Upon charge, Li is deintercalated, which can be expressed as LiTiS2 \(\to\) TiS2 + Li+ + e−. This reaction does not involve Cu. However, there is a chemical (not electrochemical) driving force for intercalation of Cu into TiS2 because Cu0.5TiS2 has lower energy than TiS2. This process can be written as TiS2 + 0.5Cu \(\to\) Cu0.5TiS2, which completes the overall Li insertion–extraction reaction loop, Li + Cu0.5TiS2 \(\leftrightarrows\) LiTiS2 + 0.5Cu.

Figure 5
figure 5

(a) A composition space for the displacement reaction material system, Li–Cu–TiS2, and the crystal structures of TiS2 with Li and/or Cu in the interstitial sites. Cu (denoted by green circles) occupies the tetrahedral sites, while Li (denoted by red circles) occupies the octahedral sites. As indicated in these crystal structures, TiS2 can intercalate Cu, Li, or their mixture. (b) Free energy per interstitial site. The bulk free energy was calculated from first principles for the solid-solution region, which was smoothly connected with a downward parabolic function along the Cu0.5TiS2–LiTiS2 edge. (c) Diffusivities calculated from first principles, which were used to calculate the mobilities in the phase-field model. (d, e) The evolution of the Li concentration (site fraction) during lithiation and delithiation, respectively. Adapted from Reference 80 with permission.

Full size image

Although the overall reaction appears simple, the actual transformation path that is taken by Li insertion and extraction processes are quite different as a result of the complex interplay between thermodynamics, kinetics, and electrochemistry in the material. In the phase diagram (Figure 5a), the single-phase region, in which Cu and Li in the TiS2 host structure form a solid solution in thermodynamic equilibrium, is identified by dark green near the TiS2 vertex, while the two-phase region, in which the Li-rich and Cu-rich phases form, is indicated by light green with tie lines connecting the equilibrium concentrations of each phase. Such phase behavior can be understood by examining the free energy or chemical potential landscape of the system. The free energy of the system, calculated by the Monte Carlo method with input from DFT, is shown in Figure 5b, where the Cu axis is stretched such that the diagram is equilateral. The gray curve in Figure 5b divides the single-phase and two-phase regions and corresponds to the boundary between the light and dark green regions in the phase diagram in Figure 5a. Note that only the left side of the gray curve was directly taken from the first-principles calculations because the energy barrier in the two-phase region is set by the interfacial energy and the desired interfacial width (a numerical parameter). In addition, the kinetic Monte Carlo method with DFT input was used to compute the diffusivity of Li and Cu shown in Figure 5c.

These available input data were used for the phase-field simulations to examine the evolution of Li/Cu concentration evolution. The governing equations describing the process, formulated to include the reaction boundary condition via SBM, are expressed for species \(i=Li, Cu\) as follows:

$$\frac{\partial {X}_{i}}{\partial t}= \frac{1}{\uppsi } \nabla \cdot \left(\uppsi {M}_{i}\nabla {\upmu }_{i}^{CH}\right)-\frac{\left|\nabla \uppsi \right|}{\uppsi } {J}_{i}{\left.\right|}_{s},$$
(6)

where \({X}_{i}\), \({\upmu }_{i}^{CH}\), and \({J}_{Li}{\left.\right|}_{s}\) are the site fraction, Cahn–Hilliard chemical potential, and the reaction flux on the surface of the particle of species \(i\), respectively. The Cahn–Hilliard chemical potential was given by

$${\upmu }_{i}^{CH}=\frac{\partial f}{\partial {X}_{i}}-{\upkappa }_{i}{\nabla }^{2}{X}_{i},$$
(7)

where \({\upkappa }_{i}\) is the gradient energy coefficient.

The reaction path can be visualized on a ternary composition triangle shown in Figure 5b, which depicts the free energy landscape. It begins at the top vertex (Cu0.5TiS2). As Li is electrochemically inserted into the particle, Cu is extruded (not shown) as Li displaces it. All the available sites are occupied, and the reaction path follows the upper right edge of the triangle (marked with green arrow). Over the intermediate composition, there is an energy barrier in the free energy that causes the two-phase behavior discussed earlier. Eventually, all available sites are occupied by Li (bottom right vertex). During the charging process, Li is extracted, which is driven by electrochemical reaction, and ultimately Cu reinserted through chemical driving force to occupy its available sites. While, in principle, these processes can occur simultaneously, Cu reinsertion is a slow process due to two reasons. First, as can be observed from the chemical potential map in Figure 5b, when Li occupies many of their available sites, there is no or little driving force for Cu insertion (see the increasing chemical potential away from the bottom edge). Second, the first-principles calculations showed that the diffusivity of Cu is more than 8 orders of magnitude smaller than that of Li.

The simulation results are shown in Figure 5d–e. Figure 5d shows the lithiation process of a Cu0.5TiS2 particle, while Figure 5e shows the delithiation process. The two dynamics are clearly not a reverse of each other. The lithiation shows decomposition of the mixture into two phases near the surface as lithiation occurs, eventually forming a core–shell structure in which the Li-rich phase surrounds the Cu-rich core. Full lithiation occurs when the core shrinks and disappears. This can be understood as follows. The free energy landscape along the Cu0.5TiS2–LiTiS2 edge has a double-well form. Since Cu only leaves the particle when Li displaces it, the reaction pathway is confined along that edge. Initially, Li and Cu form a solid solution, as nucleation is required to phase separate. However, at some point, nucleation occurs or the Li concentration reaches the spinodal point, and the surface region undergoes a phase decomposition into Li-rich and Cu-rich regions. As Li further displaces Cu, the Li-rich regions become connected, forming the shell structure. On the other hand, the delithiation process occurs with a smooth concentration gradient, a feature of diffusion within single-phase material, rather than via motion of a Li-rich/Li-poor phase boundary.

A key implication of the simulation results was that the large hysteresis incurred in this material—and plagues many displacement and conversion reaction materials—is a result of the system taking a different path in multidimensional concentration space during charge and discharge.80 The phase-field simulation was able to directly capture the reaction path hysteresis, as well as the hysteresis associated with development of concentration gradients and interfaces. While there are other origins of hysteresis at the cell level, including those arising from the ionic concentration gradient in the electrolyte especially at high rates, by far the hysteresis due to the changes in compositions/phases in the active material is the dominant component that needs to be mitigated for conversion materials. To this end, this article suggested to seek materials that (1) possess a free energy landscape that allows for the coincidence of the lithiation and delithiation reaction paths and (2) contain a species displaced by Li that is sufficiently mobile, preferably matching the mobility of Li, such that thermodynamic equilibrium is achieved sufficiently quickly. The condition (1) provides the potential thermodynamic path for the reactions, and the condition (2) enables the system to follow that path.80 Not only did the work provide fundamental insights, but it also demonstrated the capability of phase-field models to handle input regarding the material’s complex thermodynamics and kinetics and to provide quantitative predictions.

Implication and impact for battery performance and degradation

The examples provided above have shown that the complex interactions between transport, reaction, electricity, chemistry, and thermodynamics lead to highly complex evolution of the materials within battery electrodes. Insights developed based on the phase-field simulations have led to guidance for future research/development directions, both directly and indirectly. The example with the intercalation reaction in LiFePO4 has shown that the Li insertion/extraction rate of individual active particles can vary greatly from the overall rates and that it is strongly influenced by the particle size variations. It was found that, even at a low charge/discharge rate, reaction hot spots can arise, which could lead to chemical, electrochemical, and/or mechanical degradation of the material. Additionally, it showed that the particles could undergo multiple lithiation/delithiation subcycles within each half cycle, which could contribute to further degradation. The example with the displacement reaction in Li–Cu–TiS2 identified two key factors that would facilitate kinetics in displacement reaction materials: (1) sufficient driving force for the chemical insertion of the displaced component (Cu), and (2) the mobility of the displaced component that matches the mobility of Li. The idea of seeking a free energy to enable the reinsertion of the displaced metal upon Li removal is one of the important findings of the paper, which was in contrast with the traditional understanding that the challenge in displacement materials was solely the kinetics. Such insights could have only been gained through the combination of DFT, statistical mechanics, and phase-field modeling that enabled the realistic simulation of electrochemical dynamics governed by the underlying thermodynamics and kinetics of the Li–Cu–TiS2 system. Understanding the underlying mechanisms that affect performance and degradation of battery materials is an important step in building the path toward next-generation batteries.

Future outlook

Modeling and simulation have increasingly become an integral part of materials discovery, design, and optimization in recent decades. As demonstrated in this article, the phase-field modeling approach provides a key capability in understanding the details of the processes underlying charging and discharging of batteries. As novel chemistries and even different types of batteries are introduced, new mechanisms and phenomena could come into play, requiring extension of the methodologies described here. For example, in all-solid-state batteries (ASSBs), mechanical considerations such as elastic and plastic deformation and cracking, coupled with electrochemistry and transport, become a critical aspect for cycling stability.91,92,93 Recent works have used phase-field models to examine chemomechanical effects during phase transformations within an active material in the form of a single-crystalline particle,94,95 a thin film,96 and a polycrystal.97 A coupled phase-field and porous electrode theory model incorporating chemomechanical effects has also been developed.88 It is important to note that explicit consideration of the microstructures may be required to elucidate mechanical failure in ASSBs; such examination is possible using diffuse interface methods98 and would allow identification of microstructural effects on the coupling of stress, concentration, electrostatic potential, and reactions. These capabilities could be used to optimize the particle size, volume fractions, and materials selection to enhance cycling stability.99 Coupling electrochemistry to mechanics with explicit consideration of the microstructure will surely create additional challenges,100 especially on the computational resources required, but it will also catalyze the development of new numerical methods, just as microstructure-scale battery modeling led to the development of the extended SBM. In this turn, such an advancement will likely include an incorporation of machine learning, which has been shown to reduce a complex problem to a tractable one. A computationally efficient approach would be used as a part of screening and as a digital twin for scaling up laboratory-based devices into commercial products.