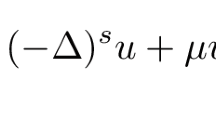Skip to main content
SpringerLink
Log in

Green’s Function for the Fractional KDV Equation on the Periodic Domain via Mittag-Leffler Function

  • Research Paper
  • Published:
Fractional Calculus and Applied Analysis Aims and scope Submit manuscript

Abstract

The linear operator c + (−Δ)α/2, where c > 0 and (−Δ)α/2 is the fractional Laplacian on the periodic domain, arises in the existence of periodic travelling waves in the fractional Korteweg-de Vries equation. We establish a relation of the Green function of this linear operator with the Mittag-Leffler function, which was previously used in the context of the Riemann-Liouville and Caputo fractional derivatives. By using this relation, we prove that the Green function is strictly positive and single-lobe (monotonically decreasing away from the maximum point) for every c > 0 and every α ∈ (0, 2]. On the other hand, we argue from numerical approximations that in the case of α ∈ (2, 4], the Green function is positive and single-lobe for small c and non-positive and non-single lobe for large c.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Boyd, Chebyshev and Fourier Spectral Methods. Dover Publishers, New York (2001).

    MATH  Google Scholar 

  2. V. Ambrosio, On the existence of periodic solutions for a fractional Schrödinger equation. Proc. AMS 146 (2018), 3767–3775.

    Article  Google Scholar 

  3. Z. Bai and H. Lü, Positive solutions for boundary value problem of nonlinear fractional differential equation. J. Math. Anal. Appl. 311 (2005), 495–505.

    Article  MathSciNet  Google Scholar 

  4. H. Bateman, Higher Transcendental Functions, Vol. III. McGraw-Hill Book Company, New York (1953).

    Google Scholar 

  5. H. Brezis, Functional Analysis, Sobolev Spaces and Partial Differental Equations. Springer, New York (2011).

    Book  Google Scholar 

  6. H. Chen, Existence of periodic traveling-wave solutions of nonlinear, dispersive wave equations. Nonlinearity 17 (2004), 2041–2056.

    Article  MathSciNet  Google Scholar 

  7. H. Chen and J. Bona, Periodic travelling wave solutions of nonlinear dispersive evolution equations. Discr. Cont. Dynam. Syst. 33 (2013), 4841–4873.

    Article  Google Scholar 

  8. M. Chugunova and D.E. Pelinovsky, Two-pulse solutions in the fifth-order KdV equation: rigorous theory and numerical approximations. Discr. Cont. Dynam. Syst B 8 (2007), 773–800.

    MathSciNet  MATH  Google Scholar 

  9. K. Claassen, M. Johnson, Nondegeneracy and stability of antiperiodic bound states for fractional nonlinear Schrödinger equations. J. Diff. Equs. 266 (2019), 5664–5712.

    Article  Google Scholar 

  10. R.J. Decker, A. Demirkaya, N.S. Manton, and P.G. Kevrekidis, Kink-antikink interaction forces and bound states in a biharmonic ϕ4 model. J. Phys. A: Math. Theor. 53 (2021), # 375702.

  11. R.J. Decker, A. Demirkaya, P.G. Kevrekidis, D. Iglesias, J. Severino, and Y. Shavit, Kink dynamics in a nonlinear beam model. Comm. Nonlin. Sci. Numer. Simul. 97 (2021), # 105747.

  12. Z. Du and C. Gui, Further study on periodic solutions of elliptic equations with a fractional Laplacian, Nonlinear Analysis 193 (2020), # 111417, 16 pp.

  13. R.L. Frank and E. Lenzmann, Uniqueness of non-linear ground states for fractional Laplacian in ℝ. Acta Math. 210 (2013), 261–318.

    Article  MathSciNet  Google Scholar 

  14. R. Garappa, The Mittag-Leffler function. MATLAB Central File Exchange, Retrieved October 31, 2020.

  15. R. Gorenflo, A. Kilbas, F. Mainardi, and S. Rogosin, Mittag- Leffler Functions, Related Topics and Applications. Springer-Verlag, Berlin (2020), Second Ed.

    Book  Google Scholar 

  16. K.A. Gorshkov and L.A. Ostrovsky, Interactions of solitons in nonintegrable systems: Direct perturbation method and applications. Physica D 3 (1981), 428–438.

    Article  Google Scholar 

  17. S. Hakkaev and A.G. Stefanov, Stability of periodic waves for the fractional KdV and NLS equations. Proc. Royal Soc. Edinburgh A 151 (2021), 1171–1203.

    Article  MathSciNet  Google Scholar 

  18. V.M. Hur and M. Johnson, Stability of periodic traveling waves for nonlinear dispersive equations. SIAM J. Math. Anal. 47 (2015), 3528–3554.

    Article  MathSciNet  Google Scholar 

  19. M.A. Johnson, Stability of small periodic waves in fractional KdV-type equations. SIAM J. Math. Anal. 45 (2013), 3168–3293.

    Article  MathSciNet  Google Scholar 

  20. A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Application of Fractional Differential Equations. Elsevier, New York (2006).

    MATH  Google Scholar 

  21. F. Olver, Asymptotics and Special Functions. AKP Classics, Massachusetts (1996).

    Google Scholar 

  22. U. Le, D. Pelinovsky, Convergence of Petviashvili-s method near periodic waves in the fractional Korteweg-De Vries equation. SIAM J. Math. Anal. 51 (2019), 2850–2883.

    Article  MathSciNet  Google Scholar 

  23. A. Lischke, G. Pang, M. Gulian, F. Song, C. Glusa, X. Zheng, Z. Mao, W. Cai, M.M. Meerschaert, M. Ainsworth, and G.E. Karniadakis, What is the fractional Laplacian? A comparative review with new results. J. Comp. Phys. 404 (2020), # 109009, 62 pp.

  24. N.S. Manton, An effective Lagrangian for solitons. Nucl. Phys. B 150 (1979), 397–412.

    Article  MathSciNet  Google Scholar 

  25. M.G. Mittag-Leffler, Sur la nouvelle fonction Eα(x). Acad. Sci. Paris 137 (1903), 554–558.

    MATH  Google Scholar 

  26. F. Natali, D. Pelinovsky and U. Le, New variational characterization of periodic waves in the fractional Korteweg-de Vries equation. Nonlinearity 33 (2020), 1956–1986.

    Article  MathSciNet  Google Scholar 

  27. F. Natali, D. Pelinovsky and U. Le, Periodic waves in the fractional modified Korteweg-de Vries equation. J. Dyn. Diff. Equat. (2021); DOI: 10.1007/s10884-021-10000-w; see also: Coorection to...; DOI: 10.1007/s10884-021-10016-2.

    Google Scholar 

  28. J.J. Nieto, Maximum principles for fractional differential equations derived from Mittag-Leffler functions. Appl. Math. Lett. 23 (2010), 1248–1251.

    Article  MathSciNet  Google Scholar 

  29. R. Parker, B. Sandstede, Periodic multi-pulses and spectral stability in Hamiltonian PDEs with symmetry. Preprint arXiv: 2010:05728 (2020).

    Google Scholar 

  30. I. Podlubny, Fractional Differential Equations. Academic Press, San Diego etc. (1999).

    MATH  Google Scholar 

  31. H. Pollard, The complete monotonic character of the Mittag-Leffler function Eα(−x). Bull. Amer. Math. Soc. 54 (1948), 1115–1116.

    Article  MathSciNet  Google Scholar 

  32. A.P. Prudnikov, Y.A. Brychkov, O.I. Marichev, Integrals And Series: Volume 1. Elementary Functions. Taylor & Francis, London (2002).

    MATH  Google Scholar 

  33. L. Roncal and P.R. Stinga, Fractional Laplacian on the torus. Commun. Contemp. Math. 18 (2016), # 1550033, 26 pp.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, L8S 4K1, Canada

    Uyen Le & Dmitry E. Pelinovsky

Authors
  1. Uyen Le
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dmitry E. Pelinovsky
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dmitry E. Pelinovsky.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Le, U., Pelinovsky, D.E. Green’s Function for the Fractional KDV Equation on the Periodic Domain via Mittag-Leffler Function. Fract Calc Appl Anal 24, 1507–1534 (2021). https://doi.org/10.1515/fca-2021-0063

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1515/fca-2021-0063

MSC 2010

Key Words and Phrases

Search

Navigation