Introduction

Genetic cerebellar ataxias are progressive rare neurological diseases (RNDs) affecting the cerebellum, often with multi-systemic damage to other neurological systems, causing debilitating impairment of gait, balance, speech, and fine motor skills. More than 100 ataxia diseases are autosomal-recessive cerebellar ataxias (ARCAs), often starting in early childhood or early adulthood. While each of them is ultra-rare, they constitute prime candidates for molecular treatment trials targeting their specific genetic defects, but robust statistical methodologies allowing to predict progression trajectories and their modification under treatment in very small samples are needed (1).

In this work, we aim to develop models to robustly capture and predict individual disease progression in RND patients. We use Autosomal Recessive Spastic Ataxia of Charlevoix-Saguenay (ARSACS) as showcase, leveraging data from the Autosomal Recessive Cerebellar Ataxia (ARCA) patient registry (2). This real-world registry includes patients at any stage of their disease, with 0 to 7 longitudinal follow-up visits. Assessment of disease severity is measured through the SARA (Scale for the Assessment and Rating of Ataxia) score, a composite score comprised of eight items evaluated by a clinical assessment developed in 2006 (3). To handle design heterogeneity, we used non-linear mixed effect models (NLMEM) to model the natural progression of the disease measured by the total SARA score, and investigate patient characteristics associated with disease evolution. A feature of real-world data is the large amount of missing covariate information at some or all visits. Several methods have been proposed to deal with missing data (4), single or multiple imputations being the most common approaches (5). Simultaneous imputation and estimation have also been proposed to infer the distribution of missing covariates in NLMEM assuming a known covariate-parameter relationship (6). Here, we combine multiple imputation with a pooled test statistic (7) to iteratively build the covariate model.

We used the final model to predict individual trajectories of disease progression over several years. In this section, we focused on patients in the early stages of disease, who would be the population of most interest in clinical trials. In addition to accounting for individual parameter uncertainty using conditional distributions and evaluating the effect of covariates, we investigated how including population parameter uncertainty influences predictions and prediction intervals.

Methods

Data

For this paper, we analysed data from the ARCA registry (2) of patients with ataxia. Patients were enrolled across more than 30 centers in 15 countries, at any stage of their disease. Disease severity was primarily measured by the Scale for the Assessment and Rating of Ataxia (SARA) score, a composite score comprised of eight items, evaluated by a clinical assessment of gait, stance, speech, sitting, fine motor, and leg movements (3). For each patient, the main variables recorded at each visit were age, SARA score, as well as other clinical scores measuring daily living activities (not analysed here). Covariates were also recorded at inclusion in the study: Age at Onset of symptoms (AOO), as reported by the patient or their caregiver, Body Mass Index (BMI), Inventory of Non Ataxia Signs (INAS (8), secondary disease progression score for non-ataxia symptoms), the genotype of the mutation (missense or loss of function mutation), and sex.

In this work, we considered the largest genetic autosomal-recessive ataxia population in the ARCA registry (extraction date: January 2022) as showcase, namely, Autosomal Recessive Spastic Ataxia of Charlevoix-Saguenay (ARSACS), comprising of 173 patients included between 2013 and 2022. The dataset included a total of 349 measurements of SARA scores ranging from 3 to 40 points (median 20.5). The follow-up varied from 0 to 6 years, with one visit for 81 patients, two visits for 44 and more than two visits in 48 patients. Median Time Since Onset of symptoms at inclusion in the registry was 35 years (Q1-Q3: 24–48). Table I summarises the covariates at inclusion. The percentage of missing values in the covariates ranged from 0 (Sex) to around 40% (INAS score).

Table I Summary of the covariates for the 173 ARSACS patients. In ARSACS, loss of function denotes a type of mutation in the SACS gene that is genetically predicted to lead to complete loss of the Sacsin protein. BMI = Body Mass Index, INAS = Inventory of Non-Ataxia Signs, AOO = Age Of Onset, N = number of patients
Full size table

Figure 1 shows the SARA scores as a function of Time Since Onset of symptoms. On average, the SARA score increases with Time Since Onset of symptoms, with large variations in the individual profiles as some patients exhibited a stable or even decreasing SARA score over time.

Fig. 1
figure 1

Plot of the SARA score as a function of TSO (time since onset of symptoms) in the 173 ARSACS patients. Solid lines represent the repeated assessments for an individual

Full size image

Modelling SARA Score

Time Since Onset (TSO) was computed as current Age minus Age of Onset (AOO). In the ARSACS population, 22 missing values of AOO were imputed to the median AOO in the data set (2 years of age), consistent with early childhood presentation of ARSACS. In the analysis, AOO was split into three clinically relevant categories: 0–7, 8–14 and 15–40 years (9).

We modelled the SARA score \({y}_{ij}\) recorded at TSO in individual i at time \({t}_{ij}\) (i = 1,…,N, j = 1,…,\({n}_{i}\)) as a continuous variable using non-linear mixed effect models (10), defined through the following equations:

$${y}_{ij}=f\left({t}_{ij},{\psi }_{i}\right)+g\left({t}_{ij},{\psi }_{i}\right){\epsilon }_{ij}$$
(1)
$$log\left({\psi }_{ik}\right)=log\left({\mu }_{k}\right)+{\beta }_{C,k}^{T}\times {C}_{i}+{\eta }_{ik}$$
(2)

where \({t}_{ij}\) represents time j for individual i, \({y}_{ij}\) the observation of individual i at time \({t}_{ij}\), \(f\left({t}_{ij},{\psi }_{i}\right)\) represents the structural model, depending on the vector of individual parameters for individual i, \({\psi }_{i}\), \(g\left({t}_{ij},{\psi }_{i}\right)\) describes the standard deviation of the residual errors, and \({\epsilon }_{ij}\sim N\)(0,1) is the residual error for the observation \({y}_{ij}\). The individual parameters were assumed to follow a log-normal distribution, with a mean equal to a linear function of fixed effects \(\mu ,\) covariate effects for parameter k \({\beta }_{C,k}\) and \({C}_{i}\), the vector of covariates for individual i. The random effects \({\eta }_{i}\) were assumed to follow a joint multinormal distribution with variance–covariance matrix \(\Omega\). We estimated the population parameters for this model, \(\theta =\left(\mu ,\beta ,\Omega ,\sigma \right)\), using the SAEM algorithm (11).

Base Model Building

Several models (linear, exponential, sigmoidal and Gompertz functions, 3 and 4 parameter logistic equations) were considered to model the progression of the SARA score as a function of TSO. The four-parameter logistic function was parameterised to include clinically relevant parameters as:

$$f\left(t\right)={S}_{max}+\left({S}_{0}-{S}_{max}\right)\times \frac{1}{1+\frac{{e}^{kt}-1}{{e}^{k{T}_{50}}-1}}$$
(3)

where \({S}_{0}\) represents the SARA score at the onset of symptoms \(\left(f\left(0\right)={S}_{0}\right)\), \({S}_{max}\) is the maximum SARA score, \({T}_{50}\) is the time when \(f\left({T}_{50}\right)=\frac{{S}_{0}+{S}_{max}}{2}\), k represents the disease progression rate (year−1). The structural model was selected using the Bayesian Information Criterion (BIC), with a diagonal variance–covariance matrix for random effects (no correlations) and a combined error model.

Additive, proportional and combined residual error models were compared, with a Likelihood Ratio Test (LRT) for nested models and BIC for non-nested models. In a third step, the structure of the covariance matrix was investigated by fitting a model with correlations on all parameters. Correlations were removed if they were less than 0.7. Finally, remaining correlations (if any) were removed using a stepwise procedure (backward-forward approach) using the LRT and removed by block when non-significant. The p-value for all LRT tests was 0.05.

Covariate Model Building Accounting for Missing Covariates

The covariate model building and final interindividual variability (IIV) selection is summarised in Fig. 2. To build the covariate model, we combined multiple imputation (5) with a stepwise algorithm including a pooled log-likelihood ratio test (LRT).

Fig. 2
figure 2

Flowchart of the approach used to build the covariate model, refine the structure of the variance–covariance matrix and obtain the final parameter estimates with their uncertainty

Full size image

First, the missing values for BMI, INAS and ARSACS genotype were imputed with Multiple Imputation using the MICE package (5). For this, we first selected the structure of each regression model using the subset with complete data for that covariate, with the non-missing covariates (AOO, Age at first visit, Sex, SARA score at first visit) and the individual parameters (Empirical Bayes Estimates, EBE) estimated from a model with no covariates (6) as regressors. Individual parameters were estimated as the mode of the conditional distribution of patient (12). Linear regressions were used for continuous covariates (INAS, BMI) and logistic regressions for categorical covariates (ARSACS genotype). For each regressor, we tested both the regressor itself and its logarithm to choose which to include in the model, based on the Akaike Information Criterion (AIC). The resulting models for each missing covariate were entered in a multivariate regression model for MICE to impute ARSACS genotype, BMI and INAS, by increasing proportion of missing information. Ten data sets were generated using this procedure.

Second, the covariate model was built with a step-wise forward–backward procedure with a pre-selection step based on a p-value for the Pearson correlation coefficient between the EBE of the model without covariates fitted above and the covariates below 0.2. In the forward–backward procedure, we used Meng and Rubin's (7) approach to compute a pooled LRT on all imputed data sets for each covariate-parameter relationship. This allows to compute a single p-value across all imputed data sets for a given covariate-parameter relationship, through a two step procedure detailed in Supplementary Materials 3. This statistic was used throughout the step-wise procedure, with a threshold set at 0.05.

Covariate effects were added iteratively with a first forward approach among the pre-selected covariates. When none of the remaining relationships were significant, a second forward approach was performed to test whether non pre-selected covariate-parameter relationships should be included. Finally, a backward approach was performed on all covariate-parameter relationships included in the model at this stage. In a final step, a backward approach was again applied to the variability components with the same procedure.

Evaluation and Uncertainty

During model building, models were evaluated with standard goodness of fit plots (population fits, individual fits, Visual Predictive Check (VPC), Normalised Prediction Distribution Errors NPDE (13) versus TSO and predictions). The parameter estimates of the final model were reported as the mean parameter estimates across all imputed data sets (7). Standard errors of estimation (SE) were estimated using case bootstrap, which resamples patients uniformly from the original data set with replacement (14). The final model was fit to 200 bootstrapped datasets for each imputed dataset (15) and the resulting distributions of the estimated population parameters pooled to obtain the overall bootstrap distribution. SE were computed as the standard deviation of this pooled distribution over the 10 imputed data sets. Bootstrap SE were also computed for the base model without covariates.

Prediction of Individual Trajectories Accounting for Uncertainty

To build individual predictions, 100 individual parameter vectors were drawn from each patient's conditional distribution in each imputed data set (1000 samples in total). Predicted SARA scores were computed for each vector up to 5 years after the last visit and pooled. Finally, for each patient and each time, we computed the 5th, 50th and 95th percentile of simulation to get a median prediction and a Prediction Interval (PI) for the trajectories.

To account for population parameter uncertainty, we repeated this procedure for each imputed data set, by first sampling 200 population parameter vectors before computing the conditional distributions and sampling 100 individual sets of parameters. The resulting 200,000 samples constituted the conditional distribution under uncertainty and were used to build individual predictions as above.

Individual predictions for the model with covariates were obtained with and without population parameter uncertainty, and with population parameter uncertainty for the model without covariates. In each case, we computed the predicted SARA score at 5 years after each patient's last visit along the width of their PI and the ratios of the predicted SARA score the ratio of the width of PI at 5 years, with and without covariates, with and without population parameter uncertainty. Individual predictions are reported in the following for the 70 patients with a maximum SARA score less than 20 points (table in supplementary materials 1).

Implementation

Analyses were performed in R version 4.2.0 (16). Parameter estimation was performed with the saemix package version 3.1 for R (17) (with 800 and 400 iterations for the first and second phases respectively, 10 chains, and 10,000 samples for the estimation of the likelihood through Importance Sampling). Multiple Imputation was performed using the MICE R package (5).

Results

Model Selection

Describing the evolution of SARA score with TSO, through a linear model yielded an intercept of 1.7 (RSE = 32%) (SARA score for TSO = 0) and a progression rate of 0.5 (RSE = 4%) points per year, but this model predicted negative SARA scores at onset in some patients or very high SARA scores as the patients grew older, which was incompatible with scores bounded between 0 and 40. An exponential model performed worse than the linear model in terms of BIC (\(\Delta\) BIC =  + 4). The four-parameter logistic equation defined in (3) resulted in a better performance (\(\Delta\) BIC = -59 compared to the linear model). The NPDE of the models displayed in Fig. 3 also showed that this model performed better than the others as it adapted to the bounded nature of the score. This structural model was therefore selected for the following. An additive error model was chosen, and we did not find significant correlations between the parameters.

Fig. 3
figure 3

NPDE (Normalised Prediction Distribution Errors) versus TSO of the models without covariates (top) and with covariates (bottom). The observed 5%, 50% and 95% percentiles are represented as solid black lines, the red band represents the simulated (1000 replicates) median npd with its 90% prediction interval, the blue line represents the simulated 5% and 95% percentiles (1000 replicates) with their 90% prediction intervals

Full size image

The individual parameter estimates from the base model without covariates were used to test for potential covariate-parameter relationships. There was no difference between parameters between the first two categories of AOO which were then regrouped as early onset (reference class: \(AOO<15.\) The initial screening process generated 8 covariate effects (sex, BMI, AOO > 15 on \({S}_{0};\) sex and AOO > 15 on \({S}_{max};\) INAS and BMI on k; AOO > 15 on \({T}_{50}),\) three covariate-parameter effects were selected during the first forward step, none during the second and none were removed during the backward procedure. The final model included 3 relationships: \({S}_{0}\) was 25% lower in men, \({S}_{max}\) was 8% higher in men compared to women (class of reference in the modelling), and \({T}_{50}\) was 35% lower in late onset patients compared to early onset patients. The parameter estimates and their residual standard errors (RSE) for the model with/without covariates can be found in Table II. All parameters of the model are well estimated with RSE under 50%. For the final model, the eta-shrinkage was of 91% for \({S}_{0}\), 73% for α and 52% for \({T}_{50}\). The residual error was slightly less than 2 points of SARA score, reflecting the intrasubject variability seen in Fig. 1.

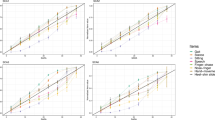
Table II Table of parameter estimates and RSE (computed using the case bootstrap with 200 samples) for the models with and without covariates for the evolution of the SARA score in 173 ARSACS patients. \({\mu }_{\psi }\) represents the fixed effect for parameter Ψ, \({\beta }_{Cov, \psi }\) the covariate effect of Cov on parameter Ψ, \({\omega }_{\psi }\) the standard deviation of random effect for parameter Ψ. The formula for individual parameter is as follows: \({\psi }_{i}={\mu }_{\psi }\times {e}^{(Cov\times {\beta }_{Cov,\psi }+{\eta }_{\psi ,i})}\), for individual i, where \({\eta }_{\psi ,i}\sim N(0,{\omega }_{\psi }^{2})\) 
Full size table

The NPDE of the models with and without covariates reported in Fig. 3 show that both models fit the data well, with no trend in the median profile. In Fig. 4, we simulated 100 parameter vectors from the population distribution of the parameters for each patient, and computed the median and the 5th-95th percentiles of the predicted SARA score for the four covariate categories. The model describes well disease progression over time in the different categories, although there are few patients with late onset.

Fig. 4
figure 4

Prediction bands of the evolution of the SARA scores versus TSO, stratified by covariate group (with women (top), males (bottom), AOO < 15 (left), AOO > 15 (right)) for the 173 ARSACS patients. Each band was obtained using 100 simulations of the random effects from the population distribution obtained with the final model to predict the evolution of SARA scores for each subject in the group over the range 0 (onset of symptoms) to 70 years after onset. The limits of the band correspond to the 90% simulation interval at each time point. The observed SARA scores are overlayed for each group, with lines joining the repeated measurements for subjects with more than one visit

Full size image

Prediction of Individual Trajectories Accounting for Uncertainty

Figure 5 shows the individual disease progression predicted for the base and covariate models, along with the prediction intervals, for one randomly selected patient in each covariate group, accounting for population parameter uncertainty. Although residual uncertainty wasn't included in these predictions, they still show considerable uncertainty 5 years after the last visit.

Fig. 5
figure 5

Examples of individual predictions with population parameter uncertainty (median + 90% PI without residual error) for the models with (red) and without (green) covariates for four patients with various covariate combination. Uncertainty covers population and individual parameter uncertainty but the predictions themselves do not include residual error

Full size image

The difference for the predictions with and without covariates is only apparent if AOO is greater than 15 years of age. Indeed, in late onset patients, the population \({T}_{50}\) was estimated to be 24.8 years instead of 38.1 years, close to the TSO at last visit recorded for these patients, and because progression is fastest around \({T}_{50},\) taking into account covariates had more impact on the predicted progression in this data set.

To better understand the effect of including covariates and/or including population parameter uncertainty on the prediction of the trajectories, we compared the predicted SARA score at 5 years and its prediction interval for all patients in the different configurations (Fig. 6). We restricted the comparison to subjects having a maximum SARA score below 20 points (70 patients), and we summarised the differences by looking at violin plots of the predicted SARA score and its width at 5 years with covariates and population uncertainty (in red): the majority of patients were predicted to increase (median + Q1-Q3) by + 2.7 points (1.9–3.6) without covariates (with uncertainty), and by + 2.9 points (1.9–3.9) with covariates (with uncertainty) 5 years after their last visit, but the uncertainty around that prediction, measured by the width of the PI, was 7.4 points (6.4–8.5) without covariates (with uncertainty) and 7.4 points (6.1–8.3) with covariates (with uncertainty).

Fig. 6
figure 6

Violin plot of the predicted SARA score and the width of 90% PI width at 5 years with uncertainty (top), and its ratio with/without uncertainty, with and without covariates (with uncertainty) (bottom), in the 70 patients with a maximum SARA score below 20

Full size image

The violin plots of the corresponding ratios comparing the model with or without covariates in yellow show that including covariates had little impact on the predicted SARA score at 5 years (median -0.2%) and on its width of PI (median: -5%). The violin plots of the corresponding ratios comparing the model with or without parameter uncertainty in purple show that including population parameter uncertainty had no impact on the predicted SARA score at 5 years (median: + 0%), and little impact on the width of its prediction interval (median: + 4% with half of the subjects varying by less than + 10%).

For more detail, in Fig. 7 we show the distribution of the two ratios, stratified by covariate category. Including covariates impacted the predicted SARA score at 5 years for the groups with AOO > 15 years, increasing the median by + 17% in women and + 22% in men, and decreased the median width of the prediction interval for the group women + AOO < 15 years (median: -9%) whereas the group man + AOO < 15 has a median ratio of 1. It could be due to the fact that, in the model with covariates, women have a higher \({S}_{0}\) (8.1) and a lower \({S}_{max}\) (34.3) than in the model with no covariates (resp 6.9 and 35.8), resulting in a slower progression, and therefore narrower prediction intervals at 5 years. Taking into account population parameter uncertainty had no impact on the predicted SARA score at 5 years, and slightly increased the width of the prediction interval for men with AOO < 15 years (median: + 6%), likely due to the fact that the parameters \({\beta }_{male,{S}_{0}}\) and \({\beta }_{male,{S}_{max}}\) have higher RSE (50% and 38% respectively) than the rest of the parameters.

Fig. 7
figure 7

Violin plot of the ratio of the predicted SARA score and the width of the 95% PI at 5 years with/without uncertainty, with and without covariates (with uncertainty) stratified by the two covariates in the model, for the 70 ARSACS patients with a maximum SARA score below 20 points, including 39 women (2 with AOO > 15) and 31 men (2 with AOO > 15)

Full size image

Discussion

In this work, we modelled the evolution of a clinician-reported outcome (SARA score) in a rare neurological disease patient group with an ultra-rare disease (ARSACS) using NLMEM. We used an innovative approach to build the covariate model in the presence of missing values for several covariates. We investigated the impact of including covariates in the model and how taking into account population parameter uncertainty affected the predicted SARA score at 5 years and its prediction intervals.

The evolution of SARA scores were best described as a non-linear function of TSO, as in (18). In the literature, sigmoid models have been used to model scores for other neurodegenerative diseases. For example, MDS-UPDRS score in Parkinson's disease were modelled with bounded functions such as the Gompertz equation (19). Three parameter logistic functions have been used to model cognitive scores CDR-SB (20) or CAMCOG (21) in Alzheimer's disease. For ataxia in particular, Jacobi et al. used mixed effect models to analyse the progression of several scores (including the SARA score) in 677 patients with Spinocereballar Ataxia (SCA) as a function of time from ataxia onset (12), and they showed that when modelling the whole disease progression, a non-linear model fitted best. Alternative models consider the change with time since first visit: Maas et al. (22) performed a multivariable linear regression on 223 patients with SCA3 to investigate predictors of disease progression, and reported that the disease progression rate was almost three times higher for patients with TSO > 10 years, with a large IIV. Using a linear model in the ARSACS dataset led to higher IIV on the rate of progression. We also tested a linear model to SARA score evolution as a function of time since first visit, which had a much higher BIC, suggesting that modelling the SARA score as a function of TSO was more informative.

Total SARA score was modelled as a continuous dependent variable, but it is actually a sum of sub-items measuring different neurological functions. An alternative could be to consider the discrete nature of the sub-scores, using Item Response Theory (IRT) (23) for example. IRT modelling was successfully applied to other composite scores for neurodegenerative diseases (23,24,25). The model involves a latent variable, which informs on the disease severity of a patient and can translate to the probability of scoring a certain grade on any sub scale. For example, a patient having a high score on the gait test could have the same total score as another patient with a lower score on the gait test, but a higher one on the fine motor movement tests, when both subscales could progress at different stages of disease severity. In the context of clinical trials, Buatois et al. (26) showed that, when modelling the MDS-UPDRS scale for patients with Parkinson's Disease, an IRT analysis yielded higher power with no assumption on the drug effect profile. Hamdan et al. (27) developed a cross-sectional IRT model to describe the disease severity in the patients from the ARCA registry. The resulting total score adding sub-items has a sigmoid shape similar to the logistic function we used, so that the total score analysis can be considered as a continuous approximation to the IRT model. Hamdan et al. (27) developed a cross-sectional IRT model to describe the disease severity in the patients from the ARCA registry. They then developed a longitudinal IRT model while investigating Markovian features (work in progress).

In our analysis, we used an innovative approach to build the covariate model in the presence of missing covariates, combining multiple imputation and a pooled test statistic. Methods have been investigated for model selection in the presence of multiple imputation. Covariates can be selected independently on each data set, with a voting at the end (28), or a pooled metric can be applied to select covariates on all imputed data sets simultaneously (7). The pooled LRT p-value we used is asymptotically equivalent the pooled p-value initially derived from Wald's test (7), and was shown to be preferable for testing random effects (29). Another advantage is that using the LRT does not require normality in the complete data model, although it may be more conservative in smaller samples (29). These two approaches were compared with others through simulation studies involving linear and logistic regression models by Wood et al. (28). They notably presented a stacking method, where all imputed data sets are merged into one data set, and a split imputation approach, where covariate selection is performed independently on each imputed data set, with a voting step at the end of the procedure. The stacking approach gave consistent estimates compared to the pooled approach we used, but a penalisation term needs to be included in the likelihood to conserve valid standard error estimates. The split imputation approach was shown to yield underestimated standard errors, and to increase the selection rate of nuisance covariates as it assumes all imputed covariates are real data. Overall, Wood et al. conclude that the pooled p-value method we used was the only one preserving type 1 error in their setting.

The pooled p-value metric used to select covariate effect uses the likelihood of the model across imputed data sets. However, since Importance Sampling was used to evaluate the likelihood of the model, some covariate-parameter relationships could have been penalised due to the stochasticity of the method. To reduce that impact, for the model fitting, at each iteration of the model building, for a given covariate-parameter candidate, the same random seed was assigned to all imputed data sets, to ensure that if only non-imputed covariates are in the model, the likelihood would be the same across all imputed data sets. Another feature is that the method penalises covariate-parameter relationships when covariates have high degree of missing information. The penalisation is twofold, first through the term r (formulas in Supplementary Materials 3), which is proportional to the average difference between the LRT evaluated at the MLE (\(\widehat{d}\)) and the LRT evaluated at the mean MLE \(\left(\overline{d}\right).\) Larger differences between the imputed data sets will translate into larger differences between the MLEs across all imputed data sets, increasing r. A second penalty occurs via \(\nu .\) When there is no difference between \(\widehat{d}\) and \(\overline{d},\) \(\nu =+\infty\), and the F-distribution will converge to a chi square distribution with k degrees of freedom (for k = 1 here, we get the standard threshold of 3.84 for the LRT at 0.05). When r increases, \(\nu\) decreases and the threshold for statistical significance will increase, increasing the p-value and making the test stricter. During covariate selection, the effect of INAS on k was likely not selected because of these two penalties (\(\overline{d}=8.9\), r = 1.25 therefore the statistic becomes D = 3.95 and with \(\nu =17,\) the threshold for statistical significance at 0.05 is 4.45). In the preselection stage, the correlation between the EBEs and the covariates were used. Out of the 24 parameter-covariate relationships, 8 were pre-selected (with the correlation), and the three final covariate effects were among the pre-selected. Although the eta-shrinkage of the EBEs of the parameters was quite high, it may not have had a big impact, since the chosen p-value threshold was large (0.2) and since, even if a covariate effect was not selected during the first stage, it is tested during the second forward step. The covariate genotype of the mutation type of ARSACS (loss of function) was not found significant in our model. It could be due to the fact that, in the complete case, 82% of patients have a loss of function mutation. For the selected covariates, our analysis showed an effect of sex and onset. In (22), for SCA3, disease progression was found to be significantly faster for men. In our model, although being a man decreases \({S}_{0}\) and increases \({S}_{max},\) with the structural model equation equation, it could be interpreted as a faster progression in men at all disease stages (of + 18% with the estimated parameters). In the end, none of the covariates with missing values were selected, so the uncertainty was computed using bootstrap on the original data set. However, a straightforward extension in the presence of imputed covariates would be to pool the bootstrap distributions over the imputed data sets to obtain the uncertainty distribution.

In our model, \(S_0\) represents the score at onset of symptoms, and was estimated to be different from 0, while \({S}_{max}\) was estimated to be around 35. We could not identify individual variability for \({S}_{max},\) implying that all patients will reach a SARA score around those values. In our model, the parameters which most influence the disease progression are k and \({T}_{50},\) which control respectively the sigmoidicity of the curve and the time to fast increase of SARA score. For example, with the parameters estimated for the model with covariates, for women, such values would correspond to an increase of SARA score ranging from 0.05 to 0.75 points/year for early onsets and 0.28–0.82 points per year for late onset patients (TSO = 5 years to\({T}_{50})\), with marginally higher values for men. An analysis of disease progression over the time of follow-up was performed by Traschütz et al. on all major genotypes from the ARCA registry (30). They modelled the evolution of the SARA score with the time since inclusion in the study using linear mixed effect models. They notably found that the slope of progression was 0.12 points/year in the ARSACS group, not statistically different from 0. This can be explained by our model where, depending on the TSO, the slope of disease progression can range from 0 to 0.98 points/year. Gagnon et al. (31) investigated the progression of the SARA score in 19 patients with ARSACS after a two year follow up, reporting a mean yearly progression of 1.3 points/year. In this study, the mean age was 38.3 years, ranging from 25 to 59 years of age, so in our model, most of these patients would be around \({T}_{50},\) at a period of fast progression, assuming an early onset. The interpretation of the effect of the selected covariates on disease progression is unclear. For example, we found that having an AOO greater than 15 years of age resulted as having a T50 13 years lower, meaning that those patients would have a rapid progression at approximately the same age as those with an AOO of 2 years. It is possible therefore that recall bias affected patients self-reporting as late onset if they discounted early symptoms of the disease.

We applied our final model to predict the individual trajectories of patients along with their prediction interval over 5 years after their last visit. Predicting patient trajectories on the individual level could be used for simulations of clinical trials, to estimate the power of a design or to predict which patients are the most informative. We limited the results presented to the patients with a SARA score below 20 points, as clinical trials with disease-modifying drugs currently focus on early or at most moderate disease stages in neurodegenerative diseases where neurodegeneration is not yet too (and likely irreversibly) advanced (32). We investigated the impact of including covariates on the individual predictions. We found that there was little impact on the individual predictions, mainly because those covariates, while being statistically significant, explained only a small portion of the IIV of the parameters of the model. The inclusion of population parameter uncertainty also had little impact on the width of prediction intervals, which we can attribute to the low uncertainty (RSE) on population parameters. This approach will however be extended to other populations in the registry, and since they have fewer patients, we expect the RSE of the population parameters to be higher.

In this work, we developed a workflow using real world data (patient registries) for a rare neurodegenerative disease, handling missing patient information as well as high heterogeneity. Such a workflow could be extended to other Autosomal Recessive Cerebellar Ataxias or other rare diseases.

In the ARSACS dataset, the increase in SARA score and the width of their PI during those 5 years were higher the closer T50 was to the TSO of the observation period (correlation coefficient: -0.65, p-value < 10–8). This suggests that patients recruited at a TSO between 30 and 50, at an intermediate stage of disease, could be the most informative when designing a clinical trial. Our model also predicts a median increase of SARA score of 3 points in 5 years, but with a median width of prediction interval of 7 points. This large uncertainty somewhat undermines the practical usefulness to predict individual progression. This could be explained by our sparse design (only about half of the patient have more than one visit), so many patient trajectories are predicted by the population parameter values, and with individual parameter SE driven mainly by the random effect on \({T}_{50}.\) On the other hand, the covariate category or the number of visits were not strongly associated with the precision of the PI in our analyses, but the dataset had mostly sparse sampling. Repeated longitudinal measurements should however help to get a more accurate prediction of their individual parameters.

In our work, we developed a method to predict individual trajectories at 5 years including uncertainty. We plan to apply this approach to an independent data set to evaluate the predictive ability of our model. In the meantime, we performed an internal evaluation analysis using simulations. Supplementary material 4 reports this evaluation, showing that individual prediction method is unbiased.

In this work, describing the evolution of the SARA score using modelling approaches on a population of ARSACS patients informed us on the heterogeneity of disease progression, which mainly depends on the time since onset. Modelling can then help clinicians determine the likely evolution for a given patient. It could also provide insight on which patients would be the most informative in the context of a clinical trial, helping with patient stratification. A perspective of this work is to investigate model-based designs as an alternative to end of treatment analyses to enhance the power of small size clinical trials.

Conclusion

In this work, we modelled disease progression in patients with a rare neurological disease, using ARSACS as showcase, and investigated the impact of the inclusion of covariates and population parameter uncertainty on individual trajectories of progression and their associated prediction intervals. We combined multiple imputation with a pooled LRT statistic method to select a covariate model with missing covariate values. Although the implementation can be somewhat complex and computationally cumbersome, it ensured missing covariates were properly accounted for. We found that covariates had a moderate impact in explaining disease progression, and that including population parameter uncertainty had little impact on the individual prediction intervals. Our current population analysis was limited by the size of the studied population and could be extended to a larger one, in order to look for other predictors of disease progression. The small impact of the inclusion of population parameter uncertainty could be explained by the low uncertainty in population parameter estimates, and the proposed workflow could be more relevant in other ataxia diagnoses with fewer patients.