Introduction

Structural failures marked by cracks and fracture are significant problems in engineering practice. If a crack occurs in a structure and no action is taken to stop its growth, the crack may propagate until the structure breaks up into pieces. Both theoretical and experimental studies leading to the arrest of crack growth are very needful.

A number of methods of arresting crack growth have been proposed. They include the application of patches to cracked site (Baker [1], O’ Donoghue and Zhuang [2]). The welding method (Ghfiri et al. [3]), the crack arrester method (Makabe et al. [4], Ayatollahi et al. [5]), the stop hole method (Song and shield [6], Murdani et al. [7], Wu et al. [8], Kim [9]). Of particular interest in this study is the stop hole method, where a circular hole is drilled at the vicinity of the crack tip in an attempt to arrest crack propagation by reducing the stress concentration near the crack tip. A survey of the techniques of evaluating the influence of the stop hole on the elastic fields show that experimental and numerical techniques have mostly been used while analytical methods have received less attention. For example, Matsumoto et al. [10], Fanni et al. [11], and Chen [12] used the finite element method to obtain an optimum crack breaker that gives maximum fatigue crack initiation life.

The endeavour in this paper is to obtain a closed form solution for the elastic fields in an orthotropic material containing a semi-infinite crack in the presence of a stop hole.

Formulation

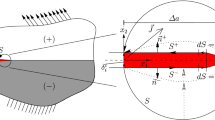
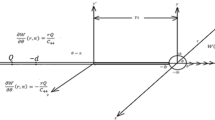
Consider the problem of an infinite elastic orthotropic material containing a semi- infinite crack the tip of which is referred to a moving coordinate system (\(x^{\prime},y^{\prime},z^{\prime}\)) space. The semi-infinite crack occupies the region defined by \(- \infty < x^{\prime} < 0\). A pair of longitudinal shear loads of magnitude \(Q\) is applied along the crack surface on an interval \(\left[ { - a\,,\, - d} \right]\) of length \(L\). A circular crack breaker (stop hole) of radius b is introduced at the center of the orthotropic material which is at the origin of a fixed coordinate system \(\left( {x,y,z} \right)\). Figure 1 illustrates the configuration of the problem under consideration.

Fig. 1
figure 1

Geometry and coordinate system of cracked medium

Full size image

Suppose that, at time \(t = 0\), the crack tip starts to move with constant velocity \(v\) along the \(x^{\prime}\)-direction and ends up at the crack breaker, attaining a displacement \(v\,t\). Suppose, also, that the disturbance due to the load is anti-plane so that it creates only an out of plane displacement and stresses in the \(z\)-direction. The problem is to investigate the influence of the circular stop hole on the stress intensity factor at the crack tip. This necessitates investigating the elastic fields at the point (x,0,0) on the boundary of the crack breaker.

Under anti-plane strain condition, the displacement components \(\left( {u,v,w} \right)\) reduce to \(\left( {0,0,w} \right)\) where \(w = w\left( {x^{\prime},y^{\prime},t} \right)\). Consequently, the only nonzero stress components \(\sigma_{{x^{\prime}z}}\) and \(\sigma_{{y^{\prime}z}}\) are given by

$$\sigma_{{x^{\prime}z}} = c_{44} \frac{\partial w}{{\partial x^{\prime}}},\,\,\,\,\,\sigma_{{y^{\prime}z}} = c_{55} \frac{\partial w}{{\partial y^{\prime}}}$$
(1)

where \(c_{44} = \mu_{xz}\) and \(c_{55} = \mu_{yz}\) are the shear moduli in the \({x}^{^{\prime}}\) and \({y}^{^{\prime}}\) directions.

Accordingly, the equation of motion takes the form

$$\frac{{\partial \sigma_{{x^{\prime}z}} }}{{\partial x^{\prime}}} + \frac{{\partial \sigma_{{y^{\prime}z}} }}{{\partial y^{\prime}}} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(2)

where \(\rho\) is the mass density of the elastic material.

Substituting the stress-displacement relations (1) into Eq. (2) and simplifying the result leads to the two-dimensional wave equation

$$\frac{{\partial^{2} w}}{{\partial x^{{\prime}{2}} }} + \frac{1}{{\eta^{2} }}\frac{{\partial^{2} w}}{{\partial y^{{\prime}{2}} }} = \frac{1}{{c^{2} }}\frac{{\partial^{2} w}}{{\partial t^{2} }}$$
(3)

where \(\eta = \left( {\frac{{C_{44} }}{{C_{55} }}} \right)^{\frac{1}{2}}\) and \(c = \left( {\frac{{C_{44} }}{\rho }} \right)^{\frac{1}{2}}\) is the wave speed.

The corresponding boundary conditions on the crack surface under anti-plane strain loading \(Q\) are as follows:

$$C_{44} \frac{\partial W}{{\partial x^{\prime}}}\left( {x^{\prime},0} \right) = \left\{ \begin{gathered} \pm Q\,\,\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,a \le x^{\prime} \le d\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,{\text{otherwise}} \hfill \\ \end{gathered} \right.$$
(4)
$$\frac{\partial W}{{\partial y^{\prime}}}\left( {b,0} \right) = 0\,\,\,\,,b > 0$$
(5)
$$w\left( {x,0} \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,x > 0$$
(6)

Solution

For a crack moving with constant velocity \(v\) in the \(x^{\prime}\)-direction, it is convenient to introduce the Galilean transformation

$$x = x^{\prime} - vt\,\,\,\,\,\,\,\,\,,\,\,\,y = \eta y^{\prime}\,\,\,\,,\,\,\,\,t^{\prime} = t$$
(7)

With this transformation, the wave equation becomes independent of time and Eq. (3) reduces to Laplace’s two-dimensional equation

$$\nabla^{2} w\left( {x,y} \right) = \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }} = 0$$
(8)

In terms of polar coordinates \(\left( {r,\,\,\theta } \right)\) which are related by.

\(x = r\cos \theta \,\,,\,\,\,\,y = r\sin \theta\), the nonzero stresses are

$$\sigma_{rz} \left( {r,\theta } \right) = C_{55} \frac{\partial W}{{\partial r}}\left( {r,\theta } \right),\;\sigma_{\theta z} \left( {r,\theta } \right) = C_{44} \frac{1}{r}\frac{\partial W}{{\partial \theta }}\left( {r,\theta } \right)$$
(9)

and Eq. (8) becomes

$$\frac{{\partial^{2} w\left( {r,\theta } \right)}}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial w\left( {r,\theta } \right)}}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }} = 0,\;r \ge b\,\,,\,\, - \pi < \theta < \pi$$
(10)

subject to the boundary conditions

$$\frac{\partial w}{{\partial \theta }}\left( {r, \pm \pi } \right) = \left\{ \begin{gathered} \frac{ \pm rQ}{{c_{44} }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a \le r \le d \hfill \\ \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Otherwise}}\,\,(\,r < a\,,\,r > d \hfill \\ \end{gathered} \right.$$
(11)
$$\frac{{\partial w\left( {b,\theta } \right)}}{\partial r} = 0$$
(12)

Let

$$\xi \left( z \right) = \frac{1}{2}\left( {\frac{z}{b} + \frac{b}{z}} \right) - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,,z = re^{i\theta }$$
(13)

Be a holomorphic function which may be expressed in terms a new set of polar coordinates \(\left(\Upsilon,\varnothing \right)\) as

$$\xi \left( z \right) = \Upsilon e^{i\phi } = \Upsilon \cos \phi + i\Upsilon \sin \phi = u(r,\theta ) + iv(r,\theta )$$
(14)

Then, using the holomorphic function defined in Eqs. (13), (10), (11) and (12) transforms to

$$\left( {\frac{{\partial^{2} }}{{\partial \Upsilon^{2} }} + \frac{1}{\Upsilon }\frac{\partial }{\partial \Upsilon } + \frac{1}{{\Upsilon^{2} }}\frac{{\partial^{2} }}{{\partial \phi^{2} }}} \right)W\left( {\Upsilon ,\phi } \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Upsilon > 0,\,\,\,\,\,\,0 \le \phi \le \pi$$
(15)

Subject to the boundary condition

$$\frac{{\partial W\left( {\Upsilon ,\pi } \right)}}{\partial \phi } = \left\{ \begin{gathered} \frac{bQ\Upsilon }{{c_{44} }}\left[ {\frac{{\left( {\Upsilon - 1} \right)}}{{\sqrt {\Upsilon \left( {\Upsilon - 2} \right)} }} + 1} \right]\,\,\,\,\,\,\,\,\,\,,\,\alpha < \Upsilon < \beta ,\,\,\,\,\alpha = \frac{1}{2}\left( {\frac{d}{b} + \frac{b}{d} + 2} \right),\beta = \frac{1}{2}\left( {\frac{d}{b} + \frac{b}{d} + 2} \right) \hfill \\ \hfill \\ \hfill \\ 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{otherwise}} \hfill \\ \end{gathered} \right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$
(16)
$$\frac{\partial W}{{\partial \phi }}\left( {\Upsilon ,\phi } \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \le \phi \le \pi$$
(17)
$$W\left( {\Upsilon ,0} \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Upsilon > 0$$
(18)

Solution of the transformed problem

Applying Mellin integral transform of \(W\left( {\Upsilon ,\phi } \right)\) defined by \(\overline{W}\left( {s,\phi } \right) = \int\limits_{0}^{\infty } {W\left( {\Upsilon ,\phi } \right)\Upsilon^{s - 1} \partial \Upsilon }\),to eqns. (15–18), the differential equation derived is

$$\frac{{d^{2} }}{{d\phi^{2} }}\overline{W}\left( {s,\phi } \right) + s^{2} \overline{W}\left( {s,\phi } \right) = 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{2} < {\text{Re}} s < 0$$
(19)

The solution of Eq. (19), subject to the boundary conditions (16–18) is

$$\overline{W}\left( {s,\phi } \right) = \frac{bQ}{{c_{44} }}{\mathfrak{M}}\left( {\beta ,\alpha ;s} \right)\frac{\sin \phi s}{{s\cos \pi s}}$$
(20)

where

$${\mathfrak{M}}\left( {\beta ,\alpha ;s} \right) = \int\limits_{\sigma }^{\tau } {\left( {\Upsilon^{s} \left( {1 - \frac{2}{\Upsilon }} \right)^{{\, - \,\,\,\,\frac{1}{2}}} - \Upsilon^{s - \,\,1} \left( {1 - \frac{2}{\Upsilon }} \right)^{{\, - \,\,\,\,\frac{1}{2}}} + \Upsilon^{s} } \right)\partial \Upsilon }$$
(21)

The inverse Mellin transform of \(\overline{W}\left( {s,\phi } \right)\) is \(W\left( {\Upsilon ,\phi } \right) = \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\overline{W}\left( {s,\phi } \right)\Upsilon^{ - s} ds}\), hence

$$W\left( {\Upsilon ,\phi } \right) = \frac{bQ}{{c_{44} }}\frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\mathfrak{M}} \left( {\beta ,\alpha ;s} \right)\frac{\sin \phi s}{{s\cos \pi s}}\Upsilon^{ - s} ds$$
(22)

Evaluating the integrals in (21) term by term using the convergent series, Nnadi [13]

$$\left( {1 - t} \right)^{{ - \frac{1}{2}}} = \sum\limits_{k = 0}^{\infty } {c_{k} t^{k} ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left| t \right| < 1} ,$$
(23)

where the coefficients are defined by

$$c_{k} = \frac{{\left( {2k} \right)!}}{{2^{2k} \left( {k!} \right)^{2} }}$$
(24)

For the first term, we have

$$\begin{gathered} \int\limits_{\alpha }^{\beta } {\rho^{s} \left( {1 - \frac{2}{\Upsilon }} \right)^{{\, - \,\,\,\,\frac{1}{2}}} } \partial \Upsilon = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \int\limits_{\alpha }^{\beta } {\Upsilon^{s - k} \partial \Upsilon } } \hfill \\ \quad \quad \quad \quad \quad \quad \quad = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\rho^{s - k + 1} }}{s - k + 1}} \right]_{\alpha }^{\beta } } = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k + 1} - \alpha^{s - k + 1} }}{s - k + 1}} \right]} \hfill \\ \end{gathered}$$
(25)

For the second term,

$$\begin{gathered} \int\limits_{\alpha }^{\beta } {\Upsilon^{s - \,\,1} \left( {1 - \frac{2}{\Upsilon }} \right)^{{\, - \,\,\,\,\frac{1}{2}}} \partial \Upsilon = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \int\limits_{\alpha }^{\beta } {\Upsilon^{s - k - 1} \partial \Upsilon } } } \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \, = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\Upsilon^{s - k} }}{s - k}} \right]_{\alpha }^{\beta } } = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k} - \alpha^{s - k} }}{s - k}} \right]} \hfill \\ \end{gathered}$$
(26)

For the third term,

$$\int\limits_{\alpha }^{\beta } {\Upsilon^{s} \partial \Upsilon = \left[ {\frac{{\Upsilon^{s + 1} }}{s + 1}} \right]_{\alpha }^{\beta } } = \frac{{\beta^{s + 1} }}{s + 1} - \frac{{\alpha^{s + 1} }}{s + 1}$$
(27)

Hence,

$${\mathfrak{M}}\left( {\beta ,\alpha ;s} \right) = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k + 1} - \alpha^{s - k + 1} }}{s - k + 1}} \right]} - \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k} - \alpha^{s - k} }}{s - k}} \right]} + \left[ {\frac{{\beta^{s + 1} }}{s + 1} - \frac{{\alpha^{s + 1} }}{s + 1} - } \right]$$
(28)

Inserting Eq. (28) into (22), we obtain

$$W\left( {\Upsilon ,\phi } \right) = \frac{bQ}{{c_{44} }}\left( {I_{\alpha \beta }^{(1)} - I_{\alpha \beta }^{(2)} + I_{\alpha \beta }^{(3)} } \right)$$
(29)

Term by term evaluation of the three terms in Eq. (27) yields

$${\mathfrak{M}}\left( {\beta ,\alpha ;s} \right) = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k + 1} - \alpha^{s - k + 1} }}{s - k + 1}} \right]} - \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \left[ {\frac{{\beta^{s - k} - \alpha^{s - k} }}{s - k}} \right]} + \left[ {\frac{{\beta^{s + 1} }}{s + 1} - \frac{{\alpha^{s + 1} }}{s + 1} - } \right]$$
(30)

Inserting Eq. (30) into (29), we obtain

$$W(\Upsilon ,\phi ) = \frac{bQ}{{c_{44} }}\left\{ {I_{\beta }^{(1)} - I_{\beta }^{(2)} + I_{\beta }^{(3)} } \right\} - \frac{bQ}{{c_{44} }}\left\{ {I_{\alpha }^{(1)} - I_{\alpha }^{(2)} + I_{\alpha }^{(3)} } \right\}$$
(31)

where

$$\mathop I\nolimits_{\beta }^{\left( 1 \right)} = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \beta^{1 - k} \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s - k + 1} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\beta }} \right)^{ - s} ds} }$$
(32)
$$\mathop I\nolimits_{\alpha }^{\left( 1 \right)} = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \alpha^{1 - k} \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s - k + 1} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\alpha }} \right)^{ - s} ds} }$$
(33)
$$\mathop I\nolimits_{\beta }^{\left( 2 \right)} = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \beta^{ - k} \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s - k} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\beta }} \right)^{ - s} ds} }$$
(34)
$$\mathop I\nolimits_{\alpha }^{\left( 2 \right)} = \sum\limits_{k = 0}^{\infty } {c_{k} 2^{k} \alpha^{ - k} \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s - k} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\alpha }} \right)^{ - s} ds} }$$
(35)
$$\mathop I\nolimits_{\beta }^{\left( 3 \right)} = \beta \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s + 1} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\beta }} \right)^{ - s} } ds$$
(36)
$$\mathop I\nolimits_{\alpha }^{\left( 3 \right)} = \alpha \frac{1}{2\pi i}\int\limits_{e - i\infty }^{e + i\infty } {\frac{\sin \phi s}{{\left( {s + 1} \right)s\cos \pi s}}\left( {\frac{\Upsilon }{\alpha }} \right)^{ - s} } ds$$
(37)

The first part of Eq. (31) represents the displacement field for \(\Upsilon < \beta\) and the second part of the same equation represents the displacement field for \(\,\Upsilon < \alpha\).

Evaluating the integrals \(\mathop I\nolimits_{\beta }^{\left( j \right)} \,\,\,and\,\,\,\,\mathop I\nolimits_{\alpha }^{\left( j \right)} \,\,\,\,\,\,\,,\,\,j = 1,\,2,3\) using residue theory and Jordan lemma,

we obtain the first part of Eq. (31) (i.e., the displacement field for \(\Upsilon < \beta\)) as

$$\begin{gathered} \frac{bQ}{{c_{44} }}\left( {\mathop I\nolimits_{\beta }^{\left( 1 \right)} - \mathop I\nolimits_{\beta }^{\left( 2 \right)} + \mathop I\nolimits_{\beta }^{\left( 3 \right)} } \right) = \frac{bQ}{{c_{44} }}\left\{ { - 2\sin \phi \Upsilon + \frac{2\beta }{\pi }\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {\frac{3}{2} - n} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} } \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {c_{1} 2^{1} - c_{2} 2^{2} } \right)\frac{1}{\pi \beta }\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{1}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} + \left( {c_{1} 2^{1} - c_{2} 2^{2} } \right)\frac{1}{\pi \beta }\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{1}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {c_{3} 2^{3} - c_{4} 2^{4} } \right)\frac{1}{{\pi \beta^{3} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{5}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} + \left( {c_{4} 2^{4} - c_{5} 2^{5} } \right)\frac{1}{{\pi \beta^{4} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{7}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {c_{5} 2^{5} - c_{6} 2^{6} } \right)\frac{1}{{\pi \beta^{5} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{9}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} + \left( {c_{6} 2^{6} - c_{7} 2^{7} } \right)\frac{1}{{\pi \beta^{6} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\beta }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{11}{2}} \right)\left( {n - \frac{1}{2}} \right)}} + ...} } \right\} \hfill \\ \end{gathered}$$
(38)

Also, the second part of Eq. (31) (i. e. the displacement field] for \(\,\Upsilon < \alpha\)) is obtained as

$$\begin{gathered} \frac{bQ}{{c_{44} }}\left( {\mathop I\nolimits_{\alpha }^{\left( 1 \right)} - \mathop I\nolimits_{\alpha }^{\left( 2 \right)} + \mathop I\nolimits_{\alpha }^{\left( 3 \right)} } \right) = \frac{bQ}{{c_{44} }}\left\{ { - 2\sin \phi \Upsilon + \frac{2\alpha }{\pi }\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\alpha }} \right)^{{n - \frac{1}{2}}} }}{{\left( {\frac{3}{2} - n} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} } \right. \hfill \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {c_{1} 2^{1} - c_{2} 2^{2} } \right)\frac{1}{\pi \alpha }\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\alpha }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{1}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} + \left( {c_{2} 2^{2} - c_{3} 2^{3} } \right)\frac{1}{{\pi \alpha^{2} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\alpha }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{3}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} \hfill \\ \left. {\quad \quad \quad \quad \quad \quad \quad \quad \quad + \left( {c_{3} 2^{3} - c_{4} 2^{4} } \right)\frac{1}{{\pi \alpha^{3} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\alpha }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{5}{2}} \right)\left( {n - \frac{1}{2}} \right)}}\,\,\,\,} + \left( {c_{4} 2^{4} - c_{5} 2^{5} } \right)\frac{1}{{\pi \alpha^{4} }}\sum\limits_{n = 1}^{\infty } {\frac{{\left( { - 1} \right)^{n + 1} \sin \left( {n - \frac{1}{2}} \right)\phi \left( {\frac{\Upsilon }{\alpha }} \right)^{{n - \frac{1}{2}}} }}{{\left( {n + \frac{7}{2}} \right)\left( {n - \frac{1}{2}} \right)}} + ...} } \right\} \hfill \\ \end{gathered}$$
(39)

Results and discussion

Stress field near the crack-tip

We investigate the tip of the crack for the stress field, using the solution obtained above.

The tip is at the origin and is approached as \(\Upsilon \to 0\). The asymptotic value of the displacement field is obtained as

$$W\left( {\Upsilon ,\phi } \right) = \frac{4bQ}{{\pi c_{44} }}\left( {\frac{H\left( \beta \right)}{{\sqrt \beta }} - \frac{H\left( \alpha \right)}{{\sqrt \alpha }}} \right)\sin \frac{\phi }{2}\Upsilon^{\frac{1}{2}}$$
(40)
$${\text{where}}\;\frac{H\left( \eta \right)}{{\sqrt \eta }} = \sqrt \eta + \frac{{\sin^{ - 1} \left( {\frac{2}{\eta }} \right)^{\frac{1}{2}} }}{\sqrt 2 } + \sqrt \eta \left( {1 - \frac{2}{\eta }} \right)^{\frac{1}{2}} - \sqrt {2c} \,\,\,,\,\,\left( {\eta = \alpha ,\,\beta } \right)$$
(41)

We introduce local polar coordinates \(\left( {R,\psi } \right)\) at the intersection of the crack breaker boundary and the \(x\)-axis that are related to the coordinates \(\left(\Upsilon ,\mathrm{ \varnothing }\right)\) through

$$\Upsilon^{\frac{1}{2}} \sin \frac{\phi }{2} = \frac{1}{\sqrt 2 }\frac{R}{b}\sin \psi \,\,\,\,\,\,\,\,\,\,\,as\,\,\Upsilon \to 0,\,\,\,\,R \to 0$$
(42)

Then, by the conformality condition \(W(\rho ,\phi ) = w(R,\psi )\) , the asymptotic displacement becomes

$$\begin{gathered} w\left( {R,\psi } \right) = \frac{4bQ}{{\pi c_{44} }}\left( {\frac{H\left( \beta \right)}{{\sqrt \beta }} - \frac{H\left( \alpha \right)}{{\sqrt \alpha }}} \right)\frac{1}{\sqrt 2 }\frac{R}{b}\sin \psi = \frac{{k_{III} }}{\sqrt \pi }\frac{1}{{c_{44} }}\frac{R}{b}\sin \psi \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$
(43)

where

$$\begin{gathered} K_{III} = \frac{{2\sqrt {2\,\,} bQ}}{\sqrt \pi }\left( {\frac{H\left( \beta \right)}{{\sqrt \beta }} - \frac{H\left( \alpha \right)}{{\sqrt \alpha }}} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$
(44)

Now,

$$\begin{gathered} \frac{{\partial w\left( {R,\psi } \right)}}{\partial \psi } = \frac{{K_{III} }}{\sqrt \pi }\frac{1}{{c_{44} }}\frac{R}{b}\cos \psi \,\,\,, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered}$$
(45)

Hence, the near crack-tip stress field is given by

$$\sigma_{\psi z} \left( {R,\psi } \right) = c_{44} \frac{1}{R}\frac{{\partial w\left( {R,\psi } \right)}}{\partial \psi } = \frac{{k_{III} }}{b\sqrt \pi }\cos \psi$$
(46)

Equation (46) shows that the near crack-tip stress field is directly proportional to mode III stress intensity factor, \({K}_{III}\) and inversely proportional to the radius of the circular hole, \(b\).

Effect of size of the circular hole on the stress field

The result (47) means that the larger the radius of the circular hole, the less the stress concentration factor. In effect, crack growth would be delayed, or even prevented. The relationship between the stress field and the radius of the crack breaker is illustrated graphically in Fig. 2. The graph shows that the larger the radius of the crack breaker, the lower the stress values at the crack tip. The physical implication is that placing a large circular hole at the crack tip would contribute to an extension of the life of the material. This result agrees with the numerical results found in [10, 11] and [12].

Fig. 2
figure 2

Variation of \(\sigma_{\psi z} \left( {R,\psi } \right)\) with \(b\)

Full size image

Effect of load application interval length on the stress intensity factor

A parametric study is introduced to investigate the effect of the length \(L\) of interval of application of the load and the radius of the crack breaker, on the stress intensity factor.

Using Eqs. (41) and (45), we obtain the normalized stress intensity factor

$$\frac{{K_{111} }}{Q} = \frac{2L\sqrt 2 }{{\sqrt \pi }}\left[ {\frac{\beta - \alpha }{{\sqrt \beta + \sqrt \alpha }} + \frac{1}{\sqrt 2 }\sin^{ - 1} \left( {\frac{{\sqrt {\frac{2}{\beta }} \sqrt {\frac{2}{\alpha }} \frac{{\left( {\beta - \alpha } \right)}}{2}}}{{\sqrt {\frac{\alpha }{2} - 1} + \sqrt {\frac{\beta }{2} - 1} }}} \right) + \frac{\beta - \alpha }{{\sqrt {\beta - 2} + \sqrt {\alpha - 2} }}} \right]\frac{b}{L}$$
(47)

As we vary the length,\(L\), of the interval \(\left[ { - \alpha , - \beta } \right]\) and substituting the corresponding values of \(\beta \,,\,\alpha\) in Eq. (47), plotting \(\frac{{k_{111} }}{Q}\) with \(\frac{b}{L}\) to have.

Conclusion

In this paper, the influence of a circular crack breaker on mode III deformation behaviour of a semi-infinite crack in a homogeneous elastic orthotropic material subjected to longitudinal shear loads is studied. The novelty of constructing a holomorphic function that mapped the circular hole into a straight line with the edge terminating at the origin as shown in Fig. 3, enabled the use of integral transform method to obtain an analytic solution of the displacement, leading to closed-form expression for the mode-III stress intensity factor,\(K_{111}\).

Fig. 3
figure 3

The transformed configuration of the original problem

Full size image

The results show that the larger the radius of the circular hole, the less the stress concentration factor. In effect, crack growth would be delayed, or even prevented and, thus, the life of the material would be extended. Further, the stress intensity factor was shown in Fig. 4 to increase with increasing length of interval of load application. Our analytical results agree with numerical results found in the literature.

As analytical solutions in closed form are desirable for accurate analysis and design due to their many advantages over numerical solutions, this study significantly contributes to the theory of antiplane crack propagation and arrest. It provides a theoretical basis for considering the use of a circular crack breaker for crack arrest [14], and the results serve as a benchmark for the purpose of judging the accuracy and efficiency of various numerical methods [15]. This study will be immensely useful to industries where orthotropic material such as fibre-reinforced composites have many applications in technology [16, 17].

Fig. 4
figure 4

Variation of \(\frac{{k_{111} }}{Q}\) with \(\frac{b}{L}\)

Full size image