Introduction

Chemical engineering draws from a wide range of disciplines such as physics, chemistry, computer science, mathematics, operations research, and the life sciences. Almost seven decades ago during World War II the rising demands for penicillin was met by co-opting chemical engineering principles to carry out large-scale fermentation. A quadruple rise in production was achieved by refining the original mold species, developing an effective growth medium, and changing the fermentation process from rudimentary surface culture to submersion in tanks [1].

These early efforts were the vanguards of current mechanistic descriptions of biological processes. Cellular metabolism is a temporally-varying process that gives rise to a wide variety of dynamical phenomena such as multiple steady states and temporal oscillations. The elucidation, and subsequent prediction of the behavior of metabolic systems is one of the major challenges of the postgenomic era [2,3,4]. To this end, significant strides have been made in recent years to construct and investigate detailed models of cellular processes [5,6,7,8]. Such a model can be treated as a “virtual laboratory” that allows one to build a characteristic description of the system and elucidate an understanding of the design principles of cellular functions, robustness, adaptability, and optimality. The insights gleaned can then be translated into the rational engineering of microbes to serve as miniature chemical factories to produce products of interest. Microbial fermentation is a popular production mode for many biofuels and biochemicals as it generally (1) relies on a sustainable feedstock (i.e., usually sugars), (2) involves a reduced environmental footprint, (3) is easily scalable, and (4) bypasses the need for complex separations.

The goal of this article is to review how chemical engineering is playing a germane role in the study of metabolic networks. We first describe the use of principles such as reaction kinetics and linear programming in modeling metabolic networks. This is followed by a description of the tools used to identify the processes that control and limit flux in biological systems. Finally, we discuss the challenges and opportunities associated with the successful establishment of microbial chemical factories.

Steady-state analysis of metabolic networks

A cell’s metabolism is described by the gamut of biochemical conversions occurring within it that work together to support life. Cells intake carbohydrates, proteins, lipids, and many small molecules and ions. These species, called metabolites, act as building materials and fuel for the cell as it grows, exports and imports materials from its environment, and replicates its genome in order to divide and multiply. A metabolic network can be used to model these reactions using principles derived from chemical kinetics. A basic premise is conservation of mass – if Xi(t) is the mass of a chemical species i at time t, then accordingly

$$ {X}_i\left(t+\Delta t\right)-{X}_i(t)=\left({v}_{i, in}-{v}_{i, out}\right)\Delta t $$

where vi, in and vi, out are the flux rates at which species i is created and consumed per unit time ∆t, respectively. Thus, as ∆t → 0, the above equation can be written as

$$ \frac{d{X}_i}{dt}={v}_{i, in}-{v}_{i, out} $$

The entire set of metabolic reactions can be represented as a stoichiometric matrix S whose entries are the stoichiometric coefficients of every metabolite i in every reaction j. A metabolic quasi-steady state is assumed, based on the fact that metabolic reactions are typically much faster compared to the time-scale of cellular growth and environmental changes. Thus, all metabolic fluxes that lead to the production and degradation of metabolites must balance, leading to the flux balance eq. [9, 10]:

$$ \mathbf{S}\bullet \mathbf{v}=\mathbf{b} $$

where v is the vector of metabolic fluxes, S the stoichiometric matrix, and b is a vector containing the net metabolite uptake/secretion rates. The resulting system is typically under-determined (due to metabolites participating in multiple reactions) and an objective function is introduced as a teleological driver of cellular metabolism. If c(v) is the objective function (usually maximizing organism growth), the resultant linear programming model is

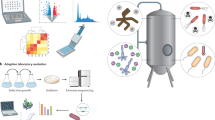
$$ \max \left\{\ c\left(\mathbf{v}\right):\mathbf{Sv}=0,\mathbf{LB}\le \mathbf{v}\le \mathbf{UB}\right\} $$

where LB and UB are vectors representing the lower and upper bounds on the reaction fluxes. The above is the most common example of flux balance analysis (FBA) [11]. To construct such a mathematical formulation, two major inputs are required – 1) information of all the metabolic enzymes existing in an organism, as this will inform the possible metabolic conversions, and 2) demands placed on the system (see Fig. 1 for an overview of the reconstruction process). This includes processes such as growth (modelled as flux through a biomass synthesis reaction), maintenance requirements, or secretion of a product of interest.

A genome-scale metabolic model (GSM) includes internal metabolic conversions as well as the reactions transporting metabolites in and out of cells. Thus, reactions can be limited by the resources available in the environment, resulting in a flexible network structure that can adapt to different ecological niches and perturbations. For instance, an E. coli cell can survive with or without oxygen, investigations of which using FBA captured the varied routes of energy production and protein biosynthesis employed under the two regimes [12]. The same metabolic model can be used in both cases by simply adjusting the bound of the reaction that transports oxygen into the cell.

FBA has been used to make significant contributions to understanding biochemical networks and metabolic engineering. Its primary goal is to design engineered organisms that can achieve higher efficiencies in metabolite overproduction through alterations in the flux distribution. This has been realized in numerous cases such as lycopene [13] and butanol [14] production in E. coli, and lysine production in Corynebacterium glutamicum [15]. FBA can also be used to improve productivity such as by optimizing process parameters and rationally designing the cell culture medium. Optimal uptake rates were first computed using FBA and then used to alter the nutrient feed composition in a hybridoma culture which reduced waste accumulation by several folds [16]. A metabolic model of E. coli was used to determine culture conditions that increased strain stability by optimizing the glucose to oxygen supply ratio [17].

FBA predictions have been found to achieve biological fidelity -- its ability to identify essential genes (i.e., genes whose deletion negates biomass synthesis) exceeds 90% in many metabolic models [18]. Thus, such analyses can be used to glean insights into an organism’s physiology by examining its metabolism quantitatively. For instance, input vs output trade-offs can be computed that describe the impact of nutrient supply rates on by-product secretion and/or growth. Such a study in E. coli predicted growth rates to increase with the nutrient supply, as is expected, but at higher growth rates the secretion of metabolites such as acetate was also predicted [19]. This is because the oxygen utilization capacity is reached at higher growth rates and the cell thus possesses surplus reductive potential. This leads to a redistribution of metabolic fluxes and by-products (such as acetate) are secreted so as to eliminate the surplus redox potential [20,21,22].

Dynamic models of metabolism

FBA considers metabolism using only reaction stoichiometry and reversibility subject to a steady-state condition. Thus, such a framework performs well when predicting the long-term response of the system to environment or genetic perturbations [23] but is unable to explain transient behavior or even how a specific metabolite state is achieved [24, 25]. In the absence of any regulatory or mechanistic information, the in silico solution space available to constraint-based models is much larger than the biologically feasible sample space [14, 15]. Thus, attempts to engineer microbial systems as in cell factories to overproduce metabolites must consider the kinetics associated with their production pathways along with the interaction of the designated pathways with the entire metabolic network.

Efforts to construct genome-scale dynamic models have been made by extending constraint-based models -- starting from stationary fluxes and introducing pseudo-kinetic behavior, such as in dynamic FBA (DFBA) [26, 27] and structural kinetic modeling [28, 29]. DFBA works by first discretizing the time period into intervals and then solving the following optimization problem at the beginning of each interval to obtain fluxes at that instant:

$$ \underset{\mathbf{v}(t)}{\max}\sum {w}_j{v}_j(t) $$

s.t.

$$ \mathbf{X}\left(t+\Delta T\right)\ge 0 $$
$$ \mathbf{v}(t)\ge 0 $$
$$ c\left(\mathbf{v}(t),\mathbf{X}(t)\right)\le 0,\forall t\in \left[{t}_0,{t}_f\right] $$
$$ \left|\mathbf{v}(t)-\mathbf{v}\left(t-\Delta T\right)\right|\le {\dot{\mathbf{v}}}_{max}\Delta T,\forall t\in \left[{t}_0,{t}_f\right] $$
$$ \mathbf{X}\left(t+\Delta T\right)=\mathbf{X}(t)+\mathbf{Sv}\Delta T $$
$$ {X}_{biomass}\left(t+\Delta T\right)={X}_{biomass}(t)+\mu {X}_{biomass}(t)\Delta T $$

Where X is the vector of metabolite concentrations (Xbiomass represents the concentration of the biomass metabolite), μ is the growth rate, and wj is the vector of weights associated with the objective function in the current time interval ∆T. t0 and tf represent the initial and final time points. The non-linearity in this formulation arises from the kinetic expressions for flux rates contained in the vector c(v(t), X(t)), usually used to constrain input fluxes. The flux values so obtained are considered to be constant over the current time interval and are then used to solve a dynamic model describing metabolite time profiles. Mahadevan et al. [26] used DFBA to describe the biphasic growth of E.coli on glucose and acetate. They could successfully predict the onset of acetate production and sequential substrate utilization where E. coli preferred glucose followed by acetate instead of simultaneous utilization. Furthermore, they could also qualitatively match the predicted rates of metabolite consumption to those measured experimentally. Since then DFBA has been used to predict the accumulation of high-value storage compounds in microalgae under varying light and nutrient conditions [30], determine optimal aerobic and anaerobic culture times and thus scale-up a batch culture of ethanol production in S. cerevisiae by 5-folds [31], and optimize glucose and ethanol production in E. coli by calculating the optimal flux profile for reactions controlled by genes under genetic perturbation [32].

Thus, DFBA as an extension of classical FBA can indeed be used to analyze the dynamic reprogramming of a network [33], especially in response to external perturbations. However, it still hinges on the inherent assumption that the time constants related to intracellular dynamics are much smaller than those describing changes in external concentrations. This is not always true for biological systems as they exhibit control on various levels and thus a direct kinetic description of metabolism that incorporates regulatory mechanisms would likely lead to a higher biological fidelity. For instance, analysis of a hybrid kinetic-FBA model of S. cerevisiae demonstrated that the inclusion of a relatively small number of enzyme kinetic expressions substantially improves the predictive accuracy of FBA, especially if these are used to describe initial reactions in the metabolism of exogenous substrates and reactions at crucial metabolic branch points [34].

Kinetic models of metabolism take the next step in this direction by using mechanistic enzyme kinetics to model network fluxes which is subject to thermodynamic and regulatory constraints and the underlying network stoichiometry. Kinetic models can thus account for changes in metabolite concentrations while capturing the non-linearities inherently present in the system [35, 36]. A set of ordinary differential equations are used to model the temporal concentration of each metabolite -

$$ \frac{d\mathbf{X}}{dt}=\mathbf{Sv}\left(\mathbf{E},\mathbf{X},\mathbf{k}\right),\mathbf{X}\left(\mathbf{0}\right)={\mathbf{X}}_{\mathbf{0}} $$

Where the reaction flux v is a function of metabolite concentrations X, kinetic parameters k, and enzyme concentrations E, and X0 represents the initial metabolite concentrations. Because many of the enzyme kinetic parameters are unknown, approximating kinetic mechanisms is a way to improve the tractability of these models when applied to large networks [37]. These include substitutes such as power-law, lin-log and log-lin kinetics, and modular rate laws (reviews of the various rate laws and their differences can be found in [38, 39]). Due to a lack of experimentally-measured kinetic parameters, many times in vitro kinetic data is used to fit and approximate in vivo enzyme kinetics [40, 41]. The thermodynamic feasibility of kinetic models can be enforced using the generalized Wegsheider condition: BT log Keq = 0, where B is the right null space of the stoichiometric matrix S [42, 43]. This enforces thermodynamic feasibility by constraining the values of Keq for every reaction such that a reaction flux can be non-zero only if the corresponding change in the reaction’s Gibbs free energy is negative.

To counter the paucity of data, a top-down modeling approach is used, wherein model parameters are adjusted iteratively using an optimization routine until the model predicted flux distribution matches the one observed. This method uses Monte Carlo modeling to reduce parameter uncertainty by replacing the use of a single set of parameters by multiple parameter sets obtained through random sampling [44,45,46]. The feasibility of these methods is improved by defining the parameter space on the basis of known in vivo information before sampling commences. Model validation in this approach involves comparing against data from a different physiological state, usually nutrient stress or a mutant strain [47]. There are three primary frameworks in existence for Monte Carlo modeling in genome-scale reconstructions – ORACLE [48,49,50], Jacobian-based structural kinetic models (SKMs) [51] and Ensemble Modeling [52,53,54,55]. The ensemble modeling approach was recently used to construct a genome-scale kinetic model of E. coli called k-ecoli457, consisting of 457 reactions, 337 metabolites, and 295 substrate-level regulatory interactions [52]. Model parameterization was done via a genetic algorithm where all available fluxomic data was simultaneously imposed. The k-ecoli457 model [52] was able to capture a wide array of perturbations, with a Pearson correlation coefficient of 0.84 between the experimental data and predicted product yields for 320 engineered strains spanning 24 product metabolites. More recently, the K-FIT decomposition based parameterization approach was introduced [56] which offers orders of magnitude improvement in parameterization times allowing for detailed a posteriori local sensitivity analyses. Despite their obvious virtues, constructing detailed kinetic models remains challenging. For instance, the latest E. coli constraint-based model contains 2719 reactions involving 1192 metabolites and spans 1515 genes (accounting for ~ 34% of the genome) [57].

The overarching goal is to be able to capture the hierarchical organization seen in biological systems, where the overall phenotype is a function of the inherent cooperativity between layers such as the transcriptome, metabolome, and proteome. Whole-cell computational models are a step in that direction and are able to predict a wide range of cellular behavior by incorporating the function of each gene, gene product, and metabolite [58, 59]. Cellular functions are split into independent modules describing processes such as DNA replication, segregation, and repair, RNA transcription, protein folding, ribosome assembly, and biochemical conversions modelled via metabolic networks. These modules are then integrated and the overall model performance validated against known properties such as organism doubling time, cellular chemical composition, and gene expression. Thus, whole cell models herald a new age of biological discovery driven by in silico modeling, but the data- and computationally-intensive inputs are a major deterrent to their construction and accessibility [60, 61].

Metabolic control analysis

Reaction properties such as rate and efficiency can be tweaked by altering metabolite concentrations and the catalytic and binding properties of enzymes. Enzymes enable high metabolic flux rates by acting as primary ‘levers’ governing a cell’s metabolism constrained by the thermodynamics and stoichiometry of the system. Drug design was one of the first paradigms under which modification of metabolism was attempted: by identifying and therapeutically targeting ‘essential metabolic pathways’ in a pathogen. This rational drug design was based on Hans Krebs’ proposition that once the exact description of a metabolic pathway has been given, the ‘pacemaker enzyme’ (i.e., the rate-limiting step) can be identified and this controls flux through the entire pathway.

However, the flux through most biological pathways has been seen to be controlled by more than one enzyme. Glycolysis, which is responsible for breaking down glucose to release energy for cellular processes and provide precursors for downstream metabolic pathways, has been found to be controlled by three enzymes – hexokinase (HK), phosphofructokinase (PFK), and pyruvate kinase (PK) [62]. These enzymes are the slowest in the pathway (Vmax values lower than the rest by at least an order of magnitude) and catalyze reactions that operate far away from equilibrium (ratio of mass-action ratio to equilibrium constant ~ 10− 3 to 10− 4). Hence, it becomes necessary to quantitatively determine the degree of control that a given enzyme exerts on the flux through the entire pathway and/or the final rate of product formation so as to be able to rationally reengineer metabolism.

Metabolic control analysis (MCA) quantifies the degree of control that a given enzyme in a pathway exerts on the flux and on the concentration of metabolites. This is done by determining the dependence of system variables (such as the rate of a reaction or the concentration of a metabolite) on enzymatic parameters such as the activity or concentration of an enzyme. Control coefficients \( {C}_{E_k}^{v_j} \) and \( {C}_{E_k}^{X_i} \) can be calculated which indicate the steady-state change in the concentration of metabolite Xi or flux vj, respectively, in response to a perturbation in the enzyme concentration or activity (Ek). Thus, the flux control coefficient (\( {C}_{E_k}^{v_j} \)) and concentration control coefficient (\( {C}_{E_k}^{X_i} \)) are defined as:

$$ {C}_{E_k}^{v_j}=\left(\frac{\partial {v}_j}{\partial\ {E}_k}\right)\left(\frac{E_{k,o}}{v_{j,o}}\right) $$
$$ {C}_{E_k}^{X_i}=\left(\frac{\partial {X}_i}{\partial\ {E}_k}\right)\left(\frac{E_{k,o}}{X_{i,o}}\right) $$

Here, \( \left(\frac{E_{k,o}}{v_{j,o}}\right) \) and \( \left(\frac{E_{k,o}}{X_{i,o}}\right) \) are scaling factors used to obtain dimensionless and normalized values of the flux coefficients. They represent the ratio between the initial values from which the slopes \( \left(\frac{d{v}_j}{\partial\ {E}_k}\right) \) and \( \left(\frac{d{X}_i}{\partial\ {E}_k}\right) \) are calculated. Two summation theorems have been shown to hold for control coefficients [63]:

$$ {\sum}_{k=1}^K{C}_{E_k}^{v_j}=1 $$
$$ {\sum}_{k=1}^K{C}_{E_k}^{X_i}=0 $$

If a small change in Ek causes a significant variation in flux vj, then the enzyme exerts high flux control. Similarly, if a minor change in vj is observed when Ek is varied a lot, then the enzyme does not exert significant flux control.

MCA has indeed been used to analyze control in a metabolic pathway and rationally identify potential enzymatic intervention targets, such as in the parasite Entamoeba histolytica which causes amebiasis in humans. E. histolytica does not have a functional mitochondrion, TCA cycle enzymes, or the oxidative phosphorylation pathway. Thus, glycolysis is the only route of generating ATP, the primary energy ‘currency’ of the cell, and thus inhibiting this pathway will potentially cripple this parasite. Saavedra et al. [64] constructed a kinetic model of this organism’s glycolytic pathway in order to determine its distribution of control. They found that the majority of control is distributed between HK and phosphoglycerate mutase (PGAM). The amoeba model was also used for evaluating the effect of inhibiting individual enzymes and its effect on flux through the entire pathway. Model predictions indicate that in order to reduce glycolytic flux and ATP levels by 50%, HK and PGAM should be inhibited by 24 and 55%, respectively, or both enzymes by 18%. In contrast, if other enzymes such as phosphofructokinase and pyruvate phosphate dikinase are targeted, their activities have to be inhibited by over 70% to achieve similar glycolytic flux reductions. These predictions were later experimentally verified [65] using reconstitution experiments which expressed glycolytic enzymes in vitro at near physiological conditions of pH, temperature, and enzymatic activity. PGAM was found to be the main flux controlling enzyme for lower glycolysis while upper glycolysis was controlled by HK, and to a much smaller extent, PFK, and ALD.

However, considerations have to be made before applying MCA to biological systems due to its dependence on the reaction flux vj being a homogeneous function of Ek, which is not necessarily always true. The summation law for flux control coefficients can be written as

$$ {E}_1\left(\frac{\partial {v}_j}{\partial\ {E}_1}\right)+{E}_2\left(\frac{\partial {v}_j}{\partial\ {E}_2}\right)+\dots +{E}_K\left(\frac{\partial {v}_j}{\partial\ {E}_K}\right)={v}_j $$

Using Euler’s theorem reveals that the above implies vj to be homogeneous with degree 1:

$$ {v}_j\left(t{E}_1,\dots, t{E}_K\right)=t{v}_j\left({E}_1,\dots, {E}_K\right) $$

However, this homogeneity is hard to realize as a change, say, in the concentration of enzyme Ek will also change components such as the concentration of free substrate which will, in turn, affect the reaction rate vj. Only for systems where enzymes are substrate saturated, i.e., where the concentrations of metabolites exceed those of the enzymes by two or three orders of magnitude does the above serve as a fair approximation (such as 70% of the enzymes measured in E. coli, yeast, and a mammalian cell line [66]). This is exemplified in the case of Rubisco, the most abundant enzyme in the world, as efforts to engineer it by modifying its catalytic efficiency or by overexpressing it, have been largely unsuccessful. Its concentration was measured to be 3–4 mM in the stroma of spinach chloroplasts [67], whereas the concentration of its substrate ribulose 1,5 bisphosphate is often lower than 0.5 mM. As expected, the kinetic rate law of the corresponding carbon-fixing reaction was found to be non-homogeneous w.r.t. Rubisco [67].

Thermodynamic analysis to predict pathway bottlenecks

MCA uses a given steady state to describe how changes in enzyme abundance (or activity) affect the pathway flux. This requires the careful calculation of enzyme kinetic properties which are experimentally laborious to measure and also differ between organisms and isozymes, which further confounds the ability to compare across pathways and/or multiple organisms. Using thermodynamics and stoichiometry to calculate a single metric called Max-min Driving Force (MDF) [68] alleviates these problems. MDF identifies reactions within a pathway whose rates are constrained by a low thermodynamic driving force and thus would need the catalyzing enzymes to be present in higher concentrations and/or be engineered to achieve higher turnovers. Furthermore, MDF can also predict if a pathway is likely to support high flux under cellular conditions, thus allowing one to select among alternative pathways as intervention targets [69, 70].

The rate of a reaction is constrained by its thermodynamic driving force, with near-equilibrium reactions requiring exponentially more enzyme to sustain the same rate as reactions operating far from equilibrium. Due to this interdependence between thermodynamic potential and flux, pathways operating near equilibrium will incur a kinetic penalty due to backward flux. Thus, MDF computes reactant concentrations that maximize the minimum driving force B associated with all reactions in a pathway:

$$ \underset{\mathbf{x},B}{\max }B $$

s.t.

$$ -\left({\mathbf{G}}^{{}^{\circ}}+ RT{\mathbf{S}}^T\mathbf{x}\right)\ge B $$
$$ \ln \left({C}_{min}\right)\le \mathbf{x}\le \ln \left({C}_{max}\right) $$

where S represents the stoichiometric matrix (rows corresponding to compounds and columns to reactions), G° is a column vector containing the standard change in Gibbs energy for a reaction j, x is a column vector of the log-concentrations of metabolites, Cmax and Cmin the maximum and minimum allowed metabolite concentrations, respectively.

MDF has been used to glean biological insights into pathways such as the TCA cycle and EMP glycolysis. An examination of the TCA pathway revealed that flux through it is constrained by malate dehydrogenase, which has a large positive standard Gibbs energy of > 30 kJ/mol at pH ≤ 7 (Fig. 2a and b). However, the TCA cycle is known to sustain high fluxes which can also vary according to the organism’s need [71]. This apparent contradiction is explained by the low physiological concentrations of oxaloacetate, the product of malate dehydrogenase, as it is channeled between it and the following enzyme in the pathway -- citrate synthase. Thus, malate dehydrogenase and citrate synthase can be treated as a single enzyme which makes the Gibbs energy drop down to below − 20 kJ/mol and removes the thermodynamic bottleneck.

Fig. 1
figure 1

Overview of the workflow involved in reconstructing genome-scale metabolic networks. The reconstruction begins with the organism’s annotated genome, from which the list of metabolic genes is extracted -- this helps quantify the gamut of biochemical conversions the organism is capable of. These set of metabolic conversions or reactions, alongside their associated enzymes and encoding genes, constitutes a draft metabolic network. This draft network is then curated, to make sure that it adheres to criteria such that every reaction is mass and charge balanced, and proceeds in the direction in which it is thermodynamically favored. Then, for constructing a constraint-based model a pseudo-steady state constraint is imposed on every metabolite and a cellular objective imposed so as to arrive at biologically relevant solutions. For constructing a kinetic model, flux through a reaction is modeled using kinetic rate laws and regulatory, thermodynamic, and stoichiometric constraints imposed

Full size image

Dash et al. [72] used MDF to examine the thermodynamic bottlenecks associated with ethanol production in C. thermocellum. They found five reactions belonging to central carbon metabolism as being limiting under high external ethanol concentrations. They further evaluated the effects of imposing a minimal set of genetic perturbations on pathway thermodynamics and energy production. In doing so they found that modifications involving ATP-linked phosphofructokinase (PFK-ATP) and NADPH linked alcohol dehydrogenase (ADH-NADPH) with NADPH linked aldehyde dehydrogenase (ALDH-NADPH) had the highest performances. The inclusion of ATP-PFK yields a higher MDF at the expense of ATP, while the ADH-NADPH reaction decouples ethanol production flux from those reactions involving NADH (Fig. 2c). ALDH-NADPH is required for ensuring NADPH production and also ensure redox balance. Interestingly, studies involving high ethanol-yielding C. thermocellum strains have shown that the cofactor specificity of ADH changes to NADPH from NADH [73].

Fig. 2
figure 2

MDF analysis of the TCA cycle (a and b) and ethanol production (c) in C. thermocellum. a Overview of the TCA cycle. The reaction between malate and oxaloacetate is catalyzed by malate dehydrogenase, which was found to be the limiting step in the pathway. b MDF as a function of pH, as calculated for the TCA cycle (‘Standard TCA’), for an oxaloacetate concentration of 10 nM (‘[OAA] = 10 nM’), and with oxaloacetate channeling included (‘OAA channeling’). c Ethanol production pathway for the best-performing strain with three interventions. Suggested interventions are shown in green while the native reaction is shown in red. For all the panels, metabolites are shown in blue. G1p, glucose-1-phosphate; g6p, glucose-6-phosphate; f6p, fructose-6-phosphate; fdp, fructose 1,6-bisphosphate; g3p, glycerol-3-phosphate; 13dpg, 3-phosphoglyceroyl phosphate; 3 pg, 3-phosphoglycerate; 2 pg, glycerate-2-phosphate; pep, phosphoenolpyruvate; pyr, pyruvate; accoa, acetyl-CoA; acald, acetaldehyde; etoh, ethanol

Full size image

Minimal protein utilization drives cellular metabolism

MDF exploits the fact that the thermodynamic driving force behind a reaction dictates its rate, where higher forces correspond to high forward and low backward fluxes. This translates into efficient enzyme usage by decreasing the amount of enzyme needed per unit of metabolic flux. However, computing enzyme demand from metabolic fluxes is not trivial as enzymes tend to not function at maximal capacity. This is mainly due to metabolites causing incomplete substrate saturation and acting as allosteric regulators (affecting enzyme turnover by binding to sites other than the active site). This becomes a cyclic inference problem as steady-state metabolite levels depend on enzyme profiles. Thus, in order to arrive at a single solution, one can look for the enzyme profile with the least cost which is needed to realize a certain flux distribution. This is well justified in biological systems, where metabolic enzymes are a limited resource and thus cells economize by synthesizing the right enzymes in the right amounts, and adapting their levels when conditions change.

A reaction rate v = Er(c) depends on enzyme level E and metabolite concentrations c through the enzymatic rate law r(c). As metabolite levels are often unknown and also vary between experimental conditions, the enzyme demand cannot simply be computed as E = v/r(c). This leads to the definition of an enzyme cost function and choosing the enzyme profile with the lowest cost, while imposing thermodynamic constraints and constraining the metabolite levels to physiological ranges. Using Michaelis-Menten kinetics, a reversible rate law can be written as

$$ v=E{k}_{cat}^{+}\frac{s/{K}_s\left(1-\frac{k_{cat}^{-}p/{K}_p}{k_{cat}^{+}s/{K}_s}\right)}{1+s/{K}_s+p/{K}_p} $$
$$ v=E{k}_{cat}^{+}\left(1-\frac{k_{cat}^{-}p/{K}_p}{k_{cat}^{+}s/{K}_s}\right)\left(\frac{s/{K}_s}{1+s/{K}_s+p/{K}_p}\right) $$
$$ v=E{k}_{cat}^{+}{\eta}^{rev}\left(\mathbf{c}\right){\eta}^{kin}\left(\mathbf{c}\right) $$

Where E is the enzyme level, \( {k}_{cat}^{+} \) is the forward catalytic constant, ƞrev is the driving force (defined as the ratio between forward and backward reaction fluxes), and ƞkin is the reduction in flux due to kinetic effects (such as substrate saturation or allosteric regulation). Thus, the enzyme demand of a single reaction j can be written as:

$$ {E}_j\left(c,{v}_j\right)=\frac{v_j}{k_{cat}^{+}{\eta}^{rev}\left(\mathbf{c}\right){\eta}^{kin}\left(\mathbf{c}\right)} $$

A burden \( {h}_{E_j} \) can be defined for each enzyme representing its molecular mass, post-translation modifications, or effects of misfolding and non-specific catalysis. To determine the demand for an entire pathway, all the reactions are summed over and the final cost function to be minimized is –

$$ q\left(\mathbf{x},\mathbf{v}\right)=\sum \limits_j{h}_{E_j}{E}_j\left(c,{v}_j\right)=\sum \limits_j{h}_{E_j}\frac{v_j}{k_{cat}^{+}{\eta}^{rev}\left(\mathbf{c}\right){\eta}^{kin}\left(\mathbf{c}\right)} $$

This function q(x, v) represents the trade-off between the fluxes which can be realized and the enzyme levels required to sustain that. Noor et al. [74] used enzyme-cost minimization (ECM) to predict enzyme levels and metabolite concentrations in E. coli using fluxes found by 13-C MFA [75]. They found that the prediction fidelity increases monotonically as more complex cost functions are used. The root-mean square error varied from 1.35 (when enzyme levels are considered to be proportional to reaction fluxes) to 0.42 (when the modular rate laws [76] are used and the form of ƞkin(c) is determined using the reaction mechanism and order of enzyme-substrate binding). However, the caveat of ECM is the a priori knowledge of reaction fluxes, which is difficult to realize on a genome-scale. Although it is true that metabolic states with a maximal specific rate constitute an elementary flux mode [77], but their enumeration is computationally intensive [78]. Furthermore, ECM relies on the assumption that the metabolic states of a cell are optimized for enzyme levels, which isn’t always true. Cells often function at sub-optimal levels for robustness or maintaining the metabolic flexibility needed for tidying over future perturbations [79].

Summary and perspectives

Metabolic engineering has been used for the analysis, design, and optimization of metabolic pathways with significant successes [13, 14, 80,81,82]. In this review we discussed metabolic engineering tools (using flux balance analysis) that enable the formulation of a cell’s metabolism as a resource allocation problem driven by biological objectives such as maximizing growth rate or energy production. The construction of genome-scale models of metabolism require, as input, the set of all known metabolic conversions (or reactions) occurring inside the organism, and the thermodynamic favorability of each. Although such constraint-based models of metabolism have found wide use and adaptation, their primary drawback is an inability to capture the dynamic behavior evinced by biological systems. To this end, conventional FBA has been augmented such as by incorporating pseudo-kinetic reaction descriptions for a subset of reaction fluxes (dynamic FBA). Kinetic models take the next step in this direction by modeling reaction fluxes as a function of metabolic concentrations, enzyme kinetic parameters, and enzyme levels themselves. Such models are able to predict the dynamic behavior of metabolic networks but at the expense of intensive data-driven or computationally expensive parameterization. Nevertheless, a kinetic description of reaction mechanisms can be used to identify major flux-controlling steps [83] and identify pathway bottlenecks (MCA and MDF). Modeling regulations at different levels of metabolism, such as enzymatic or gene expression regulation, draws heavily from control theoretic approaches and can be further extended using classical concepts such as proportional and integral control. This will enable the study of cellular processes such as robust adaptation to environmental perturbations within the well-established fields of control systems for both steady and transient states.

In nature, organisms rarely exist in isolation but interact with others in a variety of biological and ecological niches. Microbial modeling allows us to explore the co-product potential of such communities by modeling the dynamics of inter-species interactions. Microbes can interact with each other and their hosts via processes such as metabolite cross-feeding, which can link disparate pathways from individual species to give rise to novel emergent metabolic functions [84]. By intelligent design of the growth media [85], standalone growth can be negated and thus co-culture growth and product secretion can be made to be an obligatory outcome of microbial biomass synthesis. The composition of a synthetic consortia can be further tuned by using genome-scale metabolic models to scan potential members and subsequently determine the ability of the culture to synthesize desired compounds.

Conclusions

Thus, a thorough and mechanistic understanding of an organism’s cellular processes would revolutionize our abilities to repair or even guide metabolism. Synthetic biology offers the promise of replacing traditional, high carbon footprint processes fed by unsustainable feedstocks with tunable microbial reactors. Using rational approaches derived from metabolic engineering, designing clean processes that use renewable feedstocks as the raw material can also help provide feasible solutions to current problems of global warming and fossil fuel exhaustion. Indeed, a number of instances where metabolic engineering has helped sustainably improve the economy and efficiency of production processes are already available. Engineered bacteria being used to produce energy from sunlight, water, and organic wastes; synthetic molecules produced by biocatalysts being used as novel drugs and vaccines; and increasing the productivity of existing crop systems by implementing an optimal set of genetic interventions – these are but a few of the possible applications of metabolic engineering [30, 86, 87].