Abstract
This paper displays numerical simulation for bright and dark optical solitons that emerge from Fokas-Lenells equation which is studied in the context of dispersive solitons in polarization-preserving fibers. The Laplace-Adomian decomposition scheme is the numerical tool adopted in the paper. The numerical results, for bright and dark solitons, are expository and therefore supplement the analytical developments, thus far.
Similar content being viewed by others
Introduction
One of the governing models to study dispersive solitons is Fokas-Lennels equation (FLE) [1–13]. In such a model, in addition to group velocity dispersion (GVD), one considers, inter-modal dispersion as well as nonlinear dispersion thus treating it with a flavor of additional dispersive effects. There has been a plethora of analytical tools that have been implemented to study FLE. They range from semi-inverse variational principle, Lie symmetry analysis, Riccati equation approach, exp-function method, traveling wave hypothesis, trial function method and further wide varieties. This paper will be changing gears to study the model from a different perspective. One of the very many and modern numerical algorithms that will be implemented is the Laplace-Adomian decomposition integration scheme. This method has been successfully applied to variety of other models from optics [14–16]. This paper now studies FLE, for the first time, by the aid of Laplace-Adomian decomposition scheme. The details are sketched in the remainder of the paper, after introducing the model.
The Fokas-Lenells equation (FLE) in presence of perturbation terms
The dimensionless form of the perturbed Fokas-Lenells equation (FLE) is given by
This equation was first studied in [17–24] and arises in various systems such as water waves, plasma physics, solid state physics and nonlinear optics. In Eq. (1), u(x,t) represents a complex field envelope, and x and t are spatial and temporal variables, respectively. Here, the coefficient a1 is the group velocity dispersion (GVD) and a2 is the spatio-temporal dispersion (STD) the coefficient b is self-phase modulation moreover σ accounts for nonlinear dispersion. In the perturbative term of Eq. (1), the first term represents the inter-modal dispersion (IMD), the second term is the self-steepening effect and finally the last term accounts for another version of nonlinear dispersion (ND).
Bright optical solitons
The bright optical soliton solution to (1) is given by [5, 11]:
Here, ν is the soliton velocity, κ is the soliton frequency, ω is the angular velocity and θ is the phase center.
The amplitude A of the soliton in this case is given by
where, the velocity of the soliton in relation to the coefficients that appear in the Eq. (1) is
and the constraints conditions on the parameters are
In the previous context κ is any parameter that satisfies the Eq. (5).
Dark optical solitons
noindent The dark optical soliton solution to (1) is given by [5, 11]:
Here, ν is the soliton velocity, κ is the soliton frequency, ω is the angular velocity and θ is the phase center.
The amplitude B of the soliton in this case is given by
where, the velocity of the soliton in relation to the coefficients that appear in the Eq. (1) is
and the constraints conditions on the parameters are
In the previous context κ is any parameter that satisfies the Eq. (9).
The Laplace Adomian Decomposition Method (LADM)
To illustrate the basic concept of Laplace-Adomian decomposition algorithm, we consider the general form of second order nonlinear partial differential equations in the form
with initial conditions
where F is a differential operator. Now, let us decompose this operator as F=L+R+N where \(L(u)=\frac {\partial u}{\partial t}\) stands for a linear differential operator. The operators R and N are the remaining linear and nonlinear parts, respectively.
With these considerations, Eq. (10) can now be rewritten as
Solving for Lu(x,t) and applying the Laplace transform respect to t to Eq. (12), gives
Thus, Eq. (13) turns out to be equivalent to
Using Eq. (11), one get
Finally, by applying inverse Laplace transformation \(\mathcal {L}^{-1}\) on both sides of the Eq. (15), we obtain
The Laplace-Adomian decomposition algorithm assumes the solution u(x,t) can be expanded into infinite series given by
Moreover, Also the nonlinear operator N is decomposed as
Each An is an Adomian polynomial of u0,u1,…,un that can be calculated for all forms of nonlinearity according to the following formula [25–27]:
Therefore Adomian’s polynomials are given by A0=N(u0)
A1=u1N′(u0)
\(A_{2}=u_{2}N'(u_{0})+\frac {1}{2}u_{1}^{2}N''(u_{0})\)
\(A_{3}=u_{3}N'(u_{0})+u_{1}u_{2}N''(u_{0})+\frac {1}{3!}u_{1}^{3}N^{(3)}(u_{0})\)
\(A_{4}=u_{4}N'(u_{0})+\left (\frac {1}{2}u_{2}^{2}+u_{1}u_{3}\right)N''(u_{0})+\frac {1}{2!}u_{1}^{2}u_{2}N^{(3)}(u_{0})+\frac {1}{4!}u_{1}^{4}N^{(4)}(u_{0})\)
⋮
All other polynomials are calculated in a similar way.
Substituting (17) and (18) into Eq. (16) gives rise to
Hence, Eq. (20) suggests the following iterative algorithm
Finally, after determining un’s, the N-term truncated approximation of the solution is obtained as
From this analysis it is evident that, the Adomian decomposition method, combined with the Laplace transform requires less effort in comparison with the traditional Adomian decomposition method. This method considerably decreases the number of calculations. In addition, Adomian decomposition procedure is easily established without requiring to linearize the problem.
Solution of the perturbed Fokas-Lenells equation by LADM
In this section, we outline the application of LADM to obtain explicit solution of Eq. (1) with the initial conditions u(x,0)=f(x), ux(x,0)=g(x).
Let us consider the dimensionless form of the perturbed Fokas-Lenells equation Eq. (1) in an operator form
where the notation N1u=−i|u|2(bu+iσux), N2u=−λ(|u|2u)x and N3u=−μu(|u|2)x symbolize the nonlinear term, respectively. The notation Ru=−(αux+ia1uxx+ia2uxt) symbolize the linear differential operator and Lu=ut simply means derivative with respect to time.
The LADM represents solution as an infinite series of components given below,
The nonlinear terms N1u, N2u and N3u can be decomposed into infinite series of Adomian polynomials given by:
and
Here Pn, Qn and Rn are the Adomian polynomials and can be calculated by the formula given by the Eq. (19), that is,
and for every n≥1 we have
The first few Adomian polynomials are given by
Then, the Adomian polynomials corresponding to the nonlinear part Nu=N1u+N2u+N3u are
and so on for other Adomian polynomials.
By applying the Laplace transform with respect to t on both sides of the Eq. (23) and using the linearity of the Laplace transform gives:
Because of the differentiation property of Laplace transform, Eq. (31) can be written as
Thus,
By substituting (24), (25), (26) and (27) into (33), we obtain
Comparing both sides of the Eq. (34), the following relations arise:
In general, we get the following recursive algorithm
Finally, by applying inverse Laplace transformation we deduce the following recurrence formulas for each n=0,1,2,…,
Numerical simulations and graphical results
We perform numerical simulations for bright and dark optical solitions.
Application to bright optical solitions
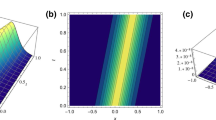
The result and the profile of four cases are shown in Table 1 and in Figs. 1, 2, 3 and 4.
Application to dark optical solitions
The result and the profile of four cases are shown in Table 2 and in Figs. 5, 6, 7 and 8.
Conclusions
This paper successfully studied FLE in polarization-preserving fibers by the aid of Laplace-Adomian decomposition scheme. The numerical scheme yielded bright and dark soliton solutions. The results thus appear with a complete spectrum of soliton solutions. Although singular solitons is a third form of solitons that emerge from this model, it does not provide any interest with any kind of numerical scheme. The results of the paper are truly encouraging to study the methodology further along. Later, this scheme will be applied to vector coupled FLE that studies solitons in birefringent fibers. Further along the model will be extended to address WDM/DWDM/UDWDM topology numerically. Such studies are currently under way.
Availability of data and materials
Not applicable.
Abbreviations
- DWDM:
-
Dense wavelength division multiplexing
- FLE:
-
Fokas-lennels equation
- GVD:
-
Group velocity dispersion
- IMD:
-
Inter-modal dispersion
- LADM:
-
Laplace-adomian decomposition method
- ND:
-
Nonlinear dispersion
- STD:
-
Spatio-temporal dispersion
- UDWDM:
-
Ultra-dense wavelength division multiplexing
- WDM:
-
Wavelength-division multiplexing
References
Biswas, A., Ekici, M., Sonmezoglu, A., Alqahtani, R. T.: Optical soliton perturbation with full nonlinearity for Fokas-Lenells equation. Optik. 165, 29–34 (2018).
Biswas, A., Yildirim, Y., Yasar, E., Zhou, Q., Mahmood, M. F., Moshokoa, S. P., Belic, M.: Optical solitons with differential group delay for coupled Fokas-Lenells equation using two integration schemes. Optik. 165, 74–86 (2018).
Biswas, A., Ekici, M., Sonmezoglu, A., Alqahtani, R. T.: Optical solitons with differential group delay for coupled Fokas–Lenells equation by extended trial function scheme. Optik. 165, 102–110 (2018).
Jawad Mohamad, A. J., Biswas, A., Zhou, Q., Moshokoa, S. P., Belic M.: Optical soliton perturbation of Fokas-Lenells equation with two integration schemes. Optik. 165, 111–116 (2018).
Biswas, A., Rezazadeh, H., Mirzazadeh, M., Eslami, M., Ekici, M., Zhou, Q., Moshokoa, S. P., Belic, M.: Optical soliton perturbation with Fokas-Lenells equation using three exotic and efficient integration schemes. Optik. 165, 288–294 (2018).
Biswas, A.: Chirp-free bright optical soliton perturbation with Fokas-Lenells equation by traveling wave hypothesis and semi-inverse variational principle. Optik. 170, 431–435 (2018).
Aljohani, A. F., Ebaid, A., El-Zahar, E. R., Ekici, M., Biswas, A.: Optical soliton perturbation with Fokas-Lenells model by Riccati equation approach. Optik. 172, 741–745 (2018).
Biswas, A., Yıldırım, Y., Yaşar, E., Zhou, Q., Moshokoa, S. P., Belic, M.: Optical soliton solutions to Fokas-Lenells equation using some different methods. Optik. 173, 21–31 (2018).
Arshed, S., Biswas, A., Zhou, Q., Moshokoa, S. P., Belic, M.: Optical solitons with polarization-mode dispersion for coupled Fokas-Lenells equation with two forms of integration architecture. Opt. Quant. Electron. 50, 304 (2018).
Bansal, A., Kara, A. H., Biswas, A., Moshokoa, S. P., Belic, M.: Optical soliton perturbation, group invariants and conservation laws of perturbed Fokas-Lenells equation. Chaos, Solitons & Fractals. 114, 275–280 (2018).
Krishnan, E. V., Biswas, A., Zhou, Q., Alfiras, M.: Optical soliton perturbation with Fokas-Lenells equation by mapping methods. Optik. 178, 104–110 (2019).
Arshed, S., Biswas, A., Zhou, Q., Khan, S., Adesanya, S., Moshokoa, S. P., Belic, M.: Optical solitons pertutabation with Fokas-Lenells equation by e x p(−ϕ(ξ))-expansion method. Optik. 179, 341–345 (2019).
Bansal, A., Kara, A. H., Biswas, A., Khan, S., Zhou, Q., Moshokoa, S. P.: Optical solitons and conservation laws with polarization-mode dispersion for coupled Fokas-Lenells equation using group invariance. Chaos, Solitons & Fractals. 120, 245–249 (2019).
González-Gaxiola, O., Biswas, A.: W-shaped optical solitons of Chen-Lee-Liu equation by Laplace-Adomian decomposition method. Opt. Quant. Electron. 50, 314 (2018).
González-Gaxiola, O., Biswas, A.: Akhmediev breathers, Peregrine solitons and Kuznetsov-Ma solitons in optical fibers and PCF by Laplace-Adomian decomposition method. Optik. 172, 930–939 (2018).
González-Gaxiola, O., Biswas, A.: Optical solitons with Radhakrishnan-Kundu-Lakshmanan equation by Laplace-Adomian decomposition method. Optik. 179, 434–442 (2019).
Fokas, A. S.: On a class of physically important integrable equations. Physica. D. 87, 145–150 (1995).
Lenells, J.: Exactly solvable model for nonlinear pulse propagation in optical fibers. Stud. Appl. Math. 123, 215–232 (2009).
Lenells, J., Fokas, A. S.: On a novel integrable generalization of the nonlinear Schrödinger equation. Nonlinearity. 22, 11–27 (2009).
Yang, C., Liu, W., Zhou, Q., Mihalache, D., Malomed, B. A.: One-soliton shaping and two-soliton interaction in the fifth-order variable-coefficient nonlinear Schrödinger equation. Nonlinear Dyn. 95, 369–380 (2019).
Triki, H., Zhou, Q., Liu, W.: W-shaped solitons in inhomogeneous cigar-shaped Bose-Einstein condensates with repulsive interatomic interactions. Laser Phys. 29, 055401 (2019).
Yang, C., Wazwaz, A. M., Zhou, Q., Liu, W.: Transformation of soliton states for a (2+1) dimensional fourth-order nonlinear Schrödinger equation in the Heisenberg ferromagnetic spin chain. Laser Phys. 29, 035401 (2019).
Aouadi, S., Bouzida, A., Daoui, A. K., Triki, H., Zhou, Q., Sha, Liu.: W-shaped, bright and dark solitons of Biswas-Arshed equation. Optik. 182, 227–232 (2019).
Zhang, Y., Yang, C., Yu, W., Mirzazadeh, M., Zhou, Q., Liu, W.: Interactions of vector anti-dark solitons for the coupled nonlinear Schrödinger equation in inhomogeneous fibers. Nonlinear Dyn. 94, 1351–1360 (2018).
Wazwaz, A. M.: A new algorithm for calculating Adomian polynomials for nonlinear operators. Appl. Math. Comput. 111(1), 33–51 (2000).
Duan, J. S.: Convenient analytic recurrence algorithms for the Adomian polynomials. Appl. Math. Comput. 217, 6337–6348 (2011).
Duan, J. S.: New recurrence algorithms for the nonclassic Adomian polynomials. Appl. Math. Comput. 62, 2961–2977 (2011).
Acknowledgments
Not applicable.
Funding
The research work of the third author (MRB) was supported by the grant NPRP 8-028-1-001 from QNRF and he is thankful for it.
Author information
Authors and Affiliations
Contributions
The original ideas and results emerged from discussions among all the authors. OGG wrote the manuscript with input from all authors. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
González-Gaxiola, O., Biswas, A. & Belic, M.R. Optical soliton perturbation of Fokas-Lenells equation by the Laplace-Adomian decomposition algorithm. J. Eur. Opt. Soc.-Rapid Publ. 15, 13 (2019). https://doi.org/10.1186/s41476-019-0111-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41476-019-0111-6